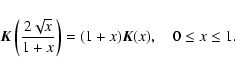... edges

In contrast with the gravitational acceleration (the gradient of 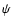$\psi$), the potential is generally finite at the edges.  

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... algebra

In particular, we use the transformation:

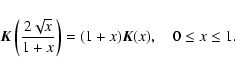$${\vec K}\left(\frac{2\sqrt{x}}{1+x}\right) = (1+x) {\vec K}(x), \quad 0 \le x \le 1.$$ (14)

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... discs

Here, discs are supposed to be objects of axis ratio $\Delta \lesssim 0.1$.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

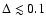... have

A careful treatment of the singular cases 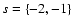$s=\{-2,-1\}$ shows that Eq. (52c) yields Eqs. (52a) and (52b).  

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... range

This range of exponents should be appropriate for most astrophysical applications (see the introduction).

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.