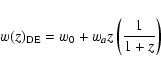A&A 490, 31-36 (2008)
DOI: 10.1051/0004-6361:200810337
Cosmography by gamma ray bursts
S. Capozziello1 - L. Izzo1,2,3
1 - Dipartimento di Scienze Fisiche, Università di Napoli
``Federico II'' and INFN Sez. di Napoli, Compl. Univ. Monte S.
Angelo, Ed. N, via Cinthia, 80126 Napoli, Italy
2 -
ICRANet and ICRA, Piazzale della Repubblica 10, 65122 Pescara, Italy
3 -
Dip. di Fisica, Università di Roma ``La Sapienza'', Piazzale Aldo
Moro 5, 00185 Roma, Italy
Received 6 June 2008 / Accepted 11 August 2008
Abstract
Aims. Relations connecting gamma ray burst quantities can be used to constrain cosmographic parameters of the Hubble law at medium-high redshifts.
Methods. We consider a sample of 27 gamma ray bursts to construct the luminosity distance to redshift relation and derive the values of the parameters q0, j0, and s0. The analysis is compared with other methods in the literature.
Results. Gamma gay bursts, if calibrated by SNeIa, seem reliable as distance indicators and give cosmographic parameters in agreement with the  CDM model.
CDM model.
Key words: gamma rays: bursts - cosmology: cosmological parameters - cosmology: distance scale
A class of very accurate standard candles, the supernovae Ia
(SNeIa), has been highly developed in the last two decades
(Branch & Tammann 1992); however, these objects are hardly detectable at
redshifts higher than z = 1.7, so the study of more distant
regions of the Universe leads to the needing to implement more
powerful standard candles. The problem becomes particularly
crucial at intermediate redshift, z = 6-7, where, up to now,
not very well-defined distance indicators are available.
In the last years, several efforts have been made in order to
implement gamma ray bursts (GRBs), the most powerful explosions in
the Universe, as standard candles, and several interesting
results have recently been achieved (e.g. Amati et al. 2008;
Basilakos &
Perivolaropoulos 2008, and references therein).
Considering the standard model of such objects, the GRB phenomenon
should originate from the black hole formation and reach huge
amounts of energy (up to 1054 erg). These events are observed
at considerable distances, so there are several efforts to frame
them into the standard of cosmological distance ladder.
In the literature, several more-detailed models give account
for the GRB formation, e.g. Meszaros (2006); Ruffini et al. (2008),
but, up to now, none of them is intrinsically capable of
connecting all the observable quantities. For this reason, GRBs
cannot be used as standard candles. Despite this shortcoming,
there are several observational correlations among the photometric
and spectral properties of GRBs. These features allow use of
GRBs as distance indicators (Schaefer 2007), even when they
cannot be fully ``enrolled'' in the class of standard candles. In
particular, it is possible to connect the peak energy of GRBs,
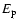 ,
with the isotropic energy released in the burst,
,
with the isotropic energy released in the burst,
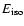 ,
and with the rest frame jet break-time of the afterglow optical
light curve, measured in days,
,
and with the rest frame jet break-time of the afterglow optical
light curve, measured in days, 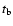 ,
(Liang & Zhang 2005):
,
(Liang & Zhang 2005):
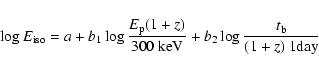 |
(1) |
where a and bi, with i=1,2, are calibration constants.
Another interesting result is the relation given by Ghirlanda et al. (2004).
It connects the peak energy 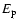 with the collimation-corrected energy, or the energy release of a GRB jet,
with the collimation-corrected energy, or the energy release of a GRB jet,
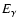 ,
where
,
where
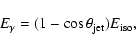 |
(2) |
with
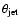 the jet opening angle, given by (Sari et al. 1999):
the jet opening angle, given by (Sari et al. 1999):
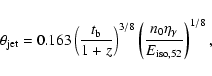 |
(3) |
where
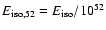 erg, n0 is the
circumburst particle density in 1 cm-3, and
erg, n0 is the
circumburst particle density in 1 cm-3, and
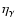 the radiative efficiency. The Ghirlanda et al. relation is
the radiative efficiency. The Ghirlanda et al. relation is
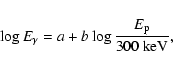 |
(4) |
where a and b are two calibration constants.
These two relations are used the most in constraining cosmology
due to their relatively small scatter, interestingly very tight
in the Ghirlanda et al. one, and the sufficient number of data
points available.
In Schaefer (2007), an example of the discrepancy between data
and theoretical curves is shown for these two relations. It is
worth noticing that the calibration of the above relations is
necessary to avoid the circularity problem: all the relations need
to be calibrated for every set of cosmological parameters. Indeed,
all GRB distances, obtained only in a photometric way, are
strictly dependent on the cosmological parameters since there is
no low-redshift set of GRBs to achieve a cosmology-independent
calibration.
Recently, Liang et al. (2008) present a calibration method
(Liang thereafter) for several GRB relations, included the above
relations (1) and (4), in a
cosmology-independent way using the SNeIa. In fact, the SNeIa are
very accurate standard candles, but their range is limited up to
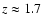 ;
hence, assuming that relations (1) and (4) work at any z and that, at the same redshift,
GRBs and SNeIa have the same luminosity distance, it becomes
possible, in principle, to calibrate GRB relations at low
redshifts. The calibration parameters are shown in Table 1.
For the
;
hence, assuming that relations (1) and (4) work at any z and that, at the same redshift,
GRBs and SNeIa have the same luminosity distance, it becomes
possible, in principle, to calibrate GRB relations at low
redshifts. The calibration parameters are shown in Table 1.
For the
 -
-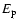 -
-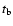 relation, the b-values in the first
line is b1 and in the second line is b2.
relation, the b-values in the first
line is b1 and in the second line is b2.
Table 1:
Parameter values obtained by Liang et al. (2008).
When our working-relations are calibrated with the Liang method,
we can compute the luminosity distance 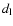 from the well-known
relation between
from the well-known
relation between 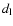 and the energy-flux ratio of the distance
indicators in consideration. Afterwards, we can use a formulation
given by Visser (2004), where the luminosity distance
and the energy-flux ratio of the distance
indicators in consideration. Afterwards, we can use a formulation
given by Visser (2004), where the luminosity distance
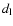 is related to the cosmographic parameters (Weinberg 1972)
by means of a Taylor series expansion for the same
is related to the cosmographic parameters (Weinberg 1972)
by means of a Taylor series expansion for the same 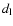 .
Such an
analysis works very well at low and intermediate redshifts, since
very good classes of standard candles are available there.
Besides, it is useful to constrain alternative theories of
gravity, as shown in Capozziello et al. (2008). Since we are
calibrating GRBs by SNeIa (in the SNeIa redshift range, the
.
Such an
analysis works very well at low and intermediate redshifts, since
very good classes of standard candles are available there.
Besides, it is useful to constrain alternative theories of
gravity, as shown in Capozziello et al. (2008). Since we are
calibrating GRBs by SNeIa (in the SNeIa redshift range, the 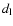 Taylor series analysis works very well), the method could also be
extended to the next step (intermediate-high redshifts) where
GRBs are expected to be suitable distance indicators. This working
hypothesis could be useful in order to link low and high redshift
ranges and then fully probe
Taylor series analysis works very well), the method could also be
extended to the next step (intermediate-high redshifts) where
GRBs are expected to be suitable distance indicators. This working
hypothesis could be useful in order to link low and high redshift
ranges and then fully probe 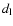 .
However, it is clear that such
a Taylor expansion, derived for low redshifts, can be problematic
for fitting GRBs at high redshifts. Here, we consider it a viable
methodological approach to link GRBs to SNeIa.
.
However, it is clear that such
a Taylor expansion, derived for low redshifts, can be problematic
for fitting GRBs at high redshifts. Here, we consider it a viable
methodological approach to link GRBs to SNeIa.
The aim of this work is to achieve the cosmographic parameters
(Weinberg 1972) using the above GRB relations and then to test
the cosmological density parameters in a 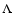 CDM model. The
only assumption that we make here is that the Universe is
described by a Friedmann-Robertson-Walker geometry and the scale
factor of the universe a(t) can be expanded in a Taylor series
(Sect. 2). In Sect. 3, after considering a sample of 27 GRBs, we use
a best-fit analysis to derive the cosmographic parameters discussed in
the previous section, adopting the so-called Chevallier,
Polarsky, Linder parameterization for the equation of state (EoS).
Discussion and conclusions are given in Sect. 4.
CDM model. The
only assumption that we make here is that the Universe is
described by a Friedmann-Robertson-Walker geometry and the scale
factor of the universe a(t) can be expanded in a Taylor series
(Sect. 2). In Sect. 3, after considering a sample of 27 GRBs, we use
a best-fit analysis to derive the cosmographic parameters discussed in
the previous section, adopting the so-called Chevallier,
Polarsky, Linder parameterization for the equation of state (EoS).
Discussion and conclusions are given in Sect. 4.
The calibration we want to achieve should be cosmologically
model-independent; hence, applying the above relations to a GRB
sample in a given z-range, we want to derive the related
cosmography. In particular, we want to obtain deceleration, jerk,
and snap parameters (Visser 2004) and compare them with the
current values deduced by other methods and observations (see, for
example, Basilakos &
Perivolaropoulos 2008; Capozziello et al.
2008, and references therein).
Being only related to the derivatives of the scale factor allows
to fit the cosmographic parameters versus the distance-redshift
relation without any a priori assumption on the underlying
cosmological model but, this fails at very high redshifts where
the Taylor expansion does not work yet.
To build a distance-redshift diagram, one has to calculate the
luminosity distance for each GRB in a given sample. In our case
the luminosity distance is
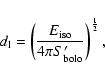 |
(5) |
where
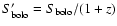 is the bolometric fluence of
gamma rays in the burst, corrected with respect to the rest
frame. The definition of
is the bolometric fluence of
gamma rays in the burst, corrected with respect to the rest
frame. The definition of
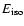 is different for each relation
used, therefore for the luminosity distance, we have
is different for each relation
used, therefore for the luminosity distance, we have
![\begin{displaymath}
d_{\rm l} = \left[\frac{10^a \left(\frac{E_{\rm p}(1+z)}{30...
...~1~{\rm day}}\right)^{b_2}}{4 \pi S'_{\rm bolo}}\right]^{1/2},
\end{displaymath}](/articles/aa/full/2008/40/aa10337-08/img25.gif) |
(6) |
adopting the Liang-Zhang relation, with a, b1, and b2given in Table 1, and
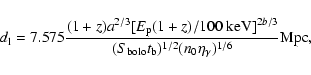 |
(7) |
for the Ghirlanda et al. relation, with a and b given in 1 (Xu et al. 2005). Note that the former gives 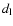 in
centimeters, therefore it divides the result for the value of 1
parsec in cm, while the latter gives
in
centimeters, therefore it divides the result for the value of 1
parsec in cm, while the latter gives 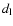 directly in Mpc.
directly in Mpc.
The luminosity distance can be connected to the Hubble series
(Weinberg 1972). Expanding the Hubble law up to the fourth order
in redshift and considering the related luminosity distance, we
get (Visser 2004)
where
 is the Hubble radius and where the
cosmographic parameters are defined as
is the Hubble radius and where the
cosmographic parameters are defined as
| H(t) |
= |
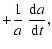 |
(9) |
| q(t) |
= |
![$\displaystyle - {1\over a} \; {{\rm d}^2 a\over {\rm d} t^2} \;\left[ {1\over a} \;
{{\rm d} a \over {\rm d} t}\right]^{-2}~,$](/articles/aa/full/2008/40/aa10337-08/img33.gif) |
(10) |
| j(t) |
= |
![$\displaystyle + {1\over a} \; {{\rm d}^3 a \over {\rm d} t^3} \; \left[ {1\over a}
\; {{\rm d} a \over {\rm d} t}\right]^{-3}~,$](/articles/aa/full/2008/40/aa10337-08/img34.gif) |
(11) |
| s(t) |
= |
![$\displaystyle + {1\over a} \; {{\rm d}^4 a \over {\rm d} t^4} \; \left[ {1\over a}
\; {{\rm d} a \over {\rm d} t}\right]^{-4}\cdot$](/articles/aa/full/2008/40/aa10337-08/img35.gif) |
(12) |
They are usually referred to as the Hubble,
deceleration, jerk, and snap parameters,
respectively. Their present values, which we denote with a
subscript 0, may be used to characterize the evolutionary status
of the Universe. For instance, q0 < 0 denotes an accelerated
expansion, while j0 allows us to distinguish among different
accelerating models; a positive value of j0 indicates that, in
the past, the acceleration reversed its sign. In this paper,
according to the WMAP observations, we assume the value of the
Hubble constant
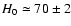 km s-1 Mpc-1 (Komatsu et al. 2008).
km s-1 Mpc-1 (Komatsu et al. 2008).
Table 2:
GRBs data sample.
The cosmographic parameters can be expressed in terms of the dark
energy density and the EoS. Following the prescriptions of the
Dark Energy Task Force, (Albrecht et al. 2006), we use the
Chevallier-Polarski-Linder parameterization (CPL) for the EoS
(Linder 2003; Chevallier et al. 2001) and assume a spatially flat Universe filled with
dust matter and dark energy. The dimensionless Hubble parameter
E(z) = H/H0 reads as
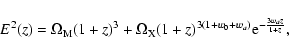 |
(13) |
with
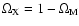 and w0 and wa the CPL
parameterization for the EoS (see Chevallier et al. 2001; Linder
2003; Capozziello et al. 2008, for details). We can have
and w0 and wa the CPL
parameterization for the EoS (see Chevallier et al. 2001; Linder
2003; Capozziello et al. 2008, for details). We can have
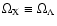 ,
with
,
with 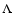 the cosmological
constant. Such a relation can be used to evaluate the cosmographic
parameters, obtaining
the cosmological
constant. Such a relation can be used to evaluate the cosmographic
parameters, obtaining
| q0 |
= |
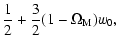 |
(14) |
| j0 |
= |
![$\displaystyle 1 + \frac{3}{2} (1 - \Omega_{\rm M}) \left [ 3w_0 (1 + w_0) + w_a \right ] \!,$](/articles/aa/full/2008/40/aa10337-08/img43.gif) |
(15) |
| s0 |
= |
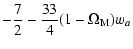 |
|
| |
|
![$\displaystyle -
\frac{9}{4} (1 - \Omega_{\rm M}) \left [ 9 + (7 - \Omega_{\rm M}) w_a \right ] w_0$](/articles/aa/full/2008/40/aa10337-08/img45.gif) |
|
| |
|
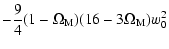 |
|
| |
|
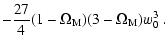 |
(16) |
For a 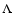 CDM-universe, where
(w0, wa) = (-1, 0), it becomes
CDM-universe, where
(w0, wa) = (-1, 0), it becomes
| q0 |
= |
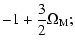 |
(17) |
| j0 |
= |
1; |
(18) |
| s0 |
= |
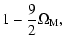 |
(19) |
that are the quantities which we are going to fit using a given
GRB sample.
Let us take a GRB sample into account that satisfies the above
relations. Unfortunately only 27 GRBs have observed jet breaks in
the Schaefer sample (Schaefer 2007). The observational
quantities of GRBs to take into account, are listed in Table 2. The luminosity distance for each of the relations is given by Eqs. (6) and (7), and then we obtain a data distribution in the luminosity distance-redshift diagram
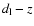 .
The errors on the data are only of a photometric
nature and, in a first analysis, we can exclude errors on the
redshift. For each GRB, we assume
.
The errors on the data are only of a photometric
nature and, in a first analysis, we can exclude errors on the
redshift. For each GRB, we assume
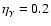 and
and
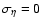 ,
(Frail et al. 2001).
,
(Frail et al. 2001).
Another version of the Hubble series can be used to improve the
data fit. If we consider the equation for the distance modulus,
![\begin{displaymath}\mu = 25 + \frac{5}{\ln~(10)}\ln~[d_{\rm l}/(1~{\rm Mpc})] + 25,
\end{displaymath}](/articles/aa/full/2008/40/aa10337-08/img53.gif) |
(20) |
and substitute the equation for 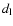 ,
we obtain a logarithmic
version of the Hubble series:
,
we obtain a logarithmic
version of the Hubble series:
This logarithmic version shows the advantage when there is no
need to transform the uncertainties on the distance modulus. With
these considerations in mind, we perform a polynomial
least-squares fit for each relation of the data assuming Taylor
series polynomials, both in distance and in logarithmic distance.
We stop at order n = 3 both for the polynomial fit and for the
logarithmic fit. In the latter case, we obtain an estimate of the
snap parameter. Note that we are using least squares since, in
absence of any better data-fitting procedure, this is the standard
procedure when assuming Gaussian distributed uncertainties.
The truncated polynomial used in the fits has the form
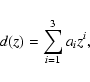 |
(22) |
and
![\begin{displaymath}\ln[d(z)/(z ~{\rm Mpc})] = \sum_{i=1}^3 b_i z^i
\end{displaymath}](/articles/aa/full/2008/40/aa10337-08/img60.gif) |
(23) |
for the logarithmic fit. In the latter case, the Hubble constant
enters as the i=1 component of the fit. As stated above, we use
H0 as a constraint (a prior).
The fits can be used to estimate the deceleration and the jerk
parameters. The logarithmic fit is better for estimating the snap
parameter through the values of the coefficients ai and biand their statistical uncertainties. The statistical
uncertainties on q0 are linearly related to the statistical
uncertainties on the parameter b1, while the statistical
uncertainties on j0 and s0 depend non-linearly on q0and its statistical uncertainty. It is worth noticing the
combination
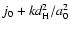 ,
which is a well-known degeneracy
in Eq. (21) (Weinberg 1972). It means that we cannot
determine j0 and
,
which is a well-known degeneracy
in Eq. (21) (Weinberg 1972). It means that we cannot
determine j0 and
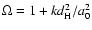 separately, but we
need an independent determination of
separately, but we
need an independent determination of 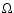 to estimate the
value of the jerk parameter.
to estimate the
value of the jerk parameter.
Table 3:
Results of the fits. LZ is for Liang-Zhang relation, GGL for the Ghirlanda et al. one.
The results of the fits are presented in Table 3,
and all of them include the error on the data. For the calculation
of the uncertainties on 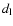 ,
we have followed the procedure
discussed in Xu et al. (2005). For example, the fractional
uncertainties on
,
we have followed the procedure
discussed in Xu et al. (2005). For example, the fractional
uncertainties on 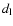 in the Ghirlanda et al. relation, without
the small angle approximation for
in the Ghirlanda et al. relation, without
the small angle approximation for
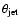 (Sari et al. 1999), are
given by
(Sari et al. 1999), are
given by
where
![$C_{\theta} = [\theta \sin{\theta} / 8 - 8 \cos{\theta}]^2$](/articles/aa/full/2008/40/aa10337-08/img80.gif) .
This shows that the uncertainties on
.
This shows that the uncertainties on 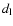 in the Ghirlanda et al.
relation are very high, due to the dependence on several
parameters. For this reason, in Fig. 1, the prediction
bounds are plotted at a
in the Ghirlanda et al.
relation are very high, due to the dependence on several
parameters. For this reason, in Fig. 1, the prediction
bounds are plotted at a 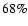 confidence level, instead of
confidence level, instead of
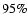 ,
as in LZ-relation.
,
as in LZ-relation.
As said above, only statistical uncertainties have been
considered and other kinds of errors (systematics of
cosmological inference, modelling errors and ``historical''
biases, Visser 2007b) have been neglected. If we do not assume
H0 as a constraint, the analysis gives H0 = 56 km s-1 Mpc-1,
which means that the data sample needs to be improved with further
GRBs to give more reliable results.
Another step would be to test the goodness of the next fit
statistics using the MATLAB package. In particular, we used the
R-square method: a value closer to 1 indicates a better fit. In
Table 4, the results of R-square are shown and the
plots of the residuals of the fits are shown in Figs. 1, 2. For the logarithmic fit, the bad
value of the R-square is caused by the logarithm of the Hubble
series, which spreads a lot of the data on the
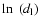 -axis. The
values
-axis. The
values 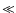 1 for the logarithmic fits are due to the
discrepancy of the data.
1 for the logarithmic fits are due to the
discrepancy of the data.
Table 4:
Goodness of the fits with the R-square.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0337fig1.eps}\end{figure}](/articles/aa/full/2008/40/aa10337-08/Timg84.gif) |
Figure 1:
Luminosity distance-redshift diagram and the residuals
of the
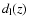 GGL fit. Note the discrepancy at high-z. The dotted lines
are the bounds predicted at
GGL fit. Note the discrepancy at high-z. The dotted lines
are the bounds predicted at 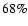 confidence level.
confidence level. |
| Open with DEXTER |
In summary, the results are in quite good agreement with the
 CDM model, giving a Universe model that accelerates in
the present epoch and that has undergone a decelerated phase in
the past. The signature of this past phase is related to the sign
change of the parameter q0 and the positive value of the jerk
parameter, unless a positive value of the spatial curvature
constant k is considered. However this occurrence is excluded by
the last observational results, which confirm a spatially flat
Universe (Komatsu et al. 2008).
CDM model, giving a Universe model that accelerates in
the present epoch and that has undergone a decelerated phase in
the past. The signature of this past phase is related to the sign
change of the parameter q0 and the positive value of the jerk
parameter, unless a positive value of the spatial curvature
constant k is considered. However this occurrence is excluded by
the last observational results, which confirm a spatially flat
Universe (Komatsu et al. 2008).
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0337fig2.eps}\end{figure}](/articles/aa/full/2008/40/aa10337-08/Timg86.gif) |
Figure 2:
Logarithmic version of the luminosity distance relation
versus redshift and the residuals of the
![$\ln~[d_{\rm l}/z~{\rm Mpc}]$](/articles/aa/full/2008/40/aa10337-08/img85.gif) LZ fit. In this version of
the Hubble series, the discrepancy is the same at every z. The
dotted lines are the bounds predicted at
LZ fit. In this version of
the Hubble series, the discrepancy is the same at every z. The
dotted lines are the bounds predicted at 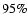 confidence
level.
confidence
level. |
| Open with DEXTER |
As said, the cosmographic parameters may also be expressed in
terms of the dark energy density and EoS parameters. Starting from
the Friedmann equation, we obtain the Hubble parameter:
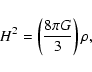 |
(25) |
where 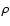 is the energy density. The continuity equation for
each cosmological component is given by the Bianchi identity
(Weinberg 1972):
is the energy density. The continuity equation for
each cosmological component is given by the Bianchi identity
(Weinberg 1972):
![\begin{displaymath}\frac{\dot{\rho}}{\rho} = -3H \left(1 + \frac{p}{\rho}\right) = -3H [ 1 + w(z)],
\end{displaymath}](/articles/aa/full/2008/40/aa10337-08/img89.gif) |
(26) |
where p is the pressure of the component considered and
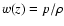 the redshift-dependent EoS for each component. The dark
energy component responsible for the observed acceleration of the
universe must have a negative EoS, (Riess et al. 2004; Allen et al. 2004). To find
the redshift-dependent EoS for each component. The dark
energy component responsible for the observed acceleration of the
universe must have a negative EoS, (Riess et al. 2004; Allen et al. 2004). To find
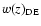 ,
we can adopt the CPL parameterization, (Linder 2003; Chevallier et al. 2001), where
,
we can adopt the CPL parameterization, (Linder 2003; Chevallier et al. 2001), where
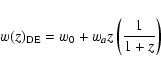 |
(27) |
with w0 and wa two parameters that enter directly into the
equations for the cosmographic parameters,
(14-16). To test the  CDM model, we
have assumed
(w0,wa)=(-1,0). Conversely, such a case can be
generalized by deducing the value of cosmographic parameters
CDM model, we
have assumed
(w0,wa)=(-1,0). Conversely, such a case can be
generalized by deducing the value of cosmographic parameters
 from polynomial fits where GRB data are
considered. Adopting our GRB sample, we obtained the following
values
from polynomial fits where GRB data are
considered. Adopting our GRB sample, we obtained the following
values
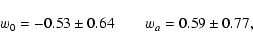 |
(28) |
which directly enter into the CPL parameterization. The errors on
the CPL parameters are directly connected with the errors on the
cosmographic parameters, as easily seen from the system (14-16).
The values of w0 and waagree, within the errors, with the 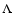 CDM model, without
assuming constraints a priori on the cosmological model.
CDM model, without
assuming constraints a priori on the cosmological model.
Starting from some relations connecting the observable quantities
of GRBs, we have used a sample of 27 GRBs to derive the
luminosity distance-redshift diagram of the Hubble law. The
relations conveniently calibrated by SNeIa to make them
independent of any cosmological models.
We have taken the Hubble law into account in the Taylor series
form, assuming the luminosity distance 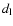 as a redshift
function whose coefficients are combinations of the cosmographic
parameters H0, q0, j0, and s0. The aim was to evaluate
such parameters starting from the GRB data. A direct analysis of
the fits leads to the conclusion that, in the error range, the
SNeIa results can also be extended at higher redshifts
(Visser 2007b). Besides, such results agree with the
as a redshift
function whose coefficients are combinations of the cosmographic
parameters H0, q0, j0, and s0. The aim was to evaluate
such parameters starting from the GRB data. A direct analysis of
the fits leads to the conclusion that, in the error range, the
SNeIa results can also be extended at higher redshifts
(Visser 2007b). Besides, such results agree with the 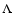 CDM
model according to Eqs. (17)-(19). In particular, the
value of the parameter q0 that we found is in agreement with
the observed
CDM
model according to Eqs. (17)-(19). In particular, the
value of the parameter q0 that we found is in agreement with
the observed
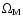 (see Table 5).
(see Table 5).
Table 5:
Cosmological density parameters.
However, the sample we used is quite poor at high redshifts and,
in some sense, this justifies the use of the method of Taylor
series which works very well at low redshifts. In particular, at
z > 6, we only have one GRB, GRB050904 (see Fig.
1). This GRB is very important in the fit results
because it affects the trend of the fits. For this reason we need
some richer sample at medium-high redshifts to constrain the
results better. However, if we had richer samples at high
redshifts, the Taylor series analysis would fail to constrain
cosmological models since an exact, and not approximated,
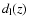 expression is needed in that case. The best constraint, however,
would be an absolute relation between several, GRB observables
which would make the GRBs a powerful standard candle at
intermediate-high redshift.
expression is needed in that case. The best constraint, however,
would be an absolute relation between several, GRB observables
which would make the GRBs a powerful standard candle at
intermediate-high redshift.
Considering these preliminary results, it seems that cosmography
by GRBs could be a useful tool in constraining self-consistent
cosmological models even if, up to now, GRBs are not standard
candles in the proper sense.
Acknowledgements
We thank the referee for the useful suggestions that improved the paper.
- Albrecht, A., et al.,
2006 [arXiv:astro-ph/0609591]
(In the text)
- Allen, S. W., Schmidtn
R. W., & Ebeling, H. 2004, MNRAS, 353, 457 [NASA ADS] [CrossRef]
- Amati, L., et al.
2008 [arXiv:0805.0377]
- Basilakos, S.,
& Perivolaropoulos, L. 2008 [arXiv:0805.0875]
- Bjornsson, G.,
Hjorth, J., Jakobsson, P., Christensen, L., & Holland, S. 2001,
ApJ, 552, L121 [NASA ADS] [CrossRef]
- Branch, D., &
Tammann, G. A. 1992, ARA&A, 30, 359 [NASA ADS] [CrossRef]
(In the text)
- Capozziello,
S., et al. 2008, to appear in PRD
[arXiv:0802.1583]
- Chevallier, M., &
Polarski, D. 2001, Int. J. Mod. Phys. D. 10, 213 [NASA ADS] [CrossRef]
- Linder, E. V. 2003, Phys.
Rev. Lett., 90, 091301 [NASA ADS] [CrossRef]
- Djorgovski, S.
G., Kulkarni, S. R., Bloom, J. S., et al. 1999b, GCN Circ.,
189 [NASA ADS] [CrossRef], http://gcn.gsfc.nasa.gov/gcn/gcn3/189.gcn3
- Frail, D. A., Kulkarni,
S.R., & Sari, R. 2001, ApJ, 562, L55 [NASA ADS] [CrossRef]
(In the text)
- Ghirlanda, G.,
Ghisellini, G., & Lazzati, D. 2004, ApJ, 616, 331 [NASA ADS] [CrossRef]
- Israel, G., Marconi,
G., & Covino, S. 1999, A&A, 348, L5 [NASA ADS]
- Jimenez, R., Band,
D., & Piran, T. 2001, ApJ, 561, 171 [NASA ADS] [CrossRef]
- Komatsu, E., Djorgovski,
S. G., & Odewahn, S. C. 2008
[arXiv:0803.0547]
(In the text)
- Kulkarni,
S. R., Djorgovski, S. G., Odewahn, S. C., et al. 1999,
Nature, 398, 389 [NASA ADS] [CrossRef]
- Li, H., Xia, J.-Q., & Liu,
J. 2008, ApJ, 680, 92 [NASA ADS] [CrossRef]
- Liang, E., & Zhang,
B. 2005, ApJ, 633, 611 [NASA ADS] [CrossRef]
(In the text)
- Liang, N., et al.
2008 [arXiv:0802.4262]
(In the text)
- Meszaros, P. 2006,
Rept. Prog. Phys., 69, 2259 [NASA ADS] [CrossRef]
- Metzger, M. R.,
Djorgovski, S. G., Kulkarni, S. R., et al. 1997,
Nature, 387, 878 [NASA ADS] [CrossRef]
- Qi, S., Wang, F., & Lu, T.
2008 [arXiv:0803.4304]
- Riess, A. G.,
Strolger, L.-G., & Tonry, J. 2004, ApJ, 607, 665 [NASA ADS] [CrossRef]
- Ruffini, R.,
et al. 2008, Gamma Ray Bursts, Proceedings XI Marcel Grossmann
Meeting (Singapore: World Scientific)
- Sari, R., Piran, T., &
Halpern, J. P. 1999, ApJ, 519, L17 [NASA ADS] [CrossRef]
(In the text)
- Schaefer,
B. E. 2007, ApJ, 660, 16 [NASA ADS] [CrossRef]
(In the text)
- Visser, M. 2004,
Class. Quant. Grav., 21, 2603 [NASA ADS] [CrossRef]
(In the text)
- Visser, M., &
Catto
 n, C. 2007a, Class. Quant. Grav., 24, 5985 [NASA ADS] [CrossRef]
n, C. 2007a, Class. Quant. Grav., 24, 5985 [NASA ADS] [CrossRef]
- Visser, M., &
Catto
 n, C. 2007b [arXiv:gr-qc/0703122]
(In the text)
n, C. 2007b [arXiv:gr-qc/0703122]
(In the text) - Weinberg, S. 1972,
Gravitation and Cosmology: Principles and applications of the
general theory of relativity (New York: Wiley)
(In the text)
- Xu, D., Dai, Z. G., &
Liang, E. W. 2005, ApJ, 633, 603 [NASA ADS] [CrossRef]
(In the text)
Copyright ESO 2008
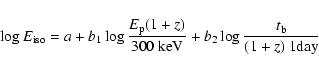
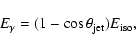
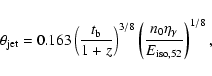
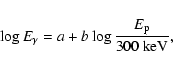
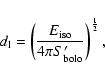
![\begin{displaymath}
d_{\rm l} = \left[\frac{10^a \left(\frac{E_{\rm p}(1+z)}{30...
...~1~{\rm day}}\right)^{b_2}}{4 \pi S'_{\rm bolo}}\right]^{1/2},
\end{displaymath}](/articles/aa/full/2008/40/aa10337-08/img25.gif)
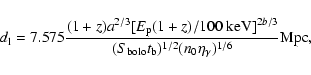
![$\displaystyle d_{\rm H} z
\Bigg\{ 1 \!+\! {1\over2}\left[1\!-\!q_0\right] {z}
-...
...ft[1\!-\!q_0\!-\!3q_0^2\!+\!j_0\!+\! \frac{k \; d_{\rm H}^2}{a_0^2} \right] z^2$](/articles/aa/full/2008/40/aa10337-08/img28.gif)
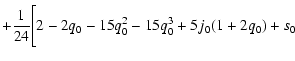
![$\displaystyle + \frac{2\; k \; d_{\rm H}^2 \; (1+3q_0)}{a_0^2}\Bigg]\; z^3 + \mathcal{O}\left(z^4\right) \Bigg\}$](/articles/aa/full/2008/40/aa10337-08/img30.gif)
![$\displaystyle - {1\over a} \; {{\rm d}^2 a\over {\rm d} t^2} \;\left[ {1\over a} \;
{{\rm d} a \over {\rm d} t}\right]^{-2}~,$](/articles/aa/full/2008/40/aa10337-08/img33.gif)
![$\displaystyle + {1\over a} \; {{\rm d}^3 a \over {\rm d} t^3} \; \left[ {1\over a}
\; {{\rm d} a \over {\rm d} t}\right]^{-3}~,$](/articles/aa/full/2008/40/aa10337-08/img34.gif)
![$\displaystyle + {1\over a} \; {{\rm d}^4 a \over {\rm d} t^4} \; \left[ {1\over a}
\; {{\rm d} a \over {\rm d} t}\right]^{-4}\cdot$](/articles/aa/full/2008/40/aa10337-08/img35.gif)
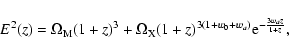
![\begin{displaymath}\mu = 25 + \frac{5}{\ln~(10)}\ln~[d_{\rm l}/(1~{\rm Mpc})] + 25,
\end{displaymath}](/articles/aa/full/2008/40/aa10337-08/img53.gif)
![$\displaystyle + \frac{1}{24} \left[-3 + 10q_0 + 9q_0^2 - 4 \left(j_0 + 1 + \frac{kd_{\rm H}^2}{a_0^2}\right)\right]z^2$](/articles/aa/full/2008/40/aa10337-08/img56.gif)
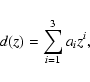
![\begin{displaymath}\ln[d(z)/(z ~{\rm Mpc})] = \sum_{i=1}^3 b_i z^i
\end{displaymath}](/articles/aa/full/2008/40/aa10337-08/img60.gif)
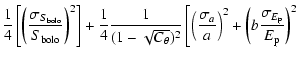
![$\displaystyle \left. +
\left( {b\frac{{\sigma _{\rm b} }}{b}\ln \frac{E_{\rm p}...
...ght)^2 \right]+ \frac{1}{4}\frac{C_{\theta }}{{(1 - \sqrt
{C_{\theta } } )^2 }}$](/articles/aa/full/2008/40/aa10337-08/img78.gif)
![$\displaystyle \times
\left[ {\left( {\frac{{3\sigma _{t_{\rm b} } }}{{t_{\rm b} }}} \right)^2
+ \left( {\frac{{\sigma _{n_0 } }}{{n_0 }}} \right)^2}\right],$](/articles/aa/full/2008/40/aa10337-08/img79.gif)
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0337fig1.eps}\end{figure}](/articles/aa/full/2008/40/aa10337-08/Timg84.gif)
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0337fig2.eps}\end{figure}](/articles/aa/full/2008/40/aa10337-08/Timg86.gif)
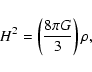
![\begin{displaymath}\frac{\dot{\rho}}{\rho} = -3H \left(1 + \frac{p}{\rho}\right) = -3H [ 1 + w(z)],
\end{displaymath}](/articles/aa/full/2008/40/aa10337-08/img89.gif)