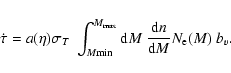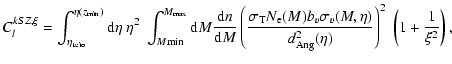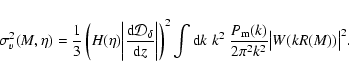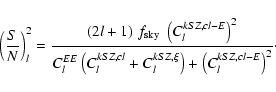A&A 490, 25-29 (2008)
DOI: 10.1051/0004-6361:200810204
Missing baryons, bulk flows, and the E-mode polarization of the Cosmic Microwave Background
C. Hernández-Monteagudo1 -
R. A. Sunyaev1,2
1 - Max Planck Institut für Astrophysik,
Karl Schwarzschild Str. 1, 85741
Garching bei München, Germany
2 -
Space Research Institute, Russian Academy of Sciences, Profsoyuznaya 84/32, 117997 Moscow, Russia
Received 15 May 2008 / Accepted 21 July 2008
Abstract
Most of the missing baryons are found in slightly overdense structures like
filaments and superclusters, but to date most of them have remained hidden
to observation. At the same time, the linear cosmological perturbation
theory predicts the existence of extended bulk flows seeded by the
gravitational attraction of linear potential wells, but again these also
remain undetected. If the peculiar motion of galaxy groups and clusters
indeed resembles that of the surrounding baryons, then the kinetic
Sunyaev-Zel'dovich (kSZ) pattern of those massive halos should be closely
correlated to the kSZ pattern of all surrounding electrons. Likewise, it
should also be correlated to the CMB E-mode polarization field generated via
Thomson scattering after reionization. We explore the cross-correlation of
the kSZ generated in groups and clusters to the all sky E-mode polarization
in the context of future CMB experiments like Planck, ACT, SPT or APEX. We
find that this cross-correlation effectively probes redshifts below z=3-4 (where most of the baryons cannot be seen), and that it arises on very large
scales (l<10). The significance with which this cross-correlation can be
measured depends on the Poissonian uncertainty associated with the number of
halos where the kSZ is measured and on the accuracy of the kSZ estimations
themselves. Assuming that Planck can provide a cosmic variance limited
E-mode polarization map at l<20 and
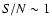 kSZ estimates can be
gathered for all clusters more massive than
kSZ estimates can be
gathered for all clusters more massive than
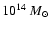 ,
then this
cross-correlation should be measured at the 2-3
,
then this
cross-correlation should be measured at the 2-3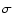 level. Further, if
an all-sky ACT or SPT type CMB experiment provides similar kSZ measurements
for all halos above
level. Further, if
an all-sky ACT or SPT type CMB experiment provides similar kSZ measurements
for all halos above
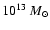 ,
then the cross-correlation total
signal to noise (S/N) ratio should be at the level of 4-5. A detection of
this cross-correlation would provide direct and definite evidence of bulk
flows and missing baryons simultaneously.
,
then the cross-correlation total
signal to noise (S/N) ratio should be at the level of 4-5. A detection of
this cross-correlation would provide direct and definite evidence of bulk
flows and missing baryons simultaneously.
Key words: cosmology: cosmic microwave background - cosmology: large-scale structure of Universe
One of the fundamental predictions of the standard cosmological model is that
baryons (and matter in general) should be moving in extended bulk flows
generated by the gravitational pull of large scale overdense regions. Despite
being potentially useful for cosmological studies
(Atrio-Barandela et al. 2008; Kashlinsky & Atrio-Barandela 2000; Atrio-Barandela et al. 2004), none of those bulk flows have been
detected to date (Benson et al. 2003), partially due to the difficulty of detecting
baryonic matter in the local universe. Indeed, the visible baryonic matter in
the various frequency ranges amounts only to one ninth of the total budget of
baryons predicted by the cosmological model (Fukugita & Peebles 2004, this is the so called
missing baryon problem). All these baryons must be found
in the present Universe, since they have been detected at large
(
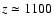 )
and intermediate redshift (
)
and intermediate redshift (
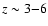 ), by means of Cosmic Microwave
Background (CMB) (Hinshaw et al. 2008) and Lyman-
), by means of Cosmic Microwave
Background (CMB) (Hinshaw et al. 2008) and Lyman- forest (McDonald et al. 2005; Croft et al. 1998)
observations. However, no conclusive observational evidence has been found at
low redshift. Some indications have been derived from the observation of
absorption lines in the direction of quasars (see Nicastro et al. (2005b,a) and
references therein), or a soft X-ray excess around clusters
(e.g., Kull & Böhringer 1999; Zappacosta et al. 2002). Cen & Ostriker (2005,1999) concluded that most of the
baryons are in a warm phase (WHIM), defined by the temperature range
forest (McDonald et al. 2005; Croft et al. 1998)
observations. However, no conclusive observational evidence has been found at
low redshift. Some indications have been derived from the observation of
absorption lines in the direction of quasars (see Nicastro et al. (2005b,a) and
references therein), or a soft X-ray excess around clusters
(e.g., Kull & Böhringer 1999; Zappacosta et al. 2002). Cen & Ostriker (2005,1999) concluded that most of the
baryons are in a warm phase (WHIM), defined by the temperature range
![$T \in [10^5, 10^7]$](/articles/aa/full/2008/40/aa10204-08/img10.gif) K. Whether most of this gas is in a diffuse phase or in small,
unresolved, collapsed objects is still an open question. Recently,
Génova-Santos et al. (2005,2008) detected a non-Gaussian cold spot when looking at the
CMB radiation in the direction of Corona Borealis, and discussed its
interpretation in the context of the thermal and the kinetic
Sunyaev-Zel'dovich effects. The thermal effect (tSZ, Sunyaev & Zeldovich 1972) expresses
the distortion that the black body CMB spectrum undergoes due to Compton
scattering on hot electrons. On the other hand, the kinetic effect
(kSZ, Sunyaev & Zeldovich 1980) describes the Thomson scattering between CMB photons and
electrons in which there is no energy exchange (and therefore it introduces
thermal or frequency independent brightness temperature fluctuations). In the
case of Corona Borealis, it was suggested that a face on filament could give
rise, via either tSZ or kSZ, to the pattern seen in the CMB maps. However, it
was shown in Hernández-Monteagudo et al. (2006b) that the tSZ is not a useful tool to track the
baryons outside the largest collapsed halos: about
K. Whether most of this gas is in a diffuse phase or in small,
unresolved, collapsed objects is still an open question. Recently,
Génova-Santos et al. (2005,2008) detected a non-Gaussian cold spot when looking at the
CMB radiation in the direction of Corona Borealis, and discussed its
interpretation in the context of the thermal and the kinetic
Sunyaev-Zel'dovich effects. The thermal effect (tSZ, Sunyaev & Zeldovich 1972) expresses
the distortion that the black body CMB spectrum undergoes due to Compton
scattering on hot electrons. On the other hand, the kinetic effect
(kSZ, Sunyaev & Zeldovich 1980) describes the Thomson scattering between CMB photons and
electrons in which there is no energy exchange (and therefore it introduces
thermal or frequency independent brightness temperature fluctuations). In the
case of Corona Borealis, it was suggested that a face on filament could give
rise, via either tSZ or kSZ, to the pattern seen in the CMB maps. However, it
was shown in Hernández-Monteagudo et al. (2006b) that the tSZ is not a useful tool to track the
baryons outside the largest collapsed halos: about 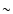 80% of the tSZ
luminosity is generated in the most massive collapsed structures, and the
80% of the tSZ
luminosity is generated in the most massive collapsed structures, and the
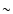 50% of baryons located in underdense or slightly overdense regions
give rise to only
50% of baryons located in underdense or slightly overdense regions
give rise to only 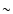 5% of the total tSZ luminosity. The kSZ is most
promising, since it does not require high gas pressure, but relative
velocities with respect to the CMB instead (which is itself a prediction of
the model). However, the drawback is that the kSZ temperature fluctuations do
not depend on the frequency, and therefore they cannot be easily distinguished
from the intrinsic CMB temperature fluctuations. However, the kSZ further
modifies the CMB photon field by introducing additional polarization, and this
should provide another way to isolate this effect.
5% of the total tSZ luminosity. The kSZ is most
promising, since it does not require high gas pressure, but relative
velocities with respect to the CMB instead (which is itself a prediction of
the model). However, the drawback is that the kSZ temperature fluctuations do
not depend on the frequency, and therefore they cannot be easily distinguished
from the intrinsic CMB temperature fluctuations. However, the kSZ further
modifies the CMB photon field by introducing additional polarization, and this
should provide another way to isolate this effect.
![\begin{figure}
\par\includegraphics[width=18cm]{0204fig1.eps}
\end{figure}](/articles/aa/full/2008/40/aa10204-08/Timg13.gif) |
Figure 1:
( Left panel) a) Visibility function versus redshift
under WMAP5 cosmogony. ( Middle panel) b) Thomson optical depth versus
redshift due to all electrons (solid line) and to those electrons contained in
halos more massive than
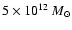 (dashed line).
( Right panel) c)
Showing square root of angular power spectra, note the
(dashed line).
( Right panel) c)
Showing square root of angular power spectra, note the 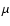 K units. Thick solid line: total CMB temperature anisotropy
amplitude. Filled circles: total kSZ induced temperature
fluctuations generated during and after reionization. Thin solid line: total
E polarization mode power spectrum. Thick dashed line: correlation term of
the Thomson scattering induced fluctuations generated in galaxy
clusters. Thin dashed line: Poisson term of the Thomson scattering induced
fluctuations in galaxy clusters. Dot-dashed line: cross-correlation between
the total E-mode polarization (thin solid line) and the correlated part of the
kSZ generated in galaxy groups and clusters (thick dashed line). K units. Thick solid line: total CMB temperature anisotropy
amplitude. Filled circles: total kSZ induced temperature
fluctuations generated during and after reionization. Thin solid line: total
E polarization mode power spectrum. Thick dashed line: correlation term of
the Thomson scattering induced fluctuations generated in galaxy
clusters. Thin dashed line: Poisson term of the Thomson scattering induced
fluctuations in galaxy clusters. Dot-dashed line: cross-correlation between
the total E-mode polarization (thin solid line) and the correlated part of the
kSZ generated in galaxy groups and clusters (thick dashed line). |
| Open with DEXTER |
In this work we exploit the anisotropic nature of the Thomson scattering (for which linear polarization is introduced in the CMB), and use it as a tool to reveal the bulk flows of the missing baryons in the low redshift universe, (z < 2-3). For that, we need to assume that the peculiar motion of clusters and groups are correlated to the velocities of the surrounding matter (just as the linear theory predicts),
and use future measurements on halos as a kSZ template for all baryons. In Sect. 2 we compute the kSZ and the polarization generated during and after reionization, and the cross-correlation between both. In Sect. 3 we compute the kSZ produced by the halo population and the signal to noise (S/N) ratio for its cross-correlation to the all-sky E-mode polarization. We discuss our results and conclude in Sect. 4. Throughout this paper, we use a cosmological parameter set corresponding to the WMAP5 + 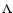 CDM model (Hinshaw et al. 2008).
CDM model (Hinshaw et al. 2008).
2 The large scale secondary anisotropies after reionization
According to WMAP data, the first stars must have reionized the IGM at around
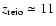 (Hinshaw et al. 2008). Since then, CMB photons and electrons have
interacted again via Thomson scattering. As during recombination, this
scattering preserves the black body spectrum of the CMB, but changes
the direction of the CMB photons, and, in the presence of a non-vanishing
quadrupole of the CMB intensity, in also induces linear polarization. This
process is the cause of a partial blurring of the anisotropies generated at
the surface of last scattering and also the generation of new anisotropies at
scales comparable to the horizon at
(Hinshaw et al. 2008). Since then, CMB photons and electrons have
interacted again via Thomson scattering. As during recombination, this
scattering preserves the black body spectrum of the CMB, but changes
the direction of the CMB photons, and, in the presence of a non-vanishing
quadrupole of the CMB intensity, in also induces linear polarization. This
process is the cause of a partial blurring of the anisotropies generated at
the surface of last scattering and also the generation of new anisotropies at
scales comparable to the horizon at
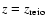 (
(
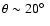 or
or
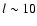 ,
Siuniaev 1977). (One should also consider that, if reionization proceeded first
in those most overdense regions hosting the first stars, then it must also
have left a patchy signature on the CMB small scale anisotropies. However, in
this work we shall neglect these small angle fluctuations). The temperature anisotropies
introduced in the CMB intensity were caused by the peculiar motions of the
scatterers (electrons) with respect to the CMB, (i.e., the kSZ effect). A simple expression
for these temperature anisotropies is given by the following integral of the
projection of the peculiar velocity along the line of sight
,
Siuniaev 1977). (One should also consider that, if reionization proceeded first
in those most overdense regions hosting the first stars, then it must also
have left a patchy signature on the CMB small scale anisotropies. However, in
this work we shall neglect these small angle fluctuations). The temperature anisotropies
introduced in the CMB intensity were caused by the peculiar motions of the
scatterers (electrons) with respect to the CMB, (i.e., the kSZ effect). A simple expression
for these temperature anisotropies is given by the following integral of the
projection of the peculiar velocity along the line of sight
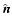 :
:
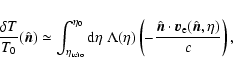 |
(1) |
(note that we are neglecting the few percent contribution of the polarization
terms). As in Seljak & Zaldarriaga (1996), in this equation 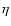 is the conformal time
(related to the coordinate time via d
is the conformal time
(related to the coordinate time via d
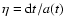 ,
with a the
cosmological scale factor), and
,
with a the
cosmological scale factor), and
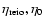 are its values at
reionization and present, respectively. Dots will denote derivatives with
respect to the conformal time. The (proper) electron peculiar velocity is
given by
are its values at
reionization and present, respectively. Dots will denote derivatives with
respect to the conformal time. The (proper) electron peculiar velocity is
given by
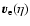 ,
and its Fourier counterpart can be related to the
underlying linear density perturbation field by means of the continuity
equation. These peculiar velocities describe the large scale bulk flows
of matter that are generated by the linear perturbations in the matter density
field. The visibility function is defined as
,
and its Fourier counterpart can be related to the
underlying linear density perturbation field by means of the continuity
equation. These peculiar velocities describe the large scale bulk flows
of matter that are generated by the linear perturbations in the matter density
field. The visibility function is defined as
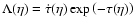 ,
with
,
with
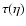 the Thomson
optical depth given by
the Thomson
optical depth given by
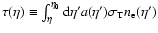 .
In this expression,
.
In this expression,
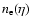 is the
background electron number density and
is the
background electron number density and
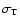 the Thomson cross section.
The Thomson opacity is given by
the Thomson cross section.
The Thomson opacity is given by
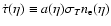 .
The visibility function
.
The visibility function
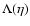 denotes the probability
that a CMB photon was last scattered at the epoch given by
denotes the probability
that a CMB photon was last scattered at the epoch given by 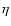 .
In
panel (a) of Fig. 1 it can be seen that the visibility function
peaks at recombination redshift
.
In
panel (a) of Fig. 1 it can be seen that the visibility function
peaks at recombination redshift
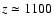 (as first predicted by
Sunyaev & Zeldovich 1970), although it has a second peak at
(as first predicted by
Sunyaev & Zeldovich 1970), although it has a second peak at
 ,
from the new Thomson scattering taking place after the stars reionize
the IGM (Siuniaev 1977). Note that the optical depth behaves differently, increasing steadily up to
the reionization redshift (solid line of panel (b) in Fig. 1).
,
from the new Thomson scattering taking place after the stars reionize
the IGM (Siuniaev 1977). Note that the optical depth behaves differently, increasing steadily up to
the reionization redshift (solid line of panel (b) in Fig. 1).
The anisotropic nature of the Thomson scattering introduces linear
polarization as long as the CMB intensity has a non-vanishing local
quadrupole. In CMB studies, it is customary to map the standard Q and Upolarization Stokes parameters on the (rotation invariant) E and B modes
(Zaldarriaga & Seljak 1997; Kamionkowski et al. 1997), which behave with opposite parity properties
versus spatial reflections. Pure Thomson scattering should produce no B mode
polarization, and hereafter this mode will be neglected. Since the
evolution of the intensity and E-mode polarization anisotropies are coupled
by the sum of the intensity quadrupole and the polarization monopole and quadrupole,
both quantities will be correlated, and
this cross-correlation has already been measured by WMAP, (Hinshaw et al. 2008).
Using a modified version of a standard Boltzmann code (like, e.g., CMBFAST
Seljak & Zaldarriaga 1996) it is straightforward to compute the temperature and E-mode
polarization anisotropies generated during and after reionization, and the cross-correlation
between them. The results,
computed under WMAP5 cosmology (Hinshaw et al. 2008), are displayed in
Fig. 1c. The total intensity (TT) and E polarization (EE) angular
power spectra are displayed by the thick and thin solid lines, respectively,
whereas the cross-correlation between the intensity and E polarization is
given by the dotted line (TE). The temperature anisotropies induced by the kSZ
during and after reionization are given by the filled circles, and the
generation of polarization at the same cosmic epochs is the responsible for
the low l (
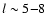 )
bump in the EE spectrum. Although the
WMAP
)
bump in the EE spectrum. Although the
WMAP![[*]](/icons/foot_motif.gif) mission has
barely measured it, the forthcoming Planck
mission has
barely measured it, the forthcoming Planck![[*]](/icons/foot_motif.gif) satellite should be able to provide an accurate estimate of the EE angular power spectrum (and this shall be our assumption hereafter).
satellite should be able to provide an accurate estimate of the EE angular power spectrum (and this shall be our assumption hereafter).
3 The clusters as probes of bulk flows
As mentioned in the Introduction, there are two major aspects of our
understanding of the local Universe that still are pending confirmation:
one is the detection of the eight ninths of baryons that have not yet been
found (Fukugita & Peebles 2004), the another is the measurement of the cosmological
bulk flows. With the advent of high resolution and high sensitivity CMB
experiments like ACT (Fowler & ACT Collaboration 2006), SPT (Ruhl et al. 2004) or APEX (Dobbs et al. 2006), bulk flows may
be detected by looking at the kSZ in galaxy clusters. These structures
contain large reservoirs of gas, which constitute sources for relatively large
values of optical depth, (
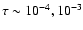 ). Nevertheless, one must
have in mind that the kSZ effect is not the only physical mechanism to be
found in clusters. Indeed, given the fact that, in these halos, gas can reach
temperatures at the level of a few KeV, inverse Compton scattering in which
hot electrons transfer energy to CMB photons (tSZ)
becomes of relevance as well. However, the brightness temperature
fluctuations introduced by this effect cross from negative to positive values at a
frequency close to 218 GHz. For this reason, this frequency becomes an ideal
window for searching for the kSZ in galaxy clusters.
). Nevertheless, one must
have in mind that the kSZ effect is not the only physical mechanism to be
found in clusters. Indeed, given the fact that, in these halos, gas can reach
temperatures at the level of a few KeV, inverse Compton scattering in which
hot electrons transfer energy to CMB photons (tSZ)
becomes of relevance as well. However, the brightness temperature
fluctuations introduced by this effect cross from negative to positive values at a
frequency close to 218 GHz. For this reason, this frequency becomes an ideal
window for searching for the kSZ in galaxy clusters.
![\begin{figure}
\par\includegraphics[width=18cm]{0204fig2.eps}
\end{figure}](/articles/aa/full/2008/40/aa10204-08/Timg39.gif) |
Figure 2:
The total S/N ratio for the correlation of the E-mode polarization with the low redshift (z<3-4) kSZ generated by bulk flows in galaxy groups and clusters. Horizontal axes display the decimal logarithm of the individual group/cluster kSZ measurement S/N ratio (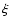 ), whereas vertical axes display the decimal logarithm of the minimum mass of groups/clusters considered. Due to Poisson/shot noise, a low choice for ), whereas vertical axes display the decimal logarithm of the minimum mass of groups/clusters considered. Due to Poisson/shot noise, a low choice for
 makes the high total S/N regions shrink, and this also happens if
makes the high total S/N regions shrink, and this also happens if
 is chosen too large and too much information is unused. The optimal minimum redshift is around
is chosen too large and too much information is unused. The optimal minimum redshift is around
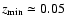 ,
and the maximum S/N ratio achievable for perfect E and kSZ surveys is ,
and the maximum S/N ratio achievable for perfect E and kSZ surveys is
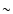 5.8. Note that we are assuming 5.8. Note that we are assuming
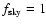 . . |
| Open with DEXTER |
The kSZ effect generated in the galaxy cluster population has been studied
extensively (Peel 2006; Bhattacharya & Kosowsky 2007; Hernández-Monteagudo et al. 2006a; Bhattacharya & Kosowsky 2008, etc.). In particular, in
Hernández-Monteagudo et al. (2006a) an analysis of the correlation properties of the cluster
peculiar motion was provided. They found that the typical correlation length
of these peculiar velocities (i.e., the typical size of a bulk flow) is
typically 20 h-1 Mpc in comoving units. This means that a large fraction
of the gas that is surrounding the clusters is actually comoving with
it. This can be envisioned as flows of matter (containing clusters, groups and
diffuse gas) falling into the (future) supercluster's potential well, and
generating a kSZ dipole pattern at its center as
different flows merge in that region (Diaferio et al. 2000). This is related to the basic assumption
of this work: peculiar motion of baryons in a given region is well
described by the peculiar motion of the largest galaxy groups and clusters
within the same region. When computing the all sky kSZ angular power spectrum
generated by clusters, Hernández-Monteagudo et al. (2006a) found that although the this could be
decomposed in four terms, only two of them give rise to most of
the power: a correlation term (generated by the bulk flows) was dominant at
the very large angular scales, whereas the anisotropy induced by the Poisson
statistics would dominate at smaller scales. Both correlation and Poisson
terms are shown by the thick and thin dashed lines in
Fig. 1c. The former has been computed using a modified version of
the CMBFAST code where the Thomson opacity generated in clusters at a given
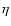 reads (Hernández-Monteagudo et al. 2006a):
reads (Hernández-Monteagudo et al. 2006a):
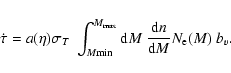 |
(2) |
The symbol
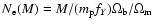 denotes the number of
electrons in a halo of mass M, with
denotes the number of
electrons in a halo of mass M, with 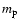 the proton mass, fY=1-Y/2 the
helium fraction correction factor and
the proton mass, fY=1-Y/2 the
helium fraction correction factor and
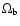 ,
,
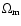 the baryon and
matter density parameters, respectively. The halo mass function d
the baryon and
matter density parameters, respectively. The halo mass function d
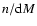 is
approximated by that of Sheth & Tormen (1999). Motivated by Peel (2006),
the velocity bias was approximated by bv = 1.3 for all halos (although the
particular choice of this parameter has very little impact on our results, as
we shall see below). We set
is
approximated by that of Sheth & Tormen (1999). Motivated by Peel (2006),
the velocity bias was approximated by bv = 1.3 for all halos (although the
particular choice of this parameter has very little impact on our results, as
we shall see below). We set
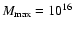
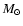 ,
and compared our
results for different choices of the minimum mass
,
and compared our
results for different choices of the minimum mass
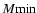 .
In the middle panel of
Fig. 1 the dashed line shows the optical depth generated by halos more
massive than
.
In the middle panel of
Fig. 1 the dashed line shows the optical depth generated by halos more
massive than
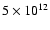
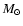 :
most of the contribution (
:
most of the contribution (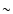 60%) comes from
z<3, and the contribution from (the more massive) galaxy groups and clusters is shifted even
further into the low z range.
On the other hand, the Poisson term can easily be found to be
60%) comes from
z<3, and the contribution from (the more massive) galaxy groups and clusters is shifted even
further into the low z range.
On the other hand, the Poisson term can easily be found to be
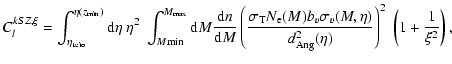 |
|
|
(3) |
where
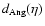 denotes angular diameter distance and
denotes angular diameter distance and
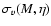 is the time dependent rms line of sight peculiar
velocity of an object of mass M,
is the time dependent rms line of sight peculiar
velocity of an object of mass M,
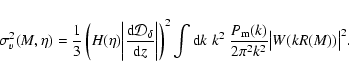 |
(4) |
The present linear matter power spectrum is given by
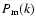 ,
the linear density
growth factor by
,
the linear density
growth factor by
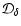 ,
the Hubble parameter by
,
the Hubble parameter by 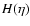 ,
and
the Fourier window function of a top hat filter corresponding to an object of
mass M by W(kR(M)) (see Hernández-Monteagudo et al. 2006a, for details). Note that in
Eq. (3),
,
and
the Fourier window function of a top hat filter corresponding to an object of
mass M by W(kR(M)) (see Hernández-Monteagudo et al. 2006a, for details). Note that in
Eq. (3), 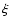 denotes the signal to noise ratio of the
kSZ detection in a single cluster/group. As noise we regard any signal
present at the cluster position that is not due to the correlated component of
the kSZ (e.g., kSZ caused by thermal velocities, tSZ residuals, intrinsic CMB,
radio source emission, IR source emission, instrumental noise, etc). Note as
well the low redshift limit given by
denotes the signal to noise ratio of the
kSZ detection in a single cluster/group. As noise we regard any signal
present at the cluster position that is not due to the correlated component of
the kSZ (e.g., kSZ caused by thermal velocities, tSZ residuals, intrinsic CMB,
radio source emission, IR source emission, instrumental noise, etc). Note as
well the low redshift limit given by
 in
Eq. (3). Therefore, this equation accounts for both the
Poissonian statistics and the error in the kSZ recovery at cluster
positions. Only in the case
in
Eq. (3). Therefore, this equation accounts for both the
Poissonian statistics and the error in the kSZ recovery at cluster
positions. Only in the case
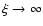 we recover the pure
Poissonian term.
we recover the pure
Poissonian term.
We are interested in the correlated component of the cluster kSZ, i.e., in the
velocity component that should be comoving with the surrounding matter. If
this is indeed the case, then the pattern of the kSZ in clusters must be very
similar to that of the kSZ generated by all electrons (filled circles in
Fig. 1), and therefore it must be closely correlated to the
E mode of the polarization anisotropies generated during and after
reionization (i.e., the low l bump). The actual amplitude of this
cross-correlation will depend on the redshift range that a given set of halos
is probing, and the signal to noise (S/N) ratio of this cross-correlation for
a particular multipole l is provided by
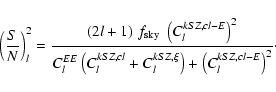 |
(5) |
The symbol
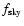 refers to the fraction of the sky covered by an
experiment, and
ClkSZ,cl and
refers to the fraction of the sky covered by an
experiment, and
ClkSZ,cl and
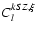 denote, respectively, the
angular power spectrum of the correlated part and the noise of the kSZ
generated in galaxy clusters. The cross-correlation between the kSZ in halos and the E-mode is
given by
ClkSZ,cl - E. If
denote, respectively, the
angular power spectrum of the correlated part and the noise of the kSZ
generated in galaxy clusters. The cross-correlation between the kSZ in halos and the E-mode is
given by
ClkSZ,cl - E. If
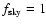 ,
the total S/N is given by the
sum of the squares of these quantities, i.e.,
,
the total S/N is given by the
sum of the squares of these quantities, i.e.,
![$S/N = \left[\sum_l
(S/N)_l^2\right]^{1/2}$](/articles/aa/full/2008/40/aa10204-08/img61.gif) .
It turns out that the actual amplitude of this S/N ratio is
strongly dependent on the relative amplitude of the Poisson term with respect
to the correlation term (and this makes the S/N independent of parameters like the
velocity bias bv). Due to the
.
It turns out that the actual amplitude of this S/N ratio is
strongly dependent on the relative amplitude of the Poisson term with respect
to the correlation term (and this makes the S/N independent of parameters like the
velocity bias bv). Due to the
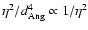 dependence in Eq. (3), the Poisson term is less
important for higher values of the minimum redshift considered
dependence in Eq. (3), the Poisson term is less
important for higher values of the minimum redshift considered
 .
Further, it depends linearly on the number density of objects, as
opposed to the correlation term, which depends on the number density
squared. Therefore, for lower values of the threshold mass
.
Further, it depends linearly on the number density of objects, as
opposed to the correlation term, which depends on the number density
squared. Therefore, for lower values of the threshold mass
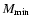 the
relative weight of the Poisson term versus the correlation one should
diminish. This is shown in Fig. 2.
Since this correlation arises around halos at low and moderate redshifts, the matter
behind this signal is different from that generating the anti cross-correlation
between CMB anisotropies and HI 21 cm observations.
the
relative weight of the Poisson term versus the correlation one should
diminish. This is shown in Fig. 2.
Since this correlation arises around halos at low and moderate redshifts, the matter
behind this signal is different from that generating the anti cross-correlation
between CMB anisotropies and HI 21 cm observations.
4 Discussion and conclusions
The horizontal axis of Fig. 2 corresponds to the S/N ratio at
which the kSZ can be determined in a single halo, i.e., 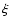 in
Eq. (3). The number of potential contaminants when measuring the
kSZ in a halo is relatively high: the tSZ has a definite spectral dependence,
and should be close to zero at
in
Eq. (3). The number of potential contaminants when measuring the
kSZ in a halo is relatively high: the tSZ has a definite spectral dependence,
and should be close to zero at 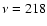 GHz, however asymmetries in the
frequency response of the experiment together with relativistic effects
(Itoh & Nozawa 2004) will inevitably leave some residuals. However, as shown in
Hernández-Monteagudo et al. (2006a), its weight relative to the kSZ decreases for the most numerous
low mass halos, for which the relativistic tSZ corrections are also less
important. Internal motion within the halos (which, as found by
Diaferio et al. 2005, is only relevant for slow halos)
should average out when integrating over the total halo solid angle. The
uncorrelated component of the kSZ could be significant in those systems where
the velocity of halos are thermalized; however this almost never happens for
the galaxy groups and clusters being targeted here, since superclusters are structures
that are not yet relaxed. Nevertheless, Peel (2006) found that, in his
cosmological simulations, the peculiar velocities of haloes showed correlation properties
that differed substantially from linear theory predictions, even at high redshift. If this is indeed the case, then the issue would be whether the baryons surrounding halos would have their peculiar velocities affected in the same way or not. We shall address this issue in future work.
The impact of IR and radio sources is a priori
significant, provided that these sources are correlated to the halos where the
kSZ is produced. However, multifrequency
observations should provide a good insight into their spectral indexes, and
therefore their contribution in the 218 GHz channel should be characterized
down to a given accuracy level. How this compares to the actual kSZ signal is
something to be reliably evaluated only once real data becomes available.
The intrinsic CMB generated at the last scattering surface is
another potential source of contamination. As shown in Fig. 6 of
Hernández-Monteagudo et al. (2006a), its residuals remain in the few
GHz, however asymmetries in the
frequency response of the experiment together with relativistic effects
(Itoh & Nozawa 2004) will inevitably leave some residuals. However, as shown in
Hernández-Monteagudo et al. (2006a), its weight relative to the kSZ decreases for the most numerous
low mass halos, for which the relativistic tSZ corrections are also less
important. Internal motion within the halos (which, as found by
Diaferio et al. 2005, is only relevant for slow halos)
should average out when integrating over the total halo solid angle. The
uncorrelated component of the kSZ could be significant in those systems where
the velocity of halos are thermalized; however this almost never happens for
the galaxy groups and clusters being targeted here, since superclusters are structures
that are not yet relaxed. Nevertheless, Peel (2006) found that, in his
cosmological simulations, the peculiar velocities of haloes showed correlation properties
that differed substantially from linear theory predictions, even at high redshift. If this is indeed the case, then the issue would be whether the baryons surrounding halos would have their peculiar velocities affected in the same way or not. We shall address this issue in future work.
The impact of IR and radio sources is a priori
significant, provided that these sources are correlated to the halos where the
kSZ is produced. However, multifrequency
observations should provide a good insight into their spectral indexes, and
therefore their contribution in the 218 GHz channel should be characterized
down to a given accuracy level. How this compares to the actual kSZ signal is
something to be reliably evaluated only once real data becomes available.
The intrinsic CMB generated at the last scattering surface is
another potential source of contamination. As shown in Fig. 6 of
Hernández-Monteagudo et al. (2006a), its residuals remain in the few 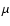 K level if the
cluster/group size is not larger than 2-3 arcmins, which should be the case
for most of clusters and groups in the sky. Therefore this source of
contamination is likely to be less relevant than the rest.
K level if the
cluster/group size is not larger than 2-3 arcmins, which should be the case
for most of clusters and groups in the sky. Therefore this source of
contamination is likely to be less relevant than the rest.
The importance of each of these contaminants will determine which range of the
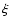 horizontal axis in Fig. 2 one should look at. Due to
the largest amplitude of Poissonian fluctuations at low values of
horizontal axis in Fig. 2 one should look at. Due to
the largest amplitude of Poissonian fluctuations at low values of
 ,
it is convenient not to consider too nearby clusters and groups. From this
figure it is possible to find at which values of
,
it is convenient not to consider too nearby clusters and groups. From this
figure it is possible to find at which values of 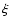 the S/N ratio starts to
be dominated by Cosmic Variance (the horizontal plateau of the contour levels
at high
the S/N ratio starts to
be dominated by Cosmic Variance (the horizontal plateau of the contour levels
at high 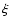 ). Likewise, the steep vertical descent of these contours at low
). Likewise, the steep vertical descent of these contours at low
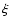 reflects the limit where S/N is exclusively limited by the accuracy of
the kSZ measurements.The requirements for a convincing detection of the
signature of the local baryon bulk flows (say S/N > 3) involve either a
large value of
reflects the limit where S/N is exclusively limited by the accuracy of
the kSZ measurements.The requirements for a convincing detection of the
signature of the local baryon bulk flows (say S/N > 3) involve either a
large value of 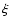 or a low value of
or a low value of
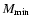 ,
but nevertheless these are
not unrealistic. For instance, the Planck satellite should provide a cleaned
CMB map in a very large fraction of the sky, and with it, estimations of the
kSZ at the cluster and group positions. These estimates should mostly be
limited by the beam size and the un-subtracted point source emission. By
looking at the Compton distortion y map (obtained from multifrequency
observations of the tSZ), one should be able to find the position of not only
the largest clusters, but also of those objects that lie closer to the
confusion limit, and whose signal can be picked up statistically via the
cross-correlation. If this y-map provides the position and the cleaned CMB
map the kSZ estimates (of at least
,
but nevertheless these are
not unrealistic. For instance, the Planck satellite should provide a cleaned
CMB map in a very large fraction of the sky, and with it, estimations of the
kSZ at the cluster and group positions. These estimates should mostly be
limited by the beam size and the un-subtracted point source emission. By
looking at the Compton distortion y map (obtained from multifrequency
observations of the tSZ), one should be able to find the position of not only
the largest clusters, but also of those objects that lie closer to the
confusion limit, and whose signal can be picked up statistically via the
cross-correlation. If this y-map provides the position and the cleaned CMB
map the kSZ estimates (of at least
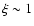 )
for all clusters more massive
than
)
for all clusters more massive
than
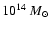 ,
then Planck alone would already yield a total S/Nbetween 2 and 3. Likewise, upcoming Dark Energy surveys like
Pan-STARRS
,
then Planck alone would already yield a total S/Nbetween 2 and 3. Likewise, upcoming Dark Energy surveys like
Pan-STARRS![[*]](/icons/foot_motif.gif) ,
DES
,
DES![[*]](/icons/foot_motif.gif) or PAU-BAO
or PAU-BAO![[*]](/icons/foot_motif.gif) , or X-ray surveys like
eROSITA
, or X-ray surveys like
eROSITA![[*]](/icons/foot_motif.gif) should probe the relevant
redshift range, and independently provide catalogs of group and cluster
candidates. At the same time, high resolution CMB experiments like ACT, SPT or
APEX would contribute more accurate kSZ estimates. Furthermore, future
B-mode polarization experiments should cover large fractions of the sky with
very high sensitivity, and provide better understanding of the E-mode of the
CMB polarization. The maximum achievable value of the total S/N is relatively
small (around 5.8), and therefore a large sky coverageis required,
since most of the signal arises at l<10. Our computations are within the
regime of linear theory. Corrections due to patchy reionization are non linear
and therefore should appear at much smaller angular scales. They should also
arise at redshifts higher than those corresponding to the kSZ addressed in
this work, (z < 3-4). We must also stress again that a cosmic variance
limited EE power spectrum has been assumed, at least in those same large
angular scales. Very soon, the Planck mission should be able to tell whether
this is a sensible assumption or not.
should probe the relevant
redshift range, and independently provide catalogs of group and cluster
candidates. At the same time, high resolution CMB experiments like ACT, SPT or
APEX would contribute more accurate kSZ estimates. Furthermore, future
B-mode polarization experiments should cover large fractions of the sky with
very high sensitivity, and provide better understanding of the E-mode of the
CMB polarization. The maximum achievable value of the total S/N is relatively
small (around 5.8), and therefore a large sky coverageis required,
since most of the signal arises at l<10. Our computations are within the
regime of linear theory. Corrections due to patchy reionization are non linear
and therefore should appear at much smaller angular scales. They should also
arise at redshifts higher than those corresponding to the kSZ addressed in
this work, (z < 3-4). We must also stress again that a cosmic variance
limited EE power spectrum has been assumed, at least in those same large
angular scales. Very soon, the Planck mission should be able to tell whether
this is a sensible assumption or not.
Acknowledgements
C.H.M. acknowledges useful conversations with D.N. Spergel.
- Atrio-Barandela,
F., Kashlinsky, A., & Mücket, J. P. 2004, ApJ, 601,
L111 [NASA ADS] [CrossRef]
- Atrio-Barandela,
F., Mücket, J. P., & Génova-Santos, R. 2008,
ApJ, 674, L61 [NASA ADS] [CrossRef]
- Battistelli, E. S.,
et al. 2006, [arXiv:astro-ph/0603702]
- Benson, B. A.,
Church, S. E., Ade, P. A. R., et al. 2003, ApJ, 592, 674 [NASA ADS] [CrossRef]
(In the text)
- Bhattacharya, S.,
& Kosowsky, A. 2007, ApJ, 659, L83 [NASA ADS] [CrossRef]
- Bhattacharya, S.,
& Kosowsky, A. 2008, Phys. Rev. D, 77, 083004 [NASA ADS] [CrossRef]
- Böhringer, H.,
Voges, W., Huchra, J. P., et al. 2000, ApJS, 129, 435 [NASA ADS] [CrossRef]
- Cen, R., &
Ostriker, J. P. 1999, ApJ, 514, 1 [NASA ADS] [CrossRef]
- Cen, R., &
Ostriker, J. P. 2005, [arXiv:astro-ph/0601008]
- Croft,
R. A. C., Weinberg, D. H., Katz, N., &
Hernquist, L. 1998, ApJ, 495, 44 [NASA ADS] [CrossRef]
-
Diaferio, A., Sunyaev, R. A., & Nusser, A. 2000, ApJ, 533,
L71 [NASA ADS] [CrossRef]
(In the text)
- Diaferio, A.,
Borgani, S., Moscardini, L., et al. 2005, MNRAS, 356,
1477 [NASA ADS] [CrossRef]
(In the text)
- Dobbs, M., Halverson, N.
W., Ade, P. A. R., et al. 2006, New Astron. Rev., 50, 960 [NASA ADS] [CrossRef]
(In the text)
- Fowler, J. W., & ACT
Collaboration 2006, BAAS, 38, 1227 [NASA ADS]
(In the text)
- Fukugita, M.,
& Peebles, P. J. E. 2004, ApJ, 616, 643 [NASA ADS] [CrossRef]
(In the text)
- Génova-Santos, R.,
Rubin o-Marti'n, J. A., Rebolo, R., et al. 2005, MNRAS,
363, 79 [NASA ADS] [CrossRef]
- Genova-Santos, R.,
et al. 2008, [arXiv:0804.0199]
-
Hernández-Monteagudo, C., Verde, L., Jimenez, R., &
Spergel, D. N. 2006a, ApJ, 643, 598 [NASA ADS] [CrossRef]
-
Hernández-Monteagudo, C., Trac, H., Verde, L., & Jimenez,
R. 2006b, ApJ, 652, L1 [NASA ADS] [CrossRef]
(In the text)
- Hinshaw, G., et al.
2008, [arXiv:0803.0732]
(In the text)
- Itoh, N., & Nozawa,
S. 2004, A&A, 417, 827 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Kamionkowski, M.,
Kosowsky, A., & Stebbins, A. 1997, Phys. Rev. D, 55,
7368 [NASA ADS] [CrossRef]
- Kashlinsky, A.,
& Atrio-Barandela, F. 2000, ApJ, 536, L67 [NASA ADS] [CrossRef]
- Kull, A., &
Böhringer, H. 1999, A&A, 341, 23 [NASA ADS]
- McDonald, P., Seljak,
U., Cen, R., et al. 2005, ApJ, 635, 761 [NASA ADS] [CrossRef]
- Nicastro, F., Mathur,
S., Elvis, M., et al. 2005a, ApJ, 629, 700 [NASA ADS] [CrossRef]
- Nicastro, F., Mathur,
S., Elvis, M., et al. 2005b, Nature, 433, 495 [NASA ADS] [CrossRef]
- Peel, A. C. 2006,
MNRAS, 365, 1191 [NASA ADS]
- Ruhl, J., Ruhl, J., Ade, P.
A. R., Carlstrom, J. E., et al. 2004, SPIE, 5498, 11 [NASA ADS]
(In the text)
- Seljak, U., &
Zaldarriaga, M. 1996, ApJ, 469, 437 [NASA ADS] [CrossRef]
(In the text)
- Sheth, R. K., &
Tormen, G. 1999, MNRAS, 308, 119 [NASA ADS] [CrossRef]
(In the text)
- Siuniaev,
R. A. 1977, Sov. Astron. Lett., 3, 268 [NASA ADS]
(In the text)
- Sunyaev,
R. A., & Zeldovich, Y. B. 1970, Ap&SS, 7, 3 [NASA ADS]
(In the text)
- Sunyaev, R. A., &
Zeldovich, Y. B. 1972, Comm. Astrophys. Space Phys., 4,
173 [NASA ADS]
(In the text)
- Sunyaev, R. A., &
Zeldovich, I. B. 1980, MNRAS, 190, 413 [NASA ADS]
(In the text)
-
Zaldarriaga, M., & Seljak, U. 1997, Phys. Rev. D, 55,
1830 [NASA ADS] [CrossRef]
- Zappacosta, L., Mannucci, F.,
Maiolino, R., et al. 2002, A&A, 394, 7 [NASA ADS] [CrossRef] [EDP Sciences]
Copyright ESO 2008
![\begin{figure}
\par\includegraphics[width=18cm]{0204fig1.eps}
\end{figure}](/articles/aa/full/2008/40/aa10204-08/Timg13.gif)
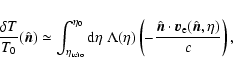
![\begin{figure}
\par\includegraphics[width=18cm]{0204fig2.eps}
\end{figure}](/articles/aa/full/2008/40/aa10204-08/Timg39.gif)