A&A 489, 1055-1063 (2008)
DOI: 10.1051/0004-6361:200810023
G. Pucacco1,![]() -
D. Boccaletti2 -
C. Belmonte3
-
D. Boccaletti2 -
C. Belmonte3
1 - Physics Department, University of Rome ``Tor Vergata", Via della Ricerca Scientifica 1, 00133 Rome, Italy
2 -
Mathematics Department, University of Rome ``La Sapienza", P.le A. Moro 2, 00185 Rome, Italy
3 -
Physics Department, University of Rome ``La Sapienza", P.le A. Moro 2, 00185 Rome, Italy
Received 22 April 2008 / Accepted 16 July 2008
Abstract
Context. We investigate periodic orbits in galactic potentials by developing analytical methods.
Aims. We evaluate the quality of the approximation of periodic orbits in the logarithmic potential constructed using perturbation theory based on Hamiltonian normal forms.
Methods. The solutions of the equations of motion corresponding to periodic orbits are obtained as series expansions computed by inverting the normalizing canonical transformation. To improve the convergence of the series, a resummation based on a continued fraction may be performed. This method is analogous to the Prendergast method, which searches for approximate rational solutions.
Results. It is shown that with a normal form truncated at the lowest order incorporating the relevant resonance it is possible to construct accurate solutions both for normal modes and periodic orbits in general position.
Key words: galaxies: kinematics and dynamics - methods: analytical
In his book on Dynamical Astronomy, Contopoulos (2004) encouraged investigation of the higher-order versions of the Prendergast (1982) method to solve non-linear differential equations. The original method was applied by Contopoulos & Seimenis (1990, hereafter CS90) to periodic orbits in the logarithmic potential and consists of approximating the exact solution with rational trigonometric functions. Even though the trigonometric series used in the rational approximation are truncated at the first non-trivial order, in CS90 it was shown that the quality of the fit to the exact result is quite good over a wide range of energy and ellipticity. On this basis, it is natural to presume that higher-order truncations would improve the quality of the prediction.
However, even the simplest version of the Prendergast (1982) method has two problematic aspects: 1) the choice of the dominant harmonic in the trigonometric series has to be made on the basis of knowledge about the orbit type under study; 2) the determination of the coefficients in the series, which depend on the parameters of the system and on initial conditions, originates from a non-linear algebraic system the solution of which must in general be performed numerically. This second aspect diminishes much of its simplicity, particularly if we attempt higher order truncations and consider the growth of the number of unknown coefficients.
In this paper, we would like to explore the link between the Prendergast-Contopoulos approach and the approximation of orbital solutions found with a resonant normal form. The motivation for this study stems from the idea of rooting a simplified version of the rational solution method into the frame of a modified normalization algorithm to devise a completely analytical approach. This step was proposed (Pucacco et al. 2008) to exploit a resummation technique based on continued fractions to speed up the convergence of series obtained in the framework of normal form perturbation theory. This technique extends the quality of predictions concerning the instability of normal modes and consequent bifurcations of families of boxlets (Belmonte et al. 2007).
In analogy with CS90, we apply this approach to investigate periodic orbits in the logarithmic potential (Binney & Tremaine 1987). We find analytical solutions to the equations of motion for the normal modes and the main low-order boxlets (``loops'' and ``bananas''). By inverting the normalizing transformation of coordinates, these solutions are either in the form of standard truncated power series or in a rational form constructed by a continued fraction truncated at the same order of the series. Knowing the ``normal form'' approximating the system under study, the procedure of creating those solutions is straightforward and does not require any further approximation or numerics.
We show that the analytic rational solutions obtained in this way offer a degree of reliability comparable, where data are available, to those of the semi-analytic treatment based on the Prendergast-Contopoulos approach. Both loops and bananas are quite well reconstructed in shape and dimension. We extend the analysis in CS90 to check also the energy conservation along the boxlets: we find that, whereas for normal modes energy is conserved within a few percent, for loops and bananas, at this level of approximation, it is not easy to go below 10%.
The plan of the paper is as follows: in Sect. 2, we briefly recall the method to construct normal forms for the logarithmic potential and in the Appendix we outline the explicit expressions of the 1:1 and 1:2 Hamiltonian and generating function. In Sect. 3, we analyze the approximation of the major-axis orbit and, in Sects. 4 and 5, we complete the same analysis for the loop and banana families respectively. In Sect. 6 we present our conclusions.
We investigate the dynamics of the potential
Normal forms for the Hamiltonian system corresponding to the potential described by Eq. (1) are constructed with standard methods (Boccaletti & Pucacco 1999; Giorgilli 2002) and were used to determine the main features of its orbit structure (Belmonte et al. 2006,2007). The starting point is the series expansion of Eq. (1) about the origin
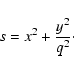 |
(4) |
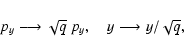 |
(5) |
The generating function of the transformation is a series of the form
It is customary to refer to the series constructed in this way as Birkhoff normal forms. The presence of terms with small denominators in the expansion forbids in general their convergence. It is therefore more effective to operate with resonant normal forms (Sanders et al. 2007; Gustavson 1966), which are still non-convergent, but have the advantage of avoiding the small divisors associated with a particular resonance. To determine the primary features of the orbital structure, we therefore approximate the frequencies with a rational number plus a small ``detuning'' (Contopoulos & Moutsoulas 1966; de Zeeuw & Merritt 1983)
A conservative strategy is of truncate at the lowest order
![]() adequate to convey some non-trivial information about the system. In the resonant case, it can be shown (Tuwankotta & Verhulst 2000) that the lowest order in the normal form capable of including the primary characterisitics of the m1:m2 resonance with double reflection symmetries is
adequate to convey some non-trivial information about the system. In the resonant case, it can be shown (Tuwankotta & Verhulst 2000) that the lowest order in the normal form capable of including the primary characterisitics of the m1:m2 resonance with double reflection symmetries is
the typical structure of the doubly-symmetric resonant normal form truncated at
![]() is (Sanders et al. 2007; Contopoulos 2004)
is (Sanders et al. 2007; Contopoulos 2004)
We are interested in the solution of the equations of motion. For a non-resonant (Birkhoff) normal form, the problem is easily solved: the coefficient
am1 m2 vanishes and K no longer has a term containing angles. Therefore, the ![]() are ``true'' conserved actions and the solutions are
are ``true'' conserved actions and the solutions are
| (20) |
In the resonant case instead, it is not possible to write the solutions in closed form. It is true that the dynamics described by the 1-d.o.f. Hamiltonian
![]() are always integrable, but, in general, the solutions cannot be written in terms of elementary functions. However, solutions can still be written down in the case of the main periodic orbits, for which
are always integrable, but, in general, the solutions cannot be written in terms of elementary functions. However, solutions can still be written down in the case of the main periodic orbits, for which
![]() are true action-angle variables. There are two types of periodic orbits that can be easily identified:
are true action-angle variables. There are two types of periodic orbits that can be easily identified:
By using the generating function Eq. (10), the solutions in terms of standard ``physical'' coordinates can be recovered (apart from possible scaling factors) inverting the canonical transformation defined by Eqs. (A.3) and (A.4). As discussed in the Appendix, the expansion Eq. (10) is composed of even-order terms only. Since in our applications we consider the 1:1 and 1:2 symmetric resonances, we have from Eq. (12) that at most
![]() so that the transformation back to the physical coordinates expressed as a series of the form
so that the transformation back to the physical coordinates expressed as a series of the form
| (21) |
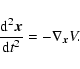 |
(27) |
In systems of the form of Eq. (6), the orbits along the symmetry axes are simple periodic orbits. It can be verified readily that these orbits correspond to the two normal modes for which either J1 or J2 vanish. If the axial orbit is stable it parents a family of ``box'' orbits. A case that is both representative and useful in galactic applications is that of the stability of the x-axis periodic orbit, the ``major-axis orbit'', if q is in the range provide by Eq. (2)). Among its possible bifurcations, the most prominent is usually that due to the 1:2 resonance between the frequency of oscillation along the orbit and that of a normal perturbation, producing the ``banana'' and ``anti-banana'' orbits (Miralda-Escudé & Schwarzschild 1989). Therefore, to derive explicit solutions for both the major-axis orbit and stable bananas (the ``pendulum-like family'' in the denomination of CS90, see Sect. 5 below), we use the 1:2 symmetric normal form.
From the expression of K reported in the Appendix, we obtain on the normal mode J2 = 0,
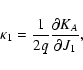 |
(30) |
To evaluate the quality of the approximation, a simple method is to follow the energy variation along the solution of the true potential of Eq. (1). We therefore compute
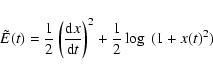 |
(36) |
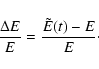 |
(39) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0023fig1.eps} \end{figure}](/articles/aa/full/2008/39/aa10023-08/Timg61.gif) |
Figure 1: Relative energy error along the major-axis orbit for two different truncations of the normal form at E=0.1. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0023fig2.eps} \end{figure}](/articles/aa/full/2008/39/aa10023-08/Timg62.gif) |
Figure 2: Relative energy error along the major-axis orbit for two different truncations of the normal form at E=0.5. |
| Open with DEXTER | |
Table 1: Relative energy variations along the major-axis orbit with different analytic predictions.
After achieving the optimal order, it is disappointing to neglect terms evaluated by a costly high-order computation. There are however other rules for ``summing'' divergent series that adopt all terms (Bender & Orszag 1978), such as the construction of Padè approximant. A related approach is the construction of continued fractions: successive approximants obtained by truncating the fraction at various order can provide an improvement in the asymptotic convergence with respect to the original series (Khovanskii 1963). From the normal form series of Eqs. (37) and (38) we can compute the truncated fractions
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0023fig3.eps} \end{figure}](/articles/aa/full/2008/39/aa10023-08/Timg76.gif) |
Figure 3: Relative energy error along the major-axis orbit for two different truncations of the continued fraction at E=0.5. |
| Open with DEXTER | |
In Fig. 3, we plot the same quantities as in Fig. 2 now derived via the continued fraction truncations: the solid line is computed with
![]() and the dashed line with
and the dashed line with
![]() .
At this energy level, the prediction using
.
At this energy level, the prediction using
![]() begins to outperform that using
begins to outperform that using
![]() .
From Table 1 we observe that the performance of
.
From Table 1 we observe that the performance of
![]() is the optimal one when going to energies higher than 0.5 and is at least as good as that of CS90 for the same range of energy.
is the optimal one when going to energies higher than 0.5 and is at least as good as that of CS90 for the same range of energy.
As a first example of a boxlet, we consider the ``loop'' orbits for which we can use the 1:1 symmetric normal form to derive explicit solutions. For moderate ellipticities (q>0.7), loops ensue as the lowest energy bifurcation due to the 1:1 resonance between the frequency of oscillation along the short (y-axis) periodic orbit and that of a normal perturbation (Miralda-Escudé & Schwarzschild 1989). From Eq. (12), for the 1:1 resonance we have
![]() so that a normal form truncated at K2 is already able to produce loops. The bifurcation curve in the (q,E)-plane starts from the point (1,0) (Scuflaire 1995; Belmonte et al. 2007) and can be expressed as the series
so that a normal form truncated at K2 is already able to produce loops. The bifurcation curve in the (q,E)-plane starts from the point (1,0) (Scuflaire 1995; Belmonte et al. 2007) and can be expressed as the series
In the normalization variables, we have a solution in the form of Eq. (19) with
For the solutions in the physical variables, we first detrmine the transformations (22)-(24) with the generating function represented by Eq. (A.11) obtaining
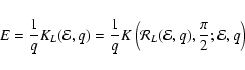 |
(61) |
| A1 | = | (66) | |
| A2 | = | (67) | |
| B1 | = | (68) | |
| B2 | = | (69) |
| a | = | (70) | |
| b | = | (71) | |
| c | = | (72) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0023fig4.eps} \end{figure}](/articles/aa/full/2008/39/aa10023-08/Timg125.gif) |
Figure 4: An orbit of the loop family at E=1.0 for q=0.9: dots correspond to the numerical solution; the continuous line corresponds to the prediction given by the continued fraction truncated at order 3; the dashed line that provided by the normal form truncated at order 3. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0023fig5.eps} \end{figure}](/articles/aa/full/2008/39/aa10023-08/Timg126.gif) |
Figure 5: The same orbit of the previous figure (dots) compared with the predictions truncated at order 5 (continued fraction, continuous line; normal form, dashed line). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0023fig6.eps} \end{figure}](/articles/aa/full/2008/39/aa10023-08/Timg127.gif) |
Figure 6: Relative energy error along the loop orbit with two different truncations of the continued fraction. |
| Open with DEXTER | |
The bifurcation of the banana orbit from the major-axis occurs along a curve in the (q,E)-plane starting from the point (1/2,0) (Scuflaire 1995; Belmonte et al. 2007). It can be expressed in terms of the series
In the normalization variables we have a solution in the form of Eq. (19) with
| (86) | |||
| (87) |
For moderate values of the bifurcation energy (and of orbital energy), corresponding to small values of q in the range indicated by the expression in Eq. (2), a simple approximation is given by the linear term in Eq. (73),
![]() ,
so that
,
so that
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0023fig7.eps} \end{figure}](/articles/aa/full/2008/39/aa10023-08/Timg156.gif) |
Figure 7: An orbit of the pendulum-like (banana) family at E=1.15 for q=0.6: the dots correspond to the numerical solution; the continuous lines correspond to the predictions truncated at order 3. |
| Open with DEXTER | |
With the choice of parameters mentioned above, in Fig. 7, we compare a numerical computation of the banana orbit (dots) with the analytic predictions (continuous lines) given by
![]() and
and
![]() .
This rational solution that originates in the continued fraction truncated at order 3, is characterized by a pair of singularities in
.
This rational solution that originates in the continued fraction truncated at order 3, is characterized by a pair of singularities in
![]() due to the presence of poles. However, the prediction is accurate overall in locating both the shape and extrema of the orbit and exceeds the accuracy of the prediction with the standard truncated series. In Fig. 9, we plot the corresponding
due to the presence of poles. However, the prediction is accurate overall in locating both the shape and extrema of the orbit and exceeds the accuracy of the prediction with the standard truncated series. In Fig. 9, we plot the corresponding
![]() (continuous line) over a half period: the abrupt increase in the relative error is evident at the poles of the solution.
(continuous line) over a half period: the abrupt increase in the relative error is evident at the poles of the solution.
In Fig. 8, we compare the numerical computation of the same orbit (dots) with the analytic predictions given by
![]() and
and
![]() .
The two predictions now almost overlap but a superior performance is achieved by the continued fraction truncation at the extrema of the orbit. In Fig. 9, we plot the corresponding
.
The two predictions now almost overlap but a superior performance is achieved by the continued fraction truncation at the extrema of the orbit. In Fig. 9, we plot the corresponding
![]() (dashed line) over a half period: the relative error is now lower than 20%, in contrast to the 30% for
(dashed line) over a half period: the relative error is now lower than 20%, in contrast to the 30% for
![]() .
.
| |
Figure 8: The same orbit as in the previous figure (dots) compared with the predictions truncated at order 5 (continuous lines): for more clarity, the y-scale has been expanded. |
| Open with DEXTER | |
A comparison with the results of CS90 is possible only in terms of the reconstruction of the shape and location of the orbit (we have used the same values of the parameters, when properly rescaled). We are able to determine that the accuracy of our analytic predictions is at least as good as that in CS90. There is no statement in CS90 about the ability of their solution in conserving energy.
We have shown how to construct approximate solutions for the main periodic orbits in the cored logarithmic potential. The guiding line has been that of exploiting normal-form expansions truncated to the first order incorporating the resonance of the given family of periodic orbits. In this way, analytic approximate solutions can be developed by a complete algorithmic procedure. Although all series are truncated to the first non-trivial orders, the solutions have a simple form only in the case of the axial orbits (normal modes). For the low-order boxlets (loops and bananas), even truncations at the first non-trivial order are cumbersome and require the use of an algebraic manipulator. However, further simplifications can be achieved if the algebraic solutions for actions and frequencies are expanded about the energy and ellipticity corresponding to the bifurcation of the family. In this case, simple expressions of the expansions can be derived, both as standard series and continued fractions.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{0023fig9.eps} \end{figure}](/articles/aa/full/2008/39/aa10023-08/Timg159.gif) |
Figure 9: Relative energy error along the banana orbit with two different truncations of the continued fraction. |
| Open with DEXTER | |
A comparison with the rational (Prendergast-Contopoulos) approach described by Contopoulos (2004), allows us to state the following conclusions: the two methods are almost equivalent in terms of the precision of the analytic prediction when evaluated to the same order (Contopoulos & Seimenis 1990). However, the normal form perturbation expansions, even if computationally heavy to compute, are completely algorithmic and analytic at every stage, whereas the evaluation of the coefficients in the rational expansions require the numerical solution of non-linear systems. We have shown that the analytic rational solutions obtained in this way offer a degree of reliability such that both loops and bananas are well reconstructed in both shape and dimension. We have extended the analysis of Contopoulos & Seimenis (1990) to check energy conservation along the boxlets: although for normal modes energy is conserved to within a few percent, for loops and bananas, at this level of approximation, it is not straightforward to achieve an accuracy better than 10%.
On the theoretical side, the usefulness of rational solutions can be explained in terms of the more rapid convergence performance of the truncated continued fractions. They are important as a resummation method of the series expansions produced in the usual way by the normalization approach. The generality of the approach enables us to confront with higher-order resonances and correspondingly higher commensurable boxlets.
In addition to the formal and algorithmic improvements, we remark on the relevance of this work to specific problems in galactic dynamics. The study of orbits in non-axisymmetric potentials is usually performed numerically; however, an exhaustive study with conventional integration methods is computer-intensive and difficult to interpret (Touma & Tremaine 1997). The availability of simple and accurate analytical recipes can be useful in several contexts in which periodic orbits and boxlets play an important role: we mention the study of the parameter space of non-axisymmetric discs (Zhao et al. 1999; Zhao 1999) and the orbit structure around massive black holes in galactic nuclei (Sridhar & Touma 1999). Even more promising is the possibility of deriving accurate solutions for periodic orbits in the triaxial case with and without rotation, for which the analysis is still at the level of the first-order averaging method applied to the 1:1:1 resonance by de Zeeuw (1985).
Acknowledgements
We thank G. Contopoulos for inspiring our original interest in this problem.
To implement the normalization algorithm, the original Hamiltonian (6) is rescaled according to
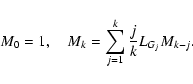 |
(A.5) |
| (A.7) |
Concerning these formulas, two remarks are in order: