A&A 489, 1091-1105 (2008)
DOI: 10.1051/0004-6361:200809649

Young star clusters in interacting galaxies - NGC 1487 and NGC 4038/4039

S. Mengel¹ - M. D. Lehnert² - N. A. Thatte³ - W. D. Vacca⁴ - B. Whitmore⁵ - R. Chandar⁶

1 - European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748 Garching, Germany
2 - Observatoire de Paris, CNRS, Université Denis Diderot, 5 place Jules Janssen, 92190 Meudon, France
3 - University of Oxford, Dept. of Astrophysics, Denys Wilkinson Building, Keble Road, GB-Oxford OX1 3RH, UK
4 - Stratospheric Observatory for Infrared Astronomy/Universities Space Research Association, NASA Ames Research Center, Moffett Field, CA 94035, USA
5 - Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, Maryland 21218, USA
6 - The University of Toledo, Toledo, OH 43606, USA

Received 25 February 2008 / Accepted 9 May 2008

Abstract
We estimate the dynamical masses of several young ($\approx$10 Myr) massive star clusters in two interacting galaxies, NGC 4038/4039 (``The Antennae'') and NGC 1487, under the assumption of virial equilibrium. These are compared with photometric mass estimates from K-band photometry assuming a standard Kroupa IMF. The clusters were selected to have near-infrared colours dominated by red supergiants, hence old enough to have survived the earliest phases of cluster evolution when the interstellar medium is rapidly swept out from the cluster, supported by there being no obvious H$\alpha$ emission associated with the clusters. All but one of the Antennae clusters have dynamical and photometric mass estimates that are within a factor $\approx$2 of one another, implying both that standard IMFs provide a good approximation to the IMF of these clusters and that there is no significant extra-virial motion, as would be expected if they were rapidly dispersing. These results suggest that almost all of the Antennae clusters in our sample have survived the gas removal phase as bound or marginally bound objects. Two of the three NGC 1487 clusters studied here have  $M_{\rm dyn}$ estimates that are significantly greater than the photometric mass estimates. At least one of these two clusters, and one in the Antennae, may be actively in the process of dissolving. The process of dissolution contributes a component of non-virial motion to the integrated velocity measurements, resulting in an estimated $M_{\rm dyn}$ that is too high relative to the amount of measured stellar light. The dissolution candidates in both galaxies are amongst the clusters with the lowest pressures/densities measured in our sample.

Key words: galaxies: interactions - galaxies: star clusters

1 Introduction

Young extragalactic star clusters are found in large numbers in interacting galaxies (e.g. Holtzman et al. 1992; Whitmore et al. 1999; Zepf & Ashman 1999; Bastian et al. 2006; Trancho et al. 2007; Mengel et al. 2005; Whitmore et al. 1993), as well as in other environments like normal spirals (Larsen et al. 2004; Larsen & Richtler 2004). Despite numerous intensive studies over the past fifteen years, the investigations of these clusters have raised more questions than they have answered.

One of the most obvious, but arguably most interesting, questions is how many of the young star clusters (YSCs) survive to old age (i.e. become globular clusters), and also what happens to the others? Most likely many clusters disperse, contributing to the general field star population. However, it remains uncertain what fraction of the general field population originated in stellar clusters.

Several studies (e.g. Bastian et al. 2006; Larsen et al. 2004) have shown that the properties of (at least some) young clusters are consistent with their being the progenitors of what we see as globular clusters today. Is it possible to identify in a population of extragalactic young star clusters those that will survive for a Hubble time? Or, to phrase the problem differently, how and with which properties was the host population of the globular clusters in today's galaxies formed?

In environments as different as those found in mergers like NGC 4038/4039 and the Milky Way, it seems that, at least up to around 100 Myr, 50-90% of the star clusters are destroyed within each decade of time. This effect has been named ``infant mortality'' (e.g. Fall et al. 2005; Lada & Lada 2003). The current hypothesis (Goodwin & Bastian 2006; Lada et al. 1984; Hills 1980; Boily & Kroupa 2003a; Whitmore 2007; Boily & Kroupa 2003b; Fall et al. 2005) is that the gas removal caused by stellar winds and supernovae unbinds some of the clusters, and that this process is only dominant out to roughly 30 Myr. Later the much slower and less destructive process of two-body relaxation becomes dominant and dissolves many of the remaining clusters.

Table 1: Integration times of all images and spectra used for the main analysis of the clusters.

More observational data are necessary to get a clearer idea of the dynamical processes at work during cluster formation and destruction. The cluster populations analysed so far with respect to their ages have not been corrected for the (unknown) cluster formation history. However, all studies which analyse statistically significant numbers of high-mass clusters (NGC 4038/4039, Mengel et al. 2005; Fall et al. 2005, M 51; Bastian et al. 2005) are of interacting systems where the star/cluster formation history is neither constant, nor a delta burst, but rather some more complex, unknown function of time. This certainly affects the age distribution of clusters and hence the destruction rate derived from it.

A different approach targets individual star clusters for intense studies of their physical parameters, with the goal of using these paramters to decide whether a star cluster is doomed or a candidate for a future GC. Our original study (Mengel et al. 2002) was of this type. We assumed that clusters are in virial equilibrium, since at ages of around 8 Myr, they have survived for many crossing times. Other studies adopted a similar assumption (Ho & Filippenko 1996a; Sternberg 1998; Ho & Filippenko 1996b). However, in the view of the high cluster destruction rate derived from recent studies, this assumption may not be universally applicable.

In this paper, we have expanded the sample of clusters for which we have performed individual and detailed analyses. With a larger sample, we hope to be able to find a diagnostic to determine the dynamical state of an extragalactic, and hence only barely resolved, star cluster without requiring high resolution spectra. Should that not be possible, we hope to identify and distinguish those techniques which might lead to more profitable results from those that are unfeasible.

We targeted the galaxies NGC 4038/4039 and NGC 1487. While the first, also called ``The Antennae'', is one of the best studied nearby mergers, NGC 1487 is less well known. It is a peculiar galaxy, with two faint tails that trace an interaction far earlier than the recent starburst. Lee & Lee (2005) conclude from their two-colour analysis of the cluster system that the merging process could have taken place 500 Myr ago. Most of the star clusters are found in three or four ``condensations'', and the brightest clusters, like those targeted for our study, are much bluer than the larger population of fainter clusters. In total, Lee & Lee (2005) found more than 500 cluster candidates in HST/WFPC2 data. Although located at approximately half the distance to the Antennae, NGC 1487 is considerably fainter: its total magnitude is comparable to the LMC.

Previous work (Mengel et al. 2002; Ho & Filippenko 1996b) has shown that stellar velocity dispersions in YSCs are typically $\approx$15 km s^-1, and therefore detailed studies of such systems require medium- to high spectral resolution observations, which are only achievable with 10 m class telescopes. Apart from near-infrared imaging for the cluster photometry, we need an estimate of the cluster size, which for objects at distances between 10 and 20 Mpc and sizes of 2-4 pc requires very high spatial resolution.

  
2 Observations and data reduction

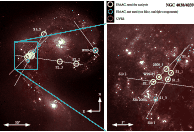	Figure 1: False-colour image of NGC 4038/4039 with HST/ACS F814W covering both the blue and the green channel, and VLT/ISAAC Ks in the red channel. Clusters that are presented in this publication are marked, using the naming convention as in W99 (those which had been listed there), or according to slit number.
Open with DEXTER

In this section we present the ground based imaging, and followup spectroscopic data obtained for the K-band bright clusters with strong CO absorption (as a consequence, the ages span a narrow range around 8.7 Myr). Table 1 lists integration times for both imaging and spectroscopy. Supporting archival images taken with the Hubble Space Telescope (HST) are also described.

  
2.1 SOFI and ISAAC imaging data

Imaging of NGC 4038/4039 was performed using ISAAC at the VLT in ON/OFF mode during the nights 15.04.2001 (Ks-band) and 16.04.2001 (CO-bandhead filter). The target fit completely onto the detector (0 $.\!\!^{\prime\prime}$1484/pixel, total field size 2 $.\mkern-4mu^\prime$5 $\times$ 2 $.\mkern-4mu^\prime$5). Seeing was excellent during both of these photometric nights (the FWHM of the PSF from coadded frames is <0 $.\!\!^{\prime\prime}$4). SOFI/NTT imaging of NGC 1487 and the Antennae covered J, H, Ks broad- and Br$\gamma$, CO2.32 $\mu$m, Pa$\beta$, and continuum NB2.28 $\mu$m, NB1.215 $\mu$m and NB2.195 $\mu$m narrow bands. Here the field size was roughly twice that of ISAAC (4 $.\mkern-4mu^\prime$9 $\times$ 4 $.\mkern-4mu^\prime$9, with a pixel size of 0 $.\!\!^{\prime\prime}$292). With the target spanning only a bit more than 2$^\prime$, an efficient on-chip offset pattern could be used. The nights were clear, and the FWHM of the PSF was between 0 $.\!\!^{\prime\prime}$7 and 1 $.\!\!^{\prime\prime}$1 for the different filters.

Reduction of the ISAAC and SOFI broad- and narrow band data was performed using the IRAF package. This included dark and sky subtraction (either using the median of several neighbouring sky images or, where this led to residuals, doing pairwise subtraction), and flat fielding by a normalized median of all sky frames. All of the on-source frames were slightly offset with respect to each other, in order to minimize the effect of pixel defects. Therefore, they had to be shifted to a common location before using the imcombine task (setting the minmax rejection algorithm to reject the highest and the lowest pixel) to combine the single frames.

The photometric standards GSPC S279-F (Ks = 12.03 mag) and S301-D (Ks = 11.79 mag) from Persson et al. (1998) were used for flux calibration of all the broad-band data. S270 was used for the ISAAC data and S301 was used for the SOFI data. The resulting Ks zeropoints were 24.28 mag and 22.27 mag, respectively.

The target clusters were selected to have a high CO(3-1) band-head absorption equivalent width (which is covered by the ISAAC and SOFI NB2.34 $\mu$m filter), which revealed clusters at ages $\approx$10 Myr, where the near-infrared emission is dominated by red supergiants. Clusters at ages that are dominated by very hot young stars do not show photospheric absorption features, or their absorption lines are rotationally broadened, making measurement of their stellar velocity dispersion very difficult. Locations of the selected clusters are shown in Figs. 1 and 2. They must be detected in at least the I-band with HST, in order to measure their size (see Sect. 3.2).

Figure 2: Left: NGC 1487 false colour image, with HST/WFPC2 F435W in the blue, HST/WFPC2 F814W in the green, and NTT/SOFI Ks in the red channel. HST images were smoothed to the FWHM of the SOFI images. Right: false-colour image with the SOFI Ks image in the red, and HST ACS/HRC F814W (not smoothed, therefore substantially better spatial resolution) in green/blue. The clusters for which we present spectra are labelled in the image on the right: clusters 1-3 were observed with ISAAC, cluster 1 additionally with UVES. During the largest fraction of the observations, the slit was oriented such that it covered all three clusters. Cluster 3 was covered during another integration that accounts for roughly 20% of its exposure time (see Table 1).

Open with DEXTER

  
2.2 Spectroscopic data

Spectroscopy was performed with ISAAC at VLT-ANTU in 04/2000, 04/2001 and 12/2001. ISAAC was configured to have an 0 $.\!\!^{\prime\prime}$3 wide slit, and a central wavelength of 2.31 $\mu$m with a total wavelength coverage from 2.25 to 2.37 $\mu$m. This was sufficient to include the ¹²CO (2-0) and (3-1) absorption bands at a spectral resolution $\lambda/\Delta\lambda \sim9000$. Observations of late-type supergiant stars were taken so that they could be used as templates for the determination of the velocity dispersions. Observations were performed by nodding along the slit and dithering the source position from one exposure to the next. B5V stars were observed several times during the night and were used to correct for the effects of atmospheric absorption.

The reduction of ISAAC spectroscopy data also made use of the IRAF data reduction package. Sky subtraction was performed by constructing the median of 3-4 frames acquired at the off-source (nodded) position and subtracting it from each source frame. If this procedure resulted in strong residuals, we simply subtracted frames in a pairwise manner (on - off). This was followed by a rejection of cosmic ray hits and bad pixels. In order to correct for tilt and slit curvature, the peak of the stellar spatial profile was traced and the displacement as a function of wavelength was fitted with a polynomial. Wavelength calibration was performed using a combination of arc discharge lamp observations and night sky lines for the identification of wavelengths.

Multiple dark-subtracted, flattened, and sky-subtracted frames for an individual object were combined by shifting-and-adding, including a rejection of highest and lowest pixels. The object spectra were then extracted from user defined apertures. The limits of the apertures were chosen to be the points where the counts in the combined spectrum had dropped to 1/10 of the peak value. The residual background (below $\approx$7% of the peak intensity for all clusters) on either side of the object aperture was fit with a line and subtracted.

For cluster NGC 1487-3, care was required in both the slit positioning and the spectrum extraction due to the nearby faint companion cluster. For most of the exposure time, the slit was oriented such that clusters 2 and 3 were lined up in this slit; in this orientation, the brightest cluster 1 was slightly offset from the slit (see Figs. 2 and 11). For 3600 s, we integrated in an almost perpendicular slit orientation that included only cluster 3. Despite trying to avoid flux from the fainter companion from entering the slit or the extraction aperture, and excellent seeing during most of the exposure time, it is likely that some unknown contribution from the companion is present in our final spectrum for cluster NGC 1487-3 (see also Sect. 3.3).

An atmospheric calibrator (B5V) was observed and reduced in the same way as the target and used to divide out the atmospheric absorption features from the spectra.

Table 2: Radial velocities and J2000 coordinates of the Antennae clusters.

Table 3: Absolute extinction corrected magnitudes, ages, velocity dispersion $\sigma$, projected half-light radius $r_{\rm hp}$. $M_{\rm dyn}$ with 1$\sigma$-uncertainties $\Delta M$, photometric mass $M_{\rm ph}$.

Results of the analysis of UVES data acquired for [W99]-2 and NGC 1487-1 were published by Mengel et al. (2002,2003). We refer the reader to those papers for a description of the data reduction and analysis. A comparison between the UVES and ISAAC results will be presented below.

  
2.3 Hubble space telescope imaging data

We use imaging observations taken with HST to estimate the size of each cluster. Observations of NGC 1487 were obtained as part of Hubble Space Telescope Cycle 11 observations (Proposal-ID 9473, PI: Vacca). We are using the F814W and F435W Advanced Camera for Surveys/High Resolution Channel (ACS/HRC) images. For the Antennae clusters we use HST/ACS-WFC images obtained as part of Proposal-ID 10188 (PI: Whitmore) in the F550M and F814W filters. In addition, we took advantage of higher resolution ACS/HRC images in the F555W filter of a supernova in the Antennae (Proposal ID 10187, PI: Smartt), which happened to include one of our target clusters ([W99]-2).

For all HST data, we use the pipeline reduced images. Total integration times are listed in Table 1. The total field coverage for the Antennae WFC F814W and F550M images was roughly 3 $.\mkern-4mu^\prime$5 $\times$ 3 $.\mkern-4mu^\prime$5, at a pixel size of 0 $.\!\!^{\prime\prime}$05/pix. The HRC images taken for NGC 1487 and the Antennae supernova had a total field size of around $31\hbox{$^{\prime\prime}$ }\times 31\hbox{$^{\prime\prime}$ }$, at a pixel size of 0 $.\!\!^{\prime\prime}$027/pix.

For photometry, we use the photometric zeropoint determined by De Marchi et al. (2004) and Sirianni et al. (2005). The reduced HST images were combined with our Ks-band images in order to create the two-colour-images shown in Figs. 1 and 2.

  
3 Analysis

  
3.1 Velocity dispersion measurements

For each cluster spectrum we estimated the Gaussian velocity dispersion $\sigma$ from the CO absorption features in the following way. An appropriate stellar template spectrum (described below) was broadened by Gaussian functions of variable $\sigma$, ranging from 0 to a few 100 km s^-1, and shifted in wavelength by radial velocities between 1400 and 1800 km s^-1. The resulting set of broadened templates were then compared with the cluster spectrum. The best fit was determined by evaluating $\chi^2$ and then searching for the minimum of the function $\chi^2$($v_{\rm r}$, $\sigma$) using a simplex downhill algorithm. Radial velocities are given in Table 2, velocity dispersions in Table 3.

It is important that the template spectrum be a good overall match in terms of stellar features to the cluster spectrum. For a star cluster that formed $\sim$10 Myr ago, late K through early M supergiant stars are expected to provide the largest contribution to the 2.3 $\mu$m flux. However population synthesis models (Leitherer et al. 1999) also show that hot main sequence stars will make a non-negligible contribution to the flux at this wavelength. Since hot O and B-type stars have an essentially featureless spectrum in our region of interest, they only represent a diluting continuum that decreases the equivalent width of the CO band-heads. This has the effect of shifting the apparent dominant stellar type towards higher effective temperatures. Starting out with a template spectrum with weak CO features leads to very low velocity dispersions, while the the opposite is true if an M5I star (which has strong band-heads) is used, with substantial differences in the results (ranging from a few up to $\approx$30 km s^-1).

We believe that no significant bias has been introduced through the selection of a stellar template and/or the wavelength range that was considered, because we have a large suite of templates that allowed us to find a good match for each cluster. For a good match the best fitting velocity dispersion was essentially independent of the selected wavelength range (see Mengel et al. 2002, for details). While we cannot rule out slight mismatches between template and cluster spectra, particularly for the low-SNR clusters S2_3 and S1_5, these should only have a slight effect on our velocity dispersion measurements, and hence $M_{\rm dyn}$ estimates.

The determination of the velocity dispersion from the UVES optical echelle data used the same procedure as for the ISAAC spectra, relying on the Calcium Triplet around 8500 Å, but also using the MgI absorption feature at 8800 Å and other weaker metal absorption lines between 8400 and 9000 Å.

Clusters [W99]-2 and NGC 1487-1 were observed with both instruments, ISAAC and UVES, in order to check the consistency of the final velocity dispersion measurements. The agreement was excellent for the Antennae cluster ( $\sigma = 13.9 \pm 2.0$ km s^-1 from ISAAC and $\sigma = 14.3\pm 0.5$ km s^-1 from UVES) and reasonable for NGC 1487-1 ( $\sigma = 12.0\pm2.0$ km s^-1 and $\sigma = 15.4\pm2.0$ km s^-1), revealing no strong systematic instrumental effect.

Our velocity dispersion measurements are summarized in Table 3. We find a range from about 7 km s^-1 to more than 20 km s^-1. For the optical echelle data the instrumental resolution is $\sigma_{\rm instrument}=3.2$ km s^-1, ensuring that the cluster line profiles are always well-resolved. The situation for the near-IR data is somewhat less straightforward, because the instrumental resolution is $\sigma_{\rm instrument}=14.2$ km s^-1, and some of our measurements lie below this value. However, as shown in Mengel et al. (2002) and Fig. 3, results are reliable and reproducible down to approximately half this value.

Figure 3 supports the assumption that the possibility to measure velocity dispersions down to half the instrumental resolution originates in the large amount of signal contained in the CO bandheads. We used our stellar spectra to create artificially broadened, noisy spectra (100 times for each sampled input velocity dispersion) and re-determined $\sigma$. We used two different wavelength ranges of equal length, one including the CO bandhead, and one that only included several metal absorption lines. The fit using the CO region has a standard deviation that is $\approx$five times smaller than that from the other region. Mean fit values from the two different wavelength regions begin to deviate around $\sigma=16$ km s^-1, with substantial deviations found below 10 km s^-1. As Fig. 3 demonstrates, the CO bandhead region allows reliable determinations of the velocity dispersion for values as low as $\approx$6 km s^-1. Since all of our measured values for the clusters in our sample are above this limit, we believe they should be valid.

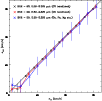	Figure 3: Results of the fits of artificially broadened spectra that had noise added corresponding to signal-to-noise-ratios ( SNRs) of 50 and 20, respectively (where SNR $\approx$ 20 is the SNR obtained for most of our clusters). At our typical S/N, strong deviations are only expected at less than half of the resolution of our data (or <6-7 km s-1).
Open with DEXTER

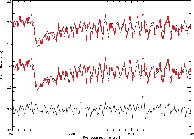	Figure 4: ISAAC spectrum of NGC 1487-1 with a good fit (using an M5I template spectrum) with a velocity dispersion of $\sigma =13.7$ km s-1 as the bottom spectrum, and a bad fit (11 km s-1) at the top. The residuals are for the good fit.
Open with DEXTER

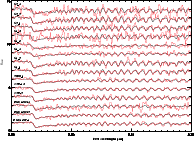	Figure 5: All ISAAC spectra, overplotted with their best fits, with labels. The region shown here generally provided the best fit.
Open with DEXTER

Figure 6: Original image, fit and residuals for two clusters (S2_2 and NGC 1487-1) for the best and a bad fit each. Pixels deviating substantially from the radial median are excluded from the fit and therefore expected to show up in the residuals, for example the two fainter objects in the top left corner of S2_2. The better fits are characterised by a smoother distribution at the central location of the cluster. For each cluster, the images are shown with the same greyscale range.

Open with DEXTER

Figures 4 and 5 show some of the fits to the observed cluster spectra. Figure 4 shows a good fit in the middle (with the corresponding residuals at the bottom), and a bad fit at the top, Fig. 5 shows the best fits for all our spectra. In general, we obtained good and stable fits for the clusters, even - surprisingly - for the low SNR spectra for S1_5 and S2_3.

  
3.2 Cluster sizes

Cluster sizes were determined from the ACS images using the routine ishape, implemented in the data reduction package baolab, developed by Larsen (Larsen 1999). The clusters all appear slightly-to-well resolved in the HST images. ishape convolves a user-provided PSF with an analytic cluster profile, and determines the minimum $\chi^2$ for a range of sizes using a simplex downhill algorithm. Outside of a clean radius, which we set to 3 pixels, ishape rejects pixels that deviate strongly from the median value of pixels at the same radius. The fit is performed out to a radius which we set to 10 pixels for most clusters, 12 pixels for [W99]-2 and N1487-1 (which were the brightest clusters of each target, therefore the SNR was sufficient out to a larger radius). We have taken into account the ellipticity that resulted for the best fit model, and determined the projected half-light radius that would correspond to a spherical model by using the average of $r_{\rm min}$ and $r_{\rm max}$. The general validity of this approach remains to be verified, but is currently justified by geometric considerations and some numerical integrations (Larsen 2003). We converted the output FWHM from ishape to a half-light radius by applying the appropriate concentration-dependent conversion factor, as described in Larsen (2001). We convert these effective radii from arcseconds to parsec by assuming distances of 19.3 Mpc (Antennae) and 9.3 Mpc (NGC 1487).

For the NGC 1487 ACS/HRC data, we created our PSF from archival data of a moderately bright star (same filter and camera as the science data) that were obtained for a completely different purpose (Proposal-ID 10198, PI: Wozniak). The Antennae ACS/WFC data contained several foreground stars that we used to generate a PSF. Despite careful shifting-and-adding, a PSF created from more than two or three stars was always slightly broader than the original PSFs. Therefore our PSF was created from only three stars. For the Antennae ACS/HRC data, it was a lucky coincidence that the supernova was located in the direct vicinity of cluster [W99]-2, thereby providing a suitable PSF reference.

Our PSFs had the following characteristics: for the Antennae images, the FWHM was 2.0 pix (0 $.\!\!^{\prime\prime}$10) for WFC/F814W, 1.89 pix (0 $.\!\!^{\prime\prime}$095) for WFC/F550M, and 2.48 pix (0 $.\!\!^{\prime\prime}$066) for HRC/F555W, where the first two were using the WFC, and the third the HRC. Only the PSF for the HRC/F555W image showed a slight deviation from a circularly symmetric Gaussian profile; there was a slight (5% of the peak) increase in the count level $\approx$3.5 pix north of the peak. The FWHM values for the PSFs used for the NGC 1487 images were 2.58 pix (0 $.\!\!^{\prime\prime}$07) in the F814W filter, and 1.97 pix (0 $.\!\!^{\prime\prime}$053) in the F435W filter. Apart from the strong Airy ring in the F814W PSF, they showed no peculiarities.

We ran ishape for distinct values of c (5, 15, 30, 100, 300), and additionally Moffat15, Moffat25 and Gaussian profiles. Best fits were typically obtained for (King 1962) profiles, with concentration parameters between c = 5 and 300. We did not generally do a two-parameter fit (optimizing c and $r_{\rm hp}$ at the same time), because we believe that this increases the risk of getting trapped in a local minimum. But for two clusters ([W99]-2 and S2_1) we did implement a two-parameter fit, and obtained satisfactory results (the concentration for the best fit lay between the two best fixed-c fits).

Examples for two cluster fits are shown in Fig. 6. The projected half-light radii that resulted from the optimization in the two different filters are listed in Table 4, together with concentrations. The agreement between the filters was excellent for all the NGC 1487 clusters, [W99]-15 and S1_2, and reasonable for [W99]-2 and S2_2. For reasons that are not clear, the agreement was not very good for three clusters, S1_5, S2_1 and S2_3. From visual inspection, the fit in F550M looked much better for S2_1, which is why we use this fit as the final value. But for the two other clusters, all fits look quite reasonable, and we used averages (with rather large uncertainties) as final values. Cluster sizes range from $\approx$1 - 8 pc, with a median size of 2.9 pc. These values are fairly typical for young star clusters (e.g. Lee et al. 2005; Larsen 2004).

  
3.3 Clusters with multiple components

For all of our clusters, faint additional point sources (or slightly resolved objects) can be detected within the slit width of 0 $.\!\!^{\prime\prime}$3 (see Fig. 7). While in most cases, these objects contribute only a few percent of the flux of the primary, we have indentified several objects where nearby clusters might have an effect on the results, but for which the magnitude of the effect is difficult to quantify. Two of the clusters (S1_3 and S1_4) were discarded from further analysis for this reason. The multiple components that show up in the ACS image (see Fig. 7) are also obvious, even though not as well resolved, in the ISAAC K-band image as extended and elongated light distributions.

This is not the case for the other two Antennae clusters with multiple components in the F814W image: for both, S1_1 and 2000_1, the light distribution looks symmetric, and there is no obvious indication of multiplicity. This could mean that the companion clusters are bluer than the main component and therefore their contribution in K-band, where we estimate both the velocity dispersion and the photometry of the cluster, may be negligible. Nevertheless, we have marked these clusters in all our analysis plots, even though their properties do not turn out to be unusual in any obvious way.

Based on the ACS images, we suspect that a nearby companion, at a distance of only 0 $.\!\!^{\prime\prime}$5 from N1487-3, may have contaminated our spectra and compromised our measured velocity dispersion. While we took into account the multiplicity when performing the photometric measurements, and derived a flux for the primary component to estimate the magnitude and photometric mass of the cluster, some flux from the companion was present within the slit and cannot be removed. We expect the contamination to have been relatively minor for the larger fraction of the integration time where the seeing was excellent (FWHM 0 $.\!\!^{\prime\prime}$3-0 $.\!\!^{\prime\prime}$4 in K-band), and more pronounced during the $\approx$30% of the integration time where the seeing was larger (FWHM 0 $.\!\!^{\prime\prime}$5-0 $.\!\!^{\prime\prime}$6 in K-band). We believe that we see the impact of an erroneously high velocity dispersion (caused by the different radial velocity of the companion cluster) in the very high ratio of $M_{\rm dyn}$/ $M_{\rm ph}$.

  
3.4 Dynamical cluster masses

The dynamical mass of each cluster is estimated using

$$M_{\rm dyn}=\frac{\eta F \sigma^2 r_{\rm hp}}{G}$$ (1)

where $\eta = \eta(c)$ is a factor that depends on the distribution of the stellar density with radius (described below), F = F(t) is a factor that evolves with time as a consequence of mass segregation in the cluster, $\sigma$ is the stellar velocity dispersion, $r_{\rm hp}$ is the projected half-light radius, and G is the gravitational constant. The function $\eta$ depends on both the cluster concentration, c, and on the mass-to-light ratio as a function of radius. We assume that it is justified to split these two dependencies into two separate parameters: $\eta = \eta(c)$ and F = F(t). To generate the relationship between the coefficient necessary to estimate the mass of the clusters, $\eta$, and the ratio of the tidal radius to the core radius (the concentration parameter, c) for a King model (Fig. 8), we solved numerically Poisson's equation yielding the density distribution for a variety of W₀ (which is the central potential divided by the velocity dispersion and characterises a King model; see e.g., Eqs. (4)-(131) from Binney & Tremaine 1987). Integrating the density profile with radius provided the mass coefficient, $\eta$. For all clusters in NGC 4038/39 and NGC 1487, the concentration values derived from the profile fitting implied a value of $\eta$ between 5.6 and 9.7.

Table 4: Projected half-light radii of all clusters that do not have very obvious multiple components.

The factor F = F(t) describes how $\eta$ varies if the mass-to-light ratio varies as a function of radius. As described in Fleck et al. (2006) their models indicate that the first 10 Myr of cluster evolution - at least for dense clusters like those in our sample - result in a steep increase in the factor $\eta$ in Eq. (1), and a more gentle increase after that. This effect is caused by mass segregation, which leads to a decrease in half-light radius, while the total mass and the half-mass radius are largely unchanged - i.e. the mass-to-light ratio varies with radius. Even though the degree of mass segregation is expected to depend on several parameters (density, IMF, upper mass cutoff, initial radius, number of stars), and only the density can be determined a priori, we think that it should be expected for our very dense, 10 Myr clusters.

We applied an average factor of $F = \eta_{\rm t} / \eta_0 = 1.3$ (derived from Fig. 14 in Fleck et al. 2006) to all our clusters. While mass segregation is expected theoretically, it should be noted that our limited spatial resolution makes it impossible to determine observationally whether these clusters have undergone mass segregation or not, because statistics and crowding will cause the highest-mass stars to appear mass segregated in any strongly centrally concentrated cluster (Ascenso 2008).

The dynamical models do not take into account the contribution of stellar binary orbital motion to the velocity dispersion; however this contribution is expected to be negligible, due to the large masses of the clusters studied here (Kouwenhoven & de Grijs 2007).

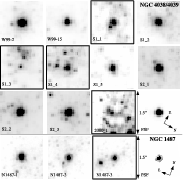	Figure 7: HST-ACS/WFC F814W images of the clusters used for our analysis. The clusters that are marked with boxes are those which have an obvious strong companion or which consist of multiple objects. This could have an impact on the measured velocity dispersion.
Open with DEXTER

  
3.5 Photometric ages and masses

We used our K-band images (see Fig. 9 for blowup images of the individual clusters) to estimate the mass of each cluster, since these suffer from significantly less extinction than the V band. We performed aperture photometry in two different ways:

Since many of our clusters sit atop a variable background (see Fig. 10), and only a small number of clusters needs to be treated, we used a manual technique of choosing an aperture size individually for each cluster where the signal from the cluster was low enough to be comparable to the noise, and selecting a background region to be representative of the background expected at the cluster location. We chose aperture sizes ranging from 1 $.\!\!^{\prime\prime}$2 to 1 $.\!\!^{\prime\prime}$8, roughly 3 to 4.4 times the FWHM of the PSF in the Antennae images. For NGC 1487, we adopted an aperture size of 3 $^{\prime\prime}$, which was also roughly four times as big as the FWHM of the images. For the clusters in NGC 4038/4039, we also computed the magnitudes using a curve of growth technique (see Mengel et al. 2005, for details). The two techniques gave identical results, except for three clusters: S1_1 is fainter by 0.1 mag using the manual technique, S1_2 is 0.2 mag brighter. Differences for those two clusters could be expected, because they are located right on the edge of a variation in background intensity. S2_1 is also brighter by 0.2 mag using the manual approach, and here the reason is not obvious. In all three cases, we used the manually determined value, but increased the uncertainty estimate in the photometry to account for the differences from the two methods.

Since the diffuse light in NGC 1487 is smooth, and none of the clusters have neighbouring clusters that might affect the photometry, we are confident in the final magnitudes derived for clusters NGC 1487-1 and NGC 1487-2. For cluster NGC 1487-3, the K-band photometry is complicated by the fact that there is a second, fainter cluster so close by that the two are only marginally separated in our near-IR images. The large uncertainty in the photometry is due to confusion from this neighboring source. To assign a K-band magnitude to the brighter cluster, we used an aperture that includes both clusters and assumed that the relative brightnesses of the two clusters are the same in I-band and K-band. The ratio of the peak counts in the acquisition image shown in Fig. 11 supports this assumption.

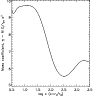	Figure 8: Variation of the mass coefficient, $\eta$, as a function of the cluster concentration, c ( $c = r_{\rm t} / r_0$). r0 is the King radius, and $r_{\rm t}$ is the tidal radius of the King model. Our clusters cover the range from $\log(c) = 0.7 {-} 2.5$.
Open with DEXTER

The absolute K band magnitudes range from -13.4 mag to -17.4 mag. The absolute extinction corrected K-band magnitudes are converted to $M_{\rm ph}$ by comparison with the absolute K-band magnitude predicted by a Starburst99 model for a 10⁶ $M_{\odot}$cluster (instantaneous burst, Kroupa IMF, solar metallicity) of the same age. Resulting photometric masses are listed in Table 3.

All clusters are fairly massive, at least compared to young star clusters in the Milky Way. For interacting galaxies, these luminosities, corresponding to photometric masses between $8\times10^4$ $M_{\odot}$ and $4.5\times10^6$ $M_{\odot}$, are not unusual. Furthermore, we selected some of the most massive clusters specifically, because, at any given age, they are the most luminous and therefore most easily accessible to high resolution spectroscopy.

The fact that the clusters in NGC 1487 are generally fainter and less massive than those in the Antennae is expected from simple statistical considerations. NGC 1487 has a relatively small number of clusters compared to the Antennae - only 1-10%. Because we targeted clusters that are amongst the brightest in each galaxy, the likelihood that a system like NGC 1487, produces one or more clusters comparable to the brightest clusters in the Antennae, is comparatively low (e.g. Whitmore 2000,2007).

We estimated the age and extinction of each cluster by comparing the broadband filter measurements, the CO(3-1) bandhead, and Br$\gamma$ and Calcium Triplet (CaT, from UVES spectroscopy) equivalent widths with the predictions of the Starburst99 (Leitherer et al. 1999; Vazquez & Leitherer 2005) evolutionary synthesis models.

Extinction turned out to be relevant, at least in K-band, only for two clusters, S1_1 (A_V=4.6 mag) and 2000_1 ( $A_{V} \approx 10$ mag). For all the other clusters, A_V is below 2 mag (with the uncertainties $\Delta A_{V} \leq 0.5$ mag), which translates to A_K below $\approx$0.2 mag, and makes potential uncertainties of $\Delta A_{K} < 0.05$ mag small in relation to the overall photometric uncertainty.

For all clusters, we determined a best fit age between 8 and 9 Myr. For clusters with ages $\approx$8.5 Myr, an alternative solution exists at 10.5 Myr for all cluster properties that are influenced by red supergiants (M_K, $W_{\rm CO}$, $W_{\rm CaT}$, V-K, etc.) because the quantities are double valued at around this age. Since M_K is the same for both ages, all our conclusions remain unchanged, because $M_{\rm ph}$, L_K/ $M_{\rm dyn}$etc. are unaffected by this uncertainty in age.

  
4 Discussion and implications

An underlying assumption of any mass estimate based on the velocity dispersion is that the cluster is self-gravitating (i.e., bound). The age of our clusters, $\approx$10 Myr, is much older than their estimated crossing times ( $t_{\rm cross} \sim r_{\rm hp}/\sigma$) of 1-few $\times$10⁵ yr, indicating that they have already survived for 20-50 crossing times. However, recent results suggest that a large fraction of clusters becomes unbound and disperses within $\approx$10-20 Myr due to the removal of interstellar material; therefore it remains possible that the clusters studied here may not be in virial equilibrium. If cluster stars are dispersing, then this extra-virial motion will lead to a measured velocity dispersion that is higher than would be measured for a bound cluster of similar mass.

One way to assess whether our clusters are gravitationally bound or show evidence for non-virial motion is to compare the L_K/Mdetermined from velocity dispersion measurements with those predicted by population synthesis models. In essence, this is a comparison of the dynamical and photometric masses. A cluster with L_K/M(based on dynamical measurements) lower than the photometric estimates (from the age of the cluster and its measured stellar light), can point to non-virial motion resulting from an expanding, dissolving cluster. In Fig. 12 we compare our estimated cluster ages and L_K/M for the Antennae and NGC 1487 clusters, with the predictions for an instantaneous burst, solar metallicity model from Starburst99 (Leitherer et al. 1999). We show predictions for L_K/M assuming two different IMFs: a Kroupa IMF (solid line) and a Salpeter IMF with $0.1~M_{\odot}$ and 100 $M_{\odot}$ lower and upper mass cutoffs respectively (dashed line). Within the measurement uncertainties, the measured properties agree with the model predictions for all but two clusters in NGC 1487 and one cluster in NGC 4038/4039. This would still be the case if we had assumed the distance to the Antennae that was determined from the tip of the red giant branch (Saviane et al. 2008) to be substantially lower than our assumed value, 13.3 rather than 19.3 Mpc. Since this lower distance would affect both estimates (lowering $M_{\rm ph}$ by a factor 2, and lowering the cluster sizes and hence $M_{\rm dyn}$ by a factor 1.45), the net effect would be that the ratio of $M_{\rm dyn}$/ $M_{\rm ph}$ needs to be corrected by a factor 1.38 (correspondingly decreasing L_K/M by a factor 0.73). In general, this would still lead to a good correspondence between the photometric and dynamical estimates, and would leave the conclusion the same.

The good agreement between evolutionary synthesis models applied to our clusters, in comparison with dynamical masses, suggests that there is no strong variation in the IMF for all but three clusters in our sample, and that they have likely survived the gas removal phase as bound stellar systems.

The two NGC 1487 clusters (red stars) and one Antennae cluster (S2_1) that are offset below the model predictions have dynamical mass estimates that are significantly higher than the photometric ones. One possible explanation is that these clusters have an IMF that is significantly steeper than Kroupa/Salpeter. There is little direct evidence for such an interpretation, and we believe that it is much more likely that these are clusters caught in the act of dissolving. The efficiency with which a cluster forms stars will impact the probability that it survives the expulsion of its natal gas. For example, clusters that form stars at lower efficiencies end up with fewer bound stars (i.e. shallower potential wells) relative to the left-over gas from formation. Such clusters, as momentum input from the massive stars expels the gas, have a lower probability of remaining bound than a cluster that formed more stars and had less remaining gas. Goodwin & Bastian (2006) explored the connection between star formation efficiency and cluster dissolution by simulating the N-body dynamics of a cluster after the expulsion of gas. Using their results (Bastian, priv. comm.), we plot the L_K/M ratios for a Kroupa IMF, solar metallicity (Starburst99 models) as the red dotted lines in Fig. 12 for the following effective star formation efficiences (eSFEs, defined as a measure of how far the cluster is out of virial equilibrium after gas expulsion): 60%, 50%, 40%, 30%, 20%, and 10%, starting from the top. eSFEs $\approx$40% and higher are predicted to result in stable clusters after 20-30 Myr, even though many clusters, at least the three between the 40% and the 60% lines, may lose a substantial amount of mass (Goodwin & Bastian 2006).

Baumgardt & Kroupa (2007) ran a grid of models with larger parameter space, varying star formation efficiency (SFE, defined in the normal way as the ratio of stellar mass over mass of stars and gas), gas expulsion time and tidal field. Even though a direct comparison to the Goodwin & Bastian (2006) results is difficult, some general conclusions are the same in both models: all clusters, even the ``survivors'', expand initially, and almost indistinguishably. After 10-20 Myr, the dissolving clusters continue to expand, while those with a sufficiently high SFE re-contract. A more gradual gas expulsion than the instantaneous expulsion assumed by Goodwin & Bastian (2006) makes it easier to remain bound.

Two clusters in in NGC 1487 and one in the Antennae, in Fig. 12, lie in or very close to regions where cluster dissolution is expected from the Goodwin & Bastian (2006) models. We consider two of them candidate dissolving clusters (which is particularly interesting because of their high mass - even though infant mortality is claimed to be mass independent, high-mass clusters are usually intuitively considered more stable against dissolution). Variations in the initial conditions, for example longer gas expulsion times or tidal fields, as explored by Baumgardt & Kroupa (2007), would shift the boundary between dissolving and surviving clusters in this plot down or up, respectively.

	Figure 9: VLT-ISAAC Ks images of Antennae clusters included in our spectroscopy slits. The clusters marked with boxes are those which have an obvious strong neighbour or which consist of multiple objects. This could have an impact on the measured velocity dispersion, and the two most obviously affected clusters (S1_3 and S1_4) were discarded from further analysis for this reason.
Open with DEXTER

	Figure 10: Blowup of the densely populated overlap region in the Antennae. In order to enhance the background, we chose a logarithmic scaling. The rectangles indicate regions that we selected manually as a reasonable assumption for the background level at the location of the nearby cluster.
Open with DEXTER

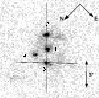	Figure 11: VLT-ISAAC Ks acquisition image of NGC 1487. It shows that the two components of Cluster 3 could be well resolved. The slit was positioned on the brighter component. Nevertheless, some flux from the fainter component entered the slit.
Open with DEXTER

The third cluster is NGC 1487-3, which is likely to have suffered effects of cluster multiplicity (see Sect. 3.3).

One of the main results of this work is that most of the clusters in our sample appear to have survived, as bound stellar systems, the gas removal phase that occurs during the life of every cluster. It is important to note that, in light of many recent works showing that many or most clusters (roughly 50% to 90%) probably do not survive the earliest phases of evolution, our study targets clusters that are likely to have survived this phase. After $\approx$10 Myr other mechanisms will continue to unbind clusters. If essentially all clusters which reach an age of $\approx$10 Myr in the Antennae are marginially bound or bound at this point, this would imply a very large number of young globular clusters. However, Fall et al. (2005) show that, at least statistically, star clusters continue to get disrupted approximately independent of mass, out to an age of $\approx$100 Myr.

Evaporation of stars resulting from two-body relaxation will eventually disrupt a number of lower mass clusters over a Hubble time. Clusters with current masses $\geq$ $\mbox{few}\times10^5~M_{\odot}$ would likely survive this process for 15 Gyr or more, assuming the typical evaporation rate of $\mu_{\rm ev} = 1 {-} 2 \times 10^{-5}$ $M_{\odot}$ yr^-1. Such a rate is plausible as it reproduces the observed turnover in the mass function of globular star clusters in many galaxies (e.g., Fall & Zhang 2001; Waters et al. 2006; Jordan et al. 2006).

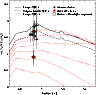Figure 12: This is a modified version of a figure from Goodwin & Bastian (2006); their Fig. 5. It shows L/M for a Starburst99 (v.5.0, 2005) SSP with a Kroupa IMF, instantaneous burst, solar metallicity (solid, black). Dotted (red) take into account the Goodwin & Bastian model results (Bastian, priv. comm.) for clusters with effective star formation efficiencies (eSFEs) below 100% (lowest line: 10%, top: 60%). The locations of our clusters are indicated (clusters with identical ages have been offset by 0.1 Myr in order to be able to see which error bar belongs to which cluster). Those that end up between the lines according to eSFEs of 20% and 50% are discussed as dissolution candidates in the text, and correspond to ratios of $M_{\rm dyn}$/ $M_{\rm ph} \geq 2.5$.

Open with DEXTER

Spectroscopic studies like the one presented here require enormous amounts of telescope time, and still result only in very few spectra. It would be much more efficient if a cluster population could be separated into ``survivors'' and ``dissolvers'' from (high resolution) imaging alone, because this would give a better handle on the infant mortality rate. Obviously, constraining the infant mortality rate is of immense relevance for the whole issue of star formation, because the currently cited cluster destruction rates range in impact from ``cluster formation is an interesting, but not very important mode of star formation'' (for destruction rates of a few tens of percent) to ``essentially all stars formed in clusters'' (for destruction rates of $\approx$90% per decade).

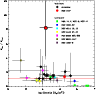Figure 13: The ratio of dynamical mass over photometric mass vs. half mass density $\rho _{\rm h}$ (taken as the log on the X-axis). High values ($\geq$2.5) of $M_{\rm dyn}$/ $M_{\rm ph}$, which may indicate dissolving clusters, seem more common at low densities. Symbols are described in the legend, diamonds and hexagons represent our data (with the open circles marking clusters that may have been influenced by nearby clusters), squares are taken from the literature: M82-F: McCrady & Graham (2007); McCrady et al. (2005), M82-A1 (1a, respectively): Smith et al. (2006); McCrady & Graham (2007), M82 MGG-9 and MGG-11: McCrady et al. (2003), NGC 1042-NC: Böker et al. (2004b,a); de Grijs et al. (2005), NGC 4212-10, 4214-13, NGC 4449-27 and NGC 4449-47: Larsen et al. (2004), NGC 5236-502, 5236-805: Larsen & Richtler (2004), NGC 6946-1447: Larsen et al. (2006,2004), NGC 1569-B: Larsen et al. (2008).

Open with DEXTER

One expectation for expanding, unbound clusters is that as they expand, their internal density should decrease. Note, however that it is impossible to determine from the size and/or concentration of these young clusters alone if they are bound or dissolving: even though unbound stars, leaving the cluster with escape velocities of tens of km s^-1 reach distances of tens or hundreds of pc in a few Myr, the half-light radius of the cluster is not immediately affected severely - even after 20 initial crossing times, the half-mass radius of a dissolving cluster is only 40% larger than that of a surviving cluster (Baumgardt & Kroupa 2007). An alternative explanation for clusters having low density is simply that they formed in a low-density environment, which is expected to lead to smaller SFEs. In any case, we might expect our clusters with non-virial motions to have low stellar densities as well. In Fig. 13, we show the estimated half-mass density $\rho _{\rm h}$ (with $r_{\rm hp}$ and $M_{\rm ph}$ as input) for the clusters versus the ratio dynamical to photometric mass. This figure shows that our two dissolving cluster candidates (i.e. those with high ratios of $M_{\rm dyn}/M_{\rm phot}$) also appear to have low stellar densities.

We have included in Fig. 13 all the data from the literature where the three parameters $M_{\rm dyn}$, $M_{\rm ph}$ (assuming a Kroupa IMF) and $r_{\rm hp}$ were provided or could easily be deduced. Most of the clusters in other publications are considerably older than 10 Myr, therefore it is not surprising that they do not show indication of cluster expansion. But the two literature clusters where the dynamical mass exceeds the photometric mass by more than a factor two (NGC 6946-1447 and NGC 5236-805) confirm the trend shown in our clusters, since they also have low densities.

Clusters with high $M_{\rm dyn}$/ $M_{\rm ph}$ likely have low values of $\rho _{\rm h}$ because they are expanding and thus the high values are due to dynamical evolution. Therefore clusters with ages around 10 Myr that have low densities are excellent candidates for clusters in the process of dissolving, although clearly some fraction of low density clusters appears to be bound at this age as well. Low density clusters that are gravitationally bound, such as found in the Milky Way (outer globular clusters, Harris 1996), the Magellanic Clouds (van den Bergh 1991), and in nearby spirals and lenticular galaxies (Larsen & Brodie 2000; Peng et al. 2006; Chandar et al. 2004), may survive longer than their higher density counterparts, since they are expected to have lower rates of relaxation-driven stellar evaporation (Chandar et al. 2007; McLaughlin & Fall 2008).

A similar picture emerges if we consider pressure instead of density: Following Elmegreen et al. (2000), we used $P \propto G M_{\rm ph}^2 / r_{\rm hp}^4$ as an estimate for the pressure in the ambient medium during cluster formation. Then SFE is expected to also scale with this parameter (Elmegreen et al. 2000). Indeed, as shown in Fig. 14, the clusters that may be disolving are amongst those with the lowest pressures in both our sample and the sample taken from the literature.

Whereas low pressure/density is not a unique identifier for dissolving cluster (since, as shown, there exist also low-density/pressure clusters with no sign of expansion), about 50% of the clusters in our plots below a density/pressure limit (10^9.5 and 10⁹, respectively) are dissolution candidates. They constitute only 20-25% of the whole sample.

In our future work, we will compare dynamical and photometric mass estimates of a larger sample, which would provide a more robust estimate of the fraction of clusters that appear as single entities, but are unbound at an age of $\approx$10 Myr.

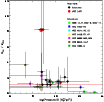	Figure 14: The ratio of dynamical mass over photometric mass vs. pressure (taken as the log on the X-axis). Symbols, references and interpretation (except now for pressure, rather than density) are the same as in Fig. 13.
Open with DEXTER

Acknowledgements

We are grateful to N. Bastian for making their modelling results available in electronic form, so we could include them in our Fig. 12. We also wish to thank the anonymous referee for constructive comments.

References

• Ascenso, J. 2008, to appear in the proceedings of the meeting, Young massive star clusters - Initial conditions and environment, ed. E. Perez, R. de Grijs, & R. M. Gonzalez Delgado, Granada, Spain, September 2007 (Dordrecht: Springer) (In the text)
• Bastian, N., Gieles, M., Lamers, H. J. G. L. M., Scheepmaker, R. A., & de Grijs, R. 2005, A&A, 431, 905 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Bastian, N., Saglia, R. P., Goudfrooij, P., et al. 2006, A&A, 448, 881 [NASA ADS] [CrossRef] [EDP Sciences]
• Baumgardt, H., & Kroupa, P. 2007, MNRAS, 380, 1589 [NASA ADS] [CrossRef] (In the text)
• Binney, J., & Tremaine, S. 1987, Galactic Dynamics, Princeton Series in Astrophysics (Princeton, NJ: Princeton University Press) (In the text)
• Boily, C. M., & Kroupa, P. 2003a, MNRAS, 338, 665 [NASA ADS] [CrossRef]
• Boily, C. M., & Kroupa, P. 2003b, MNRAS, 338, 673 [NASA ADS] [CrossRef]
• Böker, T., Sarzi, M., McLaughlin, D. E., et al. 2004a, AJ, 127, 105 [NASA ADS] [CrossRef]
• Böker, T., Walcher, C. J., Rix, H.-W., et al. 2004b, Proceedings of the conference, The Formation and Evolution of Massive Young Star Clusters, ed. H. J. G. L. M. Lamers, L. J. Smith, & A. Nota (San Francisco: Astronomical Society of the Pacific), ASP Conf. Ser., 322, 39
• Chandar, R., Whitmore, B. C., & Lee, M. G. 2004, ApJ, 611, 220 [NASA ADS] [CrossRef]
• Chandar, R., Fall, S. M., & McLaughlin, D. E. 2007, ApJ, 668, L119 [NASA ADS] [CrossRef]
• Chernoff, D. F., & Weinberg, D. M. 1990, ApJ, 351, 121 [NASA ADS] [CrossRef]
• Cohn, H. 1979, ApJ, 234, 1036 [NASA ADS] [CrossRef]
• de Grijs, R., Wilkinson, M. I., & Tadhunter, C. N. 2005, MNRAS, 361, 311 [NASA ADS] [CrossRef]
• De Marchi, G., Sirianni, M., Gilliland, R., et al. 2004, Instrument Science Report ACS 2004-8 (In the text)
• Elmegreen, B. G., Efremov, Y., Pudritz, R. E., & Zinnecker, H. 2000, Proceedings of the conference, Protostars and Planets IV (Tucson: University of Arizona Press), ed. V. Mannings, A. P. Boss, & S. S. Russell, 179 (In the text)
• Fall, S. M., & Zhang, Q. 2001, ApJ, 561, 751 [NASA ADS] [CrossRef]
• Fall, S. M. 2004 [arXiv:astro-ph/0405064]
• Fall, S. M., Chandar, R., & Whitmore, B. C. 2005, ApJ, 631, L133 [NASA ADS] [CrossRef]
• Fleck, J.-J., Boily, C. M., Lançon, A., & Deiters, S. 2006, MNRAS, 369, 1392 [NASA ADS] [CrossRef] (In the text)
• Goodwin, S. P., & Bastian, N. 2006, MNRAS, 373, 752 [NASA ADS] [CrossRef]
• Harris, W. E. 1991, ARA&A, 29, 543 [NASA ADS] [CrossRef]
• Harris, W. E. 1996, 1996, AJ, 112, 1487 [NASA ADS] [CrossRef] (In the text)
• Hills, J. G. 1980, ApJ, 235, 986 [NASA ADS] [CrossRef]
• Ho, L., & Filippenko, A. 1996a, ApJ, 466, L83 [NASA ADS] [CrossRef]
• Ho, L., & Filippenko, A. 1996b, ApJ, 472, 600 [NASA ADS] [CrossRef]
• Holtzman, J. A., Faber, S. M., Shaya, E. J., et al. 1992, AJ, 103, 691 [NASA ADS] [CrossRef]
• Jordán, A., McLaughlin, D. E., Côté, P., et al. 2006, ApJ, 651, L25 [NASA ADS] [CrossRef]
• Kouwenhoven, M. B. N., & de Grijs, R. 2007 [arXiv:0712.1748] (In the text)
• King, I. R. 1962, AJ, 67, 471 [NASA ADS] [CrossRef] (In the text)
• Krist, J. 1995, in Astronomical Data Analysis, Software, and Systems IV, ed. R. Shaw, H. E. Payne, & J. E. Hayes (San Francisco: ASP), ASP Conf. Ser., 77, 349
• Lada, C. J., & Lada, E. A. 2003, ARA&A, 41, 57 [NASA ADS] [CrossRef]
• Lada, C. J., Margulis, M., & Dearborn, D. 1984, ApJ, 285, 141 [NASA ADS] [CrossRef]
• Larsen, S. S. 1999, A&AS, 139, 393 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Larsen, S. S. 2001, AJ, 122, 1782 [NASA ADS] [CrossRef] (In the text)
• Larsen, S. S. 2003, Ishape manual, distributed with baolab-0.93.6 data reduction package (In the text)
• Larsen, S. S. 2004, A&A, 416, 537 [NASA ADS] [CrossRef] [EDP Sciences]
• Larsen, S. S., & Brodie, J. P. 2000, AJ, 120, 2938 [NASA ADS] [CrossRef]
• Larsen, S. S., & Richtler, T. 2004, A&A, 427, 495 [NASA ADS] [CrossRef] [EDP Sciences]
• Larsen, S. S., Brodie, J. P., & Hunter, D. A. 2004, AJ, 128, 2295 [NASA ADS] [CrossRef]
• Larsen, S. S., Brodie, J. P., & Hunter, D. A. 2006, AJ, 131, 2362 [NASA ADS] [CrossRef]
• Larsen, S. S., Origlia, L., Brodie, J. P., & Gallagher, J. S. 2008, MNRAS, 383, 263 [NASA ADS] (In the text)
• Larson, R. B. 1999, in Proceedings of Star Formation 1999, held in Nagoya, Japan, June 21-25, 1999, ed. T. Nakamoto, Nobeyama radio Observatory, 336
• Lee, H. J., & Lee, M. G. 2005, JKAS, 38, 345 [NASA ADS] (In the text)
• Lee, M. G., Chandar, R., & Whitmore, B. C. 2005, 130, 2128
• Leitherer, C., Schaerer, D., Goldader, J. D., et al. 1999, ApJS, 123, 3 [NASA ADS] [CrossRef] (In the text)
• Maraston, C. 2005, MNRAS, 362, 799 [NASA ADS] [CrossRef]
• McCrady, N., & Graham, J. R. 2007, ApJ, 663, 844 [NASA ADS] [CrossRef]
• McCrady, N., Gilbert, A. M., & Graham, J. R. 2003, ApJ, 596, 240 [NASA ADS] [CrossRef] (In the text)
• McCrady, N., Graham, J. R., & Vacca, W. D. 2005, ApJ, 621, 278 [NASA ADS] [CrossRef]
• McLaughlin, D. E., & Fall, S. M. 2008, ApJ, 679, 1272 [NASA ADS] [CrossRef]
• Mengel, S., & Tacconi-Garman, L. E. 2007, A&A, 466, 151 [NASA ADS] [CrossRef] [EDP Sciences]
• Mengel, S., Lehnert, M. D., Thatte, N., Tacconi-Garman, L. E., & Genzel, R. 2001, ApJ, 550, 280 [NASA ADS] [CrossRef]
• Mengel, S., Lehnert, M. D., Thatte, N., & Genzel, R. 2002, A&A, 383, 137 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Mengel, S., Lehnert, M. D., Thatte, N., & Genzel, R. 2003, SPIE, 4834, 45 [NASA ADS]
• Mengel, S., Lehnert, M. D., Thatte, N., & Genzel, R. 2005, A&A, 443, 41 [NASA ADS] [CrossRef] [EDP Sciences]
• Meurer, G. R., Heckman, T. M., Leitherer, C., et al. 1995, AJ, 110, 2665 [NASA ADS] [CrossRef]
• Peng, E. W., Côté, P., Jordán, A., et al. 2006, ApJ, 639, 838 [NASA ADS] [CrossRef]
• Persson, S. E., Murphy, D. C., Krzeminski, W., Roth, M., & Rieke, M. J. 1998, AJ, 116, 2475 [NASA ADS] [CrossRef] (In the text)
• Saviane, I., Momany, Y., Da Costa, G. S., Rich, R. M., & Hibbard, J. 2008 [arXiv:0802.1045] (In the text)
• Sirianni, M., Jee, M. J., Benítez, N., et al. 2005, PASP, 117, 1049 [NASA ADS] [CrossRef] (In the text)
• Smith, L. J., Westmoquette, M. S., Gallagher III, J. S., et al. 2006, MNRAS, 370, 513 [NASA ADS]
• Spitzer, L. Jr. 1978, Physical Processes in the Interstellar Medium (New York: Wiley-Interscience)
• Spitzer, L. Jr. 1987, Dynamical Evolution of Globular Clusters (Princeton: Princeton Univ. Press)
• Sternberg, A. 1998, ApJ, 506, 721 [NASA ADS] [CrossRef]
• Takahashi, K., & Portegies Zwart, S. F. 2000, ApJ, 535, 759 [NASA ADS] [CrossRef]
• Trancho, G., Bastian, N., Miller, B. W., & Schweizer, F. 2007, ApJ, 664, 284 [NASA ADS] [CrossRef]
• van den Bergh, S. 1991, ApJ, 369, 1 [NASA ADS] [CrossRef] (In the text)
• Vazquez, G. A., & Leitherer, C. 2005, ApJ, 621, 695 [NASA ADS] [CrossRef]
• Waters, Ch. Z., Zepf, S. E., Lauer, T. R., Baltz, E. A., & Silk, J. 2006, ApJ, 650, 885 [NASA ADS] [CrossRef]
• Whitmore, B. C. 2000 [arXiv:astro-ph/0012546]
• Whitmore, B. C. 2004, in The Formation and Evolution of Massive Young Star Clusters (San Francisco: Astronomical Society of the Pacific), ed. H. J. G. L. M. Lamers, L. J. Smith, & A. Nota, ASP Conf. Ser., 322, 419
• Whitmore, B., & Schweizer, F. 1995, AJ, 109, 960 [NASA ADS] [CrossRef]
• Whitmore, B. C., Schweizer, F., Leitherer, C., Borne, K., & Robert, C. 1993, AJ, 106, 1354 [NASA ADS] [CrossRef]
• Whitmore, B. C., Miller, B. W., Schweizer, F., & Fall, S. M. 1997, AJ, 114, 2381 [NASA ADS] [CrossRef]
• Whitmore, B. C., Zhang, Q., Leitherer, C., et al. 1999, AJ, 118, 1551 [NASA ADS] [CrossRef]
• Whitmore, B. C., Chandar, R., & Fallk, S. M. 2007, AJ, 133, 1067 [NASA ADS] [CrossRef]
• Wilson, C. D., Scoville, N., Madden, S. C., & Charmandaris, V. 2000, ApJ, 542, 120 [NASA ADS] [CrossRef]
• Zhang, Q., & Fall, S. M. 1999, ApJ, 527, 81 [NASA ADS] [CrossRef]
• Zepf, S. E., & Ashman, K. M. 1999, AJ, 118, 752 [NASA ADS] [CrossRef]