A&A 489, 1255-1262 (2008)
DOI: 10.1051/0004-6361:200809587

High-resolution spectroscopy for Cepheids distance determination^,

III. A relation between $\gamma$-velocities and $\gamma$-asymmetries

N. Nardetto¹ - A. Stoekl² - D. Bersier³ - T. G. Barnes^4,5

1 - Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
2 - CRAL, Université de Lyon, CNRS (UMR5574), École Normale Supérieure de Lyon, 69007 Lyon, France
3 - Astrophysics Research Institute, Liverpool John Moores University, Twelve Quays House, Egerton Wharf, Birkenhead, CH41 1LD, UK
4 - University of Texas at Austin, McDonald Observatory, 1 University Station, C1402, Austin, TX 78712-0259, USA
5 - currently on assignment to the National Science Foundation, 4201 Wilson Boulevard, Arlington, VA 22230, USA

Received 15 February 2008 / Accepted 1 April 2008

Abstract
Context. Galactic Cepheids in the vicinity of the Sun have a residual line-of-sight velocity, or $\gamma$-velocity, which shows a systematic blueshift of about 2 km s^-1 compared to an axisymmetric rotation model of the Milky Way. This term is either related to the space motion of the star and, consequently, to the kinematic structure of our Galaxy, or it is the result of the dynamical structure of the Cepheids' atmosphere.
Aims. We aim to show that these residual $\gamma$-velocities are an intrinsic property of Cepheids.
Methods. We observed eight galactic Cepheids with the HARPS spectroscope, focusing specifically on 17 spectral lines. For each spectral line of each star, we computed the $\gamma$-velocity (resp. $\gamma$-asymmetry) as an average value of the interpolated radial velocity (resp. line asymmetry) curve.
Results. For each Cepheid in our sample, a linear relation is found between the $\gamma$-velocities of the various spectral lines and their corresponding $\gamma$-asymmetries, showing that residual $\gamma$-velocities stem from the intrinsic properties of Cepheids. We also provide a physical reference to the stellar $\gamma$-velocity: it should be zero when the $\gamma$-asymmetry is zero. Following this definition, we provide very precise and physically calibrated estimates of the $\gamma$-velocities for all stars of our sample [in km s^-1]: $-11.3 \pm 0.3$ [R TrA], $-3.5 \pm 0.4$ [S Cru], $-1.5 \pm 0.2$ [Y Sgr], $9.8 \pm 0.1$ [$\beta$ Dor], $7.1 \pm 0.1$ [$\zeta$ Gem], $24.6 \pm 0.4$ [RZ Vel], $4.4 \pm 0.1$ [$\ell$ Car], $25.7 \pm 0.2$ [RS Pup]. Finally, we investigated several physical explanations for these $\gamma$-asymmetries like velocity gradients or the relative motion of the line-forming region compared to the corresponding mass elements. However, none of these hypotheses seems to be entirely satisfactory to explain the observations.
Conclusions. To understand this very subtle $\gamma$-asymmetry effect, further numerical studies are needed. Cepheids' atmosphere are strongly affected by pulsational dynamics, convective flows, nonlinear physics, and complex radiative transport. Hence, all of these effects have to be incorporated simultaneously and consistently into the numerical models to reproduce the observed line profiles in detail.

Key words: techniques: spectroscopic - stars: atmospheres - stars: oscillations - stars: variables: Cepheids - stars: distances

  
1 Introduction

Cepheids are very important astrophysical objects due to their well-known period-luminosity (PL) relation. Based on this relation, a multi-decade work allowed us to determine the kinematic structure of the Milky Way (in particular its rotation) and to reach cosmologically significant extragalactic distances (see Hubble Space Telescope Key Project, Freedman et al. 2001). In the second paper of this series, Nardetto et al. (2007) (hereafter Paper II) established a clear link between the distance scale and the dynamical structure of Cepheids' atmosphere through a period-projection factor (Pp) relation. Similarly, studies concerning the kinematics of the Milky Way might be closely related to the dynamical structure of Cepheids' atmosphere.

Concerning the distance scale, near-infrared interferometry currently provides a new, quasi-geometrical way to determine the distance of galactic Cepheids up to 1 kpc (see e.g. Sasselov & Karovska 1994; and Kervella et al. 2004). The basic principle of the Interferometric Baade-Wesselink method (IBW) is to compare the linear and angular size variation of a pulsating star in order to derive its distance through a simple division. The key point is that interferometric measurements in the continuum lead to angular diameters corresponding to the photospheric layer, while the linear stellar radius variation is deduced by spectroscopy, i.e., based on line-forming regions which form higher in the atmosphere. Thus, radial velocities  $V_{{\rm rad}}$, which are derived from line profiles, include the integration in two directions: over the stellar surface through limb-darkening and over the atmospheric layers through velocity gradients. All these phenomena are currently merged in one specific quantity, generally considered constant with time: the projection factor p, defined as $V_{{\rm puls}}=pV_{{\rm rad}}$, where $V_{{\rm puls}}$ is defined as the photospheric pulsation velocity (Nardetto et al. 2004). $V_{{\rm puls}}$ is then integrated with time to derive the photospheric radius variation. The precision in the distance currently obtained with the IBW method is a few percent. However, it remains strongly dependent on the projection factor. If a constant projection factor is used (generally p=1.36 for all stars) to derive the PL relation, errors of 0.10 and 0.03 on the slope and zero-point of the PL relation can be introduced. This means that distances can be overestimated by 10% for long-period Cepheids (Paper II).

In Paper II, we divide the projection factor into three sub-topics: (1) a geometrical effect related to the limb-darkening; (2) the velocity gradient within the atmosphere; and (3) the differential motion of the ``optical'' pulsating photosphere compared to the corresponding mass elements, called  $f_{{\rm o-g}}$. Even if the Pp relation was recently confirmed by HST observations (Fouqué et al. 2007), the $f_{{\rm o-g}}$ is relatively uncertain and currently entirely based on hydrodynamical calculations. Nevertheless, a key point is that this quantity should be, in principle, related to the so-called $\gamma$-velocity term. As Sabbey et al. (1995) noted, the changing depth of the spectral line-forming region over a Cepheid pulsation cycle leads to unequal extrema in the line asymmetry curve. Such phenomenon was also observed in the first paper of this series (Nardetto et al. 2006, hereafter Paper I). Spectral lines are thus not associated with the same gas particles during the pulsation cycle. Formally, they do not comply with path conservation, stated as

$$\int V_{{\rm rad}}{\rm d}\phi=0$$

where the integral is over a whole cycle. Path conservation is, however, a fundamental assumption in the BW method (Gautschy 1987).

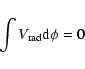
The state of the art of the BW methods, concerning the $\gamma$-velocity is the following: the $\gamma$-velocity is generally removed, i.e. the average value of the radial velocity curve is forced to zero before integrating. However, the differential motion between the line-forming region and the gas also modifies the velocity amplitude. The $f_{{\rm o-g}}$ was introduced, based on hydrodynamical models in Paper II, in order to correct this velocity amplitude effect. The next step is to find a correlation between $f_{{\rm o-g}}$ and the $\gamma$-velocity. In this paper, we will provide some indications, but the problem remains unsolved.

Table 1: Linear relations between the $\gamma$-velocities and the $\gamma$-asymmetries $V_{\gamma } = a_{{\rm0}} A_{\gamma } + b_{{\rm0}}$ for all stars. The last column corresponds to the final physically calibrated $\gamma$-velocities for each star (see Sect. 3.1 for details). The subscripts give the $1\sigma$ uncertainty.

The $\gamma$-velocities are also of great importance for the determination of the kinematic structure of the Milky Way. Galactic Cepheids in the solar vicinity show a residual line-of-sight velocity (a ``K-term'') in their radial velocities which is systematically blueshifted of about 2 km s^-1 compared to an axisymmetric rotation model of the Milky Way (Camm 1938, 1944; Parenago 1945; Stibbs 1956; Wielen 1974; Caldwell & Coulson 1987; Moffett & Barnes 1987; Wilson et al. 1991; Pont et al. 1994). Wielen (1974) found no correlation of the K-term with any obvious parameter such as period, amplitude or distance, and concluded that the K-term is an intrinsic property of Cepheid atmospheres. On the other hand, Pont et al. (1994) tried to revive Camm (1944) and Parenago's (1945) suggestion that the K-term is due to a real effect in the dynamics of the Galaxy. In addition, Butler et al. (1996) found a $\gamma$-velocity reduced by 2 km s^-1 by introducing velocity gradients in hydrostatic stellar atmospheres models. The K-term problem is still a matter of debate today.

Based on very high quality HARPS observations and careful methodology (Sect. 2), we will show that $\gamma$-velocities are due to intrinsic properties of Cepheids (Sect. 3). Finally, we discuss our results in Sect. 4.

   
2 HARPS observations

Ten stars have been observed with the HARPS spectrometer (R=120 000): R Tra, S Cru, Y Sgr, $\beta$ Dor, $\zeta$ Gem, Y Oph, RZ Vel, $\ell$ Car, RS Pup and X Sgr. X Sgr is an atypical Cepheid presenting several components in the spectral line profiles. It was studied separately by Mathias et al. (2006). Y Oph is not studied here in detail due to its insufficient phase coverage (see Paper II, Fig. 3). We thus consider 8 Cepheids in this paper.

Figure 1: Fe I 4896.4 ( $D \simeq 8$%) and Fe I 6024.1 ( $D \simeq 30$%) spectral lines evolution of $\beta$ Dor. Pulsation phases are given on the left of each profile. Wavelengths have been translated into velocities for comparison (positive velocities correspond to a redshift, motion toward us). Thesystematic difference in lines asymmetries and velocities is clear. The solid and dashed lines at $\phi =0.61$ show that modifying artificiallythe line asymmetry induces a change in the resulting centroid velocity (see Sect. 4).

Open with DEXTER

Using Kurucz models 1992 we have identified about 150 unblended spectral lines. In Paper II, we carefully selected 17 spectral lines following two criteria: (1) the continuum must to be perfectly defined for all pulsation phases of all stars, in order to avoid bias in the determination of the line depth; (2) the selected sample of lines has to cover a large range of depth. The spectral lines selected are presented in Table 1 of Paper II.

As in Paper I, we use bi-Gaussian fits to derive line asymmetries. We repeat here the main equations in order to show that there is no a priori link between the line asymmetry and our centroid method of the radial velocity determination. The centroid radial velocity ( $RV_{{\rm c}}$), or the first moment of the spectral line profile, has been estimated as

$$RV_{\rm c} = \frac{\int_{\rm line} \lambda S(\lambda) {\rm d}\lambda}{\int_{\rm line} S(\lambda) \rm d\lambda}$$ (1)

where $S(\lambda)$ is the observed line profile. Then, the radial velocity corresponding to the minimum pixel, full width at half-maximum (FWHM), and asymmetry are derived simultaneously by applying a classical $\chi^{2}$ minimization algorithm between the observed line profile ( $S(\lambda)$) and a modeled spectral line profile ( $f(\lambda)$). The corresponding reduced $\chi^{2}$ is

$${\chi_{\rm red}}^{2} = \frac{1}{N-\nu} \sum_{i=0}^{N}{\frac{(S(\lambda_i)-f(\lambda_i))^{2}}{\sigma(\lambda_i)^2}}$$ (2)

with N being the number of pixels in the spectral line, $\nu$ the number of degrees of freedom and $\sigma(\lambda_i)$ = SNR $*f(\lambda_i)$ the statistical uncertainty associated to each pixel. SNR is the estimate of the signal-to-noise Ratio in the continuum.

The analytic line profile is defined by

$$f(\lambda)= 1 - D \exp \left( \frac{4 \ln 2 (\lambda - \lamb... ...FWHM}(1+A))^2} \right) \mbox{ if } \lambda > \lambda_{{\rm m}}$$ (3)

and

$$f(\lambda)= 1 - D \exp \left( \frac{4 \ln 2 (\lambda - \lam... ...FWHM}(1-A))^2} \right) \mbox{ if } \lambda < \lambda_{{\rm m}}$$ (4)

with four free parameters: D, the depth of the line (dimensionless); $\lambda_{\rm m}$, the wavelength associated to the minimum of the line (in Å); FWHM, the Full-Width at Half-Maximum in the line (in Å); and A, the line asymmetry relative to the ${\it FWHM}$ (in %). Online tables (Nardetto et al. 2007) present the resulting values of $RV_{{\rm m}}$, $RV_{{\rm c}}$, ${\it FWHM}$, D, A, SNR, and $\chi_{{\rm red}}^2$together with the corresponding uncertainties computed from the fitting method. In the following, we will only use  $RV_{{\rm c}}$and A, which are clearly independent given the manner of their determinations.

We insist on the $RV_{{\rm c}}$ definition of the radial velocity since it is absolutely required to allow direct comparisons between $\gamma$-velocities of different spectral lines from different Cepheids. Indeed, it is the only method which provides a radial velocity independent of the rotation (projected on the line of sight) and the natural width of the spectral line (Burki et al. 1982, and Paper I).

The $RV_{{\rm c}}$ and A quantities for 17 selected spectral lines for each of the 8 stars have been interpolated over the pulsation phase using a periodic cubic spline function. The interpolation is performed either directly on the observational points (e.g. $\beta$ Dor) or using arbitrary pivot points (e.g. RZ Vel). In the latter case, a classical minimization process between the observations and the interpolated curve is used to optimize the position of the pivot points. All interpolated curves presented in this study were derived using one of these two methods. Finally, $A_{\gamma }$ and  $V_{\gamma }$ are calculated by averaging the $A(\phi)$ and $RV_{{\rm c}}(\phi)$interpolated curves, where $\phi$ is the pulsation phase. The corresponding uncertainties are defined as the average values of individual uncertainties on the observational points.

   
3 A relation between $\gamma$-velocities and $\gamma$-asymmetries

The aim of this section is to study the $\gamma$-velocities and to show that they consist of two components: one related to the space motion of the star itself, and one (the K-term) related to the dynamical structure of Cepheids' atmosphere.

  
3.1 Methodology presented in the case of $\beta$ Dor

To introduce our methodology we discuss the exemplary case of $\beta$ Dor in detail.

First, interpolated radial velocity curves derived from all spectral lines were corrected by the $\gamma$-velocity found in the Galactic Cepheid Database of the David Dunlap Observatory (Fernie et al. 1995, hereafter $V_{\gamma {\rm GCD}}$, see Table 1).

Figure 1 shows the spectral line profile of two metallic lines Fe I 4896.4 ( $D \simeq 8$% of the continuum) and Fe I 6024.1 ( $D \simeq 30$%) as a function of the pulsation phase. We translated wavelengths into velocities for comparison. We used spectral lines with different line depths for clarity, but the results are actually independent of the line depth. Two qualitative key-points concerning Fig. 1 should be mentioned: (1) the Fe I 4896.4 spectral line (smaller line depth) seems to be systematically redshifted compared to the Fe I 6024.1 spectral line (look, for instance, at the pixel minimum of each profile) and (2) its asymmetry is also systematically larger (in absolute value) from phase $\phi=0.82$ to $\phi=0.23$, while it is systematically lower (in absolute value) from phase $\phi=0.33$ to $\phi =0.61$. This leads us to the idea of a correlation between the $\gamma$-velocity and the $\gamma$-asymmetry. In Figs. 2a,b we present the corresponding interpolated radial velocity and asymmetry curves for these two spectral lines. Another line of intermediate depth is also presented (Fe I 5373, solid line). From the interpolated curves, we now calculate the $\gamma$-velocities and -asymmetries corresponding to each spectral line (horizontal lines). An anti-correlation is clearly seen.

In Fig. 2c, $RV_{{\rm c}}-A$ plots and the corresponding ( $A_{\gamma }$, $V_{\gamma }$) average values (crosses) for the three different lines are presented. Although the $RV_{{\rm c}}-A$ plots have different shapes (and this is confirmed for all spectral lines), which is the result of the dynamical structure of the Cepheid atmosphere, the average values (big crosses) are aligned, confirming the correlation found in Figs. 2a,b.

Figure 2d is a generalization of diagram (c) for all spectral lines. The $RV_{{\rm c}}-A$ curves are not included for clarity. Upper values correspond to residual $\gamma$-velocities $V_{\gamma}(i)$ of the 17 selected spectral lines i after the GCD $\gamma$-velocity correction. A linear fit is performed, and we find the relation

$$V_{\gamma}(i)-V_{\gamma {\rm GCD}}= a_{{\rm0}} A_{\gamma}(i) + b_{{\rm0}},$$

with $a_{{\rm0}}=-0.16 \pm 0.02$ [km s^-1 per %] and $b_{{\rm0}}=2.4 \pm 0.1$ [km s^-1]. The origin of the plot is taken as a reference: the $\gamma$-velocity is assumed to be zero when the $\gamma$-asymmetry is zero. This means that all points

$$(A_{\gamma}(i), V_{\gamma}(i)-V_{\gamma {\rm GCD}} )$$

are translated into

$$(A_{\gamma}(i), V_{\gamma}(i)-(V_{\gamma {\rm GCD}}+b_{{\rm0}}) )$$

which allows the definition of a physically calibrated $\gamma$-velocity for $\beta$ Dor

$$V_{\gamma\star}=V_{\gamma {\rm GCD}}+b_{{\rm0}}=7.4+2.4=9.8_{\pm 0.1} \:{\rm km\: s}^{-1} .$$

This quantity is very precise due to the very high S/N and spectral resolution of HARPS data.

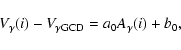
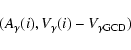
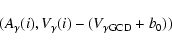
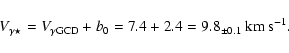
In principle, the line asymmetry and the $\gamma$-asymmetry are supposed to be the result of the dynamical structure of the Cepheid atmosphere only. The $V_{\gamma}(i) A_{\gamma}(i)$ (hereafter $V_{\gamma } A_{\gamma }$) correlation found is then a strong indication that residual $\gamma$-velocities (after correction by the GCD $\gamma$-velocities) are related to intrinsic physical properties of Cepheids' atmosphere and not to a real effect in dynamics of the Galaxy (see discussion).

3.2 V$_{\gamma }$A$_{\gamma }$ linear curves of all stars of our sample

$V_{\gamma }$ and $A_{\gamma }$ were derived for all spectral lines and for all stars of our sample using the same method as presented in the case of $\beta$ Dor.

Table 1 gives $V_{\gamma {\rm GCD}}$, the slope $a_{{\rm0}}$ of the interpolated $V_{\gamma } A_{\gamma }$ curves, the correction  $b_{{\rm0}}$ applied, and our final $\gamma$-velocities $V_{\gamma \star}$ for each star. The reduced $\chi^{2}$, defined as $\chi_{{\rm red}}^2=\frac{\chi^2}{N-\nu}$ with N being the number of spectral lines and $\nu$ the number of degrees of freedom, is also indicated. The $V_{\gamma } A_{\gamma }$ plots are shown in Fig. 3. Linear correlation curves between  $V_{\gamma }$and  $A_{\gamma }$ are found for all stars of our sample, and our  $b_{{\rm0}}$ corrections range from 0.2 to 3.6 km s^-1. The average value is $1.8 \pm 0.2$ km s^-1, which is consistent with the 2 km s^-1 ``K-term'' found in the literature. We discuss these important observational results in the next section.

  
4 Discussion

4.1 $\gamma$-velocities

The linear relation between $A_{\gamma }$ and $V_{\gamma }$ can be easily understood. The basic principle is demonstrated in Fig. 1 for the pulsation phase $\phi =0.61$. For clarity, we only present the argument for one pulsation phase.

The solid line is the bi-Gaussian fit of the Fe I 6024.1 spectral line. Artificially decreasing the bi-Gaussian asymmetry of this spectral line by the average asymmetry of the Fe I 6024.1 line, $A_{\gamma} = 7.58\%$, as shown in Fig. 1 with a dashed-line, we find that the centroid-velocity increases (i.e. is redshifted) by an amount of +1.45 km s^-1. To illustrate this, we included in Fig. 1 the computed line positions $RV_{{\rm c}}$ by vertical lines before (solid line) and after (dot-dashed line) modification of the bi-Gaussian asymmetry. Generally, we find that forcing the average line asymmetry  $A_{\gamma }$ to zero by uniformly changing the line asymmetry by the same amount at all phases alters the derived centroid velocities $RV_{{\rm c}}$ in such a way that the resulting $\gamma$-velocity becomes zero. For instance, the point ( $A_{\gamma}=7.58$%, $V_{\gamma}=1.45~$km s^-1) of the $V_{\gamma } A_{\gamma }$ linear curve of $\beta$ Dor (Fig. 3) translates into ( $A_{\gamma}=0$%, $V_{\gamma}=0~$km s^-1).

This result is obtained universally, regardless which spectral line or star is considered. Basically, we can conclude that the $\gamma$-velocities are a side-effect of the line asymmetries and related to the problem of determining line positions of asymmetric lines. This view is also supported by the high conformity of the slopes  $a_{{\rm0}}$ of the $V_{\gamma } A_{\gamma }$ relation for all sample stars (see Table 1) which (almost) agree within $1\sigma$ uncertainties.

Although this method of arbitrarily modifying the line asymmetry is a rather ad hoc method, it still allowed us to gain some insight into the origin of the $\gamma$-velocities. In particular, it shows (1) that the residual $\gamma$-velocities are related to the shapes of the spectral lines and, consequently, to an intrinsic property of Cepheids; and (2) that the main physical question is not to understand the $\gamma$-velocities, but to understand the $\gamma$-asymmetries.

Another important point is that this interpretation provides a physical meaning to the $\gamma$-velocities and, hence, a physical reference. The relation between $\gamma$-asymmetry and $\gamma$-velocity allows us to compute the contribution of the dynamical Cepheid's atmosphere to the $\gamma$-velocity. We can thus really provide a $\gamma$-velocity corresponding to the space motion of the star itself ( $V_{\gamma \star}$), independently of the dynamical structure of its atmosphere. From Table 1, we find an average systematic red-shift correction of $b_{{\rm0}}=1.8 \pm 0.2$ km s^-1 (averaged over 8 stars) between our physically calibrated $\gamma$-velocities and the ones found in the GCD, commonly used by the community. Consequently, the K-term (blueshifted) found in the literature is not due to the kinematic structure of the Galaxy, but to a bias in the previous methods of deriving the $\gamma$-velocities (cross-correlation, Gaussian fit of the spectral line), most likely due to these $A_{\gamma}V_{\gamma}$linear relations. By using only one metallic line to derive the $\gamma$-velocity, one can make, for instance, an error (or find inconsistencies) ranging from -2 to +1 km s^-1. Finally, our results are thus consistent with an axisymmetric rotation model of the Milky Way.

Figure 2: $RV_{{\rm c}}$ a) and A b) are represented as a function of the pulsation phase for three spectral lines in the case of $\beta$ Dor: Fe I 4896.4 (dashed line), Fe I 5373.7 (solid line), and Fe I 6024.1 (dot-dashed line). The $RV_{{\rm c}}$ curves include only the GCD $\gamma$-velocity correction. The actual measurements (crosses) are only indicated in the case of the Fe I 5373.7 line. The corresponding uncertainties are too small to be visible in the plot. Horizontal lines correspond to the average values  $V_{\gamma }$ and  $A_{\gamma }$of the interpolated curves, respectively. c) $RV_{{\rm c}}-A$plots and the corresponding ( $A_{\gamma }$, $V_{\gamma }$) average values (crosses) for the three different lines. Although the $RV_{{\rm c}}-A$ plots have different shapes, the average values are aligned. (d) Generalization of diagram  c) for all spectral lines. The $RV_{{\rm c}}-A$ plots are not included for clarity. The upper values are without any correction except the GCD $\gamma$-velocity. The origin of the plot is then used as a physical reference for all spectral line $\gamma$-velocities of the star (lower values). The $V_{\gamma } A_{\gamma }$ correlation found is a strong indication that $\gamma$-velocities are related to intrinsic physical properties of Cepheids' atmospheres.

Open with DEXTER

Figure 3: Same as Fig. 2d for all Cepheids of our sample. The origin of the $V_{\gamma } A_{\gamma }$ plots are used as physical references. The correction applied ( $V_{\gamma \star }=V_{\gamma }{\rm GCD}+b_{{\rm0}}$), together with the slope values ( $a_{{\rm0}}$), are indicated in Table 1. In the last panel an weighted average is done over all stars. The resulting $V_{\gamma } A_{\gamma }$ linear curve is very precise ( $a_{{\rm0}}=0.15 \pm 0.01$).

Open with DEXTER

4.2 $\gamma$-asymmetries

Different aspects of the $\gamma$-asymmetries must be pointed out.

• The $\gamma$-asymmetries are different from one spectral line to the other. This was the motivation for our  $A_{\gamma}V_{\gamma}$relations. Moreover, $A_{\gamma }$ can be positive or negative;

• given the precision of our data, we find no particular link between the line depth (i.e. where the line forms within the atmosphere, see Paper II) and the $\gamma$-asymmetries. Moreover, no relation was found between the $\gamma$-asymmetries and the wavelength;

• in order to investigate phase shifts, which might be related to the $\gamma$-asymmetries, we integrate radial velocities over time (after correcting by the corresponding $V_{\gamma}(i)$) and obtain the radius as a function of the pulsation phase for different spectral lines. Such phase shifts are observed clearly only for R TrA and RS Pup (see Fig. 4);

• one can see in Fig. 2b that the difference in asymmetry between the Fe I 6024.8 Å (dot-dashed line) and Fe I 4896.4 Å (dashed line) asymmetry curves is surprisingly almost constant with the pulsation phase. Even it is not a general rule (see solid line of Fig. 2b), this effect is frequent in our data, and seems to be important to understand the meaning of the $\gamma$-asymmetries;

• although the $A(\phi)$ and $RV_{{\rm c}}(\phi)$ curves vary in phase, there is no strict correlation between the line asymmetry $A(\phi)$ and the radial velocity $RV_{{\rm c}}(\phi)$as a function of the pulsation phase $\phi$ (see Fig. 2c). The slope and shape of the $RV_{{\rm c}}-A$ curves depend on the limb-darkening, the spectral line width, and the rotation velocity. However, the loop and the shift in asymmetry ($\gamma$-asymmetry) are mainly due to the dynamical structure of the Cepheid atmosphere. They cannot be explained by static geometrical models of pulsating stars (see Paper I for details);

• in the stellar rest frame (defined by $V_{\gamma \star}$), one has for a given spectral line and at a specific pulsation phase $\phi$, $RV_{{\rm c}}(\phi)=0$ while $A(\phi)\ne0$ or, on the contrary, $A(\phi)=0$ but $RV_{{\rm c}}(\phi)\ne0$; i.e. $RV_{{\rm c}}(\phi)=0$ does not imply $A(\phi)=0$;

• interestingly, we find a relation between the $\gamma$-asymmetries and the pulsation period of Cepheids. In particular, if we define $\langle A_{\gamma} \rangle$ as the average of the  $A_{\gamma }$ quantity over all spectral lines for a given star, then we find the following linear relation
  
  $$\langle A_{\gamma} \rangle = [-1.6 \pm 0.3]\log P +[6.7 \pm 0.9],$$
  
  
  where P is the period in days of the Cepheid. The reduced $\chi^{2}$ we obtain is 6. This relation (hereafter $\langle A_{\gamma} \rangle$) is represented by Fig. 5. We already presented such a relation in Paper I for the Fe I 6056.005 Å  spectral line. This new relation can be considered as a generalization over all spectral lines of our sample;

What could explain the observed $\gamma$-asymmetries? To answer this question, we investigate three different hypotheses: (1) the limb-darkening variation with time and within the spectral line; (2) velocity gradients; and (3) the relative motion of the line-forming region compared to the corresponding mass elements.

Figure 4: Radius (in solar radii) as a function of the pulsation phase for spectral lines of our sample. The radial velocity curves have been corrected from their $\gamma$-velocities in order to investigate phase shifts. Important differences are found from one line to the other, which are mainly due to the velocity gradient within the atmosphere. Actually, there is a linear relation between the amplitude of the radius variation and the line depth (see for instance Fig. 4 of Paper II). This indicates why it is essential to use dynamic projection factors. A phase shift is observed only for R TrA and RS Pup.

Open with DEXTER

	Figure 5: $A_{\gamma }$ averaged (without weighting) over all lines is given as a function of the pulsation period of the star. The plot is a generalization of Fig. 14a of Paper I.
Open with DEXTER

(1)

The time- and wavelength dependence of the limb-darkening within the spectral lines does not explain why the line asymmetry is not zero when the radial velocity is zero. When for instance the star is at minimum or maximum expansion (i.e. radial velocity is zero), whatever the limb-darkening distribution might be, if there are no dynamical effects within the atmosphere, then the spectral line should be symmetric. This is clearly not what we observe. Consequently, the time- and wavelength dependence of the limb-darkening may have some effects on the variation of line asymmetry over the pulsation phase, but it can not be responsible for all properties mentioned above.

(2)

Velocity gradients in the atmosphere can indeed cause an asymmetric spectral line. Line asymmetry $A(\phi)$ and radial velocity $RV_{{\rm c}}(\phi)$ basically vary in phase, even if there is not a strict correlation. This is thus a strong indication that radial velocity gradients are, to some degree, responsible for the line asymmetries in these stars. However, they cannot explain, for instance, the systematic shift in asymmetry (almost constant with the pulsation phase) observed between the 6024.8 Å and Fe I 4896.4 Å spectral line (Fig. 2). Butler et al. (1996) introduced a number of velocity gradients in their model. They found that ``the effect of this velocity gradient is to reduce the amplitude of the pulsational velocity curve at optical depth of $\tau = \frac{2}{3}$ by $20\%$ and to decrease the $\gamma$-velocity by 2 km s<sup>-1</sup> relative to the standard assumption of a comoving atmosphere''. However, the main differences they obtain in their velocity curves are near extrema. For instance, in their Fig. 11, all curves (with and without velocity gradient) vanish at the same pulsation phase. This is not what we observe in our Fig. 2a, where systematic shifts are obtained. In their study, Butler et al. (1996) applied a ``closure'' constraint: ``It is assumed that each layer of the stellar atmosphere returns to its starting position after a pulsation cycle''. Thus, let us now discuss the last hypothesis:

(3)

The relative motion of the line-forming region with respect to the corresponding mass elements. When the line-forming region moves relative to the background atmospherical structure, it will also move with respect to the background velocity field. Thus, the line experiences an apparent change in velocity, which has a comparable effect as a velocity gradient, but with a lower intensity. This explains why line-forming regions do not comply with the path conservation, as discussed in the introduction. However, this cannot explain, for instance, the systematic shift in asymmetry (or in velocity) observed between the 6024.8 Å and Fe I 4896.4 Å spectral lines. Indeed, it would mean that the line-forming regions corresponding to these two spectral lines have a systematic relative motion ( $V_{\gamma }$) compared to the background, whatever the pulsation cycle considered. Either there are cycle-to-cycle differences in the path of the line-forming regions (which we cannot confirm with our data) or one should invoke another physical explanation.

5 Conclusions

We found $\gamma$-asymmetries varying from one spectral line to another, as well as a global dependency on the period of the star or, correspondingly, on the spatial extension of the Cepheids' atmosphere. Right now, we have no clear physical explanations for this effect. Most likely, it results from a combination of several effects in the dynamical structure of the Cepheids' atmosphere, such as phase- and wavelength-dependence of the intensity distribution within the different spectral lines, velocity gradients, non-linear pulsational effects, shock fronts, and relative motions between line-forming regions (specific to each spectral line considered) and the material.

In order to further investigate the line asymmetries, improved numerical models are required. Since Cepheids' atmospheres are not in a hydrostatic state but characterized by pulsational dynamics, one has to perform non-linear, time-dependent simulations of the underlying pulsation. Snapshots from this temporal evolution (including the velocity field) can then be used to compute a detailed frequency-dependent radiative transport. In order to resolve narrow features such as shock fronts or sharp ionization regions, high spatial resolution, especially in the line-forming regions, is needed. Although convective transport plays only a minor role in the stellar structure of Cepheids in that temperature range ($\simeq$ $5500~\rm K$, see Table 2 in Paper II), there can still be considerable convective velocities (some km s^-1). As a consequence, the consistent inclusion of the convective velocity field - and of the interaction of convection with pulsation - in the numerical models might be crucial for the computation of line asymmetries. Dynamics in the circumstellar envelope (Kervella et al. 2006; Mérand et al. 2006, 2007; Nardetto et al. 2008) is also important. Confronting such models with observations (spectral line profiles, spatial- and spectral- visibility curves from interferometry) may finally lead the way to a complete picture of the relevant effects in Cepheids' atmospheres.

However, even now, we already have a clear evidence from our observed linear $A_{\gamma}V_{\gamma}$ relation that the residual $\gamma$-velocities (or K-term) seen in Cepheids are the result of the dynamical structure of their atmosphere. This provides a physical meaning to the $\gamma$-velocities and a physical reference: the $\gamma$-velocity should be zero when the $\gamma$-asymmetry is zero. This definition of the $\gamma$-velocities could be used for kinematical studies of the Galaxy, even though this method requires high signal-to-noise and high-resolution spectroscopic observations. Using only one metallic line to derive the $\gamma$-velocity can inflict errors (or inconsistencies) ranging from -2 to 1 km s^-1.

Acknowledgements

Based on observations collected at La Silla observatory, Chile, in the framework of European Southern Observatory's programs 072.D-0419 and 073.D-0136. We thanks Kervella for having provided the HARPS data and Fekety for her careful English correction of the paper. This research has made use of the SIMBAD and VIZIER databases at CDS, Strasbourg (France). This material is based in part upon work by TGB while serving at the National Science Foundation. Any opinions, findings, and conclusionsor recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation. N.N. acknowledges the Max Planck Institut for Radioastronomy for financial support.

References

• Burki, G., Mayor, M., & Benz, W. 1982, A&A, 109, 258 [NASA ADS] (In the text)
• Butler, R. P., Bell, R. A., & Hindsley, R. B. 1996, ApJ, 461, 362 [NASA ADS] [CrossRef] (In the text)
• Caldwell, J. A. R., & Coulson, I. M. 1987, AJ, 93, 1090 [NASA ADS] [CrossRef] (In the text)
• Camm, G. L. 1938, MNRAS, 99, 71 [NASA ADS] (In the text)
• Camm, G. L. 1944, MNRAS, 104,163 (In the text)
• Fernie, J. D., Beattie, B., Evans, N. R., & Seager, S. 1995, IBVS, 4148 (In the text)
• Freedman, W., Madore, B. F., Gibson, B. K., et al. 2001, ApJ, 553, 47 [NASA ADS] [CrossRef] (In the text)
• Fouqué, P., Arriagada, P., Storm, J., et al. 2007, A&A, 476, 73 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Gautschy, A. 1987, Vistas Astron., 30, 197 [NASA ADS] [CrossRef] (In the text)
• Kervella, P., Nardetto, N., Bersier, D., et al. 2004, A&A, 416, 941 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Kervella, P., Mérand, A., Perrin, G., & Coudé Du Foresto, V. 2006, A&A, 448, 623 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Kurucz, R. L. 1992, The Stellar Populations of Galaxies, IAU Symp., 149, 225 (In the text)
• Mathias, P., Gillet, D., Fokin, A., et al. 2006, A&A, 457, 575 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Mérand, A., Kervella, P., Coudé du Foresto, V., et al. 2006, A&A, 453, 155 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Mérand, A., Aufdenberg, J. P., Kervella, et al. 2007, ApJ, 664, 1093 [NASA ADS] [CrossRef] (In the text)
• Moffett, T. J., & Barnes, T. G. III 1987, PASP, 99, 1206 [NASA ADS] [CrossRef] (In the text)
• Nardetto, N., Fokin, A., Mourard, D., et al. 2004, A&A, 428, 131 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Nardetto, N., Mourard, D., Kervella, P., et al. 2006, A&A, 453, 309 [NASA ADS] [CrossRef] [EDP Sciences] (Paper I) (In the text)
• Nardetto, N., Mourard, D., Mathias, Ph., et al. 2007, A&A, 471, 661 [NASA ADS] [CrossRef] [EDP Sciences] (Paper II) (In the text)
• Nardetto, N., Mourard, D., Kervella, P., et al. 2007, yCat, 34530309N
• Nardetto, N., Groh, J. H., Kraus, S., et al. 2008, A&A, 489, 1263 [CrossRef] [EDP Sciences] (In the text)
• Parenago, P. P. 1945, PA, 53, 441 [NASA ADS] (In the text)
• Pont, F., Mayor, M., & Burki, G. 1994, A&A, 285, 415 [NASA ADS] (In the text)
• Sabbey, C. N., Sasselov, D. D., Fieldus, M. S., et al. 1995, ApJ, 446, 250 [NASA ADS] [CrossRef] (In the text)
• Sasselov, D. D., & Karovska, M. 1994, ApJ, 432, 367 [NASA ADS] [CrossRef] (In the text)
• Stibbs, D. W. N. 1956, MNRAS, 116, 453 [NASA ADS] (In the text)
• Wielen, R. 1974, A&AS, 15, 1 [NASA ADS] (In the text)
• Wilson, T. D., Barnes, T. G., Hawley, S. L., & Jefferys, W. H. 1991, ApJ, 378, 708 [NASA ADS] [CrossRef] (In the text)

 

  
Online Material

Table 2: $A_{\gamma }$ and $V_{\gamma }$ for all spectral lines of all stars.