A&A 489, 747-754 (2008)
DOI: 10.1051/0004-6361:20077928

The photospheric structure of a solar pore with light bridge

S. Giordano - F. Berrilli - D. Del Moro - V. Penza

Department of Physics, University of Rome ``Tor Vergata'', 00133 Rome, Italy

Received 22 May 2007 / Accepted 25 June 2008

Abstract
Context. Pores are among the photospheric features that form when the magnetic field emerges onto the solar surface. In pores or sunspots, light bridges are bright features that separate umbral areas into two or more irregular regions.
Aims. We study the structure of a solar pore (AR10812) with a light bridge.
Methods. We analyzed both broad-band and narrow-band images acquired with the Interferometric BI-dimensional Spectrometer at the adaptive optics channel of the NSO/Dunn Solar Telescope. Narrow-band images acquired in the photospheric Fe I 709.04 nm line were used to determine the line-of-sight velocity field.
Results. The roundish shape of the pore allows us to derive the radial profiles of both intensity and vertical velocity. The pore has a downward velocity, of about -200 m s-1, and is surrounded by an annular downflow structure with an average velocity of about -300 m s-1 with respect to the nearby quiet sun.
The light bridge shows a long narrow dark structure running along its axis. Corresponding to this dark lane, we measure a weak upflow of about 70 m s-1, flanked by a downflow of about 150 m s-1 with respect to the pore. The topology of this velocity structure resembles a convective roll.
The anticorrelation between continuum intensity and photospheric velocity may be due to the higher gas pressure in a photospheric field-free cusp, above the light bridge, located between two magnetic walls. We present an analytical model capable of reproducing the observations.

Key words: Sun: photosphere - Sun: magnetic fields - Sun: sunspots

1 Introduction

The inhomogeneous and structured aspect of the solar photosphere originates from the interaction between convective flows, which convey energy from the deeper layers of our star, and its magnetic field, emerging at its surface.

The photosphere shows a wide variety of magnetic features, ranging from the largest sunspots with field strengths of up to several kG, to the 0.1 Mm scale magnetic elements with typical field strengths of $\simeq$1500 G. In this family of magnetic structures, pores represent the link between the tiny flux tubes and complex sunspots. For a review about pores and sunspots, see Sobotka (2003) and Thomas & Weiss (2004).

Solar pores have typical diameters of a few Mm at the photosphere and exist for less than a day. The absence of a penumbra has always been interpreted as a sign of the simple magnetic structure of a magnetostatic flux tube with vertical field (Simon & Weiss 1970).

High spatial resolution osbervations indicate that pores are structured (e.g. Sobotka et al. 1999). They contain a wide variety of fine bright features, such as umbral dots or light bridges, that may indicate a convective energy transport. Knowledge of the physical processes responsible for these fine structures is a critical step in understanding their sub-photospheric structure.

Two categories of theoretical models are found to be consistent with observations: a monolithic and inhomogeneous flux tube with magnetoconvection inside (e.g. Thomas & Weiss 2004; Hulburt & Rucklidge 2000, and references therein) or a cluster of single flux tubes (Parker 1979; Choudhuri 1986). Although based on different assumptions, both models predict the presence of fine and bright features embedded in the dark umbra. According to the monolithic model, observed fine features can be related to convective motions that are not completely inhibited in the sub-photospheric layers. According to the cluster model, bright structures are signatures of field-free gas plumes penetrating from below into the photosphere.

Schüssler & Vögler (2006) simulated magnetoconvection in a sunspot umbra in which convective energy was transported by narrow upflow plumes, that became almost field-free close to the surface layers and assumed a cusplike shape in their upper parts. In intensity images, the simulations produce bright features with characteristics similar to those of umbral dots. In particular, umbral dots have an elongated shape with a central dark lane and downflows concentrated at the endpoints.

Concerning the formation of pores, observations (e.g. Wang & Zirin 1992; Keil et al. 1999) reveal that pores result from the merging of small magnetic elements, driven by supergranular and sub-surface flows. According to the model of Rucklidge et al. (1995), there exists a critical magnetic flux, below which the pore size can grow without becoming a sunspot. This model also accounts for the overlap in size between small sunspots and larger pores.

Across a pore, the magnetic field strength exhibits a variation from 600 G to 1700 G, as reported by Sutterlin et al. (1996). This behaviour was confirmed by Keppens (1996), who measured a decrease in the vertical magnetic field component from 1700 G, in the pore centre, to 900 G at its magnetic edge. Magnetic field lines are found to be almost vertical in the centres of pores, but inclined by about $40^\circ {-}80^\circ$ at their boundaries. MHD simulations of an isolated pore (Cameron et al. 2007) reproduced these values approximately for a central vertical field of 2.0-2.5 kG that decayed to 1.5 kG at the visible boundary of the pore (1.1 Mm in that simulation), where the field inclination value reached approximately $\simeq$50$^\circ$.

MHD simulations predict that intense downflows should encircle such magnetic elements, where the downflows are driven by the extra radiative cooling of the plasma surrounding the magnetic elements and fed by horizontal flows of the upper layers. Steiner et al. (1998) demonstrated that downflows should become narrower and more rapid with depth. The simulation by Cameron et al. (2007), for example, showed in the azimuthally averaged profile of the vertical velocity a downflow of -1.5 km s-1 at the photospheric level just outside the pore boundary. Several observations (e.g. Tritschler 2002; Keil et al. 1999) confirmed this prediction in the case of pores. In particular, Sankarasubramanian & Rimmele (2003) reported a $\sim $0.5 $\hbox{$^{\prime\prime}$ }$ wide annular downflow structure around a pore, which was accelerated from -200 m s-1, at $\sim $500 km above the photosphere, to -1800 m s-1 at $\sim $40 km.

Light bridges (hereafter LB) are bright irregular elongated features that divide the umbra of sunspots or pores (Thomas & Weiss 2004; Sobotka 2003), and have a wide range of variability in their morphology and physical properties. Vázquez (1973) proposed a first interpretation of photospheric LBs by claiming that they were produced by sunspot decay preceding the restoration of the granular surface. Hirzberger et al. (2002) suggested a magnetoconvective origin for LBs, since the presence of the magnetic field appeared to reduce the intensity fluctuations of the convective pattern. These findings were supported by Rimmele (1997), who measured a positive correlation between brightness and upflow velocities in a LB.

Observations indicate that LBs have a weakened field in comparison to the nearby umbra and that field strength increases while inclination decreases with height, suggesting that the background magnetic field closes above the LB in a canopy-like configuration (Jurcák et al. 2006). The magnetic canopy (Leka 1997) forms when a field-free region intrudes into the pore, so that the magnetic lines fan out over such a region and are eventually forced into a vertical direction again by the same polarity magnetic field expanding in a similar way from the other part of the umbra.

Although there are no systematic findings about the vertical velocities in LBs (Leka 1997) a correlation between brightness and upflow was reported by Rimmele (1997), which supported the idea of a sub-photospheric convection origin for the LBs. Bharti et al. (2007) demonstrated that a LB velocity structure consisted of two -500/-1400 m s-1 downflows and a 200 m s-1 upflow.

We investigate the characteristics of AR10812, a pore with a light bridge, that formed possibly by the quasi-merging of two pores of the same polarity, as derived from previous day MDI/SOHO magnetograms and continuum images. We focus our study on the line-of-sight (LOS) velocity and intensity profiles of both the pore and light bridge.

The paper is structured as follows: in Sect. 2, we describe the observations, data processing and procedure used to obtain the LOS velocity maps; in Sect. 3, we analyze the physical properties of the pore and light bridge, whose intensity behaviour we explain by means of a simple analytical model. In Sect. 4, we draw our conclusions, propose a sketch for the pore structure and view our findings.

2 Observations and data processing

2.1 Observations


  \begin{figure} \includegraphics[width=9cm,clip]{7928fig1.eps} \end{figure} Figure 1: Broad-band image of the FOV (SLAT = 11.8S, SLONG = 11.1E), including the pore, after applying a Multi Frame Blind Deconvolution (van Noort et al. 2005). The solar north is along the vertical axis.
Open with DEXTER

The data used in this paper were acquired on September, 28th 2005 (from 15:55 UT to 16:41 UT) with the Interferometric BI-dimensional Spectrometer (IBIS, Cavallini 2006), installed at the Dunn Solar Telescope (DST) at the National Solar Observatory. We observed a central region of the solar disk (SLAT = 11.8S, SLONG = 11.1E), including a pore with a light bridge (AR10812).

IBIS is a tunable narrow-band filter, composed of a series of two Fabry-Perot interferometers and a set of narrow-band interference filters, used in a classic mount and axial-mode. This instrument allows us to observe the Sun with high spatial ($\simeq$0.2 $^{\prime \prime }$), spectral ( R=200 000-270 000) and temporal resolution (acquisition rate $\simeq$3 frames s-1 at 1 k $\times$ 1k resolution).

The full dataset consists of 200 sequences, each containing a 16 image scan of the Fe I 709.04 nm line, a 14 image scan of the Fe II 722.45 nm line, and 6 spectral images of the Ca II 854.25 nm line (one line core image and 5 line wing images). For both the Fe I 709.04 nm and the Fe II 722.45 nm lines, a constant wavelength step of 3 pm was used for the scans. Each 512 $\times$ 512 pixel image (pixel scale $\simeq$0.17 $^{\prime \prime }$ pixel-1) was exposed for 25 ms. The time interval between two successive images and two successive spectral sequences was 0.3 s and 14 s, respectively.

In addition to the narrow-band images, G-band (430.5 $\pm$ 1.0 nm) and broad-band (722 $\pm$ 5 nm) images were recorded simultaneously (exposure time = 25 ms).

The High Order Adaptive Optics (HOAO) system of the DST (Rimmele 2004) was routinely used with IBIS to compensate for seeing effects. During our observations, the HOAO lock point was set on the pore, in the upper left angle of the IBIS field-of-view (FOV).


  \begin{figure} \par\includegraphics[width=13cm,clip]{7928fig2.eps} \end{figure} Figure 2: A representative synoptic panel of the analyzed sub-region. Upper left panel: broad-band intensity image. Upper right panel: Doppler velocity field computed from the Fe I 709.04 nm line scan. Bright regions (positive values) denote blueshifts. LOS velocities range between -500 m s-1 and 400 m s-1. Lower left panel: G-band intensity image. Lower right panel: Ca II wing intensity image.
Open with DEXTER

The first step in the data reduction was to correct both the data and the flatfield images for dark current and CCD non-linearity effects. We also had to consider the classical mounting of the two FPIs, which causes a systematic blueshift of the instrumental profile when moving from the optical axis towards the edge of the FOV, therefore reaching its maximum in the outermost pixels. This maximum is about 6 pm at a wavelength of 600.0 nm and about 10 pm at a wavelength of 850.0 nm. This blueshift effect has to be taken into account in the construction of the gain table.

   
2.2 LOS velocity maps

LOS velocity maps were calculated from Gaussian fits to each individual line profile at each spatial position and by transforming Doppler shifts into LOS velocities. In the following, we investigate the dynamics of the pore by limiting our analysis to the Fe I 709.04 nm line, to the Ca II wing, to the G-band, and to the broad-band images; we limit our analysis in this way because most of the fits to the Fe II 722.45 nm line in the pore region failed to converge, due to the shallowness of this line.

The Fe I 709.04 nm line is a magnetically insensitive line and is therefore suited well for Doppler measurements. We follow the convention that receding velocities are negative (see Hirzberger et al. 2003). We set the mean velocity averaged over the entire FOV to zero and therefore we do not take into account the velocity offset due to the convective blueshift (Keil et al. 1999).

The 5 min acoustic oscillations are removed by applying a $k_{\rm h}-\omega$ sub-sonic filter: we cut a cone out of the $k_{\rm h}-\omega$ space, whose outer borders correspond to 7 km s-1.

After applying the sub-sonic $k_{\rm h}-\omega$ filter to the time sequence of continuum intensity, line-core intensity and LOS velocity time-series, we select a region of interest of dimensions about 24 $\hbox{$^{\prime\prime}$ }$ $\times$ 24 $\hbox{$^{\prime\prime}$ }$ centred on the pore (Fig. 2).

By studying the velocity response functions as in Caccin et al. (1977) and Berrilli et al. (2002), we found that the major contribution to the measured velocities in Fe I 709.04 nm line originates in a layer 100 km above the photospheric surface.

To evaluate the error associated with the photometry in the Fe I 709.04 nm LOS velocity measure, we performed a Monte Carlo simulation of 105 lines, using the Fe I 709.04 nm mean profile and associated photon noise. We retrieved a photometric error of 30 m s-1.

3 Results and interpretation

The main subject of our study is a solar pore crossed by a light bridge. The pore structure is analyzed by employing both intensity and velocity maps (Fig. 2). The quasi-regular circular shape of the pore allowed us to study its global properties by analyzing the mean radial behaviour of intensity and velocity. We also investigated the dynamics and brightness profiles of the light bridge.

3.1 Global properties of the pore and nearby region

The emerging intensity and LOS velocity patterns of the observed pore and nearby region enabled us to investigate the radial structure of the pore and the convective regimes associated with different areas, inside and around the pore.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{7928fig3.eps} \end{figure} Figure 3: Plot of the Fe I 709.04 nm mean LOS velocity (upper panel) and mean continuum intensity (lower panel) as a function of radial distance from pore centre. Error bars for LOS velocity and for intensity were calculated to be standard deviations from the mean. In the lower panel, the derivative of the mean radial intensity (dotted) is also reported, which has a maximum that defines the pore boundary.
Open with DEXTER

We performed circular cuts through the geometric barycentre of the pore on the mean intensity and velocity maps. Along each circle, the azimuthal average of the intensity and velocity is computed to obtain radial profiles (Fig. 3). The mean maps were computed by averaging the 200 Fe I 709.04 nm continuum intensity and LOS velocity maps. The light bridge region was masked to exclude its contribution to the mean radial profiles.

It is worth noting that the simulated radial profiles of the emergent intensity and LOS velocity of solar pores, performed by Cameron et al. (2007), qualitatively had the same appearance as our observations (Fig. 3).

Three different regions of interest can be defined from the mean radial velocity profile. The first one, corresponding to the pore, is a quasi-plateau of about -200 m s-1, with respect to the mean granular velocity of the quiet sun. The second region, corresponding to the annular downflow surrounding the pore, is characterized by a mean value of about -300 m s-1 and rms fluctuations of $\simeq$100 m s-1. The third region is the nearby quiet sun, whose velocity was set to zero (Sect. 2.2).

The comparison of LOS velocity and intensity mean radial profiles shows that the position of the velocity minimum is beyond the pore boundary, as defined by the maximum of the intensity derivative at 2.7 $^{\prime \prime }$ from the pore centre, and just precedes the intensity plateau corresponding to the quiet sun granulation.

Using this information we define three regions. In particular, using the intensity derivative maximum, we define the pore as the region included in a circle of 2.7 $\hbox{$^{\prime\prime}$ }$ (the inner circle of Fig. 4, upper panel), excluding the light bridge. Using the velocity information, we define the rim as the region surrounding the pore up to 4.6 $\hbox{$^{\prime\prime}$ }$ from its centre (the region between the two circles in Fig. 4, upper panel). We take as reference a normal granulation region further away (from 6.1 $\hbox{$^{\prime\prime}$ }$ to 8.2 $\hbox{$^{\prime\prime}$ }$) from the pore centre.

In Fig. 4 (lower panel), we plot the time slice of the average LOS velocity in the rim region as a function of $\theta $ (azimuthal angle with respect to the pore centre).

The time slice appears irregular in space and intermittent in time. A strong downflow plume is recurrent in the upper-left boundary of the pore. Similar flow patterns in the regions surrounding magnetic elements and pores were also predicted by MHD simulations (Deinzer et al. 1984; Knölker & Schüssler 1988; Hulburt & Rucklidge 2000; Steiner et al. 1998).

Many observational studies (e.g. Sankarasubramanian & Rimmele 2003; Keil et al. 1999) have reported the presence of intense downward flows close to the edge of the pores, confirmed the results of numerical simulations and therefore support our findings.

As shown in Fig. 4 (lower panel), the downflow channels surrounding the pores are not always closed rings, but their shapes change in time. Hirzberger et al. (2003) found that the maximum velocities in the downflow channels occur in intergranular dark lanes around the pores by analyzing highly resolved Doppler maps. This finding indicates a close relation between the dynamics of these downflow channels and the convective flows close to the pores.


  \begin{figure} \includegraphics[width=9cm,clip]{7928fig4.eps} \end{figure} Figure 4: Upper panel: doppler map of the analyzed pore region averaged over the entire observation time (from 15:55 UT to 16:41 UT). The region inside the innermost circle is the pore region, the region included between the two circles is the rim region ($\sim $2 $^{\prime \prime }$ width). The ticks label the $\theta $ axis used in the projection for the time-slice diagram of the rim region. Lower panel: time slice diagram computed over the rim region.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=9.5cm,clip]{7928fig5.eps} \end{figure} Figure 5: Distributions of Fe I 709.04 nm LOS velocities in three different regions: in the quiet granular region nearby the pore (a), in the rim region (b) and inside the pore (c). All histograms have been normalized to unity area.
Open with DEXTER

To investigate the nature of convective regimes associated with the pore and its neighborhood, we compute the LOS velocity distributions in the three regions previously defined: the pore ($\sim $ $ 7\times 10^4$ pixels), the rim ($\sim $105 pixels), and the nearby region of granulation ($\sim $ $1.3\times 10^5$ pixels). The distributions are shown in Fig. 5.

The velocity distributions of both the pore and quiet granulation regions are nearly Gaussian, while the distribution relative to the rim exhibits extended non-Gaussian exponential tails.

The nearly Gaussian velocity distributions originate in regions where convection occurs in a quasi-steady condition. We observe:

a)
a broad and slightly asymmetric distribution, associated with the normal granulation, with zero mean velocity and standard deviation $\simeq$170 m s-1. The distribution shows a positive skewness that could be interpreted by a surface convection composed of upflows and downflows rather than a hierarchy of eddies (Stein & Nordlund 1998). In this scenario, the distribution can be decomposed into two Gaussian functions, corresponding to the two populations. The computed parameters for the Gaussian function describing the downflows are -50 m s-1 and 290 m s-1 for the mean value and the standard deviation, respectively. In contrast, we measure for the upflows 20 m s-1 and 380 m s-1 for the mean value and standard deviation, respectively. These values are consistent with the interpretation that upflows are warm and have low density (larger scale), while downward plasma converges into rapidly moving filamentary plumes to conserve mass (smaller scale) as it plunges into higher density layers (Stein & Nordlund 1998). This type of convection is present in quiet sun regions characterized by the presence of weak intergranular magnetic features;
b)
a broad non-Gaussian distribution with extended exponential tails due to velocities measured in the rim region. The computed mean value and standard deviation are -270 m s-1 and 140 m s-1, respectively. A variety of hypotheses can be proposed to explain exponential tails in the observed distributions. For instance, in experimental fluid systems, exponential tails can arise when the velocity magnitude exhibits an intermittent behaviour on relevant spatial or temporal scales. A similar behaviour appears to persist in the rim region time-slice (Fig. 4). The non-Gaussian distribution shape may be evidence of the presence of several convective features separated by a structured magnetic field (see Fig. 1 in Cameron et al. 2007);
c)
a narrow, negative, and slightly asymmetric distribution, associated with the pore. The measured mean value and standard deviation are -200 m s-1 and 50 m s-1, respectively.

Whenever the magnetic field inhibits the convective heat transfer in a sufficiently large volume, a pore is formed and velocity fluctuations are reduced. However, the convective energy transfer cannot be suppressed completely and upflow plumes and umbral dots naturally emerge, as pointed out by magneto-convection numerical simulations with radiative transfer under strong field conditions (Schüssler & Vögler 2006).

3.2 Fine structure and dynamics in the light bridge

The pore region observed in the G-band, in the broad-band channel of IBIS and in the red wing of the Ca II 854.25 nm line, is shown in Fig. 2. The corresponding LOS velocity pattern, computed from Doppler shifts of the Fe I 709.04 nm line, is also shown. The pore is crossed by a light bridge.

The most notable feature in the intensity maps shown in Fig. 2 is the dark lane running along the light bridge axis.

To study in detail the structure of the light bridge, we selected the highest quality image and computed three profiles through the light bridge in a direction roughly perpendicular to the dark lane. In Fig. 6 (panels a, b and c), we show the Ca II line wing, G-band, and broad-band intensity profiles. The presence of the dark structure is clearly indicated by the intensity decrease inside the light bridge.

Dark central lanes are a common feature of strong light bridges (Lites et al. 2004; Berger & Berdyugina 2003; Bharti et al. 2007). Their presence is considered to be related to an opacity effect (Spruit & Scharmer 2006; Schüssler & Vögler 2006). We discuss this aspect later in the paper.

We note that a long narrow feature inside the light bridge is also observable in our highest resolution velocity maps. The velocity profiles of the light bridge are shown in Fig. 6d. Such plots show the occurrence of a reversal in intensity and velocity, i.e. an intensity maximum along the light bridge corresponds to the most intense downward velocities. If we choose the mean velocity of the pore as a zero-point reference for the LOS velocity, as in Bharti et al. (2007), we measure a weak upflow of $\simeq$ $ 70~\rm m~s^{-1}$ along the LB axis (in correspondence of the intensity dark lane) and a downflow of $\simeq$ $-150~\rm m~s^{-1}$ along the LB boundary. Bharti et al. (2007), observing a sunspot light bridge, reported a strong downflow of up to 500-1400 m s-1 at the edge of the light bridge and an upflow of around 100-200 m s-1 in the middle part of the LB.

The observed anticorrelation between photospheric intensity and LOS velocity evokes the inverse granulation phenomenon, i.e. the inversion of temperature fluctuations with respect to the velocity field in the upper photospheric layers. However, we observe dark intensity features in continuum images, originating in the base of the photosphere, while the inverse granulation phenomenon involves intensities associated with the upper photospheric layers. The occurrence of the reversed granulation was observed around 120 km above the quiet sun photosphere by Berrilli et al. (2002), in Fe I 537.9 nm and Fe I 557.6 nm photospheric line centre images, around 140 km by Puschmann et al. (2003), using quiet sun slit-spectrograms, and around 200 km by Janssen & Cauzzi (2006), using Fe I 709.04 nm line centre images.

We therefore propose that the reported anticorrelation between the continuum intensity and the photospheric velocities, measured here and by Bharti et al. (2007), both studies of LB features associated with an active region close to the solar disk centre, is a geometric effect due to the superposition of the convective flow pattern with a field free region (i.e., with high opacity). This hypothesis could be verified by LB structures simulations or observations at different $\mu$.

As a final remark, we emphasize that the topology of the observed velocity structure along the light bridge resembles a type of roll patterns found in laboratory experiments of Rayleigh-Bénard convection and may be a signature of modified photospheric convective flows confined by two magnetic walls.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{7928fig6.eps} \end{figure} Figure 6: Plots of the light bridge intensity, in the red wing of the Ca II 854.25 nm line (a), in the G-band (b), in the broad-band channel of IBIS (c), and of the corresponding Fe I 709.04 nm line LOS velocity (d). All profiles were computed across the light bridge and shifted vertically by arbitrary amounts to improve the visualization. Vertical bars mark the light bridge boundaries.
Open with DEXTER

3.3 Interpretation of the light bridge structure

Radiative MHD simulations of light bridges by Nordlund (2007, unpublished) and Heinemann (2006), discussed in Heinemann et al. (2007), indicate how dark lanes over the centre of the light bridges are formed. The dark lanes are a consequence of hydrostatic pressure and radiative energy balance around the ``cusp'' of the magnetic field.

Following an idea proposed by Nordlund and Heinemann, we present an analytical model of the light bridge. The emergent intensity is calculated by considering contributions from the magnetic and non-magnetic areas in the non-polarized radiative transfer equation. An Eddington grey model with a source function $S_{\rm q}(\tau)$, which is linearly dependent on the optical depth $\tau$, is used for the quiet atmosphere:

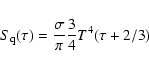\begin{displaymath}S_{\rm q}(\tau) = \frac{\sigma}{\pi}\frac{3}{4}T^4(\tau+2/3) \end{displaymath} (1)

where T is the effective temperature of the quiet sun (5780 K). We adopted for $\tau$ an exponential dependence on geometric depth z:

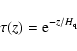\begin{displaymath}\tau(z) = {\rm e}^{-z/H_{\rm q}} \end{displaymath} (2)

where $H_{\rm q}$ is the scale height and is about 60 km (e.g. Kurucz 1994).

We use a depressed model for the magnetic atmosphere, as proposed by Spruit (1976). In our model, the optical depth $\tau_{\rm m}(z)$ is equal to:

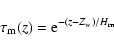\begin{displaymath}\tau_{\rm m}(z) = {\rm e}^{-(z-Z_{\rm w})/H_{\rm m}} \end{displaymath} (3)

where $H_{\rm m}$ is the scale height in the pore and $Z_{\rm w}$ is the Wilson depression, which we set to be 150 km. The relation between $\tau$ and $\tau_{\rm m}$ is $\tau_{\rm m}=w\tau^\alpha$, where $\alpha~=~H_{\rm q}/H_{\rm m}$ and $w={\rm e}^{-z_w \alpha/H_{\rm q}}$. By setting the intensity flux inside the pore to be equal to $\sigma {T^4_{\rm m}}$, where $T_{\rm m}$ is the effective temperature of the magnetic atmosphere ($\simeq$5000 K as derived by the intensity contrast measure inside and outside the pore), we obtain:

$\displaystyle S_{\rm m}(\tau) = \frac{3\sigma}{4\pi}{T^4_{\rm m}} (\tau_{\rm m} +2/3) .$     (4)

To describe the separating surface between the quiet and the magnetic regions, we use $\bar{z}(x)~=~a x^2 + z_0$, where $a=H_{\rm c}/{x_0}^2$, $H_{\rm c}$ is the cusp height, and x0 is one half of the bridge size ($\simeq$500 km). The atmosphere is described by the quiet model for $z < \bar z$ and by the magnetic model for $z >\bar z$. As a consequence, the intensity integral can be split into two terms and, by applying the variable changes between z and $\tau$, we obtain:
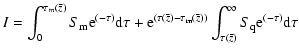$\displaystyle I = \int_{0} ^{\tau_m(\bar{z})} S_{\rm m} {\rm e}^{(-\tau)} {\rm ... ...}(\bar{z}))}\int_{\tau(\bar{z})}^{\infty} S_{\rm q} {\rm e}^{(-\tau)} \rm d\tau$     (5)

which when solved implies that
$\displaystyle I(x)\propto{{T^4_{\rm m}}} \left[5/3 - {\rm e}^{- w \tau({\bar z}... ...ht] + T^4_{\rm m} (5/3 + \tau({\bar z})) {{\rm e}^{-w \tau({\bar z})}}^\alpha .$     (6)

The computed intensity profile, convolved with the Point Spread Function of the telescope, is reported in Fig. 7. The fitting of this profile to the experimental data retrieves the free parameters values: z0=50 km, $H_{\rm c}=220$ km, and $H_{\rm m}=35$ km.

We note that the value of 220 km for the cusp height agrees with the height of about 300 km reported by Lites et al. (2004) for this type of structure.

This analytical model suggests that the dark lanes in light bridges are an effect of basic geometry and thermodynamics. The key parameters are the alignment of the structure along the line of sight and the opacity effect due to the higher gas pressure in the field-free region. The dark lanes are produced by competition between the source function (function of temperature alone) and the opacity (function of both temperature and pressure), where both quantities increase along the light bridge. The dark lane is formed when the opacity becomes the dominant effect, due to the higher gas pressure in the field-free region below the cusp.

  \begin{figure} \includegraphics[width=9cm,clip]{7928fig7.eps} \end{figure} Figure 7: Lower panel: cross-section of the light bridge structure modeled as a field free plasma region trapped by two magnetic flux tubes (grey regions). For the sake of visualization the z axis is not in scale with the x axis. The two atmospheres are shifted by $Z_{\rm w}$ (the Wilson depression). Dotted line indicates the $\tau =1$ level. Upper panel: synthetic emergent intensity (in arbitrary units) across the light bridge computed with the model and convolved with the Point Spread Function of the telescope. For comparison with profiles reported in Fig. 6 we adopt the same spatial scale.
Open with DEXTER

4 Conclusions

A pore with a light bridge (AR10812) was observed at high spatial and spectral resolution. From MDI/SOHO magnetograms and continuum images, we have established that the observed region, initially composed of two structures with the same polarity, disappeared three days after our observation. An MDI magnetogram of the observation day enabled us to relate the observed light bridge properties to the contiguity of two flux tubes of the same polarity.

To investigate the photospheric structure of the pore and nature of the bright structure inside it, we used the photospheric intensity and LOS velocity maps. In particular, we analyzed the intensity images provided by the broad-band channel of IBIS, by the red wing of Ca II 854.25 nm line and by the G-band channel, and simultaneous and cospatial Fe I 709.04 nm line LOS velocity maps.

We summarize the main results of our work as follows:

In Fig. 8 we sketch the observed pore region. We hypothesize that the pore originated from the merging of two separate magnetic structures of the same polarity both surrounded by downward flows. These downflow structures persist in the quenching region (corresponding to the light bridge), where the convection is strongly modified by the presence of a type of magnetic confinement, and also in the rim region. Similar configurations (e.g. Jurcák et al. 2006) are proposed to describe the magnetic canopy above light bridges.

As a final remark, further work is required to interpret the LOS velocity distributions in convective regimes other than those considered here.

  \begin{figure} \par\includegraphics[width=9cm,clip]{7928fig8.eps} \end{figure} Figure 8: Upper panel: schematic cross-section of the observed pore structure showing the sub-photospheric convective flows (grey layer). The sketch is drawn considering two magnetic flux tubes, each derived from the simulation by Hulburt & Rucklidge (2000). Lower panel: plot of the mean Fe I 709.04 nm LOS velocity, obtained by averaging the LOS velocity profiles, computed across the pore structure in a direction perpendicular to the light bridge (dot+spline).
Open with DEXTER

Acknowledgements
The authors thank DST/NSO staff for the efficient support in the observations. We thank K. Janssen for the IBIS data reduction pipeline, M. Sobotka for useful discussions and S. Criscuoli for helpful suggestions. We also thank the anonymous referee for the important remarks. NSO is operated by the Association of Universities for Research in Astronomy, Inc. (AURA), under cooperative agreement with the National Science Foundation. This work was partially supported by the Italian Ministry of Foreign Affairs (MAE) and by a Regione Lazio CVS (Centro per lo studio della variabilitá del Sole) PhD grant.

References

 
Copyright ESO 2008