A&A 489, 741-745 (2008)
DOI: 10.1051/0004-6361:200810146

Long-period oscillations in solar coronal bright points

H. Tian1,2 - L.-D. Xia3 - S. Li2,4


1 - Max-Planck-Institut für Sonnensystemforschung, Katlenburg-Lindau, Germany
2 - Department of Geophysics, Peking University, Beijing, PR China
3 - School of Space Science and Physics, Shandong Univ. at Weihai, Weihai, Shandong, PR China
4 - Department of Physics, Stanford University, Stanford, CA 94305, USA

Received 7 May 2008 / Accepted 20 June 2008

Abstract
Aims. By analyzing TRACE (Transition Region and Coronal Explorer) data, we investigate intensity oscillations in coronal bright points (BPs) as well as the underlying chromosphere.
Methods. A Fourier analysis is applied to a sequence of images observed in the 195 Å and 1216 Å passbands of TRACE. We produce images of Fourier power in three different period ranges (4-16 min, 20-40 min, 42-75 min). The presence of periodic oscillations are further checked by applying a wavelet analysis to a selected rectangular region in each of the three BPs.
Results. We find a clear signature of oscillations with different periods dominating in different strands of BP loops in the 195 Å passband. The oscillatory power is stronger in BPs than in the surrounding quiet Sun. In the chromospheric 1216 Å passband, oscillations in these period ranges are found mainly above the magnetic network elements, which are not necessarily associated with the coronal BPs. The wavelet analyses reveal that oscillations with periods ranging from 8 to 64 min can last for several cycles in both the BPs and the underlying chromosphere.
Conclusions. It is still unclear whether these oscillations are caused by propagating magneto-acoustic waves in loop systems associated with the BPs, or result from recurrent magnetic reconnection powering the BPs.

Key words: Sun: oscillations - Sun: corona - Sun: chromosphere - Sun: UV radiation

1 Introduction

Coronal bright points (BPs) are believed to consist of several miniature dynamic loops (Sheeley & Golub 1979) and are typically $30^{\prime\prime}$- $40^{\prime\prime}$ in size. They are characterized by locally enhanced emission in X-ray, EUV and radio wavelengths associated with the underlying bipolar magnetic field at network boundaries (Habbal et al. 1990; Brown et al. 2001; Webb et al. 1993; Madjarska et al. 2003; Tian et al. 2007; Falconer et al. 1998). The average lifetime of BPs is 20 h in EUV (Zhang et al. 2001) and 8 h in X-ray observations (Golub et al. 1974). BPs are believed to play an important role in coronal heating. They are found to be not directly related to solar wind outflow (Wilhelm et al. 2000; Xia et al. 2003).

From a theoretical point of view, the energization of BPs may result from the interaction between two magnetic fragments of opposite polarities, which can lead to magnetic reconnection and local heating of the plasma (Parnell et al. 1994; Von Rekowski et al. 2006; Priest et al. 1994). The radiation power of BPs may also be supplied by magnetic reconnection along separator field lines (Longcope 1998), or by current sheets induced by photospheric motion (Büchner 2006; Santos & Büchner 2007). McIntosh (2007) proposed a two-stage heating process, namely the forced magnetoconvection-driven reconnection occurring in cool BPs as seen in He II (304 Å), and fast separator reconnection producing hot BPs emitting in soft X-rays. This scenario has been further supported by Tian et al. (2008).

Coronal BPs have been realized to be highly dynamic and they seem to evolve on a time scale of about 6 min (Habbal et al. 1990; Sheeley & Golub 1979). Ugarte-Urra et al. (2004a) presented the first wavelet analysis for BPs and found that a BP experienced intensity variations on a time scale of 420-650 s. Ugarte-Urra et al. (2004b) extended the initial work to four BPs to confirm the oscillating nature of BPs, and found oscillation periods ranging between 600 and 1100 s.

In this contribution, we report the detection of long-period oscillations (mainly from 8 to 64 min) in three coronal BPs.

2 Observations and data analysis

The data set analyzed here contains a sequence of images observed from 01:00 to 05:00 UTC on June 14 in 1998 in two passbands (1216 Å and 195 Å) of the TRACE instrument. The pixel size is $1.0^{\prime\prime}$. Standard software for calibrating and correcting the TRACE data was applied to this data set, including removal of cosmic rays, subtraction of the dark current, normalization of the counts, and so on. We used the standard procedure Correl_Images.pro, which is available in the astronomical IDL software package, to coalign the images in the sequence. This procedure computes the 2-D cross-correlation function of two images for a range of (x, y) shifts by pixels of one image relative to the other, and obtains the best correlation between the two images. All the images were cross-correlated to an image observed at about 03:00 UTC.

We extracted a sequence of sub-images with a size of $170^{\prime\prime}\times90^{\prime\prime}$ from the original data set. There were three BPs seen in the sub-images of the 195 Å passband. The average intensity images of the studied region in the 1216 Å and 195 Å passbands can be found in Fig. 2A and E, respectively. Figure 1 shows the high-resolution ( $1.2^{\prime\prime}$) MDI magnetogram (Scherrer et al. 1995) corresponding to the studied region. The bipolar magnetic fields associated with the BPs are clearly seen in the magnetogram.


  \begin{figure} \resizebox{8.8cm}{!}{\includegraphics{0146fig1.eps}}\end{figure} Figure 1: MDI magnetogram of the studied region taken at 03:04 UTC on June 14 in 1998. The white contours correspond to bright lanes seen in the averaged image of the 1216 Å passband.
Open with DEXTER

The cadence of our TRACE data was about 70 s. For a discrete Fourier or wavelet analysis, regular time spacing is required. However, at a few moments there were irregular gaps. This problem was overcome by using a linear interpolation with the help of the INTERPOL function in the IDL software. Since our main concern is the fluctuation of the BP emissions, it is better to disregard the general trend of the increase/decrease in the time sequence of emissions.Thus, we created a sequence of running difference images, by subtracting each image from the image taken 70 s earlier. This sequence was further analyzed to search for periodic signatures.

We applied a standard Fourier analysis to the sequence of running difference images of each passband. At each spatial pixel, we obtained a frequency-power curve. Then we added the total power respectively in three different period (frequency) ranges. In this way we can obtain a power map in each period range. The three period ranges are 4-16 min, 20-40 min, and 42-75 min. The power maps can be found in Fig. 2. This Fourier analysis provides an initial insight into the oscillatory behavior and indicates potential features for wavelet analysis.


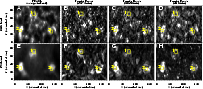  \begin{figure} \resizebox{18cm}{!}{\includegraphics{0146fig2.eps}}\end{figure} Figure 2: Panels A-D: The average intensity image of the 1216 Å passband, and maps of Fourier power in period ranges of 4-16 min, 20-40 min, and 42-75 min. Panels E-H: similar to panels A-D, but for the 195 Å passband. The regions outlined in yellow are analyzed with a wavelet transform.
Open with DEXTER

Then we selected a rectangular region in each of the three BPs, and applied a wavelet analysis to the image sequence spatially averaged in this region, in order to determine both the dominant periods of variability and how those periods vary in time. These regions are shown in Fig. 2 and outlined in yellow. The reason why we chose these three regions is that the coronal Fourier power in each region is much more significant in one period range than the other two. A first inspection of Figs. 2F-H gives us an impression that region 1, 2 and 3 has a dominant oscillatory power in the period range of 42-75 min, 20-40 min, and 4-16 min, respectively. The running difference light curves in the selected regions were smoothed over 3.5 min as we are mainly interested in those oscillations with relatively long periods. Panels (a) of Fig. 3 show these light curves.

We chose the Morlet wavelet for our analysis. The wavelet transform suffers from edge effects at both ends of the time series. This effect is important in regions defined as the ``cone of influence'' (COI). In order to check whether the periodic signatures present in the wavelet spectrum are real or not, we have to perform a significance test. Here only locations with a confidence level higher than 99% are considered real. The description of the wavelet function, COI, and significance test can all be found in Torrence & Compo (1998).

The wavelet power spectra of the three regions are shown in Fig. 3. Cross-hatched regions indicate the COI. The darker parts represent higher power, and the contours correspond to the 99% confidence level. We also averaged each wavelet power spectrum over time and plotted the global wavelet spectrum.


  \begin{figure} \par\mbox{\includegraphics[width=8.8cm]{146fig3a.eps}\includegrap... ...h=8.8cm]{146fig3e.eps}\includegraphics[width=8.8cm]{146fig3f.eps} } \end{figure} Figure 3:  Wavelet power spectra of the 1216 Å ( left side) and 195 Å ( right side) passbands for the three selected regions (corresponding to the three double-rows). a) The running difference light curve. b) Time/period variation of the wavelet power spectrum. Cross-hatched regions indicate the ``cone of influence''. The darker parts represent higher power, and the contours correspond to the 99% confidence level. c) Global wavelet.
Open with DEXTER

3 Results and discussion

The main objective of this work is to search for a signature of long-period oscillations in coronal BPs. By applying a Fourier and wavelet analysis, we find that prominent long-period oscillations do exist in our 4-h-duration data.

We can see from Figs. 2F-H that the oscillatory power is stronger in coronal BPs than in the surrounding quiet Sun, in all of the three period ranges. The chromospheric oscillatory power in different period ranges (Figs. 2B-D) is also stronger beneath coronal BPs than in the surrounding internetwork regions, which might indicate that the coronal oscillations could be a result of the upward propagating chromospheric oscillations. However, not all of the strong chromospheric oscillations have a counterpart in the corona. The stronger oscillatory power in the chromosphere seems to be located in the network elements, especially in the period range of 4-16 min. These strong oscillations might partly be due to the leakage of low-frequency photospheric oscillations through ``magneto-acoustic portals'' positioned within the network (Jefferies et al. 2006). It might provide a significant energy source to heat the quiet chromosphere (Vecchio et al. 2007).

The distribution of strong power in the 195 Å passband presented in Figs. 2F-H reveals an interesting pattern. It seems that the strong power appears as 2-4 strips in each BP. If we compare these bright strips with the magnetic polarities seen in Fig. 1, we can conclude that these strips are very likely to correspond to different strands of the loop system associated with the BP. We find that the dominant period is different in different BP and even in different strands of the same BP loop.

Ugarte-Urra et al. (2004a,b) performed a wavelet analysis for coronal BPs, and found an oscillation with a period from around 400 s up to 1100 s in BPs. Here from the wavelet spectra of the 195 Å passband in Fig. 3 we find that the oscillatory power of the BPs in our data peaks at different periods. For region 1, we find three peaks are present, corresponding to three components with periods around 16, 32, and 64 min, respectively. Each component lasts for 3-4 cycles. The dominant period for region 2 is about 32 min and it is present almost for the entire duration (about 6 cycles). A 12 min period is also significant and appears for three times, each lasting for 2-3 cycles. As for region 3, the dominant oscillation period is around 12 min, which lasts for 3 cycles before reappearing and lasts for about 10 cycles. A secondary peak at about 28 min is also found in the second half of the duration and lasts for 2-3 cycles. These periods are reported for the first time in coronal BPs.

The emission of the 1216 Å passband (50% $\rm Ly\alpha$ at $1{-}3\times10^{4}~$K, plus UV continuum at $4{-}10\times10^{3}~$K) is formed in the middle chromosphere, above the temperature minimum (McAteer et al. 2004). For each of the 3 selected regions, the wavelet result in the 1216 Å passband reveals a similar dominant period to the 195 Å passband. Although we know that the magnetic structure expands and perhaps inclines from the chromosphere to the corona, it still seems to be reasonable that the coronal oscillations might at least partly be linked to the chromospheric oscillations. We noticed in Ugarte-Urra et al. (2004b), the authors found that the BP oscillation periods are in the period range of the chromospheric network oscillations. They concluded that a fraction of the network bright points are most likely the cool footpoints of the tiny loops which comprise coronal bright points. It is also possible that this is the case in our data.

At first sight, the three main periodicities (16, 32, and 64 min) are multiples of each other, which implies that they may be different harmonics of the same mode. However, from the light curves in Fig. 3 we find clear signatures of periods around both 16 and 32 min. Thus, we think the 16-min and 32-min periods are independent. For the 64-min period observed in region 1, it is hard to draw a conclusion because it corresponds to one fourth to one third the length of our time series. Generally, we should not expect such a long period of consistency (3-4 cycles) between small-scale chromospheric and coronal structures. Further investigation of this problem is needed.

Long-period oscillations have been found in open coronal structures. Quasi-periodic perturbations with periods of 10-15 min (DeForest & Gurman 1998) and 10-25 min (Banerjee et al. 2000) were found in polar plumes. These low-frequency perturbations are explained as compressive waves (such as sound waves or slow-mode magneto-acoustic waves) propagating along the plumes (Ofman et al. 1999). Long period (20-30 min) compressional waves were also found in polar coronal holes (Banerjee et al. 2001). More recently, Popescu et al. (2005) detected very long ($\approx$170 min) and long (10-90 min) period oscillations above the solar limb. The authors suggest that these intensity fluctuations might be due to waves or a recurrent magnetic reconnection process. In closed coronal structures like AR loops, long-period oscillations have not been well investigated. BPs are small-scale closed field structures; Ugarte-Urra et al. (2004b) detected oscillations with long period ranging from 600 s to 1100 s in BPs, which were interpreted in terms of global acoustic modes driven by magnetic reconnection events.

In order to check whether or not our detected periods are within the theoretical constraints of propagating magneto-acoustic waves, we calculated the acoustic cutoff periods in the chromosphere and corona. The sound speed is given by:

 \begin{displaymath}c_{\rm s}=\left(\frac{2\gamma kT^{1/2}}{m_{\rm p}}\right)^{1/2} , \end{displaymath} (1)

where $c_{\rm s}$, $\gamma$, k, T, $m_{\rm p}$ are the sound speed, ratio of specific heat capacities, Boltzmann constant, temperature, and proton mass (Cirtain et al. 2007). We take $\gamma=5/3$, and T=104 K in the chromosphere and $T=1.3\times10^6~$K in the corona. By substituting these value into the above equation, we obtain a sound speed of about 16 km s-1 in the chromosphere, and 180 km s-1 in the corona. Using the relation $P_{\rm ac}=2\pi/(\gamma g/c_{\rm s})$ (O'Shea et al. 2006; Popescu et al. 2005), and taking a value of $\rm0.274~km~s^{-2}$ for the acceleration of gravity, we can obtain a cutoff period of 3.7 min in the chromosphere and 41.3 min in the corona.

Magneto-acoustic waves with periods below these values can propagate upwards, otherwise they will be evanescent. Some of our derived periods are lower than the coronal acoustic cutoff period and thus the corresponding oscillations could possibly propagate upwards along the loops associated with BPs. However, the chromospheric oscillation periods are all longer than the chromospheric acoustic cutoff period. And periods (e.g. the 64 min component) larger than the coronal acoustic cutoff period also exist in our data. We noticed that the acoustic cut-off period can be elevated and oscillations with longer periods can leak into higher layers of the solar atmosphere if the magnetic fields are inclined (Hansteen et al. 2006; De Pontieu et al. 2004; McIntosh & Jefferies 2006). However, we should not draw the conclusion that the long-period oscillations in our data are completely due to propagating magneto-acoustic waves.

As in Popescu et al. (2005), here we suggest another possible mechanism, recurrent magnetic reconnection, to be the cause of the periodic intensity fluctuations in our data. The energization of BPs may result from magnetic cancelation (Parnell et al. 1994; Priest et al. 1994), separator reconnection (Longcope 1998), or current sheets induced by photospheric motion (Büchner 2006; Santos & Büchner 2007). All these proposed mechanisms include magnetic reconnection, which is likely to occur continuously or intermittently at layers from the chromosphere to the corona during the entire life of a coronal BP. Repetitive or recurrent reconnection was previously suggested to cause repetitive explosive events with a period of 3-5 min (Doyle et al. 2006) and the very-long-period (170 min) oscillations above the limb (Popescu et al. 2005). It was previously suggested that separator reconnection provides energy to the BP in the lower right corner of the FOV in Fig. 3 (Brown et al. 2001). Although we do not know whether this reconnection is recurrent, we should not exclude the possibility that repetitive reconnections cause the intensity oscillations with periods ranging from 8 to 64 min in our data.

Acknowledgements

The TRACE satellite is a NASA Small Explorer that images the solar photosphere, transition region and corona with unprecedented spatial resolution and temporal continuity. We thank C. Torrence and G. P. Compo for providing the Wavelet software, which is available at URL: http://paos.colorado.edu/research/wavelets/. We also thank the anonymous referee for his/her careful reading of the paper and for the comments and suggestions.

The work of H. Tian's team at PKU is supported by the National Natural Science Foundation of China(NSFC) under contracts 40574078 and 40436015. H. Tian is now supported by China Scholarship Council for his stay in Germany. L.-D. Xia is supported by NSFC under Grant 40574064 and the Programme for New Century Excellent Talents in University (NCET).

References

 
Copyright ESO 2008