A&A 489, 617-625 (2008)
DOI: 10.1051/0004-6361:200810035
C. Brinch - R. J. van Weeren - M. R. Hogerheijde
Leiden Observatory, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands
Received 23 April 2008 / Accepted 7 July 2008
Abstract
Context. Understanding the gas abundance distribution is essential when tracing star formation using molecular line observations. Variations in density and temperature conditions can cause gas to freeze-out onto dust grains, and this needs to be taken into account when modeling a collapsing molecular cloud.
Aims. This study aims to provide a realistic estimate of the CO abundance distribution throughout the collapse of a molecular cloud. We derive abundance profiles and synthetic spectral lines that can be compared with observations.
Methods. We use a two-dimensional hydrodynamical simulation of a collapsing cloud and subsequent formation of a protoplanetary disk as input to the chemical calculations. From the resulting abundances, synthetic spectra are calculated using a molecular excitation and radiation transfer code.
Results. We compare three different methods to calculate the abundance of CO. Our models also consider cosmic ray desorption and the effects of an increased CO binding energy. The resulting abundance profiles are compared with observations from the literature and are found to agree well.
Conclusions. The resulting abundance profiles agree well with analytic approximations, and the corresponding line fluxes match the observational data. Our method to calculate abundances in hydrodynamical simulations should help comparisons with observations, and can easily be generalized to include gas-phase reaction networks.
Key words: astrochemistry - hydrodynamics - stars: formation - ISM: molecules - ISM: clouds
The study of low-mass young stellar objects (YSOs), from early protostellar cores to T Tauri stars surrounded by disks, involves observations of either the thermal emission from dust grains or molecular line emission. While dust emission yields information about the temperature profile (e.g. Draine & Lee 1984), and, through measurements of the shape of the Spectral Energy Distribution, the evolutionary stage (Adams et al. 1987; Lada & Wilking 1984), spectral lines are the only way to constrain the kinematical properties of YSOs. The interpretation of molecular lines is crucial to the understanding of protoplanetary disk formation and the distribution of angular momentum during these stages of star formation (Evans 1999). However, deriving the gas motion from spectral line profiles is complicated by degeneracies between the velocity field topology, inclination of the angular momentum axis, optical depth, and geometrical effects (Brinch et al. 2007).
In addition to these effects, molecular abundances can vary significant. The gas
abundance is determined by the ongoing chemistry driven by the co-evolving
density and temperature distributions, and to some extent also by the velocity
field. The variation in molecular abundances throughout a YSO may have a huge
impact on line profiles and therefore it is important to understand the
chemistry in interpreting these line profiles. The effect of the chemistry is
enhanced for observations of higher resolution. If observations are completed,
however, at relatively low resolution (![]() 10''), the emission is
broadened over a significant area of the object and a single average value of
abundance is adequate. However, at higher resolution, using
sub-millimeter interferometry (
10''), the emission is
broadened over a significant area of the object and a single average value of
abundance is adequate. However, at higher resolution, using
sub-millimeter interferometry (![]() 1''), the emission is averaged over a
smaller part of the object and variations in the abundance must be taken
into account.
1''), the emission is averaged over a
smaller part of the object and variations in the abundance must be taken
into account.
The problem in determining the abundance distribution was addressed before in the literature. Lee et al. (2004) adopted a semi-analytical approach using a self-similar collapse of an isothermal sphere in which they followed ``fluid-elements''. The chemistry was followed in a series of Bonnor-Ebert spheres during the pre-stellar phase and in a self-similar inside-out collapse during the protostellar phase. This model provided a good analytical description of the early stages of star formation, but, lacking any rotational velocity, no disk was formed in this scenario. Aikawa et al. (2005,2003,2001) followed the chemical evolution of contracting pre-stellar clouds using an approach similar to Lee et al. (2004) but using an isothermal cloud collapse only. Their calculations consideried only the early stages of the star formation process. Jørgensen et al. (2005,2002) introduced the ``drop model'', where chemical depletion occurs as a step function when certain temperature and density conditions of any underlying model are met. While this approach is simple yet quite successful, there may be cases where the abundance changes only gradually and a step function is no longer a good approximation. More recently, Tsamis et al. (2008) calculated the HCO+, CS, and N2H+ abundances and spectra from a simulation of an inside-out collapsing core.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{0035f1a.eps}\includegraphics[width=8.5cm,clip]{0035f1b.eps}
\end{figure}](/articles/aa/full/2008/38/aa10035-08/Timg5.gif) |
Figure 1:
The density ( left panel) and temperature ( right
panel) contours of four time snapshots of the hydrodynamical
simulation. Time progresses from left to right, top to bottom at
|
| Open with DEXTER | |
We investigate the detailed evolution of the gas-phase and solid state abundance of CO in a collapsing, rotating core. We base our study on a hydrodynamical simulation, where we follow the CO freeze-out and evaporation for a number of test particles that flow with the gas. The layout of the paper is as follows: in Sect. 2, we present our numerical simulations and equations used to solve the CO freeze-out chemistry. In Sect. 3, we present three different chemical models and compare our results with observations and the results of previous papers. Sections 4 and 5 provide discussion and a summary, respectively.
Instead of using an analytic description of the gravitational collapse and subsequent disk formation, we use a grid-based two-dimensional axis-symmetric hydrodynamical scheme. The code used was described by Yorke & Bodenheimer (1999) and we adopt in particular the J-type model described in that paper.
The initial conditions of this model are a
![]() isothermal sphere
with a temperature of 10 K and a power-law density slope of
isothermal sphere
with a temperature of 10 K and a power-law density slope of
![]() .
The cloud has an outer radius of
.
The cloud has an outer radius of
![]() m (6667 AU), and an
initial solid-body rotational perturbation of
m (6667 AU), and an
initial solid-body rotational perturbation of
![]() s-1.
The model evolves under the action of gravity, while the temperature is
solved self-consistently using an approximate radiation transfer method.
Angular momentum is transferred by artificial viscosity using an
s-1.
The model evolves under the action of gravity, while the temperature is
solved self-consistently using an approximate radiation transfer method.
Angular momentum is transferred by artificial viscosity using an
![]() -prescription (Shakura & Sunyaev 1973).
-prescription (Shakura & Sunyaev 1973).
The age of the simulated system is described in terms of the initial free-fall
timescale,
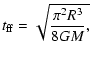 |
(1) |
The luminosity is given by the sum of the intrinsic stellar luminosity and
the accretion luminosity
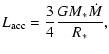 |
(2) |
The hydrodynamical simulation does not include any chemistry and we are therefore
unable to relate the state of the molecules, whether in a gas phase or locked in
an ice matrix, to the hydrodynamics. We therefore determine the abundance
by post-processing the result of the hydrodynamical calculations. We follow the
chemistry by populating the computational domain of the first snapshot with
trace particles. These particles are massless and do not interact with each
other in any way. The trace particles are positioned evenly in the radial
direction and
![]() particles are used. Every trace particle
represents the local molecular environment and carries information about the state
of the molecules (ice or gas). The particles are then allowed to follow the
flow, predetermined by the hydrodynamical calculations, and the state of the
particles is updated as temperature and density conditions change throughout
the hydrodynamical simulation. Finally, the state of the trace particles are
mapped back onto the hydro-grid at each output time step, so that a complete
history from t=0.0
particles are used. Every trace particle
represents the local molecular environment and carries information about the state
of the molecules (ice or gas). The particles are then allowed to follow the
flow, predetermined by the hydrodynamical calculations, and the state of the
particles is updated as temperature and density conditions change throughout
the hydrodynamical simulation. Finally, the state of the trace particles are
mapped back onto the hydro-grid at each output time step, so that a complete
history from t=0.0
![]() to t=2.5
to t=2.5
![]() of the CO abundance as function
of R and z is linked to the density and temperature. Taking the CO
distribution into account, we can use each of these time snapshots as input
models for our two-dimensional line excitation and radiative transfer code RATRAN (Hogerheijde & van der Tak 2000) to predict line profiles of CO and its optically thin
isotopologue C18O.
of the CO abundance as function
of R and z is linked to the density and temperature. Taking the CO
distribution into account, we can use each of these time snapshots as input
models for our two-dimensional line excitation and radiative transfer code RATRAN (Hogerheijde & van der Tak 2000) to predict line profiles of CO and its optically thin
isotopologue C18O.
Before proceeding with the freeze-out calculations, it is interesting to consider the dynamics of the trace particles to develop an understanding of the environments that the particles traverse. By a simple radial color coding of the particles, we can effectively visualize the flow within the hydrodynamical simulation and track how material is accreted onto the disk. Four snapshots of the particle distribution are shown in Fig. 3 where the shading of the particles refers to their initial distance from the center. The disk is seen to be layered vertically rather than radially, which is somewhat counterintuitive. The vertical layering occurs because material connects to the disk from above. As the disk spreads viscously due to conservation of angular momentum, a shock front propagates outwards, pushing aside infalling material. The only possible path for the particles is therefore upwards and over the disk lobe until they can rain down onto the disk at smaller radii. This rolling motion is also reflected in the strong vertical mixing inside the outer disk. However, this behavior may be an artifact of the two-dimensional nature of the hydrodynamical code. In a 3D simulation, particles should also dissipate in the azimuthal direction, which would probably change their motion.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{0035f2.eps}
\end{figure}](/articles/aa/full/2008/38/aa10035-08/Timg16.gif) |
Figure 2: The time evolution in the luminosity of the central source in the hydrodynamical simulation. This figure compares with Fig. 7 in Yorke & Bodenheimer (1999). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{0035f3.eps}
\end{figure}](/articles/aa/full/2008/38/aa10035-08/Timg17.gif) |
Figure 3:
Trace particle motion in the hydrodynamical simulation. The
particles are color-coded according to their initial radial
position. Contour lines describe the density. The vertical color bar
shows the particles initial distance from the center. The four panels ( from the
top-left to bottom-right) show the particle positions at t=0.0, 0.5,
1.5, and 2.5
|
| Open with DEXTER | |
Molecular gas abundances in general depend on reaction rates and phase transitions. However, under the physical conditions present in our model, only the latter has any significant impact on the CO abundance. The state of CO is governed by rate equations. The two main mechanisms are depletion, where gas phase molecules freeze-out onto grains, and desorption, where solid state molecules evaporate into the gas phase.
The depletion rate ![]() used in this paper is given by the equation (e.g. Charnley et al. 2001),
used in this paper is given by the equation (e.g. Charnley et al. 2001),
A similar equation can be written for the desorption of molecules. The thermal
desorption rate is given by Watson & Salpeter (1972),
A second desorption mechanism that is taken into account is cosmic-ray induced
desorption. This mechanism was first proposed by Watson & Salpeter (1972). Energetic
nuclei might eject molecules from grain surfaces by either raising the
temperature of the entire grain or by spot heating close to the impact site. The
formulation of Hasegawa & Herbst (1993) is used to calculate the cosmic ray
desorption rate,
By considering the depletion and desorption rates and defining ![]() to be the
normalized fractional depletion, we can write an equation for
to be the
normalized fractional depletion, we can write an equation for ![]() ,
,
Equation (6) is a general one and the rate functions can be changed readily to describe other reactions. In principle, van Weeren (2007) shows that an entire set of these equations can be solved simultaneously using gas phase reaction rates such as the UMIST database (Woodall et al. 2007), although computational demand becomes an issue for a full network.
To obtain abundance distributions, we evaluate Eq. (6) using the gas
temperature ![]() ,
the dust temperature
,
the dust temperature ![]() ,
and the mass density, assuming
that H2 is the main mass reservoir and that the gas-to-dust ratio is 100:1,
from the hydrodynamical simulation. We assume that the cloud has been in
hydrostatic equilibrium prior to collapse for
,
and the mass density, assuming
that H2 is the main mass reservoir and that the gas-to-dust ratio is 100:1,
from the hydrodynamical simulation. We assume that the cloud has been in
hydrostatic equilibrium prior to collapse for
![]() s). The density profile before collapse is given by a
spherical power-law of uniform temperature described in Sect. 2. Starting with a pure gas phase abundance of
s). The density profile before collapse is given by a
spherical power-law of uniform temperature described in Sect. 2. Starting with a pure gas phase abundance of
![]() molecules relative to H2, we allow the abundance to evolve for
molecules relative to H2, we allow the abundance to evolve for
![]() yr with a constant temperature of 10 K and a static density profile. The
new CO abundance then serves as the initial condition for the collapse, i.e. the start
of the hydrodynamical simulation, which defines t = 0. In the following, we
present three different ways to obtain the abundance profiles.
yr with a constant temperature of 10 K and a static density profile. The
new CO abundance then serves as the initial condition for the collapse, i.e. the start
of the hydrodynamical simulation, which defines t = 0. In the following, we
present three different ways to obtain the abundance profiles.
This approach is denoted the drop abundance model, because it follows directly from the method presented by Jørgensen et al. (2005). In this approach, we do not solve Eq. (6), but consider the rate Eqs. (3) and (4). The rate equations are inverted to obtain a characteristic timescale, and, at any given time in the simulation, this timescale is evaluated based on the current density and temperature conditions. If the freeze-out timescale is shorter than the evaporation time scale, the gas phase abundance drops to a preset level (which is sufficiently low, i.e. several orders of magnitude) but if the actual age of the cloud is shorter than the freeze-out timex scale, the gas phase abundance is kept at its initial value. Using this approach, the resulting profile is a step function where all CO is either in the gas phase or in the solid state. The movement of the trace particles does not affect the result since the abundance is determined only from the current local conditions. By ensuring that the abundance decreases by only two or three orders of magnitude and not to zero, the effect of cosmic ray desorption is modeled implicitly, even though conditions for freeze-out are met.
![\begin{figure}
\par\includegraphics[width=8.3cm]{0035f4a.ps}\\
\hspace*{3.8mm}\includegraphics[width=6.6cm]{0035f4b.eps}
\end{figure}](/articles/aa/full/2008/38/aa10035-08/Timg36.gif) |
Figure 4: This figure shows the abundance distribution of Model 1. The top panel shows the radial abundance profile through the mid-plane of the disk. The bottom panel shows the spatial abundance distribution. The shaded area is where molecules are frozen out. The unit on the y-axis of the top panel is fractional abundance. |
| Open with DEXTER | |
The result is shown in Fig. 4. The top panel shows the radial
abundance profile along the disk mid-plane (z=0), while the lower panel shows
the two dimensional distribution. The result of this drop abundance model
supports the idea of an evolution in the CO abundances from a pre-stellar core
to a Class I object, as proposed by Jørgensen et al. (2005). The maximum size of
our depleted zone is ![]() 6000 AU, just before collapse sets in, and
shrinks to
6000 AU, just before collapse sets in, and
shrinks to ![]() 500 AU (when averaged in radial and polar directions) as the
cloud collapses and the disk is formed. The inner evaporated zone has a radius
of
500 AU (when averaged in radial and polar directions) as the
cloud collapses and the disk is formed. The inner evaporated zone has a radius
of ![]() 1000 AU, in agreement with values derived in Jørgensen et al. (2005).
1000 AU, in agreement with values derived in Jørgensen et al. (2005).
The second method is similar to Model 1 except that instead of using timescales,
we use the actual rate equations that allow the trace particles to be
in a mixed state. The values for ![]() and
and ![]() are calculated for all
are calculated for all
![]() using the current
using the current
![]() and
and
![]() ,
and
Eq. (6) is solved to obtain the fraction of gas phase CO to solid
state CO for each trace particle position. In this model, we still do not
consider the history of the trace particles and the motion of the
particles is therefore irrelevant and the time dependence of
,
and
Eq. (6) is solved to obtain the fraction of gas phase CO to solid
state CO for each trace particle position. In this model, we still do not
consider the history of the trace particles and the motion of the
particles is therefore irrelevant and the time dependence of ![]() and
and ![]() in
Eq. (6) becomes negligible. Plots of the abundance distributions are shown in
Fig. 5. The profiles of Model 2 are similar to those from
Model 1, except for the gradual change from pure gas phase to pure solid state.
The inner edge in particular is described well by the step function of Model 1
because of the exponential factor in the evaporation, described by Eq. (4). The main difference between the two models is the outer edge, and
in particular at earlier times, where the gradient is more shallow.
in
Eq. (6) becomes negligible. Plots of the abundance distributions are shown in
Fig. 5. The profiles of Model 2 are similar to those from
Model 1, except for the gradual change from pure gas phase to pure solid state.
The inner edge in particular is described well by the step function of Model 1
because of the exponential factor in the evaporation, described by Eq. (4). The main difference between the two models is the outer edge, and
in particular at earlier times, where the gradient is more shallow.
![\begin{figure}
\par\includegraphics[width=8.3cm]{0035f5a.ps}\\
\hspace*{3.8mm}\includegraphics[width=7.5cm]{0035f5b.eps}
\end{figure}](/articles/aa/full/2008/38/aa10035-08/Timg41.gif) |
Figure 5: Abundance distribution of Model 2. Otherwise identical to 4. |
| Open with DEXTER | |
Our final model takes the motion of the trace particles and their chemical history into account. Freeze-out and evaporation rates are calculated dynamically for each time step and the composition of the particles is used as the initial conditions for Eq. (6). For example, the depletion in a certain area represented by a trace particle depends on where this particle has originated, which we know because the trace particles follow the flow calculated in the hydrodynamical simulation. Two trace particles may pass by the same region at the same time and experience the same desorption and depletion conditions. However, they may have originated in different areas; for example, one particle may have originated in a warmer region and the other may have travelled from a colder region, and they will then leave the location with different compositions.
Figure 6 shows the abundance distributions for this model. Surprisingly, the profiles do not differ significantly from those of Model 2. A difference only occurs when the dynamical timescale is comparable to the chemical timescale. In this case, a gas phase trace particle may move out of a depletion zone more rapidly than depletion can make any significant change to its composition, or vice versa. The evaporation front around the disk is also sharper with respect to Model 2, which causes Model 3 to appear almost like a step function in the final part of the simulation.
![\begin{figure}
\par\includegraphics[width=8.3cm]{0035f6a.ps}\\
\hspace*{3mm} \includegraphics[width=7.5cm]{0035f6b.eps}
\end{figure}](/articles/aa/full/2008/38/aa10035-08/Timg42.gif) |
Figure 6: Abundance distribution of Model 3. Otherwise similar to 4. |
| Open with DEXTER | |
We now investigate the effects of excluding the cosmic ray desorption term
(Eq. (5)) to see what effect this mechanism has on the abundances. We
also increase the CO binding energy ![]() in Eq. (4) to emulate
different ice mantle compositions. In the following, we use Model 3 as a
template.
in Eq. (4) to emulate
different ice mantle compositions. In the following, we use Model 3 as a
template.
Cosmic ray desorption ensures that depletion can never reach 100% as long as cosmic rays are able to penetrate the cloud and remove molecules from the ice matrix. If no other desorption mechanisms are present, dark cold molecular clouds will have a high degree of depletion since thermal desorption is largely ineffective at low temperatures. However, Caselli et al. (1999) found no evidence for high depletion factors and therefore some other desorption mechanism (such as for instance cosmic ray desorption) must play a certain role in these environments. However, to observe exactly how much evaporation cosmic rays account for, we calculated Model 3 without the cosmic ray desorption term. Figure 7 shows these abundance distributions. The profiles are similar to Model 3, but the amount of depletion is, as expected, about three orders of magnitude higher.
![\begin{figure}
\par\includegraphics[width=8.3cm]{0035f7a.ps}\\
\hspace*{3.8mm}\includegraphics[width=7.5cm]{0035f7b.eps}
\end{figure}](/articles/aa/full/2008/38/aa10035-08/Timg44.gif) |
Figure 7: Abundance distribution of Model 3 without cosmic ray desorption and the default binding energy of 960 K. Otherwise similar to 4. |
| Open with DEXTER | |
Including cosmic ray desorption obviously has a significant impact on the amount of gas phase molecules in the cloud, raising the gas-phase abundance substantially. However, the effect of cosmic ray desorption can be balanced by a higher binding energy between the molecule and grain surface. For example, raising the binding energy from 960 K to 1740 K compensates almost entirely for the effect of cosmic ray desorption, when the depletion is averaged over the entire model.
![\begin{figure}
\par\includegraphics[width=8.3cm]{0035f8a.ps}\\
\hspace*{3mm} \includegraphics[width=7.5cm]{0035f8b.eps}
\end{figure}](/articles/aa/full/2008/38/aa10035-08/Timg45.gif) |
Figure 8: Abundance distribution of Model 3, including cosmic rays, but with a CO binding energy of 1740 K. Otherwise similar to 4. |
| Open with DEXTER | |
An increased binding energy applies when the CO ice mantle is mixed with other species, typically water ice or NH3 ice (Fraser et al. 2004). A spread in binding energies also occurs when the ice surfaces are not even, e.g. for differently layered ices, varying mantle thicknesses and rough surfaces. If the grains are more fractal, with cavities that can trap CO molecules, it becomes more difficult to desorb the molecules, which effectively raises the binding energy. Laboratory experiments of Collings et al. (2004) detected multiple peaks in the CO desorption spectrum, implying a range of binding energies. In Fig. 8, the innermost evaporation zone is smaller by a significant margin throughout the simulation, when the binding energy is increased, in comparison to when cosmic rays are not present; this implies that the two effects can be discriminated by high-resolution observations.
We compare our results with observations of CO abundances and depletion
factors. The fractional depletion ![]() of CO for the various models are shown
in Fig. 9. The highest depletion factors occur at the end of the
pre-stellar core phase just before collapse. Observations show that depletion
factors decrease with decreasing envelope mass (Jørgensen et al. 2002). We observe
the depletion decrease after the core begins to collapse due to CO
evaporation close to the protostar. At the same time, the envelope density
decreases, which also lowers the global fractional depletion defined to be the ratio
of the total number of gas phase CO molecules to H2 molecules in the entire
model.
of CO for the various models are shown
in Fig. 9. The highest depletion factors occur at the end of the
pre-stellar core phase just before collapse. Observations show that depletion
factors decrease with decreasing envelope mass (Jørgensen et al. 2002). We observe
the depletion decrease after the core begins to collapse due to CO
evaporation close to the protostar. At the same time, the envelope density
decreases, which also lowers the global fractional depletion defined to be the ratio
of the total number of gas phase CO molecules to H2 molecules in the entire
model.
Freeze-out in the disk is most pronounced for Model 3, includes cosmic ray
desorption and a high CO binding energy. The same model but with a binding
energy of 960 K provides a low depletion factor at the onset of the
collapse. Although low values of ![]() have been measured
(e.g. Bacmann et al. 2002), most observations point toward a higher value,
have been measured
(e.g. Bacmann et al. 2002), most observations point toward a higher value,
![]() ,
in pre-stellar cores (e.g. Bergin et al. 2002; Jessop & Ward-Thompson 2001; Crapsi et al. 2004). The low value of
,
in pre-stellar cores (e.g. Bergin et al. 2002; Jessop & Ward-Thompson 2001; Crapsi et al. 2004). The low value of ![]() that we find implies that either
the binding energy is higher than 960 K or that we overestimate the cosmic ray
desorption rate. Shen et al. (2004) demonstrated that the importance of
cosmic ray heating was overestimated by previous authors. A third
possibility is that CO can be converted into other species, resulting in a
lower abundance, but since we only model CO we cannot quantify this effect.
that we find implies that either
the binding energy is higher than 960 K or that we overestimate the cosmic ray
desorption rate. Shen et al. (2004) demonstrated that the importance of
cosmic ray heating was overestimated by previous authors. A third
possibility is that CO can be converted into other species, resulting in a
lower abundance, but since we only model CO we cannot quantify this effect.
As mentioned above, a correlation was found between the amount of depletion and envelope mass. The CO abundance declines when going from a pre-stellar core, through the Class 0 phase, to a Class I object. We compare our results with the data presented by Jørgensen et al. (2002), who derived global envelope abundances for 18 sources. Their result is shown in Fig. 10, where open symbols are Class I objects, closed diamonds are Class 0 objects, and the filled squares are pre-stellar cores. Superposed on the data are curves based on our models. In the linear approximation, our models follow the same trend. The observations show no evidence of freeze-out in the Class I objects but the number of sources of this type is small and the derived envelope masses and abundances are uncertain. We also expect some intrinsic scatter due to the unique environments and characteristics of each source. The drop abundance model and Model 3, including cosmic rays and a low binding energy, have too high CO abundances (or too little depletion). Unfortunately, our simulation begins with only one solar mass and we are therefore unable to study the more massive Class 0 and pre-stellar cores.
![\begin{figure}
\includegraphics[width=8.3cm,clip]{0035f9.eps}
\end{figure}](/articles/aa/full/2008/38/aa10035-08/Timg47.gif) |
Figure 9:
The global fractional depletion in the various models. The small
bump in the curves around 0.5
|
| Open with DEXTER | |
![\begin{figure}
\includegraphics[width=8.3cm,clip]{0035f10.eps}
\end{figure}](/articles/aa/full/2008/38/aa10035-08/Timg48.gif) |
Figure 10: In this plot, we show the abundance as a function of envelope mass. Also shown in this plot are data points taken from Jørgensen et al. (2005,2002). The open symbols are Class I objects, the filled diamonds are Class 0 sources and the filled squares are pre-stellar cores. |
| Open with DEXTER | |
We can also calculate gas column densities based on our abundance distribution
models. Vertically integrated column densities,
![]() ,
are shown at four different free-fall times in
Fig. 11. The models differ mainly in the position of the evaporation
front due to the different binding energies used. The column density
profiles at t = 0 can be compared with those presented by Aikawa et al. (2005,2003,2001). Although our underlying density model is different,
the column densities are comparable, differing by an order of magnitude or
less. Aikawa et al. (2001) measured flat profiles toward the core center or
slight drops in the column within
,
are shown at four different free-fall times in
Fig. 11. The models differ mainly in the position of the evaporation
front due to the different binding energies used. The column density
profiles at t = 0 can be compared with those presented by Aikawa et al. (2005,2003,2001). Although our underlying density model is different,
the column densities are comparable, differing by an order of magnitude or
less. Aikawa et al. (2001) measured flat profiles toward the core center or
slight drops in the column within ![]() 5000 AU, which is similar to the results for our
models. The only exception is our drop abundance model (Model 1), which has an
increasing column density toward the center. The drop occurs at
5000 AU, which is similar to the results for our
models. The only exception is our drop abundance model (Model 1), which has an
increasing column density toward the center. The drop occurs at ![]() 6000 AU,
and within a 6000 AU radius we have a constant abundance. The
6000 AU,
and within a 6000 AU radius we have a constant abundance. The
![]() density decreases with the inverse square of the radius, which means that the column density
of CO increases toward the core center. This disagrees with
observations (e.g. Tafalla et al. 2004) where flat or decreasing integrated
intensity profiles are found at core centers and can be interpreted as a drop
in the column density.
density decreases with the inverse square of the radius, which means that the column density
of CO increases toward the core center. This disagrees with
observations (e.g. Tafalla et al. 2004) where flat or decreasing integrated
intensity profiles are found at core centers and can be interpreted as a drop
in the column density.
![\begin{figure}
\includegraphics[width=8.3cm,clip]{0035f11.ps}
\end{figure}](/articles/aa/full/2008/38/aa10035-08/Timg51.gif) |
Figure 11: CO gas column densities of the models discussed in this paper. These profiles are observed through a pencil beam, and need to be convolved with an appropriate beam to be directly compared with observations. |
| Open with DEXTER | |
Column densities decrease by about three orders of magnitude from the center toward
the freeze-out zone in the disk, comparable to Aikawa et al. (1996), although
column densities in our results are in general more than one order of magnitude
higher. This can be explained by the differences in the adopted disk masses.
A typical value adopted for disk masses is 10-2
![]() ,
while the
disk in our simulations increases to an unrealistically high mass of about 0.4
,
while the
disk in our simulations increases to an unrealistically high mass of about 0.4 ![]() .
Our column density distributions are also more
complicated because we do not use a simple analytic description of a non-evolving disk.
Aikawa et al. (1996) measured drops in column density due to freeze-out in the disk
around 200-300 AU, similar to our results for 100-500 AU, depending on
the model used.
.
Our column density distributions are also more
complicated because we do not use a simple analytic description of a non-evolving disk.
Aikawa et al. (1996) measured drops in column density due to freeze-out in the disk
around 200-300 AU, similar to our results for 100-500 AU, depending on
the model used.
In a similar way, we can calculate the column densities for the CO bound to ice. Plots of the ice column densities are shown in Fig. 12. Before collapse, the column density of CO ice increase inwards due to the shorter freeze-out timescales. When the central temperature rises, the column density flattens and drops, while in the protoplanetary disk the column density increases sharply. Overall, the column density drops in the envelope because of the decreasing density (which also results in a lower freeze-out rate). It is difficult to compare these results with observations since cold (unrelated) clouds, where CO is frozen out, often are located in front of protostars. Observed column densities of CO ice are often approximately 1018 cm-2 in reasonable agreement with our results.
![\begin{figure}
\includegraphics[width=8cm,clip]{0035f12.ps}
\end{figure}](/articles/aa/full/2008/38/aa10035-08/Timg54.gif) |
Figure 12: Same as Fig. 11 but for CO ice column densities. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0035f13.ps}
\end{figure}](/articles/aa/full/2008/38/aa10035-08/Timg55.gif) |
Figure 13:
Time series of CO 3-2 spectra. The top three panels show the three
different abundance models. The three lower panels show model 3,
including cosmic ray desorption using three different binding
energies. Time is shown by increasing line thickness and the four
lines correspond to the four adopted time snapshots (0.0, 0.5, 1.5,
and 2.5
|
| Open with DEXTER | |
Simulated spectral lines are a direct way to test our models because they can be compared directly to observed spectra. As mentioned in Sect. 2, we use the hydrodynamical time snapshots including the abundance distribution mapped onto the original grid as input models for our two-dimensional molecular excitation code RATRAN. This code solves the level population using an accelerated Monte Carlo method, which is then ray-traced to create frequency dependent intensity maps. After beam convolution, spectral profiles can be extracted from these and directly compared with observations. We add a mean field of 0.2 km s-1to the snapshots during the radiation transfer calculations to emulate the presence of micro-turbulence.
An in-depth analysis of spectra based on the hydrodynamical simulation is given
in a separate paper (Brinch et al. 2008) and only example spectra for
the abundance models derived in this paper are presented here. Figure
13 shows the CO J= 3-2 transition of the four time-snapshots used in
previous figures. The top three panels correspond to the
three abundance models including cosmic ray desorption, while the lower three
panels show spectra based on model 3 without cosmic ray desorption and with
increased binding energies. Figure 14 has a similar layout, but for
the less optically thick isotopologue C18O. For comparison, CO and C18O
spectra, calculated with a constant abundance profile are shown in
Fig. 15. All spectra are viewed at 90![]() inclination (edge-on;
similar to the orientation of the model in Fig. 1), and they
were convolved with a 10'' beam, a typical value for
single-dish sub-millimeter telescopes. A distance of 140 pc (Taurus star
forming region) is adopted. We use an isotopic 16O:18O ratio of 560
(Wilson & Rood 1994) to calculate all C18O spectra.
inclination (edge-on;
similar to the orientation of the model in Fig. 1), and they
were convolved with a 10'' beam, a typical value for
single-dish sub-millimeter telescopes. A distance of 140 pc (Taurus star
forming region) is adopted. We use an isotopic 16O:18O ratio of 560
(Wilson & Rood 1994) to calculate all C18O spectra.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0035f14.ps}
\end{figure}](/articles/aa/full/2008/38/aa10035-08/Timg57.gif) |
Figure 14: Similar to Fig. 13 but for C18O 3-2. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0035f15.ps}
\end{figure}](/articles/aa/full/2008/38/aa10035-08/Timg58.gif) |
Figure 15: Time series of CO and C18O spectra with a constant abundance profile. Time is represented by increasing line thickness. |
| Open with DEXTER | |
We observe that the spectra in the top row of Fig. 13 are similar to each other and also to the constant abundance profiles in Fig. 15. The reason is that CO becomes optically thick before the abundance declines and is therefore independent of the underlying abundance model. We are therefore unable to use CO spectra to distinguish between the three models and cannot determine the depletion factor using CO. An exclusion of cosmic rays or increase in the binding energy lowers the intensity of the spectra, and in this case CO can be used to constrain the models.
The line profile of the earliest snapshot (the thinnest line) is to have a boxy shape with a flat line center. This is entirely due to the hydrodynamical model, which has not yet evolved from its initial isothermal state in the region where the line get optically thick. Basically we probe the same temperature through a range of velocities, which produce the flat top. The line width in the earliest snapshot in Fig. 13 is also considerably narrower than for the other lines. This is because the velocities in the model have not yet had the time to increase from the initial solid body rotation speed.
The C18O spectra however differ considerably from those derived for a constant abundance model. When the three abundance models are compared, they also differ, although to a lesser extent, from each other. This is because the lines are optically thin and a drop in abundance has a direct impact on the spectral line, no matter at what radius the drop occurs.
The spectra shown here all simulate single-dish measurements, where the emission of the source has been smeared out by a relatively large beam. If an interferometer is used instead, beam sizes smaller than 1'' can be achieved, which allows us to map the line-of-sight column densities. With these observations, it should be possible to map abundance distributions of optically thin species and constrain our models.
The abundance profiles presented here depend on the adopted hydrodynamical model. While we believe that our results are in general applicable, details, such as the precise timescale and absolute values of the fractional depletion, depend on the initial conditions of our simulations such as mass and angular momentum and the particular hydrodynamical scheme used.
A main concern of the hydrodynamical simulation is the internal radiation transfer module used to calculate the temperature structure of the simulation. This is done with an approximate method known to overestimate the dust temperature by a few Kelvins compared with calculations by more accurate continuum radiation transfer codes (Visser, priv. comm.). While a few Kelvin may have little or no effect on the hydrodynamics and therefore the evolution of the cloud, it can certainly affect the evaporation front, which has a strong temperature dependence. While this will alter the detailed behavior of the abundances, it will not change the general trends discussed in this paper.
Although we have considered only the CO gas-phase
abundance, as mentioned in Sect. 2, our method can be easily extended
to include other species and even surface reactions. However, attempting to calculate the
entire chemical network is considerably more computationally demanding. Where
the CO models can be completed in a few hours on a standard desktop computer using
![]() trace particles, a test simulation with the entire chemical network indicated that it
would take a factor of 100 longer to complete using a factor of 1000 fewer trace
particles. Nevertheless, such large-scale chemical models present a powerful
way to obtain realistic abundance profiles for hydrodynamical simulations which
instruments such as the Atacama Large Millimeter Array (ALMA) will be able to test at high
spatial resolution.
trace particles, a test simulation with the entire chemical network indicated that it
would take a factor of 100 longer to complete using a factor of 1000 fewer trace
particles. Nevertheless, such large-scale chemical models present a powerful
way to obtain realistic abundance profiles for hydrodynamical simulations which
instruments such as the Atacama Large Millimeter Array (ALMA) will be able to test at high
spatial resolution.
We have investigated different scenarios for the depletion of CO in a collapsing cloud. We have used a hydrodynamical code to describe the dynamical evolution of the cloud and the chemistry has been solved using a trace particle approach.
Of the various models shown in Sect. 3, that which excludes cosmic ray desorption and those with higher binding energies provide the most extreme results. The drop abundance model provides a good approximation to Model 2 and 3. Therefore, if it is possible to describe observations, using a drop profile, as achieved by Jørgensen et al. (2005), it should be possible to make a hydrodynamical simulation with customized initial conditions, so that it reproduces this profile and places an observational constraint on the hydrodynamics. In cases where an analytical model has been used, the drop abundance approximation has also proven to be good.
We conclude that the freeze-out chemistry has little effect on optically thick spectral lines, especially when observed at low resolution. It is not unreasonable to model these lines using a constant abundance model regardless of the depletion. However, we should be careful when using optically thin lines to determine the average gas phase abundance that should be used in a constant abundance model, since the average abundancesderived from these lines depend on the freeze-out chemistry. The maximum discrepancy between the flat abundance profile model (Fig. 15) and the freeze-out models shown in Fig. 14 is a factor of three in the integrated intensity. Such a change in the average abundance does not affect the optically thick lines a lot, so depending on the accuracy required, it may not be unreasonable to use a flat abundance distribution to model data in which freeze-out is present.
Finally, the effect of chemical depletion is enhanced considerably when
the resolution of the observations increases, implying that it becomes more
important to model the abundance profiles accurately. This will be paticularly
important for future ALMA observations, which will have a resolution of
![]() 0.01'', for which the spatial detail will be significantly higher and
precise abundance models will be crucial for the accurate interpretation of
the data.
0.01'', for which the spatial detail will be significantly higher and
precise abundance models will be crucial for the accurate interpretation of
the data.
Acknowledgements
The authors would like to thank the anonymous referee for thorough and useful comments. C.B. is partially supported by the European Commission through the FP6 - Marie Curie Early Stage Researcher Training programme. The research of M.R.H. is supported through a VIDI grant from the Netherlands Organization for Scientific Research.