A&A 489, 763-767 (2008)
DOI: 10.1051/0004-6361:200809683
Magnetic field distribution in the quiet Sun:
a simplified model approach
F. Berrilli - D. Del Moro - B. Viticchiè
Dipartimento di Fisica, Università degli Studi di Roma ``Tor Vergata'',
Via della Ricerca Scientifica 1, 00133 Roma, Italy
Received 29 February 2008 / Accepted 27 June 2008
Abstract
Context. The quiet Sun presents magnetized plasma whose field strengths vary from zero to about 2 kG. The probability density function of the magnetic field strength B efficaciously describes the statistical properties of the quiet Sun magnetic field.
Aims. We simulate the dynamics and the evolution of quiet Sun magnetic elements to produce a probability density function of the field strengths associated with such elements.
Methods. The dynamics of the magnetic field are simulated by means of a numerical model in which magnetic elements are driven passively by an advection field characterized by spatio-temporal correlations that mimick the granulation and mesogranulation scales observed on the solar surface. The field strength can increase due to an amplification process that occurs where the magnetic elements converge. Starting from a 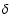 -like probability density function centered on B=30 G, we obtain magnetic field strengths of up to 2 kG (in absolute value). To derive the statistical properties of the magnetic elements, several simulation runs are performed.
-like probability density function centered on B=30 G, we obtain magnetic field strengths of up to 2 kG (in absolute value). To derive the statistical properties of the magnetic elements, several simulation runs are performed.
Results. Our model is able to produce kG magnetic fields in a time interval of the order of the granulation timescale. The mean unsigned flux density and the mean magnetic energy density of the synthetic quiet Sun reach values of
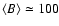 G and
G and
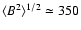 G respectively in the stationary regime. The derived probability density function of the magnetic field strength decreases rapidly from B=30 G to
G respectively in the stationary regime. The derived probability density function of the magnetic field strength decreases rapidly from B=30 G to
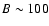 G and has a secondary maximum at B=2 kG. From this result, it follows that magnetic fields
G and has a secondary maximum at B=2 kG. From this result, it follows that magnetic fields 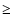 700 G dominate the unsigned flux density and magnetic energy density, although the probability density function of the field strength reaches a maximum at
700 G dominate the unsigned flux density and magnetic energy density, although the probability density function of the field strength reaches a maximum at 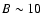 G.
G.
Conclusions. A photospheric advection field with spatio-temporal correlations, driving the magnetic elements, and reduced magnetic amplification rules are able to create a realistic probability density function of the quiet Sun magnetic field. It has been found that they naturally produce an excess of magnetic fields around 2 kG if an upper limit is imposed on the field strength.
Key words: Sun: magnetic fields - Sun: photosphere
1 Introduction
When observing the Sun in full disk magnetograms, magnetic concentrations define the network pattern
associated with the supergranular motions of photospheric plasma, while the interior of the network pattern
appears to be unmagnetized.
We know that weak polarization signals are measurable almost everywhere in the interior of network cells (Smithson 1975; Livingston & Harvey 1975). These signals are associated with the internetwork component of the solar magnetic field, also called the quiet Sun magnetic field, which covers more than 90% of the solar surface, independent of the solar activity (Harvey-Angle 1993).
Due to its large diffusion onto the solar surface, the quiet Sun magnetic field may be useful for understanding the physics of the photospheric magnetism. In fact, it could hold a large fraction of the unsigned flux density and magnetic
energy density of the solar photosphere (e.g. Stenflo 1982; Sánchez Almeida 2004; Schrijver & Title 2003; Sánchez Almeida 1998; Unno 1959).
The weak polarization signals measured in quiet Sun regions can be interpreted as the result of the linear
combination of the polarization emerging from discrete magnetic flux tubes, which are typically smaller than the angular
resolution, that fill the solar atmosphere with a complex topology (e.g. Sánchez Almeida et al. 2003; Emonet & Cattaneo 2001a).
Knowledge of the quiet Sun has been enhanced significantly by improvements in instrumentation (e.g. Sánchez Almeida et al. 1996; Lin & Rimmele 1999; Domínguez Cerdeña et al. 2003a; Lites 2002; Domínguez Cerdeña et al. 2003b; Khomenko et al. 2003), in diagnostic techniques (e.g. Stenflo 1982; Manso Sainz et al. 2004; Sánchez Almeida 2004; Socas-Navarro & Sánchez Almeida 2002; Landi degl'Innocenti 1998; Trujillo Bueno et al. 2004; Faurobert-Scholl et al. 1995; Socas-Navarro et al. 2001; Rees et al. 2000; Faurobert-Scholl 1993; Sánchez Almeida & Lites 2000; Martínez González et al. 2006b; Sánchez Almeida 2005), and numerical simulations (e.g. Vögler 2003; Stein & Nordlund 2006; Vögler & Schüssler 2007; Stein & Nordlund 2002; Cattaneo 1999; Emonet & Cattaneo 2001b; Vögler et al. 2005).
These improvements were crucial in characterizing the quiet Sun magnetic field and its different observational
parameters. One parameter, the fraction of solar surface occupied by a certain field strength, is a very powerful tool. In fact, this can be trivially translated into the probability density function (PDF) of the magnetic field strength, P(B), which is useful
in describing the statistical properties of a quiet Sun region. For example, calculating the first and the second
momentum of P(B) provides information about the mean unsigned flux density and the mean magnetic energy density (apart from a
constant factor 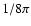 ), respectively. Using a PDF assumes implicitly a continuum for values of the magnetic field strength. The limit imposed by the pressure equilibrium between the magnetic flux tubes and photospheric plasma also defines the variability range for quiet Sun magnetic fields to be between 0 G to about 2 kG.
), respectively. Using a PDF assumes implicitly a continuum for values of the magnetic field strength. The limit imposed by the pressure equilibrium between the magnetic flux tubes and photospheric plasma also defines the variability range for quiet Sun magnetic fields to be between 0 G to about 2 kG.
Lin (1995) computed the PDF in active and quiet Sun regions using Fe I 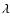 15648 and Fe I
15648 and Fe I 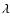 15652 lines, while Lites (2002) obtained it from the analysis of network regions and their surroundings using Fe I lines at 6300 Å. Both authors found a bimodal distribution with a dominant contribution at
15652 lines, while Lites (2002) obtained it from the analysis of network regions and their surroundings using Fe I lines at 6300 Å. Both authors found a bimodal distribution with a dominant contribution at 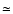 150 G and a secondary peak at
150 G and a secondary peak at 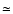 1.5 kG. In contrast, Collados (2001), studying quiet Sun regions using the same infrared lines as Lin (1995), found an exponential decline in the magnetic flux density histogram from a peak at
1.5 kG. In contrast, Collados (2001), studying quiet Sun regions using the same infrared lines as Lin (1995), found an exponential decline in the magnetic flux density histogram from a peak at 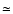 200 G and no counts for magnetic flux density
200 G and no counts for magnetic flux density 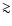 1 kG. Domínguez Cerdeña et al. (2006) developed a set of PDFs for the quiet Sun magnetic fields that was consistent with observations and magnetoconvection simulations by using information from both Hanle and Zeeman observations; their study created substantial interest because the functions increased for strong fields, just before a cut-off at
1 kG. Domínguez Cerdeña et al. (2006) developed a set of PDFs for the quiet Sun magnetic fields that was consistent with observations and magnetoconvection simulations by using information from both Hanle and Zeeman observations; their study created substantial interest because the functions increased for strong fields, just before a cut-off at
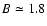 kG. This characteristic implies that strong fields are important because, even when present in a small fraction of the photosphere, they dominate the unsigned flux density and magnetic energy density. On the other hand, the magnetic field distributions proposed by Martínez González et al. (2006a,b) and Martínez González et al. (2008), which were derived from simultaneous infrared and visible observations of Fe I lines, do not present any rise for strong fields. The inversion of the Fe I
kG. This characteristic implies that strong fields are important because, even when present in a small fraction of the photosphere, they dominate the unsigned flux density and magnetic energy density. On the other hand, the magnetic field distributions proposed by Martínez González et al. (2006a,b) and Martínez González et al. (2008), which were derived from simultaneous infrared and visible observations of Fe I lines, do not present any rise for strong fields. The inversion of the Fe I 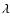 6301 and Fe I
6301 and Fe I 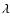 6302 profiles observed by the HINODE satellite (Orozco Suárez et al. 2007) confirms this result.
6302 profiles observed by the HINODE satellite (Orozco Suárez et al. 2007) confirms this result.
Magnetoconvection simulations provide a wide variety of quiet Sun magnetic field PDFs to be compared with those derived from observations. Simulations show, for example, exponential decays (Stein & Nordlund 2006; Vögler & Schüssler 2007; Stein et al. 2003; Cattaneo 1999), bimodal behaviors (Vögler & Schüssler 2003; Vögler et al. 2003), or an ``exponential-like core and a modest peak'' for 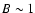 kG (Steiner 2003).
kG (Steiner 2003).
An important step is to ascertain the presence or absence of a bump for magnetic fields 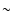 1 kG in quiet Sun magnetic field strength PDFs; since the magnetic flux and magnetic energy both scale as powers of the field strength, kG magnetic fields should play a crucial role in defining the global properties of quiet Sun magnetic fields. The connectivity between the lower and the upper solar atmosphere may indeed be defined by the larger field strength concentrations in the photosphere (Domínguez Cerdeña et al. 2006).
1 kG in quiet Sun magnetic field strength PDFs; since the magnetic flux and magnetic energy both scale as powers of the field strength, kG magnetic fields should play a crucial role in defining the global properties of quiet Sun magnetic fields. The connectivity between the lower and the upper solar atmosphere may indeed be defined by the larger field strength concentrations in the photosphere (Domínguez Cerdeña et al. 2006).
Sánchez Almeida (2007) indicated that a bump in the PDF for quiet Sun fields 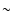 kG is to be expected if ``a magnetic amplification mechanism operates in the quiet Sun''. The author derived an equation for the temporal evolution of the PDF, whose shape can be modified by magnetic amplification and photospheric convection. In the stationary state, the model is characterized by a P(B) with a bump for strong fields.
kG is to be expected if ``a magnetic amplification mechanism operates in the quiet Sun''. The author derived an equation for the temporal evolution of the PDF, whose shape can be modified by magnetic amplification and photospheric convection. In the stationary state, the model is characterized by a P(B) with a bump for strong fields.
In our model, we implement the dynamics of a high number of photospheric magnetic elements, driven by a photospheric velocity field in which a large-scale organization (mesogranulation) is naturally derived from the cooperation of small-scale flows (granulation). The model also takes into account simplified processes that are able to amplify and limit the magnetic field strength. In Sect. 2, we describe the model, in Sect. 3, the results of the simulation are presented, while in Sect. 4, they are discussed. Finally, in Sect. 5, the conclusions are outlined.
2 The model
The model simulates the dynamics and evolution of photospheric magnetic elements driven by a photospheric velocity field characterized by spatio-temporal correlations. To reproduce these correlations, we simulated the photospheric velocity field in a way similar to that proposed by Rast (2003); it was computed by an n-body simulation that realizes the interaction between downflow plumes by considering only their mutual horizontal interaction, as in Rast (1998). The movement of each plume was determined by the advection produced by the other plumes. This model spontaneously creates stable downward plumes, organized on a mesogranular pattern, from the interaction of granular scale flows. The ratios between the mesogranular and granular spatio-temporal scales, over which the model self-organizes, agree with the ratios measured in the solar photosphere. Viticchié et al. (2006) utilized such a velocity field to drive magnetic loop footpoints in a reconnection model that reproduces the observed statistical properties nanoflares.
In the present work, the simulations start with the advection field only, without any magnetic element in the domain. When the velocity field has reached a stationary behavior, i.e. after the onset of mesogranular scale flows, the time t is set to zero and N0=500 magnetic elements are distributed at random positions over the computational domain. The magnetic elements have an associated field strength
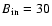 G with random orientation (
G with random orientation (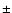 1) and size equal to the spatial resolution element. Hereafter, B represents the absolute value of the magnetic field strength. We choose such a value for
1) and size equal to the spatial resolution element. Hereafter, B represents the absolute value of the magnetic field strength. We choose such a value for
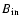 since it is approximately equal to the minimum magnetic flux density measurable nowadays (e.g. Carroll & Kopf 2008; Trujillo Bueno et al. 2004; Bommier et al. 2005).
We allow the magnetic elements to be transported passively by the photospheric velocity field towards different plume sites. At each plume site, a certain number of magnetic elements converge under the action of the advection field. When two magnetic elements, associated with B1 and B2, overlap in the same resolution element, they can produce the following two results:
since it is approximately equal to the minimum magnetic flux density measurable nowadays (e.g. Carroll & Kopf 2008; Trujillo Bueno et al. 2004; Bommier et al. 2005).
We allow the magnetic elements to be transported passively by the photospheric velocity field towards different plume sites. At each plume site, a certain number of magnetic elements converge under the action of the advection field. When two magnetic elements, associated with B1 and B2, overlap in the same resolution element, they can produce the following two results:
- 1.
- if the two elements have opposite orientations, they are substituted by a new magnetic element at the same site with an associated
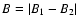 and the orientation of the strongest element. The total flux is conserved such that the spatial size of the new element remains as one resolution element. In the particular case of B1=B2, the elements cancel the effect of each other;
and the orientation of the strongest element. The total flux is conserved such that the spatial size of the new element remains as one resolution element. In the particular case of B1=B2, the elements cancel the effect of each other;
- 2.
- if the two elements have the same orientation, they are substituted by a new magnetic element in the same site with an associated B=B1+B2 and the same orientation. The total flux is again conserved and the spatial size of the new element is one resolution element.
This process implicates an amplification of the magnetic field strength. Different mechanisms have been proposed to concentrate magnetic fields in quiet Sun regions up to the kG range (e.g. Spruit 1979; Sánchez Almeida 2001; Parker 1978; Weiss 1966). As reported by Sánchez Almeida (2007), all mechanisms are abruptly diminished at the maximum field strength imposed by the gas pressure of the quiet Sun photosphere. Therefore, we place the constraint that the amplification process cannot create field strengths greater than
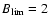 kG. We can interpret
kG. We can interpret
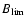 as a representative value of the maximum field strengths for quiet Sun regions (e.g. Spruit 1979; Parker 1978; Grossmann-Doerth et al. 1998; Stein et al. 2003; Domínguez Cerdeña et al. 2006; Sánchez Almeida 2007). Whenever the amplification process would produce
as a representative value of the maximum field strengths for quiet Sun regions (e.g. Spruit 1979; Parker 1978; Grossmann-Doerth et al. 1998; Stein et al. 2003; Domínguez Cerdeña et al. 2006; Sánchez Almeida 2007). Whenever the amplification process would produce
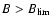 ,
the magnetic elements do not interact and remain separated.
,
the magnetic elements do not interact and remain separated.
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{9683fig1.eps}
\end{figure}](/articles/aa/full/2008/38/aa09683-08/Timg31.gif) |
Figure 1:
Illustrative representation of
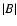 in the computational domain. Black areas represent 0 G regions; blue and sky-blue represent
in the computational domain. Black areas represent 0 G regions; blue and sky-blue represent 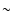 10 G regions; green represents 10 G regions; green represents 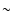 100 G regions; yellow and red represent 100 G regions; yellow and red represent 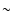 kG magnetic concentrations. The position of concentrations with kG magnetic concentrations. The position of concentrations with 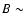 kG correspond to the position of stable downward plumes organized over mesogranular scales. kG correspond to the position of stable downward plumes organized over mesogranular scales. |
| Open with DEXTER |
We consider implicitly that the amplification mechanism operates on the same timescales as the granulation timescale (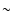 10 min). This hypothesis is consistent with the amplification timescales reported by Parker (1978) and Grossmann-Doerth et al. (1998). Up to the equipartition value of about 500 G, the amplification can be ascribed to the granular flows and five minutes are sufficient to produce kG fields from a uniform distribution of 400 G.
10 min). This hypothesis is consistent with the amplification timescales reported by Parker (1978) and Grossmann-Doerth et al. (1998). Up to the equipartition value of about 500 G, the amplification can be ascribed to the granular flows and five minutes are sufficient to produce kG fields from a uniform distribution of 400 G.
As proposed by Steiner (2003), starting from an initial PDF of
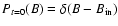 ,
the amplification process will broaden the PDF and extend it to
,
the amplification process will broaden the PDF and extend it to
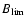 .
.
To simulate the emergence of new magnetic elements on the solar surface, we continuously add randomly located elements of random orientation and
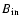 magnetic field strength. This injection process maintains the total number of magnetic elements
magnetic field strength. This injection process maintains the total number of magnetic elements  N0 and compensates for the reduction in the total number due to the concentration process.
N0 and compensates for the reduction in the total number due to the concentration process.
Figure 1 shows an illustrative representation of a snapshot of the simulation in the stationary regime: we represent the
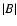 pattern emerging on the computational domain.
pattern emerging on the computational domain.
3 PDF of the quiet Sun magnetic field strengths
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9683fig2.eps} \end{figure}](/articles/aa/full/2008/38/aa09683-08/Timg34.gif) |
Figure 2:
Average maximum field strength versus evolution time t. The function is obtained by averaging the results from
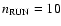 distinct simulation runs and the error bars are calculated to equal
distinct simulation runs and the error bars are calculated to equal
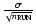 .
The horizontal dashed line represents the maximum value allowed for the magnetic flux density ( .
The horizontal dashed line represents the maximum value allowed for the magnetic flux density (
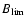 ), while the vertical dot-dashed line indicates the instant at which the model produces the first kG element. The plot shows only a part of the total time domain ( ), while the vertical dot-dashed line indicates the instant at which the model produces the first kG element. The plot shows only a part of the total time domain (
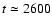 min). min). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9683fig3.eps} \end{figure}](/articles/aa/full/2008/38/aa09683-08/Timg37.gif) |
Figure 3:
Mean probability density function
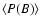 for the magnetic field strength in the stationary regime.
for the magnetic field strength in the stationary regime.
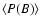 has been obtained averaging
has been obtained averaging
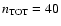 non-correlated PDFs and the error bars are calculated to equal
non-correlated PDFs and the error bars are calculated to equal
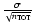 .
The histogram bin-size is 30 G. The dashed line represents the upper limit for the magnetic amplification process .
The histogram bin-size is 30 G. The dashed line represents the upper limit for the magnetic amplification process
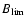 .
The maximum at B=0 G is produced by the fraction of the domain free of magnetic elements. .
The maximum at B=0 G is produced by the fraction of the domain free of magnetic elements. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9683fig4.eps} \end{figure}](/articles/aa/full/2008/38/aa09683-08/Timg39.gif) |
Figure 4:
Mean probability density function
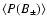 for the signed magnetic field strength in the stationary regime. The histogram bin-size is 30 G. The vertical dashed lines represent the upper and lower limits of the magnetic amplification process
for the signed magnetic field strength in the stationary regime. The histogram bin-size is 30 G. The vertical dashed lines represent the upper and lower limits of the magnetic amplification process 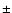
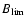 .
The maximum at B=0 G is produced by the fraction of the domain free of magnetic elements. .
The maximum at B=0 G is produced by the fraction of the domain free of magnetic elements. |
| Open with DEXTER |
To derive a PDF of the quiet Sun magnetic field strengths, we performed ten simulation runs with different advection fields and different initial distributions of magnetic elements. Each simulation reproduced the evolution of the quiet Sun for an equivalent time of about 2600 min. We considered the behavior of the model by analyzing its average maximum field strength max(B), mean unsigned flux density
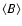 ,
and mean magnetic energy density
,
and mean magnetic energy density
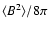 ,
as functions of the mean evolution time t:
,
as functions of the mean evolution time t:
in a similar way to Domínguez Cerdeña et al. (2006).
The model creates magnetic concentrations with B=1 kG in about 30 min and
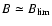 in about 200 min (Fig. 2).
in about 200 min (Fig. 2).
The quantity max(B) is unsuitable for describing the stationary regime of the magnetic element system because its value is limited. As discussed in Sect. 2, we also expect to obtain a PDF spanning the entire domain
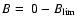 ;
the stationary regime must therefore be identified referring to the integral properties of the PDF, such as the mean unsigned flux density and the mean magnetic energy density.
;
the stationary regime must therefore be identified referring to the integral properties of the PDF, such as the mean unsigned flux density and the mean magnetic energy density.
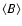 and
and
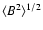 saturate exponentially at
saturate exponentially at
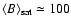 G and
G and
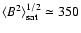 G, respectively. We interpret this saturation as an indication that the entire system has reached the stationary regime. In this regime, we compute
G, respectively. We interpret this saturation as an indication that the entire system has reached the stationary regime. In this regime, we compute
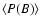 by averaging forty non-correlated PDFs. The computed
by averaging forty non-correlated PDFs. The computed
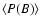 is shown in Fig. 3.
is shown in Fig. 3.
Alternatively, we could compute the mean probability density function
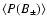 for the signed magnetic field strength by considering the direction of the magnetic fields (shown in Fig. 4). As expected, the
for the signed magnetic field strength by considering the direction of the magnetic fields (shown in Fig. 4). As expected, the
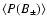 is quite symmetric with respect to zero.
is quite symmetric with respect to zero.
4 Discussion
In the previous section we presented the results of several simulations of our reduced model. We now focus on some particular points in detail.
The maximum field strength, plotted in Fig. 2, as a function of t indicates that the timescale over which kG fields are produced is approximately 30 min. This is the same timescale over which the mesogranular pattern emerged in the numerical simulation of Viticchié et al. (2006).
Different descriptions of the magnetic amplification process (Sánchez Almeida 2001; Grossmann-Doerth et al. 1998) achieved similar results: weak magnetic-field structures, in a downflow environment, develop field strengths 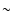 kG within a few minutes. Berrilli et al. (2005) reported that the organization of structures on mesogranular boundaries is rapid with a typical timescale of
kG within a few minutes. Berrilli et al. (2005) reported that the organization of structures on mesogranular boundaries is rapid with a typical timescale of 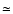 10 min.
10 min.
The analysis of the position of strong field magnetic elements in our simulation revealed that these are superimposed onto stable downward plumes on mesogranular scales (Fig. 1). Such a correlation between strong magnetic fields and the mesogranular advection scale is in agreement with Domínguez Cerdeña (2003), who found a correlation between mesogranular photospheric flows and the pattern observed in magnetograms.
The symmetry of the
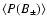 ,
reported in Fig. 4, confirms the equal probability of having concentrations of positive and negative direction. This originates in both the initial conditions and the new element addition criteria applied during the evolution. Similar symmetries have been found in simulations (e.g., Vögler & Schüssler 2007) and in observations of Martínez González et al. (2006a,2008). In the latter works the authors pointed out that such a symmetry may imply a local dynamo origin for the internetwork magnetic field, that is a magnetic field controlled by solar granulation.
,
reported in Fig. 4, confirms the equal probability of having concentrations of positive and negative direction. This originates in both the initial conditions and the new element addition criteria applied during the evolution. Similar symmetries have been found in simulations (e.g., Vögler & Schüssler 2007) and in observations of Martínez González et al. (2006a,2008). In the latter works the authors pointed out that such a symmetry may imply a local dynamo origin for the internetwork magnetic field, that is a magnetic field controlled by solar granulation.
The sharp count decay found at
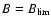 is obviously due to the ``interaction turn off'' produced by
is obviously due to the ``interaction turn off'' produced by
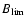 (Sect. 2). Other PDFs reported in the literature show a smooth decay of the peak for
(Sect. 2). Other PDFs reported in the literature show a smooth decay of the peak for
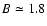 kG (Domínguez Cerdeña et al. 2006; Sánchez Almeida 2007), as expected for natural PDFs. We could reproduce this smooth decay of
kG (Domínguez Cerdeña et al. 2006; Sánchez Almeida 2007), as expected for natural PDFs. We could reproduce this smooth decay of
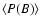 for
for
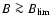 by modifying the magnetic element interaction probability, but it is not within the scope of this work to reproduce these fine details of the PDF.
by modifying the magnetic element interaction probability, but it is not within the scope of this work to reproduce these fine details of the PDF.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9683fig5.eps} \end{figure}](/articles/aa/full/2008/38/aa09683-08/Timg50.gif) |
Figure 5:
Mean probability density function
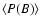 (solid line, same as Fig. 3) compared with four Pt(B) (dotted lines) calculated at different instants of the simulation. Each Pt(B) represents the mean of ten PDFs from ten simulation runs at time t. Top left: t=2160 min, top right t=2308 min, bottom left t=2464 min and bottom right: t=2593 min. The histogram bin-size is 30 G. The vertical dashed lines represent the upper and lower limits of the magnetic amplification process
(solid line, same as Fig. 3) compared with four Pt(B) (dotted lines) calculated at different instants of the simulation. Each Pt(B) represents the mean of ten PDFs from ten simulation runs at time t. Top left: t=2160 min, top right t=2308 min, bottom left t=2464 min and bottom right: t=2593 min. The histogram bin-size is 30 G. The vertical dashed lines represent the upper and lower limits of the magnetic amplification process 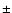
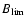 .
The maximum at B=0 G is produced by the fraction of the domain free of magnetic elements. .
The maximum at B=0 G is produced by the fraction of the domain free of magnetic elements. |
| Open with DEXTER |
To verify that the stationary regime has been reached, we compared the
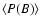 with four mean PDFs, Pt(B), representative of four different instants of the simulation during the stationary regime (Fig. 5). Each Pt(B) represents the mean of ten PDFs at a given time t. We consider the four Pt(B) to be uncorrelated because they are separated by more than 140 minutes, a time interval that is longer than three times the mean mesogranular lifetime. As shown in Fig. 5, the deviation between the
with four mean PDFs, Pt(B), representative of four different instants of the simulation during the stationary regime (Fig. 5). Each Pt(B) represents the mean of ten PDFs at a given time t. We consider the four Pt(B) to be uncorrelated because they are separated by more than 140 minutes, a time interval that is longer than three times the mean mesogranular lifetime. As shown in Fig. 5, the deviation between the
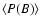 and the four Pt(B) shows no time dependence and the root mean square deviations of all four Pt(B) with respect to the
and the four Pt(B) shows no time dependence and the root mean square deviations of all four Pt(B) with respect to the
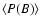 are approximately one part in a thousand.
are approximately one part in a thousand.
The values
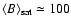 G and
G and
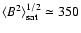 G, reached in the stationary regime, are in good agreement with the results of Domínguez Cerdeña et al. (2006). The percentages of unsigned flux density and magnetic energy density for
G, reached in the stationary regime, are in good agreement with the results of Domínguez Cerdeña et al. (2006). The percentages of unsigned flux density and magnetic energy density for 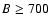 G are
G are 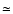
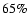 and
and 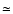
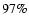 respectively, indicating a dominant role for kG fields. The percentages that we found are higher than those reported by Domínguez Cerdeña et al. (2006); these differences can be explained by referring to the steeper decrease in the
respectively, indicating a dominant role for kG fields. The percentages that we found are higher than those reported by Domínguez Cerdeña et al. (2006); these differences can be explained by referring to the steeper decrease in the
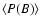 for the 0-700 G interval with respect to the log-normal trend found by these authors.
for the 0-700 G interval with respect to the log-normal trend found by these authors.
The
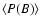 presents a maximum at
presents a maximum at
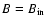 in agreement with Domínguez Cerdeña et al. (2006). This result originates in the injection value for the magnetic field strength
in agreement with Domínguez Cerdeña et al. (2006). This result originates in the injection value for the magnetic field strength
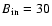 G. At
G. At
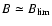 ,
the PDF presents a secondary maximum, as found by Stein et al. (2003), Domínguez Cerdeña et al. (2006), and Sánchez Almeida (2007).
,
the PDF presents a secondary maximum, as found by Stein et al. (2003), Domínguez Cerdeña et al. (2006), and Sánchez Almeida (2007).
In a similar way to Sánchez Almeida (2007), we may conclude that this secondary maximum in the
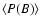 is due to the upper limit placed on the amplification process at
is due to the upper limit placed on the amplification process at
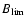 .
When a magnetic amplification process operates and a limit is placed on this process, an accumulation of field strength about the limit is expected. All assumptions of the model contribute in shaping the
.
When a magnetic amplification process operates and a limit is placed on this process, an accumulation of field strength about the limit is expected. All assumptions of the model contribute in shaping the
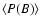 :
the strong convergence regions of the granular advection pattern create suitable conditions for amplifying the magnetic field and, at the same time, support the amplification process by gathering new magnetic elements to counteract the cancellation process. The secondary maximum of the PDF is produced by both the spatial and temporal correlations of the velocity field, which advect the magnetic elements, and the upper limit of the amplification process at
:
the strong convergence regions of the granular advection pattern create suitable conditions for amplifying the magnetic field and, at the same time, support the amplification process by gathering new magnetic elements to counteract the cancellation process. The secondary maximum of the PDF is produced by both the spatial and temporal correlations of the velocity field, which advect the magnetic elements, and the upper limit of the amplification process at
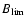 .
.
5 Conclusions
We have presented a model that reproduces the dynamics and evolution of photospheric magnetic elements. These elements are passively driven by an horizontal velocity field characterized by spatio-temporal correlations that agree with those observed in the solar photosphere. The description of the velocity field follows Rast (2003,1998).
In their evolution, the magnetic elements interact and increase their magnetic field strengths through an amplification process assumed to work on a timescale comparable with the granular timescale and able to recreate kG concentrations. The injection scale, constrained to be
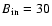 G, and the upper limit at
G, and the upper limit at
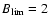 kG are both derived from observations and physical constraints (e.g. Trujillo Bueno et al. 2004; Parker 1978).
kG are both derived from observations and physical constraints (e.g. Trujillo Bueno et al. 2004; Parker 1978).
We investigated the statistical properties of the field strengths associated with the magnetic elements using a series of numerical simulations. The main conclusions are:
- 1.
- The model produces kG fields in a time interval of the order of the mesogranulation timescale. These strong fields are organized in a pattern superimposed on the mesogranulation pattern of the advection field.
- 2.
- In the stationary regime, the PDF of the magnetic field strength has a stable shape and has a secondary maximum that corresponds to the upper limit set at 2 kG.
- 3.
- The associated mean unsigned flux density and mean magnetic energy density in the stationary regime are
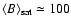 G and
G and
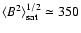 G, respectively.
G, respectively.
- 4.
- The magnetic element system described by this PDF is strongly dominated by kG magnetic fields: the fractions of unsigned flux density and magnetic energy density for
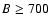 G are
G are 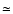
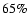 and
and 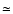
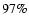 ,
respectively.
,
respectively.
The quiet Sun is certainly more complex than the model presented here. However, a more simplified approach, based on the advection field proposed by Rast (2003), reproduced the observed distributions for the released magnetic energy and waiting times of nanoflare events (Viticchié et al. 2006). In the present work, we showed how the same approach can also be applied to reproduce some of the statistical properties of the quiet Sun magnetic field.
Acknowledgements
We are very grateful to the anonymous referee for invaluable comments on the manuscript. We thank Jorge Sánchez Almeida for fruitful discussions about the topic. This paper was partially supported by Regione Lazio CVS (Centro per lo studio della variabilità del Sole) Ph.D. grant and ASI/INAF I/015/07/0 ESS grant.
- Berrilli, F., Del Moro,
D., Russo, S., Consolini, G., & Straus, T. 2005, ApJ, 632,
677 [NASA ADS] [CrossRef]
(In the text)
- Bommier, V., Derouich,
M., Landi degl'Innocenti, E., Molodij, G., &
Sahal-Bréchot, S. 2005, A&A, 432, 295 [NASA ADS] [CrossRef] [EDP Sciences]
- Carroll, T. A.,
& Kopf, M. 2008, A&A, 481, L37 [NASA ADS] [CrossRef] [EDP Sciences]
- Cattaneo, F. 1999, ApJ,
515, L39 [NASA ADS] [CrossRef]
- Collados, M. 2001, in
Advanced Solar Polarimetry - Theory, Observation, and
Instrumentation, ed. M. Sigwarth, ASP Conf. Ser., 236,
255
(In the text)
- Domínguez
Cerdeña, I. 2003, A&A, 412, L65 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Domínguez
Cerdeña, I., Kneer, F., & Sánchez Almeida, J. 2003a,
ApJ, 582, L55 [NASA ADS] [CrossRef]
- Domínguez
Cerdeña, I., Sánchez Almeida, J., & Kneer, F. 2003b,
A&A, 407, 741 [NASA ADS] [CrossRef] [EDP Sciences]
- Domínguez
Cerdeña, I., Sánchez Almeida, J., & Kneer, F. 2006,
ApJ, 636, 496 [NASA ADS] [CrossRef]
(In the text)
- Emonet, T., &
Cattaneo, F. 2001a, in Advanced Solar Polarimetry - Theory,
Observation, and Instrumentation, ed. M. Sigwarth, ASP Conf.
Ser., 236, 355
- Emonet, T., &
Cattaneo, F. 2001b, ApJ, 560, L197 [NASA ADS] [CrossRef]
- Faurobert-Scholl,
M. 1993, A&A, 268, 765 [NASA ADS]
- Faurobert-Scholl,
M., Feautrier, N., Machefert, F., Petrovay, K., & Spielfiedel,
A. 1995, A&A, 298, 289 [NASA ADS]
- Grossmann-Doerth, U.,
Schuessler, M., & Steiner, O. 1998, A&A, 337, 928 [NASA ADS]
- Harvey-Angle,
K. L. 1993, Ph.D. Thesis, Utrecht University, The
Netherlands
(In the text)
- Khomenko, E. V.,
Collados, M., Solanki, S. K., Lagg, A., & Trujillo Bueno,
J. 2003, A&A, 408, 1115 [NASA ADS] [CrossRef] [EDP Sciences]
- Landi degl'Innocenti, E.
1998, Nature, 392, 256 [NASA ADS] [CrossRef]
- Lin, H. 1995, ApJ, 446,
421 [NASA ADS] [CrossRef]
(In the text)
- Lin, H., &
Rimmele, T. 1999, ApJ, 514, 448 [NASA ADS] [CrossRef]
- Lites, B. W. 2002,
ApJ, 573, 431 [NASA ADS] [CrossRef]
- Livingston,
W. C., & Harvey, J. 1975, in BAAS, 7, 346
- Manso Sainz, R., Landi
Degl'Innocenti, E., & Trujillo Bueno, J. 2004, ApJ, 614,
L89 [NASA ADS] [CrossRef]
- Martínez
González, M. J., Collados, M., & Ruiz Cobo, B. 2006a,
ASP Conf. Ser. 358, ed. R. Casini, & B. W. Lites,
36
- Martínez
González, M. J., Collados, M., & Ruiz Cobo, B. 2006b,
A&A, 456, 1159 [NASA ADS] [CrossRef] [EDP Sciences]
- Martínez
González, M. J., Collados, M., Ruiz Cobo, B., & Beck,
C. 2008, A&A, 477, 953 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Orozco Suárez, D.,
Bellot Rubio, L. R., del Toro Iniesta, J. C., et al.
2007, ApJ, 670, L61 [NASA ADS] [CrossRef]
(In the text)
- Parker, E. N. 1978,
ApJ, 221, 368 [NASA ADS] [CrossRef]
- Rast, M. P. 1998, J.
Fluid Mechanics, 369, 125 [NASA ADS]
(In the text)
- Rast, M. P. 2003,
ApJ, 597, 1200 [NASA ADS] [CrossRef]
(In the text)
- Rees, D. E.,
López Ariste, A., Thatcher, J., & Semel, M. 2000, A&A,
355, 759 [NASA ADS]
- Sánchez Almeida, J.
1998, in Three-Dimensional Structure of Solar Active Regions, ed.
C. E. Alissandrakis, & B. Schmieder, ASP Conf. Ser.,
155, 54
- Sánchez Almeida, J.
2001, ApJ, 556, 928 [NASA ADS] [CrossRef]
- Sánchez Almeida, J.
2004, in The Solar-B Mission and the Forefront of Solar Physics,
ed. T. Sakurai, & T. Sekii, ASP Conf. Ser., 325,
115
- Sánchez Almeida, J.
2005, A&A, 438, 727 [NASA ADS] [CrossRef] [EDP Sciences]
- Sánchez Almeida, J.
2007, ApJ, 657, 1150 [NASA ADS] [CrossRef]
(In the text)
- Sánchez
Almeida, J., & Lites, B. W. 2000, ApJ, 532, 1215 [NASA ADS] [CrossRef]
- Sánchez Almeida, J.,
Landi degl'Innocenti, E., Martinez Pillet, V., & Lites,
B. W. 1996, ApJ, 466, 537 [NASA ADS] [CrossRef]
(In the text)
- Sánchez Almeida, J.,
Emonet, T., & Cattaneo, F. 2003, ApJ, 585, 536 [NASA ADS] [CrossRef]
- Schrijver,
C. J., & Title, A. M. 2003, ApJ, 597, L165 [NASA ADS] [CrossRef]
- Smithson, R. C.
1975, in BAAS, 7, 346
- Socas-Navarro, H.,
López Ariste, A., & Lites, B. W. 2001, ApJ, 553,
949 [NASA ADS] [CrossRef]
- Socas-Navarro, H.,
& Sánchez Almeida, J. 2002, ApJ, 565, 1323 [NASA ADS] [CrossRef]
- Spruit, H. C. 1979,
Sol. Phys., 61, 363 [NASA ADS] [CrossRef]
- Stein, R. F.,
& Nordlund, Å. 2002, in SOLMAG 2002. Proceedings of the
Magnetic Coupling of the Solar Atmosphere Euroconference, ed.
H. Sawaya-Lacoste, ESA SP-505, 83
- Stein, R. F.,
& Nordlund, Å. 2006, ApJ, 642, 1246 [NASA ADS] [CrossRef]
- Stein, R. F.,
Bercik, D., & Nordlund, Å. 2003, in Current Theoretical
Models and Future High Resolution Solar Observations: Preparing for
ATST, ed. A. A. Pevtsov, & H. Uitenbroek, ASP Conf.
Ser., 286, 121
- Steiner, O. 2003,
A&A, 406, 1083 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Stenflo, J. O. 1982,
Sol. Phys., 80, 209 [NASA ADS] [CrossRef]
- Trujillo Bueno, J.,
Shchukina, N., & Asensio Ramos, A. 2004, Nature, 430, 326 [NASA ADS] [CrossRef]
- Unno, W. 1959, ApJ, 129,
375 [NASA ADS] [CrossRef]
- Viticchié, B., Del
Moro, D., & Berrilli, F. 2006, ApJ, 652, 1734 [NASA ADS] [CrossRef]
(In the text)
- Vögler, A. 2003,
Ph.D. Thesis, Göttingen University, Germany
- Vögler, A.,
& Schüssler, M. 2003, Astron. Nachr., 324, 399 [NASA ADS] [CrossRef]
- Vögler, A.,
& Schüssler, M. 2007, A&A, 465, L43 [NASA ADS] [CrossRef] [EDP Sciences]
- Vögler, A., Shelyag,
S., Schüssler, M., et al. 2003, in Modelling of Stellar
Atmospheres, ed. N. Piskunov, W. W. Weiss, &
D. F. Gray, IAU Symp., 210, 157
- Vögler, A., Shelyag,
S., Schüssler, M., et al. 2005, A&A, 429, 335 [NASA ADS] [CrossRef] [EDP Sciences]
- Weiss, N. O. 1966,
R. Soc. London Proc. Ser. A, 293, 310 [NASA ADS] [CrossRef]
Copyright ESO 2008
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{9683fig1.eps}
\end{figure}](/articles/aa/full/2008/38/aa09683-08/Timg31.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9683fig2.eps} \end{figure}](/articles/aa/full/2008/38/aa09683-08/Timg34.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9683fig3.eps} \end{figure}](/articles/aa/full/2008/38/aa09683-08/Timg37.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9683fig4.eps} \end{figure}](/articles/aa/full/2008/38/aa09683-08/Timg39.gif)
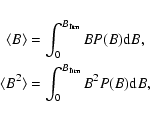
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9683fig5.eps} \end{figure}](/articles/aa/full/2008/38/aa09683-08/Timg50.gif)