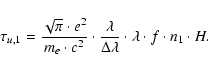A&A 489, 773-776 (2008)
DOI: 10.1051/0004-6361:200809607
On the origin of the Balmer and Lyman emission lines in solar
prominences
(Research Note)
G. Stellmacher1 -
E. Wiehr2
1 - Institut d'Astrophysique (IAP),
98bis Bvd. d'Arago, 75014 Paris, France
2 -
Institut für Astrophysik, Universität Göttingen
Friedrich-Hund-Platz 1, 37077 Göttingen, Germany
Received 19 February 2008 / Accepted 9 July 2008
Abstract
Aims. We show how the observed hydrogen Balmer and Lyman emission lines constrain the modeling of quiescent solar prominences.
Methods. We compare space observations of Lyman lines with ground-based observations of Balmer lines for quiescent solar prominences of comparable brightness defined by their H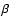 emission.
emission.
Results. The effective number densities of hydrogen atoms emitting from the same upper level u deduced from the corresponding emerging Lyman and Balmer line emissions show large differences that diminish with increasing level number and converge at the highest level numbers. Hydrogen atoms excited in 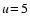 contribute 250 times less, and those in
contribute 250 times less, and those in 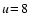 still contribute 65 times less to the Lyman than to the corresponding Balmer emission, supporting the idea of distinct spatial origin of the emissions of both series. This is also indicated by the line widths. The high optical thickness of all Lyman members allows the brightness temperature
still contribute 65 times less to the Lyman than to the corresponding Balmer emission, supporting the idea of distinct spatial origin of the emissions of both series. This is also indicated by the line widths. The high optical thickness of all Lyman members allows the brightness temperature 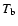 to be estimated from the spectral radiance at line center, where
to be estimated from the spectral radiance at line center, where 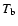 is found to be largely independent of the upper level number, in contrast to the (known) behavior of the Balmer lines.
is found to be largely independent of the upper level number, in contrast to the (known) behavior of the Balmer lines.
Key words: Sun: prominences - radiation mechanisms: thermal
The hydrogen spectrum of solar prominences is an important source
of information about the physical state and the structure of these
cool plasma clouds embedded in a hot environment. The emission
lines of this most abundant element are distributed over a wide
spectral range, reaching from the Lyman series in the EUV to the
Balmer lines in the visible and further series in the infrared
spectral regions. Large parts of the EUV Lyman lines have been
observed with the SUMER spectrograph onboard SOHO by Stellmacher et al. (2003) and by Parenti et al. (2005a).
The complete Balmer series in the visible spectral range is much
less frequently observed, since large dispersion spectrographs make
simultaneous observations over the wide spectral range from
H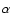 at 6563 Å to the highest Balmer members below 3880 Å
difficult. Large parts of the Balmer series have been observed
by Stellmacher (1969), Yakovkin & Zel'dina (1975), and Illing
et al. (1975). But simultaneous observations of both
the whole Lyman and the whole Balmer sequences do not exist
to our knowledge.
at 6563 Å to the highest Balmer members below 3880 Å
difficult. Large parts of the Balmer series have been observed
by Stellmacher (1969), Yakovkin & Zel'dina (1975), and Illing
et al. (1975). But simultaneous observations of both
the whole Lyman and the whole Balmer sequences do not exist
to our knowledge.
However, data of both line series from different observations may
be compared using the mean values of prominences with similar
brightness. Here, the total line radiance of the (mostly optically
thin) H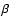 emission serves as a reasonable indicator. Such a
relation between spectroscopic data in the EUV and in the visible
spectral region may be found in De Boer et al. (1998)
and Stellmacher et al. (2003) who simultaneously observed
large parts of the Lyman lines from space and selected Balmer lines
including H
emission serves as a reasonable indicator. Such a
relation between spectroscopic data in the EUV and in the visible
spectral region may be found in De Boer et al. (1998)
and Stellmacher et al. (2003) who simultaneously observed
large parts of the Lyman lines from space and selected Balmer lines
including H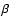 from ground.
from ground.
To compare observed Lyman and Balmer lines, we used the equation
that relates the spectral line radiance Eul, i.e. the spectral
radiance
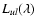 integrated over the respective emission
line, with the number density of atoms, nu, emitting from the
upper level u (Unsöld 1955):
integrated over the respective emission
line, with the number density of atoms, nu, emitting from the
upper level u (Unsöld 1955):
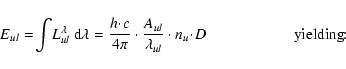 |
(1) |
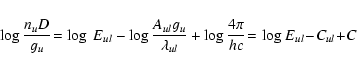 |
(2) |
where
![$C = \log~(4\pi/(h \cdot c)) = 16.8 [{\rm cgs}]$](/articles/aa/full/2008/38/aa09607-08/img17.gif) ,
Aul
are the Einstein coefficients for the spontaneous emission from upper
level u to lower level l, and
,
Aul
are the Einstein coefficients for the spontaneous emission from upper
level u to lower level l, and
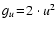 the statistical weight
of the upper level u;
the statistical weight
of the upper level u;
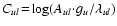 is a constant for each line and given in the NBS-tables (Wiese et al. 1966). Equation (2) relates the observed spectral line radiance
is a constant for each line and given in the NBS-tables (Wiese et al. 1966). Equation (2) relates the observed spectral line radiance
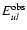 and the effective number of emitting atoms nu D. For
emission from optically thin layers, nu D is the actual number of
hydrogen atoms excited in the upper level u emitting along the
line-of-sight. In the form
and the effective number of emitting atoms nu D. For
emission from optically thin layers, nu D is the actual number of
hydrogen atoms excited in the upper level u emitting along the
line-of-sight. In the form
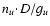 (in Eq. (2)),
this quantity may be used in the Boltzmann formula.
(in Eq. (2)),
this quantity may be used in the Boltzmann formula.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{9607fig1.eps} \end{figure}](/articles/aa/full/2008/38/aa09607-08/Timg24.gif) |
Figure 1:
Effective number of atoms,
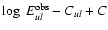 ,
emitting from the upper level
u to the lower level l, versus the line-specific emission
coefficient, ,
emitting from the upper level
u to the lower level l, versus the line-specific emission
coefficient,
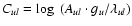 ,
from observations of the Balmer series by Stellmacher (1969; circles
for faint and triangles for brighter prominences) and by Illing et al. (1975; crosses) in comparison with observations of the Lyman
series by Parenti et al. (2005; X), by Stellmacher et al. (2003; rhombs 42-L; squares 70-H), and by Heinzel et al.
(2001; asterisks); indices give upper level numbers u. ,
from observations of the Balmer series by Stellmacher (1969; circles
for faint and triangles for brighter prominences) and by Illing et al. (1975; crosses) in comparison with observations of the Lyman
series by Parenti et al. (2005; X), by Stellmacher et al. (2003; rhombs 42-L; squares 70-H), and by Heinzel et al.
(2001; asterisks); indices give upper level numbers u. |
| Open with DEXTER |
The effective number of emitting hydrogen atoms obtained from Lyman
and from Balmer lines observations are compared in Fig. 1. Its upper
part shows means of Balmer line observations by Stellmacher (1969)
and by Illing et al. (1975), which can be considered as
characteristic of moderately bright prominences with emissions
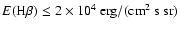 .
Substantial higher spatial resolution is achieved in the detailed
photometric data of H
.
Substantial higher spatial resolution is achieved in the detailed
photometric data of H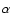 and H
and H
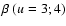 ,
obtained
by Stellmacher & Wiehr (1994). The results from observations by
Yakovkin & Zel'dina (1975) are not entered in Fig. 1 since
they represent
rare prominences with very bright emissions up to
,
obtained
by Stellmacher & Wiehr (1994). The results from observations by
Yakovkin & Zel'dina (1975) are not entered in Fig. 1 since
they represent
rare prominences with very bright emissions up to
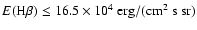 ,
like those discussed by Stellmacher & Wiehr (2005) and comparable Lyman observations do not exist.
,
like those discussed by Stellmacher & Wiehr (2005) and comparable Lyman observations do not exist.
For the faint and moderately bright prominences characterized by
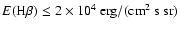 ,
EUV
observations with the SUMER instrument onboard SOHO have been taken
by De Boer et al. (1998) and by Stellmacher et al. (2003) simultaneously with ground-based data. These Lyman
data are shown in the lower part of Fig. 1 together with EUV
observations by Heinzel et al. (2001) and by Parenti et al.
(2005a).
,
EUV
observations with the SUMER instrument onboard SOHO have been taken
by De Boer et al. (1998) and by Stellmacher et al. (2003) simultaneously with ground-based data. These Lyman
data are shown in the lower part of Fig. 1 together with EUV
observations by Heinzel et al. (2001) and by Parenti et al.
(2005a).
The differences in the abscissa values for equal upper level u
of the Balmer and the Lyman lines arise from the different Einstein
coefficients Aul. The striking differences in the ordinate values
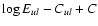 of the Lyman and the Balmer lines
reflect the largely different number of effectively emitting atoms.
Emerging Lyman lines stem from up to 250 times less emitters than
the corresponding Balmer lines from the same upper level u.
of the Lyman and the Balmer lines
reflect the largely different number of effectively emitting atoms.
Emerging Lyman lines stem from up to 250 times less emitters than
the corresponding Balmer lines from the same upper level u.
Figure 1 shows a steady decrease for the Balmer lines in the ordinate
values
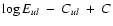 with increasing upper level
u, and this reflects the decreasing transition probabilities.
The Lyman lines show an opposite behavior of increasing ordinate values
with increasing upper level for
with increasing upper level
u, and this reflects the decreasing transition probabilities.
The Lyman lines show an opposite behavior of increasing ordinate values
with increasing upper level for 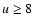 ,
approaching the values
for the Balmer lines. Only the centrally depressed Lyman lines with
,
approaching the values
for the Balmer lines. Only the centrally depressed Lyman lines with
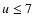 show a slight decrease in the numbers of effectively
emitting atoms for increasing u.
show a slight decrease in the numbers of effectively
emitting atoms for increasing u.
![\begin{figure}
\par\includegraphics[width=18cm]{9607fig2.eps} \end{figure}](/articles/aa/full/2008/38/aa09607-08/Timg34.gif) |
Figure 2:
SUMER spectrum of the prominence observed on July 8, 2000
by Stellmacher et al. (2003), showing the wavelength range
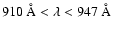 with the Lyman emissions
(
with the Lyman emissions
(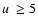 )
along the 120'' slit, which covers 20'' of the upper chromosphere
(lower image border), 30'' below the prominence, and 70'' of the
prominence body. The white line gives the spectral radiance distribution
averaged over the prominence body in a logarithmic scale. The jump
between u = 10 and u = 11 is due to the different detector coating (KBr
for larger )
along the 120'' slit, which covers 20'' of the upper chromosphere
(lower image border), 30'' below the prominence, and 70'' of the
prominence body. The white line gives the spectral radiance distribution
averaged over the prominence body in a logarithmic scale. The jump
between u = 10 and u = 11 is due to the different detector coating (KBr
for larger 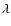 ). Note the largely constant spectral radiance
of the Lyman line centers. ). Note the largely constant spectral radiance
of the Lyman line centers. |
| Open with DEXTER |
For an interpretation of the different behavior of Balmer and Lyman
lines, we follow the NLTE calculations by Gouttebroze et al.
(1993). The analysis of the Balmer lines by Stellmacher (1969) shows
that the populations of the upper levels u > 4 follow, relative to
each other, a smooth distribution with an equilibrium temperature of
 K. This value is close to the kinetic temperature
K. This value is close to the kinetic temperature
 obtained from the line widths and is conform
to the departure coefficients bu = 1 for u > 4 calculated by
Gouttebroze et al. (1993).
obtained from the line widths and is conform
to the departure coefficients bu = 1 for u > 4 calculated by
Gouttebroze et al. (1993).
For the Lyman lines, these authors obtain a total optical prominence
thickness equivalent to
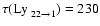 with
``conventional'' electron temperature
with
``conventional'' electron temperature
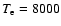 K. For higher
temperatures T = 10 000 K and T = 15 000 K (more realistic for a
prominence corona transition atmosphere), their models still lead
to values of
K. For higher
temperatures T = 10 000 K and T = 15 000 K (more realistic for a
prominence corona transition atmosphere), their models still lead
to values of
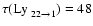 and 2.5, respectively,
even 1000 and 52 for
and 2.5, respectively,
even 1000 and 52 for
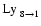 .
.
Emission lines with such high 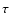 values will be limited to the outermost
(hotter) prominence regions. A rough estimate shows that the geometric
extention of the effectively emitting layers (which produce the emerging
Lyman emission) is rather small as compared to that of the (optically
thin) Balmer lines, which amounts to the whole prominence atmosphere.
values will be limited to the outermost
(hotter) prominence regions. A rough estimate shows that the geometric
extention of the effectively emitting layers (which produce the emerging
Lyman emission) is rather small as compared to that of the (optically
thin) Balmer lines, which amounts to the whole prominence atmosphere.
In general, the geometric thickness H of an emitting layer can be
estimated from
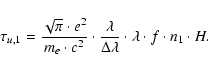 |
(3) |
With
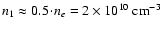 and
and
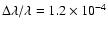 (as observed), one obtains
a geometric thickness of only H=30 km for Ly
(as observed), one obtains
a geometric thickness of only H=30 km for Ly
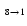 assuming a high value of
assuming a high value of
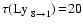 .
.
With increasing level number u, the total thickness decreases toward
that of the Lyman continuum, for which Parenti et al. (2005b)
still deduce
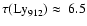 ,
and the emissions will
originate more and more in deeper (cooler) layers, thus approaching the
main regions of Balmer line emissions. This readily explains both the
`bending' of the Lyman curves in Fig. 1 and their approach to the
values of the optically thin (u > 4) Balmer lines. Upper levels
,
and the emissions will
originate more and more in deeper (cooler) layers, thus approaching the
main regions of Balmer line emissions. This readily explains both the
`bending' of the Lyman curves in Fig. 1 and their approach to the
values of the optically thin (u > 4) Balmer lines. Upper levels
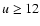 will largely be in equilibrium with the free electrons
since their energy distance to the ionization limit amounts to only
will largely be in equilibrium with the free electrons
since their energy distance to the ionization limit amounts to only
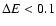 eV.
eV.
The spectral radiances at line center
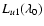 are
largely independent of u. This can be seen in the SUMER spectrum
(Fig. 2) showing the Lyman emissions (
are
largely independent of u. This can be seen in the SUMER spectrum
(Fig. 2) showing the Lyman emissions (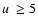 )
in the wavelength
range
)
in the wavelength
range
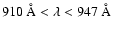 along the 120'' slit,
which covers 20'' of the upper chromosphere (lower image border),
30'' below the prominence, and 70'' of the prominence body.
Superposed is the mean spectral radiance distribution
along the 120'' slit,
which covers 20'' of the upper chromosphere (lower image border),
30'' below the prominence, and 70'' of the prominence body.
Superposed is the mean spectral radiance distribution
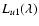 over the prominence body in a logarithmic scale.
over the prominence body in a logarithmic scale.
The almost constant central line radiances
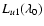 indicate largely equal brightness temperatures
indicate largely equal brightness temperatures 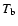 ,
which may be
derived via the Planck function. For the optically thick Lyman lines
(
,
which may be
derived via the Planck function. For the optically thick Lyman lines
(
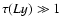 ,
hence emitted from the prominence periphery),
the spectral radiance at line center
,
hence emitted from the prominence periphery),
the spectral radiance at line center
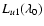 becomes
equal to the source function Su1, which we set equal to the
Planck function
becomes
equal to the source function Su1, which we set equal to the
Planck function
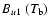 .
.
In Table 1 we give the deduced 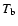 ,
together with the observed
spectral radiance at the Lyman line centers
,
together with the observed
spectral radiance at the Lyman line centers
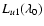 and the
total spectral line radiance
and the
total spectral line radiance
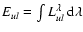 for the brightest (42-L) and the faintest (70-H) prominence regions
marked in Fig. 1 as rhombs and squares. The mean values of, respectively,
for the brightest (42-L) and the faintest (70-H) prominence regions
marked in Fig. 1 as rhombs and squares. The mean values of, respectively,
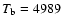 K and
K and
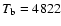 K (neglecting the centrally
most reversed line
K (neglecting the centrally
most reversed line 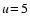 )
show a small internal scatter of only
)
show a small internal scatter of only
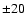 K. The radiometric accuracy of 15% for detector A in
the corresponding
K. The radiometric accuracy of 15% for detector A in
the corresponding 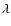 regime (Schühle et al. 2000)
introduces an uncertainty of
regime (Schühle et al. 2000)
introduces an uncertainty of
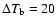 K.
K.
The 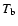 values deduced for the Lyman lines are more than 1000 K higher
than the
values deduced for the Lyman lines are more than 1000 K higher
than the
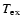 deduced from the Balmer lines, for which Stellmacher
(1969) finds
deduced from the Balmer lines, for which Stellmacher
(1969) finds
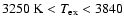 K in similarly bright prominences. Even the maximum value
K in similarly bright prominences. Even the maximum value
 K, occasionally found for the
(optically thick) H
K, occasionally found for the
(optically thick) H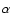 line in the brightest prominences by Stellmacher
& Wiehr (2005) is still
line in the brightest prominences by Stellmacher
& Wiehr (2005) is still 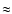 1000 K below the
1000 K below the 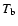 found for the
Lyman lines. This indicates that the peripheral prominence regions,
which emit the Lyman lines, are significantly hotter than the prominence
cores, which emit the Balmer lines.
found for the
Lyman lines. This indicates that the peripheral prominence regions,
which emit the Lyman lines, are significantly hotter than the prominence
cores, which emit the Balmer lines.
Since most prominences are formed by numerous tiny ``threads'' (e.g.
Lin et al. 2005), the actual spectral radiances at line center can
be expected to be higher than the observed ones. The coronal material
inbetween will not emit Lyman lines. Realistic filling factors
are still unknown. If we assume a filling of 50%, the actual spectral
radiances would be two times, for 10% filling 10 times greater than
those in Table 1. The influence of filling on the eventually deduced
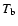 values is, however, rather weak, because the brightest Lyman line
at
values is, however, rather weak, because the brightest Lyman line
at
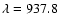 Å yields 110 K (400 K) higher
Å yields 110 K (400 K) higher 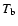 for a
50% (10%) filling.
for a
50% (10%) filling.
Such a weak influence of filling also seems to be indicated in the
various observations of different prominences. In particular, emissions
deduced from two-dimensional imaging at much higher spatial resolution
(Stellmacher & Wiehr 1999; Stellmacher & Wiehr 2000) largely follow
the same relations as from spectra of much lower spatial resolution.
Table 1:
Upper level u, wavelength
![$\lambda_0 [\AA]$](/articles/aa/full/2008/38/aa09607-08/img64.gif) ,
spectral
line radiance
,
spectral
line radiance
![$E^{\rm obs}_{\rm ul}[{\rm mW}/({\rm m}^2~{\rm s}~{\rm sr})]$](/articles/aa/full/2008/38/aa09607-08/img65.gif) ,
spectral radiance at line center
,
spectral radiance at line center
![$L_{u1}(\lambda _0)
[{\rm mW}/({\rm m}^2~{\rm s}~{\rm sr}~\AA)]$](/articles/aa/full/2008/38/aa09607-08/img66.gif) ,
and corresponding
brightness temperature
,
and corresponding
brightness temperature 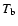 [K] for Lyman lines of the two prominence regions
given in Fig. 1 as rhombs and squares.
[K] for Lyman lines of the two prominence regions
given in Fig. 1 as rhombs and squares.
High temperatures for the Lyman emitting regions are also indicated from
the line widths. The value
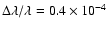 observed for the unsaturated higher Balmer lines by Stellmacher (1969)
and by Stellmacher & Wiehr (1994) correspond to
observed for the unsaturated higher Balmer lines by Stellmacher (1969)
and by Stellmacher & Wiehr (1994) correspond to
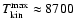 K, if purely thermally broadened, or to
7500 K for a mean non-thermal broadening of 4 km s-1.
K, if purely thermally broadened, or to
7500 K for a mean non-thermal broadening of 4 km s-1.
In contrast, the widths
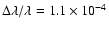 measured by Parenti et al. (2005a) for the higher Lyman
lines with u > 16, correspond to an upper limit (since optically
thick) of
measured by Parenti et al. (2005a) for the higher Lyman
lines with u > 16, correspond to an upper limit (since optically
thick) of
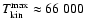 K in the case of a purely
thermal broadening. For the hydrogen formation temperature of 16 000 K,
a non-thermal broadening of 28.5 km s-1 is required, in accordance with
Stellmacher et al. (2003; Figs. 16 and 17) and with
Parenti & Vial (2007). The typical kinetic temperature of 7500 K,
deduced from the Balmer lines for the cool prominence body, would
lead to a high non-thermal broadening of 31 km s-1.
K in the case of a purely
thermal broadening. For the hydrogen formation temperature of 16 000 K,
a non-thermal broadening of 28.5 km s-1 is required, in accordance with
Stellmacher et al. (2003; Figs. 16 and 17) and with
Parenti & Vial (2007). The typical kinetic temperature of 7500 K,
deduced from the Balmer lines for the cool prominence body, would
lead to a high non-thermal broadening of 31 km s-1.
Slightly broader Lyman lines with
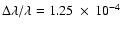 were measured by Stellmacher et al.
They discuss that the actual values may be smaller, since the intrinsic
SUMER profile seems to be underestimated. The EUV spectrograph is
particularly adapted to broad emission lines from the hot corona
rather than to narrow lines from cool prominences. Regardless of that
uncertainty, the broadening of the Lyman lines yields much higher
temperatures
were measured by Stellmacher et al.
They discuss that the actual values may be smaller, since the intrinsic
SUMER profile seems to be underestimated. The EUV spectrograph is
particularly adapted to broad emission lines from the hot corona
rather than to narrow lines from cool prominences. Regardless of that
uncertainty, the broadening of the Lyman lines yields much higher
temperatures
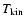 than that of the Balmer lines, in accordance
with the difference in the brightness temperatures
than that of the Balmer lines, in accordance
with the difference in the brightness temperatures 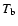 .
.
The comparison of observed Lyman and Balmer emissions from faint
through ``medium bright'' quiescent prominences, characterized by
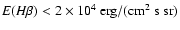 ,
shows
that the inner regions with T
,
shows
that the inner regions with T
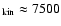 K that emit the
optically thin Balmer lines are not those with much higher T
K that emit the
optically thin Balmer lines are not those with much higher T
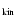 that emit the Lyman lines. Even different members of the Lyman series
will not originate in the same prominence volume. The very high
that emit the Lyman lines. Even different members of the Lyman series
will not originate in the same prominence volume. The very high
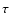 values of the first Lyman members will limit their emerging
emission to the outermost prominence periphery where excitation and
ionization are highest.
values of the first Lyman members will limit their emerging
emission to the outermost prominence periphery where excitation and
ionization are highest.
With decreasing
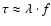 ,
higher Lyman members
will originate more and more in the deeper layers. A realistic
modeling of the Lyman and the Balmer lines will have to consider
strong gradients between the cool prominence body and its hot
periphery for temperature and (or) non-thermal velocities besides
the strong departures from LTE.
,
higher Lyman members
will originate more and more in the deeper layers. A realistic
modeling of the Lyman and the Balmer lines will have to consider
strong gradients between the cool prominence body and its hot
periphery for temperature and (or) non-thermal velocities besides
the strong departures from LTE.
Heinzel et al. (2001) propose that the reversed profiles of the
stronger Lyman lines will be related to the orientation of the
line-of-sight (LOS) with respect to the magnetic field lines:
emissions viewed across the field lines are expected to show strong
reversals. The calculations by Loucif & Magnan (1982) can be useful
for profile modeling. They treat the transfer problem of emerging
reversed lines taking spatially correlated velocity fields into
account and applying the method of addition of layers.
From our various observations, we do not find systematic differences
between prominences viewed under different aspect angles, but instead
we find the largely unique emission relations displayed in Fig. 1.
Observations at higher spatial resolution including the magnetic field
might help for adapting more refined models.
Acknowledgements
We thank Dr. F. Hessman and I. E. Dammasch and for helpful discussions;
B. Bovelet kindly performed the graphics in Fig. 1.
- De Boer, C. R.,
Stellmacher, G., & Wiehr, E. 1998, A&A, 334, 280 [NASA ADS]
(In the text)
-
Gouttebroze, P., Heinzel P., & Vial J.-C. 1993, A&AS, 99,
513 [NASA ADS]
(In the text)
- Heinzel, P.,
Schmieder, B., Vial, J.-C., & Kotrc, P. 2001, A&A, 370,
281 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Illing, R. M.
E., Landman, D. A., & Mickey, D. L. 1975, Sol. Phys., 45,
339 [NASA ADS] [CrossRef]
(In the text)
- Loucif, M. L.,
& Magnan, C. 1982, A&A, 112, 287 [NASA ADS]
(In the text)
- Lin, Y., Engvold, O.,
Rouppe van der Voort, L., Wijk, J. E., & Berger, T. E. 2005,
Sol. Phys., 226, 239 [NASA ADS] [CrossRef]
(In the text)
- Parenti, S.,
& Vial, J.-C. 2007 ApJ, 469, 1109
- Parenti,
S., Vial, J.-C., & Lemaire, P. 2005a, A&A, 443, 679 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Parenti,
S., Vial, J.-C., & Lemaire, P. 2005b, A&A, 443, 685 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
-
Schühle, U., Curdt, W., Hollandt, J., et al. 2000, Appl. Opt.,
36, 6416
-
Stellmacher, G. 1969, A&A, 1, 62 [NASA ADS]
(In the text)
- Stellmacher,
G., & Wiehr, E. 1994, A&A, 290, 655 [NASA ADS]
- Stellmacher,
G., & Wiehr, E. 2005, A&A, 431, 1069 [NASA ADS] [CrossRef] [EDP Sciences]
-
Stellmacher, G., Wiehr, E., & Dammasch, I. E. 2003, Sol. Phys.,
217, 133 [NASA ADS] [CrossRef]
- Unsöld, A.
1955, Physik der Sternatmosphären, 2 [NASA ADS].Aufl. (Berlin:
Springer)
(In the text)
- Wiese, W. L.,
Smith, M. W., Glennon, B. M. 1966, Atomic Transition Probabilities,
Vol. I, H through Ne, Nat. Stand. Ref. Data Ser., Nat. Bur. Stand.
(US) 4, U.S.-Gov. Washington DC: Printing Office
(In the text)
- Yakovkin,
N. A., & Zel'dina, M. Yu. 1975, Sol. Phys., 45, 319 [NASA ADS] [CrossRef]
(In the text)
Copyright ESO 2008
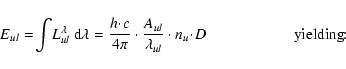
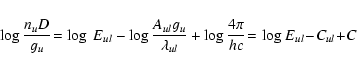
![\begin{figure}
\par\includegraphics[width=12cm,clip]{9607fig1.eps} \end{figure}](/articles/aa/full/2008/38/aa09607-08/Timg24.gif)