A&A 489, 359-375 (2008)
DOI: 10.1051/0004-6361:20078662
Core-collapse supernovae in low-metallicity environments and future all-sky transient surveys
D. R. Young1 - S. J. Smartt1 - S. Mattila1,2 - N. R. Tanvir3 - D. Bersier4 - K. C. Chambers5 - N. Kaiser5 - J. L. Tonry5
1 - Astrophysics Research Centre, School of Maths and Physics, Queen's University Belfast, Belfast BT7 1NN, Northern Ireland, UK
2 - Tuorla Observatory, University of Turku, Väisäläntie 20, 21500 Piikkiö, Finland
3 - Department of Physics and Astronomy, University of Leicester, Leicester, LE1 7RH, UK
4 - Astrophysics Research Institute, Liverpool John Moores University, Twelve Quays House, Egerton Wharf, Birkenhead, CH41 1LD, UK
5 - Institute for Astronomy, University of Hawaii, 2680 Woodlawn Drive, Honolulu, HI 96822
Received 12 September 2007 / Accepted 17 July 2008
Abstract
Aims. Massive stars in low-metallicity environments may produce exotic explosions such as long-duration gamma-ray bursts and pair-instability supernovae when they die as core-collapse supernovae (CCSNe). Such events are predicted to be relatively common in the early Universe during the first episodes of star-formation. To understand these distant explosions it is vital to study nearby CCSNe arising in low-metallicity environments to determine if the explosions have different characteristics to those studied locally in high-metallicity galaxies. Many of the nearby supernova searches concentrate their efforts on high star-formation rate galaxies, hence biasing the discoveries to metal rich regimes. Here we determine the feasibility of searching for these CCSNe in metal-poor dwarf galaxies using various survey strategies.
Methods. We determine oxygen abundances and star-formation rates for all spectroscopically typed star-forming galaxies in the Sloan Digital Sky Survey, Data Release 5, within z=0.04. We then estimate the CCSN rates for sub-samples of galaxies with differing upper-metallicity limits. Using Monte-Carlo simulations we then predict the fraction of these CCSNe that we can expect to detect using different survey strategies. We test survey capabilities using a single 2 m telescope, a network of 2 m telescopes, and the upcoming all-sky surveys of the Pan-STARRS and LSST systems.
Results. Using a single 2 m telescope (with a standard CCD camera) search we predict a detection rate of  1.3 CCSNe yr-1 in galaxies with metallicities below
1.3 CCSNe yr-1 in galaxies with metallicities below
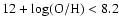 which are within a volume that will allow detailed follow-up with 4 m and 8 m telescopes (z=0.04). With a network of seven 2 m telescopes we estimate
which are within a volume that will allow detailed follow-up with 4 m and 8 m telescopes (z=0.04). With a network of seven 2 m telescopes we estimate  9.3 CCSNe yr-1 could be found, although this would require more than 1000 h of telescope time allocated to the network. Within the same radial distance, a volume-limited search in the future Pan-STARRS PS1 all-sky survey should uncover 12.5 CCSNe yr-1 in low-metallicity galaxies. Over a period of a few years this would allow a detailed comparison of their properties. We then extend our calculations to determine the total numbers of CCSNe that can potentially be found in magnitude-limited surveys with PS1 (24 000 yr-1, within
9.3 CCSNe yr-1 could be found, although this would require more than 1000 h of telescope time allocated to the network. Within the same radial distance, a volume-limited search in the future Pan-STARRS PS1 all-sky survey should uncover 12.5 CCSNe yr-1 in low-metallicity galaxies. Over a period of a few years this would allow a detailed comparison of their properties. We then extend our calculations to determine the total numbers of CCSNe that can potentially be found in magnitude-limited surveys with PS1 (24 000 yr-1, within 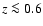 ), PS4 (69 000 yr-1, within
), PS4 (69 000 yr-1, within  )
and LSST (160 000 yr-1, within
)
and LSST (160 000 yr-1, within  )
surveys.
)
surveys.
Key words: surveys - stars: supernovae: general - gamma-rays: bursts
Upon exhausting all of its available fuel, the iron core of a massive star (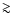 8
8 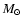 )
collapses, often giving rise to an extremely powerful, bright explosion known as a core-collapse supernova (CCSN). Under very specific circumstances these CCSNe are also thought to be associated with another very powerful and luminous event known as a long-duration gamma-ray burst (LGRB). The circumstances that permit this extraordinary
partnership are still not well understood, but it seems likely
that progenitors born in lower-metallicity environments (sub-solar) favour production of GRBs (see Fynbo et al. 2003; Tanvir et al. 2004; Fruchter et al. 2006; Stanek et al. 2006).
)
collapses, often giving rise to an extremely powerful, bright explosion known as a core-collapse supernova (CCSN). Under very specific circumstances these CCSNe are also thought to be associated with another very powerful and luminous event known as a long-duration gamma-ray burst (LGRB). The circumstances that permit this extraordinary
partnership are still not well understood, but it seems likely
that progenitors born in lower-metallicity environments (sub-solar) favour production of GRBs (see Fynbo et al. 2003; Tanvir et al. 2004; Fruchter et al. 2006; Stanek et al. 2006).
The most popular theoretical model interprets the LGRB as
being caused by the core-collapse of a specific class of massive
star. This fundamental theory, coined as the ``Collapsar'' model, was
first conceived by Woosley (1993) (also see Woosley & MacFadyen 1999). The criteria for the creation of a LGRB
resulting from the collapse of a massive star are that a black-hole
must be formed upon core-collapse, either promptly or via fall-back
of ejected material, and that an accretion disk is allowed to form
around this black-hole which acts as a ``central engine'' causing the
release of collimated relativistic jets along the rotation axis of
the black-hole
(Hirschi et al. 2006; Tchekhovskoy et al. 2008; Yoon et al. 2008). It
is these relativistic jets that form the LGRB and the associated
afterglow emission. These criteria are found to place
very specific
constraints on the type of progenitor star that can collapse to
produce a LGRB. The core of
the progenitor must be massive enough to produce a black-hole,
it must be rotating rapidly enough to form an accretion disk, and the star
needs to be stripped of
its hydrogen envelope, so that the resulting relativistic jets are
not inhibited from reaching the stellar surface. All of this points toward
rapidly rotating Wolf-Rayet stars as viable progenitors
(Woosley & Bloom 2006; Woosley & Heger 2006; Detmers et al. 2008).
Rapidly rotating O-stars which mix-up their core processed material
to produce WR stars through chemically homogeneous evolution have been
suggested to
satisfy the requirements of the collapsar model (Maeder 1987; Woosley & Heger 2006; Yoon et al. 2006; Yoon & Langer 2006).
This model prevents the depletion of angular
momentum due to mass-loss and allows a massive star to become a WR star
directly, avoiding the supergiant phase. Yoon et al. (2006) have estimated that for a
rapidly rotating star to be the progenitor of an LGRB, prior to collapse
it must have a helium core mass greater than 10 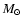 ,
that is an
initial mass greater than 25-30
,
that is an
initial mass greater than 25-30 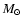 .
Woosley & Heger (2006)
have modelled the WR mass-loss rates of Vink & de Koter (2005) and
predict that the upper metallicity limit for forming LGRB may be as high
as 0.3
.
Woosley & Heger (2006)
have modelled the WR mass-loss rates of Vink & de Koter (2005) and
predict that the upper metallicity limit for forming LGRB may be as high
as 0.3 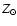 .
Apart from the single star progenitor model, a rapidly rotating massive star could lose its hydrogen envelope
and still retain a large fraction of its initial angular momentum if a close binary companion were to strip it of the envelope
rapidly enough for the progenitor to avoid spin down
(Bissaldi et al. 2007; Dainotti et al. 2007; Cantiello et al. 2007).
.
Apart from the single star progenitor model, a rapidly rotating massive star could lose its hydrogen envelope
and still retain a large fraction of its initial angular momentum if a close binary companion were to strip it of the envelope
rapidly enough for the progenitor to avoid spin down
(Bissaldi et al. 2007; Dainotti et al. 2007; Cantiello et al. 2007).
Whatever the model for the progenitor of the LGRB, prior to collapse we require a very rapidly rotating, massive WR star. These constraints lead to the prediction that LGRBs favour a lower-metallicity environment and that CCSNe found in association with an LGRB will be classified as type Ib or type Ic, characterised by an absence of hydrogen in their spectra
(Blondin & Tonry 2007; Filippenko 2003; Hamuy 2003). To date many LGRBs have revealed ``bumps'' in their afterglow emission, thought to be evidence of associated SNe (see Bloom et al. 1999; Della Valle et al. 2003; Levan et al. 2005; Galama et al. 2000). A few of these associated SNe have been adequately spectroscopically typed, all have been found to be broad-lined type Ic SNe, helping to confirm the theory that LGRBs are the result of the collapse of hydrogen-stripped massive stars (Stanek et al. 2003; Hjorth et al. 2003; Galama et al. 1998; Zeh et al. 2004). Modjaz et al. (2008) have found that the SNe type Ic-BL associated with an LGRB are found to inhabit a sample of host galaxies of significantly lower metallicity than the host galaxies of their type Ic-BL counterparts with no associated observed LGRB. Interestingly, there has not been a SN type Ic-BL without an associated observed LGRB that has been found to inhabit the same low-metallicity galaxy sample that the LGRB associated SNe inhabit.
Fruchter et al. (2006) have found that LGRBs are preferentially
found in irregular galaxies which are
significantly fainter, smaller and hence presumably of
lower-metallicity than typical CCSNe hosts.
Sollerman et al. (2005) make a similar point, stating that
the majority of LGRBs are found in extremely blue, sub-luminous
galaxies, similar to the Blue
Compact Dwarf Galaxy population.
Scannapieco (2006)
has speculated that at primordial metallicities stars of up
to 300 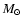 may form and if they have low mass-loss,
they may end their lives still retaining much of their original
mass. Heger & Woosley (2002) predict that those stars
within the mass range 140
may form and if they have low mass-loss,
they may end their lives still retaining much of their original
mass. Heger & Woosley (2002) predict that those stars
within the mass range 140 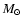 -260
-260 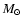 may produce pair-instability supernovae
(PISNe), huge thermonuclear explosions with energies as high as
may produce pair-instability supernovae
(PISNe), huge thermonuclear explosions with energies as high as
 1053 erg. Hence understanding SNe in low-metallicity
environments locally could offer insights into high-z GRBs and
early Universe explosions.
An indication that these exotic PISN
events may not be beyond our present day reach is the recent SN 2006gy
which has been reported to have a peak luminosity three times greater
than any other supernova ever recorded reaching a magnitude of -22
(Smith et al. 2006). Hypothesised as having had a Luminous
Blue Variable as a progenitor with an initial mass of
1053 erg. Hence understanding SNe in low-metallicity
environments locally could offer insights into high-z GRBs and
early Universe explosions.
An indication that these exotic PISN
events may not be beyond our present day reach is the recent SN 2006gy
which has been reported to have a peak luminosity three times greater
than any other supernova ever recorded reaching a magnitude of -22
(Smith et al. 2006). Hypothesised as having had a Luminous
Blue Variable as a progenitor with an initial mass of
 150
150 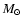 this has been suggested to be the first ever PISNe
detected (also
see Woosley et al. 2007; Ofek et al. 2007; Langer et al. 2007).
The unusual SN 2006jc defines another class of peculiar low-metallicity
event, occurring spatially coincident with an outburst thought to be
that of an LBV just two years previously (Pastorello et al. 2007),
which has also been postulated to be related to the PISN mechanism
(Woosley et al. 2007).
this has been suggested to be the first ever PISNe
detected (also
see Woosley et al. 2007; Ofek et al. 2007; Langer et al. 2007).
The unusual SN 2006jc defines another class of peculiar low-metallicity
event, occurring spatially coincident with an outburst thought to be
that of an LBV just two years previously (Pastorello et al. 2007),
which has also been postulated to be related to the PISN mechanism
(Woosley et al. 2007).
To date there
have been many surveys specifically designed to search for SNe and
depending on the motivation of an individual survey generally one of
two different survey strategies has been employed. The first of these
strategies is the pointed survey strategy; here we have a
fixed catalogue of galaxies which are all individually
observed with a cadence of a few days and scanned for fresh SNe. These
surveys included the highly successful Lick Observatory Supernova
Search (LOSS) which uses the fully robotic 0.75 m KAIT telescope to
scan a catalogue of 7500-14 000 nearby galaxies (
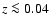 ),
aiming to observe each
individual galaxy with a cadence of 3-5 days
(Filippenko et al. 2001). With
the advent of relatively inexpensive CCD technology, the ability of
amateur astronomers to detect nearby SNe using this pointed survey
strategy has become more than substantial and a large fraction of
nearby SNe are now being discovered by this community
(Garnavich 2006).
The Southern inTermediate Redshift ESO Supernova Search (STRESS) produced a catalogue of
),
aiming to observe each
individual galaxy with a cadence of 3-5 days
(Filippenko et al. 2001). With
the advent of relatively inexpensive CCD technology, the ability of
amateur astronomers to detect nearby SNe using this pointed survey
strategy has become more than substantial and a large fraction of
nearby SNe are now being discovered by this community
(Garnavich 2006).
The Southern inTermediate Redshift ESO Supernova Search (STRESS) produced a catalogue of  43 000
(
0.05 < z < 0.6)
galaxies within 21 fields observed with the ESO Wide-Field-Imager
and searched for SNe in these hosts to determine
rates and their dependency on host galaxy colour and
redshift evolution (Botticella et al. 2008).
43 000
(
0.05 < z < 0.6)
galaxies within 21 fields observed with the ESO Wide-Field-Imager
and searched for SNe in these hosts to determine
rates and their dependency on host galaxy colour and
redshift evolution (Botticella et al. 2008).
The second strategy
employed by SN surveys is the area survey strategy; here an
area of sky is surveyed repeatedly and image subtraction used to
identify transient events including SNe. The SN Legacy Survey uses
the CFHT MegaCam imager to image four one-square degree fields to
search for SNe type Ia with the motivation of improving the sampling
of these SNe within the redshift range
0.2 < z < 1.0(Pritchet & The SNLS Collaboration 2005; Astier et al. 2006). The equation of
State SupErNova Cosmology Experiment (ESSENCE) uses the Mosaic Imager
on the Blanco 4 m telescope to survey equatorial fields, that have
preferably been observed with other wide-field surveys, to discover
SN type Ia within the redshift range
0.15 < z < 0.74(Miknaitis et al. 2007). The Nearby SN Factory uses ultra-wide
field CCD mosaic images from the Near-Earth Asteriod Tracking (NEAT) and Palomar-Quest survey
programs to perform an area survey in a bid to find SN type
Ia in the redshift range
0.03 < z < 0.08(Aldering et al. 2002). The SDSS-II Supernova Survey takes
repeated images of Stripe 82, a 300 square degree southern equatorial
strip of the sky, driven by the ambition of identifying and measuring
the lightcurves of SNe type Ia in the intermediate redshift range
0.05 < z < 0.35 (Sako et al. 2008; Frieman et al. 2008).
The Texas Supernova Search search
(Quimby et al. 2005b; Yuan et al. 2007)
is somewhat unique in that it
has a small aperture telescope (0.45 m) but very wide field (1.85 square
degrees) and is focussed on finding nearby SNe in wide area searches.
This survey discovered SN2006gy along with many other of the brightest
known SNe ever found and we shall discuss this further in
Sect. 6.
The main driver of
SN surveys that employ the pointed survey strategy is basically to
find as many SNe as possible regardless of type or characteristic. To
ensure that these surveys are as efficient as possible at
finding CCSNe, the galaxies catalogues used by the surveys generally consist
only of the most massive galaxies with the greatest star-formation
rates. As a result these galaxy catalogues
tend to be heavily biased towards galaxies with high metallicity. This
over arching high-metallicity bias has more than likely placed us in
the situation where the vast majority of CCSNe that have occurred in
low-metallicity environments (such as low-luminosity, dwarf, irregular
galaxies) have remained undetected. Prieto et al. (2008) have
matched the SAI supernova catalogue to the SDSS-DR4 catalogue of
star-forming galaxies with measured metallicities and it is clear that
the vast majority of the SNe considered have been detected in areas of
relatively high-metallicity; SN type II occurring in host galaxies
with mean metallicity
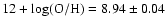 and
SN Ib/c at
and
SN Ib/c at
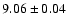 .
.
It is inherently interesting then to search for SNe specifically in
low-metallicty environments, or at least without biasing the search
to look at only high metallicity regimes.
In this paper we shall discuss several methods to
search for low-metallicity CCSN events. First we consider compiling a catalogue of nearby,
low-metallicity galaxies from pre-existing catalogues
(taking SDSS DR5 as our primary survey source)
and using either a single 2.0 m telescope or a
network of 2.0 m telescopes to perform a pointed survey of
low-metallicity galaxies in the hope of detecting a few CCSNe.
Secondly we consider
using a future all-sky transient survey such as the Panoramic Survey
Telescope and Rapid Response System (Pan-STARRS) to perform a
volume-limited survey for SNe and estimate how many may be found
in low-metallicity galaxies.
A third and final method we consider is to use a future all-sky
transient survey, limited only by
the limiting magnitude of the survey, to search for all CCSNe
including those low-metallicity events. While this paper is
primarily aimed at determining numbers of low metallicity events
that could be found, the latter calculation gives an estimate of
the total number of CCSNe that are likely to be harvested from these
upcoming surveys.
2 Creating galaxy catalogues for the various survey strategies
In order to produce catalogues of galaxies that we can use for the various survey strategies to be considered, we begin with the Sloan Digital Sky Survey (SDSS) (Adelman-McCarthy & for the SDSS Collaboration 2007). The SDSS Data
Release 5 (DR5) provides photometric
and spectroscopic data, within a wavelength range of 3500-9200 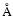 ,
for
,
for
 675 000 galaxies, over an area of 5713 square degrees of the northern
hemisphere out to a redshift
of
675 000 galaxies, over an area of 5713 square degrees of the northern
hemisphere out to a redshift
of 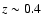 .
In general we only want to detect relatively nearby CCSNe as we want to spectroscopically type and follow these SNe with relative ease, so to this end we introduce a distance limit of z=0.04 to the SDSS spectroscopic catalogue. We have used
the SDSS DR5 website
.
In general we only want to detect relatively nearby CCSNe as we want to spectroscopically type and follow these SNe with relative ease, so to this end we introduce a distance limit of z=0.04 to the SDSS spectroscopic catalogue. We have used
the SDSS DR5 website![[*]](/icons/foot_motif.gif) to extract the out 44 041 galaxies within
z=0.04 along with data
including the petrosian magnitudes (u, g, r, i and z), the galactic extinctions in each filter determined following Schlegel et al. (1998), the spectroscopic
redshifts, the
r-band fibre magnitudes and the line intensities of H
to extract the out 44 041 galaxies within
z=0.04 along with data
including the petrosian magnitudes (u, g, r, i and z), the galactic extinctions in each filter determined following Schlegel et al. (1998), the spectroscopic
redshifts, the
r-band fibre magnitudes and the line intensities of H ,
H
,
H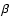 ,
[OIII]
,
[OIII]
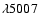 and [NII]
and [NII]
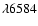 for each galaxy.
for each galaxy.
Of these 44 041 galaxies we extract out two separate samples of galaxies. The first of these samples is classified as the high signal-to-noise sample, containing galaxies with an SDSS defined line significance indicator ``nSigma''
>7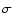 for all of the four spectral lines mentioned previously (as advised by DR5). The second sample is classified as the low signal-to-noise sample, containing galaxies that have not been included in the high signal-to-noise sample but exhibit ``nSigma'' >5
for all of the four spectral lines mentioned previously (as advised by DR5). The second sample is classified as the low signal-to-noise sample, containing galaxies that have not been included in the high signal-to-noise sample but exhibit ``nSigma'' >5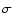 in both H
in both H and H
and H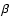 .
The high signal-to-noise sample contains 20 632 galaxies and the low signal-to-noise sample contains 8 703 galaxies.
.
The high signal-to-noise sample contains 20 632 galaxies and the low signal-to-noise sample contains 8 703 galaxies.
2.1 Removing AGN
Eventually we aim to determine a star-formation rate (SFR) for each
individual galaxy
in our sample in order to then determine their core-collapse SN rates
(CCSR).
As it is the young, massive, hot star population within each galaxy that
is the dominant source of hydrogen ionising radiation, it is possible to use
the H luminosity of these galaxies as a SFR indicator.
luminosity of these galaxies as a SFR indicator.
A difficultly arises in that many galaxies within both the high signal-to-noise and the low signal-to-noise galaxy samples will host Active Galactic Nuclei
(AGN), which will also contribute to the galaxy's H luminosity. To remove these AGN contaminated galaxies
from the high signal-to-noise galaxy sample we use the following
diagnostic line provided by Kauffmann et al. (2003) to discriminate between
purely star-forming galaxies (SFGs) and galaxies that also host AGN:
luminosity. To remove these AGN contaminated galaxies
from the high signal-to-noise galaxy sample we use the following
diagnostic line provided by Kauffmann et al. (2003) to discriminate between
purely star-forming galaxies (SFGs) and galaxies that also host AGN:
![\begin{displaymath}\log\left(\frac{[\rm {OIII}]\lambda5007}{\rm {H}\beta}\right)...
...ac{0.61}{\log([\rm {NII}]\lambda6584/\rm {H}\alpha)-0.05}+1.3
\end{displaymath}](/articles/aa/full/2008/37/aa8662-07/img29.gif) |
(1) |
Fig. 1 shows the SFGs found below this line and AGN
host galaxies above the line. We now have 18 350 high signal-to-noise SFGs. Concerning the low signal-to-noise galaxy sample, we do not have accurate enough spectral information to apply this diagnostic line to remove any unwanted AGN host galaxies. However, following the example of
Brinchmann et al. (2004) it is still possible to remove the AGN hosts from
the low signal-to-noise sample by requiring that
[NII]
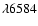 /H
/H
 and that
nSigma >7
and that
nSigma >7 in both lines. We now also have 6000 low signal-to-noise SFGs. An overview of all galaxy sub-samples can be found
in Table 1. The 17 409 unclassified galaxies are
predominantly early-type galaxies that show little signs of
recent star-formation, which is the reason that H
in both lines. We now also have 6000 low signal-to-noise SFGs. An overview of all galaxy sub-samples can be found
in Table 1. The 17 409 unclassified galaxies are
predominantly early-type galaxies that show little signs of
recent star-formation, which is the reason that H has not been detected to
the significance levels that we have required. The lack of recent star-formation within these galaxies implies that they will
also be void of any future CCSN events and hence these galaxies are not of
interest to our survey.
has not been detected to
the significance levels that we have required. The lack of recent star-formation within these galaxies implies that they will
also be void of any future CCSN events and hence these galaxies are not of
interest to our survey.
Having removed all of the AGN contaminated galaxies we now have two catalogues
of SFGs which we shall refer to from now on as the high signal-to-noise SFG (HSFG) catalogue and the low signal-to-noise SFG (LSFG) catalogue.
![\begin{figure}
\par\includegraphics[totalheight=0.2\textheight]{8662fig1.eps}
\end{figure}](/articles/aa/full/2008/37/aa8662-07/Timg31.gif) |
Figure 1:
[OIII]
 H H vs.
[NII]
vs.
[NII]
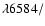 H H plot of 20 632 galaxies in our SDSS DR5 good signal-to-noise galaxy sample.
The diagnostic line from Kauffmann et al. (2003) discriminates between the purely star-forming galaxies in
our sample (those below the line) and thosehosting AGN (above the line).
plot of 20 632 galaxies in our SDSS DR5 good signal-to-noise galaxy sample.
The diagnostic line from Kauffmann et al. (2003) discriminates between the purely star-forming galaxies in
our sample (those below the line) and thosehosting AGN (above the line). |
| Open with DEXTER |
Table 1:
Hierarchy of galaxies extracted from the original SDSS
DR5 spectroscopic galaxy sample within z=0.04
![\begin{figure}
\par\includegraphics[totalheight=0.2\textheight]{8662fig2.ps}
\end{figure}](/articles/aa/full/2008/37/aa8662-07/Timg32.gif) |
Figure 2:
Comparing our Pettini & Pagel (2004) empirically calibrated oxygen abundances with those
directly measured by Izotov et al. (2006) via measuring
the electron temperature reveals that our
measurements are reliable with an rms scatter of 0.14 dex, the solid line depicting a one-to-one correspondence. Note the four outlying galaxies - see text for
details. |
| Open with DEXTER |
2.2 Measuring oxygen abundances
In order to select out low-metallicity galaxies from both the HSFG
and LSFG catalogues,
we define oxygen abundances using the empirical calibrations of
Pettini & Pagel (2004). Within the range
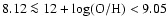 the
following empirical calibration is used:
the
following empirical calibration is used:
![\begin{displaymath}12+\log(\rm {O/H})=8.73-0.32\log\left(\frac{[\rm {OIII}]\lamb...
...07/\rm {H}\beta}{[\rm {NII}]\lambda6584/\rm {H}\alpha}\right),
\end{displaymath}](/articles/aa/full/2008/37/aa8662-07/img34.gif) |
(2) |
and below
 the following calibration is used:
the following calibration is used:
![\begin{displaymath}12+\log(\rm {O/H})=8.9+0.59\log([\rm {NII}]\lambda6584/\rm {H}\alpha).
\end{displaymath}](/articles/aa/full/2008/37/aa8662-07/img36.gif) |
(3) |
The wavelengths of the emission lines used for the flux ratios in both of these calibrations
are separated by only a small amount and therefore their ratios are free of any extinction
effects. Of the sample of 18 350 HSFGs, Izotov et al. (2006) have directly measured
metallicities for 209. They determined the
oxygen abundances by measuring the
[OIII]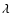 4363/[OIII]
4363/[OIII]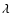 5007 line ratio to calculate an
electron temperature
5007 line ratio to calculate an
electron temperature 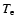 ,
and then derived the
abundances directly from the strengths of the [OII]
,
and then derived the
abundances directly from the strengths of the [OII]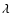 3727
(or [OII]
3727
(or [OII]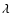 7320, 7331 when [OII]
7320, 7331 when [OII]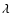 3727 was not available) and
[OIII]
3727 was not available) and
[OIII]
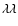 4959, 5007 emission lines. Comparing the
Izotov et al.
4959, 5007 emission lines. Comparing the
Izotov et al. 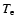 measured abundances with our Pettini & Pagel
empirically calibrated abundances we find good agreement, apart
from four outlying galaxies (see Fig. 2). These galaxies are
SDSS J124813.65-031958.2, SDSS J091731.22+415936.8, SDSS
J123139.98+035631.4 and SDSS J130240.78+010426.8.
measured abundances with our Pettini & Pagel
empirically calibrated abundances we find good agreement, apart
from four outlying galaxies (see Fig. 2). These galaxies are
SDSS J124813.65-031958.2, SDSS J091731.22+415936.8, SDSS
J123139.98+035631.4 and SDSS J130240.78+010426.8.
When viewed, these four
outliers seem to be dwarf galaxies that are in the same
line of sight as and possibly gravitationally bound
to much larger and presumably more metal rich galaxies.
Assuming that the contamination from these background galaxies has not been
adequately removed from the spectra of the dwarf galaxies by the SDSS reduction pipeline would explain
the discrepancy between the oxygen abundances measured by Izotov et al. and
our measurements. Viewing a random selection of the remaining galaxies from
the Izotov et al. sample reveal the blue compact dwarf galaxies expected from
their low-metallicity galaxy sample.
The fact that we may be over-estimating the oxygen abundances of a very
small fraction of galaxies should not concern us too much as we are trying to produce a
low-metallicity galaxy sample and not a high-metallicity sample that would then
possibly be contaminated by a few misplaced lower-metallicity galaxies. Choosing then
to ignore these four outlying galaxies we
find that our oxygen abundance measurements for the remaining
205 galaxies fall with an rms scatter of 0.14 dex from the directly
measured abundances of the Izotov et al.
Recently Prieto et al. (2008) have taken a sample of 125 958 SFGs from
SDSS DR4, with oxygen abundances derived in the same fashion as Tremonti et al. (2004) used for SFGs in DR2. The Tremonti et al. (2004) method for deriving oxygen abundance estimates an individual galaxy's metallicty via a likelihood analysis which simultaneously fits multiple optical nebular emission lines to those predicted by the hybrid stellar-population plus photoionisation models of Charlot & Longhetti (2001). A likelihood distribution of the metallicity is determined for each galaxy the median is taken as the best estimate of the galaxy metallicity. The Tremonti et al. (2004) metallicities are essentially on the Kewley & Dopita (2002) abundance scale. Matching our catalogues of HSFGs and LSFGs against the sample of 125 958 SFGs of Prieto et al. (2008), we find a common sample of 18 014 SFGs. The oxygen abundances that we measure with the Pettini & Pagel method are typically  0.2 dex below that of Tremonti et al., in agreement with the findings of Modjaz et al. (2008). The cause of this discrepancy is debated but may either be due to certain parameters that produce temperature variations not being taken into consideration when deriving
0.2 dex below that of Tremonti et al., in agreement with the findings of Modjaz et al. (2008). The cause of this discrepancy is debated but may either be due to certain parameters that produce temperature variations not being taken into consideration when deriving 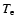 at higher-metallicity, which would lead to an under-estimation of the oxygen abundance measured on the Pettini & Pagel scale which is calibrated with
at higher-metallicity, which would lead to an under-estimation of the oxygen abundance measured on the Pettini & Pagel scale which is calibrated with 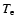 measured abundances (Stasinska 2005; Bresolin 2006), or to an unknown problem with the photoionisation models used by Tremonti et al. (Kennicutt et al. 2003).
measured abundances (Stasinska 2005; Bresolin 2006), or to an unknown problem with the photoionisation models used by Tremonti et al. (Kennicutt et al. 2003).
2.3 SN rate indicator
Having measured the metallicity for each of the galaxies in our
catalogues, we now wish to determine CCSRs. To do this we must first
determine SFRs for the galaxies and then determine the fraction of those stars
formed that will eventually end their lives as CCSNe. The
best indicator that we have for the SFR for each galaxy is its H luminosity. As alluded to previously, it is going to be the young, massive, hot stars
in purely star-forming galaxies that are the dominant source of
hydrogen ionising radiation, causing the galaxy's
H
luminosity. As alluded to previously, it is going to be the young, massive, hot stars
in purely star-forming galaxies that are the dominant source of
hydrogen ionising radiation, causing the galaxy's
H luminosity to be proportional to its recent SFR.
luminosity to be proportional to its recent SFR.
Kennicutt (1998) has determined the following calibration
between a galaxy's SFR and its H luminosity:
luminosity:
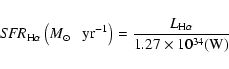 |
(4) |
where the luminosity is measured in Watts.
Derived from their model fits, Brinchmann et al. (2004) also provide likelihood distributions for
the conversion factor between the H luminosity and the SFR for galaxies of
various mass ranges. They confirm that the Kennicutt calibration is a
very good typical calibration, comparing well with
the median value for their sample. When considering the complete HSFG and
LSFG catalogues it is acceptable to assume a median mass range for the galaxies and we employ
the Kennicutt calibration. However, when considering galaxies with
relatively poor metallicity we choose to use the most
probable conversion factor for the Brinchmann et al. distribution with the lowest mass range (
luminosity and the SFR for galaxies of
various mass ranges. They confirm that the Kennicutt calibration is a
very good typical calibration, comparing well with
the median value for their sample. When considering the complete HSFG and
LSFG catalogues it is acceptable to assume a median mass range for the galaxies and we employ
the Kennicutt calibration. However, when considering galaxies with
relatively poor metallicity we choose to use the most
probable conversion factor for the Brinchmann et al. distribution with the lowest mass range (
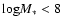 )
as this
distribution closest resembles the low-metallicity galaxies in our catalogues i.e. low-mass, blue,
dwarf, irregular galaxies.
)
as this
distribution closest resembles the low-metallicity galaxies in our catalogues i.e. low-mass, blue,
dwarf, irregular galaxies.
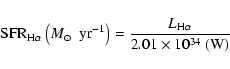 |
(5) |
SDSS provides the H equivalent line width and also the continuum flux
at the wavelength of H
equivalent line width and also the continuum flux
at the wavelength of H ,
the equivalent width times the continuum flux
giving the H
,
the equivalent width times the continuum flux
giving the H flux which is then used to determine the
H
flux which is then used to determine the
H luminosity. A problem with the SDSS data is that the measured
H
luminosity. A problem with the SDSS data is that the measured
H flux for a galaxy is only the flux which falls within the 3
flux for a galaxy is only the flux which falls within the 3
 fibre aperture of the SDSS multi-fibre spectrograph. Typically this is only a
fraction of the total galaxy flux, as the SDSS spectrograph fibre locks onto the
centre of the galaxy and any flux that falls outside of the 3
fibre aperture of the SDSS multi-fibre spectrograph. Typically this is only a
fraction of the total galaxy flux, as the SDSS spectrograph fibre locks onto the
centre of the galaxy and any flux that falls outside of the 3
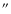 fibre
aperture is lost. Hopkins et al. (2003) have developed a very simple aperture-correction that can
be applied to the measured galaxy H
fibre
aperture is lost. Hopkins et al. (2003) have developed a very simple aperture-correction that can
be applied to the measured galaxy H luminosity to give an estimate of the total
galaxy H
luminosity to give an estimate of the total
galaxy H luminosity. The aperture-correction takes account of the ratio between
the petrosian photometric r-band galaxy magnitude and the
synthetic r-band ``fibre magnitude'' determined from the galaxy spectrum.
Hopkins et al. also provide an extinction correction to be
used when determining the galaxy H
luminosity. The aperture-correction takes account of the ratio between
the petrosian photometric r-band galaxy magnitude and the
synthetic r-band ``fibre magnitude'' determined from the galaxy spectrum.
Hopkins et al. also provide an extinction correction to be
used when determining the galaxy H SFR. The correction makes use of the Balmer decrement
and assumes the standard Galactic extinction law of
Cardelli et al. (1989). This gives
a final aperture and extinction corrected H
SFR. The correction makes use of the Balmer decrement
and assumes the standard Galactic extinction law of
Cardelli et al. (1989). This gives
a final aperture and extinction corrected H luminosity SFR indicator
for our entire galaxy sample as given in Eq. (6), and for the low-metallicity galaxy sample as given in Eq. (7),
where
luminosity SFR indicator
for our entire galaxy sample as given in Eq. (6), and for the low-metallicity galaxy sample as given in Eq. (7),
where
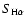 and
and
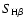 are the line
fluxes corrected for stellar absorption according to Hopkins et al. (2003).
Having now determined a SFR for each of the galaxies in our
catalogues, we can compare these rates with their oxygen abundances
(Fig. 3). It is
clear that in general the higher the galaxy SFR the higher the typical oxygen abundance. It can be reasoned that if the SFR of a galaxy is high, or has been high at any point in its history, there is an increased population of young, hot, massive stars which in turn leads to an increased rate of
CCSNe and therefore a greater rate of enrichment of the ISM. The observed high-metallicity cutoff of the SDSS galaxies is probably due to a saturation suffered by [OIII]
are the line
fluxes corrected for stellar absorption according to Hopkins et al. (2003).
Having now determined a SFR for each of the galaxies in our
catalogues, we can compare these rates with their oxygen abundances
(Fig. 3). It is
clear that in general the higher the galaxy SFR the higher the typical oxygen abundance. It can be reasoned that if the SFR of a galaxy is high, or has been high at any point in its history, there is an increased population of young, hot, massive stars which in turn leads to an increased rate of
CCSNe and therefore a greater rate of enrichment of the ISM. The observed high-metallicity cutoff of the SDSS galaxies is probably due to a saturation suffered by [OIII] 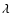 4363
4363 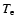 calibrated metallicities (see Kewley & Ellison 2008)
calibrated metallicities (see Kewley & Ellison 2008)
![$\displaystyle {{\it SFR}_{\rm H\alpha}}\left({M}_{\odot}{\rm ~~yr^{-1}}\right)=...
...beta}}{2.86}\right]^{2.114}\frac{L_{{\rm H}\alpha}}{1.27\times10^{34}({\rm W})}$](/articles/aa/full/2008/37/aa8662-07/img46.gif) |
|
|
(6) |
![$\displaystyle {{\it SFR}_{\rm H\alpha}}\left({M}_{\odot}{\rm ~~yr^{-1}}\right)=...
...}{2.86}\right]^{2.114}\frac{L_{{\rm H}\alpha}}{2.01\times10^{34}({\rm W})}\cdot$](/articles/aa/full/2008/37/aa8662-07/img47.gif) |
|
|
(7) |
Given a SFR, it is relatively simple to convert to a CCSR by determining
the fraction of a stellar population that will eventually collapse to create
CCSNe. Following the method used by e.g. Mattila & Meikle (2001), we use an initial mass function (IMF) for a stellar
population to calculate the fraction of this population within the mass
range 8
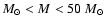 ,
the same mass range for stars predicted to end
their lives as CCSNe. From this logic the CCSR is determined as:
,
the same mass range for stars predicted to end
their lives as CCSNe. From this logic the CCSR is determined as:
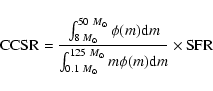 |
(8) |
where 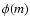 is the Salpeter IMF (Salpeter 1955) with upper and
lower mass cut-offs of
is the Salpeter IMF (Salpeter 1955) with upper and
lower mass cut-offs of
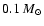 and
and
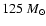 .
This conversion is
calculated to be:
.
This conversion is
calculated to be:
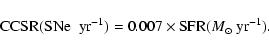 |
(9) |
![\begin{figure}
\par\includegraphics[totalheight=0.2\textheight]{8662fig3.ps}
\end{figure}](/articles/aa/full/2008/37/aa8662-07/Timg54.gif) |
Figure 3:
H determined star-formation rates using the low-mass range calibration of Brinchmann et al. (2004) of
18 350 galaxies
in our HSFG catalogue compared with their measured oxygen abundances. In general,
the greater the galaxy metallicity, the greater its star-formation rate - as
expected.
determined star-formation rates using the low-mass range calibration of Brinchmann et al. (2004) of
18 350 galaxies
in our HSFG catalogue compared with their measured oxygen abundances. In general,
the greater the galaxy metallicity, the greater its star-formation rate - as
expected. |
| Open with DEXTER |
Table 2:
The table shows the expected CCSN rates within the SDSS DR5
spectroscopic survey area (14% of the entire sky) out to a distance of 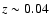 .
.
The target selection criteria for the SDSS DR5 spectroscopic sample
includes a
bright magnitude limit of 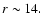 5 in order to avoid saturation and excessive
cross-talk in the spectrographs. As a result of this restriction many of
the nearby luminous galaxies have been omitted from the DR5 spectroscopic
sample. To account for these missing bright galaxies and
construct a complete galaxy catalogue we initially
select out the galaxies from the HyperLeda galaxy catalogue that match with
galaxies from the SDSS
DR5 photometric survey with magnitudes r<14.5, assuming that the HyperLeda
catalogue contains all of the nearby luminous galaxies. From this catalogue
of matched galaxies we further select out those galaxies that are not found in the
SDSS DR5 spectroscopic survey. We discover a total of 1887 nearby
luminous galaxies included in the SDSS DR5 photometric survey that have
been omited from the spectroscopic survey.
5 in order to avoid saturation and excessive
cross-talk in the spectrographs. As a result of this restriction many of
the nearby luminous galaxies have been omitted from the DR5 spectroscopic
sample. To account for these missing bright galaxies and
construct a complete galaxy catalogue we initially
select out the galaxies from the HyperLeda galaxy catalogue that match with
galaxies from the SDSS
DR5 photometric survey with magnitudes r<14.5, assuming that the HyperLeda
catalogue contains all of the nearby luminous galaxies. From this catalogue
of matched galaxies we further select out those galaxies that are not found in the
SDSS DR5 spectroscopic survey. We discover a total of 1887 nearby
luminous galaxies included in the SDSS DR5 photometric survey that have
been omited from the spectroscopic survey.
Of these 1887 galaxies we wish to know the fraction that are star-forming
galaxies. HyperLeda provides a galaxy morphological classification for a
large number of the galaxies in the catalogue and we are able to remove all
galaxies with an early-type classification, as these galaxies
will generally have very low SFRs. But note that some early-type galaxies
have HII regions and some evidence of low-level star-formation
(e.g. Moss & Whittle 2005). The mean
g-i colour of these removed early-type galaxies is 1.216, with a standard
deviation
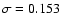 .
In an attempt to remove the remaining
non-starforming galaxies from this bright galaxy sample that do not have a morphological classification, we remove all
galaxies redward of one
.
In an attempt to remove the remaining
non-starforming galaxies from this bright galaxy sample that do not have a morphological classification, we remove all
galaxies redward of one 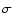 from the mean g-i colour, i.e.
g-i>1.063. This results in 1216 remaining star-forming galaxies. There is a possibility that this cut may also exclude a few starburst galaxies which have been heavily reddened due to the effects of extinction, but we are mainly concerned about low-metallicity galaxies, which are not greatly affected by extinction.
from the mean g-i colour, i.e.
g-i>1.063. This results in 1216 remaining star-forming galaxies. There is a possibility that this cut may also exclude a few starburst galaxies which have been heavily reddened due to the effects of extinction, but we are mainly concerned about low-metallicity galaxies, which are not greatly affected by extinction.
As we have no spectral information for these galaxies from SDSS DR5, it is
necessary to use an alternative indicator to estimate SFR other than the
H luminosity. The U-band luminosity can be used as a suitable
indicator as developed by Moustakas et al. (2006):
luminosity. The U-band luminosity can be used as a suitable
indicator as developed by Moustakas et al. (2006):
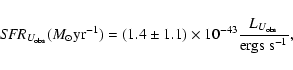 |
(10) |
where the SDSS u-band is transformed to
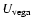 using the following
transformation from Blanton & Roweis (2007):
using the following
transformation from Blanton & Roweis (2007):
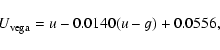 |
(11) |
and the distance moduli from HyperLeda are used to determine
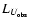 .
The
CCSR is then determined using Eq. (9). Note
that as Moustakas et al. have empirically calibrated this
U-band SFR indicator from
extinction-corrected H
.
The
CCSR is then determined using Eq. (9). Note
that as Moustakas et al. have empirically calibrated this
U-band SFR indicator from
extinction-corrected H galaxy luminosities, there is no need to
further correct this indicator for dust reddening. The 1216 bright, nearby galaxies have a resulting U-band indicated CCSR of
12.70 CCSNe yr-1.
galaxy luminosities, there is no need to
further correct this indicator for dust reddening. The 1216 bright, nearby galaxies have a resulting U-band indicated CCSR of
12.70 CCSNe yr-1.
We now have three galaxy catalogues; a HSFG catalogue and a
LSFG catalogue, with measured metallcities and CCSRs, and a nearby
galaxy catalogue containing bright galaxies not found in the SDSS
spectroscopic galaxy catalogue.
We have estimates of SFRs and CCSRs for all these galaxies.
Taking our
catalogues of 18 350 HSFGs and 6000 LSFGs and introducing various
upper limits on the individual galaxy metallicities and lower limits
on the CCSRs we are able to extract out separate galaxy
sub-samples. Table 2 displays these sub-samples,
differing both in the number of galaxies they contain and their
estimated CCSR determined from the galaxy SFRs
derived from aperture and extinction-corrected H luminosities for the HSFG and LSFG catalogues, and from U-band luminosities for the
nearby bright galaxy catalogue. For the samples of
galaxies with no metallicity constraint the SFRs have been derived using the
``typical'' calibration of Kennicutt (1998) whereas the SFRs of the
sub-samples of galaxies with constraints on metallicity have been
derived using the lowest mass range calibration of Brinchmann et al. (2004). These full catalogues or sub-samples of these catalogue can now be used to determine the feasibility of searching for low-metallicity CCSN events using various survey strategies. Figure 4 shows the cumulative
distribution of the combined CCSN rate from our HSFG and LSFG
catalogues, measured against oxygen abundance. It is clear that the
CCSR increases steeply with oxygen abundance of the galaxy sample.
luminosities for the HSFG and LSFG catalogues, and from U-band luminosities for the
nearby bright galaxy catalogue. For the samples of
galaxies with no metallicity constraint the SFRs have been derived using the
``typical'' calibration of Kennicutt (1998) whereas the SFRs of the
sub-samples of galaxies with constraints on metallicity have been
derived using the lowest mass range calibration of Brinchmann et al. (2004). These full catalogues or sub-samples of these catalogue can now be used to determine the feasibility of searching for low-metallicity CCSN events using various survey strategies. Figure 4 shows the cumulative
distribution of the combined CCSN rate from our HSFG and LSFG
catalogues, measured against oxygen abundance. It is clear that the
CCSR increases steeply with oxygen abundance of the galaxy sample.
3 Strategy 1: a pointed survey of catalogued low-metallicity galaxies
When determining the feasibility of using a pointed low-metallicity survey to search for CCSNe in a catalogue of low-metallicity galaxies we consider using the fully robotic 2.0 m
Liverpool Telescope situated at the Observatorio del Roque de los Muchachos,
La Palma. We shall also consider the using of a network of similar sized telescopes.
There are three characteristics that we require of the galaxy catalogue that we shall use with this survey strategy; firstly, it must contain only a few hundred galaxies as too many galaxies in the catalogue would hinder our ability to observe each individual
galaxy frequently enough to ensure that we detect any SN that it may
host. Secondly, we require that the galaxies are of
sufficiently low metallicity in order to determine how the CCSNe that
they host differ from those hosted by their higher metallicity counterparts.
Finally, the galaxies must exhibit a suitably high enough CCSR to increase
the probability of detecting these CCSNe. The latter two requirements somewhat
contradict each other because metallicity
tends to scale with SFR in SFGs and therefore requiring a
low-metallicity
galaxy sample implies that we require galaxies with lower
SFRs, and hence lower CCSRs. It is
therefore essential that we produce a galaxy catalogue that can act as
a compromise between these two conflicting requirements.
![\begin{figure}
\par\includegraphics[totalheight=0.3\textheight]{8662fig4.ps}
\end{figure}](/articles/aa/full/2008/37/aa8662-07/Timg61.gif) |
Figure 4:
Cumulative distribution of the combined CCSN rate from our HSFG and LSFG catalogues, measured against oxygen abundance. It is clear that as oxygen abundance increases so to does the rate of CCSNe. |
| Open with DEXTER |
For the purpose of this survey strategy we decide that the galaxy catalogue that
optimally fits our requirements is the sub-sample of the HSFG cataglogue that
contain galaxies with oxygen abundances of less than 8.2 dex and a CCSR greater than 1 CCSNe every 1000 years. This low-metallicity catalogue contains
727 galaxies, a suitable number for a pointed survey, with an estimated
CCSR of 2.8 CCSNe yr-1. It should be noted that this galaxy catalogue is extracted solely from the 5713 square degrees of the sky that
SDSS DR5 spectroscopic survey covers, that is 14% of the entire sky.
It can be assumed that the rest of the sky contains similar density of
these low-metallicity galaxies. We shall return to this point later.
3.1 Monte-Carlo simulations
Of the estimated 2.8 CCSNe yr-1 that this
low-metallicity galaxy catalogue will produce, we will only be able to detect a fraction
of these due to the practical limiting factors of a pointed survey. The
reason that a given SN would not be detected is simply due to its faintness at the point of
observation. The factors that will influence the
likelihood that
a SN will be detected when observed within our search are: whether
or not the galaxy that hosts the
CCSN is observable during the period of time when the CCSN
is
detectable, the type of CCSN (IIP, IIL, Ib, Ic or IIn) observed and its intrinsic
brightness, the distance to the host galaxy, the extinction towards the CCSN, the exposure time and the age of the CCSN when observed (affected by the
cadence of the observations).
By running a Monte-Carlo simulation, constrained by each of these parameters,
to randomly produce a sample of 100 000 possible SNe observable
within our search, we can infer the fraction of CCSNe that we should
actually detect.
In order for the Monte-Carlo simulation (MCS) to accurately reproduce the
relative rates of the different types of CCSNe, we
use the observed rates compiled by Smartt et al. (200), given in
Table 3. These rates have been compiled within a time and volume-limited
sample, accounting for all SNe discovered within the eight year period between 1999 January 1
and 2006 December 2006 in galaxies with a recessional velocity
<
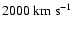 .
Apart from those SNe that
inhabit environments of heavy extinction or first observed late into their
evolution, it is expected that within this appointed distance limit
(
.
Apart from those SNe that
inhabit environments of heavy extinction or first observed late into their
evolution, it is expected that within this appointed distance limit
(
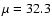 )
all known types of SNe should have been bright enough to
have been detected, implying that these relative rates are
as free from any Malmquist bias as possible. CCSNe of type IIb have been merged with type Ib/c,
and type IIn have been divided between those with a plateau phase in the
tail of their lightcurves, IIn/P, and those with a linear phase, IIn/L.
)
all known types of SNe should have been bright enough to
have been detected, implying that these relative rates are
as free from any Malmquist bias as possible. CCSNe of type IIb have been merged with type Ib/c,
and type IIn have been divided between those with a plateau phase in the
tail of their lightcurves, IIn/P, and those with a linear phase, IIn/L.
Table 3:
Relative CCSRs taken from
Smartt et al. (2007).
We also supply template lightcurves of the various SNe for the MCS. For type IIP we use 1999em as our template, taking the data from Hamuy et al. (2001). For type IIL we use 1998S,
taking data for the rise to maximum light from Liu et al. (2000) and
data for the tail from Fassia et al. (2000). For type Ib/c we use
2002ap, taking data from Foley et al. (2003). For
SNe of type IIn, we suggest that it is appropriate to divide the relative rate evenly
between type IIn that exhibit a plateau phase in their
lightcurves and those that exhibit a linear phase, type IIn/P and
type IIn/L respectively. For the type IIn/P, we use
1994Y as the template taking data from Ho et al. (2001), allowing
1998S to provide the rise to maximum light. For type IIn/L we use 1999el as the
template taking data from Di Carlo et al. (2002), again allowing 1998S
to provide the rise to maximum light (see Fig. 5 for comparison).
The following conversion from Blanton & Roweis (2007) is used to transform the data for the
lightcurves to the Sloan g-band (note magnitudes are to be in AB system):
|
g=B-0.03517-0.3411(B-V).
|
(12) |
The SN absolute magnitude distributions of Richardson et al. (2002) are used in the MCS to provide weighted,
random distributions of peak magnitudes for the
SNe (Table 4). Equation (12) is again
used to transform these distributions to the g-band, taking
a (B-V) colour from the epoch of peak g-magnitude from our template
lightcurves. 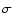 is the range in the peak magnitude distribution and g-band magnitudes are given in the AB system. When choosing a filter to perform a SN search with the Liverpool telescope the r-band is superior to the g-band because it has a greater filter throughput, the CCD detector is more responsive in the r-band and also SNe are generally brighter in the r-band especially later in their evolution. However, the Richardson et al. distributions of
SN peak magnitudes are given in the B-band which we can transform to the g-band but not to the r-band. It is for this reason that we simulate a SN survey in the g-band and then with these results we can then hypothesise the outcome of a search in the r-band.
is the range in the peak magnitude distribution and g-band magnitudes are given in the AB system. When choosing a filter to perform a SN search with the Liverpool telescope the r-band is superior to the g-band because it has a greater filter throughput, the CCD detector is more responsive in the r-band and also SNe are generally brighter in the r-band especially later in their evolution. However, the Richardson et al. distributions of
SN peak magnitudes are given in the B-band which we can transform to the g-band but not to the r-band. It is for this reason that we simulate a SN survey in the g-band and then with these results we can then hypothesise the outcome of a search in the r-band.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{8662fig5.ps}
\end{figure}](/articles/aa/full/2008/37/aa8662-07/Timg65.gif) |
Figure 5:
Template lightcurves used within the Monte-Carlo
simulation. Lightcurves for SNe of type IIP are according to 1999em, type IIL to 1998S, type Ib/c to 2002ap, type IIn/P to 1994Y and
type IIn/L to 1999el. Note that allmagnitudes are in the AB system. |
| Open with DEXTER |
Table 4:
Peak magnitude distributions from Richardson et al. (2002).
A major factor influencing the detection efficiency of any SN
search is the time between consecutive
observations of a galaxy hosting a SN. As this
time increases, so does the likelihood that we will not observe the
SN until it is well advanced along its lightcurve. This could result
in the magnitude dropping below our detection limit, hence failing to be detected in the
search. There are three parameters that affect the cadence of our
search and
that need to be included in the MCS. The first of these is the probability
that the SN will be in solar conjunction for a
fraction, if not all, of the time that it
remains detectable by our search. To account for this factor, we use
the celestial coordinates of the 727 galaxies within our low-metallicity galaxy catalogue and an almanac for the Liverpool Telescope to determine the fraction
of the year that each individual galaxy is observable, producing a
distribution with a mean fraction of 0.380. We then use this
distribution in the MCS to allocate a random amount of time to the
cadence of observation of each SN, to account for cases where a
SN would be unobservable and hence undetectable because its host galaxy is behind the sun.
The second factor that affects the cadence is the
number of nights that cannot be used by the Liverpool Telescope to
perform our search. Reasons why the telescope could not be used on any
particular night include weather, technical
difficulties and scheduled maintenance nights. To
compensate for these nights in our MCS, we have taken nightly reports
from the Liverpool Telescope website![[*]](/icons/foot_motif.gif) , from 2005 August 1 to 2006 July 31,
and use these reports to determine a distribution of nights (58
, from 2005 August 1 to 2006 July 31,
and use these reports to determine a distribution of nights (58 of nights in total) that
can be used for our search. This distribution of usable nights is included in our MCS when considering the cadence of observations.
of nights in total) that
can be used for our search. This distribution of usable nights is included in our MCS when considering the cadence of observations.
The final factor that will affect the cadence of observations, is the
number of galaxies that we aim to observe every night. This number is
influenced by the amount of telescope time dedicated to our
search each night; the
greater the amount of time on the telescope each night, the greater the number of galaxies we can observe per
night and the higher the cadence of observations. The number of galaxies
that can be observed each night is also affected by exposure time. The
benefit of increasing the exposure time is that we can search to a deeper magnitude limit, meaning
that fainter SNe are detectable and SNe are detectable for a greater period of time. It is essential therefore to run a number of MCSs in order to find
the optimal balance between the exposure time given to each galaxy and
the cadence of observations and hence enabling us to detect the greatest fraction of
CCSNe hosted by our low-metallicity galaxy catalogue.
The final two parameters placed in our MCS are the host galaxy distances and
the extinction toward the SNe. The MCS will attribute to each SN a random host galaxy
distance, out to the distance limit of our search, which is z=0.04 (assuming the galaxies within
our search are spread homogeneously and isotropically throughout this
volume). Considering that the majority, if not all, of the galaxies
within our catalogue are low-luminosity, blue, dwarf galaxies with relatively
low metallicities, we assume that host galaxies will have produced very
little dust and will not contribute a great deal to any extinction toward
the CCSN.
To this end we simply attribute a typical Galactic extinction to each
SN (
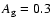 ).
).
![\begin{figure}
\par\includegraphics[width=12cm,clip]{8662fig6.ps}
\end{figure}](/articles/aa/full/2008/37/aa8662-07/Timg70.gif) |
Figure 6:
Percentage of CCSNe
detected from our MCSs for a differing number of hours observing per night
(labeled to the right of the plot). The percentage of CCSNe detected
increases as the nightly observing time increases, as this increases the
cadence of observations. As the individual exposure time per galaxies
increases, the limiting magnitude of the search deepens but the cadence of
observations decreases. There is therefore an optimal point at which
the exposure time and cadence of observation are balanced to detect the maximum
percentage of SNe. |
| Open with DEXTER |
We note that a fraction of SNe remain undetected within spiral galaxies that are not observed face on (e.g. Cappellaro et al. 2003). This is due to the fact that the average extinction attributed to SNe in spiral galaxies with higher inclination angles is higher than that of face on spiral galaxies, making the
SNe fainter and more difficult to detect. Implementation of a correction for this effect into the MCS, using a similar method to that of Riello & Patat (2005), could easily result in an under-estimation of the CCSRs observed in low-metallicity galaxies as these tend not be to grand-design spiral galaxies but rather dwarf, irregular galaxies where the effect of galaxy inclination would be negligible. We have therefore decided not to attempt to correct for this effect. This may make our
predictions for the SN discovery rates in the full galaxy catalogues
(with no metallicity limit) somewhat optimistic. However this may not lead to a significant over-estimate of events, as the SFRs that we calculate come from the observed galaxy H luminosities and in inclined spirals these will also be lower than in face on targets.
luminosities and in inclined spirals these will also be lower than in face on targets.
3.4 Monte Carlo simulation results for a Single 2.0 m telescope
Having included each of these parameters in the MCS, we randomly
generate 100 000 SNe that would potentially be observable within
our search. The information gained about each SN produced by the simulation include
its type and its apparent magnitude at the point of observation. It is only if this magnitude is
above the limiting magnitude of our search can we register the SN as being
detected.
By running the MCS multiple times for (a) the varying number of hours we aim to
observe with the LT every night and (b) the varying amount of exposure time
that we dedicate to each individual galaxy, we can determine the optimal
values of these parameters that shall enable us to detect the greatest
fraction of the CCSNe that we have predicted our low-metallicity galaxy
will produce. The results can be seen in Fig. 6.
Studying the results of the MCSs we suggest that the
difference between the percentage of CCSNe detected while aiming to observe one
hour per night as opposed to two hours per night or more is not enough to
justify the extra observing time as the
fraction of CCSN detected only increases by a few percent. As the detection rates are double valued either side of the peak
detection rate, we suggest using a shorter exposure time in order to
increase cadence and thereby increase the probability of
discovering CCSNe earlier in their evolution as opposed to later.
Aiming to observe one hour a night using 60 s exposures allows each galaxy to be observed once every  17 days while accessible with LT and enables 29.6% of CCSNe to be detected with
our search. When considering the catalogue of 727 low-metallicity galaxies which produce 2.8 CCSNe yr-1, this equates to a detected CCSN rate of
0.8 SNe yr-1
and requires a total amount of 154 h yr-1 telescope time. Remembering that the r-band is superior to the g-band for performing a SN search, we note that given a 60 s exposure the AB limiting magnitudes for the Liverpool telescope are g = 18.7 mag and r = 19.0 mag. Given the average cadence of observations determined by our chosen survey parameters, a typical SN will be observed
17 days while accessible with LT and enables 29.6% of CCSNe to be detected with
our search. When considering the catalogue of 727 low-metallicity galaxies which produce 2.8 CCSNe yr-1, this equates to a detected CCSN rate of
0.8 SNe yr-1
and requires a total amount of 154 h yr-1 telescope time. Remembering that the r-band is superior to the g-band for performing a SN search, we note that given a 60 s exposure the AB limiting magnitudes for the Liverpool telescope are g = 18.7 mag and r = 19.0 mag. Given the average cadence of observations determined by our chosen survey parameters, a typical SN will be observed
 73 days post-explosion with g-r=0.8 mag.
Given the difference in limiting magnitudes and the typical g-r colour at the point of observation, we expect to detect SNe that are 1.1 mag
fainter with an r-band search than we would with a g-band search. Assuming that the template SN lightcurves and the distribution of SN peak magnitudes are similar in the r-band as compared to the g-band, we re-run the g-band MCS with a limiting magnitude 1.1 mag fainter than previously used. From this simulation we predict that using the r-band will allow for
73 days post-explosion with g-r=0.8 mag.
Given the difference in limiting magnitudes and the typical g-r colour at the point of observation, we expect to detect SNe that are 1.1 mag
fainter with an r-band search than we would with a g-band search. Assuming that the template SN lightcurves and the distribution of SN peak magnitudes are similar in the r-band as compared to the g-band, we re-run the g-band MCS with a limiting magnitude 1.1 mag fainter than previously used. From this simulation we predict that using the r-band will allow for 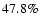 of CCSNe to be detected with our search. Again considering the catalogue of 727 low metallicity HSFGs which produce 2.8 CCSNe yr-1, this equates to a detected CCSN rate of
1.3 SNe yr-1.
of CCSNe to be detected with our search. Again considering the catalogue of 727 low metallicity HSFGs which produce 2.8 CCSNe yr-1, this equates to a detected CCSN rate of
1.3 SNe yr-1.
Assuming a typical Galactic extinction of
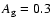 (
(
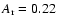 )
and an exposure
time of 60 s we estimate that the absolute
limiting magnitude (
)
and an exposure
time of 60 s we estimate that the absolute
limiting magnitude ( significance) for this search at a distance of 20 Mpc will be
significance) for this search at a distance of 20 Mpc will be
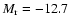 ,
at 70 Mpc it will be
,
at 70 Mpc it will be
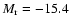 and at 150 Mpc it will be
and at 150 Mpc it will be
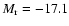 .
We plan to use the method of image matching and subtraction (see Alard & Lupton 1998) to detect SNe throughout this survey. Assuming original
images with equal depth, the process of image subtraction increases the
noise by roughly a factor of
.
We plan to use the method of image matching and subtraction (see Alard & Lupton 1998) to detect SNe throughout this survey. Assuming original
images with equal depth, the process of image subtraction increases the
noise by roughly a factor of 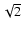 .
In addition, the detection of
SNe inside their host galaxies will be always more difficult due to
image subtraction residuals caused by uncertainties in the alignment and
matching of the two images. Since we wish to avoid a large fraction of
spurious detections, we require the relatively high significance level
of 25
.
In addition, the detection of
SNe inside their host galaxies will be always more difficult due to
image subtraction residuals caused by uncertainties in the alignment and
matching of the two images. Since we wish to avoid a large fraction of
spurious detections, we require the relatively high significance level
of 25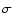 from the limiting magnitude of our search.
from the limiting magnitude of our search.
3.5 Surveying with a network of 2.0 m telescopes
As discussed previously SDSS DR5 covers only  14% of the
entire sky. If we presently had the ability to compile a catalogue of low-metallicity
galaxies for the whole sky as complete as that for the area of the SDSS DR5
spectroscopic survey and a collection of seven 2.0 m telescopes (or
three to four 2.0 m telescopes with double the time allocation) we would expect to detect
roughly 7 times the CCSNe detected solely by the LT, i.e.
14% of the
entire sky. If we presently had the ability to compile a catalogue of low-metallicity
galaxies for the whole sky as complete as that for the area of the SDSS DR5
spectroscopic survey and a collection of seven 2.0 m telescopes (or
three to four 2.0 m telescopes with double the time allocation) we would expect to detect
roughly 7 times the CCSNe detected solely by the LT, i.e.
 9.3 CCSNe/yr. We could consider using a network of six to eight 2.0 m robotic telescopes similar to the RoboNet global network of 2.0 m
telescopes consisting of the LT and the Faulkes Telescope North and the
Faulkes Telescope South to perform this kind of survey. Another advantage of using a network of telescopes in both the northern and southern hemispheres as opposed to a single telescope is that we gain a greater sky coverage and can therefore target a greater number of galaxies within our search.
9.3 CCSNe/yr. We could consider using a network of six to eight 2.0 m robotic telescopes similar to the RoboNet global network of 2.0 m
telescopes consisting of the LT and the Faulkes Telescope North and the
Faulkes Telescope South to perform this kind of survey. Another advantage of using a network of telescopes in both the northern and southern hemispheres as opposed to a single telescope is that we gain a greater sky coverage and can therefore target a greater number of galaxies within our search.
The two obstacles that we would encounter if we were to use this strategy to search for CCSNe are firstly the generous amount of telescope
time that we would require ( 1000 h yr-1) and secondly the present lack of
data required to compile an all sky galaxy catalogue. Compiling a catalogue
of all galaxies listed in the 2dF, 6dF, LEDA and SDSS DR5 within the redshift range
0<z<0.04 results in a catalogue containing a total of 103 549 individual galaxies, only a fraction of which will be star-forming. Apart from this we shall have to wait for PS1, the prototype
1.8 m telescope of the Panoramic Survey Telescope and
Rapid Response System (Pan-STARRS), which shall cover an area of 3
1000 h yr-1) and secondly the present lack of
data required to compile an all sky galaxy catalogue. Compiling a catalogue
of all galaxies listed in the 2dF, 6dF, LEDA and SDSS DR5 within the redshift range
0<z<0.04 results in a catalogue containing a total of 103 549 individual galaxies, only a fraction of which will be star-forming. Apart from this we shall have to wait for PS1, the prototype
1.8 m telescope of the Panoramic Survey Telescope and
Rapid Response System (Pan-STARRS), which shall cover an area of 3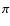 of
the sky to a depth exceeding that of SDSS DR5, in order to compile a far more
complete all-sky low-metallicity galaxy catalogue.
of
the sky to a depth exceeding that of SDSS DR5, in order to compile a far more
complete all-sky low-metallicity galaxy catalogue.
4 Strategy 2: volume-limited searches with the Pan-STARRS all sky surveys
Having considered a dedicated pointed low-metallicity galaxy survey to search for CCSNe both with one and with a network of 2.0 m telescopes, we
now turn our attention to an all-sky survey. Pan-STARRS is a
set of four 1.8 m telescopes with wide field optics, each with a 7 square
degree field of view, which will be constructed by the University of Hawaii. The
prototype telescope PS1 has now achieved first light and
is set to go online during 2008. PS1 will have the capability of
surveying
the whole available sky in less than a week at a rate of 6000 square degrees per
night, covering 30 000 square degrees of the sky per cycle
(Chambers & Denneau 2007).
Included in the list of tasks that the PS1 image reduction pipeline will
perform is the subtraction of every image from a reference image in order to
produce a database of residual transient objects that will include moving objects and static
variables such as SNe.
There are two different strategies that one would employ to search for
SNe (or transients of any type), these are volume-limited searches and
magnitude-limited searches. We will consider both of these. A volume-limited search has the advantage that it can quantify true rates of
transients. In addition the radial limit can be chosen so that the
target discoveries are bright enough to be followed in multi-wavelength
studies with complementary facilities (e.g. spectroscopic and photometric
follow-up with 2-8 m telescopes).
4.1 Monte Carlo simulations
Of all the modes in which PS1 shall be run the 3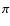 Steradian Survey
(covering 30 000 square degrees of the sky)
shall be the most effective when searching for nearby CCSNe. The survey aims to cover that whole sky 60 times in 3 years, that is 12 times
in each of the five filters g, r, i, z and y. This aim has already
taken historic weather patterns on Haleakala into consideration. The footprint of the survey
completely covers the entire footprint of the SDSS DR5 spectroscopic
survey and the AB limiting magnitude (25
Steradian Survey
(covering 30 000 square degrees of the sky)
shall be the most effective when searching for nearby CCSNe. The survey aims to cover that whole sky 60 times in 3 years, that is 12 times
in each of the five filters g, r, i, z and y. This aim has already
taken historic weather patterns on Haleakala into consideration. The footprint of the survey
completely covers the entire footprint of the SDSS DR5 spectroscopic
survey and the AB limiting magnitude (25 )
in the g-band is stated
to be 21.5 mag for a single 60 s exposure (Chambers & Denneau 2007).
)
in the g-band is stated
to be 21.5 mag for a single 60 s exposure (Chambers & Denneau 2007).
Having an adapted MCS produce 100 000 potential SNe over the
redshift range of our galaxy samples (0<z<0.04) will again help us
to estimate the fraction of potentially observable CCSNe that we will
actually detect with PS1. We assume that we can take the
fraction of CCSNe detected in the g-band as the typical fraction that
would be detected in each of the five filters; indeed running the adapted MCS detailed in Sect. 5.1 in an attempt to produce the detected CCSN rates of this nearby sample in all five filters, were the K-corrections essentially behave as colour corrections at such low redshift, results in predicted detection efficiencies extremely close to those found if considering only the g-band. Concerning the cadence we have also taken the PS1 survey strategy into consideration (Chambers & Denneau 2007), see
Fig. 9.
A random extinction is assigned to each of the CCSNe
using a weighted distribution based on CCSRs taken from Mattila & Meikle (2001) and
Schmidt et al. (1994). However for
low metallicity galaxies ( 8.2 dex)
only a typical Galactic extinction of
8.2 dex)
only a typical Galactic extinction of
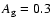 is assigned to the CCSNe, as at these metallicities we expect the galaxies
to be relatively dust free.
is assigned to the CCSNe, as at these metallicities we expect the galaxies
to be relatively dust free.
We must also consider the fact that Pan-STARRS shall be covering a large fraction of the sky that is obscured by the Galactic Plane, a total of  7500 square degrees of the Pan-STARRS area. Any SN that is located with a line-of-sight through the Galactic Plane shall be extinguished above the typical Galactic extinction assumed. To allow for this we take the extinctions, as determined by Schlegel et al. (1998), of
7500 square degrees of the Pan-STARRS area. Any SN that is located with a line-of-sight through the Galactic Plane shall be extinguished above the typical Galactic extinction assumed. To allow for this we take the extinctions, as determined by Schlegel et al. (1998), of  1500 points positioned homogeneously across the expanse of the Galactic Plane visible with Pan-STARRS and determine a distribution of extinctions to be folded into the MCS for any SN falling behind the Galactic Plane. The cumulative distribution of these extinctions can be seen in
Fig. 7.
1500 points positioned homogeneously across the expanse of the Galactic Plane visible with Pan-STARRS and determine a distribution of extinctions to be folded into the MCS for any SN falling behind the Galactic Plane. The cumulative distribution of these extinctions can be seen in
Fig. 7.
![\begin{figure}
\par\includegraphics[totalheight=0.2\textheight]{8662fig7.ps}
\end{figure}](/articles/aa/full/2008/37/aa8662-07/Timg80.gif) |
Figure 7:
Cumulative distribution of 1500 extinctions as measured through the fraction of the Galactic Plane which lies within the Pan-STARRS survey area. |
| Open with DEXTER |
Table 5:
Estimated intrinsic and detectable CCSRs within the
SDSS DR5 survey area and z<0.04. Also shown are the rates extended to the PS1 survey area.
For the full galaxy catalogue (within
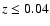 )
we can expect to detect 66.9
)
we can expect to detect 66.9 of all
CCSNe. When considering the lower metallicity samples we can expect to
detect 74.2
of all
CCSNe. When considering the lower metallicity samples we can expect to
detect 74.2 of CCSNe. The predicted detectable CCSRs for both the full galaxy catalogue
and for the lower-metallicity samples can be found in Table 5.
of CCSNe. The predicted detectable CCSRs for both the full galaxy catalogue
and for the lower-metallicity samples can be found in Table 5.
These results are a vast improvement on the rates predicted for the
catalogued galaxy surveys with both a single 2.0 m telescope and a network
of 2.0 m telescopes. Considering that the Pan-STARRS survey area is
 5.25 that of SDSS DR5 and given a complete galaxy catalogue of that
area, we can expect to detect a total of
5.25 that of SDSS DR5 and given a complete galaxy catalogue of that
area, we can expect to detect a total of  570 CCSNe yr-1, roughly 13 of which
will be from host galaxies with
570 CCSNe yr-1, roughly 13 of which
will be from host galaxies with
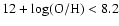 .
We would
expect that the PS1 survey itself will provide a photometric catalogue
of at least the quality the depth of SDSS DR5 (most likely signficcantly
better) over the whole sky and hence provide us with a means to identify
SNe in nearby, faint blue hosts.
Our estimate of
number of CCSNe expected to be detected in the low-metallicity galaxy sample can be considered as a lower
limit as there may be many more blue, compact, dwarf galaxies that have
not been detected and catalogued by SDSS DR5.
The number of CCSNe expected to be detected
by PS1 in low-metallicity galaxies is hence about 50%
times more than would be possible using a network of seven
2.0 m telescope in a dedicated pointed survey with 1000 h of dedicated
time. It would this seem much more efficient to use the PS1 survey
to discover these are objects than invest in a dedicated pointed survey
with large numbers of 2.0 m telescopes with standard CCD cameras
and fields of view.
.
We would
expect that the PS1 survey itself will provide a photometric catalogue
of at least the quality the depth of SDSS DR5 (most likely signficcantly
better) over the whole sky and hence provide us with a means to identify
SNe in nearby, faint blue hosts.
Our estimate of
number of CCSNe expected to be detected in the low-metallicity galaxy sample can be considered as a lower
limit as there may be many more blue, compact, dwarf galaxies that have
not been detected and catalogued by SDSS DR5.
The number of CCSNe expected to be detected
by PS1 in low-metallicity galaxies is hence about 50%
times more than would be possible using a network of seven
2.0 m telescope in a dedicated pointed survey with 1000 h of dedicated
time. It would this seem much more efficient to use the PS1 survey
to discover these are objects than invest in a dedicated pointed survey
with large numbers of 2.0 m telescopes with standard CCD cameras
and fields of view.
Eventually three more 1.8 m telescopes identical to PS1 will be added to
the Pan-STARRS network to create PS4. These four telescopes will be trained
on the same area of the sky simultaneously
to effectively perform a deeper all-sky
survey (with the same observing strategy as PS1),
giving a co-added 25 limiting magnitude of g=22.2.
limiting magnitude of g=22.2.
At an apparent limiting magnitude of
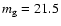 ,
PS1 has an absolute limiting
magnitude
,
PS1 has an absolute limiting
magnitude
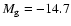 at the boundary of our search (z=0.04). For PS4 we would push the boundary of our search out to the point where the
absolute limiting magnitude is identical to that of our search with PS1 in
order to detect the same fraction of CCSNe as we have predicted for PS1.
This distance limit is calculated to be z=0.056.
Using the same
survey strategy as previously suggested for PS1 and introducing
the new limiting magnitude and distance limit, we predict that PS4 should discover a total of
at the boundary of our search (z=0.04). For PS4 we would push the boundary of our search out to the point where the
absolute limiting magnitude is identical to that of our search with PS1 in
order to detect the same fraction of CCSNe as we have predicted for PS1.
This distance limit is calculated to be z=0.056.
Using the same
survey strategy as previously suggested for PS1 and introducing
the new limiting magnitude and distance limit, we predict that PS4 should discover a total of  1308 CCSNe yr-1,
1308 CCSNe yr-1,
 18.3 CCSNe yr-1 being found in galaxies with
18.3 CCSNe yr-1 being found in galaxies with
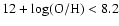 .
These results
can be found in Table 6.
.
These results
can be found in Table 6.
Table 6:
Estimated intrinsic and detectable CCSRs within the SDSS
DR5 survey area and z<0.056. Also shown are the rates extended to the PS4 survey area.
5 Strategy 3: magnitude-limited searches
with future all-sky surveys
Thus far when considering the Pan-STARRS survey to search for CCSNe
we have limited ourselves to the known galaxy
population within
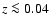 .
If our aim is to detect
all of the CCSNe that we possibly can then we are by no
means utilizing the Pan-STARRS survey to its greatest
potential. The galaxy catalogue employed is
taken from SDSS DR5 and is therefore limited by a comparatively
shallow depth compared to the depth to which Pan-STARRS will be
able to detect CCSNe (Chambers & Denneau 2007).
.
If our aim is to detect
all of the CCSNe that we possibly can then we are by no
means utilizing the Pan-STARRS survey to its greatest
potential. The galaxy catalogue employed is
taken from SDSS DR5 and is therefore limited by a comparatively
shallow depth compared to the depth to which Pan-STARRS will be
able to detect CCSNe (Chambers & Denneau 2007).
![\begin{figure}
\par\includegraphics[totalheight=0.2\textheight]{8662fig8.ps}
\end{figure}](/articles/aa/full/2008/37/aa8662-07/Timg85.gif) |
Figure 8:
The galaxy distribution for the SDSS DR5 spectroscopic
survey galaxy sample. The solid curve represents the absolute magnitude
limit as a function of redshift given that the SDSS DR5 apparent magnitude
limit for the sample is r=17.77. An absolute magnitude limit of
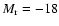 is reached at at redshift of 0.033 (dashed line). There is a clear
drop in the galaxy density at this redshift, indicated by the dashed line,
and we choose to use this limit as the completeness limit of the SDSS DR5
galaxy sample.
is reached at at redshift of 0.033 (dashed line). There is a clear
drop in the galaxy density at this redshift, indicated by the dashed line,
and we choose to use this limit as the completeness limit of the SDSS DR5
galaxy sample. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{8662fig9.ps}
\end{figure}](/articles/aa/full/2008/37/aa8662-07/Timg86.gif) |
Figure 9:
A schematic depicting the cadence of observation for any
given point in the sky, taken from the Pan-STARRS observation strategy
(Chambers & Denneau 2007). One Pan-STARRS year of 12 lunar months, approximately
352 days, is represented by a circle. With each observation epoch a double exposure is taken in order to
identify Near Earth Objects. |
| Open with DEXTER |
A far more powerful method that we could implement with
Pan-STARRS to detect CCSNe is to perform simply a magnitude-limited search
to detect CCSNe
over the whole sky and to as large distances as possible
following the example of surveys such as the
Nearby SN Factory (Copin et al. 2006). The inherent
difficulties that we will encounter with this kind of survey will
be trying to distinguish SNe from all other transient events and
variables such as classical novae, asteroids and AGN and further
distinguishing CCSNe from the thermonuclear (type Ia) SNe.
Assuming that it may be possible to overcome these
difficulties (and that we can probabilistically classify transient events)
we can
estimate how many CCSNe that we shall be able to detect with PS1, PS4 and
also compare these rates with the likes of the Large Synoptic Survey
Telescope (LSST) set to come online in 2016.
5.1 Adapted Monte-Carlo simulations
In order to determine the total CCSRs that we are to expect from the all-sky
surveys PS1, PS4 and LSST, we must first ascertain to what redshift depth our SDSS
DR5 galaxy sample is relatively complete to. When targeting galaxies for the
spectroscopic survey SDSS DR5 has a lower magnitude limit of r=17.77.
This apparent magnitude limit equates to an absolute galaxy magnitude
limit of
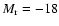 being reached at a redshift of z=0.033. The
galaxy density distribution for SDSS DR5 can be seen in
Fig. 8. There is a clear drop in the observed galaxy density at this
redshift and we choose to set this limit as the completeness limit of the
SDSS DR5 galaxy sample.
being reached at a redshift of z=0.033. The
galaxy density distribution for SDSS DR5 can be seen in
Fig. 8. There is a clear drop in the observed galaxy density at this
redshift and we choose to set this limit as the completeness limit of the
SDSS DR5 galaxy sample.
Table 7:
The 25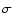 AB limiting magnitudes for PS1, PS4 and LSST.
AB limiting magnitudes for PS1, PS4 and LSST.
With this completeness limit in mind we can now extrapolate the complete local
galaxy sample out to the observable redshift limits for the individual
CCSN surveys that we are considering. We assume that the galaxy
distribution throughout the observable universe is both homogeneous and
isotropic. To determine the observable redshift limits of each of the suggested
CCSN searches it is necessary to model the CCSN detection distribution
for each of the surveys. This is made possible by using an adapted MCS to determine
the percentage of CCSNe that would be detected as a function of redshift.
The variant parameters included in the MCS that define one distribution from another are the
cadence and the limiting magnitudes of the survey. For PS1 and PS4 we
set the cadence to reflect the observing strategy for Pan-STARRS
(Fig. 9) and the 25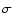 limiting magnitudes outlined by
Chambers & Denneau (2007), assuming that the limiting magnitude of PS4 is
achieved via co-adding four PS1 images (see Table 7).
limiting magnitudes outlined by
Chambers & Denneau (2007), assuming that the limiting magnitude of PS4 is
achieved via co-adding four PS1 images (see Table 7).
The current LSST configuration sets the telescope at an 8.4 m diameter with
a 9.6 square degree field-of-view. It is planned that LSST will survey the whole
of the observable sky every 3 nights, eventually covering a total of
20 000 square
degrees. The primary focus of the survey is to detect transients and in
order to detect fast faint events the sky will be surveyed with
duplicate pairs of 15 s exposures. Using the LSST exposure calculator
this equates to the 25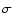 limiting magnitudes per single exposure as found in Table 7.
limiting magnitudes per single exposure as found in Table 7.
When considering a magnitude-limited survey it is important to note that we shall
detect CCSNe at relatively large redshifts compared to the volume-limited survey that we have previously discussed. With this increase in
survey depth we now encounter parameters in our search that we have
previously neglected due to fact that our searches have been relatively
nearby. These parameters that now have to be considered in our MCS are all
functions of redshift and hence could be neglected at low-redshift. They are the
star-formation history (SFH) of the universe, the redshifting
of light emitted by the CCSNe, the broadening of the CCSNe
lightcurves due to time-dilation and finally the retardation
of the CCSN rates again due to time-dilation.
Star-formation history: as star-formation was more prolific earlier
in the Universe's history than it is at present, star-formation is seen to
increase as redshift increases (at least to moderate redshifts of
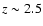 ). It is also important to note that approximately 50
). It is also important to note that approximately 50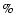 of all local star formation activity is obscured, while at a redshift of
of all local star formation activity is obscured, while at a redshift of 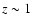 this fraction could be as high as 80
this fraction could be as high as 80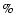 (Takeuchi et al. 2005). To incorporate the SFH of the universe into our simulations, but also taking into account that a greater fraction of this star-formation will be obscured by dust at higher redshifts, we include the far-ultraviolet (FUV) SFR evolution determined by Schiminovich et al. (2005), see Eq. (13). Compared with all other indicators of SFR, the FUV luminosity is the most inhibited by dust and therefore we would hope that by using this indicator we would only consider the star-formation that will give rise to CCSNe that are not so extinguished as to be invisible to our search.
(Takeuchi et al. 2005). To incorporate the SFH of the universe into our simulations, but also taking into account that a greater fraction of this star-formation will be obscured by dust at higher redshifts, we include the far-ultraviolet (FUV) SFR evolution determined by Schiminovich et al. (2005), see Eq. (13). Compared with all other indicators of SFR, the FUV luminosity is the most inhibited by dust and therefore we would hope that by using this indicator we would only consider the star-formation that will give rise to CCSNe that are not so extinguished as to be invisible to our search.
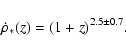 |
(13) |
K corrections: comparing the bolometric fluxes of objects at various redshifts presents no
difficulty as we are comparing the total flux emitted by the objects at all
wavelengths. However, in practice we measure only a fraction of the total
flux of an object, redshifted to the observed wavelength and transmitted through a given
bandpass. This presents us with a challenge when we wish to simulate the
total number of CCSNe that an all-sky survey will detect, as we have so
far only considered their rest-frame (or emitted-frame) magnitudes but we
must now consider their redshifted-frame (or observed-frame)
magnitudes. To do
this we need to calculate a transformation known as the K correction
(Oke & Sandage 1968; Hogg et al. 2002), which transform between
emitted-frame and observed-frame magnitudes:
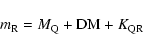 |
(14) |
![$\displaystyle K_{\rm QR}= -2.5{\rm log}_{10} \left[\frac{1}{[1+z]}\phantom{\fra...
...ambda}([1+z]\lambda_{\rm em})Q(\lambda_{\rm em}){\rm d}\lambda_{\rm em}}\right]$](/articles/aa/full/2008/37/aa8662-07/img91.gif) |
|
|
(15) |
where 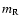 is the apparent magnitude the the object as measured through observed-frame
bandpass,
is the apparent magnitude the the object as measured through observed-frame
bandpass, 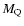 is the absolute magnitude of the object as measured through the emitted-frame
bandpass, DM is the distance modulus of the object considered as
determined from its luminosity
distance and
is the absolute magnitude of the object as measured through the emitted-frame
bandpass, DM is the distance modulus of the object considered as
determined from its luminosity
distance and
 is the K correction that transforms between these
magnitudes. The K correction can be understood as the difference in
magnitude between two identical objects placed at the same distance; one traveling at a redshift of
z relative to the observer and measured through the observed-frame
bandpass, the other at rest relative to the observer and measured through the
emitted-frame bandpass.
is the K correction that transforms between these
magnitudes. The K correction can be understood as the difference in
magnitude between two identical objects placed at the same distance; one traveling at a redshift of
z relative to the observer and measured through the observed-frame
bandpass, the other at rest relative to the observer and measured through the
emitted-frame bandpass.
We choose to use the K correction as derived by Hogg et al. (2002) to account for the redshifting of the SN light in our MCS; see
Eq. (15), where
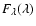 is the spectral density of flux of the
object considered taken from spectral data (measured in erg cm-2 s-1 Å-1).
is the spectral density of flux of the
object considered taken from spectral data (measured in erg cm-2 s-1 Å-1).
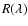 and
and
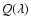 are the observed-frame and emitted-frame filter
total throughput functions, both
depending on the various parameters of the survey considered including the total
throughput of the atmosphere, the reflectivity of the telescope
mirrors, the transmission of the corrector optics and filters and the quantum
efficiency of the camera detector.
are the observed-frame and emitted-frame filter
total throughput functions, both
depending on the various parameters of the survey considered including the total
throughput of the atmosphere, the reflectivity of the telescope
mirrors, the transmission of the corrector optics and filters and the quantum
efficiency of the camera detector.
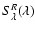 and
and
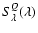 are the spectral density of flux for the AB zero-magnitude standard source, which
is a synthetic source equal to 3631 Jy (where 1 Jy = 10-26 W m-2 Hz-1) for all frequencies (Oke & Gunn 1983), as measured
through the observed-frame and emitted-frame filters respectively.
are the spectral density of flux for the AB zero-magnitude standard source, which
is a synthetic source equal to 3631 Jy (where 1 Jy = 10-26 W m-2 Hz-1) for all frequencies (Oke & Gunn 1983), as measured
through the observed-frame and emitted-frame filters respectively.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{8662fig10.eps}
\end{figure}](/articles/aa/full/2008/37/aa8662-07/Timg100.gif) |
Figure 10:
A third order polynomial is fitted to each set of K correction data,
 and
and
 ,
for each CCSNe
type and each redshift position sampled over the entire redshift range of
the all-sky surveys considered. This example is of the ,
for each CCSNe
type and each redshift position sampled over the entire redshift range of
the all-sky surveys considered. This example is of the
 correction
for type IIL SNe as sampled at a redshift of z=0.2.
correction
for type IIL SNe as sampled at a redshift of z=0.2. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{8662fig11.ps}
\end{figure}](/articles/aa/full/2008/37/aa8662-07/Timg101.gif) |
Figure 11:
The solid lines show CCSN detection distributions for PS1,
PS4 and LSST, the dashed lines the absolute magnitude limits of the surveys
as a function of redshift. At a absolute limiting magnitude of
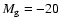 the PS1, PS4 and LSST reach their respective limiting redshifts
depths of
the PS1, PS4 and LSST reach their respective limiting redshifts
depths of 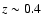 , ,
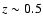 and
and 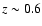 . . |
| Open with DEXTER |
It is essential to provide our MCS with
K corrections for each of the CCSNe simulated in order to determine
accurate apparent magnitudes as measured through each of the five Pan-STARRS
filters. As the K correction varies for each filter considered we must
produce five K corrections for each CCSN;
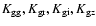 and
and
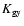 .
Any
given CCSN produced by the simulation is placed at a random redshift and is
first observed at a random point in its evolution, therefore we require
K corrections
over the entire redshift range of our surveys, for every possible epoch of
observation and for every CCSN type. It is then imperative that we have enough spectral information for each type of
CCSN considered in order to cover the shear expanse of the parameters
involved in calculating the K corrections. We require spectral information
covering a large range of the evolution of each CCSN type including the rise
to maximum light and through to over 300 days post-explosion in order to
accommodate for the maximum time separating two consecutive observations in the same
filter according to the Pan-STARRS observation strategy implemented in the
MCS (see Fig. 9). As the K correction evolves with time we also require spectral data for a large
number of epochs in order to achieve good time resolution over the evolution
of each CCSN. Finally, a wide range in wavelength coverage is required in
order to provide enough information to determine K corrections for all five
bandpasses whenever possible, remembering that the spectral data shall be
redshifted according to the distance appointed to the CCSN by the MCS.
.
Any
given CCSN produced by the simulation is placed at a random redshift and is
first observed at a random point in its evolution, therefore we require
K corrections
over the entire redshift range of our surveys, for every possible epoch of
observation and for every CCSN type. It is then imperative that we have enough spectral information for each type of
CCSN considered in order to cover the shear expanse of the parameters
involved in calculating the K corrections. We require spectral information
covering a large range of the evolution of each CCSN type including the rise
to maximum light and through to over 300 days post-explosion in order to
accommodate for the maximum time separating two consecutive observations in the same
filter according to the Pan-STARRS observation strategy implemented in the
MCS (see Fig. 9). As the K correction evolves with time we also require spectral data for a large
number of epochs in order to achieve good time resolution over the evolution
of each CCSN. Finally, a wide range in wavelength coverage is required in
order to provide enough information to determine K corrections for all five
bandpasses whenever possible, remembering that the spectral data shall be
redshifted according to the distance appointed to the CCSN by the MCS.
For CCSNe of type IIP we have used the spectra of SN1999em
(Baron et al. 2000; Hamuy et al. 2001; Leonard et al. 2001), for
type IIL the spectra of SN1998S are used (Fassia et al. 2000; Pozzo et al. 2004; Fransson et al. 2005) and for type Ib/c the spectra of
SN2002ap are used (Gal-Yam et al. 2002) supplemented with spectra from
SN1990B (Matheson et al. 2001, and Asiago Catalogue) and SN1998bw
(Patat et al. 2001) in order to attain the time coverage required. Due
to the fact that type IIn/P and IIn/L are relatively rare, there is not enough
spectral data to cover both the time and wavelength coverage required to
determine a full range of K corrections for these CCSNe. To compensate for
this lack of data we allow the type IIn/P SN population to be represented
by type IIP SNe and the type IIn/L population to be represented by type IIL
SNe, adapting the Smartt et al. (2007) rates appropriately for the MCS.
Having calculated the thousands of possible K corrections allowed by the
relevant parameters of the MCS, we then fit a third
order polynomial to each set of K correction data defined by CCSN type,
filter and redshift in order to provide a K correction for all epochs
required by the MCS (See Fig. 10)
These polynomials are read by the MCS in order to determine a final accurate
apparent magnitude in each of the five filters, for each CCSN as measured at its specific redshift and
point in its evolution.
Time dilation: the broadening of the CCSN lightcurves due to time dilation at relatively
high redshift can be described simply as watching the CCSN
evolve in ``slow motion'' with respect to our frame of reference. This
enables us to sample the lightcurve of the CCSN with a greater frequency
within its frame of reference relative to our frame of reference. The
cadence hence goes as:
 |
(16) |
The same argument leads to a retardation of the detected CCSN rates,
giving:
 |
(17) |
Figure 11 shows the CCSN detection distributions for PS1, PS2
and LSST. Beyond the redshift limit where an absolute limiting magnitude
of Mg=-20 is attained the surveys will cease to detect all but the most
extreme of CCSNe were luminosity is concerned and hence it is at this
limit that we choose to mark the boundary of the observable universe when
considering CCSNe. These redshift limits are 0.37, 0.50 and 0.59 for PS1,
PS4 and LSST respectively.
Assuming that the galaxy density is homogeneous and isotropic
throughout the volumes contained by these redshifts, we extrapolate our
nearby local sample of galaxies and their predicted CCSRs to both the sky coverage areas and the respective redshifts for the
three surveys, taking into account the SFH of the universe, the
redshifting of light from distant CCSNe and the
time-dilation of both the CCSN lightcurves and the CCSRs. Using the CCSN detection distributions obtained from the
MCSs we then determine the detected CCSR for each of the surveys. The
results can be found in Table 8.
Table 8:
Predicted CCSRs for PS1, PS4 and LSST.
6 Discussion and comparison with other surveys
Having considered three different survey strategies designed to search
for CCSNe, specifically in low-metallicity environments (a
pointed survey of catalogued low-metallicity galaxies
using both a single and a network of
2.0 m telescopes, a volume-limited survey using the Pan-STARRS all-sky
surveys and finally a magnitdue limited survey using future all-sky
surveys), it is now appropriate to compare these different
strategies, the numbers of CCSNe we expect to detect and the various
limitations of each strategy.
Using a single 2.0 m telescope or a network of seven 2.0 m telescopes to
perform a pointed survey of low-metallicty galaxies
within z=0.04 we expect to
detect approximately 1.3 CCSNe yr-1 and 9.3 CCSNe yr-1 respectively in host galaxies of very low-metallicity,
exhibiting oxygen abundances
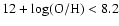 .
When
considering the relative numbers of similar events that we would hope
to detect using a volume-limited
survey with PS1 we estimate that we
would detect approximately 12.5 CCSNe yr-1 and, extending
the search to z=0.056, PS4 would detect 18.3 CCSNe yr-1. A drawback of the pointed low-metallicity survey is the
fact that
.
When
considering the relative numbers of similar events that we would hope
to detect using a volume-limited
survey with PS1 we estimate that we
would detect approximately 12.5 CCSNe yr-1 and, extending
the search to z=0.056, PS4 would detect 18.3 CCSNe yr-1. A drawback of the pointed low-metallicity survey is the
fact that  1000 h of telescope time would be required of the
network of seven 2.0 m telescopes. Unlike the network of 2.0 m
telescopes, the all-sky surveys have the additional
advantage of not
being limited by the number of galaxies that they can feasibly observe
and as a result shall be capable of observing CCSN events in all
environments and not only those in the lowest-metallicity host
galaxies, helping us to reduce the possibility of missing any rare
CCSN events of extreme interest and also gaining the capability of
determining accurate relative rates of SNe within a large but limited
volume, expecting to detect a total of
1000 h of telescope time would be required of the
network of seven 2.0 m telescopes. Unlike the network of 2.0 m
telescopes, the all-sky surveys have the additional
advantage of not
being limited by the number of galaxies that they can feasibly observe
and as a result shall be capable of observing CCSN events in all
environments and not only those in the lowest-metallicity host
galaxies, helping us to reduce the possibility of missing any rare
CCSN events of extreme interest and also gaining the capability of
determining accurate relative rates of SNe within a large but limited
volume, expecting to detect a total of  570 CCSNe yr-1 with PS1 and
570 CCSNe yr-1 with PS1 and  1300 CCSNe yr-1 with PS4.
1300 CCSNe yr-1 with PS4.
To estimate the amount of 8.0 m telescope time that we would require to
spectroscopically follow the  13 CCSNe found with the PS1 volume-limited survey in low-metallicity environments (
13 CCSNe found with the PS1 volume-limited survey in low-metallicity environments (
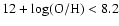 ), we consider a CCSN occurring at the average
distance of the survey, that is
), we consider a CCSN occurring at the average
distance of the survey, that is  120 Mpc. Depending on how
early we catch this SN, we hope to observe it at various epochs during
its evolution and into its tail phase. Suggesting an average absolute
magnitude of -15 for these epochs equates as an observed apparent
magnitude of 20.7 at 120 Mpc, including a typical galactic extinction
of 0.3 mag. To determine the time required from a typical 8.0 m
telescope for spectroscopic follow-up we use the VLT FORS2 exposure
time calculator, selecting a suitable grism and requiring a
signal-to-noise of 50 per spectral element for each spectrum. To reach
this signal-to-noise level we would require a
120 Mpc. Depending on how
early we catch this SN, we hope to observe it at various epochs during
its evolution and into its tail phase. Suggesting an average absolute
magnitude of -15 for these epochs equates as an observed apparent
magnitude of 20.7 at 120 Mpc, including a typical galactic extinction
of 0.3 mag. To determine the time required from a typical 8.0 m
telescope for spectroscopic follow-up we use the VLT FORS2 exposure
time calculator, selecting a suitable grism and requiring a
signal-to-noise of 50 per spectral element for each spectrum. To reach
this signal-to-noise level we would require a  3000 s on
source integration. If we were to spectroscopically follow the
13 events, requiring 5 epochs of observations per SN, we would then
require
3000 s on
source integration. If we were to spectroscopically follow the
13 events, requiring 5 epochs of observations per SN, we would then
require  70 h of 8.0 m telescope time per year.
70 h of 8.0 m telescope time per year.
An obstacle that would hinder both the pointed survey of
low-metallicity galaxies and the volume-limited Pan-STARRS surveys is
the incompleteness of any galaxy catalogue that could presently be
produced. In the former case one would obviously need an all-sky
target list for a pointed survey as we have demonstrated that the SDSS
footprint does not have enough low-metallicity galaxies to make a
search particularly fruitful (only 1.3 CCSNe yr-1 is likely to
be found). In the case of the wide area search of Pan-STARRS one would
ideally like to quantify all potential low-metallicity systems within
a local volume of the Universe so that new discoveries can be quickly
cross-matched and the optical transients in these galaxies immediately
selected for follow-up. Hence it would be extremely useful to have an
SDSS DR5 type catalogue over the entire sky. As previously discussed
(see Sect. 3.5) it is currently possible to compile a catalogue of
 105 galaxies within the sky area covered by Pan-STARRS and
within the redshift range z<0.04. This catalogue is far from
complete, however when PS1 completes a full cycle of sky observations
we would have a deep photometric catalogue with which to search for
CCSNe and classify the host galaxies.
105 galaxies within the sky area covered by Pan-STARRS and
within the redshift range z<0.04. This catalogue is far from
complete, however when PS1 completes a full cycle of sky observations
we would have a deep photometric catalogue with which to search for
CCSNe and classify the host galaxies.
![\begin{figure}
\par\includegraphics[width=18cm,clip]{8662fig12.ps}
\end{figure}](/articles/aa/full/2008/37/aa8662-07/Timg104.gif) |
Figure 12:
Of the 12 SNe discovered by the Nearby Supernova Factory that were hosted by SFGs in the SDSS DR5 catalogue, 5 were hosted by galaxies with 12 + log(O/H) < 8.4. The host shown are SDSS J140737.23+384047 (SN 2007fg), SDSS J160205.11+294338 (SN 2007fz), SDSS J135042.68 + 400208 (SNF20080324-010), SDSS J154404.32+275335 (SNF20080515-004) and SDSS J150031.40+552210 (SNF20080614-002). |
| Open with DEXTER |
It will be challenging to identify and select genuine CCSNe in the
magnitude-limited, all sky-surveys. Without a defined volume limit it
becomes impossible to describe accurate relative rates of SNe and
without the prior knowledge of the SN hosts it will be very difficult
to segregate CCSNe from the large numbers of other transitory events,
especially more distant SNe type Ia in apparently faint (but perhaps
intrinsically bright) hosts. Most of the SNe are likely to be too
distant to have any catalogued host and one of the challenges is to
classify objects from the information gathered in the all-sky surveys
themselves e.g. lightcurve matching, identification and photometric
redshift measurement of the host, estimated energy of the transient.
If it is possible to overcome these challenges the numbers of detected
CCSNe expected from these unbiased, all-sky and magnitude-limited
surveys shall overwhelm those numbers from the other survey strategies
far above an order of magnitude (see Table 8).
A pioneering survey in this area has been the Texas Supernova Search
(TSS), which has now evolved into the ROTSE Supernova Verification
Project (RSVP)
(Quimby et al. 2005b; Yuan et al. 2007). The Robotic Optical
Transient Search Experiment (ROTSE) presently consists of four 0.45 m
robotic telescope located around the globe, each with a 1.85 square
degree field of view, dedicated to detecting and observing optical
transients, with an emphasis on GRBs. The TSS has used the ROTSE-IIIb
(MacDonald Observatory Texas) to perform a
wide-field search for nearby SNe.
The RSVP uses all four ROTSE-III telescopes
to discover SNe and other transient variables, by imaging areas of
the sky that host nearby galaxy clusters. The typical cadence is
1-3 days with a typical limiting magnitude of  18.5 mag. To date
the ROSTE-IIIb telescope has discovered 50 SNe in total at mean redshift
of z=0.049; 34 type Ia and 16 type II (5 of which have been
classified as Ic and 5 as IIn). The most remarkable result of this
small scale SN survey is that they have claim over the discovery of
the three most luminous SN ever detected; SN2006tf (-20.7 mag),
SN2006gy (-22 mag) and SN2005ap (-22.7 mag). SN 2006tf and SN 2006gy
were both classified as a type IIn (Quimby 2006; Quimby et al. 2007a) and possibly had Luminous Blue Variable (LBV)
star progenitors with explosions speculated to have been triggered by
pulsation pair instability (Woosley et al. 2007; Smith et al. 2006,2008). SN 2005ap was classified as
a type II (Quimby et al. 2005a) and exhibited a broad H
18.5 mag. To date
the ROSTE-IIIb telescope has discovered 50 SNe in total at mean redshift
of z=0.049; 34 type Ia and 16 type II (5 of which have been
classified as Ic and 5 as IIn). The most remarkable result of this
small scale SN survey is that they have claim over the discovery of
the three most luminous SN ever detected; SN2006tf (-20.7 mag),
SN2006gy (-22 mag) and SN2005ap (-22.7 mag). SN 2006tf and SN 2006gy
were both classified as a type IIn (Quimby 2006; Quimby et al. 2007a) and possibly had Luminous Blue Variable (LBV)
star progenitors with explosions speculated to have been triggered by
pulsation pair instability (Woosley et al. 2007; Smith et al. 2006,2008). SN 2005ap was classified as
a type II (Quimby et al. 2005a) and exhibited a broad H P-Cygni profile. The explosion of the progenitor, which still had its
Hydrogen envelope intact, was possibly powered by either a GRB type
engine or a pair-instability eruption
(Quimby et al. 2007b). Although these type of super-luminous SNe
may be intrinsically rare, it is more likely that they have remained
undiscovered in the past due to the fact that they have been missed or
misclassified as AGN in pointed surveys as they have occurred close to
the cores of bright galaxies. The image-subtraction techniques used by
area surveys, such as TSS and RSVP, will ensure that these types of
interesting events will continue to be discovered.
Taking a spectrum of the SN type IIn 1998S
at peak (Fassia et al. 2000) and redshifting it to estimate the
K-corrections that SNe similar to 2006gy would require at various
redshifts, we predict that we would detect these events to
P-Cygni profile. The explosion of the progenitor, which still had its
Hydrogen envelope intact, was possibly powered by either a GRB type
engine or a pair-instability eruption
(Quimby et al. 2007b). Although these type of super-luminous SNe
may be intrinsically rare, it is more likely that they have remained
undiscovered in the past due to the fact that they have been missed or
misclassified as AGN in pointed surveys as they have occurred close to
the cores of bright galaxies. The image-subtraction techniques used by
area surveys, such as TSS and RSVP, will ensure that these types of
interesting events will continue to be discovered.
Taking a spectrum of the SN type IIn 1998S
at peak (Fassia et al. 2000) and redshifting it to estimate the
K-corrections that SNe similar to 2006gy would require at various
redshifts, we predict that we would detect these events to 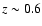 for PS1,
for PS1, 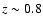 for PS4 and
for PS4 and 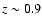 for LSST. For PS4 and
LSST these limits correspond to a search volume
for LSST. For PS4 and
LSST these limits correspond to a search volume  2.9 and
2.9 and
 4.4 times greater than PS1.
4.4 times greater than PS1.
The Nearby Supernova Factory (NSF) uses ultra-wide
field CCD mosaic images from the Near-Earth Asteriod Tracking (NEAT) and Palomar-Quest survey
programs with the aim of finding low-redshift SNe Ia
(Aldering et al. 2002). Within the volume-limited (z<0.04) search with PS1 we predict relative-rates of SNe II, SNe Ib/c and SNe IIn as 57.8%, 38.2% and 4.0% and at mean redshifts of 0.0318, 0.0316 and 0.0321 respectively. In its lifetime the NSF had discovered and classified 85 CCSNe within z<0.04 with relative-rates of SNe II, SNe Ib/c and SNe IIn of 67.1%, 20.0% and 12.9% at mean redshifts
of 0.0283, 0.0292 and 0.0284 respectively. The reason that the relative-rates of CCSNe types predicted by our PS1 volume-limited search and those discovered by the NSF are somewhat discrepant may be due in part to the photometric screening of SN candidates that the NSF perform prior to spectroscopically classifying candidates. The NSF aim to find young SNe Ia that are nearby yet are within the Hubble-flow and therefore seem to classify SN candidates that are on the rise and that are close to the limiting-magnitude of their search (
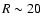 mag),
as can be seen from the relative-magnitude distributions of classified SNe in
Table 9. However it could be argued that because of the high-metallicity bias of many current and historic SN searches, the relative-rates of nearby CCSNe compiled by Smartt et al. (200), and used in our simulations, are also biased toward higher metallicity. A high-metallicity bias in these relative-rates would be seen as an over-estimation of the true SN Ib/c to
SN II ratio; as seen when compared to the relative-rates discovered by the NSF. Further evidence supporting this hypothesis results from cross-matching NSF discovered SNe with our catalogue of SDSS DR5 SFGs within z<0.04. A total of
12 CCSNe are matched with SDSS galaxies, 5 of which occurring in galaxies with 12 + log(O/H) < 8.4 (see Fig. 12). This high fraction of CCSNe discovered in low-metallicity environments may again be due to selection criteria of the NSF (possibly looking for SNe occurring in apparently faint hosts) but remains encouraging for our plans to search for low-metallicity CCSNe with future all-sky surveys.
mag),
as can be seen from the relative-magnitude distributions of classified SNe in
Table 9. However it could be argued that because of the high-metallicity bias of many current and historic SN searches, the relative-rates of nearby CCSNe compiled by Smartt et al. (200), and used in our simulations, are also biased toward higher metallicity. A high-metallicity bias in these relative-rates would be seen as an over-estimation of the true SN Ib/c to
SN II ratio; as seen when compared to the relative-rates discovered by the NSF. Further evidence supporting this hypothesis results from cross-matching NSF discovered SNe with our catalogue of SDSS DR5 SFGs within z<0.04. A total of
12 CCSNe are matched with SDSS galaxies, 5 of which occurring in galaxies with 12 + log(O/H) < 8.4 (see Fig. 12). This high fraction of CCSNe discovered in low-metallicity environments may again be due to selection criteria of the NSF (possibly looking for SNe occurring in apparently faint hosts) but remains encouraging for our plans to search for low-metallicity CCSNe with future all-sky surveys.
Table 9:
Comparison between the relative magnitudes of CCSNe we predict with a volume-limited (z<0.04) search with PS1 and those discovered within the same volume by the Nearby Supernova Factory.
Another future all-sky survey that has potential for SNe discoveries is
Gaia: the European Space Agency's ``super-Hipparcos'' satellite with
the objective of creating the most precise three-dimensional map of
the Galaxy (Perryman 2005). The satellite shall have many
other additional capabilities including the ability to detect
nearby SNe (within a few hundred Mpc), and predicted for launch in
December 2011 it is a potential competitor of Pan-STARRS and LSST. Belokurov & Evans (2003) have performed a feasibility study
similar to this study for Gaia and have predicted that the satellite
shall detect  1420 CCSNe yr-1 using a magnitude-limited
survey strategy. Capable of detecting objects brighter than 20th magnitude,
1.5 mag brighter than the g=21.5 limit for PS1,
Gaia has the ability to survey a volume of only an eighth of the depth
that PS1 shall survey. Belokurov & Evans (2003) employed a galaxy
catalogue which more than likely neglected low-luminosity galaxies,
which would result in the CCSN rate being under-predicted by a factor
of up to
1420 CCSNe yr-1 using a magnitude-limited
survey strategy. Capable of detecting objects brighter than 20th magnitude,
1.5 mag brighter than the g=21.5 limit for PS1,
Gaia has the ability to survey a volume of only an eighth of the depth
that PS1 shall survey. Belokurov & Evans (2003) employed a galaxy
catalogue which more than likely neglected low-luminosity galaxies,
which would result in the CCSN rate being under-predicted by a factor
of up to  2 fewer SNe. Hence if we scale the
Belokurov & Evans numbers by
2 fewer SNe. Hence if we scale the
Belokurov & Evans numbers by  16, the final
numbers should be comparable with our PS1 estimates, predicting
16, the final
numbers should be comparable with our PS1 estimates, predicting
 22 720 CCSNe yr-1, which is very close to the rate
that we have predicted for PS1 using our MCSs,
22 720 CCSNe yr-1, which is very close to the rate
that we have predicted for PS1 using our MCSs,  24 000 CCSNe yr-1 (see Table 8). However, we note
that these numbers are likely somewhat over optimistic due to the
treatment of host galaxy extinction in our MCS.
24 000 CCSNe yr-1 (see Table 8). However, we note
that these numbers are likely somewhat over optimistic due to the
treatment of host galaxy extinction in our MCS.
Having determined oxygen abundances, star-formation rates and CCSN rates for all
spectroscopically typed star-forming galaxies in the Sloan Digital Sky
Survey Data Release 5 within z=0.04, we have used Monte-Carlo simulations to predict the fraction of
these CCSNe that we can expect to detect using different survey
strategies. Using a single 2 m telescope (with a standard CCD camera)
search we predict a detection rate of
 1.3 CCSNe yr-1 in galaxies with metallicities below
1.3 CCSNe yr-1 in galaxies with metallicities below
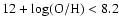 which are within a volume that will allow
detailed follow-up with 4 m and 8 m telescopes (z=0.04). With a
network of seven 2 m telescopes we estimate
which are within a volume that will allow
detailed follow-up with 4 m and 8 m telescopes (z=0.04). With a
network of seven 2 m telescopes we estimate  9.3 CCSNe yr-1
could be found, although this would require more than
1000 h of telescope time allocated to the network.
Within the same radial distance, a
volume-limited search with the future Pan-STARRS
PS1 all-sky survey should uncover 12.5 CCSNe yr-1 in low metallicity
galaxies. Over a period of a a few years this would allow a detailed comparison of their properties. We have also extended our
calculations to determine the total numbers of CCSNe that can potentially be
found in magnitude-limited surveys
with PS1 (24 000 yr-1, within
9.3 CCSNe yr-1
could be found, although this would require more than
1000 h of telescope time allocated to the network.
Within the same radial distance, a
volume-limited search with the future Pan-STARRS
PS1 all-sky survey should uncover 12.5 CCSNe yr-1 in low metallicity
galaxies. Over a period of a a few years this would allow a detailed comparison of their properties. We have also extended our
calculations to determine the total numbers of CCSNe that can potentially be
found in magnitude-limited surveys
with PS1 (24 000 yr-1, within
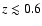 ),
PS4 (69 000 yr-1, within
),
PS4 (69 000 yr-1, within
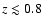 )
and LSST (160 000 yr-1, within
)
and LSST (160 000 yr-1, within
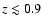 ) surveys.
) surveys.
All considered, a final strategy chosen to searching for CCSNe in low-metallicity environments shall realistically involve both a volume-limited and a magnitude-limited all-sky survey in order to include a volume-limited galaxy sample with which to accurately determine relative SN rates and have some prior knowledge of the host galaxy characteristics, but yet not exclude the potential of detecting rare CCSN events that would have otherwise been missed had we only considered the volume-limited survey strategy.
With the huge number of CCSNe predicted to be detected, these all-sky surveys are set to serve as a catalyst concerning our understanding of CCSNe; including their varying characteristics with metallicity, the relative rates of the various types of SNe and of extremely rare events similar to SN 2006jc, SN 2006gy and more than likely events the nature of which have not yet been observed.
Acknowledgements
Funding for the Sloan Digital Sky Survey (SDSS) and SDSS-II has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, the U.S. Department of Energy, the National Aeronautics and Space Administration, the Japanese Monbukagakusho, and the Max Planck Society, and the Higher Education Funding Council for England. The SDSS Web site is http://www.sdss.org/
The SDSS is managed by the Astrophysical Research Consortium (ARC) for the Participating Institutions. The Participating Institutions are the American Museum of Natural History, Astrophysical Institute Potsdam, University of Basel, University of Cambridge, Case Western Reserve University, The University of Chicago, Drexel University, Fermilab, the Institute for Advanced Study, the Japan Participation Group, The Johns Hopkins University, the Joint Institute for Nuclear Astrophysics, the Kavli Institute for Particle Astrophysics and Cosmology, the Korean Scientist Group, the Chinese Academy of Sciences (LAMOST), Los Alamos National Laboratory, the Max-Planck-Institute for Astronomy (MPIA), the Max-Planck-Institute for Astrophysics (MPA), New Mexico State University, Ohio State University, University of Pittsburgh, University of Portsmouth, Princeton University, the United States Naval Observatory, and the University of Washington.
This research has made use of the CfA Supernova Archive, which is funded in part by the National Science Foundation through grant AST 0606772.
This work, conducted as part of the award ``Understanding the lives of
massive stars from birth to supernovae'' (S.J. Smartt) made under the
European Heads of Research Councils and European Science Foundation
EURYI (European Young Investigator) Awards scheme, was supported by
funds from the Participating Organisations of EURYI and the EC Sixth
Framework Programme. S.J.S. and D.R.Y. thank the Leverhulme Trust and
DEL for funding. S.M. acknowledges financial support from the Academy of Finland, project 8120503.
- Adelman-McCarthy,
J. K., & for the SDSS Collaboration 2007, in press
[arXiv:0707.3380]
(In the text)
- Alard, C., &
Lupton, R. H. 1998, ApJ, 503, 325 [NASA ADS] [CrossRef]
(In the text)
- Aldering, G., Adam,
G., Antilogus, P., et al. 2002, in Survey and Other Telescope
Technologies and Discoveries, ed. J. A. Tyson, &
S. Wolff, Proc. SPIE, 4836, 61
(In the text)
- Astier, P.,
Guy, J., Regnault, N., et al. 2006, A&A, 447, 31 [NASA ADS] [CrossRef] [EDP Sciences]
- Baron, E., Branch, D.,
Hauschildt, P. H., et al. 2000, ApJ, 545, 444 [NASA ADS] [CrossRef]
- Belokurov, V. A.,
& Evans, N. W. 2003, MNRAS, 341, 569 [NASA ADS] [CrossRef]
(In the text)
- Bissaldi, E., Calura,
F., Matteucci, F., Longo, F., & Barbiellini, G. 2007, in press
[arXiv:astro-ph/0702652]
- Blanton, M. R.,
& Roweis, S. 2007, AJ, 133, 734 [NASA ADS] [CrossRef]
(In the text)
- Blondin, S., &
Tonry, J. L. 2007, ApJ, 666, 1024 [NASA ADS] [CrossRef]
- Bloom, J. S.,
Kulkarni, S. R., Djorgovski, S. G., et al. 1999,
Nature, 401, 453 [NASA ADS] [CrossRef]
- Botticella,
M. T., Riello, M., Cappellaro, E., et al. 2008, A&A,
479, 49 [NASA ADS] [CrossRef] [EDP Sciences]
- Bresolin, F. 2006,
ArXiv Astrophysics e-prints
- Brinchmann, J.,
Charlot, S., White, S. D. M., et al. 2004, MNRAS,
351, 1151 [NASA ADS] [CrossRef]
(In the text)
- Cantiello, M.,
Yoon, S.-C., Langer, N., & Livio, M. 2007, A&A, 465,
L29 [NASA ADS] [CrossRef] [EDP Sciences]
- Cappellaro, E.,
Barbon, R., & Turatto, M. 2003, in press
[arXiv:astro-ph/0310859]
(In the text)
- Cardelli, J. A.,
Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345,
245 [NASA ADS] [CrossRef]
(In the text)
- Chambers, K. C.,
& Denneau, L. J. 2007
(In the text)
- Charlot, S., &
Longhetti, M. 2001, MNRAS, 323, 887 [NASA ADS] [CrossRef]
(In the text)
- Copin, Y., Blanc, N.,
Bongard, S., et al. 2006, New Astron. Rev., 50, 436 [NASA ADS] [CrossRef]
(In the text)
- Dainotti,
M. G., Bernardini, M. G., Bianco, C. L., et al.
2007, A&A, 471, L29 [NASA ADS] [CrossRef] [EDP Sciences]
- Della Valle,
M., Malesani, D., Benetti, S., et al. 2003, A&A, 406,
L33 [NASA ADS] [CrossRef] [EDP Sciences]
- Detmers, R. G.,
Langer, N., Podsiadlowski, P., & Izzard, R. G. 2008,
ArXive-prints, 804
- Di Carlo, E., Massi,
F., Valentini, G., et al. 2002, ApJ, 573, 144 [NASA ADS] [CrossRef]
(In the text)
- Fassia, A., Meikle,
W. P. S., Vacca, W. D., et al. 2000, MNRAS,
318, 1093 [NASA ADS] [CrossRef]
(In the text)
- Filippenko, A. V.
2003, in From Twilight to Highlight: the Physics of Supernovae, ed.
W. Hillebrandt, & B. Leibundgut, 171
- Filippenko,
A. V., Li, W. D., Treffers, R. R., & Modjaz, M.
2001, in ASP Conf. Ser. 246, IAU Colloq. 183: Small Telescope
Astronomy on Global Scales, ed. B. Paczynski, W.-P. Chen,
& C. Lemme, 121
(In the text)
- Foley, R. J.,
Papenkova, M. S., Swift, B. J., et al. 2003, PASP,
115, 1220 [NASA ADS] [CrossRef]
(In the text)
- Fransson, C., Challis,
P. M., Chevalier, R. A., et al. 2005, ApJ, 622,
991 [NASA ADS] [CrossRef]
- Frieman, J. A.,
Bassett, B., Becker, A., et al. 2008, AJ, 135, 338 [NASA ADS] [CrossRef]
- Fruchter, A. S.,
Levan, A. J., Strolger, L., et al. 2006, Nature, 441,
463 [NASA ADS] [CrossRef]
- Fynbo,
J. P. U., Jakobsson, P., Möller, P., et al.
2003, A&A, 406, L63 [NASA ADS] [CrossRef] [EDP Sciences]
- Gal-Yam, A., Ofek,
E. O., & Shemmer, O. 2002, MNRAS, 332, L73 [NASA ADS] [CrossRef]
(In the text)
- Galama, T. J.,
Vreeswijk, P. M., van Paradijs, J., et al. 1998, Nature,
395, 670 [NASA ADS] [CrossRef]
- Galama, T. J.,
Tanvir, N., Vreeswijk, P. M., et al. 2000, ApJ, 536,
185 [NASA ADS] [CrossRef]
- Garnavich, P. M.
2006, Journal of the American Association of Variable Star
Observers (JAAVSO), 35, 42 [NASA ADS]
(In the text)
- Hamuy, M. 2003, ArXiv
Astrophysics e-prints
- Hamuy, M., Pinto,
P. A., Maza, J., et al. 2001, ApJ, 558, 615 [NASA ADS] [CrossRef]
(In the text)
- Heger, A. &
Woosley, S. E. 2002, ApJ, 567, 532 [NASA ADS] [CrossRef]
(In the text)
- Hirschi, R., Meynet,
G., & Maeder, A. 2006, ArXiv Astrophysics e-prints
- Hjorth, J., Sollerman,
J., Møller, P., et al. 2003, Nature, 423, 847 [NASA ADS] [CrossRef]
- Ho,
W. C. G., Van Dyk, S. D., Peng, C. Y.,
et al. 2001, PASP, 113, 1349 [NASA ADS] [CrossRef]
(In the text)
- Hogg, D. W.,
Baldry, I. K., Blanton, M. R., & Eisenstein,
D. J. 2002, in press [arXiv:astro-ph/0210394]
- Hopkins, A. M.,
Miller, C. J., Nichol, R. C., et al. 2003, ApJ, 599,
971 [NASA ADS] [CrossRef]
(In the text)
- Izotov,
Y. I., Stasinska, G., Meynet, G., Guseva, N. G., &
Thuan, T. X. 2006, A&A, 448, 955 [NASA ADS] [CrossRef] [EDP Sciences]
- Kauffmann, G.,
Heckman, T. M., Tremonti, C., et al. 2003, MNRAS, 346,
1055 [NASA ADS] [CrossRef]
(In the text)
- Kennicutt, Jr.,
R. C. 1998, ARA&A, 36, 189 [NASA ADS] [CrossRef]
- Kennicutt, Jr.,
R. C., Bresolin, F., & Garnett, D. R. 2003, ApJ, 591,
801 [NASA ADS] [CrossRef]
(In the text)
- Kewley, L. J.,
& Dopita, M. A. 2002, ApJS, 142, 35 [NASA ADS] [CrossRef]
(In the text)
- Kewley, L. J.,
& Ellison, S. L. 2008, ArXiv e-prints, 801
(In the text)
- Langer, N., Norman,
C. A., de Koter, A., et al. 2007, in press
[arXiv:0708.1970]
- Leonard, D. C.,
Filippenko, A. V., Ardila, D. R., & Brotherton,
M. S. 2001, ApJ, 553, 861 [NASA ADS] [CrossRef]
- Levan, A., Nugent, P.,
Fruchter, A., et al. 2005, ApJ, 624, 880 [NASA ADS] [CrossRef]
- Liu, Q.-Z., Hu,
J.-Y., Hang, H.-R., et al. 2000, A&AS, 144, 219 [NASA ADS] [CrossRef] [EDP Sciences]
- Maeder, A.
1987, A&A, 178, 159 [NASA ADS]
- Matheson, T.,
Filippenko, A. V., Li, W., Leonard, D. C., & Shields,
J. C. 2001, AJ, 121, 1648 [NASA ADS] [CrossRef]
(In the text)
- Mattila, S., &
Meikle, W. P. S. 2001, MNRAS, 324, 325 [NASA ADS] [CrossRef]
(In the text)
- Miknaitis, G.,
Pignata, G., Rest, A., et al. 2007, ApJ, 666, 674 [NASA ADS] [CrossRef]
(In the text)
- Modjaz, M., Kewley,
L., Kirshner, R. P., et al. 2008, AJ, 135, 1136 [NASA ADS] [CrossRef]
(In the text)
- Moss, C., &
Whittle, M. 2005, MNRAS, 357, 1337 [NASA ADS] [CrossRef]
(In the text)
- Moustakas, J.,
Kennicutt, Jr., R. C., & Tremonti, C. A. 2006, ApJ,
642, 775 [NASA ADS] [CrossRef]
(In the text)
- Ofek, E. O.,
Cameron, P. B., Kasliwal, M. M., et al. 2007, ApJ,
659, L13 [NASA ADS] [CrossRef]
- Oke, J. B., &
Sandage, A. 1968, ApJ, 154, 21 [NASA ADS] [CrossRef]
- Oke, J. B., &
Gunn, J. E. 1983, ApJ, 266, 713 [NASA ADS] [CrossRef]
(In the text)
- Pastorello, A.,
Smartt, S. J., Mattila, S., et al. 2007, Nature, 447,
829 [NASA ADS] [CrossRef]
(In the text)
- Patat, F., Cappellaro,
E., Danziger, J., et al. 2001, ApJ, 555, 900 [NASA ADS] [CrossRef]
(In the text)
- Perryman,
M. A. C. 2005, in Astrometry in the Age of the Next
Generation of Large Telescopes, ed. P. K. Seidelmann, &
A. K. B. Monet, ASP Conf. Ser., 338, 3
(In the text)
- Pettini, M., &
Pagel, B. E. J. 2004, MNRAS, 348, L59 [NASA ADS] [CrossRef]
(In the text)
- Pozzo, M., Meikle,
W. P. S., Fassia, A., et al. 2004, MNRAS, 352,
457 [NASA ADS] [CrossRef]
- Prieto, J. L.,
Stanek, K. Z., & Beacom, J. F. 2008, ApJ, 673,
999 [NASA ADS] [CrossRef]
(In the text)
- Pritchet, C. J.,
& The SNLS Collaboration 2005, in Observing Dark Energy, ed.
S. C. Wolff, & T. R. Lauer, ASP Conf. Ser., 339,
60
- Quimby, R. 2006,
Central Bureau Electronic Telegrams, 644, 1 [NASA ADS]
- Quimby, R., Mondol,
P., Hoeflich, P., et al. 2005a, Central Bureau Electronic
Telegrams, 116, 1 [NASA ADS]
(In the text)
- Quimby, R. M.,
Castro, F., Gerardy, C. L., et al. 2005b, BAAS, 37,
1431 [NASA ADS]
- Quimby, R., Castro,
F., Mondol, P., Caldwell, J., & Terrazas, E. 2007a, Central
Bureau Electronic Telegrams, 793, 1 [NASA ADS]
- Quimby, R. M.,
Aldering, G., Wheeler, J. C., et al. 2007b, ApJ, 668,
L99 [NASA ADS] [CrossRef]
(In the text)
- Richardson, D.,
Branch, D., Casebeer, D., et al. 2002, AJ, 123, 745 [NASA ADS] [CrossRef]
(In the text)
- Riello, M., &
Patat, F. 2005, MNRAS, 362, 671 [NASA ADS] [CrossRef]
(In the text)
- Sako, M., Bassett, B.,
Becker, A., et al. 2008, AJ, 135, 348 [NASA ADS] [CrossRef]
- Salpeter, E. E.
1955, ApJ, 121, 161 [NASA ADS] [CrossRef]
(In the text)
- Scannapieco, E. 2006,
in press [arXiv:astro-ph/0609208]
(In the text)
- Schiminovich, D.,
Ilbert, O., Arnouts, S., et al. 2005, ApJ, 619, L47 [NASA ADS] [CrossRef]
(In the text)
- Schlegel, D. J.,
Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef]
(In the text)
- Schmidt, B. P.,
Kirshner, R. P., Eastman, R. G., et al. 1994, ApJ,
432, 42 [NASA ADS] [CrossRef]
(In the text)
- Smartt,
S. J., Eldridge, J. J., Crockett, R. M., &
Mound, J. R. 2008, MNRAS, submitted
(In the text)
- Smith, N., Chornock,
R., Li, W., et al. 2008, ArXiv e-prints, 804
- Smith, N., Li, W.,
Foley, R. J., et al. 2006, in press
[arXiv:astro-ph/0612617]
(In the text)
- Sollerman, J.,
Östlin, G., Fynbo, J. P. U., et al. 2005, New
Astron., 11, 103 [NASA ADS] [CrossRef]
(In the text)
- Stanek, K. Z.,
Gnedin, O. Y., Beacom, J. F., et al. 2006, Acta
Astron., 56, 333 [NASA ADS]
- Stanek, K. Z.,
Matheson, T., Garnavich, P. M., et al. 2003, ApJ, 591,
L17 [NASA ADS] [CrossRef]
- Stasinska, G.
2005, A&A, 434, 507 [NASA ADS] [CrossRef] [EDP Sciences]
- Takeuchi,
T. T., Buat, V., & Burgarella, D. 2005, A&A, 440,
L17 [NASA ADS] [CrossRef] [EDP Sciences]
- Tanvir, N. R.,
Barnard, V. E., Blain, A. W., et al. 2004, MNRAS,
352, 1073 [NASA ADS] [CrossRef]
- Tchekhovskoy, A.,
McKinney, J. C., & Narayan, R. 2008, ArXiv e-prints,
803
- Tremonti, C. A.,
Heckman, T. M., Kauffmann, G., et al. 2004, ApJ, 613,
898 [NASA ADS] [CrossRef]
(In the text)
- Vink,
J. S., & de Koter, A. 2005, A&A, 442, 587 [NASA ADS] [CrossRef] [EDP Sciences]
- Woosley, S. E.
1993, ApJ, 405, 273 [NASA ADS] [CrossRef]
(In the text)
- Woosley,
S. E., & MacFadyen, A. I. 1999, A&AS, 138,
499 [NASA ADS] [CrossRef] [EDP Sciences]
- Woosley,
S. E., & Bloom, J. S. 2006, ARA&A, 44, 507 [NASA ADS] [CrossRef]
- Woosley, S. E.,
& Heger, A. 2006, ApJ, 637, 914 [NASA ADS] [CrossRef]
- Woosley, S. E.,
Blinnikov, S., & Heger, A. 2007, Nature, 450, 390 [NASA ADS] [CrossRef]
- Yoon, S., Langer, N.,
Cantiello, M., Woosley, S. E., & Glatzmaier, G. A.
2008, ArXiv e-prints, 801
- Yoon, S.-C., &
Langer, N. 2006, in Stellar Evolution at Low Metallicity: mass
Loss, Explosions, Cosmology, ed. H. J. G. L. M.
Lamers, N. Langer, T. Nugis, & K. Annuk, ASP
Conf. Ser., 353, 63
- Yoon, S.-C.,
Langer, N., & Norman, C. 2006, A&A, 460, 199 [NASA ADS] [CrossRef] [EDP Sciences]
- Yuan, F., Akerlof, C.,
Quimby, R., et al. 2007, in American Astronomical Society
Meeting Abstracts, 211, 105.05
- Zeh, A., Klose, S.,
& Hartmann, D. H. 2004, ApJ, 609, 952 [NASA ADS] [CrossRef]
Copyright ESO 2008
![\begin{displaymath}\log\left(\frac{[\rm {OIII}]\lambda5007}{\rm {H}\beta}\right)...
...ac{0.61}{\log([\rm {NII}]\lambda6584/\rm {H}\alpha)-0.05}+1.3
\end{displaymath}](/articles/aa/full/2008/37/aa8662-07/img29.gif)
![\begin{figure}
\par\includegraphics[totalheight=0.2\textheight]{8662fig1.eps}
\end{figure}](/articles/aa/full/2008/37/aa8662-07/Timg31.gif)
![\begin{figure}
\par\includegraphics[totalheight=0.2\textheight]{8662fig2.ps}
\end{figure}](/articles/aa/full/2008/37/aa8662-07/Timg32.gif)
![\begin{displaymath}12+\log(\rm {O/H})=8.73-0.32\log\left(\frac{[\rm {OIII}]\lamb...
...07/\rm {H}\beta}{[\rm {NII}]\lambda6584/\rm {H}\alpha}\right),
\end{displaymath}](/articles/aa/full/2008/37/aa8662-07/img34.gif)
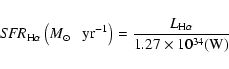
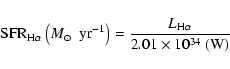
![$\displaystyle {{\it SFR}_{\rm H\alpha}}\left({M}_{\odot}{\rm ~~yr^{-1}}\right)=...
...beta}}{2.86}\right]^{2.114}\frac{L_{{\rm H}\alpha}}{1.27\times10^{34}({\rm W})}$](/articles/aa/full/2008/37/aa8662-07/img46.gif)
![$\displaystyle {{\it SFR}_{\rm H\alpha}}\left({M}_{\odot}{\rm ~~yr^{-1}}\right)=...
...}{2.86}\right]^{2.114}\frac{L_{{\rm H}\alpha}}{2.01\times10^{34}({\rm W})}\cdot$](/articles/aa/full/2008/37/aa8662-07/img47.gif)
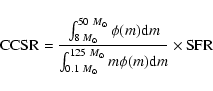
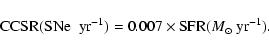
![\begin{figure}
\par\includegraphics[totalheight=0.2\textheight]{8662fig3.ps}
\end{figure}](/articles/aa/full/2008/37/aa8662-07/Timg54.gif)
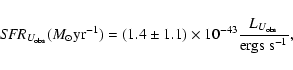
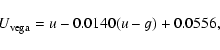
![\begin{figure}
\par\includegraphics[totalheight=0.3\textheight]{8662fig4.ps}
\end{figure}](/articles/aa/full/2008/37/aa8662-07/Timg61.gif)
![\begin{figure}
\par\includegraphics[width=12cm,clip]{8662fig5.ps}
\end{figure}](/articles/aa/full/2008/37/aa8662-07/Timg65.gif)
![\begin{figure}
\par\includegraphics[width=12cm,clip]{8662fig6.ps}
\end{figure}](/articles/aa/full/2008/37/aa8662-07/Timg70.gif)
![\begin{figure}
\par\includegraphics[totalheight=0.2\textheight]{8662fig7.ps}
\end{figure}](/articles/aa/full/2008/37/aa8662-07/Timg80.gif)
![\begin{figure}
\par\includegraphics[totalheight=0.2\textheight]{8662fig8.ps}
\end{figure}](/articles/aa/full/2008/37/aa8662-07/Timg85.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{8662fig9.ps}
\end{figure}](/articles/aa/full/2008/37/aa8662-07/Timg86.gif)
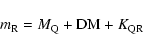
![$\displaystyle K_{\rm QR}= -2.5{\rm log}_{10} \left[\frac{1}{[1+z]}\phantom{\fra...
...ambda}([1+z]\lambda_{\rm em})Q(\lambda_{\rm em}){\rm d}\lambda_{\rm em}}\right]$](/articles/aa/full/2008/37/aa8662-07/img91.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{8662fig10.eps}
\end{figure}](/articles/aa/full/2008/37/aa8662-07/Timg100.gif)
![\begin{figure}
\par\includegraphics[width=9cm,clip]{8662fig11.ps}
\end{figure}](/articles/aa/full/2008/37/aa8662-07/Timg101.gif)