|
Polarisation |
General expression for |
Approximation for |
| T=0 |
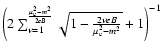 |
|
|
|
|
|
|
|
|
eB/(2mT) for |
|
|
|
... |
|
Polarisation |
General expression for |
Approximation for |
| T=0 |
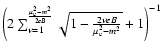 |
|
|
|
|
|
|
|
|
eB/(2mT) for |
|
|
|
... |