A&A 489, 207-216 (2008)
DOI: 10.1051/0004-6361:20078431
The photon dominated region in the IC 348 molecular cloud
K. Sun1 - V. Ossenkopf1,2 - C. Kramer1 - B. Mookerjea3 - M. Röllig4 - M. Cubick1 - J. Stutzki1
1 - I. Physikalisches Institut, Universität zu Köln, Zülpicher Straße 77, 50937 Köln, Germany
2 - SRON Netherlands Institut for Space Research, PO Box 800, 9700 AV Groningen, The Netherlands
3 - Department of Astronomy & Astrophysics, Tata Institute of Fundamental Research, Homi Bhabha Road, Mumbai 400 005, India
4 -
Argelander-Institut für Astronomie, Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
Received 7 August 2007 / Accepted 17 July 2008
Abstract
Aims. In this paper we discuss the physical conditions of clumpy nature in the IC 348 molecular cloud. We show that the millimeter and sub-millimeter line emission from the IC 348 molecular cloud can be modelled as originating from a photon dominated region (PDR).
Methods. We combine new observations of fully sampled maps in [C I] at 492 GHz and 12CO 4-3, taken with the KOSMA 3 m telescope at about 1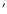 resolution, with FCRAO data of 12CO 1-0, 13CO 1-0 and far-infrared continuum data observed by HIRES/IRAS. To derive the physical parameters of the region we analyze the line ratios of [C I] 3P1-3P
0/12CO 4-3, [C I]3P1-3P
0/13CO 1-0, and 12CO 4-3/12CO 1-0. A first rough estimate of abundance is obtained from an LTE analysis. To understand the [C I] and CO emission from the PDRs in IC 348, we use a clumpy PDR model. With an ensemble of identical clumps, we constrain the total mass from the observed absolute intensities. Then we apply a more realistic clump distribution model with a power law index of 1.8 for clump-mass spectrum and a power law index of 2.3 for mass-size relation.
resolution, with FCRAO data of 12CO 1-0, 13CO 1-0 and far-infrared continuum data observed by HIRES/IRAS. To derive the physical parameters of the region we analyze the line ratios of [C I] 3P1-3P
0/12CO 4-3, [C I]3P1-3P
0/13CO 1-0, and 12CO 4-3/12CO 1-0. A first rough estimate of abundance is obtained from an LTE analysis. To understand the [C I] and CO emission from the PDRs in IC 348, we use a clumpy PDR model. With an ensemble of identical clumps, we constrain the total mass from the observed absolute intensities. Then we apply a more realistic clump distribution model with a power law index of 1.8 for clump-mass spectrum and a power law index of 2.3 for mass-size relation.
Results. We provide detailed fits to observations at seven representative positions in the cloud, revealing clump densities between
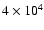 cm-3 and
cm-3 and
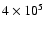 cm-3 and C/CO column density ratios between 0.02 and 0.26. The derived FUV flux from the model fit is consistent with the field calculated from FIR continuum data, varying between 2 and 100 Draine units across the cloud. We find that both an ensemble of identical clumps and an ensemble with a power law clump mass distribution produce line intensities which are in good agreement (within a factor
cm-3 and C/CO column density ratios between 0.02 and 0.26. The derived FUV flux from the model fit is consistent with the field calculated from FIR continuum data, varying between 2 and 100 Draine units across the cloud. We find that both an ensemble of identical clumps and an ensemble with a power law clump mass distribution produce line intensities which are in good agreement (within a factor 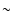 2) with the observed intensities. The models confirm the anti-correlation between the C/CO abundance ratio and the hydrogen column density found in many regions.
2) with the observed intensities. The models confirm the anti-correlation between the C/CO abundance ratio and the hydrogen column density found in many regions.
Key words: ISM: clouds - ISM: dust, extinction - ISM: structure - ISM: individual objects: IC 348
Photon Dominated Regions (PDRs) are surfaces of molecular clouds
where chemistry and heating are regulated by far-ultraviolet (FUV)
photons (6.0 eV <
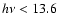 eV) (Hollenbach & Tielens 1999). Gas cooling
happens mainly via the fine structure lines of [O I],
[C II], [C I] and the rotational lines of CO
(Kaufman et al. 1999). The form of carbon changes with increasing depth
from the surface of the PDR from C+ through C0 to CO.
Therefore emission from [C II], [C I] and the
rotational lines of CO can be used as probes of temperature,
density and column density in the PDRs (Mookerjea et al. 2006; Kramer et al. 2004). In
particular, the two fine structure lines of neutral atomic carbon
at 492 and 809 GHz give information on intermediate regions
between atomic and molecular gas, since they trace both physical
regimes. Initial homogeneous plane-parallel steady-state models of
PDRs predicted that PDRs are confined to the FUV irradiated
surfaces of molecular clouds. However, observations detected
widespread [C II] and [C I] emission, thus
suggesting that PDR surfaces are formed deeply inside the
molecular clouds. One possible explanation is in terms of the
clumpiness of the molecular clouds which allows for deeper
penetration of FUV radiation so that PDRs are formed at the
surfaces of the clumps present throughout the molecular cloud
(Mookerjea et al. 2006; Howe et al. 1991; Stutzki et al. 1988). In addition, an explanation has
also been proposed in terms of the dynamics of the ISM: a. clouds
are suddenly shielded from FUV fields (Störzer et al. 1997); b.
time-dependent chemistry of the PDRs (Oka et al. 2004).
eV) (Hollenbach & Tielens 1999). Gas cooling
happens mainly via the fine structure lines of [O I],
[C II], [C I] and the rotational lines of CO
(Kaufman et al. 1999). The form of carbon changes with increasing depth
from the surface of the PDR from C+ through C0 to CO.
Therefore emission from [C II], [C I] and the
rotational lines of CO can be used as probes of temperature,
density and column density in the PDRs (Mookerjea et al. 2006; Kramer et al. 2004). In
particular, the two fine structure lines of neutral atomic carbon
at 492 and 809 GHz give information on intermediate regions
between atomic and molecular gas, since they trace both physical
regimes. Initial homogeneous plane-parallel steady-state models of
PDRs predicted that PDRs are confined to the FUV irradiated
surfaces of molecular clouds. However, observations detected
widespread [C II] and [C I] emission, thus
suggesting that PDR surfaces are formed deeply inside the
molecular clouds. One possible explanation is in terms of the
clumpiness of the molecular clouds which allows for deeper
penetration of FUV radiation so that PDRs are formed at the
surfaces of the clumps present throughout the molecular cloud
(Mookerjea et al. 2006; Howe et al. 1991; Stutzki et al. 1988). In addition, an explanation has
also been proposed in terms of the dynamics of the ISM: a. clouds
are suddenly shielded from FUV fields (Störzer et al. 1997); b.
time-dependent chemistry of the PDRs (Oka et al. 2004).
IC 348 is a young open cluster northeast of the Perseus cloud at
a distance of 316 pc (Herbig 1998). The IC 348 cluster has about
300 stellar members, with spectral types from B5 to late M, as
found from observations in X-rays (Preibisch & Zinnecker 2001; Preibisch et al. 1996),
near-infrared (Luhman et al. 1998,2005; Najita et al. 2000; Lada & Lada 1995), and optical
(Herbig 1998; Luhman et al. 2003). Lada et al. (2006) constructed
optical-infrared spectral energy distributions (SEDs) for all
known members of the cluster by combining the Spitzer Space
Telescope and ground-based observations. The IC 348 molecular
cloud prominently shows up in the CO 3-2 survey of the Perseus
molecular cloud complex (Sun et al. 2006). The FUV radiation of its
youngest member, HD 281159, a B 5 V star, heats the surrounding
gas and dust. Surveys for molecular outflows revealed so far four
bipolar outflows powered by deeply embedded young sources
(Tafalla et al. 2006; Eislöffel et al. 2003). Jørgensen et al. (2007) estimated the current star
formation efficiency of 10%-15% for the whole Perseus cloud
using Spitzer mid-infrared data and SCUBA sub-millimeter maps.
Sun et al. (2006) observed IC 348 in four low-J CO transitions
as part of their 7.1 square degree survey of the entire Perseus
molecular cloud and quantified the spatial structure of the
emission in terms of its power spectrum, applying the
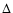 -variance method (Stutzki et al. 1998) to the integrated
intensity maps. The
-variance method (Stutzki et al. 1998) to the integrated
intensity maps. The 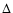 -variance spectra of the overall
region was found to follow a power law with an index of
-variance spectra of the overall
region was found to follow a power law with an index of
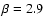 -3.0; while sub-regions of Perseus gave different power
spectral indices. The active star forming regions showed higher
indices typical for large condensations; lower indices were
derived for dark clouds, representing more filamentary structure.
IC 348 as an exception, showed a rather filamentary structure
corresponding to the smallest value of
-3.0; while sub-regions of Perseus gave different power
spectral indices. The active star forming regions showed higher
indices typical for large condensations; lower indices were
derived for dark clouds, representing more filamentary structure.
IC 348 as an exception, showed a rather filamentary structure
corresponding to the smallest value of
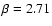 in 13CO 2-1.
in 13CO 2-1.
In this paper we present large-scale (
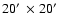 )
fully-sampled maps of the [C I] 3P1-3P0 (hereafter [C I]) and 12CO 4-3 emission from the IC 348 molecular cloud. At a common resolution of 70
)
fully-sampled maps of the [C I] 3P1-3P0 (hereafter [C I]) and 12CO 4-3 emission from the IC 348 molecular cloud. At a common resolution of 70
 ,
we have combined our data with the 12CO 1-0, 13CO 1-0 data from the Five College Radio Astronomy Observatory (FCRAO) (Ridge et al. 2003), and the far-infrared (FIR) continuum data from HIRES/IRAS. The goal of the analysis is to understand the extent to which the observed line emission from IC 348 can be understood in the framework of a photon dominated region.
,
we have combined our data with the 12CO 1-0, 13CO 1-0 data from the Five College Radio Astronomy Observatory (FCRAO) (Ridge et al. 2003), and the far-infrared (FIR) continuum data from HIRES/IRAS. The goal of the analysis is to understand the extent to which the observed line emission from IC 348 can be understood in the framework of a photon dominated region.
Section 2 describes the KOSMA observations and the complementary datasets used for analysis. Section 3 discusses the general observational results. A Local Thermodynamic
Equilibrium (LTE) analysis of the observed line intensities is presented in Sect. 4. A comparison with clumpy PDR models is presented in Sect. 5.
Section 6 summarizes the results.
![\begin{figure}
\par\mbox{\includegraphics[angle=-90,width=6cm,clip]{8341_1.eps}\...
...8341_2.eps}\includegraphics[angle=-90,width=6cm,clip]{8341_3.eps} }
\end{figure}](/articles/aa/full/2008/37/aa8431-07/Timg29.gif) |
Figure 1:
Velocity integrated intensities of [C I] emission (color) overlayed with contours of a) 12CO 4-3, b) 12CO 1-0 and c) 13CO 1-0
integrated intensities at a common angular resolution of 70
 .
The center of the maps is at .
The center of the maps is at
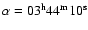 , ,
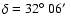 (J2000). All tracers are integrated from
(J2000). All tracers are integrated from
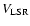 2 km s-1 to 14 km s-1. Contours range between 20% to 90% with a step of 10% of the peak intensities that are 73 K km s-1 for 12CO 4-3, 72 K km s-1 for 12CO 1-0 and 31 K km s-1 for 13CO 1-0. The seven filled triangles indicates the positions where we carry out a detailed PDR analysis later. The open pentacle symbol denotes the position of HD 281159.
2 km s-1 to 14 km s-1. Contours range between 20% to 90% with a step of 10% of the peak intensities that are 73 K km s-1 for 12CO 4-3, 72 K km s-1 for 12CO 1-0 and 31 K km s-1 for 13CO 1-0. The seven filled triangles indicates the positions where we carry out a detailed PDR analysis later. The open pentacle symbol denotes the position of HD 281159. |
| Open with DEXTER |
2 Datasets
We have used the Kölner Observatorium für Sub-Millimeter
Astronomie (KOSMA) 3-m sub-millimeter telescope on Gornergrat,
Switzerland (Kramer et al. 1998a; Winnewisser et al. 1986) to observe the emission of the
fine structure line of neutral carbon at 492 GHz and 12CO
4-3 at 461 GHz. We have used the Sub-Millimeter Array Receiver
for Two frequencies (SMART) on KOSMA for these observations
(Graf et al. 2002). SMART is an eight-pixel dual-frequency SIS-heterodyne receiver capable of observing in the 650 and 350 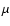 m atmospheric windows (Graf et al. 2002). The IF signals were
analyzed with two
m atmospheric windows (Graf et al. 2002). The IF signals were
analyzed with two 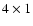 GHz array-acousto-optical spectrometers with a spectral resolution of 1.5 MHz (Horn et al. 1999). The typical double side band receiver noise temperature at 492 GHz is about 150 K. The observations were performed in position-switched On-The-Fly (OTF) between December 2004 and February 2005. Owing to technical difficulties the higher frequency channel of SMART could not be used at the time of these observations.
GHz array-acousto-optical spectrometers with a spectral resolution of 1.5 MHz (Horn et al. 1999). The typical double side band receiver noise temperature at 492 GHz is about 150 K. The observations were performed in position-switched On-The-Fly (OTF) between December 2004 and February 2005. Owing to technical difficulties the higher frequency channel of SMART could not be used at the time of these observations.
We observed a fully sampled map of the IC 348 molecular cloud
centered at
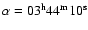 ,
,
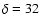 $^$06
$^$06 (J2000), extending over
(J2000), extending over
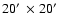 .
For the observations, we used the position-switched
on-the-fly (OTF) mode (Beuther et al. 2000) with a sampling of 29
.
For the observations, we used the position-switched
on-the-fly (OTF) mode (Beuther et al. 2000) with a sampling of 29
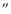 .
The emission-free off position was selected from the 13CO
1-0 FCRAO map, which is (-8
.
The emission-free off position was selected from the 13CO
1-0 FCRAO map, which is (-8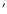 ,
10
,
10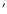 )
relative to the map
center. We estimate the pointing accuracy to be better than
10
)
relative to the map
center. We estimate the pointing accuracy to be better than
10
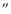 .
The half power beam width (HPBW) and the main beam
efficiency (
.
The half power beam width (HPBW) and the main beam
efficiency (
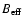 )
were derived from continuum scans of
the Sun and the Jupiter. The HPBW at both frequencies is 60
)
were derived from continuum scans of
the Sun and the Jupiter. The HPBW at both frequencies is 60
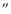 and the main beam efficiency is 50%. The forward efficiency
and the main beam efficiency is 50%. The forward efficiency
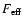 of the telescope is
of the telescope is 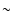 90%. Atmospheric
calibration was done by measuring the atmospheric emission at the
OFF-position and using a standard atmospheric model to fit the
opacity taking into account the sideband imbalance
(Cernicharo 1985; Hiyama 1998).
90%. Atmospheric
calibration was done by measuring the atmospheric emission at the
OFF-position and using a standard atmospheric model to fit the
opacity taking into account the sideband imbalance
(Cernicharo 1985; Hiyama 1998).
All data presented in this paper are in units of main beam temperature
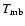 ,
calculated from the observed calibrated antenna temperature
,
calculated from the observed calibrated antenna temperature
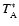 using the
derived beam and forward efficiencies,
using the
derived beam and forward efficiencies,
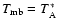 (
(
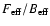 ). Based on observations of reference sources such as W 3 and DR 21 we estimate the accuracy of the absolute intensity calibration to be better than 15%. The data reduction was carried out using the GILDAS
). Based on observations of reference sources such as W 3 and DR 21 we estimate the accuracy of the absolute intensity calibration to be better than 15%. The data reduction was carried out using the GILDAS![[*]](/icons/foot_motif.gif) software package.
software package.
We have used the FCRAO 12CO 1-0 and 13CO 1-0 datasets with an resolution of 46
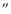 presented by Ridge et al. (2003) for comparison. For comparison, we have smoothed all CO and C I
data to a common resolution of 70
presented by Ridge et al. (2003) for comparison. For comparison, we have smoothed all CO and C I
data to a common resolution of 70
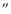 assuming that both the FCRAO and KOSMA telescopes have a Gaussian beam.
assuming that both the FCRAO and KOSMA telescopes have a Gaussian beam.
Further, we have obtained HIRES processed IRAS maps of the dust continuum emission at 60 and 100 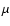 m (Aumann et al. 1990). The dust continuum maps have resolution of 1
m (Aumann et al. 1990). The dust continuum maps have resolution of 1
 5, which is only slightly worse than that of our submillimeter datasets.
5, which is only slightly worse than that of our submillimeter datasets.
3 Observational results
Figure 1 presents maps of integrated intensities of [C I], 12CO 1-0, 13CO 1-0 and 12CO 4-3 observed in IC 348. All maps are integrated over the velocity
range
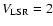 km s-1 to 14 km s-1.
km s-1 to 14 km s-1.
The energy of the upper level for the [C I] 1-0 transition
is 24 K and the critical density for this transition is
103 cm-3 for collisions with molecular H2(Schröder et al. 1991). This implies that [C I] 1-0 is easily
excited and the line is easily detectable even when emitted by
moderate density interstellar gas exposed to the average
interstellar radiation field. Previous observations have found the
[C I] to be extended and well correlated with the low-JCO emission (see a review by Mookerjea et al. 2006; Preibisch et al. 1996; Schneider et al. 2003). In
IC 348 the [C I] emission peaks to the southwest of the
mapped region with a value of 24 K km s-1 and we detect
[C I] emission over a large region with a homogeneous
intensity distribution at a level of 65% of the peak intensity.
The [C I] emission is extended towards the east and
northeast of the mapped region. This is consistent with the
clumpy UV irradiated cloud scenario.
![\begin{figure}
\par\includegraphics[angle=-90,width=17cm,clip]{8341_4.eps}\end{figure}](/articles/aa/full/2008/37/aa8431-07/Timg41.gif) |
Figure 2:
Spectra of the four different tracers on those six positions along the cut from the northern edge of the cloud into the cloud, and on the seventh position at the south of the cloud.
[C I] spectra in all the positions have been multiplied by 3. All panels have the same x axis from 3.5 km s-1 to 14.5 km s-1 and the same y axis from -0.5 K to 30.5 K. |
| Open with DEXTER |
The 12CO 4-3 emission peaks at almost the same position as
[C I] with an intensity of  66 K km s-1.
However, the morphology of the 12CO 4-3 emission is
different to that of [C I]. We find secondary maxima in the
north and a steeper decay of the emission to the south. The
distribution of the 12CO 4-3 emission agrees very well with
that of 12CO 3-2 (Sun et al. 2006). We attribute the
difference in the intensity distributions of [C I] and
12CO 4-3 to the fact that 12CO 4-3 emission arises
from regions of higher temperature and density, while [C I]
emission can arise also from embedded PDR surfaces with moderate
to low density within the molecular clouds.
66 K km s-1.
However, the morphology of the 12CO 4-3 emission is
different to that of [C I]. We find secondary maxima in the
north and a steeper decay of the emission to the south. The
distribution of the 12CO 4-3 emission agrees very well with
that of 12CO 3-2 (Sun et al. 2006). We attribute the
difference in the intensity distributions of [C I] and
12CO 4-3 to the fact that 12CO 4-3 emission arises
from regions of higher temperature and density, while [C I]
emission can arise also from embedded PDR surfaces with moderate
to low density within the molecular clouds.
The distribution of the 12CO 1-0 emission shows the same
global structure as the 12CO 4-3 emission, but it is
considerably more extended. This is consistent with the fact that
12CO 1-0 traces lower temperature and density. The
morphologies of [C I] and 13CO 1-0 appear to be very
similar, implying that they trace the same material and both lines
are effectively column density tracers.
We selected seven positions within IC 348 for a more detailed
study. Six of the seven positions are oriented along a cut from
the northern edge of the cloud, past HD 281159 and into the
clouds. The seventh position is at the southeast edge of the
cloud. Though emission at the seventh position (southern rim) is
weak, it is clearly detected. The selected positions vary in their
physical and chemical conditions. Spectra of [C I],
12CO 4-3, 12CO 1-0 and 13CO 1-0 at those seven
positions are displayed in Fig. 2.
Table 1:
The observed integrated line intensities (in erg s-1 sr-1 cm-2) and line ratios at the seven selected positions. The errors on the integrated intensity are
estimated to be  15%.
15%.
The [C I] emission is centered at a velocity of 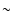 8 km s-1. The lowest [C I] main beam brightness temperature (
8 km s-1. The lowest [C I] main beam brightness temperature (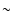 2 K) occurs at the southern rim (9
2 K) occurs at the southern rim (9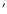 ,
-10
,
-10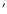 ), while the highest temperatures of 7.0 K and 6.7 K are observed at the position of the [C I] peak (-1
), while the highest temperatures of 7.0 K and 6.7 K are observed at the position of the [C I] peak (-1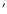 ,
-3
,
-3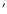 )
and the western rim (-5
)
and the western rim (-5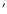 ,
-7
,
-7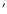 ), respectively. The line widths of [C I] spectra at the seven positions range between 2.0 km s-1 and 2.6 km s-1.
), respectively. The line widths of [C I] spectra at the seven positions range between 2.0 km s-1 and 2.6 km s-1.
The 12CO 4-3 main beam brightness temperature varies between 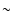 3.6 K at southern rim and 16.4 K at [C I] peak. The line width of the 12CO 4-3 spectra ranges between
2.0 km s-1 and 2.7 km s-1.
3.6 K at southern rim and 16.4 K at [C I] peak. The line width of the 12CO 4-3 spectra ranges between
2.0 km s-1 and 2.7 km s-1.
Both the 12CO 1-0 and 13CO 1-0 spectra consist of two velocity components: one is at 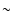 7 km s-1 and the other lies at
7 km s-1 and the other lies at 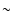 8 km s-1. The two components are most
prominently visible at the southern rim, map center and the [C I] peak. For the 8 km s-1 component at the [C I] peak, the 13CO 1-0 spectrum peaks at the dip of
the 12CO 1-0 spectrum, which may indicate self-absorption effect for this component.
8 km s-1. The two components are most
prominently visible at the southern rim, map center and the [C I] peak. For the 8 km s-1 component at the [C I] peak, the 13CO 1-0 spectrum peaks at the dip of
the 12CO 1-0 spectrum, which may indicate self-absorption effect for this component.
Table 1 presents the integrated intensities and line
ratios at the seven selected positions. Figure 3
shows the variation of the integrated intensities and their ratios
at these seven positions.
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{8431_5.eps} \end{figure}](/articles/aa/full/2008/37/aa8431-07/Timg48.gif) |
Figure 3:
The top panel a) presents the normalized integrated intensities of [C I], 12CO 4-3, 12CO 1-0 and 13CO 1-0 in the seven selected positions. The typical errors of the intensities are about 15%, resulting in errors of the line ratios of about 21%; b) displays integrated line intensity ratios. The x axes of all panels are the relative distance to the northern rim (8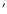 ,
6 ,
6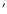 )
position. The southern rim is plotted in a separate box. )
position. The southern rim is plotted in a separate box. |
| Open with DEXTER |
In Fig. 3a we see that the intensities of
[C I], 13CO 1-0 and 12CO 4-3 lines show
similar trends, only the falling off of the intensity of 12CO
4-3 is somewhat less drastic than [C I], 13CO 1-0.
As opposed to the single peak seen in [C I], 13CO 1-0
and 12CO 4-3, the 12CO 1-0 intensity profile shows
two peaks with comparable intensities, one at the northern rim and
the other at the position of the [C I] peak.
Three independent line ratios, i.e., [C I] / 12CO
4-3, [C I] / 13CO 1-0 and 12CO 4-3 / 12CO
1-0, are presented in Table 1 and
Fig. 3b (in erg s-1 sr-1 cm-2).
The largest [C I] / 12CO 4-3 ratio (1.21) occurs at
the southern rim and the second (0.67) and third (0.41) largest
are at the western rim and [C I] peak, while the ratios at
the other four positions are 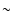 0.25. When comparing with
other star forming regions like W 3 Main, S 106 and Orion A
etc. (see Table 3 by Kramer et al. 2004), the [C I] /
12CO 4-3 ratio at the other five positions are within the
range found in those star forming regions except for the western
and southern rim. The highest ratio at the southern rim is close
to the ratio found at the center of M 51 and the nucleus position
of NGC 4826 (Israel & Baas 2002). The 12CO 4-3 / 12CO 1-0 ratio peaks at [C I] peak and decreases for the positions further away with increasing distance. The [C I] / 13CO 1-0 ratios are rather constant except for the western rim.
0.25. When comparing with
other star forming regions like W 3 Main, S 106 and Orion A
etc. (see Table 3 by Kramer et al. 2004), the [C I] /
12CO 4-3 ratio at the other five positions are within the
range found in those star forming regions except for the western
and southern rim. The highest ratio at the southern rim is close
to the ratio found at the center of M 51 and the nucleus position
of NGC 4826 (Israel & Baas 2002). The 12CO 4-3 / 12CO 1-0 ratio peaks at [C I] peak and decreases for the positions further away with increasing distance. The [C I] / 13CO 1-0 ratios are rather constant except for the western rim.
4 LTE analysis
Figure 4 shows a map of the 12CO 4-3 / 12CO 1-0
line ratio in terms of line integrated temperatures (K km s-1)
overlaid by 12CO 4-3 integrated intensities. The ratio has
its minimum of 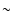 0.3 at the edges of the cloud; ratios of
0.3 at the edges of the cloud; ratios of
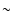 0.9 are found at the 12CO 4-3 peaks; maximum ratios
between 1.1 and 1.5 occur close to HD 281159.
0.9 are found at the 12CO 4-3 peaks; maximum ratios
between 1.1 and 1.5 occur close to HD 281159.
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{8431_6.eps}\end{figure}](/articles/aa/full/2008/37/aa8431-07/Timg49.gif) |
Figure 4:
The color plot represents the 12CO 4-3 / 12CO
1-0 line intensity ratio (in units of K km s-1) observed
in the IC 348 cloud. The contours show the 12CO 4-3 line
intensity spaced at 10% intervals from 20% to 90% relative to
the peak intensity of 73 K km s-1. White pixels in the
figure denote positions where either of the line intensities falls
below the 3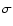 threshold.
threshold. |
| Open with DEXTER |
Table 2:
Results of the LTE analysis. The excitation temperature
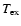 is listed in Col. (2); Col. (3)-(5) present C, CO and H2 column densities; the C/CO ratio is listed in Col. (6). The uncertainties of the column densities are derived
by varying the integrated intensities by
is listed in Col. (2); Col. (3)-(5) present C, CO and H2 column densities; the C/CO ratio is listed in Col. (6). The uncertainties of the column densities are derived
by varying the integrated intensities by 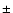 15%.
15%.
For a rough estimate of the column densities and for an easy
comparison to other [C I] studies (e.g. Little et al. 1994; Bensch et al. 2003; Plume et al. 2000) we first apply a Local Thermodynamic
Equilibrium analysis. Assuming LTE and optically thick emission,
the 12CO 4-3 / 12CO 1-0 ratio of 0.3 corresponds to an
excitation temperature
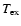 of
of 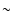 10 K. The ratio
grows to 0.85 for
10 K. The ratio
grows to 0.85 for
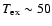 K and remains almost
constant at even higher temperatures. Considering the calibration
uncertainty, we set
K and remains almost
constant at even higher temperatures. Considering the calibration
uncertainty, we set
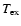 to 50 K in all the positions
where the ratio falls above 0.85. We note that [C I] and
12CO often have different excitation temperatures. However,
N(C)
to 50 K in all the positions
where the ratio falls above 0.85. We note that [C I] and
12CO often have different excitation temperatures. However,
N(C)
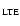 only changes by 20% when the assumed
excitation temperature varies between 20 and 150 K. For the first
order estimation, it is therefore reasonable to use the 12CO
excitation temperature also for [C I]. With the 12CO
excitation temperatures and the assumption of optically thin
[C I] and 13CO 1-0 emission, we then obtain the
column density of C, N(C)
only changes by 20% when the assumed
excitation temperature varies between 20 and 150 K. For the first
order estimation, it is therefore reasonable to use the 12CO
excitation temperature also for [C I]. With the 12CO
excitation temperatures and the assumption of optically thin
[C I] and 13CO 1-0 emission, we then obtain the
column density of C, N(C)
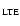 ,
and 13CO,
N(13CO)
,
and 13CO,
N(13CO)
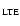 ,
from the integrated line
intensities. Using the relative abundance ratio
[12CO]/[13CO] of 65 (Langer et al. 1990) we translate the
13CO column densities into CO column densities. H2column densities are derived from the [CO]/[H2] abundance
ratio of
,
from the integrated line
intensities. Using the relative abundance ratio
[12CO]/[13CO] of 65 (Langer et al. 1990) we translate the
13CO column densities into CO column densities. H2column densities are derived from the [CO]/[H2] abundance
ratio of
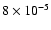 (Frerking et al. 1982). The results are summarized in
Table 2.
(Frerking et al. 1982). The results are summarized in
Table 2.
The resulting map of C/CO column density ratios is presented in
Fig. 5. In most of the cloud, the C/CO ratio falls below
0.1. Higher values (up to 1.5) occur at the rim of the cloud where
the 13CO 1-0 emission is more diffuse. Values as low as 0.02
are found at the southwest of the cloud and along the ridge to the
northeast. As 13CO 1-0 roughly traces the H2 column
density, this plot indicates an anti-correlation between the C/CO
ratio and the H2 column density. This is consistent with the
conclusion of Mookerjea et al. (2006) that the [C I] line is not a
tracer of optical extinction, total H2 column density or
total mass in the beam.
The seven positions, for which we perform a detailed analysis
within the context of a PDR model, exhibit C/CO column density
ratios between about 0.05 and 0.5, i.e. they cover a relatively
wide range (see Table 2). The ratios measured within the
full map cover almost the full range cited so far in the
literature with values as low as 0.03 in parts of G34.3
(Little et al. 1994) and as high as 1.5 seen in the Polaris Flare
(Bensch et al. 2003).
5 PDR modelling
In the next step we attempt to obtain a self-consistent model for
the physical and chemical structure of the cloud matching the
observed C/CO ratios. We will use a clumpy PDR model to
self-consistently compute the abundance of the species and their
excitation determining the line strength. The model is constrained
by the strength of the UV field, which can be independently
estimated, and by the known geometry, provided by the complex,
filamentary, and clumpy structure of the region.
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{8431_7.eps}\end{figure}](/articles/aa/full/2008/37/aa8431-07/Timg85.gif) |
Figure 5:
The C/CO column density ratio overlaid by 13CO 1-0 integrated intensities contours. The contour levels are spaced at 10% intervals from 20% to 90% relative to the peak intensity of 31 K km s-1. White pixels in the figure denote positions where the 13CO 1-0 intensities fall below the 3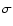 threshold.
threshold. |
| Open with DEXTER |
5.1 FUV intensity
We use HIRES processed 60 and 100 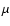 m IRAS data (Aumann et al. 1990)
to generate a far-infrared intensity map
m IRAS data (Aumann et al. 1990)
to generate a far-infrared intensity map
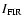 in
IC 348. It represents the far-infrared intensity between
42.5
in
IC 348. It represents the far-infrared intensity between
42.5 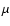 m and 122.5
m and 122.5 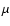 m as measured by the filter curves of
the two IRAS data sets (Nakagawa et al. 1998). Following
Kaufman et al. (1999), we assume that the total FUV flux,
m as measured by the filter curves of
the two IRAS data sets (Nakagawa et al. 1998). Following
Kaufman et al. (1999), we assume that the total FUV flux,
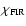 ,
absorbed by the dust grains is re-radiated in
the far-infrared. In this way we estimate the FUV field from the
far-infrared field (cf. Kramer et al. 2005):
,
absorbed by the dust grains is re-radiated in
the far-infrared. In this way we estimate the FUV field from the
far-infrared field (cf. Kramer et al. 2005):
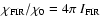 ,
where
,
where
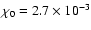 erg s-1 cm-2 (Draine & Bertoldi 1996; Draine 1978). The derived
spatial distribution of the FUV intensity is presented in
Fig. 6. In the mapped region, the FUV field
erg s-1 cm-2 (Draine & Bertoldi 1996; Draine 1978). The derived
spatial distribution of the FUV intensity is presented in
Fig. 6. In the mapped region, the FUV field
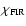 varies between about 1 and 100 Draine units.
For the seven selected positions
varies between about 1 and 100 Draine units.
For the seven selected positions
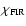 is listed in
Table 3.
is listed in
Table 3.
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{8431_8.eps} \end{figure}](/articles/aa/full/2008/37/aa8431-07/Timg89.gif) |
Figure 6:
FUV intensity distribution (contours) in IC 348 estimated from the IRAS FIR fluxes, overlayed on the [C I] integrated intensities (colors). The FUV intensity
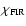 contour levels run from 5, 10, 20 to 100 by steps of 20 Draine units,
contour levels run from 5, 10, 20 to 100 by steps of 20 Draine units,  . . |
| Open with DEXTER |
The primary source of UV radiation in the cloud is HD 281159.
Assuming that the star is a black body at an effective temperature
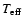 corresponding to its spectral type, we can
estimate the FUV flux independently (Kramer et al. 1996; Beuther et al. 2000). A
B 5 V star has an effective temperature
corresponding to its spectral type, we can
estimate the FUV flux independently (Kramer et al. 1996; Beuther et al. 2000). A
B 5 V star has an effective temperature
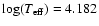 and a total luminosity L of
and a total luminosity L of
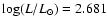 (de Jager & Nieuwenhuijzen 1987). The FUV luminosity
(de Jager & Nieuwenhuijzen 1987). The FUV luminosity
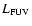 and the FUV flux
and the FUV flux
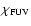 are defined as
are defined as
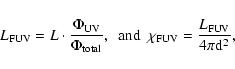 |
(1) |
where
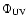 is the FUV flux between 6 eV and 13.6 eV,
is the FUV flux between 6 eV and 13.6 eV,
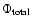 is the total flux, and d is the distance
to the UV source. We compute the distance d in two ways: for the
point close to HD 281159 we use the optical radius of the cluster
IC 348 of about 0.37 pc (Herbig 1998) as the minimum distance
between star and cloud. For all other points we assume that star
and cloud are located in the same plane so that the distance is
directly given by the observed separation. Finally we normalize
the FUV field to units of
is the total flux, and d is the distance
to the UV source. We compute the distance d in two ways: for the
point close to HD 281159 we use the optical radius of the cluster
IC 348 of about 0.37 pc (Herbig 1998) as the minimum distance
between star and cloud. For all other points we assume that star
and cloud are located in the same plane so that the distance is
directly given by the observed separation. Finally we normalize
the FUV field to units of 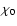 .
The resulting FUV fields,
.
The resulting FUV fields,
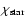 ,
are also listed in Table 3 for
the seven selected positions.
,
are also listed in Table 3 for
the seven selected positions.
We see that both methods provide consistent FUV field values.
Because of the uncertainty of the distance between star and cloud
we consider the values
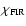 ,
derived from the HIRES
data, somewhat more reliable so that we will use them in the
following. The FUV field
,
derived from the HIRES
data, somewhat more reliable so that we will use them in the
following. The FUV field 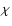 at the seven positions ranges from
about 1 to 90 Draine units.
at the seven positions ranges from
about 1 to 90 Draine units.
Molecular clouds are known for their highly filamentary and
clumpy, often self-similar structure over a wide range of scales
(Dame et al. 2001; Stutzki et al. 1988; Heyer et al. 1998). The observed structure further
breaks up into substructures with every step of increased spatial
resolution (Falgarone & Phillips 1996; Bensch et al. 2001). For IC 348, the self-similar
structure was directly measured in terms of the 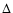 -variance
by Sun et al. (2006). In such a cloud, the UV field can penetrate
deeply into the cloud forming PDRs at many internal surfaces. The
cloud is basically filled by surfaces (Ossenkopf et al. 2007). This
explains the observed [C I] and even [C II] emission
deep within molecular clouds (Meixner & Tielens 1993; Howe et al. 1991; Stutzki et al. 1988; Stacey et al. 1993).
We can simulate such a structure by an ensemble of individual
clumps, each of them being small compared to the overall cloud,
leaving enough ``empty'' regions to permit a deep penetration of
the UV field (Stutzki et al. 1998).
-variance
by Sun et al. (2006). In such a cloud, the UV field can penetrate
deeply into the cloud forming PDRs at many internal surfaces. The
cloud is basically filled by surfaces (Ossenkopf et al. 2007). This
explains the observed [C I] and even [C II] emission
deep within molecular clouds (Meixner & Tielens 1993; Howe et al. 1991; Stutzki et al. 1988; Stacey et al. 1993).
We can simulate such a structure by an ensemble of individual
clumps, each of them being small compared to the overall cloud,
leaving enough ``empty'' regions to permit a deep penetration of
the UV field (Stutzki et al. 1998).
![\begin{figure}
\par\mbox{\includegraphics[angle=-90,width=7cm,clip]{8431_9.eps}\includegraphics[angle=-90,width=7cm,clip]{8431_10.eps} }
\end{figure}](/articles/aa/full/2008/37/aa8431-07/Timg99.gif) |
Figure 7:
Comparison of the observed line intensity ratios [C I]/12CO 4-3, [C I]/13CO 1-0 and 12CO 4-3/12CO 1-0 at (1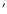 ,
-1 ,
-1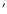 )
with the single clump KOSMA - )
with the single clump KOSMA - 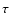 PDR model calculations. The left figure shows the fit of clump mass and density at a fixed FUV field
PDR model calculations. The left figure shows the fit of clump mass and density at a fixed FUV field 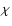 of 101.5; the right one presents the fit of FUV field and clump density at a fixed clump mass of 10
of 101.5; the right one presents the fit of FUV field and clump density at a fixed clump mass of 10
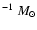 .
The central solid contours represent the observed intensity ratios, the outer dashed two give those for a 20%
uncertainty. The grey-scale images indicate the reduced .
The central solid contours represent the observed intensity ratios, the outer dashed two give those for a 20%
uncertainty. The grey-scale images indicate the reduced 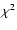 of the fit. The position of the minimum reduced
of the fit. The position of the minimum reduced 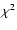 is marked by a white cross. The horizontal light blue line in the
right panel shows the FUV flux
is marked by a white cross. The horizontal light blue line in the
right panel shows the FUV flux
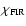 from the HIRES data.
from the HIRES data. |
| Open with DEXTER |
In the following we test two different clump ensembles with
respect to their ability to reproduce the observed line
intensities.
All individual clumps in the PDRs are modelled using the spherical
KOSMA - 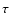 PDR model (Röllig et al. 2006; Störzer et al. 1996; Röllig et al. 2007). The
model computes the chemical and temperature structure of a clump
illuminated by an isotropic FUV radiation field and cosmic rays.
The emission from the model is calculated as a function of the gas
density, FUV radiation field and mass of the clumps (implicitly
specifying the clump size). The model clumps are assumed to have a
power-law density profile of n(r)
PDR model (Röllig et al. 2006; Störzer et al. 1996; Röllig et al. 2007). The
model computes the chemical and temperature structure of a clump
illuminated by an isotropic FUV radiation field and cosmic rays.
The emission from the model is calculated as a function of the gas
density, FUV radiation field and mass of the clumps (implicitly
specifying the clump size). The model clumps are assumed to have a
power-law density profile of n(r) 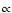 n0 r-1.5for
n0 r-1.5for
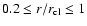 and n(r) = const. for
and n(r) = const. for
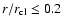 .
n0 is the density at the clump
surface called clump density, which is about half of the
clump averaged density
.
n0 is the density at the clump
surface called clump density, which is about half of the
clump averaged density
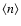 :
:
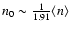 .
.
The PDR models are pre-computed on a regular grid with equidistant
logarithmic steps. The FUV field 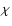 covers the range from
100, 100.5, ..., 105.5, 106.0 Draine units; The
clump densities range from 102.0, 102.5, ..., 105.5,
106.0 cm-3; and the clump masses
covers the range from
100, 100.5, ..., 105.5, 106.0 Draine units; The
clump densities range from 102.0, 102.5, ..., 105.5,
106.0 cm-3; and the clump masses
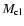 cover
cover
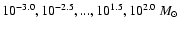 .
.
In a first approach we will assume that the cloud is composed of a
collection of identical clumps, so that the full ensemble is
characterized by the parameter set of the individual clumps and
their number only. To determine the properties of the individual
clumps we perform a 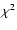 fit of the three line intensity
ratios given in Table 1, using a spherical PDR model
in a three-dimensional parameter space spanned by the FUV field,
the clump mass, and density. The results for the seven selected
positions are summarized in Table 3.
Figure 7 presents an example of the
fit of the three line intensity
ratios given in Table 1, using a spherical PDR model
in a three-dimensional parameter space spanned by the FUV field,
the clump mass, and density. The results for the seven selected
positions are summarized in Table 3.
Figure 7 presents an example of the 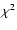 fitting
for the map center (1
fitting
for the map center (1 ,
-1
,
-1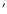 ). The left panel shows a
cut through the parameter space for a fixed UV field,
demonstrating the fit of clump mass
). The left panel shows a
cut through the parameter space for a fixed UV field,
demonstrating the fit of clump mass
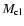 and clump density
n0. The right panel presents the corresponding fit for the
FUV field
and clump density
n0. The right panel presents the corresponding fit for the
FUV field 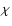 and the clump density n0. We see that all
line ratios are good density tracers, but hardly constrain the
clump mass as expected. The clump density has to fall between 2.5
and
and the clump density n0. We see that all
line ratios are good density tracers, but hardly constrain the
clump mass as expected. The clump density has to fall between 2.5
and
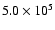 cm-3. But the reduced
cm-3. But the reduced 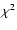 only
changes between 1 and 2.5 when the clump mass varies from
10-2.0 to 10
only
changes between 1 and 2.5 when the clump mass varies from
10-2.0 to 10
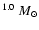 .
This general behaviour
applies to all positions analyzed. The clump densities at the
seven positions vary between
.
This general behaviour
applies to all positions analyzed. The clump densities at the
seven positions vary between
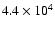 to
to
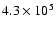 cm-3. The highest clump density occurs at
positions of the ridge and the map center. The clump masses are
not well constrained, the best fitting values fall between 0.1 and
0.4
cm-3. The highest clump density occurs at
positions of the ridge and the map center. The clump masses are
not well constrained, the best fitting values fall between 0.1 and
0.4 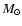 .
The fitted FUV flux
.
The fitted FUV flux
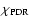 agrees with
agrees with
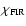 derived from the FIR continuum in most positions.
The maximum deviations by a factor three correspond to the maximum
deviation that we got comparing the FIR continuum with the stellar
radiation estimate.
derived from the FIR continuum in most positions.
The maximum deviations by a factor three correspond to the maximum
deviation that we got comparing the FIR continuum with the stellar
radiation estimate.
Table 3:
Physical parameters at selected positions in Fig 1, obtained by fitting the observed intensity ratios to the single clump KOSMA - 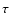 PDR models.
Cols. (2)-(5) list the fitted clump densities, clump mass, clump radius and FUV field; Col. (6) is the minimum reduced
PDR models.
Cols. (2)-(5) list the fitted clump densities, clump mass, clump radius and FUV field; Col. (6) is the minimum reduced 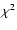 of the PDR fit; the FUV field derived from the FIR
continuum
of the PDR fit; the FUV field derived from the FIR
continuum
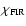 and that from the stellar radiation
and that from the stellar radiation
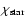 are in Cols. (7) and (8); The distance to HD 281159 used for the calculation of
are in Cols. (7) and (8); The distance to HD 281159 used for the calculation of
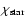 is
listed in Col. (9).
is
listed in Col. (9).
The total number of clumps in the beam
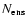 is
calculated by comparing the observed absolute line integrated
intensities with the models, correcting for the beam filling
factor
is
calculated by comparing the observed absolute line integrated
intensities with the models, correcting for the beam filling
factor![[*]](/icons/foot_motif.gif) . A 70
. A 70
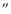 beam corresponds to a diameter of
0.10 pc at the distance of IC 348. The clump size obtained from
the best fit models found in the previous section ranges from 0.01
to 0.02 pc. The beam filling factor
beam corresponds to a diameter of
0.10 pc at the distance of IC 348. The clump size obtained from
the best fit models found in the previous section ranges from 0.01
to 0.02 pc. The beam filling factor
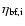 of each
clump is calculated as
of each
clump is calculated as
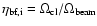 ,
where
,
where
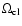 and
and
 are the solid angles of a clump and the
beam.
are the solid angles of a clump and the
beam.
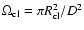 is the
solid angle of the individual clump. D is the distance of the
cloud; assuming a Gaussian beam shape,
is the
solid angle of the individual clump. D is the distance of the
cloud; assuming a Gaussian beam shape,
 is
computed as
is
computed as
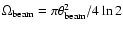 ,
where
,
where
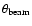 is the FWHM of our beam. The
intensity correction for a single clump is
is the FWHM of our beam. The
intensity correction for a single clump is
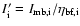 ,
where
,
where
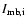 is the beam averaged
line intensity for that single clump. Since [C I] is the
most optically thin one among our four tracers, we use its line
intensity to derive the number of clumps in the beam
is the beam averaged
line intensity for that single clump. Since [C I] is the
most optically thin one among our four tracers, we use its line
intensity to derive the number of clumps in the beam
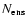 (see Table 4) by dividing the observed
intensities
(see Table 4) by dividing the observed
intensities
![$I_{\rm [C {\sc i}]obs}$](/articles/aa/full/2008/37/aa8431-07/img124.gif) by the intensities for a
single clump
by the intensities for a
single clump
![$I_{\rm [C {\sc i}]mod,i}$](/articles/aa/full/2008/37/aa8431-07/img125.gif)
![\begin{displaymath}N_{\rm ens} = \frac{I_{\rm [C {\sc i}]obs}}{I_{\rm [C {\sc i}...
...]mod,i}}
\times \frac{\Omega_{\rm beam}}{\Omega_{\rm cl}}\cdot
\end{displaymath}](/articles/aa/full/2008/37/aa8431-07/img126.gif) |
(2) |
Then we use
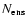 to calculate the ratios R of line
intensities between model ensemble and observations for the other
tracers:
to calculate the ratios R of line
intensities between model ensemble and observations for the other
tracers:
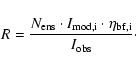 |
(3) |
The R values are listed in Table 4. This allows easy judgment of the quality of the model fit. Considering the calibration uncertainty, a perfectly fitting model yields a ratio R of
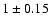 .
All three remaining tracers from Ensemble 1 have a good agreement
between the modelled and observed absolute line intensities.
.
All three remaining tracers from Ensemble 1 have a good agreement
between the modelled and observed absolute line intensities.
Table 4:
Results of ensemble of identical clumps, Ensemble case 1. The mass and FUV field for each single clump are listed in Cols. (2) and (3); Cols. (4)-(6) present the line intensity
ratios between the ensemble models and observations of 12CO 4-3, 12CO 1-0 and 13CO 1-0; the C, CO and H2 column densities from the ensembles are presented in Cols. (7)-(9); Col. (10) is the C/CO ratios. The total number of the clumps in the ensemble and ensemble mass are listed in Cols. (11) and (12); Col. (13) lists the beam filling factor of each clump. The total ensemble mass
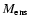 listed in the table is computed as
listed in the table is computed as
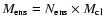 ,
where
,
where
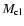 is the mass of a clump.
is the mass of a clump.
Table 5:
Results of ensembles with a clump mass distribution and mass-size distribution, Ensemble case 2. Column (2)-(4) present the ratios (in erg s-1 sr-1 cm-2) of the
modelled and observed line intensities for 12CO 4-3, 12CO 1-0 and 13CO 1-0; The mean clump ensemble density
 and the fitted FUV field
and the fitted FUV field
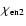 are
presented in Cols. (5) and (6). The C, CO and H2 column densities from the ensembles are presented in Cols. (7)-(9); Col. (10) is the C/CO ratios. The total masses are listed in Col. (11); Col. (12) is the minimum reduced
are
presented in Cols. (5) and (6). The C, CO and H2 column densities from the ensembles are presented in Cols. (7)-(9); Col. (10) is the C/CO ratios. The total masses are listed in Col. (11); Col. (12) is the minimum reduced 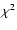 of the fit.
of the fit.
Representing the clumpy structure of the cloud by an ensemble of
identical clumps is, of course, an oversimplification. A realistic
clump size and mass distribution should be taken into account.
Large-scale CO maps present the clumpy structure of the ISM with a
mass distribution following a power law
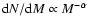 ,
where N is the number of clumps and
,
where N is the number of clumps and
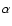 has a value around 1.8 (Kramer et al. 1998b). Furthermore, the
observations also show that there is a strong correlation of the
density and mass of the clumps corresponding a mass-size relation
has a value around 1.8 (Kramer et al. 1998b). Furthermore, the
observations also show that there is a strong correlation of the
density and mass of the clumps corresponding a mass-size relation
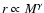 with
with
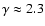 (Heithausen et al. 1998). For an ensemble of randomly positioned clumps with a power law mass spectrum, there is a relation among the power law spectral index
(Heithausen et al. 1998). For an ensemble of randomly positioned clumps with a power law mass spectrum, there is a relation among the power law spectral index 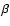 of the power spectrum,
of the power spectrum, 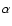 and
and 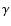 :
:
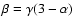 (Stutzki et al. 1998). Using the
(Stutzki et al. 1998). Using the 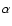 and
and 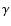 values above,
values above,
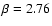 ,
which is close to the power law index
,
which is close to the power law index
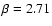 of 13CO 2-1 in IC 348 found by Sun et al. (2006).
of 13CO 2-1 in IC 348 found by Sun et al. (2006).
In this section we assume these characteristics to be universal
and model the emission by ensemble averaging the PDR single clump
results over such a clump distribution (Cubick et al. 2008; Cubick 2005) to
reproduce the observed line intensities. The remaining parameter
space is then given by the FUV field input
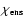 ,
the
total mass within the beam
,
the
total mass within the beam
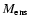 ,
the average clump
ensemble density
,
the average clump
ensemble density
 ,
and the minimum and maximum
clump masses,
,
and the minimum and maximum
clump masses,
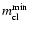 and
and
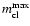 .
.
To constrain the fit to a three-dimensional parameter space also
for this case, we fix the clump mass limits. The upper mass limit
has to reflect the total mass of the clump distribution because a
spectral index
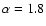 corresponds to a top-heavy function,
i.e. a distribution where most of the mass is contained in the few
most massive clumps. We assume that the total mass obtained from
the Ensemble 1 model also provides a reasonable guess for the
total mass in Ensemble 2, consequently setting the upper mass
limit
corresponds to a top-heavy function,
i.e. a distribution where most of the mass is contained in the few
most massive clumps. We assume that the total mass obtained from
the Ensemble 1 model also provides a reasonable guess for the
total mass in Ensemble 2, consequently setting the upper mass
limit
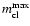 to half of the total mass of
Ensemble 1. We set the lower mass limit,
to half of the total mass of
Ensemble 1. We set the lower mass limit,
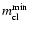 ,
to 10
,
to 10
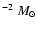 .
These
small clumps can only exist transiently and evaporate on a time
scale of
.
These
small clumps can only exist transiently and evaporate on a time
scale of 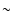 5000 yrs (Kramer et al. 2008). The choice of the lower
mass limit is not critical for the fit. Cubick et al. (2008) studied
the dependencies of the model output on the clump mass limits and
found that mainly high - J CO transitions (like 12CO 8-7)
are sensitive to the lower clump mass limit.
5000 yrs (Kramer et al. 2008). The choice of the lower
mass limit is not critical for the fit. Cubick et al. (2008) studied
the dependencies of the model output on the clump mass limits and
found that mainly high - J CO transitions (like 12CO 8-7)
are sensitive to the lower clump mass limit.
The actual fit is performed analogously to the ensemble 1 case.
The results are presented in Table 5. We find a
reasonable agreement between the modelled line intensities from
Ensemble 2 and the observed ones. The intensity ratios between
model and observations range between 0.7 and 2.0. The fitted FUV
field
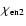 from Ensemble 2 is consistent with the
field
from Ensemble 2 is consistent with the
field
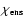 from Ensemble 1 and that derived from the
FIR continuum in most positions. The maximum deviation occurs at
the northern rim.
from Ensemble 1 and that derived from the
FIR continuum in most positions. The maximum deviation occurs at
the northern rim.
The reduced 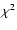 values are similar for both ensembles at
values less than 5. In spite of the somewhat more complex model,
the fit is not better than for an ensemble of identical clumps
(Ensemble 1).
values are similar for both ensembles at
values less than 5. In spite of the somewhat more complex model,
the fit is not better than for an ensemble of identical clumps
(Ensemble 1).
![\begin{figure}
\par\includegraphics[width=8cm,angle=0,clip]{8431_11.eps}\includegraphics[width=8cm,angle=0]{8431_12.eps}\end{figure}](/articles/aa/full/2008/37/aa8431-07/Timg147.gif) |
Figure 8:
Observed (filled symbols) and modelled line intensities
of 12CO, 13CO, and [C I] from both Ensemble case
1 (drawn lines with open symbols) and Ensemble case 2 (dotted lines, open symbols with a cross inside) at the northern rim ( left panel) and the southern rim ( right panel). To better display the data, we artificially shift the [C I] frequency by +40 GHz for the observed intensity. |
| Open with DEXTER |
To compare the observed absolute line intensities with the model
prediction, we show two examples of observed and modelled
integrated intensities versus frequency, namely the cooling curves
of 12CO, 13CO (upto J = 9-8) and [C I] for the
best-fit of both Ensemble 1 and Ensemble 2 models at the northern
rim and the southern rim (see Fig. 8). At those two
positions the modelled and observed line intensities agree very
well. Figure 8 also provides a prediction for line
intensities of [C I] 3P2-3P1,
12CO 7-6, 13CO 8-7, etc. Figure 8 indicates
that the tracers studied in this paper do not allow to draw any
conclusion about the clump size spectrum that best fits the
observations. Both Ensemble 1 and 2 fit the observed data equally
well. On the other hand, they give very different predictions for
the higher J CO lines. The line intensities predicted for
Ensemble 2 are noticeably larger than those predicted for Ensemble 1 (see Fig. 8). The 13CO 8-7 line, tracing the column densities of the warm gas, is predicted to be very
sensitive to the differences between the two models, allowing to
discriminate between them.
Based on the CO and H2 column densities from the PDR
analysis, we find the averaged CO relative abundance [CO]/[H2] is 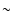
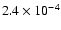 ,
which is 3 times larger
than the canonical ratio [CO]/[H2] of
,
which is 3 times larger
than the canonical ratio [CO]/[H2] of
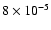 (Frerking et al. 1982) that we used in the LTE analysis. The beam averaged
C/CO abundance ratio (Table 5) varies by a factor 10
between 0.03 at the northern rim, which shows the highest column
density of all studied positions of
(Frerking et al. 1982) that we used in the LTE analysis. The beam averaged
C/CO abundance ratio (Table 5) varies by a factor 10
between 0.03 at the northern rim, which shows the highest column
density of all studied positions of
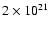 cm-2, and
0.26 at the southern rim, which shows the lowest H2 column
density of
cm-2, and
0.26 at the southern rim, which shows the lowest H2 column
density of
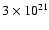 cm-2. The observed anti-correlation
between C/CO and N(H2) and also the absolute values resemble
those found in many other Galactic molecular clouds as compiled
recently by Mookerjea et al. (2006). They used the KOSMA-
cm-2. The observed anti-correlation
between C/CO and N(H2) and also the absolute values resemble
those found in many other Galactic molecular clouds as compiled
recently by Mookerjea et al. (2006). They used the KOSMA-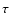 model to
interpret data taken in the Cepheus B star forming region. They
suggested that the emission of high column density peaks is
dominated by massive clumps exhibiting low C/CO ratios, while
positions of low column densities are dominated by smaller clumps,
exhibiting higher C/CO ratios. This scenario is confirmed in
IC 348 by a more complete analysis using clump mass ensembles
following the canonical mass and size distributions. However, the
scatter of the present data is large. Observations of the higher
lying transitions of [C I] and CO are needed to further
improve the analysis.
model to
interpret data taken in the Cepheus B star forming region. They
suggested that the emission of high column density peaks is
dominated by massive clumps exhibiting low C/CO ratios, while
positions of low column densities are dominated by smaller clumps,
exhibiting higher C/CO ratios. This scenario is confirmed in
IC 348 by a more complete analysis using clump mass ensembles
following the canonical mass and size distributions. However, the
scatter of the present data is large. Observations of the higher
lying transitions of [C I] and CO are needed to further
improve the analysis.
6 Summary and conclusions
We have presented fully sampled [C I] and 12CO 4-3
maps of the IC 348 molecular cloud, covering a region of
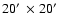 .
The observed 12CO
4-3/12CO 1-0 ratios vary between 0.2 and 1.5. High
12CO 4-3/12CO 1-0 ratios occur near the B 5 star, at
the cloud center and northern edge of the cloud.
.
The observed 12CO
4-3/12CO 1-0 ratios vary between 0.2 and 1.5. High
12CO 4-3/12CO 1-0 ratios occur near the B 5 star, at
the cloud center and northern edge of the cloud.
We have estimated the FUV field from the FIR continuum intensities
obtained from the 60 and 100 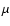 m HIRES/IRAS images. The FUV
field in the whole observed region ranges between 1 and 100 Draine
units. We also used HD 281159, the primary source of UV radiation
in this region, to estimate the FUV field for the seven studied
regions and the FUV field varies between 3 to 40 Draine units.
m HIRES/IRAS images. The FUV
field in the whole observed region ranges between 1 and 100 Draine
units. We also used HD 281159, the primary source of UV radiation
in this region, to estimate the FUV field for the seven studied
regions and the FUV field varies between 3 to 40 Draine units.
Using a clumpy PDR model based on the spherical KOSMA - 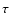 PDR
model we fitted the observed line intensities and intensity ratios
at seven selected positions. The observed intensity ratios provide
a strong constraint on the clump densities. They fall between
PDR
model we fitted the observed line intensities and intensity ratios
at seven selected positions. The observed intensity ratios provide
a strong constraint on the clump densities. They fall between
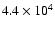 cm-3 and
cm-3 and
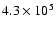 cm-3. The FUV
field fitted in the model falls between 2 to 100 Draine units,
consistent with independent estimates for the FUV field derived
from the FIR continuum maps by IRAS and from the stellar
radiation. We found that both an ensemble of identical clumps
(Ensemble 1) and a model using a clump size and mass distribution
following the typically observed scaling (Ensemble 2) produce line
intensities which are in good agreement (within a factor
cm-3. The FUV
field fitted in the model falls between 2 to 100 Draine units,
consistent with independent estimates for the FUV field derived
from the FIR continuum maps by IRAS and from the stellar
radiation. We found that both an ensemble of identical clumps
(Ensemble 1) and a model using a clump size and mass distribution
following the typically observed scaling (Ensemble 2) produce line
intensities which are in good agreement (within a factor 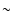 2)
with the observed intensities. The models confirm the
anti-correlation between C/CO abundance ratio and hydrogen column
density found in many regions and explained by Mookerjea et al. (2006).
2)
with the observed intensities. The models confirm the
anti-correlation between C/CO abundance ratio and hydrogen column
density found in many regions and explained by Mookerjea et al. (2006).
The results of this study strengthen the picture of molecular
clouds as highly fragmented, surface dominated objects. Although
Ensemble 2 is the natural case in this picture, Ensemble 1 fits
the observed intensities equally well. We predicted line
intensities for [C I], CO, and 13CO transitions for
both cases, which can be tested by future observations. The higher
J CO lines are needed to decide on the necessity of the clump
mass and size distributions and to determine the clump mass limits
(Cubick et al. 2008).
Acknowledgements
We thank Naomi Ridge for allowing us to use the FCRAO low-J CO data in IC 348. We used the NASA/IPAC/IRAS/HIRES data reduction facilities. This material is based on work supported by the
Deutsche Forschungs Gemeinschaft (DFG) via grant SFB 494. This research has made use of NASA Astrophysics Data System.
- Aumann, H. H.,
Fowler, J. W., & Melnyk, M. 1990, AJ, 99, 1674 [NASA ADS] [CrossRef]
(In the text)
- Bensch, F., Stutzki, J.,
& Ossenkopf, V. 2001, A&A, 366, 636 [NASA ADS] [CrossRef] [EDP Sciences]
- Bensch, F.,
Leuenhagen, U., Stutzki, J., & Schieder, R. 2003, ApJ, 591,
1013 [NASA ADS] [CrossRef]
- Beuther, H., Kramer,
C., Deiss, B., & Stutzki, J. 2000, A&A, 362, 1109 [NASA ADS]
(In the text)
- Cernicharo, J. 1985,
ATM: A program to compute theoretical atmospheric opacity for
frequency <1000 GHz, Tech. Rep., IRAM
- Cubick, M. 2005, The
contribution of photon dominated regions to the far-infrared
emission of the Milky Way: construction of PDR models, Diploma
thesis, Universität zu Köln
- Cubick, M.,
Röllig, M., Ossenkopf, V., Kramer, C., & Stutzki, J. 2008,
A&A, submitted
- Dame, T. M.,
Hartmann, D., & Thaddeus, P. 2001, ApJ, 547, 792 [NASA ADS] [CrossRef]
- de Jager, C., &
Nieuwenhuijzen, H. 1987, A&A, 177, 217 [NASA ADS]
(In the text)
- Draine, B. T. 1978,
ApJS, 36, 595 [NASA ADS] [CrossRef]
- Draine, B. T., &
Bertoldi, F. 1996, ApJ, 468, 269 [NASA ADS] [CrossRef]
- Eislöffel, J.,
Froebrich, D., Stanke, T., & McCaughrean, M. J. 2003, ApJ,
595, 259 [NASA ADS] [CrossRef]
- Falgarone, E., &
Phillips, T. G. 1996, ApJ, 472, 191 [NASA ADS] [CrossRef]
- Fiege, J. D., &
Pudritz, R. E. 2000, MNRAS, 311, 105 [NASA ADS] [CrossRef]
- Frerking, M. A.,
Langer, W. D., & Wilson, R. W. 1982, ApJ, 262,
590 [NASA ADS] [CrossRef]
(In the text)
- Gehman, C. S.,
Adams, F. C., & Watkins, R. 1996, ApJ, 472, 673 [NASA ADS] [CrossRef]
- Graf, U. U.,
Heyminck, S., Michael, E. A., et al. 2002, in Millimeter
and Submillimeter Detectors for Astronomy, ed. T. G. Phillips,
& J. Zmuidzinas, Proc. SPIE, Hawaii/USA, 4855, 99, 167
(In the text)
- Heithausen, A.,
Bensch, F., Stutzki, J., Falgarone, E., & Panis, J. F.
1998, A&A, 331, 65 [NASA ADS]
(In the text)
- Herbig, G. H. 1998,
AJ, 497, 736 [NASA ADS] [CrossRef]
(In the text)
- Heyer, M. H., Brunt,
C., Snell, R. L., et al. 1998, ApJS, 115, 241 [NASA ADS] [CrossRef]
- Hiyama, S. 1998,
Seitenbandkalibration radioastonomischer Linienbeobachtungen,
Diploma thesis, Universität zu Köln
- Hollenbach, D. J.,
& Tielens, A. G. G. M. 1999, Rev. Mod. Phys.,
71, 173 [NASA ADS] [CrossRef]
(In the text)
- Horn, J., Siebertz, O.,
Schmülling, F. et al. 1999, Exp. Astron., 9, 17 [NASA ADS] [CrossRef]
(In the text)
- Howe, J. E.,
Jaffe, D. T., Genzel, R., & Stacey, G. J. 1991, ApJ,
373, 158 [NASA ADS] [CrossRef]
- Israel, F. P., &
Baas, F. 2002, A&A, 383, 82 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Jørgensen,
J. K., Johnstone, D., Kirk, H., & Myers, P. C. 2007, ApJ,
656, 293 [NASA ADS] [CrossRef]
(In the text)
- Kaufman, M., Wolfire,
M., Hollenbach, D., & Luhman, M. 1999, ApJ, 527, 795 [NASA ADS] [CrossRef]
(In the text)
- Klessen, R. S., &
Burkert, A. 2000, ApJS, 128, 287 [NASA ADS] [CrossRef]
- Kramer, C., Stutzki, J.,
& Winnewisser, G. 1996, A&A, 307, 915 [NASA ADS]
- Kramer, C., Degiacomi,
C., Graf, U., et al. 1998a, in Advanced Technology MMV, Radio,
and Terahertz Telescopes, ed. T. Phillips, Proc. SPIE,
Kona/Hawaii/USA, 3357, 71
- Kramer, C., Stutzki,
J., Röhrig, R., & Corneliussen, U. 1998b, A&A, 329,
249 [NASA ADS]
(In the text)
- Kramer, C., Jakob,
H., Mookerjea, B., et al. 2004, A&A, 424, 887 [NASA ADS] [CrossRef] [EDP Sciences]
- Kramer, C.,
Mookerjea, B., Bayet, E., et al. 2005, A&A, 441, 961 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Kramer, C., Cubick, M.,
Röllig, M., et al. 2008, A&A, 477, 547 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Lada, E. A., &
Lada, C. J. 1995, AJ, 109, 1682 [NASA ADS] [CrossRef]
- Lada, C. J.,
Muench, A. A., & Luhman, K. L., et al. 2006, AJ,
131, 1574 [NASA ADS] [CrossRef]
(In the text)
- Langer, W. D., &
Penzias, A. A. 1990, ApJ, 357, 477 [NASA ADS] [CrossRef]
(In the text)
- Little,
L. T., Gibb, A. G., Heaton, B. D., Ellison,
B. N., & Claude, S. M. X. 1994, MNRAS, 271,
649 [NASA ADS]
- Luhman, K. L.,
Rieke, G. H., Lada, C. J., & Lada, E. A. 1998,
ApJ, 508, 347 [NASA ADS] [CrossRef]
- Luhman,
K. L., Stauffer, J. R., & Muench, A. A.,
et al. 2003, ApJ, 593, 1093 [NASA ADS] [CrossRef]
- Luhman, K. L.,
Lada, E. A., Muench, A. A., & Elston, R. J.
2005, ApJ, 618, 810 [NASA ADS] [CrossRef]
- Meixner, M., & Tielens,
A. G. G. M. 1993, ApJ, 405, 216 [NASA ADS] [CrossRef]
- Mookerjea, B., Kramer,
C., Röllig, M., & Masur, M. 2006, A&A, 456, 235 [NASA ADS] [CrossRef] [EDP Sciences]
- Najita, J. R.,
Tiede, G. P., & Carr, J. S. 2000, ApJ, 541, 977 [NASA ADS] [CrossRef]
- Nakagawa, T., Yui,
Y. Y., Doi, Y., et al. 1998, ApJS, 115, 259 [NASA ADS] [CrossRef]
(In the text)
- Nakajima, Y., & Hanawa,
T. 1996, ApJ, 467, 321 [NASA ADS] [CrossRef]
- Oka, T., Iwata, M.,
Maezawa, H., et al. 2004, ApJ, 602, 803 [NASA ADS] [CrossRef]
(In the text)
- Ossenkopf, V.,
Röllig, M., Cubick, M., & Stutzki, J. 2007, Molecules in
Space & Laboratory, Paris, ed. J. L. Lemaire, & F.
Combes, 95
(In the text)
- Ostriker, E. C.,
Stone, J. M., & Gammie, C. F. 2001, ApJ, 546,
980 [NASA ADS] [CrossRef]
- Padoan, P., Juvela, M.,
Bally, J., & Nordlund, A&A, 1998, ApJ, 504, 300 [NASA ADS] [CrossRef]
- Plume, R.,
Bensch, F., Howe, J. E., et al. 2000, ApJ, 539, L133 [NASA ADS] [CrossRef]
- Preibisch, T., &
Zinnecker, H. 2001, AJ, 122, 866 [NASA ADS] [CrossRef]
- Preibisch, T., Zinnecker,
H., & Herbig, G. H. 1996, A&A, 310, 456 [NASA ADS]
- Ridge, N. A.,
Wilson, T. L., Megeath, S. T., Allen, L. E., &
Myers, P. C. 2003, AJ, 126, 286 [NASA ADS] [CrossRef]
(In the text)
- Röllig, M.,
Ossenkopf, V., Jeyakumar, S., & Stutzki, J. 2006, A&A, 451,
917 [NASA ADS] [CrossRef] [EDP Sciences]
- Röllig, M.,
Abel, N. P., Bell, T., et al. 2007, A&A, 467,
187 [NASA ADS] [CrossRef] [EDP Sciences]
- Schneider, N.,
Simon, R., Kramer, C., et al. 2003, A&A, 406, 915 [NASA ADS] [CrossRef] [EDP Sciences]
- Schröder, K.,
Staemmler, V., Smith, M. D., Flower, D. R., & Jaquet,
R. 1991, J. Phys. B, 24, 2487 [NASA ADS] [CrossRef]
(In the text)
- Stacey, G. J.,
Jaffe, D. T., Geis, N., et al. 1993, ApJ, 404, 219 [NASA ADS] [CrossRef]
- Stutzki, J.,
Stacey, G. J., Genzel, R., et al. 1988, ApJ, 332,
379 [NASA ADS] [CrossRef]
- Stutzki, J., Bensch,
F., Heithausen, A., Ossenkopf, V., & Zielinsky, M. 1998,
A&A, 336, 697 [NASA ADS]
(In the text)
- Störzer, H.,
Stutzki, J., & Sternberg, A. 1996, A&A, 310, 592 [NASA ADS]
- Störzer, H.,
Stutzki, J., & Sternberg, A. 1997, A&A, 323, 13 [NASA ADS]
(In the text)
- Sun, K., Kramer,
C., Ossenkopf, V., et al. 2006, A&A, 451, 539 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Tafalla, M., Kumar,
M. S. N., & Bachiller, R. 2006, A&A, 456,
179 [NASA ADS] [CrossRef] [EDP Sciences]
- Winnewisser, G., Bester,
M., & Ewald, R. 1986, A&A, 167, 207 [NASA ADS]
Copyright ESO 2008
![\begin{figure}
\par\mbox{\includegraphics[angle=-90,width=6cm,clip]{8341_1.eps}\...
...8341_2.eps}\includegraphics[angle=-90,width=6cm,clip]{8341_3.eps} }
\end{figure}](/articles/aa/full/2008/37/aa8431-07/Timg29.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=17cm,clip]{8341_4.eps}\end{figure}](/articles/aa/full/2008/37/aa8431-07/Timg41.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{8431_5.eps} \end{figure}](/articles/aa/full/2008/37/aa8431-07/Timg48.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{8431_6.eps}\end{figure}](/articles/aa/full/2008/37/aa8431-07/Timg49.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{8431_7.eps}\end{figure}](/articles/aa/full/2008/37/aa8431-07/Timg85.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{8431_8.eps} \end{figure}](/articles/aa/full/2008/37/aa8431-07/Timg89.gif)
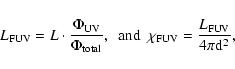
![\begin{figure}
\par\mbox{\includegraphics[angle=-90,width=7cm,clip]{8431_9.eps}\includegraphics[angle=-90,width=7cm,clip]{8431_10.eps} }
\end{figure}](/articles/aa/full/2008/37/aa8431-07/Timg99.gif)
![\begin{displaymath}N_{\rm ens} = \frac{I_{\rm [C {\sc i}]obs}}{I_{\rm [C {\sc i}...
...]mod,i}}
\times \frac{\Omega_{\rm beam}}{\Omega_{\rm cl}}\cdot
\end{displaymath}](/articles/aa/full/2008/37/aa8431-07/img126.gif)
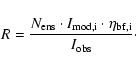
![\begin{figure}
\par\includegraphics[width=8cm,angle=0,clip]{8431_11.eps}\includegraphics[width=8cm,angle=0]{8431_12.eps}\end{figure}](/articles/aa/full/2008/37/aa8431-07/Timg147.gif)