Table 3: Two-Absorber fits for XMM- Newton and Chandra.
Parameter XMM Chandra Simult. XMM Chandra XMM Chandra

$\Gamma$		 $\rm 2.08_{-0.03} ^{+0.03}$ $\rm 1.84_{-0.02} ^{+0.02}$ $\rm 2.00_{-0.01} ^{+0.01}$ ... ... $\rm 2.13_{-0.02}^{+0.02}$ $\rm 1.83_{-0.02} ^{+0.02}$

Norm$^{\rm a}$		 $\rm 1.41_{-0.03} ^{+0.03}$ $\rm 1.18_{-0.02} ^{+0.02}$ $\rm 1.34_{-0.01} ^{+0.01}$ ... ... $\rm 1.50_{-0.02}^{+0.02}$ $\rm 1.17_{-0.02} ^{+0.02}$

$\rm N_{\rm H}(1)$$^{\rm b}$		 $\rm 5.72_{-0.19} ^{+0.21}$ $\rm 6.05_{-0.19} ^{+0.19}$ $\rm 7.34_{-0.15} ^{+0.18}$ ... ... ... ...

$\log\xi(1)$		 $\rm 1.15_{-0.15} ^{+0.14}$ $\rm 1.50_{-0.12} ^{+0.03}$ $\rm 1.50_{-0.04} ^{+0.02}$ ... ... ... ...

Fe		 $\rm 3.14_{-0.25} ^{+0.27}$ $\rm 4.79_{-0.22} ^{+0.23}$ $\rm 2.85_{-0.10} ^{+0.10}$ ... ... ... ...

$\rm N_{\rm H}(2)$$^{\rm b}$		 $\rm 4.75_{-0.89} ^{+1.20}$ $\rm 2.74_{-1.15} ^{+0.68}$ $\rm 5.49_{-0.54} ^{+0.71}$ ... ... ... ...

$\log\xi(2)$		 $\rm 3.03_{-0.04} ^{+0.15}$ $\rm 3.10_{-0.12} ^{+0.23}$ $\rm 3.00_{-0.01} ^{+0.04}$ ... ... ... ...

$\chi ^2$/(d.o.f.)		 296.1/(286) 186.5/(180) 647.9/(473) 373.8/(293) 274.1/(187) 298.5/(291) 189.3/(185)

$P_{\rm global}[{\rm Two~Abs}]$		 0.35 0.38 $4\times 10^{-8}$ $7\times 10^{-4}$ $2 \times 10^{-5}$ 0.39 0.43

$\chi^2(1$- $2~{\rm keV})$/(d.o.f.)		 44.9/(35) 48.9/(52) 135.1/(87) 65.7/(35) 69.4/(52) 43.9/(35) 49.3/(52)

$P_{(1-2~{\rm keV})}[{\rm Two~Abs}]$		 0.14 0.65 $4\times 10^{-4}$ $7\times 10^{-4}$ 0.05 0.17 0.63

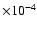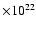
The error parameters are 90% confidence limits. The Fe abundance is the same for both absorbers. (a) Power-law normalization, $\times 10^{-4}$ photons keV-1 cm-2 s-1 at 1 keV in the observed frame. (b) Column density of the component, $\times 10^{22}$  ${\rm cm}^{-2}$.

Source LaTeX | All tables | In the text