A&A 489, 403-412 (2008)
DOI: 10.1051/0004-6361:200809969

Abundances of four open clusters from solar stars^,,

G. Pace^1,2 - L. Pasquini³ - P. François⁴

1 - Centro de Astrofisica, Universidade do Porto, Rua das Estrellas, 4150-762 Porto, Portugal
2 - Aryabhatta Research Institute of Observational Sciences, Manora Peak, Nainital, 263129 Uttaranchal, India
3 - European Southern Observatory, Karl Schwarzschildstr. 2, Garching bei München, Germany
4 - Observatoire de Paris, 64 Avenue de l'Observatoire, 75014 Paris, France

Received 14 April 2008 / Accepted 16 June 2008

Abstract
Aims. We present the abundance measurements of several elements (Fe, Ca, Na, Ni, Ti, Al, Cr, Si) for 20 solar-type stars belonging to four Galactic open clusters: NGC 3680, IC 4651, Praesepe, and M 67. Oxygen abundances were in addition measured for most stars in each cluster apart from IC 4651. For NGC 3680, accurate abundance determinations using high-resolution spectra covering a large spectral domain are computed for the first time.
Methods. We used UVES high-resolution, high signal-to-noise (S/N) ratio spectra and performed a differential analysis with respect to the sun, by measuring equivalent widths and assuming LTE.
Results. The most surprising result is a measurement of significant supersolar metallicity for Praesepe ( $\rm [Fe/H]=0.27\pm 0.10$). As for the other clusters, we confirm a supersolar metallicity for IC 4651 ( $\rm [Fe/H]=0.12\pm 0.05$), a solar metallicity for M 67 ( $\rm [Fe/H]=0.03\pm 0.04$) and a slight subsolar metallicity for NGC 3680 ( $\rm [Fe/H]=-0.04\pm 0.03$). We find that the abundance ratios of almost all elements are solar, with the notable exception of oxygen in NGC 3680 and Praesepe, supersolar in the former cluster ( $\rm [O/Fe]=0.2\pm 0.05$) and as low as $\rm [O/Fe]=-0.4\pm 0.1$ in the latter. Observations of several objects per cluster is required to obtain robust results, especially for those elements with a limited number of suitable lines.

Key words: stars: abundances - Galaxy: open clusters and associations: individual: NGC 3680 - Galaxy: open clusters ans associations: individual: IC 4651 - Galaxy: open clusters and associations: individual: Praesepe - Galaxy: open clusters and associations: individual: M 67

1 Introduction

Understanding the chemical evolution of the Galaxy requires both the development of theoretical models and comparison of their predictions with observational results. Several different models have been created of increasingly more complex and realistic scenarios, for instance including two infall episodes that formed the halo-thick disk and thin disk (François et al. 2004; Chiappini et al. 1997,2001). Observationally, new-generation telescopes such as VLT and Keck and the availability of multi-object spectroscopy have enabled a significant amount of high quality spectroscopic data to be gathered.

A long-standing question concerns the existence and evolution of the chemical abundance gradient in the Galactic disk. Galactic open clusters are probably the best tool for understanding whether and how the gradient slope changes with time because they have formed at all epochs. Their distances can be measured more accurately and are less affected by observational biases than other classes of objects.

Dias & Lépine (2005) identified the birthplace of 612 open clusters and determined the spiral pattern rotation speed of the Galactic disk. The possibility of tracing open clusters back to where they formed is interesting because, coupled with metallicity measurements, allow us to reconstruct the chemical distribution of the Galactic disk in the past. Dias & Lépine (2005) based their work on large photometric databases in the visible. They achieve important conclusions on the structure and dynamics of the spiral arms, but to estimate precisely the deviation of open cluster motions from circular orbits, and improve the scale of Galactocentric distances at the place of birth, a more complete and precise database of age, distance, proper motion and radial velocity determinations is required. Unprecedented opportunities are provided by deep photometric surveys in the infrared, such as UKIDSS (Lawrence et al. 2007) and VISTA (McPherson et al. 2006). These surveys can be used to complete deep, precise and homogeneous open cluster databases of location in the 3-D space, age, and reddening. The calibration of photometric metallicity indicators could be used for clusters not observable with high-resolution spectroscopy.

Open clusters have the added advantage of providing a sample of coeval stars that formed from the same material, which means, in particular for main-sequence stars, that they should have the same atmospheric chemical composition. As a result, the chemical composition of an open cluster can be studied by several stellar spectra. With all these advantages, open clusters are ideal objects to probe the chemical evolution of the Galactic disk. A large dataset, spanning as wide a range of Galactocentric distances and ages, as possible, is of course required.

Finally, clusters are at the basis of our understanding of stellar evolution, and their colour-magnitude diagrams, and well-determined abundances can be used to test stellar evolution models directly (see e.g. Nordstroem et al. 1997).

To date, accurate chemical composition data have been determined for only a few open clusters using high resolution spectra of a number of primarily giant stars (Gratton 2000). The situation is evolving rapidly due to coordinated efforts using facilities available at 8-M-class telescopes (Bragaglia & Tosi 2006; Randich et al. 2005). This work combines with other efforts attempting to establish a robust open-cluster metallicity scale. Random and systematic errors have given rise to - sometimes dramatic - discrepancies in abundance determinations of a given open cluster as computed from different groups. We confirm that this is no longer the case when comparing independent metallicity measurements from high resolution spectroscopy.

   
2 Observations and data reduction

The data used were primarily collected to study the chromospheric activity evolution of solar-type stars (Pace & Pasquini 2004). The sample includes two stars in NGC 3680, five in IC 4651, seven in Praesepe, and six in M 67. The targets were chosen to be main sequence stars, and to have a high probability of being members of the clusters and not known to be binaries at the time of observations. Our selection was completed using the reference works of Nordstroem et al. (1996) for NGC 3680, Meibom et al. (2002) for IC 4651, and several sources for M 67, including Latham et al. (1992) for the binary determination in this cluster. From the sample originally collected and used in Pace & Pasquini (2004), one M 67 star was excluded because it turned out to be a binary (Randich et al. 2006). Our stars have colours in the range 0.51 < (B-V)₀ < 0.72, which includes the solar colour evaluated around B-V = 0.65 (see e.g. Pasquini et al. 2008). We note that the paucity of stars observed in NGC 3680 is due to the fact that, as shown by Nordstroem et al. (1997), this cluster has few single G stars members, since most of its low mass members have dispersed during its lifetime.

Star names are taken from Eggen (1969) for NGC 3680, Anthony-Twarog et al. (1988) and Eggen (1971) for IC 4651, Sanders (1977) for M 67, and Klein Wassink (1927) for Praesepe.

The spectra were obtained during the ESO observing run 66.D-0457 with the UVES spectrograph at the focus of Kueyen 2 of the VLT (Dekker et al. 2000). While we used the blue part of the spectra to determine the level of chromospheric activity, we did also record red spectra simultaneously for the range between 480 and 680 nm. Given the higher flux of stars in this range, we could reduce the width of the UVES red slit to 0.4 arcsec, to achieve a resolution of R=100 000 at red wavelengths, while maintaining a high S/N ratio in this wavelength range. With some variation from star to star and between different regions of the spectra, the S/N ratio/pixel is about 130 for Praesepe stars and 80 for all other stars. The spectra were reduced with the UVES pipeline (Modigliani et al. 2004), and then analysed using both MIDAS and IDL routines

   
3 Abundance analysis

Abundance measurements were completed by measuring equivalent widths (EWs) and using OSMARCS models (Edvardsson et al. 1993), in a standard-LTE analysis. We used the line list from Randich et al. (2006), from which suitable lines in the EW-range 5-140 mÅ were selected. EW measurements were performed by using an IDL program developed by one of the authors (G.P.), which operates semi-automatically to allow a visual control of the fit of each selected line.

We first completed the chemical analysis of the Sun for EW measurements determined by Randich et al. (2006), and the well-known values of temperature and gravity (see e.g. Stix 2002). The solar EW measurements used were obtained for an UVES spectrum of a resolution R=45 000. A comparison with EW measurements for the UVES archive solar spectrum acquired for the same configuration as our sample spectra, indicated that variations in resolution power between R=45 000 and R=100 000 do not have any detectable effect on the EWs, and we therefore preferred to employ published measurements. We attempted to describe the data using several values for the microturbulence and eventually chose the value that provided the flattest trend in the EW versus abundance diagram, namely 1.1 km s^-1. Our results are available at CDS in electronic form (Table 1) containing the following information. Column 1 lists the wavelength, Col. 2 indicates the element chemical symbol, Col. 3 ionization stage, Col. 4 indicates the EW measurement, and Col. 5 provides the corresponding chemical abundance. While the correlation coefficient between [Fe/H] and EW is close to 0, namely 0.02, that between [Fe/H] and the excitation potential ($\chi$) is -0.42, and the difference between Fe  I and Fe  II is approximately -0.05 dex. These numbers differ significantly from zero. Small inaccuracies in the model that reproduces the atmospheric temperature stratification, rather than the limits of the LTE assumption, could be responsible for the slope in the [Fe/H] versus $\chi$ diagram and for a poor ionization equilibrium, since lines of different excitation potential tend to form in different layers of the solar atmosphere (Grevesse & Sauval 1999).

By performing a differential analysis line by line with respect to the Sun, we expect to reduce significantly the spurious trends and restore the ionisation equilibrium when evaluating the stellar parameters, provided that the structure of the stellar photosphere does not differ significantly from solar, which is a reasonable assumption since our targets are solar-type stars.

For stars studied, atmospheric parameters that reproduce most effectively excitation and ionisation equilibria were selected from a broad grid of guess values.

The temperature estimates about which the grids were constructed, were computed first for existing photometry, in particular V-H, V-J and V-K colours. V-magnitudes were taken from the reference papers in Sect. 2 for IC 4651, from Nordstroem et al. (1997) for NGC 3680, from Montgomery et al. (1993) for M 67, and from Jones & Stauffer (1991) for Praesepe, with the exception of KW 368 and KW 208, whose V-magnitudes are taken instead from Jones & Cudworth (1983) and Johnson (1952) respectively. We then adopted J, H, and K magnitudes from the 2 MASS catalogue (Skrutskie et al. 2006). Each of the V-H, V-J, and V-K colours were transformed into a temperature estimation using a calibration defined by Ramírez & Meléndez (2005), and the three values were averaged.

The comparison between photometric and spectroscopic temperatures indicated that the colour-colour and colour- temperature transformations could be affected by systematic error, and that the colour excess adopted for IC 4651 could be underestimated (see Sect. 4.4).

As for gravity, we used the values expected for a dwarf according to: 1) the previously determined photometric temperature; 2) the stellar ages, i.e. those of the parent cluster given in Carraro & Chiosi (1994) and, only for Praesepe, in the WEBDA database; and 3) the solar metallicity isochrones of Girardi et al. (2000). Microturbulence was allowed to vary in the range from $\approx$0.7 to $\approx$1.7 km s^-1. Temperature, gravity and microturbulence velocity were set equal those values for which no significant trend in the computed iron abundances was present, neither as a function of the excitation potential of the line nor as a function of its EW, and for which the iron abundances derived using the Fe  I and Fe  II lines provided similar results to within the margins of error. The correlation coefficients of EW versus abundance and $\chi$ versus abundance are in general $\approx$0.1 or smaller, always smaller than 0.3, and Fe  I and Fe II provide consistent measurements that agree to within 0.03 dex. Praesepe stars are an exception because we were unable to find parameters as good as those obtained for the other stars and consistent with the photometric data, and in some cases accepted correlation coefficients as high as 0.5. The explanation for this is that we have used the same line list for all the sample, therefore Praesepe stars, which are more metal rich and have an EW range that is shifted towards larger values, have a higher percentage of lines that are close to saturation and fewer weak lines, hence a less constrained microturbulence. Furthermore, microturbulence is significantly higher in Praesepe stars than in the others. Differences in the structure of the photosphere, due to higher metallicity and rotation velocity, could produce a higher microturbulence. In any case, as we see, our measurement of a significantly higher chemical abundance for these stars is robust.

For each tentative combination of temperature, gravity, and microturbulence values of the grid, the metallicity was initially set to solar, and then iteratively substituted with the average abundance corresponding to the Fe  I lines, until convergence was achieved. Furthermore, for each measured line, the abundances were calculated differentially with respect to the sun. This, in addition to the afore-mentioned more robust parameter determination, allows us to compensate for errors in the $\log~gf$ values (Langer et al. 1998).

The steps in the grid values are 20 K for temperature, 0.02 dex for $\log ~G$, and 0.02 km s^-1 for $\xi$. We used between 54 and 64 Fe  I and between 9 and 11 Fe  II lines for each star. For only three Praesepe stars, no higher than 7 or 8 Fe  II lines could be measured reliably, and for one star, no more than 42 Fe  I lines.

As expected, we found a correlation between microturbulence and temperature obtained as described above. Praesepe stars, as already discussed, have a significantly higher microturbulence value; we therefore calibrated two different linear T-versus-$\xi$relationships, one for Praesepe, and one for the remaining stars.

We fine-tuned the parameters, to ensure that $\xi$ was as close as possible to the value expected from the calibrations, and the gravity as consistent as possible with the spectroscopic temperature, not anymore with the photometric one.

We calibrated the T-versus-$\xi$ relationship for the second time, with the finally adopted parameters, not using Praesepe stars. The result is:

$$\xi=-5.42+6.30\cdot\frac{T_{\rm eff}}{T_{\odot}},\ \ \ \ \sigma=0.06$$

here $\sigma$ represents the standard deviation of datapoints about the fit. For the remainder of the paper, we refer to  $\xi_{\rm fit}$as the microturbulence values derived from the fit above.

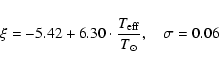
Abundances were finally recomputed by assuming the fine-tuned parameters.

In cluster stars, we measured the abundance of oxygen, which is treated separately, iron, calcium, aluminum, sodium, nickel, titanium, chromium, and silicon. As for iron lines, we used solar measurements as reference values for all of our [X/H] estimates of cluster stars, computing for all elements the difference between the stellar and the solar value for each line measured.

Oxygen abundances, instead, were derived from measured EWs of the O  I 6300.30 Å forbidden line employing the same method used by Randich et al. (2006). Specifically, we employed MOOG (Sneden 1973, version 2002) and Kurucz model atmospheres (Kurucz 1993). We used the driver blend, which allowed us to take into account the contribution of the blending Ni  I 6300.34 feature to the measured EWs of the 6300.3 Å feature. As input to MOOG, we used the results of our analysis for stellar parameters and iron and nickel abundances. For the oxygen and nickel lines we employed ${\it gf}$-values equal $\log~{\it gf}=-9.717$ and $\log~{\it gf}=-2.11$, respectively, following Allende Prieto et al. (2001) and Johansson et al. (2003) (see Randich et al. 2006, for additional details).

Because of the cluster radial velocities, we did not need to correct for the presence of telluric lines for NGC 3680, Praesepe, and M 67; on the other hand, telluric lines severely affected the spectra of IC 4651 stars, and we were unable to correct for this due to the unavailability of suitable standard stars. Finally, for three stars in Praesepe and one in M 67 we were unable to measure the O  I line.

Table 2: Comparison between our solar abundances (second Col.) and those of Grevesse & Sauval (2000) (third column). For iron, the abundance value obtained using ionised lines is also given. The number of lines and the standard deviation of the measurements for each species are also reported in the fourth and in the fifth column respectively. When only three or two lines are measured (sodium and aluminum), half of the difference between the maximum and minimum value is reported instead of the standard deviation.

   
4 The results

The results for the Sun are summarised in Table 2, those for the cluster stars in Table 3.

The results shown in Table 2 were obtained for the (T=5780, G=4.40, $\xi= 1.1$) model. In Col. 1 we indicate the element and ionization stage. In Col. 2 we wrote our results, and in Col. 3 the values from Grevesse & Sauval (2000) are given as comparison.

For each star, the mean abundance values of all elements studied, apart from oxygen are given in Table 3, along with the error calculated by the analysis described in Sect. 4.1. The standard deviation corresponding to the measurements of the different lines, and the number of lines measured for each element are also given (when no more than three lines could be measured, half the difference between the highest and lowest values is given instead of the standard deviation). All values refer to neutral-element lines. The stars are grouped by cluster, and for each cluster one abundance is obtained by averaging the abundance of all stars. The relative standard deviation is also computed, apart from for NGC 3680, for which only 2 stars were observed. In this case, half of the difference between the two stellar abundances is given. These standard deviations indicate the robustness of our analysis. Only in four cases (aluminum in Praesepe and M 67 and titanium and chromium in M 67) the cluster abundance dispersion is larger than 0.07 dex. Furthermore, we note that the dispersion in the stellar abundances of M 67 is significantly enhanced by Sanders 1287, which always shows the lowest chemical content. Its case is worth further investigation. On the other hand, the maximum difference for stars belonging to the same cluster can easily exceed 0.1 dex, which implies that caution should be taken when deriving conclusions based on a small number of objects. To represent errors in the final values, we use the standard deviations of the stellar abundance measurements in each cluster.

Since for Praesepe, in the parameter determination, higher EW-[Fe/H] and $\chi$-[Fe/H] correlations are sometimes found, we assume the more conservative average error estimate for its single stars originating in the analysis described in Sect. 4.1 of 0.10 dex. By doing so we account for the possibility of a systematic component in the parameter determination of Praesepe stars.

   
4.1 Errors

There are three sources of measurement errors in our abundance analysis:

-

error in EW measurements;

-

error in atmospheric parameters;

-

error in $\log {\it gf}$ values.

The last item is the least significant, since it should be almost eliminated when subtracting the solar abundances from the stellar ones. On the other hand, EW measurements and atmospheric parameter determinations are affected by errors that are not necessarily negligible for in the stellar and the solar estimations.

   
4.1.1 Errors in equivalent width measurements and log gf

Errors in EW measurements are due mostly to the uncertainty in the choice of the continuum; we should therefore underestimate these significantly by using the Cayrel formula (Cayrel et al. 1988). They are by far the most significant contributors to the dispersion in the abundance measurements for different lines of the same element. Divided by the square root of the number of lines, the dispersion in the abundance measurements has to be quadratically added to the other contributions to compute the global error.

   
4.1.2 Errors in the parameter atmosphere

To evaluate the uncertainty in the parameters, we used the differences between those derived in our spectral analysis, $T_{\rm spec},\ \ G_{\rm spec}$, and $\xi_{\rm spec}$; and the computed ones, $T_{\rm phot},\ \ G_{\rm phot}$, and $\xi_{\rm fit}$. The evaluations of $T_{\rm phot}$ and $G_{\rm phot}$ and the linear regression used to compute  $\xi_{\rm fit}$, were discussed in Sect. 3. The uncertainty in the gravity was calculated to be the quadratic average (equal to the standard deviation) of $G_{\rm spec}-G_{\rm phot}$. We adopted the rms of the $\xi_{\rm spec} - \xi_{\rm fit}$ differences to represent the uncertainty in $\xi$. We remind the reader that the linear fit indicating  $\xi_{\rm fit}$ as a function of temperature was computed without using Praesepe stars. The uncertainty in the microturbulence, which is higher, was computed separately using the same formula.

For the temperature, we used a slightly modified approach; if we had proceeded in the same way, we would have overestimated the uncertainty in temperature and been unable to determine the errors in the reddening, which may contribute to the differences $T_{\rm spec}-T_{\rm phot}$. We therefore computed the mean value of $T_{\rm spec}-T_{\rm phot}$ for each cluster, and assumed that the mean value was due to an incorrect evaluation of the reddening. Only after subtracting this value from each term did we proceed in evaluating the standard deviation of $T_{\rm spec}-T_{\rm phot}$.

The final values for the uncertainty in the parameters are: $\Delta T=110$ K, $\Delta G=0.07$ log (gr cm s^-2), $\Delta \xi=0.06$ km s^-1, $\Delta \xi=0.18$ km s^-1 for Praesepe

4.1.3 Errors in the final abundance values

To evaluate the uncertainty in the final abundance due to the error in a particular atmospheric parameter ( $T_{\rm eff}$, $\log ~G$ or $\xi$), we repeated the entire chemical analysis twice: in the first analysis, we increased the value of the parameter, and in the second analysis, decreased its value, by an amount equal to the error in the parameter computed as described in Sect. 4.1.2, while all other parameters were kept constant. We then completed a similar procedure to determine the errors in the EW measurements and $\log~{\it gf}$ (see Sect. 4.1.1) and we finally added quadratically all the contributions.

However, as discussed above, we propose that a more robust estimate of our final errors in the abundances are represented by the standard deviation values. The abundance measurements of different stars belonging to the same cluster actually represent independent evaluations of the same quantity, which is the cluster abundance. The error analysis in this section is supposed to determine which parameters influence the final determination most significantly, and confirm whether our method for evaluating such parameters is robust.

We find that the uncertainty in the temperature dominates the final error, since the other contributions are in most cases marginal or even negligible, and that the assumed uncertainty of 110 K, which is due to the different methods of measurement for photometric and spectroscopic data, appears to slightly overestimate the errors.

As for the EW, although for a single line, the measurement error can reach up to $\sim$$20 \%$, having at our disposal many lines means that its contribution to the total error is far less important than the uncertainty in the temperature.

According to these tests, silicon is more insensitive than the other elements to the uncertainties. It is remarkable as shown in Table 3 the dispersion in measurements of [Si/H] for each cluster is among the smallest, and is the smallest dispersion value for all elements for IC 4651 and NGC 3680 despite the small number of lines used. This again points towards a good consistency in our analysis.

Table 4: Table of the typical errors associated with abundance measurements of iron (about sixty Fe I lines), sodium (two or three lines), and nickel (about twenty lines).

Table 5: EWs of the 6300.30 Å O  I line derived oxygen abundances. In both columns, the global cluster errors for the cluster refer to the standard deviations in the abundances originating in the single stars, while reported errors in single star abundance measurements come from the uncertainty in the EWs. See the text for the errors due to the parameter uncertainty.

4.2 Oxygen

The measured EWs of the 6300.30 Å line, and derived n(O) and [O/Fe] values are listed in Table 5. We recall from Randich et al. (2006) that by using the same method and log-gf values, we derive a solar oxygen abundance $n({\rm O})_{\odot}=8.66$.

The listed errors in n(O) values include the contribution of uncertainties in the measured EWs of the forbidden line and errors in Ni abundances (which are, however, negligible). The uncertainties in stellar parameters, i.e. $\Delta T = \pm 110$ K, $\Delta G = \pm 0.07$ dex, and $\Delta \xi = \pm 0.06$ km s^-1, correspond respectively to the uncertainties $\Delta n({\rm O})=-0.08/0.05$, $\pm$0.04, and $\pm$0.02. The uncertainty of $\pm$0.19 km s^-1 for the microturbulence velocity in Praesepe stars, corresponds, instead, to $\Delta n({\rm O})=0.06$/-0.07.

Based on a single, faint line, these measurements are affected by considerable uncertainty. On the other, hand the average value for each cluster has a standard deviation that is smaller than the typical uncertainty in the [O/Fe] estimation of each single star.

4.3 Comparison with published data

In this section, we provide an overview of the published data about chemical abundances in our target clusters, and compare them with our results. The content of the section is summarised in Table 6, in which we do not consider photometric and low-resolution spectroscopy studies. We add the data compilation for Collinder 261, NGC 6253, and Berkeley 29, which have been studied twice, to compare results from independent sets of chemical analysis and verify the overall reliability of abundance measurements from high-resolution spectroscopy.

4.3.1 NGC 3680

For this cluster Anthony-Twarog & Twarog (2004) obtained a measurement of [Fe/H] = -0.14 $\pm$ 0.03, which was in agreement with the measurement of Pasquini et al. (2001) of [Fe/H] = - $0.17\pm0.12$. The former analysis was based on CCD photometry for the intermediate-band uvbyCaH$\beta$, and the latter was instead based on a small part of a high dispersion spectrum of a single giant.

Friel et al. (2002) published radial velocities and metallicities for 39 clusters older than the Hyades. They used spectra of resolution 4 Å FWHM. We studied two clusters in their target list, M 67 and NGC 3680, for which they measured [Fe/H] = -0.15 and -0.19 dex respectively, with a standard error of 0.05 dex for both values. They studied 25 stars in M 67 and 7 in NGC 3680. The contrast with our result is significant, but both our measurements and those of Friel et al. (2002) point to a difference of about 0.05 dex between the two clusters, NGC 3680 being more metal poor. The disagreement between eech of the afore-mentioned measurements of the metallicity in NGC 3680 and that of [Fe/H] = +0.11 given by Nordstroem et al. (1997) based on uvby$\beta$ photometry, cannot be attributed entirely to measurement errors.

Our measurement of a slightly metal-poor composition ([Fe/H] = - $0.04\pm0.03$) is the first to our knowledge based on high-resolution spectra of a wide wavelength range.

Figure 1: Comparisons between iron line EW measurements of stars with different abundances and with similar (spectroscopic) temperatures. Two Praesepe stars are compared respectively with a star in IC 4651 (KW 326 versus AMC 4220, left panel) and in M 67 (KW 100 versus Sanders 1092, right panel). Fe  I and Fe  II lines are plotted with different symbols. KW 100 and Sanders 1092 have virtually the same temperature. AMC 4220 is evaluated to be about 100 K hotter than KW 326, which reduces the effect of the metallicity difference on the EW ratios between the two stars.

Open with DEXTER

Table 7: Results of our revised abundance analyses of Praesepe stars. In the upper part of the table, theoretical parameters are used (temperature from the photometry, gravity from the models and the temperature and microturbulence from the fit). In the lower part of the table, we adopted the most reliable measurements of parameters found by ignoring constraints from photometry or models. Also these analyses confirm the high metallicity of Praesepe is evident.

4.3.2 IC 4651

For IC 4651 several measurement of metallicity are available. Pasquini et al. (2004) obtained their results using UVES spectra. They observed twenty stars, including both dwarfs and giants. A considerable effort was made to study stars corresponding to the region around the turn off. They measured an iron abundance of [Fe/H] =  $0.10\pm 0.03$, in excellent agreement with ours. Carretta et al. (2004) observed 4 clump stars with the high-resolution spectrograph FEROS at the focus of the ESO 1.5-m telescope, and measured [Fe/H] =  $0.11\pm0.01$. In this case, the agreement in the measurement of iron abundance is excellent, and it is remarkable that the same iron content is found for both giants and dwarfs. Meibom et al. (2002) also measured [Fe/H] = 0.1 dex, using uvby$\beta$ data. For this cluster, the measurements of [Fe/H] obtained by independent studies appear to be in remarkably good agreement.

As far as other elements are concerned, we can compare our measurements with those of Pasquini et al. (2004), who measured abundances for several elements in common with our study. The measurements for main sequence stars are in good agreement (within 0.03 dex) with our own for calcium, aluminum, and nickel. The discrepancy found between our measurements of sodium abundances is also within the margins of error (0.06 dex, which corresponds to approximately 1$\sigma$). For the remaining elements (silicon, titanium and chromium) the difference ranges from 0.09 to 0.11 dex. We note that, while we consider only data for main-sequence stars, the values given in Table 9 from Pasquini et al. (2004) correspond to the overall cluster abundance, and the agreements between our measurements and theirs are poorer. Within a margin of uncertainty of 2$\sigma$, all the results show a substantial solar-scaled mixture.

4.3.3 M 67

For this cluster Tautvaisiene et al. (2000) obtained [Fe/H] = - $0.03\pm0.03$ by analysing evolved stars, including helium core-burning stars of the clump. Hobbs & Thorburn (1991) measured [Fe/H] = - $0.04\pm 0.12$. A similar value of [Fe/H] = -0.05 was found using calibrations of the ultraviolet excess at (B-V)₀=0.06 as a function of [Fe/H] (Montgomery et al. 1993). Friel & Boesgaard (1992) acquired spectra at a resolution of 0.25 Å for three M 67 dwarf stars of [Fe/H] values of -0.07, 0.05 and 0.03. Yong et al. (2005) collected spectra at a resolution of 28 000 for K-giant members of several open clusters, including 3 stars in M 67. Iron abundances measured using Fe  I lines for these stars are: 0.03, -0.05, and -0.01 dex. They provided a final result for the cluster, taking account of measurements obtained using the Fe  II lines, of $0.02\pm0.14$.

These results all agree reasonably with our own. Finally, a study on M 67, based also on UVES spectra of main-sequence stars (Randich et al. 2006), measured [Fe/H] =  $0.03\pm0.03$, which agrees with our measurement of $0.03\pm 0.04$.

For the remaining elements, the comparison with Randich et al. (2006) is also very satisfactory: the discrepancies are in most cases (aluminum, calcium, titanium and nickel) within 0.02 dex, and only for oxygen and sodium do the measurements differ by as much as 0.08 and 0.07 dex, respectively. We recall that we used the same line list but different synthesis code and model atmosphere from those adopted by Randich et al. (2006).

The measurement of Yong et al. (2005), despite the agreement in the measurement of the iron abundance, infer abundance ratios that are systematically higher than ours. The disagreement is twice as large as their quoted rms errors, or more, as in the cases of aluminum, sodium and titanium.

Our conclusion is that all studies completed are in good agreement in their measurement of the M 67 iron content, which is equal to the solar value, and most of them reach the same conclusion also for the abundance of other elements. However, disagreement between some element abundance measurements does exist, in particular for aluminum and sodium. We note that for these two elements the abundances rely only on few lines, and that the Yong et al. (2005) analysis is based only on giant stars. Furthermore, for these two elements, discrepancies between the abundances for dwarfs and giants in the same cluster have been observed (see e.g. Randich et al. 2006).

4.3.4 Praesepe

Former studies of the metallicity of this cluster measured either barely supersolar or definitely supersolar. Our result is in agreement with those of the latter group. Boesgaard & Budge (1988) used high resolution spectra (0.1-0.2 Å) of five F dwarfs and one spectroscopic binary taken at the Palomar 5-m Hale telescope, and measured $\rm [Fe/H]=0.13\pm 0.07$. Boesgaard (1989) reanalysed three of the five Praesepe F dwarf spectra presented in Boesgaard & Budge (1988), selecting those with low rotational velocities and well determined temperatures. They found [Fe/H] values of 0.033, 0.106, and 0.147, which implied a revised value for the mean cluster metallicity of $\rm [Fe/H]=0.092\pm 0.067$. Friel & Boesgaard (1992) also measured Praesepe's mean metallicity and their result was $\rm [Fe/H]=0.038\pm 0.039$. They studied two stars in common with Boesgaard (1989), with which the result agreed very well (0.033 and 0.016 dex of difference in the measurements). In this case a disagreement with our measurement of $\rm [Fe/H]=0.27$ is clearly evident.

For this cluster, An et al. (2007) obtained from spectroscopy a moderate supersolar metallicity ( $\rm [Fe/H]=0.11 \pm0.03$ dex), which is the adopted value: however they measured a higher value from photometric analysis ( $\rm [Fe/H]=0.20 \pm0.04$ dex). To measure both sets of measurements, they adopted published reddening data and performed simultaneous parameter determination.

Figure 1 shows comparisons between iron line EW measurements in one Praesepe star and one star in IC 4651 (left panel) and one in M 67 (right panel). For the comparisons, we chose two pairs of stars whose temperatures, derived from the spectral analysis, differed by only 110 K and 10 K. We display the comparison of sets of measurements for KW 326 against AMC 4220 (in the left panel), and KW 100 against Sanders 1092 (in the right panel of Fig. 1). The differences between the EWs are of about 15$\%$ for KW 326 and AMC 4220 and even higher for KW 100 and Sanders 1092.

We repeated the chemical analysis of Praesepe stars using two different combinations of parameters in addition to those adopted. First, we used the values computed in Sect. 3, namely  $T_{\rm phot}$, $G_{\rm phot}$, and  $\xi_{\rm fit}$. Then, we used the combination of parameters that flatten the EW versus abundance and the $\chi$ versus abundance trends. The latter is the combination of parameters that we would have obtained by means of the spectral analysis if we had ignored photometric data. They differ from the adopted values because the adopted values were adjusted to ensure closer agreement with the values of  $T_{\rm phot}$, $G_{\rm phot}$, and  $\xi_{\rm fit}$, as explained in Sect. 3.

In both cases, and for each and every star, the abundance analysis confirmed that the cluster was metal-rich, as can be seen in Table 7. We can confidently conclude Praesepe shows an enhanced average metallicity of not lower than $\approx$0.2 dex, which implies that it is closer in metallicity to the Hyades than previously understood (see Sect. 5).

Table 8: Comparison between spectroscopic and computed values, i.e. photometric temperatures and gravities computed assuming photometric temperatures. The photometric temperatures are computed by means of the infrared magnitudes from the 2MASS catalogue (shown in the second, third and fourth column), which were converted into TCS colours, and the available V magnitudes (shown in fifth column).

   
4.4 Comparison between photometric and spectroscopic temperatures

In Table 8, we show the photometric data adopted, the stellar parameters derived from these photometric data and the spectroscopic parameters. The mean $T_{\rm spec}-T_{\rm phot}$ values are 120, 325, 122, and 169 K for NGC 3680, IC 4651, Praesepe, and M 67 respectively. With the exception of two Praesepe stars, the photometric temperature is always lower than the spectroscopic one. Praesepe suffers little extinction, and its mean $T_{\rm spec}-T_{\rm phot}$value, as for NGC 3680, is amongst the lowest. However, it is also the only cluster for which the stellar values of this quantity are scattered about the average value, which is unsurprising, since, as discussed in Sect. 4.1.2, there were more problems in the determination of the spectroscopic parameters for Praesepe stars. The systematic bias towards positive $T_{\rm spec}-T_{\rm phot}$ has three possible causes: errors in the colour-temperature transformation, errors in the adopted cluster reddening, and some systematic effect in determining the spectroscopic temperature. While the error in the cluster extinction depends on the individual cluster, the other sources of systematic errors should affect all stars in a similar way. All clusters have a similar average $T_{\rm spec}-T_{\rm phot}$, apart from IC 4651 for which this quantity is $\approx$150 K higher than in M 67 and $\approx$200 K higher than in the other two clusters. It is natural to suggest that this is due to an underestimation of the B-V colour excess adopted for IC 4651 (Anthony-Twarog & Twarog 1987). If this is the case, a value about 0.04 higher, i.e. E(B-V) of between 0.12 and 0.13 mag, is the correct value. Similar conclusions were reached by Pasquini et al. (2004) and Biazzo et al. (2007).

4.5 Summary

For most elements and all clusters, our results infer, or are at least consistent with, solar-scaled abundances in all four target clusters, regardless of whether we consider $\alpha$ elements (oxygen, silicon, calcium, and titanium), iron-peak elements (iron, chromium and nickel), or the odd-Z elements aluminum and sodium. Among the few elements that are an exception to these trends, oxygen is 0.4 dex below its solar-scaled value in Praesepe and 0.2 above this value for NGC 3680. Subsolar (slightly outside the margins of errors) metallicities were also measured for aluminum in NGC 3680 and IC 4651, and nickel in NGC 3680.

   
5 The metallicity gradient and the age-metallicity relationship

The comparison of our metallicity measurements with other high-quality data analyses made in Sect. 4.4, clearly shows that these studies agree within the quoted errors even when they employ different model atmospheres and methods of analysis. In Table 9, we compile all the open cluster abundance measurements to our knowledge, obtained using high-resolution spectroscopic analysis. For our target clusters, abundance data and relative errors are taken from the present work, regardless of whether or not other results are also available. For M 67 and IC 4651, our results are, however, almost indistinguishable from the mean literature value. For Collinder 261, Berkeley 29, and NGC 6253, we indicate the average of the two determinations in Table 6 and half of the differences between them as abundance estimation and relative error respectively. The results are shown with their references, the instruments used, and the spectral resolution. Cluster ages and Galactocentric distances are also given. For the latter values, in the cases in which we used the WEBDA database, we adopted the distance and the Galactic coordinates from the database, and assumed a solar distance from the Galactic centre of 8 kpc, to be consistent with Bragaglia & Tosi (2006).

We considered only one study of Hyades cluster, i.e. Paulson et al. (2003), which was nevertheless extensive (almost one hundred target stars) and measured $\rm [Fe/H]=0.13 \pm 0.05$  dex. The history of the metallicity measurements for Hyades is summarised by Takeda (2008) (see Fig. 8 of this paper): they range from $\approx$0.1 to $\approx$0.2 dex, Takeda's analysis favouring the higher results.

The other element abundance ratios given in Paulson et al. (2003) are solar within $1 \sigma$, emphasising the similarity between Hyades and Praesepe.

The abundance data and the Galactocentric distances in Table 9 have been displayed in the Galactocentric-distance versus metallicity diagram of Fig. 2. The Hyades abundance used in this figure was 0.16 dex, with an error bar of 0.04 dex, to take into account both the aforementioned result of Paulson et al. (2003) (0.13 dex), and the higher estimations at around 0.2 dex given by other authors. Error bars along the x-axis are difficult to evaluate: it would indeed be unwise to extend the limits of the statistical analysis too far, although several kpc can easily be reached for the most distant clusters. Homogeneous and reliable photometry and open cluster parameter determination are as important as the robustness of the metallicity measurements. Of the four datapoints from this work in Fig. 2, only Praesepe departs significantly above the -0.06-dex/kpc-steep linear fit. The only other two clusters that have an exceptionally high iron content are the very metal rich NGC 6253 and NGC 6791, whose abundances are also solar scaled for most of the elements (Carretta et al. 2007; Sestito et al. 2007). Anyway, these three clusters are very different from one another as far as age and location are concerned. In particular the relatively young and close-by Praesepe has not formed significantly inside the Galactic disk and drifted outwards later on, as suggested for NGC 6791 (Carretta et al. 2007).

It is worth mentioning that the most metal rich clusters analysed so far, NGC 6253 and NGC 6791, to which we add Praesepe, are all very subsolar in oxygen, which may lead us to conclude that they formed out of material enriched by type Ia supernovae. However, this suggestion is not supported by the abundance ratios of the other alpha elements, which are in general solar in value.

Figure 2: Abundance gradient as resulting from high-spectroscopy open cluster chemical analyses. Data plotted and relative error bars are as in Table 9; for Hyades only, we have adopted in this figure a different value, i.e. $0.16 \pm 0.04$ dex, which takes into account also other estimations of about 0.2 dex. The y-axis of the filled symbol points refer to our datapoints. The line represents the -0.06 dex/kpc relation.

Open with DEXTER

6 Conclusions

This work is one of several aimed at collecting high-precision abundance measurements in open clusters, based on high-resolution and high-signal-to-noise spectra. We present data for four clusters, and confirm all of the abundance trends present in the literature for IC 4651 and M 67. For these clusters, all determinations agree to within a few hundredths of dex, irrespective of whether dwarfs or giants have been observed. We report slightly different abundances for NGC 3680 and mostly Praesepe, which is shown to be substantially metal rich.

The modern iron determinations agree very well in most of cases, though there is still no precise agreement about the extent to which Praesepe and Hyades are supersolar. Metallicity measurements for open clusters are in general consistent, irrespective of the analysis method and research group. As for abundance ratios of elements other than iron, significant differences between the results of the different groups still arise.

The dispersion within each cluster is limited to a few hundredths of a dex, and differences of up to 0.1 dex or more are measured between the individual stars. These differences have to be interpreted as being due to limitations in the observations and in the analysis rather than true, intrinsic chemical variations in the cluster composition. Caution should therefore be taken when adopting analyses that consider only one or a few stars per cluster.

We find a significant supersolar metallicity for IC 4651 ( $\rm [Fe/H]=0.12\pm 0.05$) and a solar metallicity for M 67 ( $\rm [Fe/H]=0.03\pm 0.04$) and a slightly subsolar metallicity for NGC 3680 ( $\rm [Fe/H]=-0.04\pm 0.03$). The surprising result is that of Praesepe, which is as metal rich as $\rm [Fe/H]=0.27\pm 0.10$. The photometric analysis of An et al. (2007) also indicates that Praesepe is metal rich. The reasons for the discrepancy with other results need to be further investigated.

For other elements, the composition is solar within the errors for all elements and for all the clusters, except for aluminum (subsolar in NGC 3680 and IC 4651), nickel (also subsolar in NGC 3680), and oxygen. We find [O/Fe] to be $\approx$0.2 and $\approx$-0.4 in NGC 3680 and Praesepe respectively, and just $\approx$$1 \sigma$ below the solar value in M 67.

We confirm the extraordinarily similar overall chemical composition of the Sun and the star cluster M 67.

Acknowledgements

We are greatly indebted to Sofia Randich for her contribution to the data analysis presented here and for many useful comments. Jorge Melendez, Nuno Santos, Valentina D'Orazi and K. Sinha deserve to be warmly thanked for their valuable feedback. Our analysis presented here was based on observations obtained at the ESO Very Large Telescope (VLT). This publication made use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation; and from the WEBDA database, created by J.-C. Mermilliod and now operated at the institute for Astronomy of the University of Vienna. The SIMBAD astronomical database and the NASA's Astrophysics Data System Abstract Service have also been extensively used. G.P. acknowledges the support of the project PTDC/CTE-AST/65971/2006 of the Portuguese FCT and that of Indian DST, L.P. acknowledges ESO DGDF.

References

• Allende Prieto, C., Lambert, D. L., & Asplund, M. 2001, ApJ, 556, L63 [NASA ADS] [CrossRef] (In the text)
• An, D., Terndrup, D. M., Pinsonneault, M. H., et al. 2007, ApJ, 655, 233 [NASA ADS] [CrossRef] (In the text)
• Anthony-Twarog, B. J., Mukherjee, K., Twarog, B. A., & Caldwell, N. 1988, AJ, 95, 1453 [NASA ADS] [CrossRef] (In the text)
• Anthony-Twarog, B. J., & Twarog, B. A. 1987, AJ, 94, 1222 [NASA ADS] [CrossRef] (In the text)
• Anthony-Twarog, B. J., & Twarog, B. A. 2004, AJ, 127, 1000 [NASA ADS] [CrossRef] (In the text)
• Barrado y Navascués, D., Deliyannis, C. P., & Stauffer, J. R. 2001, ApJ, 549, 452 [NASA ADS] [CrossRef]
• Biazzo, K., Pasquini, L., Girardi, L., et al. 2007, A&A, 475, 981 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Boesgaard, A. M. 1989, ApJ, 336, 798 [NASA ADS] [CrossRef] (In the text)
• Boesgaard, A. M., & Budge, K. G. 1988, ApJ, 332, 410 [NASA ADS] [CrossRef] (In the text)
• Bragaglia, A., & Tosi, M. 2006, AJ, 131, 1544 [NASA ADS] [CrossRef]
• Bragaglia, A., Gratton, R. G., Carretta, E., et al. 2001, AJ, 122, 207 [NASA ADS] [CrossRef]
• Bragaglia, A., Sestito, P., Villanova, S., et al. 2008, A&A, 480, 79 [NASA ADS] [CrossRef] [EDP Sciences]
• Carraro, G., & Chiosi, C. 1994, A&A, 287, 761 [NASA ADS] (In the text)
• Carraro, G., Bresolin, F., Villanova, S., et al. 2004, AJ, 128, 1676 [NASA ADS] [CrossRef]
• Carretta, E., Bragaglia, A., Gratton, R. G., & Tosi, M. 2004, A&A 422, 951 [NASA ADS] [CrossRef] (In the text)
• Carretta, E., Bragaglia, A., Gratton, R. G., & Tosi, M. 2005, A&A, 441, 131 [NASA ADS] [CrossRef] [EDP Sciences]
• Carretta, E., Bragaglia, A., & Gratton, R. G. 2007, A&A, 473, 129 [NASA ADS] [CrossRef] [EDP Sciences]
• Cayrel, R., Cayrel de Strobel, G., & Campbell, B. 1988, The Impact of Very High S/N Spectroscopy on Stellar Physics, IAU Symp., 132, 449 (In the text)
• Chiappini, C., Matteucci, F., & Gratton, R. 1997, ApJ, 477, 765 [NASA ADS] [CrossRef]
• Chiappini, C., Matteucci, F., & Romano, D. 2001, ApJ, 554, 1044 [NASA ADS] [CrossRef]
• Dekker, H., D'Odorico, S., Kaufer, A., Delabre, B., & Kotzlowski, H. 2000, Proc. SPIE, 4008, 534 [NASA ADS] (In the text)
• Dias, W. S., & Lépine, J. R. D. 2005, ApJ, 629, 825 [NASA ADS] [CrossRef] (In the text)
• Edvardsson, B., Andersen, J., Gustafsson, B., et al. 1993, A&A, 275, 101 [NASA ADS] (In the text)
• Eggen, O. J. 1969, ApJ, 155, 701 [NASA ADS] [CrossRef] (In the text)
• Eggen, O. J. 1971, ApJ, 166, 87 [NASA ADS] [CrossRef] (In the text)
• Ford, A., Jeffries, R. D., & Smalley, B. 2005, MNRAS, 364, 272 [NASA ADS] [CrossRef]
• François, P., Matteucci, F., Cayrel, R., et al. 2004, A&A, 421, 613 [NASA ADS] [CrossRef] [EDP Sciences]
• Friel, E. D., & Boesgaard, A. M. 1992, ApJ, 387, 170 [NASA ADS] [CrossRef] (In the text)
• Friel, E. D., & Janes, K. A. 1993, A&A, 267, 75 [NASA ADS] (In the text)
• Friel, E. D., Janes, K. A., Tavarez, M., et al. 2002, AJ, 124, 2693 [NASA ADS] [CrossRef] (In the text)
• Friel, E. D., Jacobson, H. R., Barrett, E., et al. 2003, AJ, 126, 2372 [NASA ADS] [CrossRef]
• Friel, E. D., Jacobson, H. R., & Pilachowski, C. A. 2005, AJ, 129, 2725 [NASA ADS] [CrossRef]
• Girardi, L., Bressan, A., Bertelli, G., & Chiosi, C. 2000, A&AS, 141, 371 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Gratton, R. 2000, Stellar Clusters and Associations: convection, Rotation, and Dynamos, ASP Conf. Ser., 198, 225 (In the text)
• Grevesse, N., & Sauval, A. J. 1999, A&A, 347, 348 [NASA ADS] (In the text)
• Grevesse, N., & Sauval, A. J. 2000, Origin of Elements in the Solar System, Implications of Post-1957 Observations, 261 (In the text)
• Hobbs, L. M., & Thorburn, J. A. 1991, AJ, 102, 1070 [NASA ADS] [CrossRef] (In the text)
• Hobbs, L. M., Thorburn, J. A., & Rodriguez-Bell, T. 1990, AJ, 100, 710 [NASA ADS] [CrossRef]
• King, J. R., & Hiltgen, D. D. 1996, AJ, 112, 2650 [NASA ADS] [CrossRef]
• Klein Wassink, W. J. 1927, Publications of the Kapteyn Astronomical Laboratory Groningen, 41, 1 [NASA ADS] (In the text)
• Johansson, S., Litzén, U., Lundberg, H., & Zhang, Z. 2003, ApJ, 584, L107 [NASA ADS] [CrossRef] (In the text)
• Johnson, H. L. 1952, ApJ, 116, 640 [NASA ADS] [CrossRef] (In the text)
• Jones, B. F., & Cudworth, K. 1983, AJ, 88, 215 [NASA ADS] [CrossRef] (In the text)
• Jones, B. F., & Stauffer, J. R. 1991, AJ, 102, 1080 [NASA ADS] [CrossRef] (In the text)
• Kurucz, R. 1993, ATLAS9 Stellar Atmosphere Programs and 2 km s^-1 grid. Kurucz CD-ROM No. 13 (Cambridge, Mass.: Smithsonian Astrophysical Observatory) (In the text)
• Langer, G. E., Fischer, D., Sneden, C., & Bolte, M. 1998, AJ, 115, 685 [NASA ADS] [CrossRef] (In the text)
• Latham, D. W., Mathieu, R. D., Milone, A. A. E., & Davis, R. J. 1992, Evolutionary Processes in Interacting Binary Stars, 151, 471 [NASA ADS] (In the text)
• Lawrence, A., Warren, S. J., Almaini, O., et al. 2007, MNRAS, 379, 1599 [NASA ADS] [CrossRef] (In the text)
• McPherson, A. M., et al. 2006, Proc. SPIE, 6267 (In the text)
• Meibom, S., Andersen, J., & Nordström, B. 2002, A&A, 386, 187 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Modigliani, A., Mulas, G., Porceddu, I., et al. 2004, The Messenger, 118, 8 [NASA ADS] (In the text)
• Montgomery, K. A., Marschall, L. A., & Janes, K. A. 1993, AJ, 106, 181 [NASA ADS] [CrossRef] (In the text)
• Nordstroem, B., Andersen, J., & Andersen, M. I. 1996, A&AS, 118, 407 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Nordstroem, B., Andersen, J., & Andersen, M. I. 1997, A&A, 322, 460 [NASA ADS] (In the text)
• Pace, G., & Pasquini, L. 2004, A&A, 426, 1021 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Pasquini, L., Randich, S., & Pallavicini, R. 2001, A&A, 374, 1017 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Pasquini, L., Randich, S., Zoccali, M., et al. 2004, A&A, 424, 951 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Pasquini, L., Biazzo, K., Bonifacio, P., Randich, S., & Bedin, L. 2008, [arXiv:0807.0092] (In the text)
• Paulson, D. B., Sneden, C., & Cochran, W. D. 2003, AJ, 125, 3185 [NASA ADS] [CrossRef] (In the text)
• Platais, I., Melo, C., Mermilliod, J.-C., et al. 2007, A&A, 461, 509 [NASA ADS] [CrossRef] [EDP Sciences]
• Ramírez, I., & Meléndez, J. 2005, ApJ, 626, 465 [NASA ADS] [CrossRef] (In the text)
• Randich, S., Bragaglia, A., Pastori, L., et al. 2005, The Messenger, 121, 18 [NASA ADS]
• Randich, S., Sestito, P., Primas, F., Pallavicini, R., & Pasquini, L. 2006, A&A, 450, 557 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Sanders, W. L. 1977, A&AS, 27, 89 [NASA ADS] (In the text)
• Sestito, P., Bragaglia, A., Randich, S., et al. 2006, A&A, 458, 121 [NASA ADS] [CrossRef] [EDP Sciences]
• Sestito, P., Randich, S., & Bragaglia, A. 2007, A&A, 465, 185 [NASA ADS] [CrossRef] [EDP Sciences]
• Shen, Z.-X., Jones, B., Lin, D. N. C., Liu, X.-W., & Li, S.-L. 2005, ApJ, 635, 608 [NASA ADS] [CrossRef]
• Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] (In the text)
• Sneden, C. 1973, ApJ, 184, 839 [NASA ADS] [CrossRef] (In the text)
• Stix, M. 2002, The sun: an introduction - 2n [NASA ADS]d ed. /Michael Stix. Berlin: Springer, QB 521 .S75, (In the text)
• Takeda, Y. 2008, The Metal-Rich Universe, La Palma, June 2006, ed. G. Israelian, & G. Meynet (Cambridge Contemporary Astrophysics Series), in press (In the text)
• Tautvaisiene, G., Edvardsson, B., Tuominen, I., & Ilyin, I. 2000, A&A, 360, 499 [NASA ADS] (In the text)
• Tautvaisiene, G., Edvardsson, B., Puzeras, E., & Ilyin, I. 2005, A&A, 431, 933 [NASA ADS] [CrossRef] [EDP Sciences]
• Taylor, B. J., & Joner, M. D. 2002, A&AS 200, 902
• Villanova, S., Carraro, G., Bresolin, F., & Patat, F. 2005, AJ, 130, 652 [NASA ADS] [CrossRef]
• Yong, D., Carney, B. W., & Teixera de Almeida, M. L. 2005, AJ, 130, 597 [NASA ADS] [CrossRef] (In the text)

 

  
Online Material

Table 3: Table of the computed abundances, all from the neutral-element lines. In the rows with the average the standard deviation refers to the different stellar values within the cluster (for NGC 3680 we give half of the difference between the two stellar values). In the other rows the standard deviations refer to the measurements from he different lines. When no more than 3 lines are used for a given element, half the difference between the largest and the smallest values, rather than the standard deviation, is given. In the case of Praesepe the errors adopted are higher than the standard deviation: 0.10 dex.

Table 6: Literature data about high-resolution spectroscopic studies of clusters that have more than one high-resolution entry. Errors refer to the rms dispersion between stellar values, or half of the full spread when only two or three stars are studied. From Cols. 1 to 8 we indicate the abundance measurements. In Col. 9, the number of stars used is given; in Col. 10, the reference, in Cols. 11 and 12, we indicate, respectively, the spectral resolution and the instrument and/or the observatory.

Table 9: Compilation of high-resolution studies on open clusters. The first panel shows the results of the abundance analyses, while the second one summarises dataset and clusters' properties, showing, in the given order, the number of stars used, the reference (i.e. number in the bibliography and ``PPF'' for the present study; some of the cited references for the abundances are compilations of the results obtained by the same group), the spectral resolution power, the instrument and/or the telescope employed, clusters' Galactocentric distances and ages. The two latter values are flagged with a letter according to the reference used: F for Friel & Janes (1993), B for Bragaglia & Tosi (2006), C for Carraro & Chiosi (1994) and W for the WEBDA database.