A&A 489, 419-427 (2008)
DOI: 10.1051/0004-6361:200809777
The directivity of solar type III bursts at hectometer and kilometer wavelengths: Wind-Ulysses observations
X. Bonnin - S. Hoang - M. Maksimovic
Observatoire de Paris, LESIA, UMR 8109 CNRS, 92195 Meudon, France
Received 13 March 2008 / Accepted 28 May 2008
Abstract
We investigate the directivity of solar type III radio bursts at
hectometer and kilometer wavelengths using radio data recorded
simultaneously by the Wind and Ulysses spacecraft which are widely
separated in heliocentric longitude and latitude. From the
positions of the associated flares and the solar wind speed and
plasma density measured aboard the spacecraft, we estimate the
location of the type III radio sources along the approximately
spiral magnetic field lines connected to the flare sites. Using
the ratios of the radio flux densities measured from 1995 to 2005
at the same frequencies (940-80 kHz) on these spacecraft, we have
for the first time derive the average directivity diagram of type
III bursts in two dimensions, longitude and latitude relative to
the emission source. This diagram is found to exhibit no
significant variation with the solar activity. The diagram in
longitude is found to shift east of the local magnetic field
direction at the source. The angular width and eastward shift of
the diagram are observed to increase with decreasing frequencies;
around 800 kHz, its full width at maximum/10 level is about
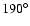 and its eastward shift
and its eastward shift 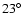 .
The diagram in
latitude, obtained uniquely thanks to the out-of-ecliptic orbit of
Ulysses, shows no significant variation with latitude.
.
The diagram in
latitude, obtained uniquely thanks to the out-of-ecliptic orbit of
Ulysses, shows no significant variation with latitude.
Key words: Sun: radio radiation - Sun: particle emission - plasmas - methods: data analysis
It is generally agreed that the solar type III radio bursts are
generated by suprathermal electrons (
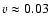 to 0.3 c),
ejected from solar active regions, accelerated in the low corona,
and traveling outward along open magnetic field lines into the
interplanetary medium (IPM). Along their path, these electrons
develop ``bump-on-tail'' distribution unstable to the production
of Langmuir waves at the local plasma frequency
to 0.3 c),
ejected from solar active regions, accelerated in the low corona,
and traveling outward along open magnetic field lines into the
interplanetary medium (IPM). Along their path, these electrons
develop ``bump-on-tail'' distribution unstable to the production
of Langmuir waves at the local plasma frequency
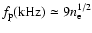 ,
where
,
where 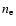 is the plasma density in cm-3. Some
of the Langmuir wave energy is then converted through nonlinear
wave-wave interactions into electromagnetic waves at the
fundamental and/or second harmonic of
is the plasma density in cm-3. Some
of the Langmuir wave energy is then converted through nonlinear
wave-wave interactions into electromagnetic waves at the
fundamental and/or second harmonic of 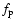 .
Since the energetic
electrons are guided along the open field lines, the ``bump-on-tail'' instability occurs essentially along these lines.
As a result, the type III emission is expected to radiate
primarily in about the magnetic field direction. On the other
hand, the propagation of radio waves through the inhomogeneous IPM
is controlled by large-scale structures (refraction and focusing)
and small-scale inhomogeneities (random scattering) of the plasma
density. These propagation effects are likely to significantly
modify the primary directivity of the radio emission, resulting in
a very different apparent directivity that is actually observed.
.
Since the energetic
electrons are guided along the open field lines, the ``bump-on-tail'' instability occurs essentially along these lines.
As a result, the type III emission is expected to radiate
primarily in about the magnetic field direction. On the other
hand, the propagation of radio waves through the inhomogeneous IPM
is controlled by large-scale structures (refraction and focusing)
and small-scale inhomogeneities (random scattering) of the plasma
density. These propagation effects are likely to significantly
modify the primary directivity of the radio emission, resulting in
a very different apparent directivity that is actually observed.
Knowledge of the emission directivity is of very important when
studying the emission mechanism and ubiquitous propagation effects in
the medium, particularly at low frequency. The first stereoscopic
observations of the type III directivity were carried out at 169 kHz by Caroubalos & Steinberg (1974) and Caroubalos et al. (1974) from the Earth and
Soviet planetary probe Mars-3. A thorough documentation of these
works at high frequencies was made by Poquérusse (1984). At
lower frequencies, namely at the hectometer and kilometer
wavelengths, the widespread visibility of the type III emission
was reported by MacDowall (1982), Dulk et al. (1985), and Lecacheux et al. (1989), using longitudinally separated spacecraft in the
ecliptic plane, ISEE-3 and Voyagers. The first stereoscopic
directivity measurements were reported by Poquérusse et al. (1996) and Hoang et al. (1997), using
comparisons of flux densities measured between the ARTEMIS
ground-based radio spectrograph around 150 MHz and the radio
receiver (1.25-940 kHz) on the Ulysses spacecraft at the highest frequencies.
Due to intensity intercomparisons performed between two very
different frequency domains, these authors had to assume the radio
spectrum to remain unchanged for all bursts, on the one hand, and,
on the other, to select bursts occurring only near the
Sun-Earth line for the ground-based spectrograph to always be set
in the direction of the burst maximum intensity for comparison.
In this paper, we present the first stereoscopic measurement of
the hectometer and kilometer type III directivity using radio data
acquired simultaneously by the Wind and Ulysses spacecraft at the same
frequencies. The advantage in combining them for stereoscopic
radio observations is twofold: (1) Ulysses is widely separated
from Wind in heliocentric longitude and latitude. (2) Both radio
receivers are well-calibrated and can operate a common list of
frequencies for accurate intercomparisons. The second requirement
alleviates the difficulties mentioned above, encountered by
Poquérusse et al. (1996) and Hoang et al. (1997) in their works based on intensity comparisons
between two very different frequency domains. In Sect. 2 we
describe the observations and data selection. In Sect. 3 we
explain our method for measuring the directivity of the type II
burst. Section 4 presents the results discussed in Sect. 5. In Sect. 6, we give a summary and conclusions.
We use radio data from the Unified Radio and Plasma Wave (URAP)
experiment on Ulysses (Stone et al. 1992) and the WAVES instrument
on Wind (Bougeret et al. 1995). The radio receiver on Wind (RAD1,
20-1040 kHz, 3 kHz bandwidth) can be commanded to operate on
nearly all the 12 frequency channels of the high-band receiver on
Ulysses (52-940 kHz, 3 kHz bandwidth): 940, 740, 540, 387,
272, 196, 148, 120, 100, 81, 63, and 52 kHz. Both these receivers
are well-calibrated and have the 2-D direction-finding using the
spacecraft spin modulation of the radio signal (Manning & Fainberg 1980; Fainberg et al. 1985).
For direction-finding, the antenna system used on Ulysses
(spin period 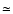 12 s) consists of the spin-axis electric
monopole of 7.5 m and spin-plane electric dipole of
12 s) consists of the spin-axis electric
monopole of 7.5 m and spin-plane electric dipole of
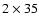 m; on
Wind (spin period
m; on
Wind (spin period 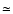 3 s), it is composed of the spin-axis
electric dipole of
3 s), it is composed of the spin-axis
electric dipole of
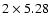 m and spin-plane electric dipole of
m and spin-plane electric dipole of
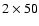 m.
m.
In the present study, we have selected type III bursts observed
simultaneously by Wind and Ulysses between 1995 and 2005, a period
spanning the 1996 minimum and 2001 maximum of the solar cycle 23.
During that time, Ulysses made two orbits over the Sun's poles and
explored wide ranges of distance, latitude, and longitude in the
heliocentric Earth ecliptic (HEEC) coordinate system. Wind moved
along its distant in-ecliptic prograde orbits around Earth to
successively explore the Earth's magnetosphere and solar wind. We
have considered bursts observed only when Wind was located in the
solar wind well upstream of the Earth's bow shock, when the bursts
were not polluted by terrestrial kilometric radiation, were
relatively simple, isolated, and intense enough (at least 4 dB
above background) so that their intensity time profiles at each
frequency could be measured reliably at both spacecraft. In all cases,
the background was first substracted by using quiet periods
between bursts. The importance of properly measuring the burst
intensity time profiles will appear clearer in Sect. 3.2.
Another criterion used in selecting type III bursts is their
association with solar flares within NOAA active regions (AR).
This association allows us to know, within about 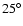 ,
the
position of bursts near the Sun, as further explained in Sect. 3.1. For that purpose, we searched for a solar H
,
the
position of bursts near the Sun, as further explained in Sect. 3.1. For that purpose, we searched for a solar H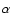 and/or X flare could be associated in time with each
selected type III. The associated solar flare was identified
within an AR visible on the Sun using the Solar Geophysical
Database
(http://sgd.ngdc.noaa.gov/sgd/jsp/solarindex.jsp).
Whenever an ambiguity existed on the burst position near the Sun,
we checked it by using the direction-finding on the Wind radio
receiver, and when available, meter wave type III bursts recorded
by the RadioHeliograph at Nançay (France)
(http://secchirh.obspm.fr).
and/or X flare could be associated in time with each
selected type III. The associated solar flare was identified
within an AR visible on the Sun using the Solar Geophysical
Database
(http://sgd.ngdc.noaa.gov/sgd/jsp/solarindex.jsp).
Whenever an ambiguity existed on the burst position near the Sun,
we checked it by using the direction-finding on the Wind radio
receiver, and when available, meter wave type III bursts recorded
by the RadioHeliograph at Nançay (France)
(http://secchirh.obspm.fr).
Finally, from about 2000 bursts initially selected for the study,
we are left with about 1000 bursts could be unambiguously
associated with an identified AR. This type III data set does
serve as a basis for measuring the radiation diagram as will be
described below.
In this section we derive the 2-D directivity
diagram of the hectometric and kilometric type III using the burst
data set described above.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{9777fig1.eps}\end{figure}](/articles/aa/full/2008/37/aa09777-08/Timg29.gif) |
Figure 1:
Geometry of observation. ( Left panel) Type III
source on the spiral open magnetic field line and the locations of
Wind and Ulysses in the HEEC (Heliocentric Earth Ecliptic)
coordinate system xyz. ( Right panel) Source-centered reference
frame x'y'z': the x'-axis is tangent to the open magnetic field
line passing the source anti-sunward; the z'-axis is in the plane
defined by the x'-axis and the vertical to the ecliptic plane,
oriented to ecliptic North; the y'-axis completes
the orthogonal right-handed coordinate system. The direction of
Wind and Ulysses is defined by the longitude  and
latitude
and
latitude  relative to the source frame.
relative to the source frame. |
| Open with DEXTER |
To derive the radiation diagram, we need to know the 3-D position
in the IPM of the type III source from which we can define the
different viewing directions for Ulysses and Wind. To determine
the position, we follow the method described by Saito et al. (1977)
and Leblanc et al. (1998). We assume that the solar flare
electrons responsible for the type III follow the approximately
Archimedean spiral open magnetic field lines rooted in the Sun
near the center of the associated ARs (see Sect. 2) and
spreading outward into the IPM at the same constant heliolatitudes
as the ARs. In the HEEC coordinates
the spiral field lines can be expressed as
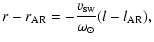 |
|
|
(1) |
where the subscript AR denotes the related active region, r is
the heliodistance,
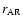 the reference distance of the spiral
field line rooted in the AR (assumed at 1 solar radius), lthe heliolongitude,
the reference distance of the spiral
field line rooted in the AR (assumed at 1 solar radius), lthe heliolongitude,
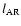 the longitude of the footpoint
of the spiral (assumed to be the AR's center),
the longitude of the footpoint
of the spiral (assumed to be the AR's center),
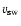 the solar
wind speed, and
the solar
wind speed, and
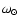 the solar corotational angular
speed of
the solar corotational angular
speed of
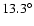 per day.
per day.
We can estimate the value of
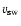 using solar wind speed recorded
in situ at Wind (Ogilvie et al. 1995) located near Earth. If we assume that these spirals remain unchanged, i.e.,
with negligible radial and temporal evolution, then the value of
using solar wind speed recorded
in situ at Wind (Ogilvie et al. 1995) located near Earth. If we assume that these spirals remain unchanged, i.e.,
with negligible radial and temporal evolution, then the value of
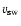 is measured by Wind at the time
is measured by Wind at the time 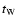 when the spiral line rooted in the associated AR passes the spacecraft by corotation.
when the spiral line rooted in the associated AR passes the spacecraft by corotation.
Similarly, we can represent the plasma conditions all along the
spiral paths travelled by the type III electrons, using the plasma
density measured in situ at Wind (Ogilvie et al. 1995) at the time 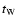 and the fact that in the IPM the
density decreases closely as r-2 (McComas et al. 1992; Issautier et al. 1998). This procedure allows complete
determination of the position of the type III sources along the
spiral field lines at different frequencies.
and the fact that in the IPM the
density decreases closely as r-2 (McComas et al. 1992; Issautier et al. 1998). This procedure allows complete
determination of the position of the type III sources along the
spiral field lines at different frequencies.
Figure 1 illustrates the geometry of observation. Figure 1 (left
panel) shows the type III source along the spiral magnetic field
line and the locations of Wind and Ulysses in the HEEC coordinate
system xyz. Figure 1 (right panel) defines the new observation
reference frame centered at the type III source: the x'-axis is
tangent to the open magnetic field line passing the source
anti-sunward; the z'-axis is in the plane defined by the x'-axis
and the vertical to the ecliptic plane, oriented in the direction
of ecliptic North; the y'-ais completes the orthogonal
right handed coordinate system. In the source-centered reference
frame just defined, the new coordinates of the observing spacecraft (with
index i = U for Ulysses, W for Wind) are: the spacecraft Cartesian
components
x'i, y'i, z'i, which are transformed from the spacecraft
HEEC Cartesian coordinates
xi, yi, zi; and the coordinates of
the spacecraft relative to the source frame, namely its longitude
 with
with
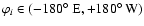 ,
its latitude
,
its latitude
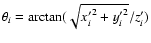 with
with
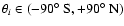 ,
and its distance to the source
,
and its distance to the source
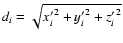 .
.
At the antenna terminals of each spacecraft with index i, we measure
the source flux density time profile,
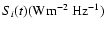 .
Figure 2 shows an example of a type III burst observed by Wind
(top) and Ulysses (bottom) on 17 June 1996 at a frequency of 196
kHz. The continuous curve above the background level represents the actual
burst flux density profile. The lower curve,
denoted above as Si(t), shows the same data, but with the
background removed. The burst onset time,
.
Figure 2 shows an example of a type III burst observed by Wind
(top) and Ulysses (bottom) on 17 June 1996 at a frequency of 196
kHz. The continuous curve above the background level represents the actual
burst flux density profile. The lower curve,
denoted above as Si(t), shows the same data, but with the
background removed. The burst onset time,
 ,
defines the
time at which the burst intensity rises significantly from
background. The end time,
,
defines the
time at which the burst intensity rises significantly from
background. The end time,
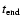 ,
is the time when the burst
intensity goes down to the background level.
,
is the time when the burst
intensity goes down to the background level.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{9777fig2.eps}\end{figure}](/articles/aa/full/2008/37/aa09777-08/Timg43.gif) |
Figure 2:
The flux density time profile of a type III
burst observed by Wind ( top) and Ulysses ( bottom) on 17 June 1996
at 196 kHz. The continuous curve above background represents the
actual burst intensity profile. The lower curve (full circles),
denoted
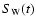 and
and
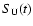 ,
shows the same burst profile, but
with the background removed. The burst is seen to occur between
the onset time ,
shows the same burst profile, but
with the background removed. The burst is seen to occur between
the onset time
 and end time
and end time
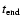 (see text for
exact definition).
(see text for
exact definition). |
| Open with DEXTER |
In the source reference frame defined above in Fig. 1 (right panel), we can
determine the energy density
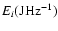 radiated by the
source at frequency f with flux density Si(t) from
radiated by the
source at frequency f with flux density Si(t) from
 to
to
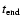 (Fig. 2), per unit solid angle in the
direction
(Fig. 2), per unit solid angle in the
direction
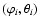 of the spacecraft at distance di:
of the spacecraft at distance di:
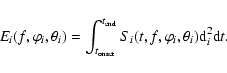 |
(2) |
This can be defined as
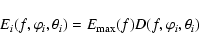 |
(3) |
where
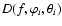 is the radiation diagram of the
event at f, normalized to 1 in the direction of maximum
intensity, and
is the radiation diagram of the
event at f, normalized to 1 in the direction of maximum
intensity, and
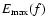 the energy spectrum of the event taken
in the direction of maximum intensity at each frequency.
the energy spectrum of the event taken
in the direction of maximum intensity at each frequency.
From the above, it is clear that we cannot use the measurements of the energy density from a single spacecraft to derive the directivity, since the energy
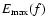 varies widely from one event to another. Then for measuring the radiation diagram, we consider the radio energy ratios at a frequency f between Ulysses (index U) and
Wind (index W) in order to eliminate
varies widely from one event to another. Then for measuring the radiation diagram, we consider the radio energy ratios at a frequency f between Ulysses (index U) and
Wind (index W) in order to eliminate
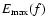 ,
which is not actually measured, such as,
,
which is not actually measured, such as,
Equations (4) and (5) imply that the measured energy ratios, 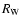 and
and 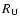 ,
are equal to the ratio of the radiation diagram
observed by the two spacecraft in two different directions
,
are equal to the ratio of the radiation diagram
observed by the two spacecraft in two different directions
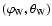 and
and
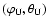 .
It is
noteworthy that it is not redundant to use both
.
It is
noteworthy that it is not redundant to use both
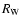 and
and 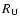 because they put two times more constraints on the
diagram to be measured, as we shall see in the next section.
because they put two times more constraints on the
diagram to be measured, as we shall see in the next section.
In this section, we derive the radiation diagram
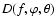 from the measurements of the radio energy ratios,
from the measurements of the radio energy ratios, 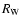 and
and
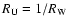 (Eqs. (4) and (5)), made simultaneously by Wind in the direction
(Eqs. (4) and (5)), made simultaneously by Wind in the direction
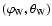 and
Ulysses in the direction
and
Ulysses in the direction
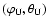 relative to the
source frame, as illustrated in Fig. 1.
For that purpose, we fit a model function with 2 fitting parameters, which will be explained and justified in Sect. 4.2, to the energy ratios
relative to the
source frame, as illustrated in Fig. 1.
For that purpose, we fit a model function with 2 fitting parameters, which will be explained and justified in Sect. 4.2, to the energy ratios 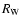 and
and 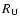 .
In the next section, in order to guide the choice of the model diagram to be fitted to observations, we highlight the complex dependency of the observables
.
In the next section, in order to guide the choice of the model diagram to be fitted to observations, we highlight the complex dependency of the observables 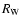 and
and 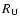 upon the directions
upon the directions
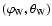 and
and
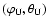 of Wind and Ulysses.
of Wind and Ulysses.
Table 1:
Characteristics of the type III radiation diagram.
![\begin{figure}
\par\includegraphics[width=15cm]{9777fig3.eps}\end{figure}](/articles/aa/full/2008/37/aa09777-08/Timg84.gif) |
Figure 3:
(a) Type III burst energy ratios R measured
from Wind (circles) and Ulysses (triangles), at all selected
frequencies and for all relative latitudes  of the
spacecraft,
of the
spacecraft,
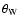 and
and
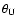 ,
as a function of
the longitudes ,
as a function of
the longitudes  of Wind and Ulysses,
of Wind and Ulysses,
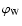 and and
 ,
relative to the source (in coordinates x'y'z',
Fig. 1). Different absolute values of latitude ,
relative to the source (in coordinates x'y'z',
Fig. 1). Different absolute values of latitude  are
indicated by a color bar. Averaged values of R in
are
indicated by a color bar. Averaged values of R in 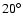 bins
of longitude
bins
of longitude  are plotted as black full circles. (b)
Energy ratios R measured from Wind (circles) and Ulysses
(triangles), at all selected frequencies and for all relative
longitudes
are plotted as black full circles. (b)
Energy ratios R measured from Wind (circles) and Ulysses
(triangles), at all selected frequencies and for all relative
longitudes  of the spacecraft,
of the spacecraft,
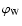 and and
 ,
as a function of the
latitudes ,
as a function of the
latitudes  of Wind and Ulysses,
of Wind and Ulysses,
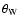 and
and
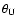 ,
relative to the source.
Different absolute values of ,
relative to the source.
Different absolute values of  indicated by the color bar.
Averaged values of R in
indicated by the color bar.
Averaged values of R in 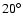 bins of
bins of  plotted as
black full circles.
plotted as
black full circles.
|
| Open with DEXTER |
To show how the energy ratios 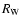 and
and 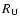 and the related
diagram D may depend on the observing direction (
and the related
diagram D may depend on the observing direction (
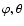 ), Fig. 3 represents the data
), Fig. 3 represents the data 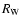 and
and 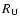 as functions of the observing longitude
as functions of the observing longitude
 and latitude
and latitude  .
Figure 3a displays measurements
of
.
Figure 3a displays measurements
of 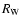 and
and 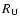 at all frequencies selected between 940 and 80
kHz as a function of
at all frequencies selected between 940 and 80
kHz as a function of
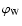 and
and
 respectively, for
different absolute values of
respectively, for
different absolute values of
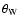 and
and
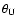 ,
respectively (coded by the color bar
scale). Similarly Fig. 3b shows measurements of
,
respectively (coded by the color bar
scale). Similarly Fig. 3b shows measurements of 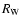 and
and
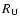 at all frequencies selected as a function of
at all frequencies selected as a function of
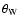 and
and
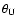 ,
respectively, for different absolute values of
,
respectively, for different absolute values of
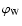 and
and
 .
To check for any dependence on
direction (
.
To check for any dependence on
direction (
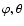 )
of the R data, their averaged
values in
)
of the R data, their averaged
values in 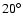 bins of the abscissae
bins of the abscissae  and
and  are also shown.
are also shown.
As can be seen from Fig. 3b, R shows a slight variation with
the observing latitude  :
the
:
the  averaged values of
R tend to lie approximately around
a flat maximum at low latitudes and decrease slightly by a factor
of 6 towards higher latitudes. In contrast, Fig. 3a displays a
stronger dependence by R on the observing longitude
averaged values of
R tend to lie approximately around
a flat maximum at low latitudes and decrease slightly by a factor
of 6 towards higher latitudes. In contrast, Fig. 3a displays a
stronger dependence by R on the observing longitude  :
the
:
the  averaged values of R decrease from
a maximum at small longitudes to a minimum at large longitudes by
a factor of 25. Furthermore, the relative latitude
averaged values of R decrease from
a maximum at small longitudes to a minimum at large longitudes by
a factor of 25. Furthermore, the relative latitude  appears to be uniformly distributed about the
appears to be uniformly distributed about the  variation
trend of R: this means that the variation of R with
variation
trend of R: this means that the variation of R with  is independent of
is independent of  .
.
Figure 3a suggests that the energy ratios R and
radiation diagram D, to a first approximation, are only
functions of the observing longitude  and frequency f.
From Eqs. (4) and (5), and omitting f for brevity, the
and frequency f.
From Eqs. (4) and (5), and omitting f for brevity, the 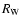 and
and 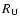 data can be expressed by the model
functions:
data can be expressed by the model
functions:
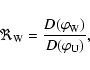 |
(6) |
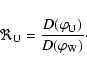 |
(7) |
For the radiation diagram
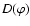 itself, we take an
empirical model function of the form
itself, we take an
empirical model function of the form
![\begin{displaymath}D(\varphi) = 10^{a[\cos(\varphi - \varphi_0) - 1]},
\end{displaymath}](/articles/aa/full/2008/37/aa09777-08/img89.gif) |
(8) |
where  is the observing longitude (
is the observing longitude (
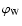 ,
,
 ),
), 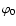 the longitude of the maximum intensity
(normalized to 1), and a the amplitude of the
cosine diagram. Here, a defines the full angular width
the longitude of the maximum intensity
(normalized to 1), and a the amplitude of the
cosine diagram. Here, a defines the full angular width
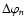 at the maximum/n level of the diagram such that
at the maximum/n level of the diagram such that
![\begin{displaymath}\frac {1}{n} = 10^{a[\cos(\mathbf{\Delta\varphi_{\it n} /2}) - 1]},
\end{displaymath}](/articles/aa/full/2008/37/aa09777-08/img91.gif) |
(9) |
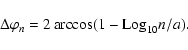 |
(10) |
The choice of the model diagram in Eq. (8) is simply based on the shape with a single beam exhibited by the
observed 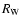 and
and 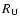 represented in Fig. 3. It is worth noticing that the observed diagram is nothing compared to
the primary diagram at the source because of the ubiquitous propagation effects in the medium, which are
expected to strongly distort and smooth out any sophisticated primary diagram that exists.
represented in Fig. 3. It is worth noticing that the observed diagram is nothing compared to
the primary diagram at the source because of the ubiquitous propagation effects in the medium, which are
expected to strongly distort and smooth out any sophisticated primary diagram that exists.
We then fit the model functions
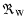 and
and
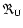 ,
with the two
fitting parameters a and
,
with the two
fitting parameters a and 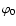 ,
to the measured
,
to the measured 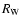 and
and
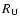 data (Eqs. (4) and (5) and Fig. 3a), by the
Levenberg-Marquardt nonlinear least-squares method (Press et al. 1992).
The results of the diagram fitting are shown in Fig. 4
for five groups of two frequencies: (a) 940-740, (b) 540-388, (c)
272-196, (d) 148-124, and (e) 104-80 kHz. The diagram
data (Eqs. (4) and (5) and Fig. 3a), by the
Levenberg-Marquardt nonlinear least-squares method (Press et al. 1992).
The results of the diagram fitting are shown in Fig. 4
for five groups of two frequencies: (a) 940-740, (b) 540-388, (c)
272-196, (d) 148-124, and (e) 104-80 kHz. The diagram
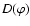 (Eq. (8)) obtained with the fitted values of a and
(Eq. (8)) obtained with the fitted values of a and
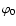 is plotted as log
is plotted as log
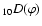 vs.
vs.  .
These values of a and
.
These values of a and 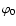 are also given
in each panel of Fig. 4 and in Table 1. Since we have no direct
measurements of the diagram itself, which is obtained by fitting to
the actually measured data
are also given
in each panel of Fig. 4 and in Table 1. Since we have no direct
measurements of the diagram itself, which is obtained by fitting to
the actually measured data 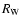 and
and 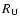 ,
we represent the diagram data by
,
we represent the diagram data by
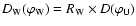 and
and
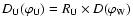 .
For illustration, these data are averaged in
.
For illustration, these data are averaged in
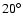 bins of
bins of  and plotted as a function of
and plotted as a function of  in Fig. 4. As expected,
the fitted curve of the diagram can be seen to clearly pass
through the averaged diagram data points to within the scatter
bars.
in Fig. 4. As expected,
the fitted curve of the diagram can be seen to clearly pass
through the averaged diagram data points to within the scatter
bars.
![\begin{figure}
\par\includegraphics[width=11cm,clip]{9777fig4.eps}\end{figure}](/articles/aa/full/2008/37/aa09777-08/Timg98.gif) |
Figure 4:
The diagram in longitude  relative to
the source, with the fitted values of the amplitude a and shift
relative to
the source, with the fitted values of the amplitude a and shift
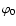 ,
is plotted as a continuous line as ,
is plotted as a continuous line as
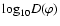 vs. vs.  ,
in different frequency ranges. The diagram data (see
definition in the text) are averaged in ,
in different frequency ranges. The diagram data (see
definition in the text) are averaged in 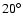 bins of
bins of
 and plotted (black circles with scatter bars) vs.
and plotted (black circles with scatter bars) vs.
 .
As the frequency decreases, the shift .
As the frequency decreases, the shift 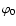 to
east of the local magnetic field direction increases and the
amplitude a of the cosine diagram decreases.
to
east of the local magnetic field direction increases and the
amplitude a of the cosine diagram decreases. |
| Open with DEXTER |
In Fig. 4, the derived value of the amplitude a of the cosine
diagram gives the full angular width
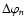 of the
diagram at maximum/n level (see Eq. (10)). The derived
of the
diagram at maximum/n level (see Eq. (10)). The derived
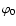 indicates an eastward tilt of the radiation diagram
from the local magnetic field direction at the source. As the
frequency decreases, the eastward shift
indicates an eastward tilt of the radiation diagram
from the local magnetic field direction at the source. As the
frequency decreases, the eastward shift 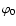 increases and
the amplitude a decreases (consequently the diagram width
increases and
the amplitude a decreases (consequently the diagram width
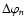 increases). Table 1 summarizes the results of
the diagram fitting assuming the emission source at the
fundamental (F), together with the diagram widths
increases). Table 1 summarizes the results of
the diagram fitting assuming the emission source at the
fundamental (F), together with the diagram widths
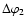 (at maximum/2) and
(at maximum/2) and
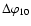 (at
maximum/10) as computed from Eq. (10). In the table, the
fitting parameters
(at
maximum/10) as computed from Eq. (10). In the table, the
fitting parameters 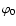 and a are given with their
numerical uncertainties for the five groups of two frequencies.
The present diagram observations essentially confirm previous
results of Hoang et al. (1997) on the
angular width and eastward shift of the type III emission diagram,
but provide more accurate diagrams thanks to systematic
comparisons of Wind and Ulysses radio burst data at the same
frequencies and in all directions. Further consideration of these
diagram characteristics will be given in Sect. 5.
and a are given with their
numerical uncertainties for the five groups of two frequencies.
The present diagram observations essentially confirm previous
results of Hoang et al. (1997) on the
angular width and eastward shift of the type III emission diagram,
but provide more accurate diagrams thanks to systematic
comparisons of Wind and Ulysses radio burst data at the same
frequencies and in all directions. Further consideration of these
diagram characteristics will be given in Sect. 5.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{9777fig5.eps}\end{figure}](/articles/aa/full/2008/37/aa09777-08/Timg99.gif) |
Figure 5:
The diagram in latitude  relative to
the source, with the fitted values of the amplitude and shift, is
plotted as a continuous line as
relative to
the source, with the fitted values of the amplitude and shift, is
plotted as a continuous line as
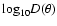 vs.
vs.  ,
in
different frequency ranges. The diagram data (see definition in
the text) are averaged in ,
in
different frequency ranges. The diagram data (see definition in
the text) are averaged in 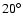 bins of
bins of  and plotted
(black circles with scatter bars) vs.
and plotted
(black circles with scatter bars) vs.  .
No significant tilt
is seen in the diagram. A weak directivity is observed equatorward
at highest frequencies. At low frequency, the diagram is nearly
isotropic. .
No significant tilt
is seen in the diagram. A weak directivity is observed equatorward
at highest frequencies. At low frequency, the diagram is nearly
isotropic. |
| Open with DEXTER |
In this section, we examine the latitude dependence of the
radiation diagram in more detail. From the above section and
Eqs. (4) and (5), we may express the energy
ratios differently as measured between Wind (W) and Ulysses (U) (at f) by
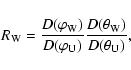 |
(11) |
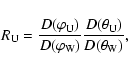 |
(12) |
where the model diagram function 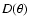 has the same form as
has the same form as
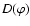 of Eq. (8). Then by removing the longitude
of Eq. (8). Then by removing the longitude
 dependence from the diagram, we can obtain the energy
ratios that are functions of the latitude
dependence from the diagram, we can obtain the energy
ratios that are functions of the latitude  alone as
alone as
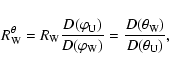 |
(13) |
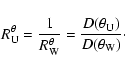 |
(14) |
The
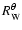 and
and
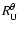 ratios can then be expressed by the empirical model functions, which depend on the
latitude
ratios can then be expressed by the empirical model functions, which depend on the
latitude  alone:
alone:
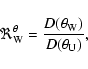 |
(15) |
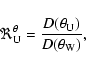 |
(16) |
with
![\begin{displaymath}D(\theta) = 10^{b[\cos(\theta - \theta_0) - 1]},
\end{displaymath}](/articles/aa/full/2008/37/aa09777-08/img109.gif) |
(17) |
where 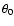 is the latitude
is the latitude  of the maximum intensity
(normalized to 1), and b the amplitude of the
cosine diagram.
of the maximum intensity
(normalized to 1), and b the amplitude of the
cosine diagram.
We then fit the model functions
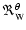 and
and
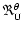 ,
with the fitting parameters b and
,
with the fitting parameters b and 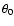 ,
to the measured
,
to the measured
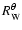 and
and
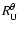 - Eqs. (13)
and (14). The results of the diagram fitting are shown in Fig. 5
for the five groups of two frequencies: (a) 940-740, (b) 540-388,
(c) 272-196, (d) 148-124, and (e) 104-80 kHz. The diagram
- Eqs. (13)
and (14). The results of the diagram fitting are shown in Fig. 5
for the five groups of two frequencies: (a) 940-740, (b) 540-388,
(c) 272-196, (d) 148-124, and (e) 104-80 kHz. The diagram
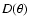 (Eq. (17)) obtained with the fitted values of band
(Eq. (17)) obtained with the fitted values of band 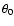 is plotted in continuous line as
is plotted in continuous line as
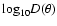 vs.
vs.  .
These values of b and
.
These values of b and
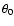 are also displayed in each panel of Fig. 5. Since we
have no direct measurements of the diagram that is obtained by
least-squares fitting to the actually measured data
are also displayed in each panel of Fig. 5. Since we
have no direct measurements of the diagram that is obtained by
least-squares fitting to the actually measured data
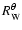 and
and
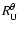 ,
we represent the
diagram data by
,
we represent the
diagram data by
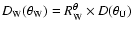 and
and
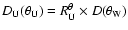 .
For
illustration, the latter data are averaged in
.
For
illustration, the latter data are averaged in  bins of
bins of
 and plotted as a
function of
and plotted as a
function of  in Fig. 5. The fitted curve of the diagram
can be seen, as expected, to pass through the diagram's averaged
data points to within the scatter bars. From the figure, there is
no significant tilt
in Fig. 5. The fitted curve of the diagram
can be seen, as expected, to pass through the diagram's averaged
data points to within the scatter bars. From the figure, there is
no significant tilt  of the diagram maximum from
of the diagram maximum from
 latitude, in contrast to the longitude
latitude, in contrast to the longitude  case. The
amplitude b of the cosine diagram
case. The
amplitude b of the cosine diagram 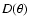 is also much
smaller than the amplitude a of the diagram
is also much
smaller than the amplitude a of the diagram
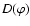 and
decreases rapidly towards lower frequencies. This will be
discussed further in Sect. 5.3.
and
decreases rapidly towards lower frequencies. This will be
discussed further in Sect. 5.3.
We now address different effects that may affect the type III
radiation diagram we have found above.
From Fig. 4 we find that the radiation diagram axis shifts
significantly to east from the local magnetic field direction, in
agreement with previous observations of Poquérusse et al. (1996)
and Hoang et al. (1997). This eastward shift of the diagram axis out of the spiral magnetic
field lines traveled by the type III electrons is not consistent
with what should be expected from the plasma emission mechanism of
the type III bursts that are emitted in that magnetic field
direction. Following Poquérusse et al. (1996) and referring to
Fig. 6, we can interpret the eastward shift of the diagram axis
as follows. The type III electron streams travel outward along
open-field lines from the associated flare sites in active regions
through complex coronal structures of closed-field lines. Along
these open-field lines, the solar wind escapes faster than in the
surrounding areas. At some distance farther out, when the spiral
open-field lines start to deviate by a few degrees from the radial
direction, the faster wind along the type III electron
trajectories catches up with the ambient slower wind, and thus
produces a density compression that leads to a transverse density
gradient
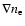 directed west of the spiral field
direction, like in the well-known corotating interaction regions
(CIRs). This in turn results in a refractive index gradient
directed west of the spiral field
direction, like in the well-known corotating interaction regions
(CIRs). This in turn results in a refractive index gradient
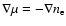 ,
oriented eastward in the opposite
sense of the density gradient, and so bends radiation in the
eastward direction as observed.
,
oriented eastward in the opposite
sense of the density gradient, and so bends radiation in the
eastward direction as observed.
It is well known that, in the CIR density compression regions observed in the solar wind, westward density gradients actually exists
(e.g., Schwenn & Marsch 1990, Fig. 3.10; Lacombe et al. 2000, Fig. 2).
On the other hand, that the eastward shift of the diagram
increases with decreasing frequency (Fig. 4 and Table 1), i.e.,
at larger heliocentric distance, implies that the density gradient
(or density compression) along the CIR-like path traveled by the
type III electrons is presumably stronger farther away from the
sun. This seems to be suggested by three-dimensional
magnetohydrodynamic models of solar wind large-scale structures
(Pizzo 1994).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9777fig6.eps}\end{figure}](/articles/aa/full/2008/37/aa09777-08/Timg116.gif) |
Figure 6:
Schematic interpretation of the eastward
(equatorward) shift of the type III emission diagram in longitude
(latitude) relative to the local open-field direction at the
source. The type III electrons travel outward along spiral
open-field lines from the associated flare sites in active
regions. Along these paths, the solar wind escapes faster than in
the surrounding areas filled with structures of closed-field
lines. At some distance farther out, the faster wind catches up
with the ambient slower wind and produces a density compression
that leads to a transverse density gradient
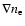 directed westward (poleward) of the open-field direction. This in
turn results in a refractive index gradient directed westward (poleward) of the open-field direction. This in
turn results in a refractive index gradient
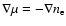 ,
oriented eastward (equatorward) in the opposite sense of
the density gradient. Radiation is thus bent in the eastward
(equatorward) direction as observed. ,
oriented eastward (equatorward) in the opposite sense of
the density gradient. Radiation is thus bent in the eastward
(equatorward) direction as observed.
|
| Open with DEXTER |
As summarized in Table 1, the angular width of the type III
radiation diagram increases with decreasing observing
frequencies. This is presumably due to propagation effects at work in the IPM: refraction by regular density gradient and
scattering by random density fluctuations. Computer simulations of
these propagation effects have been performed for several decades,
among other emission features, on the directivity at hectometer
and kilometer wavelengths (e.g., Steinberg 1972; Thejappa et al. 2007).
Using a simple model of isotropic point
source and different density relative fluctuations with Gaussian
distribution (Steinberg 1972) or power-law distribution
(Thejappa et al. 2007), by computer Monte Carlo
simulations these authors could qualitatively reproduce the
anisotropic shape and large width of the apparent directivity
diagram of the type III at low frequency.
There can be no doubt therefore that, on the grand average,
propagation effects are likely to strongly affect the primary
diagram of the type III source. Detailed propagation computations,
taking additional parameters into account such as the source
angular size and beaming, are necessary before attempting to
deduce any information on the radiation diagram of the primary
source (e.g., Zheleznyakov & Zaitsev 1970).
Furthermore, since energy loss due to electron collisions can be
neglected in the IPM, we might expect propagation effects to be
negligible in the radiation transfer at low frequency, while they
do strongly distort the radiation diagram because of angular
scattering undergone by radio waves. We can thus reasonably assume
that the total energy radiated in space by the emission source is
not much affected by propagation. This consideration is worthy of
note when estimating the efficiency of the mode conversion in the
type III emission mechanism.
As can be seen from Fig. 5, the amplitude of the latitude
diagram is found to be much smaller than that of the longitude
diagram illustrated in Fig. 4: this is consistent with the
dominant effect of the longitude in the type III directivity
diagram. On the other hand, this amplitude decreases rapidly from
higher frequencies to lower frequencies, the diagram in latitude
becomes isotropic at low frequency. At highest frequencies, the
latitude diagram is slightly anisotropic, decreasing from maximum
around  latitude to about maximum/6 at high latitude.
This latitude behavior of the emission, which increases towards
low latitude (equatorward), was also observed by Hoang et al. (1997).
As observed, this latitudinal directivity appears to be contrary to that expected
from a plasma density distribution more or less concentrated in a
dense and narrow solar equatorial band as actually observed at
high latitude (see Issautier et al. 1997, and references therein).
Indeed, such a plasma density distribution presents a latitudinal
component of the density gradient directed towards low latitude
and consequently should bend radiation in the opposite sense,
i.e., towards high latitude (poleward).
latitude to about maximum/6 at high latitude.
This latitude behavior of the emission, which increases towards
low latitude (equatorward), was also observed by Hoang et al. (1997).
As observed, this latitudinal directivity appears to be contrary to that expected
from a plasma density distribution more or less concentrated in a
dense and narrow solar equatorial band as actually observed at
high latitude (see Issautier et al. 1997, and references therein).
Indeed, such a plasma density distribution presents a latitudinal
component of the density gradient directed towards low latitude
and consequently should bend radiation in the opposite sense,
i.e., towards high latitude (poleward).
To explain the equatorward directivity, as in the case of the
eastward shift of the longitude diagram discussed in Sect. 5.1
and shown in Fig. 6, we speculate on a poleward component of the
local density gradient
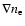 along the type III electron
open-field tube. As a result, this will produce a refractive index
gradient
along the type III electron
open-field tube. As a result, this will produce a refractive index
gradient
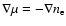 and bend radiation
equatorwards.
and bend radiation
equatorwards.
From stereoscopic observations of type III bursts (see Dulk 2000, and references therein), it has been
suggested that type III bursts radiate at both the fundamental (F)
and harmonic (H), but with different directivities: at small
(longitude) angles from the spiral type III electron trajectory,
the radiation at a given frequency is initially at F and followed
later on by H; at large angles, only H is observed. These F and H
directivities have been established by Monte Carlo simulation of
radio wave propagation in the IPM (Thejappa et al. 2007).
As a consequence, the directivity we measure at the same frequency
f might consist of both the fundamental
F and harmonic H radiation near the diagram axis; and way off the diagram axis, it might
consist of H radiation alone. To check for that effect, we
performed the data analysis by restricting the observing longitude
angles to a range between 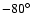 and
and 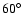 around the
diagram axis. The results found indicate higher values of the
diagram amplitude a and lower ones for the angular width
around the
diagram axis. The results found indicate higher values of the
diagram amplitude a and lower ones for the angular width
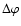 than in the case of a widespread longitude range,
and thus point to the F narrower diagram on top of the H wider
diagram.
than in the case of a widespread longitude range,
and thus point to the F narrower diagram on top of the H wider
diagram.
To check for a possible variation of the radiation diagram with
the solar cycle, we have divided the whole period of observation
from 1995 to 2005 into two subperiods of equal duration spanning
the 1996 minimum and 2001 maximum separately. We then
performed the diagram data analysis on each of these subperiods.
The comparison of the results found for the two subperiods and the
whole period show no significant difference between the diagrams
measured during the minimum and maximum phases of the solar cycle.
Using radio data recorded simultaneously by the Wind and Ulysses
spacecraft from 1995 to 2005 at the same frequencies between 940
and 80 kHz, we have derived for the first time the average
radiation diagram of the solar hectometric and kilometric type III
bursts in two dimensions (longitude and latitude relative to the
source). No variation with the solar cycle has been detected in
the diagrams derived separately from the minimum and maximum
activity phases.
The full angular width of the diagram in longitude at the
maximum/10 level is about 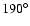 at 940-740 kHz and increases
to nearly
at 940-740 kHz and increases
to nearly 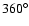 at 104-80 kHz. The axis of the diagram is
found to shift eastward from the local magnetic field direction at
the source by an angle increasing from
at 104-80 kHz. The axis of the diagram is
found to shift eastward from the local magnetic field direction at
the source by an angle increasing from 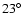 at 940-740 kHz
to
at 940-740 kHz
to 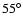 at 104-80 kHz. This eastward shift is interpreted to
be the result of refraction by a westward density gradient due to
a local density compression region along the open magnetic field
lines above the associated active regions.
at 104-80 kHz. This eastward shift is interpreted to
be the result of refraction by a westward density gradient due to
a local density compression region along the open magnetic field
lines above the associated active regions.
The diagram in latitude, obtained uniquely thanks to the
out-of-ecliptic exploration of Ulysses, shows no poleward
directivity that should be expected from the interplanetary
plasma density distribution, more or less spherical, that exists
at latitudes above the ecliptic plane. On the contrary, at the highest
frequencies this diagram is observed to decrease slightly towards
higher latitudes; at lower frequencies, it becomes nearly
isotropic with latitudes. The absence of a poleward directivity in
latitude is possibly due to a local poleward density gradient
that results in a local equatorward refractive index gradient
bending radiation towards low latitudes.
Our study has confirmed previous findings of Hoang et al. (1997) from the Ulysses/URAP radio receiver and
ARTEMIS ground-based radio spectrograph. Moreover, it has provided
more accurate measurements of the average radiation diagram of the
type III bursts and new insights into the propagation of radio waves
and solar particles along open magnetic field lines above active
regions and in corotating interaction regions. In this respect,
our results implying transverse density compression bring new
constraints to hydrodynamic models dealing with solar wind
structures (see Forsyth & Gosling 2001, and references therein).
Precise knowledge of this diagram obtained with our study will be valuable for studying both the emission mechanism and the
propagation in interplanetary space of the type III bursts. The
data analysis tool developed for the present study can be easily applied
to the STEREO duo-spacecraft mission to investigate solar radio
emissions.
Acknowledgements
The Wind/WAVES investigation is a
collaboration of the Observatoire de Paris, NASA/GSFC, and the
University of Minnesota. The Ulysses/URAP investigation is a joint
project of NASA/GSFC, the Observatoire de Paris, the University of
Minnesota, and the CETP, Velizy, France. The French contribution to
these projects is supported by the CNES and CNRS. Part of the data
used in this study comes from the Centre des Données de la
Physique des Plasmas (CDPP) in Toulouse, France. We are grateful to
Catherine Lacombe and Carine Briand for careful reading of the
manuscript and helpful comments. S.H. thanks Michel
Poquérusse for interesting discussions on the type III
emission directivity.
- Bougeret,
J.-L., Kaiser, M. L., Kellogg, P. J., et al. 1995,
Space Sci. Rev., 71, 231 [NASA ADS] [CrossRef]
(In the text)
-
Caroubalos, C., & Steinberg, J. L. 1974, A&A, 32,
245 [NASA ADS]
(In the text)
-
Caroubalos, C., Poquérusse, M., & Steinberg, J. L.
1974, A&A, 32, 255 [NASA ADS]
(In the text)
- Dulk, G. A.
2000, in Radio Astronomy at Long Wavelengths, ed. R. G. Stone,
K. W. Weiler, M. L. Goldstein, & J.-L. Bougeret,
115
(In the text)
- Dulk, G. A.,
Steinberg, J. L., Lecacheux, A., Hoang, S., & MacDowall,
R. J. 1985, A&A, 150, L28 [NASA ADS]
(In the text)
- Fainberg,
J., Hoang, S., & Manning, R. 1985, A&A, 153, 145 [NASA ADS]
- Forsyth,
R. J., & Gosling, J. T. 2001, Corotating and
transient structures in the heliosphere (The heliosphere near solar
minimum. The Ulysses perspective, ed. A. Balogh, R.
G. Marsden and E. J. Smith, Springer-Praxis Books in
Astrophysics and Astronomy (London: Springer), 107
(In the text)
- Hoang, S.,
Poquérusse, M., & Bougeret, J.-L. 1997, Sol. Phys.,
172, 307 [NASA ADS] [CrossRef]
(In the text)
-
Issautier, K., Meyer-Vernet, N., Moncuquet, M., & Hoang, S.
1997, Sol. Phys., 172, 335 [NASA ADS] [CrossRef]
(In the text)
-
Issautier, K., Meyer-Vernet, N., Moncuquet, M., & Hoang, S.
1998, J. Geophys. Res., 103, 1969 [NASA ADS] [CrossRef]
- Lacombe, C.,
Salem, C., Mangeney, A., et al. 2000, Ann. Geophys., 18,
852 [NASA ADS] [CrossRef]
(In the text)
- Leblanc, Y.,
Dulk, G. A., & Bougeret, J.-L. 1998, Sol. Phys., 183,
165 [NASA ADS] [CrossRef]
(In the text)
-
Lecacheux, A., Steinberg, J.-L., Hoang, S., & Dulk, G. A.
1989, A&A, 217, 237 [NASA ADS]
(In the text)
-
MacDowall, R. J. 1982, Master's Thesis, University of
Maryland
(In the text)
- Manning, R.,
& Fainberg, J. 1980, Space Sci. Instrum., 5, 161 [NASA ADS]
- McComas,
D. J., Bame, S. J., Feldman, W. C., Gosling,
J. T., & Phillips, J. L. 1992,
Geophys. Res. Lett., 19, 1291 [NASA ADS] [CrossRef]
- Ogilvie,
K. W., Chornay, D. J., Fritzenreiter, R. J.,
et al. 1995, Space Sci. Rev., 71, 55 [NASA ADS] [CrossRef]
(In the text)
- Pizzo, V. J.
1994, J. Geophys. Res., 99, 4185 [NASA ADS] [CrossRef]
(In the text)
-
Poquérusse, M. 1984, Ph.D. Thesis, University Paris 7
(In the text)
-
Poquérusse, M., Hoang, S., Bougeret, J.-L., & Moncuquet,
M. 1996, in Amer. Inst. Phys. Conf. Ser. 382, ed.
D. Winterhalter, J. T. Gosling, S. R. Habbal,
W. S. Kurth, & M. Neugebauer, 62
(In the text)
- Press,
W. H., Teukolsky, S. A., Vetterling, A. W. T.,
& Flannery, B. P. 1992, Numerical Recipes in C: The Art of
Scientific Computing (Cambridge University Press)
(In the text)
- Saito, K.,
Poland, A. I., & Munro, R. H. 1977, Sol. Phys.,
55, 121 [NASA ADS] [CrossRef]
(In the text)
- Schwenn, R.,
& Marsch, E. 1990, Physics of the Inner Heliosphere I.
Large-Scale Phenomena (Physics of the Inner Heliosphere I)
(In the text)
-
Steinberg, J.-L. 1972, A&A, 18, 382 [NASA ADS]
(In the text)
- Stone,
R. G., Bougeret, J. L., Caldwell, J., et al. 1992,
A&AS, 92, 291 [NASA ADS]
(In the text)
- Thejappa,
G., MacDowall, R. J., & Kaiser, M. L. 2007, ApJ, 671,
894 [NASA ADS] [CrossRef]
(In the text)
-
Zheleznyakov, V. V., & Zaitsev, V. V. 1970, Sov.
Astron., 14, 250 [NASA ADS]
(In the text)
Copyright ESO 2008
![\begin{figure}
\par\includegraphics[width=12cm,clip]{9777fig1.eps}\end{figure}](/articles/aa/full/2008/37/aa09777-08/Timg29.gif)
![\begin{figure}
\par\includegraphics[width=12cm,clip]{9777fig2.eps}\end{figure}](/articles/aa/full/2008/37/aa09777-08/Timg43.gif)
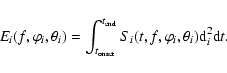
![\begin{figure}
\par\includegraphics[width=15cm]{9777fig3.eps}\end{figure}](/articles/aa/full/2008/37/aa09777-08/Timg84.gif)
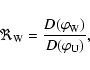
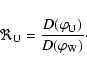
![\begin{displaymath}D(\varphi) = 10^{a[\cos(\varphi - \varphi_0) - 1]},
\end{displaymath}](/articles/aa/full/2008/37/aa09777-08/img89.gif)
![\begin{displaymath}\frac {1}{n} = 10^{a[\cos(\mathbf{\Delta\varphi_{\it n} /2}) - 1]},
\end{displaymath}](/articles/aa/full/2008/37/aa09777-08/img91.gif)
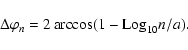
![\begin{figure}
\par\includegraphics[width=11cm,clip]{9777fig4.eps}\end{figure}](/articles/aa/full/2008/37/aa09777-08/Timg98.gif)
![\begin{figure}
\par\includegraphics[width=12cm,clip]{9777fig5.eps}\end{figure}](/articles/aa/full/2008/37/aa09777-08/Timg99.gif)
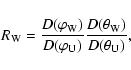
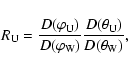
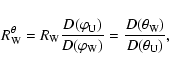
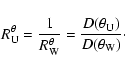
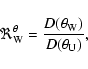
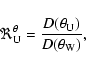
![\begin{displaymath}D(\theta) = 10^{b[\cos(\theta - \theta_0) - 1]},
\end{displaymath}](/articles/aa/full/2008/37/aa09777-08/img109.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9777fig6.eps}\end{figure}](/articles/aa/full/2008/37/aa09777-08/Timg116.gif)