Table 1: Multiply imaged systems considered in this work.
Id RA Dec $z_{\rm phot}$ $\Delta(z_{\rm phot})$ $z_{\rm mod}$ rms (s) rms (i) $z_{\rm free}$

1.1		 198.77725 51.81934 $\rm0.965_{-0.240}^{+0.075}$ - 0.8885- - 0.27 1.95  
1.2 198.77482 51.81978 $\rm0.940_{-0.096}^{+0.102}$ ...        
1.3 198.77414 51.81819 $\rm0.995_{-0.087}^{+0.051}$ ...        
1.4 198.77671 51.81767 $\rm0.740_{-0.078}^{+0.129}$ ...        
1.5 198.76206 51.81331 $\rm0.915_{-0.090}^{+0.108}$ ...        
2.2 198.77156 51.81174 $\rm 2.310_{-0.381}^{+0.456}$ [1.9-2.8] $\rm 2.24_{-0.14}^{+0.25}$ 0.09 0.39 $\rm 3.98_{-0.52}^{+1.30}$
2.3 198.76970 51.81186 $\rm 2.225_{-0.657}^{+0.195}$ ...        
3.1 198.76696 51.83205 - [3.31-3.37] $\rm 3.32_{-0.01}^{+0.03}$ 0.15 1.22 $\rm 4.85_{-0.71}^{+0.65}$
3.2 198.76634 51.83190 $\rm 3.350_{-0.036}^{+0.024}$ ...        
3.3 198.75824 51.82982 $\rm 3.350_{-0.036}^{+0.024}$ ...        
4.1 198.76564 51.82653 - [2.03-2.48] $\rm 2.03_{-0.00}^{+0.03}$ 0.17 0.51 $\rm 2.46_{-0.11}^{+0.12}$
4.2 198.76075 51.82487 $\rm 2.255_{-0.222}^{+0.216}$ ...        
4.3 198.77666 51.82797 - ...        
5.1 198.76602 51.82677 - [2.03-2.48] $\rm 2.03_{-0.00}^{+0.03}$ 0.21 0.64 $\rm 2.36_{-0.08}^{+0.14}$
5.2 198.76041 51.82489 $\rm 2.315_{-0.186}^{+0.171}$ ...        
5.3 198.77591 51.82807 - ...        
6.1 198.77984 51.82640 $\rm 2.595_{-0.159}^{+0.144}$ [2.43-2.79] $\rm 2.78_{-0.06}^{+0.00}$ 0.30 0.84 $\rm 4.98_{-0.49}^{+0.45}$
6.2 198.76890 51.82580 $\rm 2.535_{-0.117}^{+0.258}$ ...        
6.3 198.75652 51.81947 $\rm 2.625_{-0.135}^{+0.108}$ ...        
7.1 198.77074 51.83087 $\rm 3.490_{-0.108}^{+0.132}$ [2.52-3.62] $\rm 3.59_{-0.18}^{+0.02}$ 0.28 2.59 $\rm 5.63_{-0.56}^{+0.02}$
7.2 198.76614 51.83010 $\rm 2.960_{-0.183}^{+0.354}$ ...        
7.3 198.75869 51.82814 $\rm 3.200_{-0.675}^{+0.210}$ ...        
8.1 198.77250 51.83045 $\rm 2.805_{-0.090}^{+0.174}$ [2.61-2.98] $\rm 2.97_{-0.05}^{+0.00}$ 0.30 1.63 $\rm 5.53_{-0.61}^{+0.08}$
8.2 198.76608 51.82949 $\rm 2.770_{-0.108}^{+0.207}$ ...        
8.3 198.75863 51.82740 $\rm 2.725_{-0.117}^{+0.198}$ ...        
9.1 198.77176 51.83030 - [2.40-3.37] $\rm 3.36_{-0.07}^{+0.04}$ 0.24 1.29 $\rm 5.53_{-0.61}^{+0.08}$
9.2 198.76690 51.82957 $\rm 2.995_{-0.378}^{+0.195}$ ...        
9.3 198.75813 51.82708 $\rm 3.000_{-0.603}^{+0.366}$ ...        
10.1 198.78708 51.81424 $\rm 3.100_{-0.162}^{+0.324}$ [2.40-3.42] $\rm 2.41_{-0.01}^{+0.07}$ 0.21 1.62 $\rm 3.79_{-0.28}^{+0.25}$
10.2 198.78352 51.81138 $\rm 2.595_{-0.189}^{+0.117}$ ...        
10.3 198.76242 51.80954 $\rm 2.705_{-0.261}^{+0.189}$ ...        
11.1 198.78648 51.81322 $\rm 3.045_{-0.138}^{+0.102}$ [2.40-3.42] $\rm 2.47_{-0.04}^{+0.06}$ 0.25 2.13 $\rm 3.79_{-0.27}^{+0.27}$
11.2 198.78564 51.81247 $\rm 3.155_{-0.099}^{+0.078}$ ...        
11.3 198.76242 51.80954 $\rm 2.705_{-0.261}^{+0.189}$ ...        
15.1 198.76284 51.81246 $\rm 2.440_{-0.231}^{+0.171}$ [2.21-2.67] $\rm 2.67_{-0.09}^{+0.00}$ 0.37 0.93 $\rm 5.58_{-0.71}^{+0.26}$
15.2 198.76704 51.82128 $\rm 2.440_{-0.153}^{+0.231}$ ...        
15.3 198.78821 51.82176 - ...        
15.4 198.77519 51.81155 - ...        
16.1 198.76356 51.81164 $\rm 2.710_{-0.324}^{+0.216}$ [2.50-2.92] $\rm 2.70_{-0.08}^{+0.10}$ 0.27 0.73 $\rm 5.04_{-0.52}^{+0.44}$
16.2 198.76774 51.82101 - ...        
16.3 198.78838 51.82097 $\rm 2.750_{-0.165}^{+0.171}$ ...        
16.4 198.77558 51.81128 - ...        
We have found 13 distinct multiply imaged systems. Coordinates are given in degrees (J 2000.0). When the photometry is reliable in each band, we report the corresponding photometric redshift estimates, with error bars quoting the 3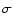$\sigma$ confidence level. 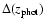$\Delta(z_{\rm phot})$ corresponds to the redshift range allowed by the photometric redshift estimation and that will be used as a prior in the optimization (i.e. 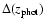for each system, the redshift will be let free and allowed to vary between $\Delta(z_{\rm phot})$). For system 1 however we fix the redshift to the measured one, 0.8885. 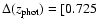The photometric estimate $\Delta(z_{\rm phot}) = [0.725$-1.04] is in agreement with the spectroscopic measurement. $z_{\rm mod}$ corresponds to the redshift inferred from the optimization procedure. We report both the rms in the source plane and the rms in the image plane. The mean scatters are given for the whole system, not for each individual image composing a system. 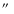The total rms is equal to 0.26 $\hbox {$^{\prime \prime }$ }$ (source plane) and 1.45 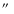$\hbox {$^{\prime \prime }$ }$ (image plane). 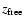$z_{\rm free}$ corresponds to the redshift inferred from the optimization when all redshift but system 1 are assigned a flat prior between 0.28 and 6 (see Sect. 5.3).

Source LaTeX | All tables | In the text