A&A 489, 115-133 (2008)
DOI: 10.1051/0004-6361:200809644
N. J. Rodriguez-Fernandez1 - F. Combes2
1 - IRAM, 300 rue de la Piscine, 38406 St. Martin d'Hères, France
2 - LERMA, Observatoire de Paris, 61 Av de l'Observatoire, 75014 Paris, France
Received 25 February 2008 / Accepted 26 June 2008
Abstract
Context. The gas distribution and dynamics in the inner Galaxy present many unknowns, such as the origin of the asymmetry of the lv-diagram of the Central Molecular Zone (CMZ). On the other hand, there is recent evidence in the stellar component of the presence of a nuclear bar that may be slightly lopsided.
Aims. Our goal is to characterize the nuclear bar observed in 2MASS maps and to study the gas dynamics in the inner Milky Way taking into account this secondary bar.
Methods. We have derived a realistic mass distribution by fitting the 2MASS star count map with a model including three components (disk, bulge and nuclear bar) and we have simulated the gas dynamics in the deduced gravitational potential using a sticky-particles code.
Results. Our simulations of the gas dynamics successfully reproduce the main characteristics of the Milky Way for a bulge orientation of ![]() -
-![]() with respect to the Sun-Galactic Center (GC) line and a pattern speed of 30-40 km s-1 kpc-1. In our models the Galactic Molecular Ring (GMR) is not an actual ring but the inner parts of the spiral arms, while the 3-kpc arm and its far side counterpart are lateral arms that extend around the bar. Our simulations reproduce, for the first time, the parallelogram shape of the lv-diagram of the CMZ as the gas response to the nuclear bar. This bar should be oriented by an angle of
with respect to the Sun-Galactic Center (GC) line and a pattern speed of 30-40 km s-1 kpc-1. In our models the Galactic Molecular Ring (GMR) is not an actual ring but the inner parts of the spiral arms, while the 3-kpc arm and its far side counterpart are lateral arms that extend around the bar. Our simulations reproduce, for the first time, the parallelogram shape of the lv-diagram of the CMZ as the gas response to the nuclear bar. This bar should be oriented by an angle of
![]() -
-![]() with respect to the Sun-GC line and its mass amounts to (2-5.5) 109
with respect to the Sun-GC line and its mass amounts to (2-5.5) 109 ![]() .
We show that the observed asymmetry of the CMZ cannot be due to lopsidedness of the nuclear bar as suggested by the 2MASS maps.
.
We show that the observed asymmetry of the CMZ cannot be due to lopsidedness of the nuclear bar as suggested by the 2MASS maps.
Conclusions. We do not find clear evidence of lopsidedness in the stellar potential. We propose that the observed asymmetry of the central gas layer can be due to the infalling of gas into the CMZ in the
![]() -complex.
-complex.
Key words: Galaxy: structure - Galaxy: center - Galaxy: kinematics and dynamics - ISM: kinematics and dynamics - methods: numerical
Studying the structure and the dynamics of the Milky Way galaxy is necessary to understand its formation and evolution. For example, the large scale star formation rate, the gas transfer to the nucleus and the fueling of the central super-massive black hole are strongly influenced by the large scale dynamics of the Galaxy.
At least three components are needed to explain the rotation curve of the Galaxy: a disc, a bulge and a massive dark halo. In near-infrared images, the bulge is a triaxial structure difficult to distinguish from a bar.
The first direct evidence of the barred nature of the Milky Way was found by Blitz & Spergel (1991). The analysis of COBE/DIRBE data (Freudenreich 1998; Binney et al. 1997; Dwek et al. 1995) supported Blitz & Spergel results.
Dwek et al. (1995) found that the peanut-shaped bulge seen in the COBE image is best fitted by boxy Gaussians functions.
Since COBE, direct evidence of the bar has increased based on photometric surveys and star counts in the near-infrared (see for instance López-Corredoira et al. 2000, 2005; Babusiaux & Gilmore 2005, and references therein).
Although there is a consensus on the triaxial nature of the bulge, the actual shape and the inclination is still under debate with currently no clear agreement among different authors. The inclination angles found range from
![]() -
-![]() (Lopez-Corredoira et al. 1997; Freudenreich 1998; Binney et al. 1991) to
(Lopez-Corredoira et al. 1997; Freudenreich 1998; Binney et al. 1991) to
![]() -
-![]() (Sevenster 1999; López-Corredoira et al. 2001; Weiner & Sellwood 1999) with a number of works giving values in the range
(Sevenster 1999; López-Corredoira et al. 2001; Weiner & Sellwood 1999) with a number of works giving values in the range ![]() -
-![]() (Bissantz & Gerhard 2002; López-Corredoira et al. 2005; Mulder & Liem 1986; Fux 1999; Babusiaux & Gilmore 2005; Binney et al. 1997; Bissantz et al. 2003; Englmaier & Gerhard 1999).
(Bissantz & Gerhard 2002; López-Corredoira et al. 2005; Mulder & Liem 1986; Fux 1999; Babusiaux & Gilmore 2005; Binney et al. 1997; Bissantz et al. 2003; Englmaier & Gerhard 1999).
In addition to the bar-like boxy-bulge, some recent works have also proposed the existence of another bar that would be longer and thinner than the bulge (Picaud et al. 2003; López-Corredoira et al. 2007; Benjamin et al. 2005; López-Corredoira et al. 2001). As with the bulge, the near side of this long and thin bar would also be located in the first Galactic quadrant. In contrast, the long bar would be oriented at an angle of
![]() with respect to the line of sight towards Galactic center.
In the present paper we will not discuss this component as the mass should be dominated by the bulge. Hereafter, we will refer to the triaxial boxy bulge as the ``large bar'' or simply ``bulge''.
with respect to the line of sight towards Galactic center.
In the present paper we will not discuss this component as the mass should be dominated by the bulge. Hereafter, we will refer to the triaxial boxy bulge as the ``large bar'' or simply ``bulge''.
Due to the difficulty of measuring stellar velocities, most of our knowledge of the Galactic dynamics comes from spectroscopic observations of the atomic and molecular interstellar medium (Liszt & Burton 1978; Scoville 1972; Dame et al. 2001; Rougoor & Oort 1960; Bally et al. 1987). The gas exhibit large non-circular motion in the inner Galaxy. Among the possible explanations for these kinematics, de Vaucouleurs (1964) proposed a gas response to a bar potential. This explanation has also been discussed in other observational works such as those of Kerr (1967); Bania (1977) or Liszt & Burton (1978). Nevertheless, it is the comparison of the observations with numerical simulations of the gas dynamics that have allowed us to better understand the structure of the Galaxy and to derive important dynamical information, such as the pattern speed of the bar. The first attempt was that of Mulder & Liem (1986) solving the gas-dynamical equations to obtain the gas flow in a weak bar for the whole Galaxy.
A major step in our understanding of the gas kinematics in the Galactic Center was
the paper by Binney et al. (1991). These authors compared of the CO(1-0) and HI longitude-velocity diagrams (hereafter lv-diagram) of Bally et al. (1987) and Burton & Liszt (1978), with the lv locus of closed stellar orbits in a bar potential (X1 and X2 orbits).
The lv-diagram of the molecular gas in the inner
![]() of the Galaxy shows a parallelogram shape that resembles the lv locus of the cusped X1 orbit for a bar with an inclination of
of the Galaxy shows a parallelogram shape that resembles the lv locus of the cusped X1 orbit for a bar with an inclination of
![]() .
In spite of the globally successful interpretation of the CO and HI lv-diagrams, the Binney et al. (1991) model cannot account for the observed asymmetry of the CO parallelogram, which is lopsided towards positive longitudes while the modeled parallelograms are centered at longitude
.
In spite of the globally successful interpretation of the CO and HI lv-diagrams, the Binney et al. (1991) model cannot account for the observed asymmetry of the CO parallelogram, which is lopsided towards positive longitudes while the modeled parallelograms are centered at longitude ![]() .
In addition the expected upper right vertex of the locus of the cusped X1 orbit has a velocity close to 0, while the upper right vertex of the observed CO parallelogram shown in Fig. 2 of Binney et al. (1991) has a velocity of
.
In addition the expected upper right vertex of the locus of the cusped X1 orbit has a velocity close to 0, while the upper right vertex of the observed CO parallelogram shown in Fig. 2 of Binney et al. (1991) has a velocity of ![]() km s-1.
km s-1.
The qualitative insight into the gas dynamics that one could obtain by comparing the lv-diagram of the gas with that of a few stellar orbits should be tested by performing simulations of the gas dynamics that take into account the dissipative nature of the gas clouds. This was done by Jenkins & Binney (1994), who tried to reproduce the lv-diagram of the CMZ using a sticky-particles code but with moderate success.
Using a combination of SPH and collisionless particles, Lee et al. (1999) were able to reproduce an inner ring with the right inclination in the lv-diagram and also some of the gas clouds with non-circular velocities in the range
![]() .
.
To our knowledge, the works by Binney et al. (1991); Jenkins & Binney (1994) and Lee et al. (1999) are the only dynamical models that have tried to interpret the dynamics of the complex Galactic center region (the central 500 pc). Other Galactic dynamics models have been mainly devoted to larger scales, from the works of Mulder & Liem (1986) and Wada et al. (1994) to the more recent works by Fux (1999); Englmaier & Gerhard (1999); Weiner & Sellwood (1999) and Bissantz et al. (2003). The bar pattern rotation speed for most of those models are in the range of 40 to 60 km s-1 kpc-1. The corotation radius is estimated to be in the range 3-4 kpc by some works (Habing et al. 2006; Bissantz et al. 2003; Englmaier & Gerhard 1999) and in the range 4-5 kpc by other works (Combes 1996; Sevenster 1999; Fux 1999). In contrast, Binney et al. (1991) placed the corotation at 2.4 kpc and found a pattern speed of 80 km s-1 kpc-1. As pointed out by Combes (1996), the discrepancy between the Binney et al. estimation and other estimations can be due to the fact that the molecular gas distribution in the Galactic center region used by Binney et al. could be the response to a small nuclear bar instead of the large bar of the Galaxy.
Indeed, there is recent evidence of the presence of a distinct structure in the nuclear region of the Galaxy. The star counts map made by Alard (2001) with 2MASS data shows an excess of counts in the inner four degrees of the Galaxy that resembles a small nuclear bar. This bar could be lopsided with the barycenter displaced to negative longitudes. Nishiyama et al. (2005) have also found evidence of a structure different to the large bar or bulge in the inner degrees of the Galaxy.
In the present paper, we investigate the gas response to the mass distribution inferred from the 2MASS data. In particular, we model the central mass distribution as a small nuclear bar. We are interested in the role of this nuclear bar in explaining the differences between the results of previous works (Combes 1996; Binney et al. 1991; Fux 1999). We also want to study whether a lopsided nuclear bar could explain the apparent lopsidedness of the molecular gas distribution in the nuclear region, whose complex dynamics are far from being understood. Therefore, we have modeled the 2MASS star counts maps of Alard fitting different parametric functions using three components: a disc, bulge/bar and nuclear bar. We use that mass distribution to determine the galactic stellar potential and to model the gas dynamics using a N-body code that takes into account cloud collisions.
Nested bars are common in external galaxies. As much as one third of barred galaxies have a secondary nuclear bar (Laine et al. 2002). In some cases the secondary bar is coupled with the primary bar (Shaw et al. 1993) while in other cases the two bars rotate with different speeds (Wozniak et al. 1995). The present paper is the first one dealing with the gas flow in the Milky Way nested bars and we will assume that both bars are dynamically coupled (they rotate with the same speed). As we discuss in Sect. 8, this seems a good assumption since our simulations explain for the first time some characteristics of the inner Galaxy.
The paper is organized as follows: in the next section we summarize our understanding of the distribution and kinematics of the interstellar gas. In Sects. 3 and 4 we present the 2MASS star counts model and the fits to the data. The gas dynamics simulations are described in Sect. 5, and the results are presented in Sects. 6 and 7. We discuss the nature of the nuclear bar in Sect. 8. Our conclusions are summarized in Sect. 9.
![\begin{figure}
\par\includegraphics[angle=-90,width=16cm]{9644f1.eps}\end{figure}](/articles/aa/full/2008/37/aa09644-08/Timg44.gif) |
Figure 1:
Longitude-velocity (lv) diagram of the CO(1-0) emission (Dame et al. 2001). The solid lines trace the position of some remarkable features such as the locus of the spiral arms, the 3-kpc arm and the Connecting Arm. The black dashed lines indicate the contour of the Galactic Molecular Ring. The solid circles are the terminal velocities measurements of Fich et al. (1989) using CO while the triangles are the terminal velocities determined from the HI data of Burton & Liszt (1993).
The boxes mark the position of the Sagittarius, Scutum, Norma and Centaurus tangent points, located respectively at
|
| Open with DEXTER | |
In this section we summarize visible structures in the longitude-velocity diagram (hereafter lv-diagram) of the interstellar gas. The large scale lv-diagram derived from observations of the CO(1-0) line by Dame et al. (2001) is shown in Fig. 1 while Fig. 2 shows the lv-diagram of the nuclear region derived also from CO(1-0) observations by Bally et al. (1987). We also discuss the plausible face on view of the Galaxy. The different features discussed here will be used in the following sections to compare with our simulations of the gas dynamics.
The terminal velocity curve (TVC) is not a kinematic feature in itself as many independent features contribute to this curve at different Galactic longitudes.
However, we discuss it here since it has been used to constrain several dynamical models of the Milky Way (Bissantz et al. 2003; Binney et al. 1991; Weiner & Sellwood 1999; Englmaier & Gerhard 1999).
There have been different determinations of the TVC using CO and HI data (Alvarez et al. 1990; Fich et al. 1989; Burton & Liszt 1993; Clemens 1985). The dispersion of the TVC points derived by different authors is typically 10 km s-1 (see for instance Fig. 6 of Bissantz et al. 2003).
The TVC measurements by Fich et al. (1989) and Burton & Liszt (1993) are shown in Fig. 1 and in the figures showing the simulation results. In addition, in Fig. 1 we have indicated with boxes the Sagittarius, Scutum, Norma and Centaurus tangent points, located respectively at
![]() and
and ![]() (see for instance Dame et al. 2001; Englmaier & Gerhard 1999).
(see for instance Dame et al. 2001; Englmaier & Gerhard 1999).
Many works have studied the spiral structure of the Galaxy using different tracers such as HII regions, atomic and molecular gas or photometric observations in different bands from the near to the far infrared. The different models of the spiral arms have two arms (Bash 1981, using HII regions; Drimmel & Spergel 2001, using K-band observations; Benjamin 2008, using Spitzer), three (Kulkarni et al. 1982; Nakanishi & Sofue 2003, using HI) or four arms (Georgelin & Georgelin (1976) using HI regions; Nakanishi & Sofue (2006) using CO or Drimmel (2000) using the 240 micron luminosity).
Deprojecting a given data set to find the face on view of the Galaxy is a difficult task in particular for the inner Galaxy. For instance, the kinematical distances based in the rotation curve are not accurate due to the presence of important non-circular motion.
Furthermore, after performing the deprojection there is an uncertainty as to how different structures are associated with a common arm (see Nakanishi & Sofue 2006). Different authors have even fitted different spirals to the same data.
A plausible explanation for the discrepancy between the two arms derived from stellar tracers (K band) and the four arms that are found in most of the interstellar tracers is that the Milky Way has two stellar spiral arms but the gas response is a four-armed spiral (Drimmel 2000).
In any case, the major arms are logarithmic with pitch angles of ![]() -
-![]() .
In addition, to these grand-design spirals there is a more
flocculent structure giving a number of minor arms like the Local Arm, which is a small arm linked to the Perseus spiral arm. In order to compare with our simulations, in Figs. 8, 9 and 10 we have traced the sketch of the logarithmic spiral arms of Nakanishi & Sofue (2006), which are very similar to the classical spirals of Georgelin & Georgelin (1976).
The locus of different spiral arms in the lv-diagram are shown in Fig. 1. The Carina arms deserves a special mention since the Carina tangent point is clearly seen at
.
In addition, to these grand-design spirals there is a more
flocculent structure giving a number of minor arms like the Local Arm, which is a small arm linked to the Perseus spiral arm. In order to compare with our simulations, in Figs. 8, 9 and 10 we have traced the sketch of the logarithmic spiral arms of Nakanishi & Sofue (2006), which are very similar to the classical spirals of Georgelin & Georgelin (1976).
The locus of different spiral arms in the lv-diagram are shown in Fig. 1. The Carina arms deserves a special mention since the Carina tangent point is clearly seen at
![]() .
.
The determinations of the speed of the spiral pattern give values in the range from 13.5 to 59 km s-1 kpc-1 (Bissantz et al. 2003; Lin et al. 1969; Martos et al. 2004; Fernández et al. 2001; Debattista et al. 2002). Thus, the spiral pattern speed could be lower that the bar one.
The so-called Galactic Molecular Ring (GMR) is one of the most prominent structures in the lv-diagram (Fig. 1). The locus of the GMR is more or less a diagonal line that passes trough the origin as a circular ring would do. If the GMR is a real ring, it could be associated with a resonance. Binney et al. (1991) proposed that the GMR could be located at the Outer Linblad Resonance. Other models that place the corotation farther out have suggested that the GMR could be better explained by the Ultra Harmonic Resonance (Combes 1996).
However, the real spatial distribution of the GMR is not known and it could be composed of imbricated spiral arms instead of being an actual ring. Some authors (see for instance Englmaier & Gerhard 1999) consider that, if formed by several arms, the GMR should be located outside of the corotation since they exhibit almost circular velocities. In their face-on deprojection of the neutral and molecular gas distribution, Nakanishi & Sofue (2006) found that the GMR seems to be the inner part of the Sgr-Carina arm (the far-side of the GMR) and the Scutum-Crux arm (the near-side of the GMR).
The 3-kpc arm is clearly seen in the lv-diagram of Fig. 1 with a velocity of -53 km s-1 at ![]() .
The name of this feature comes from a tangent point at
.
The name of this feature comes from a tangent point at
![]() that corresponds to a distance of
that corresponds to a distance of ![]() 3 kpc. This arm is located in between the Sun and the GC since the clouds in the arm absorb the radiation from the continuum sources in the GC. The 3-kpc arm cannot be explained with a combination of rotation and expansion (Burke & Tuve 1964) and has been interpreted as a stationary density wave in a barred potential (Mulder & Liem 1986). The simulations of Fux (1999) suggest that it is a lateral arm that surrounds the bar while, in the simulations by Englmaier & Gerhard (1999), it would be a small arm arising from the extremity of the bar.
3 kpc. This arm is located in between the Sun and the GC since the clouds in the arm absorb the radiation from the continuum sources in the GC. The 3-kpc arm cannot be explained with a combination of rotation and expansion (Burke & Tuve 1964) and has been interpreted as a stationary density wave in a barred potential (Mulder & Liem 1986). The simulations of Fux (1999) suggest that it is a lateral arm that surrounds the bar while, in the simulations by Englmaier & Gerhard (1999), it would be a small arm arising from the extremity of the bar.
Sevenster (1999) and Habing et al. (2006) propose a different explanation. Sevenster (1999) found old stars associated with the 3-kpc arm. They interpret the fact that both old stars and gas follow the same trajectories as the probe as that the arm would be the locus of closed orbits and not a spiral density wave maximum. They propose that the 3-kpc arm has its origin near one of the two points where the bar meets its corotation radius and that the arm can be a channel to transport gas from the corotation to the GC and to fuel the star formation in cloud complexes like Sgr B2.
The recent discovery of the far-side counterpart of the 3-kpc arm by Dame & Thaddeus (2008) will certainly contribute to our understanding of the exact nature of these features (see Sect. 6.3).
The ``Connecting Arm'' is clearly seen in Fig. 1 as a feature with high inclination with a velocity of ![]() 100 km s-1 at
100 km s-1 at
![]() and more than 250 km s-1 at
and more than 250 km s-1 at ![]() .
The name ``Connecting Arm'' comes from the fact that it seems to be connected to the nuclear ring.
This is a very puzzling structure that has not been discussed much in the literature (see Fux 1999, for a short summary).
On the one hand, Burton & Liszt (1978) and Liszt & Burton (1980) suggested that the Connecting Arm could be the edge of the HI ring found at a radius of
.
The name ``Connecting Arm'' comes from the fact that it seems to be connected to the nuclear ring.
This is a very puzzling structure that has not been discussed much in the literature (see Fux 1999, for a short summary).
On the one hand, Burton & Liszt (1978) and Liszt & Burton (1980) suggested that the Connecting Arm could be the edge of the HI ring found at a radius of ![]() 1 kpc (see below).
On the other hand, in one of his simulations, Fux (1999) obtained a feature in the lv-diagram that resembles the Connecting Arm. In that simulation, the Connecting Arm-like feature is the locus of the off-axis shocks or dustlanes (since in the optical images of barred galaxies the off-axis shocks are seen as dust lanes). Marshall et al. (2008) also interpret the Connecting Arm as the near side dustlane.
1 kpc (see below).
On the other hand, in one of his simulations, Fux (1999) obtained a feature in the lv-diagram that resembles the Connecting Arm. In that simulation, the Connecting Arm-like feature is the locus of the off-axis shocks or dustlanes (since in the optical images of barred galaxies the off-axis shocks are seen as dust lanes). Marshall et al. (2008) also interpret the Connecting Arm as the near side dustlane.
However, in another of the simulations discussed by Fux (1999) the locus of the dustlane in the lv-diagram is a vertical feature extending approximately from a velocity of 0 km s-1 to 200 km s-1 at an almost constant longitude (see his Figs. 15 and 16). This looks like the ``clumps'' discussed by Bania (1977). These clumps are cloud complexes found at
![]() and
and
![]() that exhibit a huge velocity dispersion of
that exhibit a huge velocity dispersion of ![]() 200 km s-1 in a very narrow range of longitude. A portion of the clump located at
200 km s-1 in a very narrow range of longitude. A portion of the clump located at
![]() (known as Clump 2) is shown in Fig. 2. The Clump 2 has been interpreted as a dustlane by Stark & Bania (1986), while in the Fux (1999) interpretation, Banias's clumps would be gas clouds that are about to enter the dustlane shocks, although the actual dustlane would be the Connecting Arm as mentioned above. This is also the interpretation of Liszt (2008,2006), who have studied in detail the spatial and velocity structure of all these features.
(known as Clump 2) is shown in Fig. 2. The Clump 2 has been interpreted as a dustlane by Stark & Bania (1986), while in the Fux (1999) interpretation, Banias's clumps would be gas clouds that are about to enter the dustlane shocks, although the actual dustlane would be the Connecting Arm as mentioned above. This is also the interpretation of Liszt (2008,2006), who have studied in detail the spatial and velocity structure of all these features.
The HI emission in the GC region can be modeled as a tilted circular ring with an inner radius of ![]() 300 pc and outer radius of 1-1.5 kpc (Burton & Liszt 1978). This first model was improved by Liszt & Burton (1980), who discussed that an elongated ring could also explain the observations.
The spatial distribution of the interstellar gas in the innermost 3 kpc of the Galaxy has recently been reviewed by Ferrière et al. (2007). The model that they consider more plausible, despite its inherent uncertainties, is that of Liszt & Burton (1980) since an elongated ring seems to be easier to understand if it is composed of gas clouds moving in elongated X1 orbits. Therefore, they modeled the HI ring as an elliptical ring with a semi-major axis of 1.6 kpc, and an axis ratio of 3.1, with an inner hole with semi-axis of 800 pc
300 pc and outer radius of 1-1.5 kpc (Burton & Liszt 1978). This first model was improved by Liszt & Burton (1980), who discussed that an elongated ring could also explain the observations.
The spatial distribution of the interstellar gas in the innermost 3 kpc of the Galaxy has recently been reviewed by Ferrière et al. (2007). The model that they consider more plausible, despite its inherent uncertainties, is that of Liszt & Burton (1980) since an elongated ring seems to be easier to understand if it is composed of gas clouds moving in elongated X1 orbits. Therefore, they modeled the HI ring as an elliptical ring with a semi-major axis of 1.6 kpc, and an axis ratio of 3.1, with an inner hole with semi-axis of 800 pc ![]() 258 pc that encloses the Central Molecular Zone (see below).
258 pc that encloses the Central Molecular Zone (see below).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9644f2.eps}\end{figure}](/articles/aa/full/2008/37/aa09644-08/Timg55.gif) |
Figure 2: Upper panel: longitude-velocity (lv) diagram of the CO(1-0) emission in the Central Molecular Zone using data of Bally et al. (1987) and integrating all negative Galactic latitudes. The solid lines trace the position of some remarkable features such as Clump 2, or structures K and J of Rodriguez-Fernandez et al. (2006). The dashed line indicates the contour of the very crowded central region. Lower panel: integrated intensity map. |
| Open with DEXTER | |
The Central Molecular Zone (hereafter CMZ) refers to the central accumulation of gas in the inner hundreds of parsec of the Galaxy.
This gas is mainly molecular and extends continuously from approximately
![]() to
to ![]() (see Fig. 2). The spatial distribution is not symmetric due to the prominent cloud complex located at
(see Fig. 2). The spatial distribution is not symmetric due to the prominent cloud complex located at
![]() (hereafter
(hereafter
![]() -complex) that lacks a negative longitude counterpart. Figure 2 also shows the lv-diagram of the CMZ. This plot has been obtained integrating the CO(1-0) data of Bally et al. (1987) for negative Galactic longitudes to reveal a number of kinematical component such as Clump 2 (at
-complex) that lacks a negative longitude counterpart. Figure 2 also shows the lv-diagram of the CMZ. This plot has been obtained integrating the CO(1-0) data of Bally et al. (1987) for negative Galactic longitudes to reveal a number of kinematical component such as Clump 2 (at
![]() ), and the features K and J discussed by Rodriguez-Fernandez et al. (2006).
), and the features K and J discussed by Rodriguez-Fernandez et al. (2006).
The kinematics of the inner region are very complex with a high fraction of the gas exhibiting non-circular velocities. Figure 2 shows with a dashed line the contour of the inner CMZ that contains the feature M of Rodriguez-Fernandez et al. (2006) and the inner arms found by Sofue (1995). This contour resembles a parallelogram but it is not the parallelogram that inspired the Binney et al. (1991) work.
The whole lv-diagram shown in Fig. 2 is very different to that used by Binney et al. (1991).
These authors integrated the CO data of Bally et al. (1987) over positive and negative latitudes and studied the region
![]() .
In their Fig. 2, the feature K is not clearly detached from the inner lv parallelogram and they considered that it is part of a larger lv parallelogram. However, following the analysis of the Bally et al. (1987) data by Rodriguez-Fernandez et al. (2006), we conclude that feature K is a distinct kinematic feature. This conclusion is also supported by the large scale (
.
In their Fig. 2, the feature K is not clearly detached from the inner lv parallelogram and they considered that it is part of a larger lv parallelogram. However, following the analysis of the Bally et al. (1987) data by Rodriguez-Fernandez et al. (2006), we conclude that feature K is a distinct kinematic feature. This conclusion is also supported by the large scale (
![]() )
CO(1-0) survey by Bitran et al. (1997), whose lv-diagram shows clearly that the feature K extends to
)
CO(1-0) survey by Bitran et al. (1997), whose lv-diagram shows clearly that the feature K extends to
![]() where it is connected to the Connecting Arm.
where it is connected to the Connecting Arm.
Interestingly, when one compares the lv parallelograms of the X1 orbits displayed in Fig. 3 of Binney et al. (1991) to the parallelogram shown in our Fig. 2, the upper right vertex is in good agreement, showing velocities of ![]() 0 km s-1. Thus, one of the apparent discrepancies (see Sect. 1) between the Binney et al. (1991) model and the CO lv-diagram disappears.
0 km s-1. Thus, one of the apparent discrepancies (see Sect. 1) between the Binney et al. (1991) model and the CO lv-diagram disappears.
![\begin{figure}
\par\includegraphics[width=6cm,clip]{9644f3.eps}\end{figure}](/articles/aa/full/2008/37/aa09644-08/Timg61.gif) |
Figure 3: Sketch of the different coordinates systems and angles used to define the bars in the Galactic plane. The z and z' axis are coincident and the z>0 semiaxis is in the northern Galactic hemisphere. |
| Open with DEXTER | |
We have modeled the 2MASS star count map of Alard (2001) to determine a realistic stellar potential. In this section we summarize the methods and the main conclusions of Alard's work.
Using the H and K bands and assuming that we know the intrinsic color of the sources (H and K), one can correct for extinction one of the bands as follows:
![\begin{displaymath}m_K^{\rm corr}=m_K- [ A_K/(A_H-A_k)][(m_H-m_K)-(H-K)]
\end{displaymath}](/articles/aa/full/2008/37/aa09644-08/img62.gif) |
(1) |
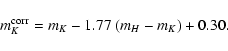 |
(2) |
| (3) |
In this section we describe how we have modeled the 2MASS star count map.
The number of stars in a volume dV located at x with a magnitude in the interval M and
![]() is:
is:
| (4) |
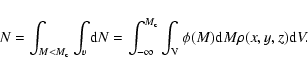 |
(5) |
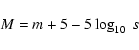 |
(6) |
Our model of the density distribution is given by three components: a triaxial bulge or large bar, an exponential disk and a small nuclear bar. The exact functional form of each component is given below.
We use the exponential disc of Wainscoat et al. (1992), which is defined as:
From the COBE/DIRBE images we know that the bulge of the Milky Way is boxy (Dwek et al. 1995). The 2MASS data confirm this result (López-Corredoira et al. 2005). Therefore, we have adopted a boxy Gaussian (Dwek et al. function G2) to represent the bulge:
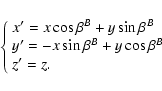 |
(10) |
In contrast to the bulge, the small nuclear bar found by Alard does not seem to be boxy. Therefore we have taken a triaxial Gaussian function (Dwek et al. function G1) to represent this component:
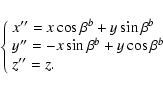 |
(13) |
Finally, we must also convert
![]() to
to
![]() since we want to model the star counts in Galactic coordinates (l,b) and to integrate along the line of sight (s). If (x,y,z) is a right-handed reference frame centered in the galactic center, with the plane of the sky in the xz-plane with x>0 for l<0, and z>0 towards the Galactic north pole, and assuming that the sun is located at
(x,y,z)=(0,-D,0) then:
since we want to model the star counts in Galactic coordinates (l,b) and to integrate along the line of sight (s). If (x,y,z) is a right-handed reference frame centered in the galactic center, with the plane of the sky in the xz-plane with x>0 for l<0, and z>0 towards the Galactic north pole, and assuming that the sun is located at
(x,y,z)=(0,-D,0) then:
We have computed the integral in magnitudes from
![]() to
to
![]() with
with
![]() .
The integral of the distance along the line of sight s has been computed up to
.
The integral of the distance along the line of sight s has been computed up to
![]() using a variable step
using a variable step ![]() :
:
 |
(16) |
We have fitted the star count map using the model described above.
This model has 14 free parameters corresponding to the disc (
![]() ), the bulge (
), the bulge (
![]() )
and the nuclear bar (
)
and the nuclear bar (
![]() ).
).
The star count equation is evaluated for an initial guess of the density function parameters. A ![]() parameter is computed as the difference of the star count data points (
parameter is computed as the difference of the star count data points (
![]() )
and the model (
)
and the model (
![]() ),
),
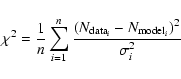 |
(17) |
We have not attempted to fit all the free parameters at once.
First, we fitted a star count model with the disc and the boxy bulge to a reduced data set consisting of one point every 10 pixels (one data point every ![]() ).
In the disc region, we took one point every 5 pixels (
).
In the disc region, we took one point every 5 pixels (
![]() )
across the disc.
Finally, we neglected the data points in the inner region (
)
across the disc.
Finally, we neglected the data points in the inner region (
![]() )
since they are clearly dominated by the nuclear bar.
This reduced data set contains 1494 points and is shown in Fig. 4.
The error of these data points used to calculate
)
since they are clearly dominated by the nuclear bar.
This reduced data set contains 1494 points and is shown in Fig. 4.
The error of these data points used to calculate ![]() was estimated to be 15% as explained above.
was estimated to be 15% as explained above.
We have fitted the data for fixed values of the bulge angle (
![]() deg) and the disc radial scale (
deg) and the disc radial scale (
![]() kpc). The results obtained for the other free parameters are shown in Table 1.
For all
kpc). The results obtained for the other free parameters are shown in Table 1.
For all ![]() ,
the best fits are always obtained with
,
the best fits are always obtained with
![]() kpc.
This is in agreement with the radial scale length of the disc derived from previous studies in the infrared, which have values in the range from 1.9 (2MASS López-Corredoira et al. 2005) to 2.6 (COBE Freudenreich 1998).
Regarding the angle of the bulge, the best fit is obtained for
kpc.
This is in agreement with the radial scale length of the disc derived from previous studies in the infrared, which have values in the range from 1.9 (2MASS López-Corredoira et al. 2005) to 2.6 (COBE Freudenreich 1998).
Regarding the angle of the bulge, the best fit is obtained for ![]() ,
although
,
although ![]() is only 2.8% higher for
is only 2.8% higher for
![]() (Fig. 4 shows the best fit with
(Fig. 4 shows the best fit with
![]() ). This is also in agreement with other studies of the structure of the inner Galaxy.
Dwek et al. (1995) derived angles in the range
). This is also in agreement with other studies of the structure of the inner Galaxy.
Dwek et al. (1995) derived angles in the range ![]() -
-![]() depending on the function assumed to represent the bulge (they found
depending on the function assumed to represent the bulge (they found ![]() with the same boxy Gaussian that we use here), while Freudenreich (1998) derived angles in the range of
with the same boxy Gaussian that we use here), while Freudenreich (1998) derived angles in the range of ![]() -
-![]() also using COBE/DIRBE data. A high angle of
also using COBE/DIRBE data. A high angle of ![]() has also been measured from the 2 Micron Galaxy Survey (TMGS) by López-Corredoira et al. (2000). On the other hand, the work of López-Corredoira et al. (2005) using 2MASS data found
has also been measured from the 2 Micron Galaxy Survey (TMGS) by López-Corredoira et al. (2000). On the other hand, the work of López-Corredoira et al. (2005) using 2MASS data found
![]() -
-![]() .
.
The shape of the bulge as given by the best fit with
![]() is x0/x0:y0/x0:z0/x0=1:0.5:0.3 while the best fit with
is x0/x0:y0/x0:z0/x0=1:0.5:0.3 while the best fit with
![]() has axis ratios of 1:0.55:0.4 which are in perfect agreement with those derived by
López-Corredoira et al. (2005), also with 2MASS data or by López-Corredoira et al. (2000) with TMGS data. In contrast, other studies have favored somewhat thinner bulges with ratios of 1:0.3-0.4:0.3 (Freudenreich 1998; Dwek et al. 1995; Bissantz et al. 2003).
has axis ratios of 1:0.55:0.4 which are in perfect agreement with those derived by
López-Corredoira et al. (2005), also with 2MASS data or by López-Corredoira et al. (2000) with TMGS data. In contrast, other studies have favored somewhat thinner bulges with ratios of 1:0.3-0.4:0.3 (Freudenreich 1998; Dwek et al. 1995; Bissantz et al. 2003).
![\begin{figure}
\par\includegraphics*[bb= 304 47 527 343 , angle=-90,width=9cm]{9644f4.eps}\end{figure}](/articles/aa/full/2008/37/aa09644-08/Timg120.gif) |
Figure 4:
Thin solid contours represent the star counts map. Thick dashed lines are the best fit obtained with a star count model with
|
| Open with DEXTER | |
Table 1: Results of the fits to the star counts data of Fig. 4 using an exponential disc and a triaxial boxy-Gaussian bulge.
In the second data set we have also included the star counts in the innermost region of the Galaxy (
![]() ).
We have taken one point every 3 pixels (
).
We have taken one point every 3 pixels (
![]() )
across the disc.
The data set is shown in Fig. 5. It contains 1734 points.
From Fig. 1 of Alard (2001) it is clear that the dispersion of the star count map in the nuclear region is narrower than in the bulge. We have estimated a
)
across the disc.
The data set is shown in Fig. 5. It contains 1734 points.
From Fig. 1 of Alard (2001) it is clear that the dispersion of the star count map in the nuclear region is narrower than in the bulge. We have estimated a ![]() of 5% for these data points.
of 5% for these data points.
We have fitted the data using our star count model with three components: disc, bulge and nuclear bar. We have taken as a starting point the best fits for
![]() ,
20
,
20![]() ,
35
,
35![]() ,
45
,
45![]() and 60
and 60![]() derived in the previous section (all the parameters of the disc and the bulge are fixed except the factors
derived in the previous section (all the parameters of the disc and the bulge are fixed except the factors ![]() ). The best fit results for the parameters of the nuclear bar are summarized in Table 2. The full set of results for the nuclear bar fits are listed in Tables 3-6.
). The best fit results for the parameters of the nuclear bar are summarized in Table 2. The full set of results for the nuclear bar fits are listed in Tables 3-6.
The best fits are found with a thick triaxial bar with typical axis ratios of 1:(0.7-0.8):(0.5-0.6) and ![]() in the interval 60-120 for all the
in the interval 60-120 for all the ![]() .
This implies that the parameters of the nuclear bar can indeed be constrained independently of the bulge and that
.
This implies that the parameters of the nuclear bar can indeed be constrained independently of the bulge and that
![]() .
Globally, the best fit is obtained with
.
Globally, the best fit is obtained with
![]() and a nuclear bar with
and a nuclear bar with
![]() -
-![]() .
Some examples of good fits are shown in Fig. 5.
.
Some examples of good fits are shown in Fig. 5.
![\begin{figure}
{\includegraphics*[angle=-90,width=15cm]{9644f5a.eps} }
{\includegraphics*[angle=-90,width=15cm]{9644f5b.eps} }
\end{figure}](/articles/aa/full/2008/37/aa09644-08/Timg125.gif) |
Figure 5:
Upper panels: thin solid contours represent the star count map. Thick dashed lines are the best fit obtained with a star count model with
|
| Open with DEXTER | |
Finally, we have also performed fits with a lopsided nuclear bar (
![]() ).
The results are shown in Tables 3-6 and they are
summarized in Table 2. The best fits are still obtained with a nuclear bar that is almost perpendicular to the Sun-GC line. The symmetry center of the bar would be shifted by 22-25 pc towards the third Galactic quadrant if
).
The results are shown in Tables 3-6 and they are
summarized in Table 2. The best fits are still obtained with a nuclear bar that is almost perpendicular to the Sun-GC line. The symmetry center of the bar would be shifted by 22-25 pc towards the third Galactic quadrant if
![]() -
-![]() while it would be shifted by the same quantity but towards the fourth quadrant if
while it would be shifted by the same quantity but towards the fourth quadrant if
![]() -
-![]() .
.
Table 2: Summary of the parameters of the nuclear bar as derived from the best fits to the 2MASS star count data.
We have used the code of Combes & Gerin (1985) to simulate the motion of gas clouds in the potential obtained from the mass distribution inferred with the star count model. This code has already been used successfully to understand the gas distribution and dynamics of a number of galaxies such as M100 (Garcia-Burillo et al. 1998), or NGC 4736 (Gerin et al. 1991; Mulder & Combes 1996).
The potential is obtained from the mass distribution derived in the previous section, using standard FFT techniques in a Cartesian grid of
![]() cells. The cells are cubic with a linear size of 58.6 pc, therefore the physical size of the grid is
cells. The cells are cubic with a linear size of 58.6 pc, therefore the physical size of the grid is
![]() kpc3. This is good compromise to model the large scale dynamics at least to a radius of 10 kpc and to have a good enough spatial resolution to study the Galactic center.
kpc3. This is good compromise to model the large scale dynamics at least to a radius of 10 kpc and to have a good enough spatial resolution to study the Galactic center.
As described by Combes & Sanders (1981), the interaction between periodically reproduced
images is avoided following the scheme of Hohl & Hockney (1969), i.e. the potential computations are done in a grid 8 times bigger, of
![]() cells. The disk mass is truncated at 15 kpc in radius, and the mass distribution is assumed spherical outside, so that its influence in the center is cancelled. This is equivalent to assuming that a spherical dark halo dominates the mass outside. This assumption should have a negligible influence on the dynamics of the inner Galaxy, which is the main interest of this paper.
cells. The disk mass is truncated at 15 kpc in radius, and the mass distribution is assumed spherical outside, so that its influence in the center is cancelled. This is equivalent to assuming that a spherical dark halo dominates the mass outside. This assumption should have a negligible influence on the dynamics of the inner Galaxy, which is the main interest of this paper.
The stellar potential is decomposed into its axisymmetric and non-axisymmetric parts. The axisymmetric potential is calculated in radial bins using the averaged mass in the bin. The non-axisymmetric part of the potential is calculated with a mass distribution corresponding to the difference between the total mass and the axisymmetric distribution.
The stellar number density derived in the previous section should be multiplied by a factor f to obtain the total mass density. This factor accounts for the mass of the stars detected by 2MASS but also for the mass of those stars that are not counted in the 2MASS maps.
In addition, we have to introduce a dark halo to explain the observed velocities at large radii. The total density used is then:
Figure 6 shows an example of a rotation curve. The modeled curve compares well with the rotation curve derived from observations of the interstellar gas for radii larger than 2 kpc. The agreement seems worse for small radii. However the comparison in this region is not straightforward. On the one hand, the measured curve has been derived using the tangent point method assuming that the clouds move in circular orbits, which is not true in the innermost region. In addition, this curve depends on the position of the observer in the Galaxy. On the other hand, the modeled rotation curve has been derived with the axisymmetrical potential and with an azimuthal average of the non-axisymmetrical potential. This rotation curve is an average curve independent of the position of the observer.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.5cm]{9644f6.eps}\end{figure}](/articles/aa/full/2008/37/aa09644-08/Timg144.gif) |
Figure 6:
Rotation curve obtained with the halo and the scaling discussed in Sect. 5.1 for a bulge and nuclear bar orientation of
|
| Open with DEXTER | |
Figure 7 gives the rotation velocity ![]() as a function of galactocentric radius. It also shows the
as a function of galactocentric radius. It also shows the
![]() curves (where
curves (where ![]() is the epicyclic frequency). For a given bar pattern speed
is the epicyclic frequency). For a given bar pattern speed
![]() ,
these curves give the location of the corotation (
,
these curves give the location of the corotation (
![]() ), the Outer
Lindblad resonance (
), the Outer
Lindblad resonance (
![]() ), the Inner Lindblad resonances (
), the Inner Lindblad resonances (
![]() )
and the Ultra Harmonic Resonance (
)
and the Ultra Harmonic Resonance (
![]() ).
).
![\begin{figure}
\par\includegraphics*[angle=-90, width=8.5cm]{9644f7.eps}\end{figure}](/articles/aa/full/2008/37/aa09644-08/Timg153.gif) |
Figure 7: Angular frequencies as a function of radius in the epicyclicapproximation for the potential discussed in Sect. 5.1. |
| Open with DEXTER | |
The gas clouds are modeled as particles that are initially launched in the axisymmetric potential with a velocity corresponding to the circular velocity of the potential at the radius of the particle.
The initial radial distribution is an exponential disk with a radial scale of 2 kpc.
The non-axisymmetric part of the potential is then introduced gradually multiplying by the factor
![]() with a time delay of
with a time delay of ![]() Myr. The angular speed of the non-axisymmetrical pattern,
Myr. The angular speed of the non-axisymmetrical pattern,
![]() ,
is constant along the simulation.
,
is constant along the simulation.
We do not use a mass spectrum for the clouds and we do not simulate star formation.
The simulations typically contain 106 particles. The effects of gas self-gravitation are neglected. The clouds move as test particles in the stellar potential except when they collide inelastically. The forces due to the stellar potential are evaluated every 1 Myr and the particles are moved according to them. The particles are followed in three dimensions but the collisions are computed in a two-dimensional grid with
![]() cells.
Clouds in the same grid cell can collide. The relative velocity of two collision partners loses 60% of its absolute value in the collision. A detailed discussion of the collisional schema can be found in Combes & Gerin (1985) and Casoli & Combes (1982).
cells.
Clouds in the same grid cell can collide. The relative velocity of two collision partners loses 60% of its absolute value in the collision. A detailed discussion of the collisional schema can be found in Combes & Gerin (1985) and Casoli & Combes (1982).
Figures 8 and 9 show face-on views and the lv-diagram for a grid of models with ![]() from
from ![]() to
to ![]() and pattern speeds from 20 to 50 km s-1 kpc-1.
For an easy comparison with observations, we have overlaid in the lv-diagrams the TVC points, the boxes indicating the tanget points and the solid and dashed lines shown in Fig. 1.
We have also plotted the four logarithmic spirals of Nakanishi & Sofue (2006) in the face-on views. The models shown in Figs. 8 and 9 exhibit a number of common characteristics.
The galaxies have two major spiral arms but they also exhibit a second pair of less prominent spiral arms. In the inner
and pattern speeds from 20 to 50 km s-1 kpc-1.
For an easy comparison with observations, we have overlaid in the lv-diagrams the TVC points, the boxes indicating the tanget points and the solid and dashed lines shown in Fig. 1.
We have also plotted the four logarithmic spirals of Nakanishi & Sofue (2006) in the face-on views. The models shown in Figs. 8 and 9 exhibit a number of common characteristics.
The galaxies have two major spiral arms but they also exhibit a second pair of less prominent spiral arms. In the inner ![]() 4 kpc, there are arms that extend around the bar forming an oval (hereafter lateral arms). The density of gas inside this oval decreases to a radius of
4 kpc, there are arms that extend around the bar forming an oval (hereafter lateral arms). The density of gas inside this oval decreases to a radius of ![]() 1 kpc, where there is a ring.
This ring is connected to the lateral arms by the off-axis arms (or dustlanes).
In the inner hundreds of parsecs there is a nuclear condensation of gas.
1 kpc, where there is a ring.
This ring is connected to the lateral arms by the off-axis arms (or dustlanes).
In the inner hundreds of parsecs there is a nuclear condensation of gas.
The Milky Way galaxy is a very complex system and up to now there are no simulations of the gas dynamics that can explain all the observed features, neither quantitatively nor qualitatively.
Englmaier & Gerhard (1999) have compared their models to the terminal velocity curve, they have also compared the position the arm tangent points in the CO lv-diagram, at
![]() and
and ![]() .
The two lv-diagrams presented by Fux (1999) were selected by the global resemblance to the lv-diagram s obtained from CO and HI data. They reproduce qualitatively the 3-kpc arm and the Connecting Arm. Weiner & Sellwood (1999) constrained their models by comparing them with the HI terminal velocity curve.
Finally, Bissantz et al. (2003) used mainly the terminal velocity curve and some voids in the observed lv-diagram to compare with their simulations.
To select the best models, in the present work we have compared with: i) the terminal velocity curve, ii) the inclination of the GMR in the lv-diagram, iii) the existence or not of the 3 kpc arm and when it exists, its inclination and absolute velocity iv) the arm tangent points v) the shape and size of the HI 1kpc ring.
.
The two lv-diagrams presented by Fux (1999) were selected by the global resemblance to the lv-diagram s obtained from CO and HI data. They reproduce qualitatively the 3-kpc arm and the Connecting Arm. Weiner & Sellwood (1999) constrained their models by comparing them with the HI terminal velocity curve.
Finally, Bissantz et al. (2003) used mainly the terminal velocity curve and some voids in the observed lv-diagram to compare with their simulations.
To select the best models, in the present work we have compared with: i) the terminal velocity curve, ii) the inclination of the GMR in the lv-diagram, iii) the existence or not of the 3 kpc arm and when it exists, its inclination and absolute velocity iv) the arm tangent points v) the shape and size of the HI 1kpc ring.
Figure 8 shows face-on views and lv-diagrams for a grid of models with
![]() and pattern speeds from 20 to 50 km s-1 kpc-1.
The model with
and pattern speeds from 20 to 50 km s-1 kpc-1.
The model with
![]() km s-1 kpc-1 reproduces some spiral tangent points and has an inner lateral arm with the inclination of the 3-kpc arm, however it does not reproduce the terminal velocity curve nor the velocity of the 3-kpc arm, for instance.
At the other extreme, the model with
km s-1 kpc-1 reproduces some spiral tangent points and has an inner lateral arm with the inclination of the 3-kpc arm, however it does not reproduce the terminal velocity curve nor the velocity of the 3-kpc arm, for instance.
At the other extreme, the model with
![]() km s-1 kpc-1 does not reproduce satisfactorily either the terminal velocity curve or the GMR or the 3-kpc arm.
km s-1 kpc-1 does not reproduce satisfactorily either the terminal velocity curve or the GMR or the 3-kpc arm.
In contrast, the models with
![]() and 40 km s-1 kpc-1 give a very good overall representation of the Galaxy. Both reproduce satisfactorily the spiral tangent points at
and 40 km s-1 kpc-1 give a very good overall representation of the Galaxy. Both reproduce satisfactorily the spiral tangent points at
![]() within
within
![]() and
and ![]() km s-1, approximately.
In addition, the model with
km s-1, approximately.
In addition, the model with
![]() km s-1 kpc-1 reproduces very well the Carina arm and its tangent point at
km s-1 kpc-1 reproduces very well the Carina arm and its tangent point at ![]()
![]() .
However, the locus of the inner spiral arms and the 3-kpc arm in the modeled lv-diagram are too steep in comparison with the observed lv-diagram.
In contrast, the GMR and the the 3-kpc arm is very well reproduced from
.
However, the locus of the inner spiral arms and the 3-kpc arm in the modeled lv-diagram are too steep in comparison with the observed lv-diagram.
In contrast, the GMR and the the 3-kpc arm is very well reproduced from
![]() to
to ![]() by the model with
by the model with
![]() km s-1 kpc-1.
In particular the 3-kpc arm is reproduced with both the correct inclination and the velocity within
km s-1 kpc-1.
In particular the 3-kpc arm is reproduced with both the correct inclination and the velocity within ![]() 10 km s-1.
In addition, the terminal velocity curve for
10 km s-1.
In addition, the terminal velocity curve for
![]() is very well reproduced.
Given the difficulty of the task, it will not be realistic to give a very narrow interval for the bar pattern speed; from our best models we conclude that the most probable value for
is very well reproduced.
Given the difficulty of the task, it will not be realistic to give a very narrow interval for the bar pattern speed; from our best models we conclude that the most probable value for
![]() should be in the range 30-40 km s-1 kpc-1.
However, since this work is devoted to the inner Galaxy structure and kinematics, in the following we will mainly discuss models with
should be in the range 30-40 km s-1 kpc-1.
However, since this work is devoted to the inner Galaxy structure and kinematics, in the following we will mainly discuss models with
![]() km s-1 kpc-1 since they explain the terminal velocity curve, the 3-kpc arm and the GMR better than the model with
km s-1 kpc-1 since they explain the terminal velocity curve, the 3-kpc arm and the GMR better than the model with
![]() km s-1 kpc-1.
km s-1 kpc-1.
![\begin{figure}
\par\includegraphics[angle=-90, width=14cm]{9644f8a.eps}\par\includegraphics[angle=-90, width=14cm]{9644f8b.eps}\end{figure}](/articles/aa/full/2008/37/aa09644-08/Timg169.gif) |
Figure 8:
Simulations for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90, width=14.3cm]{9644f9a.eps}\par\includegraphics[angle=-90, width=14.3cm]{9644f9b.eps}\end{figure}](/articles/aa/full/2008/37/aa09644-08/Timg170.gif) |
Figure 9:
Simulations for
|
| Open with DEXTER | |
Figure 9 shows face-on views and lv-diagrams for a grid of models with constant ![]() km s-1 kpc-1 and
km s-1 kpc-1 and ![]() of 45
of 45![]() ,
35
,
35![]() ,
20
,
20![]() and 10
and 10![]() (
(![]() is constant to 90
is constant to 90![]() for all the models). For
for all the models). For
![]() ,
the velocity along the line of sight is too low to explain the high non-circular velocities of the 3 kpc arm (-53 km s-1 at
,
the velocity along the line of sight is too low to explain the high non-circular velocities of the 3 kpc arm (-53 km s-1 at ![]() )
and the observed arm is not reproduced in the lv diagram.
In contrast, the 3-kpc arm and the inclination of the GMR is well reproduced for
)
and the observed arm is not reproduced in the lv diagram.
In contrast, the 3-kpc arm and the inclination of the GMR is well reproduced for ![]() from 20
from 20![]() to 45
to 45![]() .
Nevertheless, the model with
.
Nevertheless, the model with
![]() does not correctly reproduce the positive velocity terminal curve. In addition, there is no ring at 1 kpc in the face-on view.
does not correctly reproduce the positive velocity terminal curve. In addition, there is no ring at 1 kpc in the face-on view.
Once again, we cannot give a very narrow interval of angles for the inclination angle of the bar since the analysis, as in other published works, is still rather qualitative.
We reckon that the inclination of the bar should be in the range of 20![]() to 35
to 35![]() , with some preference for 20
, with some preference for 20![]() since the quantitative agreement of the 3-kpc arm and the terminal velocity curve is better.
Therefore, the model with
since the quantitative agreement of the 3-kpc arm and the terminal velocity curve is better.
Therefore, the model with
![]() km s-1 kpc-1 and
km s-1 kpc-1 and
![]() will be considered as our standard model in the rest of the paper.
will be considered as our standard model in the rest of the paper.
The inclination of the bar derived from our models is in good agreement with previous determinations (López-Corredoira et al. 2005; Binney et al. 1997; Fux 1999, see also Sect. 1).
Regarding the bar pattern speed, our simulations give results that are lower than those of
Englmaier & Gerhard (1999) or Bissantz et al. (2003), which suggest
![]() -60 km s-1 kpc-1, but in good agreement with the results of Weiner & Sellwood (1999),
-60 km s-1 kpc-1, but in good agreement with the results of Weiner & Sellwood (1999),
![]() km s-1 kpc-1, or Fux (1999).
In his self-consistent gas and star simulations, Fux found that the pattern speed evolves from 50 to 30 km s-1 kpc-1.
Taking into account our potential, a pattern speed of 30 or 40 km s-1 kpc-1 gives a corotation radius of 7 and 5 kpc, respectively (see Fig. 7).
Therefore, the corotation radius is well beyond the bar extremity, which is the characteristic of a slow bar (see for instance Sellwood & Sparke 1988).
km s-1 kpc-1, or Fux (1999).
In his self-consistent gas and star simulations, Fux found that the pattern speed evolves from 50 to 30 km s-1 kpc-1.
Taking into account our potential, a pattern speed of 30 or 40 km s-1 kpc-1 gives a corotation radius of 7 and 5 kpc, respectively (see Fig. 7).
Therefore, the corotation radius is well beyond the bar extremity, which is the characteristic of a slow bar (see for instance Sellwood & Sparke 1988).
To explain the fact that the dustlanes in the inner spiral arms of some galaxies are located in the concave section of the arms, and assuming that the bars are fast (i.e., they extend to the corotation), Sellwood & Sparke (1988) proposed the existence of different speeds for the bar and the spiral patterns. Indeed, for the Milky Way some works have derived low rotations speeds of 13-20 km s-1 kpc-1 for the spiral pattern (Amaral & Lepine 1997; Lin et al. 1969; Morgan 1990). Gas flow models with independent speeds for the bar and the spiral patterns have been presented by Bissantz et al. (2003), who discussed that different speeds for the spiral and the bar patterns could explain some regions devoid of gas in the lv-diagram. However, the overall agreement of their lv-diagrams with observations is not better than other models like that of Fux (1999) or our models, which are able to reproduce quantitatively features as the 3-kpc arm.
It is interesting to remark that our simulations favor a relatively slow bar and not a fast bar as assumed by Sellwood & Sparke (1988).
Furthermore, the pattern speed of the relatively slow bar models (30-40 km s-1 kpc-1, Fux 1999; Weiner & Sellwood 1999, this work) is comparable to
several determinations of the spiral pattern speed that give values of 30-35 km s-1 kpc-1 (Mishurov & Zenina 1999; Lépine et al. 2001; Fernández et al. 2001).
On the other hand, Ibata & Gilmore (1995) have measured a rotation speed of ![]() km s-1 kpc-1 for the bulge in the 0.7<R<3.5 kpc region.
Therefore, at present there are still many uncertainties regarding the speeds of the different patterns and it is not clear whether the spirals and the bar are decoupled or they turn at the same speeds.
Simulations with an independent pattern speed for the spirals would be needed to study this question in detail but this is beyond the scope of the current paper, which is mainly devoted to the inner Galaxy.
km s-1 kpc-1 for the bulge in the 0.7<R<3.5 kpc region.
Therefore, at present there are still many uncertainties regarding the speeds of the different patterns and it is not clear whether the spirals and the bar are decoupled or they turn at the same speeds.
Simulations with an independent pattern speed for the spirals would be needed to study this question in detail but this is beyond the scope of the current paper, which is mainly devoted to the inner Galaxy.
To obtain further insight into the structure and the dynamics of the Galaxy, we present below a more detailed analysis of the model with
![]() km s-1 kpc-1 and
km s-1 kpc-1 and
![]() .
We have selected different structures in the face-on view and we show the locus of the different structures in the lv-diagram (Fig. 10).
.
We have selected different structures in the face-on view and we show the locus of the different structures in the lv-diagram (Fig. 10).
![\begin{figure}
\par\includegraphics*[angle=-90, width=16cm]{9644f10a.eps}\par\includegraphics*[angle=-90, width=16cm]{9644f10b.eps}\end{figure}](/articles/aa/full/2008/37/aa09644-08/Timg174.gif) |
Figure 10:
Simulations for |
| Open with DEXTER | |
As already mentioned in Sect. 2.2, it is uncertain whether the GMR is an actual ring or it is composed by imbricated spiral arms. In our models the radius of the GMR (4-5 kpc) corresponds exactly with the position of the Ultra-Harmonic resonance for
![]() km s-1 kpc-1 (Fig. 7).
However, we do not support the idea that the GMR is a resonant ring.
km s-1 kpc-1 (Fig. 7).
However, we do not support the idea that the GMR is a resonant ring.
As shown in the upper panels of Fig. 10, in our models the GMR is composed of the inner parts of the spiral arms, which at those radii show almost circular motion. This is in agreement with the face-on views of the CO and HI data of Nakanishi & Sofue (2006), who have proposed that the GMR is formed by the Scutum-Crux arm (near side of the GMR) and the inner part of the Sgr-Carina (far side of the GMR). Englmaier & Gerhard (1999) discussed that if formed by imbricated arms, the GMR should be outside the corotation, assuming that there cannot exist significant circular orbits inside the corotation to produce a feature resembling a circular ring. However, this statement only holds for fast bars, for which all the region inside the corotation is dominated by the bar. In contrast, in our models with a relatively slow bar, the inner part of the spiral arms is inside the corotation radius and exhibits almost circular motion.
The lower panels of Fig. 10 show the locus of the lateral arms that surround the bar. The two dot-dashed lines in the lv-diagram are the fit to the 3-kpc arm and to its far-side counterpart as given by Dame & Thaddeus (2008). As already mentioned, the locus of the lateral arms in the lv-diagram reproduce quite well the structure of the 3-kpc arm. This is in agreement with Fux (1999), who has already proposed that the 3-kpc arm could be a lateral arm. On the other hand, Fux (1999) proposed that the ``135 km s-1 arm'' is the far side counterpart of the 3-kpc arm. However, our models predict a far side counterpart of the 3-kpc arm whose locus in the lv-diagram is almost symmetrical to the 3-kpc arm. This is in perfect agreement with the recently found far 3-kpc arm (Dame & Thaddeus 2008). The full implications of the new finding by Dame & Thaddeus (2008) will be presented elsewhere.
The fact that the 3-kpc arms are lateral arms imply that they cannot be a channel to transport gas from the corotation to the CMZ as suggested by Habing et al. (2006), at least not directly.
In contrast to the 3-kpc arms, the dustlanes do contribute to the transport of gas to the inner regions. In our models the locus of the dustlanes in the lv-diagram are vertical structures with velocities from ![]() 0 km s-1 to more than 100 km s-1. The maximum velocity increases as l decreases.
These vertical structures in the lv-diagram resemble the Clumps found by Bania (1977) and discussed recently by Liszt (2008,2006).
Nevertheless, our models do not reproduce the Galactic longitude of the observed Clumps (5.5
0 km s-1 to more than 100 km s-1. The maximum velocity increases as l decreases.
These vertical structures in the lv-diagram resemble the Clumps found by Bania (1977) and discussed recently by Liszt (2008,2006).
Nevertheless, our models do not reproduce the Galactic longitude of the observed Clumps (5.5![]() and 3.1
and 3.1![]() ).
We confirm that Banias's Clumps are probably shocked gas in the dustlanes, which was the original interpretation of Stark & Bania (1986) for the ``Clump 2''.
The fact that the Clumps are composed of gas undergoing the dustlane shocks is also suggested by observational evidences, both kinematical (linewidths, velocity gradients, Stark & Bania 1986; Liszt 2006) and chemical (Rodriguez-Fernandez et al. 2006).
Taking into account the discrete appearance of Bania's clumps at two Galactic longitudes, it is likely that the dust lanes of the Milky Way are patchy, as is commonly observed in external galaxies.
).
We confirm that Banias's Clumps are probably shocked gas in the dustlanes, which was the original interpretation of Stark & Bania (1986) for the ``Clump 2''.
The fact that the Clumps are composed of gas undergoing the dustlane shocks is also suggested by observational evidences, both kinematical (linewidths, velocity gradients, Stark & Bania 1986; Liszt 2006) and chemical (Rodriguez-Fernandez et al. 2006).
Taking into account the discrete appearance of Bania's clumps at two Galactic longitudes, it is likely that the dust lanes of the Milky Way are patchy, as is commonly observed in external galaxies.
Fux (1999) and Marshall et al. (2008) have proposed a slightly different interpretation. They propose that the Connecting Arm is the locus of the near side dustlane in the lv-diagram.
However, the linewidths of the gas in the Connecting Arm do not show the velocity dispersion expected in the dustlane shocks (see for instance Reynaud & Downes 1998).
Indeed probably both Bania's clumps and the Connecting Arm are related to the dustlane. We reckon that Bania's Clumps are clouds that are undergoing the strong shocks expected in the dustlanes while the Connecting Arm is most likely the post-shocked and accelerated gas (see also the discussion in Liszt 2006).
Indeed, in our simulations the maximum velocity of the gas in the dustlanes increases as l decreases with the same steep of the Connecting Arm.
Observationally, this interpretation is supported by the fact that the Clump at
![]() seems to be connected to to Connecting Arm at a negative latitude (see Bitran et al. 1997). The situation was less clear for ``Clump 2'' at
seems to be connected to to Connecting Arm at a negative latitude (see Bitran et al. 1997). The situation was less clear for ``Clump 2'' at
![]() since it is found at positive latitudes.
However, this apparent problem has been solved with the recent discovery by Liszt (2008) of an emission feature with the same inclination in the lv-diagram as the Connecting Arm but at positive latitude.
In addition it seems connected to Clump 2.
In any case, the Clump 2 exhibits a rich shock chemistry as expected for gas in the dustlane shocks (Rodriguez-Fernandez et al. 2006)
since it is found at positive latitudes.
However, this apparent problem has been solved with the recent discovery by Liszt (2008) of an emission feature with the same inclination in the lv-diagram as the Connecting Arm but at positive latitude.
In addition it seems connected to Clump 2.
In any case, the Clump 2 exhibits a rich shock chemistry as expected for gas in the dustlane shocks (Rodriguez-Fernandez et al. 2006)
Figure 11 shows the face-on view of the inner 2 kpc of the modeled galaxies and the lv-diagrams for different orientations of the nuclear bar. All the other parameters are the same as those discussed in the previous section and the large scale face on views and lv-diagram s are the same, independent of the orientation of the nuclear bar.
The dustlanes end in a ring and inside this ring there is a small bar-like structure that is connected to the ring by two small spiral arms. The HI ring has an inner and outer radius of 300 pc and 800 pc, respectively, in excellent agreement with the HI observations of Liszt & Burton (1980) (see their Fig. 3). The ring is almost circular. In some simulations we have also found elliptical rings with the major axis approximately perpendicular to the large bar. Therefore, the ring is not supported by X1 orbits elongated in the direction of the large bar (see a review of the different proposed models in Ferrière et al. 2007).
In the central hundreds of parsecs there is an elongated structure that corresponds to the gas response to the nuclear bar and that resembles the observed CMZ.
We have analyzed the shape of the lv-diagram as a function of the nuclear bar orientation.
Figure 11 shows the lv-diagram obtained for nuclear bar orientations from 0![]() ,
to 15
,
to 15![]() ,
30
,
30![]() and 45
and 45![]() .
Our modeled lv-diagrams do not reproduce the components K and J of Rodriguez-Fernandez et al. (2006).
In contrast, the lv-diagram of the CMZ is a parallelogram that resembles the observed one (Fig. 2). The inclination of the observed parallelogram is very well reproduced for an angle of
.
Our modeled lv-diagrams do not reproduce the components K and J of Rodriguez-Fernandez et al. (2006).
In contrast, the lv-diagram of the CMZ is a parallelogram that resembles the observed one (Fig. 2). The inclination of the observed parallelogram is very well reproduced for an angle of ![]() .
After the Binney et al. (1991) paper, Jenkins & Binney (1994) tried to reproduce the parallelogram discussed by Binney et al. (1991) using n-body simulations but with little success. To our knowledge, this is the first time that numerical simulations of the gas dynamics of the Milky Way naturally reproduce the parallelogram of the lv-diagram of the CMZ. This is probably due to the accurate potential that we have determined with the deep 2MASS data.
.
After the Binney et al. (1991) paper, Jenkins & Binney (1994) tried to reproduce the parallelogram discussed by Binney et al. (1991) using n-body simulations but with little success. To our knowledge, this is the first time that numerical simulations of the gas dynamics of the Milky Way naturally reproduce the parallelogram of the lv-diagram of the CMZ. This is probably due to the accurate potential that we have determined with the deep 2MASS data.
The orientation angle of the small bar inferred from our simulations is in excellent agreement with our models of the 2MASS star counts and with the face on view of the CMZ inferred from CO and OH data by Sawada et al. (2004).
We conclude that the observed CMZ is most likely the gas response to the nuclear bar and that the orientation of the nuclear bar is
![]() .
.
![\begin{figure}
\par\includegraphics[angle=-90, width=14.3cm,clip]{9644f11a.eps}\...
...eps}\par\includegraphics[angle=-90, width=14.3cm,clip]{9644f11d.eps}\end{figure}](/articles/aa/full/2008/37/aa09644-08/Timg177.gif) |
Figure 11:
Simulations for
|
| Open with DEXTER | |
In the simulations discussed above, the velocity dispersion of the CMZ is well reproduced for a mass of the nuclear bar of
![]() (Sect. 5.1).
However, the terminal velocities of the HI ring do not match the observed ones.
For further insight into the nuclear bar mass we have increased its value in order to reproduce the terminal velocities of the HI ring.
In these models, the shape of the different mass components is still given by the fits to the 2MASS star counts map (Tables 3-6). However, we have considered different scaling factors for the nuclear bar and for the bulge and disc. Thus, instead of Eq. (18), the total density is given by:
(Sect. 5.1).
However, the terminal velocities of the HI ring do not match the observed ones.
For further insight into the nuclear bar mass we have increased its value in order to reproduce the terminal velocities of the HI ring.
In these models, the shape of the different mass components is still given by the fits to the 2MASS star counts map (Tables 3-6). However, we have considered different scaling factors for the nuclear bar and for the bulge and disc. Thus, instead of Eq. (18), the total density is given by:
It is difficult to reproduce both the terminal velocities of the CMZ and HI ring, however from the previous considerations we conclude that the mass of the nuclear bar should be in the range (2-
![]() .
.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.5cm]{9644f12.eps}\end{figure}](/articles/aa/full/2008/37/aa09644-08/Timg185.gif) |
Figure 12:
Same as Fig. 6 but with a nuclear bar mass of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics*[bb=48 71 306 746, angle=-90, width=14cm]{9644f13.eps}\end{figure}](/articles/aa/full/2008/37/aa09644-08/Timg186.gif) |
Figure 13:
Simulations results for
|
| Open with DEXTER | |
The nuclear bar in the star count map of Alard (2001) seems to be shifted towards negative longitudes (in contrast to the gas distribution that seems to be shifted towards positive longitudes). Our star count model shows that fits with a lopsided nuclear bar have a ![]() that is 9
that is 9![]() lower than the
lower than the ![]() for models that do not allow a lopsided bar. The symmetry center of the bar could be shifted by 22-25 pc with respect to the dynamical center of the Galaxy.
for models that do not allow a lopsided bar. The symmetry center of the bar could be shifted by 22-25 pc with respect to the dynamical center of the Galaxy.
We have studied the gas response to a lopsided nuclear bar in order to investigate whether the observed asymmetry of the CMZ could be explained by a lopsided nuclear bar as inferred from the 2MASS data. As discussed by Morris & Serabyn (1996) the signature of a m=1 mode in the Galactic center would be a shift of the gas distribution in l but also a shift of the velocity centroid of the lv-diagram.
Figure 14 shows a simulation of the gas flow in the potential computed from the fit to the 2MASS star counts map with
![]() (for which x1=0.023 kpc).
The lv-diagram of the gas shows a parallelogram whose sides show the good inclination.
The simulated parallelogram is only slightly asymmetric in l and v.
To better understand the effect of a lopsided nuclear bar, we have also computed a simulation with the same nuclear bar but artificially shifted by 90 pc along its major axis towards the third Galactic quadrant (x1=0.090 kpc). The results are also shown in Fig. 14.
The lv-diagram is still only slightly asymmetric in v but now it is clearly asymmetric in l. The gas response to the lopsided stellar bar follows the star distribution and it is lopsided towards negative longitudes as well.
To obtain an lv-diagram with a parallelogram similar to that of the CO data shown in Fig. 2, the nuclear bar should be lopsided towards the first quadrant.
This is shown in Fig. 14, where
x1=-0.090 kpc.
However, such a bar is not compatible with the 2MASS star counts.
(for which x1=0.023 kpc).
The lv-diagram of the gas shows a parallelogram whose sides show the good inclination.
The simulated parallelogram is only slightly asymmetric in l and v.
To better understand the effect of a lopsided nuclear bar, we have also computed a simulation with the same nuclear bar but artificially shifted by 90 pc along its major axis towards the third Galactic quadrant (x1=0.090 kpc). The results are also shown in Fig. 14.
The lv-diagram is still only slightly asymmetric in v but now it is clearly asymmetric in l. The gas response to the lopsided stellar bar follows the star distribution and it is lopsided towards negative longitudes as well.
To obtain an lv-diagram with a parallelogram similar to that of the CO data shown in Fig. 2, the nuclear bar should be lopsided towards the first quadrant.
This is shown in Fig. 14, where
x1=-0.090 kpc.
However, such a bar is not compatible with the 2MASS star counts.
We conclude that, both from the fits to the 2MASS data and from the numerical simulations of the gas dynamics, there is no clear evidence of an intrinsic lopsidedness in the stellar potential. The observed asymmetry of the gas distribution in the CMZ cannot be explained as the gas response to a lopsided nuclear bar in the way suggested by Alard's map.
![\begin{figure}
\par\includegraphics[angle=-90, width=14cm]{9644f14a.eps}\par\inc...
...44f14b.eps}\par\includegraphics[angle=-90, width=14cm]{9644f14c.eps}\end{figure}](/articles/aa/full/2008/37/aa09644-08/Timg187.gif) |
Figure 14:
Simulations for
|
| Open with DEXTER | |
Although the origin of the asymmetry of the CMZ is a long-standing problem, it has not been discussed much in the literature. Two exceptions are the papers by Combes (1996) and Morris & Serabyn (1996). The first paper proposed that the observed asymmetry could be due to a m=1 mode of the potential since lopsidedness is commonly observed in the central regions of external galaxies. The second paper discusses how the effect of the presence of a m=1 mode in the Galactic center would be an asymmetry of the CMZ both in longitude and in velocity. However, we have shown in the previous section that the possible lopsidedness of the stellar distribution cannot explain the observed asymmetry of the CMZ. Furthermore, there is no clear evidence of an intrinsic asymmetry of the stellar potential. Regarding the gas, the distribution is clearly asymmetric in l but the parallelogram of Fig. 2 is rather symmetric in v. In addition, the structures found by Sofue (1995) that seem to be the signature of a quasi-circular ring inside the CMZ and that could be the nuclear bar equivalent to the HI ring, do not show an asymmetry in v.
Indeed our simulations propose an alternative explanation for the asymmetric distribution of the CMZ in which the stellar potential in the GC is strictly symmetric. The simulations show that the HI ring can be connected to the CMZ by a pair of small spiral arms. For instance, the simulation with
![]() (second row of Fig. 11) shows that the clouds in the arm seen at negative longitudes will be seen in the lv-diagram outside of the observed parallelogram while the clouds in the arm seen at
positive longitudes ``fill'' the observed parallelogram at the position of the
(second row of Fig. 11) shows that the clouds in the arm seen at negative longitudes will be seen in the lv-diagram outside of the observed parallelogram while the clouds in the arm seen at
positive longitudes ``fill'' the observed parallelogram at the position of the
![]() -complex.
Observations of the molecular gas in external galaxies show that, in contrast to most numerical simulations, the gas distribution in real galaxies is rarely symmetric.
This could also be the case in the Milky Way.
The apparent asymmetry of the CMZ can be due to material falling into the CMZ from the HI ring through only one of the inner spiral arms.
In this context, strong shocks are expected in the interaction region: the
-complex.
Observations of the molecular gas in external galaxies show that, in contrast to most numerical simulations, the gas distribution in real galaxies is rarely symmetric.
This could also be the case in the Milky Way.
The apparent asymmetry of the CMZ can be due to material falling into the CMZ from the HI ring through only one of the inner spiral arms.
In this context, strong shocks are expected in the interaction region: the
![]() -complex.
-complex.
Observationally, the
![]() -complex looks very different to the Sgr's cloud complexes. For instance, in the lb map of Fig. 2, it is clear that the gas distribution from Sgr C to Sgr B is rather symmetric and thin.
The asymmetry in l is indeed exclusively due to the
-complex looks very different to the Sgr's cloud complexes. For instance, in the lb map of Fig. 2, it is clear that the gas distribution from Sgr C to Sgr B is rather symmetric and thin.
The asymmetry in l is indeed exclusively due to the
![]() -complex.
Furthermore, the
-complex.
Furthermore, the
![]() -complex shows an unusual latitude extension, much higher that the rest of the CMZ.
The velocity structure of this cloud complex is also unusual, showing a wide velocity dispersion (the
-complex shows an unusual latitude extension, much higher that the rest of the CMZ.
The velocity structure of this cloud complex is also unusual, showing a wide velocity dispersion (the
![]() -complex is indeed the most prominent feature in the lv-diagram). The chemistry also gives us interesting hints as to the nature of this cloud complex.
On the one hand, Hüttemeister et al. (1998) have found that the highest abundances of the shock tracer molecule SiO are found at one of the extremities of the CMZ: in the
-complex is indeed the most prominent feature in the lv-diagram). The chemistry also gives us interesting hints as to the nature of this cloud complex.
On the one hand, Hüttemeister et al. (1998) have found that the highest abundances of the shock tracer molecule SiO are found at one of the extremities of the CMZ: in the
![]() -complex.
They have already proposed that this cloud complex represents the scenario of strong shocks due to gas falling into the CMZ.
On the other hand, Rodriguez-Fernandez et al. (2006) have presented a more complete study of the SiO emission in all the kinematical structures of the GC.
They have detected SiO in at least one cloud of each kinematical structure.
However, the only feature where they detected high abundances of SiO in every observed cloud is the
-complex.
They have already proposed that this cloud complex represents the scenario of strong shocks due to gas falling into the CMZ.
On the other hand, Rodriguez-Fernandez et al. (2006) have presented a more complete study of the SiO emission in all the kinematical structures of the GC.
They have detected SiO in at least one cloud of each kinematical structure.
However, the only feature where they detected high abundances of SiO in every observed cloud is the
![]() -complex. In agreement with Hüttemeister et al. (1998); Rodriguez-Fernandez et al. (2006) have measured the highest SiO abundances in this region.
Therefore, the lb distribution, the velocity structure, and the chemistry imply that the cloud complex giving rise to the observed asymmetry of the CMZ (the
-complex. In agreement with Hüttemeister et al. (1998); Rodriguez-Fernandez et al. (2006) have measured the highest SiO abundances in this region.
Therefore, the lb distribution, the velocity structure, and the chemistry imply that the cloud complex giving rise to the observed asymmetry of the CMZ (the
![]() -complex) shows significant differences to other CMZ complexes.
In particular, it shows the signature of strong shocks.
Therefore, we suggest that the observed asymmetry of the CMZ can be the result of gas falling into the CMZ and not due to an intrinsic asymmetry of the stellar potential. This explanation is also supported by our detailed simulations of the stellar structure and the gas dynamics.
-complex) shows significant differences to other CMZ complexes.
In particular, it shows the signature of strong shocks.
Therefore, we suggest that the observed asymmetry of the CMZ can be the result of gas falling into the CMZ and not due to an intrinsic asymmetry of the stellar potential. This explanation is also supported by our detailed simulations of the stellar structure and the gas dynamics.
Double bars are commonly observed in external galaxies (Elmegreen et al. 1996; Wozniak et al. 1995; Shaw et al. 1993). Around 28% of barred galaxies have a secondary bar (Erwin & Sparke 2002; Laine et al. 2002). Nuclear or secondary bars are objects of prime interest to explain the gas inflow towards the center of a galaxy and the fueling of Active Galactic Nuclei (Shlosman et al. 1989).
Several works have studied the stellar orbits that support nested bars (Maciejewski & Sparke 1997,2000) and their stability (El-Zant & Shlosman 2003). In addition, double barred galaxies have been the subject of a number of numerical simulations of star and gas dynamics that have shown a plethora of phenomena, such as: i) secondary bars forming in purely stellar discs (Rautiainen et al. 2002) or only in the presence of gas (Combes 1994); ii) secondary bars forming before (Rautiainen & Salo 1999) or after the primary bars (Combes 1994; Englmaier & Shlosman 2004; Heller et al. 2007); iii) decoupled secondary bars rotating slower (Heller et al. 2001) or faster (Friedli & Martinet 1993; Rautiainen et al. 2002; Englmaier & Shlosman 2004; Combes 1994) than the primary bar; iv) two misaligned bars rotating at the same speed (Combes 1994; Shaw et al. 1993).
The secondary bars rotating at the same speed as the primary bars have been explained by Shaw et al. (1993) and Combes (1994) as follows: the gas clouds tend to shift from the closed X1 orbits to the perpendicular X2 orbits of the primary bar. However, dissipative collisions between the gas clouds reduce the orthogonality of this phase shift and the gas settles in a leading phase-shifted bar. If the gas fraction is high, its gravitational influence is then sufficient to modify the stellar component and to form a secondary bar that is still coupled to the primary bar.
If the secondary and primary bars remain coupled and they continue rotating with the same speed, the bars will align or form an angle of 90![]() since the primary bar exerts a gravitational torque on the secondary bar and vice-versa (Friedli & Martinet 1993).
Alternatively, the secondary bar may increase its rotation speed.
Thus, the coupled phase can be a precursor of a future decoupled phase. The dynamical process from coupled to decoupled gaseous nuclear bars has been studied by Heller et al. (2001); Englmaier & Shlosman (2004)
and, more recently, by Heller et al. (2007), who have carried out the first simulations of the formation of nested bars from cosmological initial conditions. In these simulations a secondary bar forms in response to the gas inflow along the stellar primary bar. This gaseous bar is initially corotating with the primary bar. Subsequent mass inflow strengthens the bar giving rise to even more rapid gas inflow. During this process the secondary bar shrinks in size and the pattern speed increases at a rate inversely proportional to the bar size.
The pattern speeds of the two bars are such that the secondary bar corotation coincides with the primary bar inner Lindblad resonance, suggesting that non-linear interactions between the two bars are at play (Tagger et al. 1987).
since the primary bar exerts a gravitational torque on the secondary bar and vice-versa (Friedli & Martinet 1993).
Alternatively, the secondary bar may increase its rotation speed.
Thus, the coupled phase can be a precursor of a future decoupled phase. The dynamical process from coupled to decoupled gaseous nuclear bars has been studied by Heller et al. (2001); Englmaier & Shlosman (2004)
and, more recently, by Heller et al. (2007), who have carried out the first simulations of the formation of nested bars from cosmological initial conditions. In these simulations a secondary bar forms in response to the gas inflow along the stellar primary bar. This gaseous bar is initially corotating with the primary bar. Subsequent mass inflow strengthens the bar giving rise to even more rapid gas inflow. During this process the secondary bar shrinks in size and the pattern speed increases at a rate inversely proportional to the bar size.
The pattern speeds of the two bars are such that the secondary bar corotation coincides with the primary bar inner Lindblad resonance, suggesting that non-linear interactions between the two bars are at play (Tagger et al. 1987).
Our simulations are the very first attempt to model the Milky Way with two nested bars and have been performed assuming a common pattern speed for both bars. Therefore, we cannot study in detail the coupling and the evolution of the nuclear bar.
Nevertheless, these simulations explain many characteristics of the Galaxy at scales from the disk to the nuclear region, some for the first time, such as the parallelogram of the CMZ.
Therefore, the observational data are compatible with a scenario of coupled bars rotating with the same speed.
Our results imply that the nuclear bar is leading the large primary bar by
![]() ,
as expected in this context (Combes 1994).
Thus, the decoupling of the nuclear bar can still not be effective in the Milky Way.
The dynamical decoupling of the two bars will be the subject of a forthcoming paper.
,
as expected in this context (Combes 1994).
Thus, the decoupling of the nuclear bar can still not be effective in the Milky Way.
The dynamical decoupling of the two bars will be the subject of a forthcoming paper.
We have presented gas flow models in the mass distribution derived from 2MASS
star counts using a model with three components (disk, bulge and nuclear bar).
Our dynamical models are the first ones that include a central mass cusp (the nuclear bar) constrained by observations.
For the first time, we have obtained good models of the Milky Way from the scales of the spiral arms to the Central Molecular Zone (CMZ) in the Galactic center (GC).
The best models are found for a bulge orientation of 20-35![]() with respect to the Sun-GC line and a pattern speed of 30-40 km s-1 kpc-1.
This places the corotation radius at 5-7 kpc.
The simulations reproduce:
with respect to the Sun-GC line and a pattern speed of 30-40 km s-1 kpc-1.
This places the corotation radius at 5-7 kpc.
The simulations reproduce:
In our simulations, the CMZ is the gas response to the nuclear bar.
These simulations reproduce, for the first time, the parallelogram shape of the lv-diagram of the CMZ.
Using this shape we have been able to constrain the nuclear bar orientation, which is of
![]() -
-![]() with respect to the Sun-GC line, in excellent agreement with the 2MASS fits and the results of Sawada et al. (2004).
We have also studied the observed asymmetry of the CMZ and conclude that it cannot be due to the lopsidedness of the nuclear bar as suggested by the 2MASS maps. Gas dynamical simulations in a lopsided potential cannot
reproduce the observations, and we do not see strong direct evidence in the 2MASS data of an intrinsic lopsidedness of the stellar potential.
with respect to the Sun-GC line, in excellent agreement with the 2MASS fits and the results of Sawada et al. (2004).
We have also studied the observed asymmetry of the CMZ and conclude that it cannot be due to the lopsidedness of the nuclear bar as suggested by the 2MASS maps. Gas dynamical simulations in a lopsided potential cannot
reproduce the observations, and we do not see strong direct evidence in the 2MASS data of an intrinsic lopsidedness of the stellar potential.
We propose an alternative scenario to explain the observed asymmetry of the CMZ.
The asymmetry can be due to gas falling into the CMZ through the inner spiral arm in the
![]() -complex region. We have also discussed that the
-complex region. We have also discussed that the
![]() -complex shows significant differences with the, otherwise symmetric, CMZ that extends from Sgr C to Sgr B. In particular, the
-complex shows significant differences with the, otherwise symmetric, CMZ that extends from Sgr C to Sgr B. In particular, the
![]() -complex shows all the signatures of the shocks expected if it is an interaction region where new material is falling into the CMZ.
-complex shows all the signatures of the shocks expected if it is an interaction region where new material is falling into the CMZ.
In our models both bars rotate with the same pattern speed. The success of these models in explaining many characteristics of the Milky Way, such as the Central Molecular Zone (CMZ) imply that the observations are compatible with that assumption. Furthermore, in our models the nuclear bar leads the large bar by
![]() as expected for coupled nested bars (Combes 1994).
Therefore, in spite of the high mass of the nuclear bar (10-25% of the mass of the bulge) the dynamical decoupling my still not be effective.
However, this question requires further studies and gas flow models with two pattern speeds or self-consistent gas and star dynamics simulations.
as expected for coupled nested bars (Combes 1994).
Therefore, in spite of the high mass of the nuclear bar (10-25% of the mass of the bulge) the dynamical decoupling my still not be effective.
However, this question requires further studies and gas flow models with two pattern speeds or self-consistent gas and star dynamics simulations.
Acknowledgements
We thank Katia Ferrière for a critical reading of the manuscript and Tom Dame for sharing with us his finding of the far-side counterpart of the 3-kpc arm before publication. We also thank the anonymous referee for useful comments that have improved the paper, in particular regarding the phenomena of several pattern speeds and nested bars in other galaxies. The early stages of this work have benefited from support by a Marie Curie Fellowship of the European Community program ``Improving Human Research Potential and the Socio-economic Knowledge base'' under contract number HPMF-CT-2002-01677.
Table 3:
Results of the fits to the star count data of Fig. 5 using a disc, bulge and nuclear bar. The following parameters have been taken from Table 1 and kept fixed:
![]() .
The bar angle
.
The bar angle ![]() is also fixed, the other parameters are free and used to obtain the best fit to the data.
The first set of results have been obtained with x1 fixed to 0. In the second set of results x1 is a free parameter.
is also fixed, the other parameters are free and used to obtain the best fit to the data.
The first set of results have been obtained with x1 fixed to 0. In the second set of results x1 is a free parameter.
Table 4:
Same as Table 3 but with
![]() .
The first set of results have been obtained with x1 fixed to 0. In the second set of results x1 is a free parameter.
.
The first set of results have been obtained with x1 fixed to 0. In the second set of results x1 is a free parameter.
Table 5:
Same as Table 3 but with
![]() .
The first set of results have been obtained with x1 fixed to 0. In the second set of results x1 is a free parameter.
.
The first set of results have been obtained with x1 fixed to 0. In the second set of results x1 is a free parameter.
Table 6:
Same as Table 3 but with
![]() .
The first set of results have been obtained with x1 fixed to 0. In the second set of results x1 is a free parameter.
.
The first set of results have been obtained with x1 fixed to 0. In the second set of results x1 is a free parameter.