A&A 488, 1109-1115 (2008)
DOI: 10.1051/0004-6361:20078835
Supergranules over the solar cycle
N. Meunier1 - T. Roudier2 - M. Rieutord3
1 - Laboratoire d'Astrophysique de l'Observatoire de Grenoble, Université Joseph Fourier, CNRS, BP 43, 38041 Grenoble Cedex, France
2 -
Laboratoire d'Astrophysique de Toulouse-Tarbes, Université de Toulouse, CNRS, 57 avenue d'Azereix,
65000 Tarbes, France
3 -
Laboratoire d'Astrophysique de Toulouse-Tarbes, Université de Toulouse, CNRS, 14 avenue Édouard Belin,
31400 Toulouse, France
Received 11 October 2007 / Accepted 17 June 2008
Abstract
Context. The origin of supergranulation has not been understood yet. Contradictory results have been obtained in the past concerning the relation between supergranule properties (mostly cell size) and the solar cycle.
Aims. We propose to study the variation in supergranule cell sizes and velocity fields over the solar cycle, as well as the intensity variation inside supergranules.
Methods. We define supergranule cells from maps of horizontal velocity field divergences. The flow fields are derived from MDI/SOHO intensity maps. The intensity variation in supergranules are compared to the variation inside granules resulting from a numerical simulation. The variation in these profiles with the cell size and over the solar cycle is also analysed.
Results. We find that cell sizes are smaller on average at cycle maximum. We also find that the slope between Log (
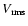 )
and Log (R) is weakly correlated with the spot number (i.e. the global activity level) but anti-correlated with the local magnetic field. We also confirm the decrease in the intensity variation from cell centre to the boundary, which puts a lower limit on the temperature variation of 0.57
)
and Log (R) is weakly correlated with the spot number (i.e. the global activity level) but anti-correlated with the local magnetic field. We also confirm the decrease in the intensity variation from cell centre to the boundary, which puts a lower limit on the temperature variation of 0.57 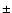 0.06 K. This temperature difference is of 1.03
0.06 K. This temperature difference is of 1.03 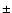 0.05 K when considering the areas of strongest divergence and strongest convergence. We observe a strong similarity in the intensity variation inside supergranules and granules. A significant variation with the cell size is observed, also similar to that in granules, but the variation over the solar cycle is not significant.
0.05 K when considering the areas of strongest divergence and strongest convergence. We observe a strong similarity in the intensity variation inside supergranules and granules. A significant variation with the cell size is observed, also similar to that in granules, but the variation over the solar cycle is not significant.
Conclusions. The sign of the variation in supergranule cell sizes over the solar cycle is in agreement with what can be expected from the influence of the magnetic field. The observed intensity variations show that a common process could be the origin of both granules and supergranules.
Key words: Sun: granulation - Sun: photosphere - Sun: activity - Sun: magnetic fields - Sun: general
The classical explanation of the origin of supergranulation as a
consequence of a convective instability driven by the heat released
by the
second ionisation of helium (Simon & Weiss 1968) has been challenged in the
past by a number of authors (e.g. Rieutord et al. 2000; Rast 2003; Rieutord et al. 2008). Other
results such as the wave-like properties of supergranules
(Schou 2003; Gizon et al. 2003), which could be related to the super-rotation
of supergranules, also questions the very origin of supergranules.
In this context, the study of the relation between the dynamical cells
on a supergranular scale and the magnetic field should provide some
interesting constraints. There are two approaches to studying the
relation between a given solar structure (for example supergranulation)
and the activity level. The first is to associate the activity level
with the local magnetic
field (at a given time). This has been done in a number of papers
(Wang et al. 1996; Sýkora 1970; Wang 1988; Raju & Singh 2002; Hagenaar et al. 1997), using magnetograms or Ca II K
images to determine supergranule boundaries. In that case one finds
how the local magnetic field influences the local flow fields.
The second approach is to associate, in an appropriate way, the activity
level with the phase of the cycle. Contrary to the preceding one,
this approach is global and integrates the magnetic flux over the whole Sun,
from active region to the network and the intranetwork magnetic fields.
Some factors may lead to a different result, for example a variable proportion of the different magnetic components over the solar cycle. On a similar subject, it can be noted that, although the variation of granule size with the local activity level is well-determined (e.g. Title et al. 1992, for a difference between quiet sun and plages), the variation over the solar cycle is much more difficult to study (Muller et al. 2007).
The temporal variation in the supergranule size has been studied by
Berrilli et al. (1999); Sýkora (1970); Muenzer et al. (1989); Singh & Bappu (1981); Komm et al. (1995); here again, magnetograms or
Ca II K images were used. These studies found either a correlation or
an anti-correlation with the solar cycle. DeRosa & Toomre (2004) are the only ones
who used, like Meunier et al. (2007a), the divergence of the horizontal velocity
fields to characterise supergranules, but they studied only two periods
of different activity levels. They found smaller cell sizes at a time
of high activity.
The aim of the present work is to study the
variations of supergranulation in more detail over the solar cycle, using a technique
that is independent of the magnetic network for cell determination. As
the origin of supergranulation is still an open question, it is very
interesting to have insight into its relationship with the magnetic
field and the solar cycle.
After briefly describing the data sets and the analysis in Sect. 2, we
study the variation of the cell size over the solar cycle in Sect. 3. All
works on the variation of supergranules over the solar cycle performed
up to now have concentrated on the cell size. Our objective is to
extend this analysis to other properties of supergranules. Therefore,
in Sect. 4, we also focus on the variation in the dynamics over time,
with the study of the velocity fields, and of the scale relationship
between the velocity and the cell size. Finally, in Sect. 5, we study
the intensity variation in supergranules, as in Meunier et al. (2007b)
but on a much larger data set. We also compare the supergranular intensity
profiles with that obtained for simulated granules. We conclude in Sect. 6.
Table 1:
Number of 1-h data sets for each time series, and
the monthly spot number at the time of each series (SIDC, 1996-2006).
We use high-resolution MDI/SOHO (Scherrer et al. 1995) intensity maps
obtained during the last solar cycle. The pixel size is 0
 605 and the
field-of-view 620
605 and the
field-of-view 620
 303
303
 .
The temporal cadence is 1 min. All images are remapped on a grid with constant steps in longitude
and latitude. We study 12 time series covering the solar cycle between
August 1996 and July 2006. The details (dates, number of 1-h data
sets in each series) are given in Table 1. Figure 1
shows the variations of the spot number over that period as well as the
localisation of the 12 time series. The spot number is used here as to
indicate the global activity level and essentially the phase of
the cycle, as opposed to the local activity level in individual cells.
.
The temporal cadence is 1 min. All images are remapped on a grid with constant steps in longitude
and latitude. We study 12 time series covering the solar cycle between
August 1996 and July 2006. The details (dates, number of 1-h data
sets in each series) are given in Table 1. Figure 1
shows the variations of the spot number over that period as well as the
localisation of the 12 time series. The spot number is used here as to
indicate the global activity level and essentially the phase of
the cycle, as opposed to the local activity level in individual cells.
Only cells outside active regions are considered. This leads to 54 501
determination, which are not completely independent due
to their long lifetime (see Sect. 4 of Meunier et al. 2007b, for a discussion).
We studied in detail the variations of the instrumental conditions over the
whole period using several criteria, and found that these instrumental
variations did not affect significantly our results.
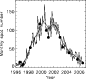 |
Figure 1:
Monthly sunspot number during solar cycle 23 (thin solid line), provided by SDIC (1996-2006). The 3-month smoothed monthly sunspot number is shown as a thick line. The 12 time series studied in this paper (see Table 1) are indicated as filled circles. |
| Open with DEXTER |
For each hourly data set, the 60 intensity maps are aligned with the
map at the centre of the data set. Intensity maps are corrected for
large-scale gradients and 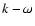 filtered (with a cut-off at 6 km s-1)
before applying a local correlation-tracking (LCT) algorithm. This last
step provides velocity and divergence maps. These divergence maps are
averaged over 1 h and smoothed with a Gaussian whose full-width at
half-maximum is 10.2 Mm so as to exhibit supergranular cells. With no
smoothing, they exhibit the mesogranular scale. The validity of this
approach is discussed in Meunier et al. (2007b,c).
filtered (with a cut-off at 6 km s-1)
before applying a local correlation-tracking (LCT) algorithm. This last
step provides velocity and divergence maps. These divergence maps are
averaged over 1 h and smoothed with a Gaussian whose full-width at
half-maximum is 10.2 Mm so as to exhibit supergranular cells. With no
smoothing, they exhibit the mesogranular scale. The validity of this
approach is discussed in Meunier et al. (2007b,c).
The intensity levels in the original data are different for each time
series and they are therefore normalised in the following by removing any
variation in the average intensity over the cycle. To define the
localisation inside the supergranular cells, we use two parameters:
the normalised divergence
 ,
which is 0 at the
position of the maximum divergence inside the cell (diverging flows)
and 1 at the position of minimum divergence (converging flows),
and the relative distance to cell centre
,
which is 0 at the
position of the maximum divergence inside the cell (diverging flows)
and 1 at the position of minimum divergence (converging flows),
and the relative distance to cell centre
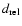 .
This last
parameter is not only weighted by the cell radius, but also defined
in such a way that it is 1 over the whole boundary of
each cell (see Fig. 2 of Meunier et al. 2007b); therefore,
.
This last
parameter is not only weighted by the cell radius, but also defined
in such a way that it is 1 over the whole boundary of
each cell (see Fig. 2 of Meunier et al. 2007b); therefore,
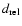 take
values between 0 and 1. This difference in definition (strongest
converging flows versus whole boundary) leads to different variations
in the following, as values of 1 for
take
values between 0 and 1. This difference in definition (strongest
converging flows versus whole boundary) leads to different variations
in the following, as values of 1 for
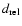 correspond to mean
values of
correspond to mean
values of
 significantly less than 1. This is due to
the intermittent behaviour of the converging flows and network features,
which do not fill all the boundaries of the cells.
significantly less than 1. This is due to
the intermittent behaviour of the converging flows and network features,
which do not fill all the boundaries of the cells.
In a previous work (Meunier et al. 2007b), we defined a parameter
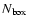 ,
which gives the number of pixel with a magnetic field below 3 G (the noise level in our magnetograms) in a box of 7
,
which gives the number of pixel with a magnetic field below 3 G (the noise level in our magnetograms) in a box of 7 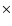 7 pixels around a given pixel: high values of this parameter (within the limit of the maximum value of 49) indicate very quiet regions. The size of the box has been chosen in order to correspond to the granular scale. We use this parameter to characterise the pixel selection.
7 pixels around a given pixel: high values of this parameter (within the limit of the maximum value of 49) indicate very quiet regions. The size of the box has been chosen in order to correspond to the granular scale. We use this parameter to characterise the pixel selection.
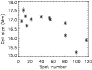 |
Figure 2:
Average cell size R (in Mm) as a function of the monthly spot number. |
| Open with DEXTER |
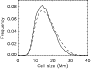 |
Figure 3:
Cell size distribution at cycle maximum (solid line) and cycle minimum (dashed line). We consider the time series from 2000 to 2004 for cycle maximum and the time series 1996, 1997, and 2006 for the cycle minimum. |
| Open with DEXTER |
We first discuss the variation in the cell size on the supergranular
scale. Figure 2 shows this variation. There is a clear
anti-correlation of the cell size variation with the sunspot number,
with a correlation of 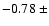 0.03. Here, and in the following, the
uncertainties in the correlation have been computed using a Monte Carlo
simulation and are at the 1-
0.03. Here, and in the following, the
uncertainties in the correlation have been computed using a Monte Carlo
simulation and are at the 1-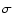 level. Therefore, supergranules are
smaller at cycle maximum. Here and in the following sections,
the spot number is used as an indicator of the phase of the solar
cycle. If we use the spot area, for example, which may be a better indicator
of the total flux at any given time, the anti-correlation remains significant
at -0.68
level. Therefore, supergranules are
smaller at cycle maximum. Here and in the following sections,
the spot number is used as an indicator of the phase of the solar
cycle. If we use the spot area, for example, which may be a better indicator
of the total flux at any given time, the anti-correlation remains significant
at -0.68 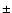 0.03.
0.03.
Furthermore, the relationship does not seem linear, with a flat curve
up to a spot number of 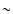 60 (i.e. in the middle of the variation
range of the spot number), and then a rapid decrease.
60 (i.e. in the middle of the variation
range of the spot number), and then a rapid decrease.
Figure 3 shows two cell size distributions, one covering the
cycle maximum and one covering the cycle minimum. The average cell size
is 17.06 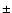 0.04 Mm at cycle minimum and 16.11
0.04 Mm at cycle minimum and 16.11 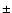 0.05 at cycle maximum.
As observed by Meunier et al. (2007a) for the study of supergranular cell size
versus the local magnetic field (at any given time), the difference in cell
size is mostly due to the tail of the distribution toward large sizes,
while the peak of the distributions remains at the same position.
0.05 at cycle maximum.
As observed by Meunier et al. (2007a) for the study of supergranular cell size
versus the local magnetic field (at any given time), the difference in cell
size is mostly due to the tail of the distribution toward large sizes,
while the peak of the distributions remains at the same position.
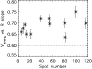 |
Figure 4:
Slope of Log (
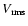 )
in cells versus Log (R), as a function of the monthly spot number, on the supergranular scale. )
in cells versus Log (R), as a function of the monthly spot number, on the supergranular scale. |
| Open with DEXTER |
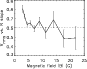 |
Figure 5:
Slope of Log (
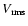 )
in cells versus Log (R), as a function of the magnetic field level in the cells |B| on the supergranular scale. The horizontal dotted line at 0.6 corresponds to the Bolgiano-Obukhovexponent. )
in cells versus Log (R), as a function of the magnetic field level in the cells |B| on the supergranular scale. The horizontal dotted line at 0.6 corresponds to the Bolgiano-Obukhovexponent. |
| Open with DEXTER |
In this section we focus on the relationship between the cell size R and the
rms velocity
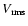 inside the cell. We studied this relationship in
Meunier et al. (2007c) on a smaller data set (March 1997), following the work of
Krishan et al. (2002) and found a slope of 0.66
inside the cell. We studied this relationship in
Meunier et al. (2007c) on a smaller data set (March 1997), following the work of
Krishan et al. (2002) and found a slope of 0.66 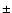 0.02 between Log (R) and Log (
0.02 between Log (R) and Log (
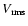 )
on the supergranular scale. Here, we consider a much larger data
set. We can therefore refine the values and study the variation of this
slope with the phase of the solar cycle (i.e. with the spot number here)
or with the local magnetic field. This allows us to see whether this
relationship is purely dynamical or if it is influenced by the magnetic field.
)
on the supergranular scale. Here, we consider a much larger data
set. We can therefore refine the values and study the variation of this
slope with the phase of the solar cycle (i.e. with the spot number here)
or with the local magnetic field. This allows us to see whether this
relationship is purely dynamical or if it is influenced by the magnetic field.
The slope between Log (R) and Log (
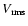 )
on the supergranular scale is shown in Fig. 4 as a function of the spot number. The correlation with the monthly spot number is 0.48
)
on the supergranular scale is shown in Fig. 4 as a function of the spot number. The correlation with the monthly spot number is 0.48 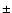 0.15 in the case of supergranulation. This correlation is, however, very sensitive to specific points. For example, if one removes the 2000 October point (spot number around 100), the correlation falls to 0.27
0.15 in the case of supergranulation. This correlation is, however, very sensitive to specific points. For example, if one removes the 2000 October point (spot number around 100), the correlation falls to 0.27 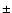 0.19, which becomes poorly significant. The positive correlation with the global activity level is therefore very weak. Furthermore, the correlation with another indicator, the spot area, is also small (from 0.48 to 0.23).
0.19, which becomes poorly significant. The positive correlation with the global activity level is therefore very weak. Furthermore, the correlation with another indicator, the spot area, is also small (from 0.48 to 0.23).
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{8835fig6.ps}\end{figure}](/articles/aa/full/2008/36/aa8835-07/Timg20.gif) |
Figure 6:
Left column: intensity variation in supergranules (for
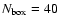 )
versus the normalised divergence ( upper panel) and versus the relative distance to cell centre ( lower panel) in arbitrary units. Right panel: same for simulated granules. )
versus the normalised divergence ( upper panel) and versus the relative distance to cell centre ( lower panel) in arbitrary units. Right panel: same for simulated granules. |
| Open with DEXTER |
We also study the variations in this slope with the local magnetic field in Fig. 5. The
local magnetic field is characterised by the average of the magnetic field in absolute value over
the cell, |B|. We do see a small variation, with a smaller exponent on larger activity levels,
i.e. an anti-correlation with the local activity level in the cell. The correlation
is
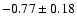 .
The first 5 points of the curves represent 85% of all cells, for a
correlation of -0.90
.
The first 5 points of the curves represent 85% of all cells, for a
correlation of -0.90 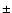 0.07. Also, we now have an exponent significantly larger than 0.6. For example, the cells with a magnetic field below 4 G represents 30% of the cells, and all points in Fig. 4 are above 0.6.
0.07. Also, we now have an exponent significantly larger than 0.6. For example, the cells with a magnetic field below 4 G represents 30% of the cells, and all points in Fig. 4 are above 0.6.
It is interesting to estimate the respective contribution of the different components of the magnetic field
to this correlation. We find that the intranetwork field inside the
cells has no influence (correlation very close to zero),
but that the network field seems to control this variation.
We first consider the total data set in order to derive intensity profiles, which should be much
more precise than in Meunier et al. (2007b) because of the greater amount of data.
The total amount of data can be analysed to derive the intensity profiles as a function of the normalised divergence (top left of Fig. 6) and as a function of the relative distance to cell centre (bottom left of Fig. 6).
The plots are shown for a parameter
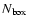 of 40, but profiles are quite similar for higher values (i.e. for a more restrictive pixel selection). The intensity decrease between the cell centre and the cell boundary is clearly visible, with a close to linear relation in the case of the divergence, and a flat curve close to cell centre in the case of the relative distance to cell centre.
of 40, but profiles are quite similar for higher values (i.e. for a more restrictive pixel selection). The intensity decrease between the cell centre and the cell boundary is clearly visible, with a close to linear relation in the case of the divergence, and a flat curve close to cell centre in the case of the relative distance to cell centre.
The temperature differences derived from the average intensity for normalised divergences
 and for relative distance
and for relative distance
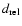 less than 0.1 and more than 0.9 are shown in Fig. 7. There is a nice trend as
less than 0.1 and more than 0.9 are shown in Fig. 7. There is a nice trend as
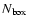 is increasing, showing a greater temperature difference for quieter regions. The temperature difference is always positive, i.e. a higher temperature at cell centre. Therefore we obtain a temperature difference of 1.03
is increasing, showing a greater temperature difference for quieter regions. The temperature difference is always positive, i.e. a higher temperature at cell centre. Therefore we obtain a temperature difference of 1.03 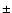 0.05 K when considering the divergence and 0.57
0.05 K when considering the divergence and 0.57 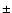 0.06 K when considering the relative distance to cell centre. This shows that the temperature difference is significantly greater when comparing zones of diverging and converging flows (flow field definition of the cells) than when comparing the cell centre and the cell boundary (cell geometry).
0.06 K when considering the relative distance to cell centre. This shows that the temperature difference is significantly greater when comparing zones of diverging and converging flows (flow field definition of the cells) than when comparing the cell centre and the cell boundary (cell geometry).
In Meunier et al. (2007b), we also considered the variation in the minimum intensity around each pixel on the granular scale (here 7  7 pixels), as well as the maximum intensity. Our objective was to retrieve some information on the localisation of the intensity changes, i.e. between granules and intergranules. At this spatial resolution, the intensity contrast of granules with respect to their sizes (Hirzberger et al. 1997) are in fact not detectable, as we find from simulations of granulation degraded at the spatial resolution of our data.
The observed variations, a strong increase in the minimum intensity and strong decrease in the maximum intensity, are therefore not likely to be merely due to variation in size of granules across supergranules. Both amplitudes are greater (by a factor 2) than the intensity variations. The global intensity decrease therefore mostly stems from the intensity variation inside granules, and the intensity in intergranules shows the opposite behaviour.
Another consequence is that the influence of intergranule and granule properties (for example different formation heights) are probably not significant, which reinforces the interpretation of the intensity variations as temperature variations. The influence of the magnetic field was also discussed in detail in Meunier et al. (2007b). Although we cannot exclude another source for the intensity variations, we think it very likely that these variations are related to temperature variations.
7 pixels), as well as the maximum intensity. Our objective was to retrieve some information on the localisation of the intensity changes, i.e. between granules and intergranules. At this spatial resolution, the intensity contrast of granules with respect to their sizes (Hirzberger et al. 1997) are in fact not detectable, as we find from simulations of granulation degraded at the spatial resolution of our data.
The observed variations, a strong increase in the minimum intensity and strong decrease in the maximum intensity, are therefore not likely to be merely due to variation in size of granules across supergranules. Both amplitudes are greater (by a factor 2) than the intensity variations. The global intensity decrease therefore mostly stems from the intensity variation inside granules, and the intensity in intergranules shows the opposite behaviour.
Another consequence is that the influence of intergranule and granule properties (for example different formation heights) are probably not significant, which reinforces the interpretation of the intensity variations as temperature variations. The influence of the magnetic field was also discussed in detail in Meunier et al. (2007b). Although we cannot exclude another source for the intensity variations, we think it very likely that these variations are related to temperature variations.
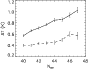 |
Figure 7:
Temperature variation versus the number of pixels
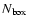 below 3 G on the granular scale for the pixel selection, for the normalised divergence (solid line) and the relative distance to cell centre (dashed line).
below 3 G on the granular scale for the pixel selection, for the normalised divergence (solid line) and the relative distance to cell centre (dashed line). |
| Open with DEXTER |
We now compare the previous intensity profiles with those derived inside granules, for which the
convective origin is accepted. We thus use a simulation of granulation performed by
Rieutord et al. (2001,2002).
This simulation is based on the radiation-hydrodynamics code developed by Stein & Nordlund (1998). This simulation of compressible convection is performed with radiative transfer treated at LTE with grey opacities, including contributions from spectral lines. The horizontal resolution is 95 km and the aspect ratio of the simulation is about 10. More details can be found in Rieutord et al. (2002).
Granules are determined with a similar technique to the one used for supergranules. The intensity profiles as a function of
 and
and
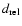 are shown in Fig. 6 (right panel).
The shape of the intensity profile versus
are shown in Fig. 6 (right panel).
The shape of the intensity profile versus
 is different from that
obtained for supergranules. Here the shape at small
is different from that
obtained for supergranules. Here the shape at small
 is very
specific and exhibits a maximum around 0.1-0.2, which is not visible for supergranules. This shows that the organisation of the velocity field inside the cells is quite different for granules and supergranules.
is very
specific and exhibits a maximum around 0.1-0.2, which is not visible for supergranules. This shows that the organisation of the velocity field inside the cells is quite different for granules and supergranules.
However, the shape of the intensity profile versus
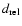 is surprisingly very similar to what is obtained for supergranules. It also exhibits a plateau close to cell centre (up to
is surprisingly very similar to what is obtained for supergranules. It also exhibits a plateau close to cell centre (up to
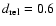 in the case of granules and up to
in the case of granules and up to
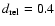 in the case of supergranules) and then a sharp decrease. This suggests that the intensity variations inside the cells are quite similar.
in the case of supergranules) and then a sharp decrease. This suggests that the intensity variations inside the cells are quite similar.
It is not the first time that the properties of supergranules and
granules are directly compared. For example, Schrijver et al. (1997) compared the size distribution of supergranules and granules after a normalisation. They concluded that, in both cases, the spatial distribution of cells were compatible with a random distribution of upflows and that the downflows at the boundary were defined by the competing strength between flows from adjacent cells.
We are not aware of any direct comparison between intensity profiles
of observed and modelled granules. This should be interesting as it
would allow us to go further in our interpretation, especially if some
differences are found. This kind of comparison is beyond the scope of
the present work and it should be noted that, given the small size of
granules, the influence of the seeing is crucial when using ground-based
observations. The current observations of Hinode may allow such a
study, at least for the variation with
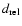 .
(The horizontal
velocity field on such scales and at disk centre is not accessible
using Dopplergrams.)
.
(The horizontal
velocity field on such scales and at disk centre is not accessible
using Dopplergrams.)
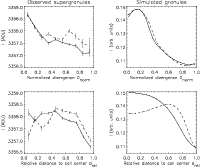 |
Figure 8:
Left column: intensity variation in supergranules (for
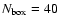 )
versus the normalised divergence ( upper panel) and versus the relative distance to cell centre ( lower panel), in arbitrary units, in two cases: for supergranular cell sizes below 22 Mm (solid line) and for supergranular cells larger than 22 Mm (dashed line). Right panel: same for simulated granules in two cases: for simulated granule sizes below 1.3 Mm (solid line) and for simulated granule sizes larger than 1.3 Mm (dashed line). )
versus the normalised divergence ( upper panel) and versus the relative distance to cell centre ( lower panel), in arbitrary units, in two cases: for supergranular cell sizes below 22 Mm (solid line) and for supergranular cells larger than 22 Mm (dashed line). Right panel: same for simulated granules in two cases: for simulated granule sizes below 1.3 Mm (solid line) and for simulated granule sizes larger than 1.3 Mm (dashed line). |
| Open with DEXTER |
It would be useful to determine what kind of law relates the sizes of
cells to the temperature variation. Figure 8 shows the intensity
variations across supergranules for small and large cells separately. It
is too noisy to detect a clear variation in the temperature difference as
a function of the cell size. When considering the normalised divergence,
the intensity difference between the centre and the boundary is not very
large. However, we note an intensity excess in the case of large
cells in the outer part of the cells. When considering the distance to
cell centre, however, the intensity difference between centre and boundary
is quite noticeable, with less of an intensity difference for larger cells.
As in the previous section, we compare this size-dependent intensity
difference with that observed for granules. The intensities for small and
large simulated granules are shown in Fig. 8 (right panel).
For the normalised divergence, the intensity seems fairly independent of
the granule size. This invariance is much clearer here for granules than for supergranules.
As for the distance to cell centre, we observe in large granules a decrease in the intensity at cell centre compared to smaller granules. This is not new and has been observed before in large granules observed at high spatial resolution. What is very interesting is that the two curves in the lower panel of Fig. 8 are quite similar between supergranules and granules: so here again, there is a strong similarity between granules and supergranules.
Finally, because we have covered a complete solar cycle, we should be able to determine whether the intensity contrast inside supergranules varies during the solar cycle. This is important because the influence of the magnetic field on this measurement remains significant: with more magnetic flux at cycle maximum, we expect the intensity contrast to be lower at cycle maximum (due to the brightness enhancement related to the magnetic network).
When looking at the intensity variation independently for cycle maximum and for cycle minimum, the intensities are on average higher at cycle maximum, but the intensity differences are quite similar.
Furthermore, when studying the temperature difference for different values of
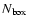 ,
we do not observe the decrease in intensity contrast at cycle
maximum, which could be caused by more magnetic flux. In fact, there is a weak trend toward a small increase in this intensity contrast at cycle maximum, but it is hardly significant.
,
we do not observe the decrease in intensity contrast at cycle
maximum, which could be caused by more magnetic flux. In fact, there is a weak trend toward a small increase in this intensity contrast at cycle maximum, but it is hardly significant.
We have studied the variation of supergranule sizes over a solar cycle, as
well as the properties of the velocity field inside these cells and the
intensity variations. Our measurements are independent of the magnetic
network, in contrast to most previous works.
We first conclude
that supergranules are smaller on average at cycle maximum than at cycle minimum. The tail of the cell
distribution is longer (toward the large cell sizes) at cycle minimum. This agrees with
the result of DeRosa & Toomre (2004), who studied two short periods in the solar cycle, and with that of Meunier et al. (2007a), who found smaller cell sizes when the local activity level
was higher. This can be expected from the influence of the Lorentz force.
It also agrees with the simulation of the magnetic network made by Crouch et al. (2007).
Second, we find that the power-law relationship between cell size and velocity field
significantly depends on the local activity level (defined as the average
magnetic field inside the cell, including the network at the boundary). Therefore this power law between cell size and velocity is not
purely due to hydrodynamical effects. It shows that the magnetic field has a stronger influence inside large cells compared to small
cells, leading to a change in the slope. On the other hand, the variation
with the phase of the solar cycle is not significant.
There is no theoretical result in the literature that provides a relation between the magnetic
field and the exponent that we are studying here.
Depending on the type of magnetic field (strong guide field or small-scale magnetic fields), a constant exponent or an increasing exponent with the magnetic field has been obtained, and the understanding of our observations remains a completely opened question.
In Meunier et al. (2007c), we interpreted our result by a possible Bolgiano-Obukhov turbulence origin of supergranulation. This was very interesting because turbulence in a stratified medium was attractive for explaining supergranulation as they may be shallow structures (November 1994). This interpretation does not hold any longer with this larger data set, however, because the exponent is now much larger (close to 1 for
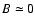 )
than 0.6.
This agrees with the results obtained by Rincon (2007), who shows that, in the case of the Sun, the typical scale for the Bolgiano-Obukhov turbulence was instead in the granule-mesogranule range. This means that another scaling may take place in the case of supergranulation (Rincon, private communication).
)
than 0.6.
This agrees with the results obtained by Rincon (2007), who shows that, in the case of the Sun, the typical scale for the Bolgiano-Obukhov turbulence was instead in the granule-mesogranule range. This means that another scaling may take place in the case of supergranulation (Rincon, private communication).
Finally, we confirm the decrease in the intensity from cell centre
to boundary observed by Meunier et al. (2007b). We derive a lower limit of
the temperature difference of 1.03 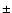 0.05 K between area of
maximum divergence and maximum convergence and of 0.57
0.05 K between area of
maximum divergence and maximum convergence and of 0.57 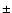 0.06 K
between the cell centre and the boundary. This result
is not incompatible with previous measurements of these variations
(Beckers 1968; Foukal & Fowler 1984; Lin & Kuhn 1992; Frazier 1970), which gave an increase of the intensity
toward the boundary, as these were strongly influenced by the magnetic
network; in fact, we studied this dependence in detail in Meunier et al. (2007b). Our
results are, however, close to those of Rast (2003), who independently
followed a similar technique (i.e. eliminating the magnetic network).
0.06 K
between the cell centre and the boundary. This result
is not incompatible with previous measurements of these variations
(Beckers 1968; Foukal & Fowler 1984; Lin & Kuhn 1992; Frazier 1970), which gave an increase of the intensity
toward the boundary, as these were strongly influenced by the magnetic
network; in fact, we studied this dependence in detail in Meunier et al. (2007b). Our
results are, however, close to those of Rast (2003), who independently
followed a similar technique (i.e. eliminating the magnetic network).
The shape of the variations with the divergence, despite the common
decrease, presents some differences with that of granules. However,
the variation versus the distance to the cell centre is very close to
what is observed for granules. The variation in these intensity profiles
for different categories of cell sizes confirms this conclusion.
The variations over the solar cycle are not significant.
Even if our results show that supergranules do not entirely
result from hydrodynamical effects, unlike granules, the similarities
with granules are nevertheless
striking and need further investigation. Progress will be
possible when the intensity and velocity profiles of these two structures have both been observed, which is delicate for granules, and modelled, which is still a challenge for supergranules (e.g. Benson et al. 2006).
Acknowledgements
SOHO is a mission of international cooperation between the European Space
Agency (ESA) and NASA. The monthly sunspot number
as been provided by
the SIDC-team, World Data Centre for the Sunspot Index, Royal Observatory of Belgium, Monthly Report on the International Sunspot Number, online catalogue of the sunspot index: http://www.sidc.be/sunspot-data/, 1996-2006.
- Beckers, J. M. 1968,
Sol. Phys., 5, 309 [NASA ADS] [CrossRef]
- Benson, D., Stein,
R. F., & Nordlund, A. 2006, AAS/Solar Physics Division
Meeting, 37, 30.03
(In the text)
- Berrilli, F., Ermolli,
I., Florio, A., & Pietropaolo, E. 1999, A&A, 344, 965 [NASA ADS]
- Crouch, A. D.,
Charbonneau, P., & Thibault, K. 2007, ApJ, 662, 715 [NASA ADS] [CrossRef]
(In the text)
- DeRosa, M. L., &
Toomre, J. 2004, ApJ, 616, 1242 [NASA ADS] [CrossRef]
(In the text)
- Foukal, P., & Fowler,
L. 1984, ApJ, 281, 442 [NASA ADS] [CrossRef]
- Frazier, E. N. 1970,
Sol. Phys., 14, 89 [NASA ADS] [CrossRef]
- Gizon, L., Duvall,
T. L., & Schou, J. 2003, Nature, 421, 43 [NASA ADS] [CrossRef]
- Hagenaar, H. J.,
Schrijver, C. J., & Title, A. M. 1997, ApJ, 481,
988 [NASA ADS] [CrossRef]
- Hirzberger, J.,
Vázquez, M., Bonet, J. A., Hanslmeier, A., & Sobotka,
M. 1997, ApJ, 480, 406 [NASA ADS] [CrossRef]
(In the text)
- Komm, R. W., Howard,
R. F., & Harvey, J. W. 1995, Sol. Phys., 158,
213 [NASA ADS]
- Krishan, V., Paniveni,
U., Singh, J., & Srikanth, R. 2002, MNRAS, 334, 230 [NASA ADS] [CrossRef]
(In the text)
- Lin, H., & Kuhn,
J. R. 1992, Sol. Phys., 141, 1 [NASA ADS] [CrossRef]
- Meunier, N., Roudier,
T., & Tkaczuk, R. 2007a, A&A, 466, 1123 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Meunier, N., Tkaczuk, R.,
& Roudier, T. 2007b, A&A, 463, 745 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Meunier, N., Tkaczuk,
R., Roudier, T., & Rieutord, M. 2007c, A&A, 461, 1141 [NASA ADS] [CrossRef] [EDP Sciences]
- Muenzer, H., Schroeter,
E. H., Wöhl, H., & Hanslmeier, A. 1989, A&A, 213,
431 [NASA ADS]
- Muller, R.,
Hanslmeier, A., & Saldaña-Muñoz, M. 2007, A&A,
475, 717 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- November,
L. J. 1994, Sol. Phys., 154, 1 [NASA ADS] [CrossRef]
(In the text)
- Raju, K. P., &
Singh, J. 2002, Sol. Phys., 207, 11 [NASA ADS] [CrossRef]
- Rast, M. P. 2003, in
Local and Global Helioseismology: the Present and Future, ed.
H. Sawaya-Lacoste, ESA SP-517, 163
- Rieutord, M., Roudier,
T., Malherbe, J. M., & Rincon, F. 2000, A&A, 357,
1063 [NASA ADS]
- Rieutord, M.,
Roudier, T., Ludwig, H.-G., Nordlund, Å., & Stein, R.
2001, A&A, 377, L14 [NASA ADS] [CrossRef] [EDP Sciences]
- Rieutord, M., Ludwig,
H.-G., Roudier, T., Nordlund, Å. & Stein, R. 2002, Nuovo
Cimento C Geophys. Space Phys. C, 25, 523 [NASA ADS]
- Rieutord, M.,
Meunier, N., Roudier, T., et al. 2008, A&A, 479, L17 [NASA ADS] [CrossRef] [EDP Sciences]
- Rincon, F. 2007, in
IAU Symp., 239, ed. F. Kupka, I. Roxburgh, &
K. Chan, 58
(In the text)
- Scherrer, P. H.,
Bogart, R. S., Bush, R. I., et al. 1995,
Sol. Phys., 162, 129 [NASA ADS] [CrossRef]
(In the text)
- Schou, J. 2003, ApJ,
596, L259 [NASA ADS] [CrossRef]
- Schrijver, C., Hagenaar,
H., & Title, A. 1997, ApJ, 475, 328 [NASA ADS] [CrossRef]
(In the text)
- Simon, G. W., &
Weiss, N. O. 1968, Zeit. für Astrophys., 69, 435 [NASA ADS]
(In the text)
- Singh, J., & Bappu,
M. K. V. 1981, Sol. Phys., 71, 161 [NASA ADS] [CrossRef]
- Stein, R. F., &
Nordlund, Å. 1998, ApJ, 499, 914 [NASA ADS] [CrossRef]
(In the text)
- Sýkora, J. 1970, Sol.
Phys., 13, 292 [NASA ADS] [CrossRef]
- Title, A. M., Topka,
K. P., Tarbell, T. D., et al. 1992, ApJ, 393,
782 [NASA ADS] [CrossRef]
(In the text)
- Wang, H. 1988, Sol. Phys.,
117, 343 [NASA ADS] [CrossRef]
- Wang, H., Tang, F.,
Zirin, H., & Wang, J. 1996, Sol. Phys., 165, 223 [NASA ADS] [CrossRef]
Copyright ESO 2008





![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{8835fig6.ps}\end{figure}](/articles/aa/full/2008/36/aa8835-07/Timg20.gif)

