A&A 488, 1031-1046 (2008)
DOI: 10.1051/0004-6361:200809885
E. Caffau1 - H.-G. Ludwig1,2 - M. Steffen3 - T. R. Ayres4 - P. Bonifacio1,2,5 - R. Cayrel6 - B. Freytag7,8 - B. Plez8,9
1 - GEPI, Observatoire de Paris, CNRS, Université Paris Diderot, 92195
Meudon Cedex, France
2 -
CIFIST Marie Curie Excellence Team
3 -
Astrophysikalisches Institut Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany
4 -
Center for Astrophysics and Space Astronomy, University of Colorado
389 UCB (CASA), Boulder, CO 80309-0389, USA
5 -
Istituto Nazionale di Astrofisica, Osservatorio Astronomico di Trieste, via Tiepolo 11,
34143 Trieste, Italy
6 -
GEPI, Observatoire de Paris, CNRS, Université Paris Diderot, 61 Av. de l'Observatoire, 75014
Paris, France
7 -
CRAL,UMR 5574: CNRS, Université de Lyon, École Normale Supérieure de Lyon,
46 allée d'Italie, 69364 Lyon Cedex 7, France
8 -
Department of Physics and Astronomy, Uppsala University, Box 515, 751
20 Uppsala, Sweden
9 -
GRAAL, CNRS UMR 5024, Université Montpellier II, 34095 Montpellier Cedex 5, France
Received 1 April 2008 / Accepted 28 May 2008
Abstract
Context. The solar oxygen abundance has undergone a major downward revision in the past decade, the most noticeable one being the update including 3D hydrodynamical simulations to model the solar photosphere. Up to now, such an analysis has only been carried out by one group using one radiation-hydrodynamics code.
Aims. We investigate the photospheric oxygen abundance considering lines from atomic transitions. We also consider the relationship between the solar model used and the resulting solar oxygen abundance, to understand whether the downward abundance revision is specifically related to 3D hydrodynamical effects.
Methods. We performed a new determination of the solar photospheric oxygen abundance by analysing different high-resolution high signal-to-noise ratio atlases of the solar flux and disc-centre intensity, making use of the latest generation of CO5BOLD 3D solar model atmospheres.
Results. We find
![]() .
The lower and upper values represent extreme assumptions on the role of collisional excitation and ionisation by neutral hydrogen for the NLTE level populations of neutral oxygen. The error of our analysis is
.
The lower and upper values represent extreme assumptions on the role of collisional excitation and ionisation by neutral hydrogen for the NLTE level populations of neutral oxygen. The error of our analysis is ![]() (0.04
(0.04![]() 0.03) dex, the last being related to NLTE corrections, the first error to any other effect. The 3D ``granulation effects'' do not play a decisive role in lowering the oxygen abundance.
0.03) dex, the last being related to NLTE corrections, the first error to any other effect. The 3D ``granulation effects'' do not play a decisive role in lowering the oxygen abundance.
Conclusions. Our recommended value is
![]() ,
considering our present ignorance of the role of collisions with hydrogen atoms on the NLTE level populations of oxygen. The reasons for lower O abundances in the past are identified as (1) the lower equivalent widths adopted and (2) the choice of neglecting collisions with hydrogen atoms in the statistical equilibrium calculations for oxygen.
,
considering our present ignorance of the role of collisions with hydrogen atoms on the NLTE level populations of oxygen. The reasons for lower O abundances in the past are identified as (1) the lower equivalent widths adopted and (2) the choice of neglecting collisions with hydrogen atoms in the statistical equilibrium calculations for oxygen.
Key words: Sun: abundances - Sun: photosphere - line: formation - hydrodynamics - convection - radiative transfer
Oxygen is the most abundant element after hydrogen and helium and is the main product of type II supernovae. In the studies of chemical abundances in stars and in interstellar and intergalactic matter, it is common to use the solar or solar system abundances as a reference. Unlike many other elements, oxygen is volatile and is therefore incompletely condensed in meteorites, where it is present in the form of oxides. As a consequence, the only available reference is the solar photospheric oxygen abundance.
In spite of its high cosmic abundance, there are not many atomic oxygen lines that are suitable for spectroscopic abundance determinations. Oxygen in the solar photosphere is mainly present in the neutral state. The permitted resonance and low-excitation energy lines lie in the vacuum ultraviolet, many at wavelength shortward of the Lyman break. High-resolution spectra of the Sun at these wavelengths are not available. However, even if they were available, the line blending and heavy saturation of most of these lines would make them unsuitable for abundance measurements. In the optical or near infrared range, there are only a few O I lines that can be used; however, all the permitted lines are of high excitation and many of these are blended. There are three forbidden lines that arise from the ground state or very low lying levels, which, however, are very weak, and they are all more or less blended with other atomic or molecular lines. This makes the determination of the solar oxygen abundance a rather complex matter that requires special care.
Because of its high cosmic abundance, oxygen is one of the major contributors to the internal opacity of matter at solar-like chemical composition. It also plays a special role, together with nitrogen and carbon, in the energy production in the Sun. This implies that the solar oxygen abundance has a direct impact on the internal structure and evolutionary behaviour of the Sun. A solar model with reduced abundance of CNO elements has lower central density and opacity (Watson & Guzik 2006) and thus evolves more slowly than a model with higher abundances. In the late evolution of the Sun, the CNO cycle becomes the main source of energy, and a reduced abundance of these elements, together with the lower central densities, implies a higher central burning temperature for the Sun.
The oscillatory properties of the Sun are strongly dependent on the metal content. In fact, the use of helioseismic data has been suggested for deriving Z (Antia & Basu 2006).
The solar oxygen abundance has
undergone several major downward revisions
over the years, starting from
the value of Lambert (1978), A(O) = 8.92![]() .
The influential review of Anders & Grevesse (1989) still provided a value
near this measurement (A(O) =
.
The influential review of Anders & Grevesse (1989) still provided a value
near this measurement (A(O) =
![]() ), but
nine years later it underwent a downward update by 0.1 dex
(Grevesse & Sauval 1998), then was subject to another downward revision by almost
0.1 dex due to Holweger (2001), another downward revision by Allende Prieto et al. (2001),
and finally was lowered again
down to the extremely low value of A(O) = 8.66 recommended
by Asplund et al. (2004).
The last result is supported by Meléndez (2004) and Socas-Navarro & Norton (2007).
However, the recent result of
Ayres et al. (2006, A(O) = 8.84), based on CO infrared lines,
is a countertrend.
), but
nine years later it underwent a downward update by 0.1 dex
(Grevesse & Sauval 1998), then was subject to another downward revision by almost
0.1 dex due to Holweger (2001), another downward revision by Allende Prieto et al. (2001),
and finally was lowered again
down to the extremely low value of A(O) = 8.66 recommended
by Asplund et al. (2004).
The last result is supported by Meléndez (2004) and Socas-Navarro & Norton (2007).
However, the recent result of
Ayres et al. (2006, A(O) = 8.84), based on CO infrared lines,
is a countertrend.
The very low abundance advocated by Asplund et al. (2004), together with the downward revision of the solar abundances of all the other elements by Asplund and collaborators (Asplund et al. 2005, and references therein), has created serious problems for solar models to explain the helioseismic data (Bahcall et al. 2005a; Guzik et al. 2006; Bahcall et al. 2005b).
So far, the only three analyses of the solar oxygen abundance that take the effects of photospheric inhomogeneities (granulation effects) into account are those of Holweger (2001), Allende Prieto et al. (2001), and Asplund et al. (2004). The recommended oxygen abundances differ by almost 0.1 dex. According to our analysis based on 3D CO5BOLD solar models, the granulation effects do not lead to a systematic lowering of the oxygen abundance. The 3D corrections we find are small and, for the majority of the lines, positive.
We present here a new and independent determination of the solar
oxygen abundance, with particular emphasis on a latest generation 3D
CO5BOLD![]() solar model, which, we believe, helps in understanding
possible underlying systematic errors in the modelling
of the solar photosphere.
The line-by-line analysis is presented with full details
in the next sections. However, the paper is organised
in such a way that the reader not interested in such details
may skip directly to the discussion and conclusions in Sect. 6.
solar model, which, we believe, helps in understanding
possible underlying systematic errors in the modelling
of the solar photosphere.
The line-by-line analysis is presented with full details
in the next sections. However, the paper is organised
in such a way that the reader not interested in such details
may skip directly to the discussion and conclusions in Sect. 6.
The atomic data on oxygen lines is reviewed in detail in Sect. 2.1 of
Asplund et al. (2004, hereafter A04). For the lines in common we adopt the same
data, and we refer the reader to that paper for further details. In addition
to the atomic lines used by A04 we make use of two IR lines: the 1316 nm
line, for which we adopt the
![]() of Biémont et al. (1991), and the 1130 nm
line, for which we use the NIST value of
of Biémont et al. (1991), and the 1130 nm
line, for which we use the NIST value of
![]() = 0.076, the same value used
by Holweger (2001). The adopted atomic data are summarised in
Table 1.
= 0.076, the same value used
by Holweger (2001). The adopted atomic data are summarised in
Table 1.
For the collisional broadening constants
![]() given in Table 1, we
paid particular attention in our 3D spectrum synthesis computations
to the Van der Waals broadening of the oxygen lines
to obtain as realistic line profiles as possible. While this
broadening process is important for the strength of strong lines it
also plays a role for the shape of weak lines. From that perspective
we deemed appropriate to provide the actual values that we employed. Whenever
available we preferred Van der Waals broadening constants obtained from the
theory of Anstee & O'Mara (1995), Barklem & O'Mara (1997), Barklem et al. (1998a), and summarised in Barklem et al. (1998b). Hereafter,
we collectively refer to the description as the ``ABO theory''.
ABO theory predicts a slightly different temperature dependence of the
broadening effects than does classical theory. It is
customary to give the broadening constants for a Maxwellian (relative) velocity
distribution at 104 K. We did not implement the ABO theory in our 3D
spectrum synthesis code, but instead opted to ignore the slight differences
in the temperature dependences and to choose a reference temperature of
5500 K at which we evaluated the broadening constants from ABO theory.
This ensures that our classical implementation provided the ABO value at
this temperature. The reference temperature was chosen as characteristic of
the lower photospheric layers of the Sun. This is the reason we give the
broadening constants in a non-standard fashion with reference to 5500 K
in Table 1.
given in Table 1, we
paid particular attention in our 3D spectrum synthesis computations
to the Van der Waals broadening of the oxygen lines
to obtain as realistic line profiles as possible. While this
broadening process is important for the strength of strong lines it
also plays a role for the shape of weak lines. From that perspective
we deemed appropriate to provide the actual values that we employed. Whenever
available we preferred Van der Waals broadening constants obtained from the
theory of Anstee & O'Mara (1995), Barklem & O'Mara (1997), Barklem et al. (1998a), and summarised in Barklem et al. (1998b). Hereafter,
we collectively refer to the description as the ``ABO theory''.
ABO theory predicts a slightly different temperature dependence of the
broadening effects than does classical theory. It is
customary to give the broadening constants for a Maxwellian (relative) velocity
distribution at 104 K. We did not implement the ABO theory in our 3D
spectrum synthesis code, but instead opted to ignore the slight differences
in the temperature dependences and to choose a reference temperature of
5500 K at which we evaluated the broadening constants from ABO theory.
This ensures that our classical implementation provided the ABO value at
this temperature. The reference temperature was chosen as characteristic of
the lower photospheric layers of the Sun. This is the reason we give the
broadening constants in a non-standard fashion with reference to 5500 K
in Table 1.
Alternatively, we computed Van der Waals broadening constants from
the approximation implemented in the Kurucz routine WIDTH (see Ryan 1998).
In short, the WIDTH approximation is the following:
![]() ,
where
S is the number of electrons in the ion under consideration and
Z is the nuclear charge (for neutral oxygen S=8 and Z=8).
Then
,
where
S is the number of electrons in the ion under consideration and
Z is the nuclear charge (for neutral oxygen S=8 and Z=8).
Then
![]() ,
where v is the average relative velocity of the atom with respect to
the perturber (Gray 2005, Eq. (11.28)). The results are listed in
Table 1.
,
where v is the average relative velocity of the atom with respect to
the perturber (Gray 2005, Eq. (11.28)). The results are listed in
Table 1.
Table 1: Atomic parameters of the oxygen lines included in our analysis.
Our analysis is based on a time-dependent 3D hydrodynamical model of the solar photosphere, as well as on a number of standard 1D hydrostatic models. The 3D model was computed with the CO5BOLD code (Wedemeyer et al. 2004; Freytag et al. 2002,2003). An overview of the numerics, aspects of the methodology of its application, and basic validity tests can be found in Ludwig et al. (2008).
The 3D model used has a box size of
![]() Mm3 and a resolution of
Mm3 and a resolution of
![]() grid points, and it spans a
range in optical depth of about
grid points, and it spans a
range in optical depth of about
![]() .
The
multi-group opacities used by CO5BOLD are based on monochromatic opacities
stemming from the MARCS stellar atmosphere package (Gustafsson et al. 2007,2003)
provided as a function of gas pressure and temperature with high wavelength
resolution. For the calculation of the opacities, solar elemental abundances
according to Grevesse & Sauval (1998) are assumed, with the exception of CNO for which values
close to the recommendation of Asplund et al. (2005) are adopted
(specifically, A(C) = 8.41, A(N) = 7.80, A(O) = 8.67).
The monochromatic opacities are binned into representative opacity groups
(Ludwig 1992; Ludwig et al. 1994; Vögler 2004; Nordlund 1982). The solar CO5BOLD model applied here uses twelve bins; to our knowledge, this is the highest
wavelength resolution hitherto applied in a 3D stellar atmosphere model.
.
The
multi-group opacities used by CO5BOLD are based on monochromatic opacities
stemming from the MARCS stellar atmosphere package (Gustafsson et al. 2007,2003)
provided as a function of gas pressure and temperature with high wavelength
resolution. For the calculation of the opacities, solar elemental abundances
according to Grevesse & Sauval (1998) are assumed, with the exception of CNO for which values
close to the recommendation of Asplund et al. (2005) are adopted
(specifically, A(C) = 8.41, A(N) = 7.80, A(O) = 8.67).
The monochromatic opacities are binned into representative opacity groups
(Ludwig 1992; Ludwig et al. 1994; Vögler 2004; Nordlund 1982). The solar CO5BOLD model applied here uses twelve bins; to our knowledge, this is the highest
wavelength resolution hitherto applied in a 3D stellar atmosphere model.
The equation of state takes the ionisation of hydrogen and helium into consideration, as well as the formation of H2 molecules according to Saha-Boltzmann statistics. It ignores the ionisation of the metals, which is of minor importance (<1 %) for the bulk thermodynamic properties. Relevant thermodynamic quantities - in particular gas pressure and temperature - are tabulated as a function of gas density and internal energy. To ensure accuracy in higher derivatives (like the adiabatic sound speed) analytical first derivatives are tabulated as well.
The tabulated EOS is only used for the computation of the bulk thermodynamic quantities (like gas pressure, temperature, sound speed, specific heats) needed in the hydrodynamical simulations. The electron pressure is not relevant in this context. In contrast, for the post facto spectrum synthesis from selected snapshots, a precise calculation of the electron pressure is important. A more detailed LTE EOS, including the formation of H- and the multiple ionisation of all individual metals, is employed for this purpose.
We emphasise that our finally obtained oxygen abundance is not used to alter the 3D model atmosphere consistently. Besides the substantial computational efforts, we believe that the feedback would be very small, in particular since oxygen is not a significant electron contributor. We tested the feedback in the spectral synthesis: changing the oxygen abundance by 0.1 dex or changing the oscillator strength by 0.1 dex gave line strengths of the 630 nm forbidden oxygen line differing by only 0.1%.
For statistically representing the solar atmosphere, we selected 19 snapshots
equidistantly spaced in time covering in total 1.2 h of solar time. The
snapshots are separated in time enough so that their flow patterns are
largely uncorrelated. They have been further selected to have statistical
properties close to the properties of the whole ensemble of available snapshots.
We restricted
ourselves to a subset of the available 3D data to keep the computational
burden manageable.
Here, in Fig. 1, we only show a comparison of the average CO5BOLD
model with the 3D model used by A04 in their re-determination of the solar oxygen
abundance. The CO5BOLD model was averaged on surfaces of equal Rosseland
optical depth. The Rosseland scale was subsequently transformed to an optical
depth scale at 500 nm in the continuum to allow a direct comparison to the model
published by A04. This is not exactly identical to an averaging on
![]() surfaces as done by A04, but we consider the involved
inconsistencies immaterial for the present discussion. For further comparison
and a benchmark, we added the empirical Holweger-Müller solar
model (Holweger 1967; Holweger & Müller 1974, hereafter HM) to the plot. In the low photospheric layers
(
surfaces as done by A04, but we consider the involved
inconsistencies immaterial for the present discussion. For further comparison
and a benchmark, we added the empirical Holweger-Müller solar
model (Holweger 1967; Holweger & Müller 1974, hereafter HM) to the plot. In the low photospheric layers
(
![]() ), the average CO5BOLD stratification follows the HM model
rather closely. As a consequence, the CO5BOLD model reproduces the observed
solar centre-to-limb variation in the continuum remarkably well (see Ludwig et al. 2008).
In this region the A04 model has a steeper
temperature gradient and becomes gradually cooler than the HM model. Towards
lower optical depth, the CO5BOLD model becomes increasingly cooler than the
HM model, while the A04 model approaches the HM stratification due to the
different mean temperature gradients of the models. In any case, both
hydrodynamical models stay systematically cooler than the HM model. In the
higher photosphere (
), the average CO5BOLD stratification follows the HM model
rather closely. As a consequence, the CO5BOLD model reproduces the observed
solar centre-to-limb variation in the continuum remarkably well (see Ludwig et al. 2008).
In this region the A04 model has a steeper
temperature gradient and becomes gradually cooler than the HM model. Towards
lower optical depth, the CO5BOLD model becomes increasingly cooler than the
HM model, while the A04 model approaches the HM stratification due to the
different mean temperature gradients of the models. In any case, both
hydrodynamical models stay systematically cooler than the HM model. In the
higher photosphere (
![]() ), the CO5BOLD model exhibits larger
temperature fluctuations than the A04 model.
), the CO5BOLD model exhibits larger
temperature fluctuations than the A04 model.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{9885fig1.eps}\end{figure}](/articles/aa/full/2008/36/aa09885-08/Timg22.gif) |
Figure 1: Comparison of the temperature structures of the CO5BOLD model used in this work, the 3D model of A04, and the Holweger-Müller model. For the 3D models the RMS fluctuations (thin lines) around the mean (thick lines) are indicated. |
| Open with DEXTER | |
It is unclear which of the 3D models provides the better representation of the solar photosphere. Nonetheless, we think the differences seen in Fig. 1 provide an estimate of the systematic uncertainties that are present in the current generation of hydrodynamical model atmospheres.
As a reference we also used several 1D LTE plane parallel solar model atmospheres:
The global effect produced by many weak lines is similar to that of an additional continuous opacity. In principle it is possible to do an appropriate ``re-normalisation'' of the spectrum and compare this to a synthetic spectrum computed without including these very weak lines. We tested this procedure with 1D synthetic spectra and found it to be acceptable, at least as a first approximation, introducing errors in the derived abundance of less than 0.01 dex. Therefore our approach has been to use this technique for the 3D analysis, keeping only a minimal number of lines (n < 10) in the computation.
![\begin{figure}
\resizebox{9cm}{!}{\includegraphics[draft = false]
{9885fig2.eps}}\end{figure}](/articles/aa/full/2008/36/aa09885-08/Timg31.gif) |
Figure 2:
The equivalent width contribution function,
dEW/d |
| Open with DEXTER | |
Departures from LTE are non-negligible for several permitted O I
lines, most noticeably for the 777 nm triplet.
At present our 3D-NLTE line formation code
by Steffen & Cayrel (see Cayrel et al. 2007) is not
capable of treating oxygen, and we defer full 3D-NLTE
computations to a future paper.
However, in the case of O I lines, 1D computations
should yield a reliable estimate of departures from LTE.
In fact the line formation range in the solar photosphere
is very similar in 3D and
![]() models, respectively,
for the oxygen triplet (see Fig. 2), and also
for the other infrared oxygen lines.
This is not necessarily valid for other elements and other stellar
models. For instance, 3D-NLTE and 1D-NLTE contribution functions
of the 670.8 nm 7Li line are very different for a metal-poor
model at
models, respectively,
for the oxygen triplet (see Fig. 2), and also
for the other infrared oxygen lines.
This is not necessarily valid for other elements and other stellar
models. For instance, 3D-NLTE and 1D-NLTE contribution functions
of the 670.8 nm 7Li line are very different for a metal-poor
model at
![]() = 6240 K,
= 6240 K,
![]() = 4.0,
= 4.0,
![]() = -2.0 (Cayrel et al. 2007).
Even if the mean vertical stratification of oxygen is very similar
in 1D and 3D, horizontal inhomogeneities could introduce a difference between
1D and 3D NLTE corrections. The error due to the 1D approximation needs
to be quantified by future detailed 3D-NLTE calculations.
= -2.0 (Cayrel et al. 2007).
Even if the mean vertical stratification of oxygen is very similar
in 1D and 3D, horizontal inhomogeneities could introduce a difference between
1D and 3D NLTE corrections. The error due to the 1D approximation needs
to be quantified by future detailed 3D-NLTE calculations.
The similarity between NLTE corrections computed in 1D and 3D is confirmed by the results in Table 2 of A04. We suspect that the two corrections would have been even closer if the authors had used a model with the mean temperature structure of their 3D model as a background model for their 1D-NLTE computations.
For the present paper we decided to compute 1D-NLTE corrections
based on the
![]() model (rather than on
model (rather than on
![]() )
and to
use the Kiel code (Steenbock & Holweger 1984), together with the oxygen
model atom described in Paunzen et al. (1999).
We also compared our NLTE corrections with those
computed by Holweger (2001) and A04.
)
and to
use the Kiel code (Steenbock & Holweger 1984), together with the oxygen
model atom described in Paunzen et al. (1999).
We also compared our NLTE corrections with those
computed by Holweger (2001) and A04.
Table 2: Ni I isotopic splitting.
There are several high-resolution, high signal-to-noise
ratio (S/N) spectra both of the solar flux and of
the disc-centre intensity, and we decided to make use
of all of them. The choice of using more than one solar atlas
stems the fact that, even if S/N is very high for solar spectra,
the abundances obtained from different spectra do not always
agree within one ![]() ,
highlighting the existence of systematic
differences, which are not fully understood.
,
highlighting the existence of systematic
differences, which are not fully understood.
Considering the six oxygen lines at 630, 636, 777 and 844 nm,
we measure the following wavelength shifts, with respect to
the laboratory wavelengths:
for the Kurucz flux ![]()
![]() ,
for the Neckel flux
,
for the Neckel flux
![]()
![]() and
for the Delbouille intensity
and
for the Delbouille intensity
![]()
![]() .
Our results are in good agreement with the Allende Prieto & Garcia Lopez (1998)
data that present a
.
Our results are in good agreement with the Allende Prieto & Garcia Lopez (1998)
data that present a ![]() of 238
of 238
![]() with an average of 286
with an average of 286
![]() for iron lines in the Neckel flux spectrum.
for iron lines in the Neckel flux spectrum.
It is not the purpose of the present paper to investigate the convective shifts of oxygen lines. What we did want to do was point out the systematic differences in absolute wavelengths between the various solar atlases. This makes it mandatory to leave the wavelength shift as a free parameter when performing line-profile fitting.
To derive oxygen abundances, we measured the equivalent width (EW) of the oxygen lines and, when possible, fitted the line profile. EWs were computed by direct numerical (trapezoidal) integration or by integration of a fitted Gaussian or Voigt profile, using the IRAF task splot. The results are summarised in Table 3.
All line profile fitting was performed through ![]() minimisation
using the code described in Caffau et al. (2005).
Besides the oxygen abundance, the level
of the continuum and a wavelength shift were also left as free parameters
in the fitting procedure.
For 1D models, the macro turbulence has to be fixed a priori.
The whole line profile or only a selected range can be fitted,
as was done, for example, for the 926 nm line because of the
presence of a residual of a telluric line in one of the wings.
minimisation
using the code described in Caffau et al. (2005).
Besides the oxygen abundance, the level
of the continuum and a wavelength shift were also left as free parameters
in the fitting procedure.
For 1D models, the macro turbulence has to be fixed a priori.
The whole line profile or only a selected range can be fitted,
as was done, for example, for the 926 nm line because of the
presence of a residual of a telluric line in one of the wings.
A change in the Van der Waals broadening constant ![]() ,
input to the line formation code, can produce lines with different
shapes (more or less broadened) but also of different EW.
For instance if we change the
,
input to the line formation code, can produce lines with different
shapes (more or less broadened) but also of different EW.
For instance if we change the
![]() of the 636 nm [OI] line
from the standard input value for Linfor3D -8.145to the value of -8.364provided by the WIDTH approximation (Ryan 1998),
the difference in EW is 0.2%.
Considering the oxygen triplet, the EW increases by
4% to 5% (depending on the oxygen abundance)
if we change the
of the 636 nm [OI] line
from the standard input value for Linfor3D -8.145to the value of -8.364provided by the WIDTH approximation (Ryan 1998),
the difference in EW is 0.2%.
Considering the oxygen triplet, the EW increases by
4% to 5% (depending on the oxygen abundance)
if we change the
![]() from -7.57 as derived
from ABO theory
to -7.74 as obtained from the WIDTH approximation.
We adopted the following strategy. For the transitions for
which the broadening data were available from ABO
we computed the
from -7.57 as derived
from ABO theory
to -7.74 as obtained from the WIDTH approximation.
We adopted the following strategy. For the transitions for
which the broadening data were available from ABO
we computed the
![]() according to the ABO theory; when not available,
we used the WIDTH approximation that is the one also used inside
the SYNTHE code. We point out that, contrary to naive expectations,
the broadening effect is not completely negligible for
weak lines, as also pointed out by Ryan (1998).
In the 615 nm line, for instance, a change
in
according to the ABO theory; when not available,
we used the WIDTH approximation that is the one also used inside
the SYNTHE code. We point out that, contrary to naive expectations,
the broadening effect is not completely negligible for
weak lines, as also pointed out by Ryan (1998).
In the 615 nm line, for instance, a change
in
![]() of 0.16 dex, from -7.164 to -7.004,
produces, for an oxygen abundance of 8.66, a difference in EW of 1%.
In contrast, the [OI] lines are insensitive to the value
adopted for
of 0.16 dex, from -7.164 to -7.004,
produces, for an oxygen abundance of 8.66, a difference in EW of 1%.
In contrast, the [OI] lines are insensitive to the value
adopted for
![]() .
.
Concerning the quadratic Stark broadening, even strong lines,
such as the oxygen triplet lines, are not very sensitive to the parameter ![]() .
In fact a change by a factor 2 in
.
In fact a change by a factor 2 in ![]() produces
a change in the strongest line of the triplet
of
-0.01+0.006 dex in the oxygen abundance
according to WIDTH combined with the ATLAS model.
Even the shape of the line is affected by this change very little,
only the wings being appreciably different in the synthetic spectra.
produces
a change in the strongest line of the triplet
of
-0.01+0.006 dex in the oxygen abundance
according to WIDTH combined with the ATLAS model.
Even the shape of the line is affected by this change very little,
only the wings being appreciably different in the synthetic spectra.
Table 3: Solar LTE oxygen abundance for individual lines as derived from different spectra and model atmospheres.
Since the emphasis of this work is on the 3D analysis, we analysed all the observed spectra with CO5BOLD+Linfor3D. For comparison we considered the 1D computations for EWs for all the observed spectra, but we mostly limited the 1D line-profile fitting to the Kurucz flux, when available, or to the Delbouille intensity.
As in Caffau & Ludwig (2007), we defined the ``3D corrections'' as
the difference A(O)![]() - A(O)
- A(O)
![]() ,
because the 3D effect is best captured when comparing
the 3D and the
,
because the 3D effect is best captured when comparing
the 3D and the
![]() models (which share the
same input physics) and using the same line formation code,
Linfor3D. The resulting ``3D corrections'' depend
on the choice of both the mixing-length parameter,
models (which share the
same input physics) and using the same line formation code,
Linfor3D. The resulting ``3D corrections'' depend
on the choice of both the mixing-length parameter,
![]() ,
and the micro-turbulence parameter,
,
and the micro-turbulence parameter, ![]() ,
necessary for defining
the 1D model. The micro-turbulence is only important for the
stronger lines, in our case the triplet lines.
In this study we considered two values of the micro-turbulence,
,
necessary for defining
the 1D model. The micro-turbulence is only important for the
stronger lines, in our case the triplet lines.
In this study we considered two values of the micro-turbulence,
![]() and 1.5
and 1.5
![]() (see Table 3).
Apart from the triplet lines, the difference
in abundance when considering the two
(see Table 3).
Apart from the triplet lines, the difference
in abundance when considering the two ![]() is at most 0.02 dex.
For the triplet, a different choice in
is at most 0.02 dex.
For the triplet, a different choice in ![]() is translated into
a change in the 1D abundance by up to 0.04 dex.
Higher micro-turbulence produces stronger lines in synthetic spectra,
so that the oxygen abundance obtained is lower.
In the present work we gave preference to
is translated into
a change in the 1D abundance by up to 0.04 dex.
Higher micro-turbulence produces stronger lines in synthetic spectra,
so that the oxygen abundance obtained is lower.
In the present work we gave preference to ![]()
![]() .
Concerning the
.
Concerning the
![]() model for the mixing-length parameter, we took
model for the mixing-length parameter, we took
![]() .
Most of the lines are formed in layers that are not
strongly affected by convection, hence by the choice of the mixing-length parameter.
However, this is not true for the 615 nm line, which is formed in deep
photospheric layers.
For testing this aspect, we considered three representative lines: the
strongest line of the triplet at
777.1 nm, the stronger forbidden line at 630 nm, and the line at 615 nm.
We changed the mixing-length parameter by
+1.0-0.5 with respect to our
preferred
value of 1.0. With this change in
.
Most of the lines are formed in layers that are not
strongly affected by convection, hence by the choice of the mixing-length parameter.
However, this is not true for the 615 nm line, which is formed in deep
photospheric layers.
For testing this aspect, we considered three representative lines: the
strongest line of the triplet at
777.1 nm, the stronger forbidden line at 630 nm, and the line at 615 nm.
We changed the mixing-length parameter by
+1.0-0.5 with respect to our
preferred
value of 1.0. With this change in
![]() ,
the change in the
,
the change in the
![]() oxygen abundance (for fixed equivalent width in the synthetic flux
spectra)
for the forbidden and the triplet line is small
-0.003+0.011 for the
forbidden line and
-0.003+0.018 for the triplet line.
In contrast, we find a change in abundance of
-0.045+0.080 for the 615 nm line.
This clearly indicates that, for some lines, the 3D-1D
corrections depend on the mixing-length parameter assumed in the 1D
comparison model.
oxygen abundance (for fixed equivalent width in the synthetic flux
spectra)
for the forbidden and the triplet line is small
-0.003+0.011 for the
forbidden line and
-0.003+0.018 for the triplet line.
In contrast, we find a change in abundance of
-0.045+0.080 for the 615 nm line.
This clearly indicates that, for some lines, the 3D-1D
corrections depend on the mixing-length parameter assumed in the 1D
comparison model.
For completeness, we also provide differences using other 1D models, either with Linfor3D or with SYNTHE. We point out, however, that these differences also depend on code specific disparities such as different opacities, partition functions, radiative transfer schemes, etc, and thus serve mainly to illustrate the magnitude of systematic modelling uncertainties.
Besides the fact that Holweger (2001) computed 1D-non-LTE and A04 3D-non-LTE, the differences in the two NLTE computations is the way in which excitation and ionisation by inelastic collisions with hydrogen atoms is accounted for. Holweger (2001) accounts for them by using the formalism of Steenbock & Holweger (1984), which is a generalisation of the one in Drawin (1969). A04 instead totally ignore them.
The two reasons favouring ignoring collisions
with hydrogen atoms are (i) the larger cross-section
for collisions with electrons and (ii) the fact that
electrons have much higher velocities, thereby making
collisions with ![]() far more frequent.
On the other hand, the ratio of hydrogen atoms
to electrons is often as high as 104 or even 105.
Under these circumstances, it appears difficult to deny
the role of collisions with hydrogen atoms.
far more frequent.
On the other hand, the ratio of hydrogen atoms
to electrons is often as high as 104 or even 105.
Under these circumstances, it appears difficult to deny
the role of collisions with hydrogen atoms.
In our solar model,
![]() is almost flat at 104 in the
outer layers, it is about
is almost flat at 104 in the
outer layers, it is about
![]() at
at
![]() and then drops dramatically
to
and then drops dramatically
to ![]() 70 at
70 at
![]() .
One should therefore expect that the role of collisions
with hydrogen atoms is different for lines having
different line formation depths.
.
One should therefore expect that the role of collisions
with hydrogen atoms is different for lines having
different line formation depths.
Since the Steenbock & Holweger (1984) formalism is the only
practical way to include the effects of collisions
with hydrogen atoms,
it has become customary in NLTE codes to adopt it
and to introduce the scaling factor
![]() .
A zero value for this scaling factor is equivalent
to ignoring the process.
For some species, like Na and Li, for which laboratory data
exist, it is known that the classical Drawin formula (Drawin 1969)
leads to overestimating the collisional rates
(see Asplund et al. 2004, and references therein).
Unfortunately, no laboratory data exists for collisions of neutral
hydrogen with oxygen. Inspection
of the literature shows that very different choices for
.
A zero value for this scaling factor is equivalent
to ignoring the process.
For some species, like Na and Li, for which laboratory data
exist, it is known that the classical Drawin formula (Drawin 1969)
leads to overestimating the collisional rates
(see Asplund et al. 2004, and references therein).
Unfortunately, no laboratory data exists for collisions of neutral
hydrogen with oxygen. Inspection
of the literature shows that very different choices for
![]() are made for different species.
For example Gehren et al. (2001) advocate
are made for different species.
For example Gehren et al. (2001) advocate
![]() for Fe I
in the Sun.
for Fe I
in the Sun.
Allende Prieto et al. (2004) have used the centre-to-limb variations of
the 777 nm O I triplet to constrain the role
of collisions with hydrogen atoms.
Their ![]() analysis of synthetic NLTE profiles computed
from their 3D hydrodynamical simulation favours
analysis of synthetic NLTE profiles computed
from their 3D hydrodynamical simulation favours
![]() .
In several papers the Kiel group has adopted
.
In several papers the Kiel group has adopted
![]() (Stürenburg & Holweger 1991; Solanki & Steenbock 1988; Stürenburg & Holweger 1990),
mainly based on the unpublished work of Steenbock.
In the present paper we present NLTE corrections
for
(Stürenburg & Holweger 1991; Solanki & Steenbock 1988; Stürenburg & Holweger 1990),
mainly based on the unpublished work of Steenbock.
In the present paper we present NLTE corrections
for
![]() and discuss the implications.
and discuss the implications.
We here consider the possible errors that affect the analysis
of the oxygen abundance in each line.
We will take the following errors into account for each line:
``
![]() error'', ``broadening theory error'',
``blending error'', ``NLTE correction error'', ``statistical error''.
error'', ``broadening theory error'',
``blending error'', ``NLTE correction error'', ``statistical error''.
The uncertainties are summarised in Table 4. The column ``total error'' of this table considers the global uncertainty that we attribute to each line. This value is the quadratic sum of all the uncertainties. The error related to the NLTE computations is not included in Table 4 because it is considered as a systematic error. Details of the derived NLTE corrections are instead listed in Table 5.
In this section we give the details of the analysis of each of the considered transitions. The results are summarised in Tables 3 and 4. Initially, we also considered the 557 nm forbidden line, but discarded it because both the Delbouille intensity and the Kurucz flux show an asymmetry in the line profile, caused by the presence of C2 lines, as pointed out by Lambert (1978). Unfortunately the molecular data for these C2 lines is still not of sufficient quality to allow a reliable synthesis of the profile.
Table 4: Oxygen LTE abundance for each line with the error estimates.
This weak line (see Fig. 3) arises from the ground level
and is immune to departures from LTE, so it has
always been considered a primary indicator of the photospheric
oxygen abundance. However, it is blended with an Ni I line and
lies next to two stronger lines![]() ,
whose wings can influence the EW of the oxygen line if not
taken into account properly.
In Fig. 4 the contribution of nickel is
compared to the blend [O I]+Ni I
according to a 3D synthetic spectrum.
,
whose wings can influence the EW of the oxygen line if not
taken into account properly.
In Fig. 4 the contribution of nickel is
compared to the blend [O I]+Ni I
according to a 3D synthetic spectrum.
![\begin{figure}
\resizebox{9cm}{!}{\includegraphics[clip=true,angle=0]{9885fig3.eps}}\end{figure}](/articles/aa/full/2008/36/aa09885-08/Timg70.gif) |
Figure 3: The four observed spectra we used for the analysis of the [O I] 630 nm line. The Kurucz flux spectrum, KF, and the Neckel flux, NF, and Neckel intensity, NI, spectra plotted here are the normalised spectra provided by Kurucz (2005a) and Neckel (1999); the NI is shifted up by 0.1 for clarity, while the Delbouille intensity, DI, has been normalised and then shifted up by 0.1. The vertical line indicates the laboratory wavelength of the oxygen line. We recall that KF is corrected for gravitational redshift while NF is not, explaining the large wavelength differences between the two flux atlases. |
| Open with DEXTER | |
![\begin{figure}
\resizebox{9cm}{!}{\includegraphics[clip=true,angle=0]{9885fig4.eps}}\end{figure}](/articles/aa/full/2008/36/aa09885-08/Timg71.gif) |
Figure 4: The contribution of Ni I line (dashed line) with A(Ni) = 6.25 is compared to the combined [O I]+Ni I blend (solid line) for disc-centre according to the Linfor3D computation with A(O) = 8.66. |
| Open with DEXTER | |
The blending nickel line exhibits a complex isotopic structure
(see Table 2).
The two main components are 58Ni I and 60Ni I,
with an isotopic ratio of 0.38
and ![]() of 630.0335 nm and 630.0355 nm,
respectively (see Bensby et al. 2004).
Each component of the nickel blend is assumed to have
of 630.0335 nm and 630.0355 nm,
respectively (see Bensby et al. 2004).
Each component of the nickel blend is assumed to have
![]() = -2.11(Johansson et al. 2003).
The two other even isotopic components, 62Ni I
and 64Ni I, can be inserted in the line list as well,
even if this does not change the line shape significantly,
assuming that their shift with respect to the other even components
has the same value as the shift between 58Ni I
and 60Ni I (about 0.002 nm, see Rosberg et al. 1993).
Rosberg et al. (1993) studied the isotope splitting of the even components of
Ni II and showed that the splitting is equidistant for
any of the even components of Ni II they studied.
We assume the same behaviour for Ni I.
We adopted A(Ni) = 6.25 (Grevesse & Sauval 1998) and consider it as a fixed parameter
in the oxygen abundance determination.
= -2.11(Johansson et al. 2003).
The two other even isotopic components, 62Ni I
and 64Ni I, can be inserted in the line list as well,
even if this does not change the line shape significantly,
assuming that their shift with respect to the other even components
has the same value as the shift between 58Ni I
and 60Ni I (about 0.002 nm, see Rosberg et al. 1993).
Rosberg et al. (1993) studied the isotope splitting of the even components of
Ni II and showed that the splitting is equidistant for
any of the even components of Ni II they studied.
We assume the same behaviour for Ni I.
We adopted A(Ni) = 6.25 (Grevesse & Sauval 1998) and consider it as a fixed parameter
in the oxygen abundance determination.
The observed solar spectra were renormalised
in order to remove the silicon and iron contributions, and
the EW of the observed spectra were computed with the program
splot. The oxygen abundances obtained from the curve-of-growth
computed with Linfor3D are reported in Table 3.
Note that the abundance obtained from HM+Linfor3D is only
slightly higher by ![]() 0.015 dex. On the other hand,
both 1D ATLAS and MARCS models, in combination with
the WIDTH line formation code, imply a
lower oxygen abundance by 0.03 dex.
In this respect both MARCS and ATLAS models
behave in a similar way to the LHD model.
As can be deduced from Table 3,
the difference 3D-
0.015 dex. On the other hand,
both 1D ATLAS and MARCS models, in combination with
the WIDTH line formation code, imply a
lower oxygen abundance by 0.03 dex.
In this respect both MARCS and ATLAS models
behave in a similar way to the LHD model.
As can be deduced from Table 3,
the difference 3D-
![]() is considerably smaller than
the difference 3D-
is considerably smaller than
the difference 3D-
![]() ,
meaning that the latter difference
is dominated by the different mean temperature structures
rather than by horizontal temperature fluctuations.
,
meaning that the latter difference
is dominated by the different mean temperature structures
rather than by horizontal temperature fluctuations.
We disagree on the sign of the 3D-1D correction for this
line with what was previously found by A04,
whose results
imply a 3D correction A(O)![]() - A(O)
- A(O)
![]() of
-0.04 dex for the flux, while we find a value of +0.03 dex (see
above).
Our 3D correction for this line is about +0.05 dex for the flux and +0.07 dex
for the intensity spectra. The influence of the micro-turbulence is completely
negligible for this line.
of
-0.04 dex for the flux, while we find a value of +0.03 dex (see
above).
Our 3D correction for this line is about +0.05 dex for the flux and +0.07 dex
for the intensity spectra. The influence of the micro-turbulence is completely
negligible for this line.
From this line, fixing A(Ni) = 6.25, the 3D oxygen abundance is
![]() if we consider all four spectra. If we consider only
the two flux spectra A(O)
if we consider all four spectra. If we consider only
the two flux spectra A(O)
![]() ,
and A(O)
,
and A(O)
![]() from the two disc-centre spectra.
Fitting the line profile of the solar intensity and flux
spectra with a CO5BOLD+Linfor3D grid of synthetic spectra, we obtain an
oxygen abundance which perfectly agrees with the results
from the EWs (Table 3) within 0.01 dex
(see Fig. 5).
from the two disc-centre spectra.
Fitting the line profile of the solar intensity and flux
spectra with a CO5BOLD+Linfor3D grid of synthetic spectra, we obtain an
oxygen abundance which perfectly agrees with the results
from the EWs (Table 3) within 0.01 dex
(see Fig. 5).
Even if not able to reproduce the line shape satisfactorily, the 1D fits agree with the 3D results, further supporting the notion that the 3D correction is small. The line fit using SYNTHE slightly underestimates the oxygen abundance (HM model A(O) = 8.67, MARCS model A(O) = 8.65 ATLAS model A(O) = 8.61), in agreement with the above result based on matching the EW with 1D models.
![\begin{figure}
\resizebox{9cm}{!}{\includegraphics[clip=true,angle=0]{9885fig5.eps}}\end{figure}](/articles/aa/full/2008/36/aa09885-08/Timg78.gif) |
Figure 5: The 3D fit of the [OI] 630 nm line. The observed spectra (diamonds, their size indicating the observational noise level) are superimposed on the best fit 3D synthetic line profile (solid). From top to bottom, the spectra are: Delbouille intensity (DI), Neckel intensity (NI), Neckel flux (NF), and Kurucz flux (KF). |
| Open with DEXTER | |
Since this oxygen line is blended with the neutral nickel line, a possible approach is to use a multi parameter fit, with oxygen and nickel abundance, wavelength shift, and continuum level as free parameters. We attempted this, but the result was not satisfactory because wavelength shift and nickel abundance turned out to be closely correlated parameters, thus producing a range of degenerate solutions for the best fit. However, if the wavelength scale can be established by other methods, the degeneracy is removed and both the nickel and the oxygen abundance can be found from line fitting (see Ayres 2008, and Sect. 6 below).
Since an error in the parameters of the nickel line
introduces an error of the oxygen abundance,
we computed two additional 3D grids
where we varied the Ni I abundance by ![]() dex
with respect to its fiducial value of 6.25.
Noting that the error of the solar nickel abundance is 0.04 dex (Grevesse & Sauval 1998),
and the error of the
dex
with respect to its fiducial value of 6.25.
Noting that the error of the solar nickel abundance is 0.04 dex (Grevesse & Sauval 1998),
and the error of the
![]() value of this line is
0.06 dex (Johansson et al. 2003), a variation of
value of this line is
0.06 dex (Johansson et al. 2003), a variation of ![]() dex in the
strength of the nickel line takes the possible uncertainties into account.
Our evaluation of the systematics induced in the oxygen abundance shows
that a difference of
dex in the
strength of the nickel line takes the possible uncertainties into account.
Our evaluation of the systematics induced in the oxygen abundance shows
that a difference of ![]() in the nickel abundance produces a
difference in the oxygen abundance of
-0.03+0.05
(resulting in A(O) = 8.66, 8.74 respectively) in the fitting of the Kurucz flux.
Similar values are obtained for the Delbouille intensity
(a
in the nickel abundance produces a
difference in the oxygen abundance of
-0.03+0.05
(resulting in A(O) = 8.66, 8.74 respectively) in the fitting of the Kurucz flux.
Similar values are obtained for the Delbouille intensity
(a ![]() change in nickel implies
change in nickel implies ![]() change in oxygen abundance).
change in oxygen abundance).
Our adopted oxygen abundance for this line comes from the average value
of the four observed spectra, and it is
A(O) =
![]() (see Table 4 for details).
The systematic error is the quadratic sum of the
(see Table 4 for details).
The systematic error is the quadratic sum of the
![]() error and the error related to blends and uncertainties in
the continuum placement.
The error due to the broadening theory is completely negligible for this
line, being of the order of 10-4 dex.
The final result is A(O) =
error and the error related to blends and uncertainties in
the continuum placement.
The error due to the broadening theory is completely negligible for this
line, being of the order of 10-4 dex.
The final result is A(O) =
![]() .
.
This line lies on the red wing of a Ca I auto-ionisation line (see Fig. 6). Several CN lines are present in the range. For C and N abundances we adopted 8.39 and 7.80, respectively. Their contribution to the EW of the [OI] 636 line, according to our ATLAS+SYNTHE synthesis, is 0.05 pm in flux and 0.03 pm in intensity. With a CO5BOLD+Linfor3D synthetic spectrum, the CN molecules happen to come out stronger by 20% with respect to the 1D ATLAS+SYNTHE result. This implies a difference of only 0.002 dex in the derived oxygen abundance, which is far from being able to explain the 0.1 dex difference between the oxygen abundance provided by this line (see below) and that of the 630 nm forbidden line (see Table 3).
At first we tried to remove the contribution of all the blending lines by dividing the observed spectrum by a 1D synthetic spectrum computed with all relevant atomic and molecular lines (including the Ca I auto-ionisation line) except oxygen. We obtained an oxygen abundance (A(O) = 8.78), inconsistent with what was derived from the other forbidden line (A(O) = 8.68). This is at variance with what was found by A04, according to their analysis, the difference in abundance is only 0.02 dex. This can stem from the differences in the EWs. But a difference of 0.06 pm in EW for this line can hardly explain the difference in A(O). A difference must rely on the spectral-synthesis code used in the two analysis. Next, we normalised the spectrum following the profile of the Ca I auto-ionisation line. From the EW measured from this normalised spectrum, we subtracted the contribution due to CN molecules and obtained the oxygen abundances reported in Table 3. Our oxygen abundance for this line relies therefore only on the EW approach.
We point out that the three spectra observed from Kitt Peak (Neckel and Kurucz) imply a higher oxygen abundance than the one observed from the Jungfraujoch (Delbouille). Moreover, for the [OI] 630 nm line there is also a difference between the two intensities: in the Neckel intensity spectrum the line is stronger than in the Delbouille spectrum, even if the effect is less evident. We considered the hypothesis that the difference in height above sea level of the two sites could have induced a higher telluric contribution in the spectra taken at the site of lower elevation. But since there is no evidence of a telluric contribution from the inspection of spectra taken at different air mass, we discarded this hypothesis. More likely, the differences in the spectra might be related to different levels of solar activity at the time of the respective observations (cf. Livingston et al. 2007).
The fact that the oxygen abundance derived from the two forbidden lines clearly does not agree is disturbing. Obviously, deficiencies in the solar model atmospheres cannot be responsible. In fact, 3D and HM show a similar discrepancy (see Table 3). Presumably, the problem is related to our imperfect knowledge of the blend line contributions. A possible solution is offered by the work of Ayres (2008).
![\begin{figure}
\resizebox{9cm}{!}{\includegraphics[clip=true,angle=0]{9885fig6.eps}}\end{figure}](/articles/aa/full/2008/36/aa09885-08/Timg83.gif) |
Figure 6: The Kurucz flux spectrum around the [OI] 636.378 nm line with the identification of the stronger lines. |
| Open with DEXTER | |
Our adopted oxygen abundance for this line, taking
all the measurements into account, is
![]() ,
which is A(O) =
,
which is A(O) =
![]() (see Table 4 for details).
(see Table 4 for details).
![\begin{figure}
\resizebox{9cm}{!}{\includegraphics[clip=true,angle=0]{9885fig7.eps}}\end{figure}](/articles/aa/full/2008/36/aa09885-08/Timg86.gif) |
Figure 7: The O I 615 nm Mult. 10 lines in the four observed spectra used in this work. Symbols are as in Fig. 3. The three vertical lines indicate the laboratory wavelength of the lines. |
| Open with DEXTER | |
These lines of Mult. 10 lie in a very complex spectral region (see Fig. 7), close to a rather strong iron line and in the range of many CN lines, which make the continuum placement problematic. The EW was measured using the de-blending capability of splot, with which we accounted for the presence of the neighbouring Fe I line. The EW is very sensitive to the placement of the continuum. The oxygen abundance is then obtained from matching this EWwith the 3D curve-of-growth.
Our adopted LTE oxygen abundance for this line is 8.63 for the disc-centre spectra and 8.64 for the flux spectra. For both disc-centre and flux we estimate a global systematic error of 0.21 dex, while the statistical error is 0.01 for flux and 0.03 for intensity (see Table 4 for details). We neglect any possible error related to the molecular data because we think they are included in the error associated with the continuum level placement.
The
![]() results overestimate the oxygen abundance by
about +0.03 dex (flux); in other words, the 3D correction
is negative, -0.03 dex.
Only for this line do we find a negative 3D correction, and this is
a consequence of
the effect of horizontal temperature fluctuations, 3D-
results overestimate the oxygen abundance by
about +0.03 dex (flux); in other words, the 3D correction
is negative, -0.03 dex.
Only for this line do we find a negative 3D correction, and this is
a consequence of
the effect of horizontal temperature fluctuations, 3D-
![]() ,
being appreciable only in this case. This, in turn, is a consequence of the high
excitation potential of this line, which implies that it forms in the
deep photosphere and is highly sensitive to temperature fluctuations.
,
being appreciable only in this case. This, in turn, is a consequence of the high
excitation potential of this line, which implies that it forms in the
deep photosphere and is highly sensitive to temperature fluctuations.
Using the Holweger-Müller model, the oxygen abundance is even 0.14 dex higher than the 3D result. For comparison, the corresponding abundance difference is 0.12 dex for ATLAS+WIDTH, and 0.06 dex for MARCS+WIDTH.
Figure 8 shows the EW contribution function
(following Magain 1986)
of the 3D disc-centre synthetic spectrum for the 615.8 nm line
in comparison with the 630.0 nm and 777.1 nm
lines, together with the temperature structures
of the 3D and
![]() models.
The 615.8 nm line is formed deep inside the photosphere.
models.
The 615.8 nm line is formed deep inside the photosphere.
![\begin{figure}
\resizebox{9cm}{!}{\includegraphics[clip=true,angle=0]{9885fig8.eps}}\end{figure}](/articles/aa/full/2008/36/aa09885-08/Timg87.gif) |
Figure 8:
The average temperature profile (left ordinate) of the 3D model
(solid line) and the temperature profile of the
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[clip=15cm,clip]{9885fig9.eps}\end{figure}](/articles/aa/full/2008/36/aa09885-08/Timg88.gif) |
Figure 9: The O I 777 nm triplet in the four observed spectra used in this work. Symbols are as for Fig. 3. |
| Open with DEXTER | |
Table 5:
NLTE corrections for all the lines,
for different values of ![]() ,
the corrections
from Holweger (2001) and A04 for comparison.
,
the corrections
from Holweger (2001) and A04 for comparison.
For the 1D synthetic spectra we have the possibility of including all the relevant atomic and molecular lines and thus perform line profile fitting. We performed this exercise only on the Kurucz flux: an ATLAS+SYNTHE grid provides A(O) = 8.75. This result is consistent with those based on EW measurements as reported above.
The abundance derived from this line is uncertain because the continuum placement is difficult and the atomic parameters of the blend lines in the range are not well known. We note that Holweger (2001) has discarded this line in his analysis of the solar oxygen abundance. We decided to keep it among possible oxygen abundance indicators, although the large associated error gives it a low weight.
These three strong lines (see Fig. 9) lie in a clean region of the spectrum and do not suffer any blending from other atomic or molecular lines or any telluric absorption. The strength of these lines places them on the saturation part of the curve-of-growth, which, however, is not really flat and still provides a reasonable abundance sensitivity for these lines. The lines have relatively extended wings, such that the wings of neighbouring lines overlap. The EW of each line is affected by this effect by 1% to 2.5% (the 777.4 nm line being the most affected). The triplet lines arise from a high excitation level (9.146 eV) and are very sensitive to departures from LTE. From Table 3 it is evident that the LTE oxygen abundance obtained from CO5BOLD+Linfor3D for the three lines is greater for the fluxes than for the intensities, which is consistent with the fact that NLTE corrections are greater for flux than for intensity (see Table 5).
The 3D correction (expected to be similar in LTE and NLTE) is
about +0.05 dex for flux and +0.10 dex for intensity (assuming a
micro-turbulence ![]()
![]() ).
ATLAS+WIDTH implies the same abundances as CO5BOLD+Linfor3D, while the
abundances using the MARCS model are 0.06 dex lower.
Therefore we conclude, as for that of the forbidden lines,
that the direction of our 3D correction is opposite
to what is found by A04
using the MARCS solar model
as the 1D reference: while we find A(3D)-A(1D
).
ATLAS+WIDTH implies the same abundances as CO5BOLD+Linfor3D, while the
abundances using the MARCS model are 0.06 dex lower.
Therefore we conclude, as for that of the forbidden lines,
that the direction of our 3D correction is opposite
to what is found by A04
using the MARCS solar model
as the 1D reference: while we find A(3D)-A(1D
![]() ) = +0.06,
they find A(3D)-A(1D
) = +0.06,
they find A(3D)-A(1D
![]() ) = -0.06.
) = -0.06.
Since the lines are on the saturation part of the
curve-of-growth, they are sensitive to the
micro-turbulence ![]() adopted in the 1D analysis.
The difference due to a change from 1.0
adopted in the 1D analysis.
The difference due to a change from 1.0
![]() to 1.5
to 1.5
![]() produces a difference of -0.04 dex
(for 777.1 nm) in both
produces a difference of -0.04 dex
(for 777.1 nm) in both
![]() and
and
![]() models.
models.
The fit of the line profile is problematic. The shape of the line is affected by NLTE effects (A04), so even the CO5BOLD+Linfor3D LTE synthetic spectra cannot reproduce the shape of the observed line very well, which is narrower than the synthetic spectra. For this reason our abundance analysis for these lines relies on EWs and not on line profile fitting.
Our adopted LTE oxygen abundances for the three
lines of the triplet as obtained by matching the measured
EWs with the 3D curve-of-growth are the following
(see Tables 3 and 4 for details).
From flux spectra:
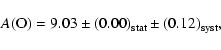
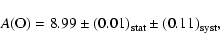
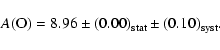
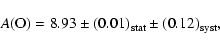
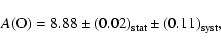
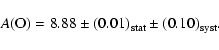
![\begin{figure}
\resizebox{9cm}{!}{\includegraphics[clip=true,angle=0]{9885fig10.eps}}\end{figure}](/articles/aa/full/2008/36/aa09885-08/Timg97.gif) |
Figure 10: The O I 844 nm line in the four observed spectra used in this work. Symbols are as for Fig. 3. The vertical line indicates the laboratory wavelength position of the line. |
| Open with DEXTER | |
This line (see Fig. 10) is blended mainly by an iron line for which the atomic data are not well known. Also in this case we tried to divide the observed spectrum by a 1D ATLAS+SYNTHE synthetic one. The spectrum obtained, should only contain oxygen, has a shape that does not agree with the CO5BOLD+Linfor3D synthetic line profile on the blue side, where the Fe I blend line lies, but the agreement is good on the red side.
A de-blending EW computation is not always stable,
however our ``de-blended'' EW provides
an oxygen abundance in the range 8.80 to 8.84,
depending on the observed spectrum considered.
That an over-plot of the observed spectrum, ``as is'' with the
CO5BOLD+Linfor3D synthetic spectra suggests a value of 8.86 for
the oxygen abundance and suggests that a fit with the CO5BOLD+Linfor3D grid avoiding the blue wing gives A(O) = 8.80,
indicates that our EW is nevertheless useful for the abundance
determination (see Table 3).
The 3D correction is +0.03 dex for flux and +0.07 dex
for disc-centre intensity (![]()
![]() ).
).
Using a 1D ATLAS+SYNTHE grid, we fitted both the observed Kurucz flux spectrum ``as is'' and the ``divided-out'' spectrum containing only the oxygen line (obtained by dividing by a synthetic spectrum of only the blend lines), and obtained A(O) = 8.79 and 8.73, respectively. Using a 1D HM+SYNTHE grid in the same way, we obtained instead A(O) = 8.82 and 8.76, respectively.
Our adopted LTE oxygen abundance from this line is:
A(O) =
![]() from the flux spectra,
and
A(O) =
from the flux spectra,
and
A(O) =
![]() from disc-centre
intensity spectra (see Table 4 for details).
from disc-centre
intensity spectra (see Table 4 for details).
![\begin{figure}
\resizebox{9cm}{!}{\includegraphics[clip=true,angle=0]{9885fig11.eps}}\end{figure}](/articles/aa/full/2008/36/aa09885-08/Timg100.gif) |
Figure 11: The observed Delbouille (DI) and Wallace (WI) disc-centre intensity spectra of the O I 926 nm line. |
| Open with DEXTER | |
In the Kurucz flux spectrum, as in the Neckel flux and intensity spectra,
the O I 926 nm line is contaminated by a telluric line.
The intensity spectra of Delbouille (see Fig. 11) and Wallace
have been processed to subtract the telluric contribution.
The subtraction is probably not completely
successful, since the profile still shows some distortion.
Nevertheless, the spectra can be fitted reasonably well. Although the
Delbouille spectrum has a higher signal-to-noise (about 5000), the
Wallace spectrum (S/N about 500) shows less residual distortion after
the subtraction of the telluric line. For this reason
the EW was only computed from the Wallace intensity spectrum,
providing an oxygen abundance of A(O) = 8.75 in 3D.
The 3D correction in this case is +0.06 dex (![]()
![]() ).
).
We also did line-fitting restricted to a range that excludes the
portion of the line that is affected by the telluric absorption.
The fit of the Delbouille spectrum with a CO5BOLD+Linfor3D grid
gives A(O) = 8.67. The 3D fitting of the Wallace spectrum results in
A(O) = 8.71. Fitting the Delbouille and Wallace spectra with an
ATLAS+SYNTHE grid, we obtain A(O) = 8.68 and 8.66, respectively.
With the Holweger-Müller+SYNTHE grid, we have instead A(O) = 8.74
and 8.73, respectively![]() .
.
For this line our adopted LTE oxygen abundance is
A(O) =
![]() (see Table 4 for details).
(see Table 4 for details).
![\begin{figure}
\resizebox{9cm}{!}{\includegraphics[clip=true,angle=0]{9885fig12.eps}}\end{figure}](/articles/aa/full/2008/36/aa09885-08/Timg102.gif) |
Figure 12: The observed disc-centre intensity spectrum used for the O I 1130 nm line. The vertical line indicates the laboratory wavelength position of the line. |
| Open with DEXTER | |
In the Kurucz flux atlas and in both Neckel spectra, the O I 1130 nm line is blended by a telluric absorption. The Wallace intensity spectrum has been cleaned from telluric absorption, but its S/N is only about 80, inferior to the Kitt Peak FTS scans we considered, and insufficient for our purposes.
Our analysis of this line therefore relies on a special reduction of FTS
scans obtained from the NSO Digital Archive (see Fig. 12).
The O I 1130 nm line, and the companion 1316 nm multiplet
described below, fall in the shoulders of very strong telluric absorptions
and require a careful correction for the blending.
One of us (TRA) examined the NSO/FTS catalogue of
observations and identified a suitable series of scans, taken on the 13th
and 14th of September 1983. Each scan was a co-add of two interferograms
totalling 5 minutes exposure, through a 5
![]() diameter
aperture, at disc-centre. The datasets are listed as ``8309NNr0.XXX''
where ``NN'' is the day (13 or 14), and ``XXX'' is a scan number. Hereafter,
these will be described as ``NN.XXX' for simplicity. Scan 13.004 was
taken in the early morning at about 09:00 local time, at a moderate
airmass of 1.7. Scan 13.011 was acquired close to local noon at a low
airmass of 1.14. Scan 13.015 was taken later in the afternoon, again
at a moderate airmass of 1.5. On the following day, scan 14.007 was
collected at about 09:00 local time at an airmass of 1.7, while
scan 14.010 was taken about an hour before local noon, at a lower airmass
of 1.27. The spectral resolution of these data is very high, around
diameter
aperture, at disc-centre. The datasets are listed as ``8309NNr0.XXX''
where ``NN'' is the day (13 or 14), and ``XXX'' is a scan number. Hereafter,
these will be described as ``NN.XXX' for simplicity. Scan 13.004 was
taken in the early morning at about 09:00 local time, at a moderate
airmass of 1.7. Scan 13.011 was acquired close to local noon at a low
airmass of 1.14. Scan 13.015 was taken later in the afternoon, again
at a moderate airmass of 1.5. On the following day, scan 14.007 was
collected at about 09:00 local time at an airmass of 1.7, while
scan 14.010 was taken about an hour before local noon, at a lower airmass
of 1.27. The spectral resolution of these data is very high, around
![]() ,
and the S/N is very high as well, >103,
taking only the Poisson noise into account and ignoring other
sources of uncertainty.
Owing to the excellent frequency stability of the FTS scans, pairs taken at
low and high airmass can be registered very precisely to the telluric
absorptions, and ratioed to eliminate the solar component. The ratio
can be modelled as an exponential attenuation factor, and then applied
back to the observed spectra as a correction for the telluric component.
By subjecting this technique to various combinations of the low and high
airmass scans, one can average over slight variations in the atmospheric
attenuation factor in the morning versus the afternoon (owing, say, to
increases in the humidity due to solar heating), and possible slight
changes in the solar component due to 5 min oscillations, convection,
and the like.
All these effects contribute to the deterioration of the information
content of the spectrum and may be effectively thought of as ``noise''.
This source of noise
is in fact much more than the pure Poisson noise in the spectrum.
The dispersion in the derived solar profiles
is a rough measure of the uncertainty of the telluric correction
procedure and of intrinsic solar variations. For the O I 1130 nm
line, the corresponding S/N is about 15.
We refer to this S/N ratio as ``equivalent S/N''.
,
and the S/N is very high as well, >103,
taking only the Poisson noise into account and ignoring other
sources of uncertainty.
Owing to the excellent frequency stability of the FTS scans, pairs taken at
low and high airmass can be registered very precisely to the telluric
absorptions, and ratioed to eliminate the solar component. The ratio
can be modelled as an exponential attenuation factor, and then applied
back to the observed spectra as a correction for the telluric component.
By subjecting this technique to various combinations of the low and high
airmass scans, one can average over slight variations in the atmospheric
attenuation factor in the morning versus the afternoon (owing, say, to
increases in the humidity due to solar heating), and possible slight
changes in the solar component due to 5 min oscillations, convection,
and the like.
All these effects contribute to the deterioration of the information
content of the spectrum and may be effectively thought of as ``noise''.
This source of noise
is in fact much more than the pure Poisson noise in the spectrum.
The dispersion in the derived solar profiles
is a rough measure of the uncertainty of the telluric correction
procedure and of intrinsic solar variations. For the O I 1130 nm
line, the corresponding S/N is about 15.
We refer to this S/N ratio as ``equivalent S/N''.
The line is blended with a weaker iron line at
![]() nm,
nm,
![]() = -2.381 from Kurucz's Cowan-code computations,
whose contribution is 17% (for an ATLAS+SYNTHE synthetic spectrum
with A(O) = 8.60) to the complete EW of the blend.
From fitting with a CO5BOLD+Linfor3D grid we derived an oxygen abundance
of A(O) = 8.76. The corresponding value obtained from fitting with ATLAS+SYNTHE
is A(O) = 8.75. The EW-based abundance determination gives a fully consistent
result, A(O) = 8.75. The 3D correction is +0.04 dex (
= -2.381 from Kurucz's Cowan-code computations,
whose contribution is 17% (for an ATLAS+SYNTHE synthetic spectrum
with A(O) = 8.60) to the complete EW of the blend.
From fitting with a CO5BOLD+Linfor3D grid we derived an oxygen abundance
of A(O) = 8.76. The corresponding value obtained from fitting with ATLAS+SYNTHE
is A(O) = 8.75. The EW-based abundance determination gives a fully consistent
result, A(O) = 8.75. The 3D correction is +0.04 dex (![]()
![]() ).
Our adopted LTE oxygen abundance for this line is:
A(O) =
).
Our adopted LTE oxygen abundance for this line is:
A(O) =
![]() (see Table 4 for details).
(see Table 4 for details).
![\begin{figure}
\resizebox{9cm}{!}{\includegraphics[clip=true,angle=0]{9885fig13.eps}}\end{figure}](/articles/aa/full/2008/36/aa09885-08/Timg107.gif) |
Figure 13: The observed disc-centre intensity spectrum used for the analysis of the O I 1316 nm line. The vertical lines indicate the laboratory wavelengths of the three O I lines discussed in the text. |
| Open with DEXTER | |
As shown in Fig. 13, three oxygen lines can be found in this multiplet,
at ![]() 1316.3889 nm, 1316.4858 nm, and 1316.5131 nm.
The strongest one (1316.4858 nm) is blended
with one of the other oxygen lines (1316.5131 nm).
For the three lines we adopt for
1316.3889 nm, 1316.4858 nm, and 1316.5131 nm.
The strongest one (1316.4858 nm) is blended
with one of the other oxygen lines (1316.5131 nm).
For the three lines we adopt for
![]() values of
-0.28, -0.250, -0.728, respectively, according to Biémont et al. (1991).
values of
-0.28, -0.250, -0.728, respectively, according to Biémont et al. (1991).
The Wallace intensity solar spectrum has an S/N of about 700, but the spectrum is poorly rectified, making the continuum placement very uncertain. We decided not to use this spectrum but rather the Kitt Peak FTS scans mentioned above (Sect. 5.3.7), which have a higher S/N (>103) and are well-rectified. For the 1316 nm feature the equivalent S/N for the strongest of the lines, having a central depth of about 5%, is about 25, somewhat higher than for the 1130 nm line. From fitting this spectrum, we obtain A(O) = 8.75 with a 3D grid for all three lines. With an ATLAS+SYNTHE grid, the fit gives A(O) = 8.77.
For this line our LTE adopted abundance is
A(O) =
![]() .
.
The best estimate of the solar oxygen abundance
is obtained by a suitable average of the abundances
derived from the individual lines.
Our adopted oxygen abundances are summarised in
Table 4, together with associated
errors, while corrections for departures
from LTE are listed in Table 5.
A different choice in the collision efficiency with H-atoms,
quantified by the scaling factor ![]() (see Sect. 5.1),
produces a different value in the solar oxygen abundance.
A weighted mean
(see Sect. 5.1),
produces a different value in the solar oxygen abundance.
A weighted mean
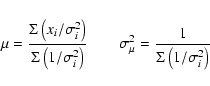 |
(1) |
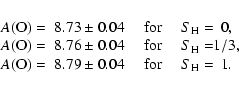 |
(2) |
If we consider the NLTE abundance in column 6 of Table 5,
corresponding to
![]() ,
excluding the 615 nm line, we find a
line to line scatter of 0.13 dex, so compatible with the 1
,
excluding the 615 nm line, we find a
line to line scatter of 0.13 dex, so compatible with the 1![]() error
bars we attribute to the individual lines. The same range in A(O) is
obtained for
error
bars we attribute to the individual lines. The same range in A(O) is
obtained for
![]() .
The 615 nm line requires a lower abundance
and would increase the overall scatter, but, as we discussed in the section
devoted to this line, this line is particularly problematic.
.
The 615 nm line requires a lower abundance
and would increase the overall scatter, but, as we discussed in the section
devoted to this line, this line is particularly problematic.
The lowest abundance after the 615 nm line is coming from the forbidden oxygen line at 630 nm. The relatively low oxygen abundance it implies is sensitive to the abundance of nickel, which we assumed to be 6.25, the presently recommended value. Had we adopted the equivalent width of 4.3 pm, which A04 attribute to the oxygen contribution to the 630 nm line, we would have obtained A(O) = 8.78, moving the result closer to the other lines and becoming fully consistent with forbidden oxygen line at 636 nm.
We do not show comparisons between line profile shapes of synthetic and observed spectra
because we cannot reproduce the observed features due to blends, as
is the case for the 636, 844, and 926 nm lines; the triplet is
affected by NLTE corrections. Since our NLTE computation is based on the
![]() model, we cannot reproduce the profile of the triplet lines accurately. The
infrared lines, after correction for telluric absorption, have low S/N so
that visual comparison to synthetic profiles is not particularly illuminating. Only
for the 630 nm forbidden line can the observed line profile shape be
compared to the synthetic 3D spectrum, and this is shown in
Fig. 5 for all four observed profiles.
model, we cannot reproduce the profile of the triplet lines accurately. The
infrared lines, after correction for telluric absorption, have low S/N so
that visual comparison to synthetic profiles is not particularly illuminating. Only
for the 630 nm forbidden line can the observed line profile shape be
compared to the synthetic 3D spectrum, and this is shown in
Fig. 5 for all four observed profiles.
Our results must be compared with those
of Holweger (2001), A04, and to the one
of Ayres (2008).
Holweger (2001) provides A(O) =
![]() ,
thus
,
thus ![]() 0.05 dex lower than our weighted
mean for
0.05 dex lower than our weighted
mean for
![]() ,
right within one
,
right within one ![]() of his error bar.
The mean oxygen abundance obtained
from the atomic lines by A04,
A(O)=8.65, and our weighted mean, for
of his error bar.
The mean oxygen abundance obtained
from the atomic lines by A04,
A(O)=8.65, and our weighted mean, for
![]() ,
differ of +0.08 dex.
,
differ of +0.08 dex.
One of us (Ayres 2008) has recently carried out an independent analysis
specifically of the 630 nm O I forbidden line, taking a different
approach than followed in the present work. Here, we have allowed the
wavelength scale in the vicinity of the 630 nm feature to float, to
accommodate the Ni I blend at its nominal abundance. With this approach
we obtain an excellent match to the observed line-shape, although Ni I
accounts for a larger fraction of the equivalent width of the full feature
(see Fig. 4) than would be inferred from the original analysis
of the forbidden oxygen line by Allende Prieto et al. (2001, their Fig. 1). Curiously, we
obtain nearly the same oxygen abundance as Allende Prieto et al. (2001), even though here the
O I component occupies a smaller fraction of the full equivalent width.
At the time Allende Prieto et al. (2001) performed their analysis, the oscillator strength of
the Ni transition was not known precisely, and they left the product
![]() as a free fitting parameter. They obtained a
contribution corresponding to a low nickel abundance of A(Ni) = 6.05, i.e. a
rather small contribution, using today's accepted value of the oscillator
strength of the Ni transition. It is conceivable that the difficulty in the
continuum placement are responsible for the disparate findings.
as a free fitting parameter. They obtained a
contribution corresponding to a low nickel abundance of A(Ni) = 6.05, i.e. a
rather small contribution, using today's accepted value of the oscillator
strength of the Ni transition. It is conceivable that the difficulty in the
continuum placement are responsible for the disparate findings.
Ayres (2008) took the alternative fitting
approach of fixing the wavelength scale and allowing the Ni I abundance
to float. Although the absolute velocity calibrations of the solar atlases and
specially reduced spectra we have described earlier can be uncertain
by hundreds of m s-1, Ayres circumvented that deficiency by adjusting
an observed FTS spectrum to match 3D-synthesised cores of several Fe I
absorption lines in the immediate vicinity of the [O I] 630 nm feature
(the 3D model was a single CO5BOLD snapshot in this case). This procedure
moves the blend bluewards of the result we obtained here, leading to a higher
fraction of the equivalent width contributed by O I, and lowering the
fraction of Ni I (by about 30%). The inferred oxygen abundance
is larger than obtained here, A(O) =
![]() .
Ayres's approach relies
on an accurate prediction of the relative core velocities of the Fe I
and O I (+ Ni I) features by the 3D model, and assumes that the
Ni I abundance can be treated as a free parameter.
.
Ayres's approach relies
on an accurate prediction of the relative core velocities of the Fe I
and O I (+ Ni I) features by the 3D model, and assumes that the
Ni I abundance can be treated as a free parameter.
In both cases, it is important to note that the CO5BOLD model provides a different conversion between fractional O I equivalent width and inferred oxygen abundance than the 3D simulations reported by Allende Prieto et al. (2001) and subsequent studies also using the Stein-Nordlund class of models. The differences might be related to the different temperature gradients of the 3D models (e.g., as exhibited by the 1D average stratifications shown in Fig. 1) since a main factor governing the strength of a weak photospheric line is the temperature gradient in the line formation zone. Another factor introducing systematic uncertainties is the spectral synthesis. Meléndez (2004) applied the spectral synthesis code MOOG (Sneden 1973) in his determination of the solar oxygen abundance. Besides mainly targeting OH molecular lines in the infrared, he recalculated the oxygen abundance from the forbidden oxygen line at 630 nm based on the average 3D model of A04 and their equivalent width, as well as oscillator strength, obtaining A(O) = 8.75. According to our calculations, horizontal temperature fluctuations have essentially no effect on the resulting equivalent width of the line in disc-integrated spectra so that Meléndez' value can be directly compared to the value of 8.69 quoted by A04. We are left with the uncomfortable conclusion that differences in the spectral synthesis can introduce differences as large as 0.06 dex in the derived oxygen abundance.
The weighted mean of the abundances derived from several O I lines in the solar spectrum implies a solar oxygen abundance in the range A(O) = 8.73 to A(O) = 8.79, depending on the actual influence of collisions by neutral hydrogen atoms on the NLTE level populations of oxygen. The lower abundance is obtained by a total neglect of such collisions, the higher abundance is obtained by assuming the rather large cross sections provided by the recipe of Steenbock & Holweger (1984), which may be considered an upper limit to the efficiency of these collisions. Any treatment of neutral hydrogen collisions intermediate between these two extremes will provide an oxygen abundance in the above range.
Apart from this systematic uncertainty of the NLTE corrections, we
regard the determination of A(O) as very robust, with a total error in the
weighted mean of 0.07 dex. Considering our present ignorance on the
actual role of collisions by neutral hydrogen, we believe that it is
reasonable to assume that the true value lies somewhere in between these
two extreme assumptions.
Therefore, assuming
![]() ,
our recommended value
for the solar oxygen abundance is the mean of the two,
A(O) =
,
our recommended value
for the solar oxygen abundance is the mean of the two,
A(O) =
![]() .
.
Our recommended oxygen abundance is a downward revision
with respect to that of Grevesse & Sauval (1998). Using that set of
solar abundances the solar metallicity is
![]() .
If we take that set of solar abundances and change only the oxygen
abundance to our recommended value,
.
If we take that set of solar abundances and change only the oxygen
abundance to our recommended value, ![]() drops to 0.016.
On the other hand, our oxygen abundance is an upward revision
relative to what was recommended by
A04. By taking
the solar abundances of Asplund et al. (2005) but our oxygen abundance,
we find
drops to 0.016.
On the other hand, our oxygen abundance is an upward revision
relative to what was recommended by
A04. By taking
the solar abundances of Asplund et al. (2005) but our oxygen abundance,
we find
![]() .
Clearly the latter result is influenced
by the general downward revision of all the solar
abundances advocated by Asplund and collaborators.
Having found a higher solar oxygen abundance by using CO5BOLD models,
and having been unable to confirm the downward revision of phosphorus
(Caffau et al. 2007b) and sulphur (Caffau & Ludwig 2007; Caffau et al. 2007a),
it seems not unlikely that, also for other elements, a CO5BOLD based
analysis would imply higher abundances than recommended by Asplund et al. (2005).
.
Clearly the latter result is influenced
by the general downward revision of all the solar
abundances advocated by Asplund and collaborators.
Having found a higher solar oxygen abundance by using CO5BOLD models,
and having been unable to confirm the downward revision of phosphorus
(Caffau et al. 2007b) and sulphur (Caffau & Ludwig 2007; Caffau et al. 2007a),
it seems not unlikely that, also for other elements, a CO5BOLD based
analysis would imply higher abundances than recommended by Asplund et al. (2005).
We should compare our result with solar oxygen abundances deduced
by other means. Delahaye & Pinsonneault (2006) obtain A(O) =
![]() (CNNe)
from the seismic properties; the latter uncertainty is related to the abundance of C, N, and Ne.
Antia & Basu (2006) using the helioseismically measured sound speed profile obtained
(CNNe)
from the seismic properties; the latter uncertainty is related to the abundance of C, N, and Ne.
Antia & Basu (2006) using the helioseismically measured sound speed profile obtained
![]() ,
but the method does not permit the abundance of a single element to be deduced.
Chaplin et al. (2007) using the frequencies of low-degree acoustic oscillations of the Sun
obtained Z in the range 0.0187-0.0229.
Basu & Antia (2008) find
Z = 0.016, again from helioseismic considerations.
As we can see, all the results obtained from the properties of the solar
interior favour a ``high'' solar metallicity, and therefore a ``high''
oxygen abundance.
In the same line are the results obtained in the
work of Turck-Chièze et al. (2004): they find a better agreement
when they compare the seismic model (Z = 0.017) to the solar model with
the abundances of Holweger (2001) (Z = 0.015) with respect to the model
with A04 abundances (Z = 0.012).
,
but the method does not permit the abundance of a single element to be deduced.
Chaplin et al. (2007) using the frequencies of low-degree acoustic oscillations of the Sun
obtained Z in the range 0.0187-0.0229.
Basu & Antia (2008) find
Z = 0.016, again from helioseismic considerations.
As we can see, all the results obtained from the properties of the solar
interior favour a ``high'' solar metallicity, and therefore a ``high''
oxygen abundance.
In the same line are the results obtained in the
work of Turck-Chièze et al. (2004): they find a better agreement
when they compare the seismic model (Z = 0.017) to the solar model with
the abundances of Holweger (2001) (Z = 0.015) with respect to the model
with A04 abundances (Z = 0.012).
The downward revision of the solar Z by Asplund et al. (2005)
is generally considered to mainly stem from the use of
3D models, as opposed to 1D models used in older
analysis (e.g. Allende Prieto 2007).
The result of our analysis reveals, however, that
this is not the case at least for oxygen.
The 3D corrections for the O I lines are small,
and for all lines, except for the 615.8 nm line, they are positive,
indicating that the 3D model provides a higher abundance
than the corresponding
![]() model (see Table 3).
The average 3D correction, if we consider all the oxygen lines,
is +0.049 assuming a micro-turbulence
model (see Table 3).
The average 3D correction, if we consider all the oxygen lines,
is +0.049 assuming a micro-turbulence ![]()
![]() in the
in the
![]() model,
and +0.066 when
model,
and +0.066 when ![]()
![]() .
.
Closer inspection shows that the lower oxygen abundance of A04
is essentially a result of using lower equivalent widths, on average, and
of the choice of
![]() (larger NLTE corrections), which are both
acting in the downward direction. The differences between the Stein &
Nordlund model employed by A04
and our CO5BOLD model (see
Fig. 1) are not essential for the resulting oxygen
abundance. The fact that our oxygen abundance with
(larger NLTE corrections), which are both
acting in the downward direction. The differences between the Stein &
Nordlund model employed by A04
and our CO5BOLD model (see
Fig. 1) are not essential for the resulting oxygen
abundance. The fact that our oxygen abundance with
![]() is 0.08 dex
higher is entirely due to our measured equivalent widths, which are larger. If
we use the CO5BOLD model and the equivalent widths of A04,
we find A(O) = 8.67 when averaging the oxygen abundances for the atomic lines, very
close to their result. Therefore, the 3D corrections quoted by
A04 are in the opposite direction to ours due to
the different choice of 1D reference model.
is 0.08 dex
higher is entirely due to our measured equivalent widths, which are larger. If
we use the CO5BOLD model and the equivalent widths of A04,
we find A(O) = 8.67 when averaging the oxygen abundances for the atomic lines, very
close to their result. Therefore, the 3D corrections quoted by
A04 are in the opposite direction to ours due to
the different choice of 1D reference model.
A04 argued that their suggested low O abundance would place the Sun on the same oxygen level as is observed in the local interstellar medium and nearby B stars. However, it is not at all obvious that the Sun's chemical composition should reflect its immediate surroundings since it might have migrated towards larger galactic radii from its place of formation (Wielen et al. 1996) of higher metallicity. Moreover, the Sun harbours a planetary system, and it is now well-established that planet-hosting stars have, on average, higher metallicities than stars with no planets. Ecuvillon et al. (2006) present a uniform analysis of oxygen abundances in a volume-limited sample of 59 stars with no planets and compare it to a sample of 96 planet-hosting stars. The mean oxygen abundance of the sample of planet-hosting stars is 8.77, while the mean oxygen abundance of the sample of stars with no planets is 8.67. Thus our recommended solar oxygen abundance places the Sun in a very popular position among planet-hosting stars in the solar neighbourhood.
To improve our knowledge of the solar oxygen abundance, one should focus in the first place on the collisions with hydrogen atoms, both theoretically and experimentally. To the readers who have been following the saga of the solar abundances for some time it is perhaps not surprising to find that the measurement of high accuracy equivalent widths is still an open issue. One should try to better constrain the placement of the continuum, and the influence of the blending lines.
Acknowledgements
This paper is dedicated to the late Hartmut Holweger who accompanied the initial phases of the oxygen project with encouragement and advice. We thank Sveneric Johansson for his input on the isotopic splitting of nickel lines. We are grateful to Martin Asplund for providing us with the full details of his analysis. Furthermore, we are grateful to Robert Kurucz for providing the revised version of his solar flux atlas. We wish to thank Rosanna Faraggiana for many fruitful discussions on the topic of abundance determinations. Special thanks also go to Inga Kamp for giving us the Kiel code and the oxygen model atom and helping us in their use. E.C., H.G.L., and P.B. acknowledge support from EU contract MEXT-CT-2004-014265 (CIFIST).