A&A 488, 1125-1132 (2008)
DOI: 10.1051/0004-6361:200809833
Forced oscillations of coronal loops driven by EIT waves![[*]](/icons/foot_motif.gif)
I. Ballai1 - M. Douglas1 - A. Marcu2
1 - Solar Physics and Space Plasma Research Centre
(SP2RC), Dept. of Applied Mathematics, University of Sheffield,
Hicks Building, Hounsfield Road, Sheffield, S3 7RH, UK
2 - Babes-Bolyai University, Dept. of Theoretical and
Computational Physics, 1 Kogalniceanu, 400084 Cluj-Napoca, Romania
Received 24 March 2008 / Accepted 9 July 2008
Abstract
Aims. We study the generation of transversal oscillations in coronal loops represented as a straight thin flux tube under the effect of an external driver modelling the global coronal EIT wave. We investigate how the generated oscillations depend on the nature of the driver, and the type of interaction between the two systems.
Methods. We consider the oscillations of a magnetic straight cylinder with fixed-ends under the influence of an external driver modelling the force due to the global EIT wave. Given the uncertainties related to the nature of EIT waves, we first approximate the driver by an oscillatory force in time and later by a shock with a finite width.
Results. Results show that for a harmonic driver the dominant period in the generated oscillation belongs to the driver. Depending on the period of driver, compared to the natural periods of the loop, a mixture of standing modes harmonics can be initiated. In the case of a non-harmonic driver (modelling a shock wave), the generated oscillations in the loop are the natural periods only. The amplitude of oscillations is determined by the position of the driver along the tube. The full diagnosis of generated oscillations is achieved using simple numerical methods.
Key words: magnetohydrodynamics (MHD) - Sun: corona - waves
Latest high-resolution coronal observations have shown that
coronal structures are very dynamic entities with flows and waves
propagating along them. Waves and oscillations in coronal loops
have received increased attention in the last few years due to the
possibility to use the observed properties to diagnose not only
the magnetic field in these structures, but also the
sub-resolution space distribution of loops, plasma properties,
etc. (e.g. Roberts et al. 1984; Aschwanden et al. 1999;
Nakariakov et al. 1999; Banerjee et al. 2007; Verth et al.
2007; Arregui et al. 2008; Verth & Erélyi 2008). One specific type of oscillations observed in coronal loops is the fast kink
mode which disturbs the symmetry axis of the loop (for a full
description of these waves see, e.g. Edwin & Roberts 1983) and
it is nearly incompressible.
Many of kink waves and oscillations have their origin in the
interaction of coronal loops with various external sources and
drivers (see, e.g. Hindman & Jain 2008; Erdélyi & Hargreaves 2008). One of the possible explanations of oscillations in coronal
loops and/or prominence fibrils is that they have their origin in
the interaction of these loops with global coronal waves, e.g. EIT
waves. EIT waves (Thompson et al. 1999) are waves generated by
sudden energy releases (flares, coronal mass ejections, etc.) and
they are able to propagate over very large distances in the solar
low corona.
Observational evidence for large-scale coronal impulses initiated
during the early stage of a flare and/or CME has been provided by
the EIT instrument onboard SOHO, TRACE/EUV, STEREO/EUVI. EIT waves
propagate in the quiet Sun with speeds of 250-400 km s-1at an almost constant altitude. At a later stage in their
propagation EIT waves can be considered as a freely propagating
wavefront which is observed to interact with coronal loops (see,
e.g. Wills-Davey & Thompson 1999). Using TRACE/EUV 195 Å observations, Ballai et al. (2005) have shown
that EIT waves - seen in this wavelength - are waves with average
periods of the order of 400 s. Since at the height where the
EUV lines are formed, the magnetic field can be considered
vertical, EIT waves were interpreted as fast magnetohydrodynamic
(MHD) waves. This interpretation was confirmed using
multi-wavelength STEREO/EUVI observations by Long et al. (2008).
Recently, Attrill et al. (2007a,b) proposed that the diffuse EIT
coronal bright fronts are due to driven magnetic reconnections
between the skirt of the expanding CME magnetic field and the
favorably orientated quiet Sun magnetic field. According to this
latter model, the propagation process of the front consists of a
sequence of successive reconnection events.
Although a large consensus was reached on the trigger mechanism of
these global coronal waves and effects EIT waves can generate, the
nature of these large scale disturbances is still unknown, despite
the multitudes of models. The main reason of this uncertainty is
the lack of high temporal and spatial resolution as well as the
limited field of view (in the case of TRACE/EUV).
The present paper investigates the temporal and spatial variations
of transversal oscillations in a coronal loop under the influence of
an external driver representing the coronal global EIT waves.
Strictly speaking a coronal loop application would require the
consideration of an external magnetic field. However, we consider
this study as a starting point in a much more complex analysis. Due
to the uncertainties in resolving the nature of EIT waves, we will
discuss separately the cases of a harmonic driver and a driver of a
finite width with a pulse-like temporal distribution. It should be
noted here that the study of the present papers apply not only to
EIT waves as external driver, but it could be applied to any
external source.
In the next section we introduce the working model and derive the
governing equation of transversal oscillations based on the
principle of force equilibrium in conjunction with the continuity of
mass and magnetic flux. The governing equation is solved for the a
driving force when its particular form is not specified. Section 3
is devoted to the study of the periodical motion of the coronal loop
under the influence of a few particular drivers. Finally, in Sect. 4 we summarize our results and discuss some possible key extensions
which were neglected here but they could be added to this model in
subsequent studies.
Let us suppose that a flux tube is situated in a magnetic free
environment and it is under the effect of gravity. This model could approximate (in the first order) a magnetic loop
in the solar corona. We consider
the magnetic rope in the thin-flux-tube approximation inclined at an arbitrary angle with
respect to the vertical. Let us suppose the
directions 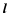 and
and 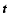 to be oriented along the loop
and in a transversal direction. We assume that the EIT wave is
acting with a force
to be oriented along the loop
and in a transversal direction. We assume that the EIT wave is
acting with a force 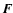 (per unit volume) on the tube and the direction of
this force is directed along the x-axis. For the sake of
simplicity all dissipative effects are neglected. A schematic representation of
the model is shown in Fig. 1.
(per unit volume) on the tube and the direction of
this force is directed along the x-axis. For the sake of
simplicity all dissipative effects are neglected. A schematic representation of
the model is shown in Fig. 1.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9833fig1.eps}\end{figure}](/articles/aa/full/2008/36/aa09833-08/Timg5.gif) |
Figure 1:
A schematic representation of the working model. The straight flux tube, arbitrarily
inclined with respect to the vertical direction, is under the influence of different forces which will generate transversal oscillations in the coronal loop which has fixed ends in the dense photosphere. |
| Open with DEXTER |
Part of the discussion of this paper is using the model and
derivation developed by Spruit (1981) where the transversal waves
were studied in a magnetic flux tube in the convective
zone/photosphere.
Any vector 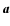 can be decomposed with respect to the
parallel and perpendicular direction of the tube such as
can be decomposed with respect to the
parallel and perpendicular direction of the tube such as
The forces acting on the tube are the pressure force, the Lorentz
force, the gravitational force and the force from the EIT wave. These
forces are going to be decomposed along the two characteristic
directions. We suppose that the homogeneous magnetic field is untwisted and
it has a single component, along the tube, i.e.
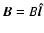 .
.
The parallel component of the motion is driven by the parallel
components of acting forces. Since the Lorentz force has no field
aligned component, it will appear only in the perpendicular
direction. The parallel force equilibrium requires that
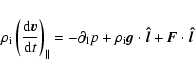 |
(1) |
where the operator
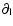 is defined as
is defined as
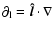 and
and
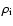 is the density inside the loop.
Along the perpendicular direction the forces acting on the tube
will be
is the density inside the loop.
Along the perpendicular direction the forces acting on the tube
will be
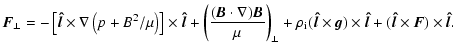 |
|
|
(2) |
According to Spruit (1981), the Lorentz force can be simply
written as
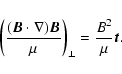 |
(3) |
We suppose that the tube is in equilibrium with its environment
and the total pressure inside the tube is balanced by the
external pressure, i.e.
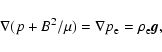 |
(4) |
where 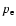 and
and
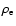 are the pressure and density outside the
tube. With this in mind, the perpendicular component of the
forces acting on the tube becomes
are the pressure and density outside the
tube. With this in mind, the perpendicular component of the
forces acting on the tube becomes
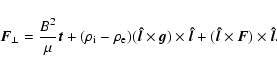 |
(5) |
The perpendicular component of forces acts to move the plasma mass
(per unit volume) of
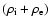 in the tube and in the
exterior. Therefore the equilibrium of forces in the transversal
direction can be simply given as
in the tube and in the
exterior. Therefore the equilibrium of forces in the transversal
direction can be simply given as
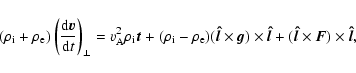 |
(6) |
where we introduced the internal Alfvén speed
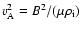 .
It should be mentioned that in the
original derivation by Spruit (1981) the appearance of the term
containing
.
It should be mentioned that in the
original derivation by Spruit (1981) the appearance of the term
containing
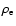 on the left hand side of Eq. (6)
was attributed to the apparent increase of tube's inertia.
Combining Eqs. (1) and (6), the total
equation of motion is given by
on the left hand side of Eq. (6)
was attributed to the apparent increase of tube's inertia.
Combining Eqs. (1) and (6), the total
equation of motion is given by
 |
|
|
|
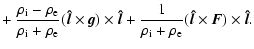 |
|
|
(7) |
Let us write the Cartesian components of the unit vectors
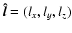 and
and
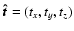 ,
so the
cartesian components of Eq. (7) can be written as
,
so the
cartesian components of Eq. (7) can be written as
These equations must be supplemented by the continuity and
induction equations which can be combined into a single equation
of the form
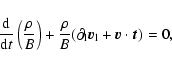 |
(9) |
where
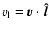 and
and
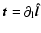 .
Now suppose that the flux tube is nearly
vertical and let us denote the horizontal displacement of the tube
by
.
Now suppose that the flux tube is nearly
vertical and let us denote the horizontal displacement of the tube
by 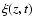 .
In order to simplify the mathematics we suppose
that these displacements are small. According to Spruit (1981) the
components of the unit vector
.
In order to simplify the mathematics we suppose
that these displacements are small. According to Spruit (1981) the
components of the unit vector
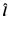 and
and
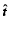 can be
written as
can be
written as
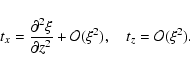 |
(10) |
In addition we assume that the tube is in the xz-plane, so we
choose ly=ty=0. Now the remaining two equations of the system
(8) reduce to
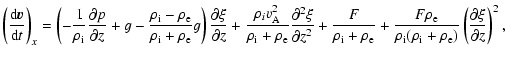 |
|
|
(11) |
and
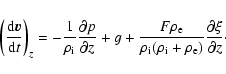 |
(12) |
In the above equations we restricted ourselves to linear motion
only. Next we assume that the vertical displacements are small and
of the same order as 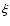 .
In order to obtain a closed equation,
in addition, we assume that the force, F acting externally on
the tube is of the same order as
.
In order to obtain a closed equation,
in addition, we assume that the force, F acting externally on
the tube is of the same order as 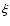 .
Collecting terms of the
same order (with respect to
.
Collecting terms of the
same order (with respect to 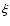 )
in the two equations we obtain
that
)
in the two equations we obtain
that
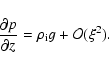 |
(13) |
After inserting these two relations back into Eq. (11)
we obtain
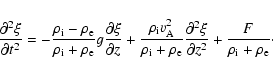 |
(14) |
The above equation describes the propagation of transversal
oscillations of a vertical flux tube when the oscillations are
driven by an external force, F. Similar to Spruit (1981), the
first termon the right hand side is due to stratification and is
proportional to the buoyancy force, while the second term is due
to the restoring force due to the magnetic tension in the tube.
This equation (without the external force) has been originally
derived by Lamb (1932). Equation (14) is similar to the
equation derived by Spruit (his Eq. (29)) apart from the
driving term on the right hand side of our equation. The
propagation of kink modes described by a KG equation was studied
earlier by, e.g. Musielak & Ulmschneider (2003), Erdélyi &
Hargreaves (2008) & Hargreaves (2008).
In what follows we are going to solve Eq. (14) for a
coronal loop when the driving force is due to the incident EIT
wave. Before presenting the solutions we introduce a new function,
Q, defined as
![$\xi=Q\exp~[\lambda z]$](/articles/aa/full/2008/36/aa09833-08/img45.gif) and we choose the value of
the parameter
and we choose the value of
the parameter 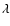 such that all first derivatives with
respect to z vanish. After a straightforward calculation we
obtain that when
such that all first derivatives with
respect to z vanish. After a straightforward calculation we
obtain that when
the governing Eq. (14) reduces to
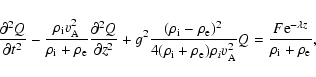 |
(15) |
which is a nonhomogeneous Klein-Gordon (KG) equation. A
nonhomogeneous KG equation has been also derived earlier by Rae
& Roberts (1982) and the inhomogeneous part described the effect
of the external medium. In their analysis the inhomogeneous part
was neglected by considering a situation where the temporal
variations of the parameters outside the loop are very slow
compared to changes inside the tube. For kink modes, Roberts
(2004) has obtained a similar equation.
The transversal waves described by Eq. (15) will
propagate with the speed given by the second term on the left hand
side
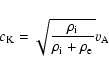 |
(16) |
which is the kink speed. This quantity has been previously
discussed within the context of wave propagation in magnetic flux
tubes by, e.g. Edwin & Roberts (1983). The coefficient of the
third term has dimension of s-2 and its square root is given
by
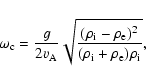 |
(17) |
and constitutes the cut-off frequency for kink modes propagating
in coronal loops. For typical coronal parameters (
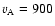 km s-1,
km s-1,
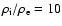 )
the cut-off frequency of kink
oscillations is about 0.13 mHz. With these new notations, Eq.
(15) becomes
)
the cut-off frequency of kink
oscillations is about 0.13 mHz. With these new notations, Eq.
(15) becomes
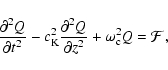 |
(18) |
where
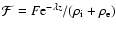 .
.
Employing a normal mode analysis (
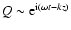 )
for
the homogeneous part of Eq. (18), the dispersion
relation of these linear waves is given as
)
for
the homogeneous part of Eq. (18), the dispersion
relation of these linear waves is given as
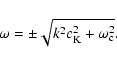 |
(19) |
Due to the particular k-dependence of the dispersion relation
waves are dispersive, i.e. waves with larger wavelength (shorter k) propagating faster. The group speed of these waves is given
as
so, waves with smaller wave number will have smaller group speed,
the maximum of the group speed (at
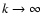 )
being
)
being
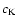 .
.
Equation (18) has been studied in the context of pulse
propagation in the solar photosphere and chromosphere (see, e.g.
Roberts & Webb 1978; Rae & Roberts 1982; Kalkofen et al. 1994;
Sutmann et al. 1998; Hassan & Kalkofen 1999; Musielak &
Ulmschneider 2001, 2003; Hindman & Jain 2008; Erdélyi & Hargreaves 2008). The solution of the KG equation represents the
propagation of a wave with the speed 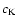 followed by a wake
oscillating with the frequency
followed by a wake
oscillating with the frequency
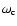 .
.
An extension of the KG equation has been discussed by Ballai et al. (2006) when the dissipation (kinematic viscosity in their
analysis) modified the KG equation into a Klein-Gordon-Burgers
equation where the dissipative term was given as a mixed (space
and time) derivative.
In what follows we present an analytical solution to Eq.
(18) in the most general form and particular solutions
will be deducted. Let us suppose that the boundary and initial
conditions used for solving Eq. (18) are given by
Q(0,t)=Q(L,t)=0,
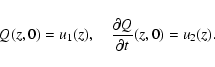 |
(20) |
First we apply the Laplace transform to Eq. (18) and we
obtain
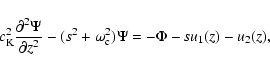 |
(21) |
where 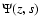 and
and 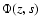 are the Laplace transforms of
the functions Q(z,t) and
are the Laplace transforms of
the functions Q(z,t) and
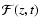 defined as
defined as
Given the nature of the boundary conditions we further apply a
finite Fourier sine transform defined as
where we introduced
After applying the Fourier sine transform we obtain
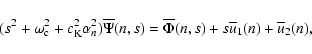 |
(22) |
where the functions with an overline represent the Fourier
transformed functions. From Eq. (22) we obtain that
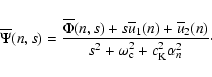 |
(23) |
Now we apply an inverse Fourier transform which results in
In order to obtain Q(z,t), we need to apply an inverse Laplace
transform to the function 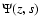 .
When calculating this
transform we will take into account the results of the convolution
theorem, i.e.
.
When calculating this
transform we will take into account the results of the convolution
theorem, i.e.
as well as the inverse Laplace transforms of the quantities
and
with
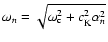 being the
natural frequency of the loop and the mode corresponding to n=0being the cut-off frequency. It is interesting to note that the
ratio of periods corresponding to the fundamental mode (n=1) and
the first harmonic (n=2) is given by
being the
natural frequency of the loop and the mode corresponding to n=0being the cut-off frequency. It is interesting to note that the
ratio of periods corresponding to the fundamental mode (n=1) and
the first harmonic (n=2) is given by
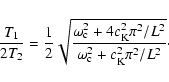 |
(25) |
Due to the presence of the cut-off frequency this period ratio is
not 1 but is slightly smaller, however it can approach the
observed period ratio (Verwichte et al. 2004; McEwan et al. 2006)
if the cut-off is made unrealistically high. For typical coronal
and loop conditions, the natural periods of a loop of L = 200 Mm
and
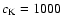 km s-1 are 400 s, 200 s, and 133 s,
respectively while for a 300 Mm loop these periods will be in a
ratio
600/300/200. If the length is fixed at 200 Mm and let
the kink speed to be 1100 km s-1 the periods of the first
three modes will be
364/182/121. It should be pointed out that
Eq. (25) is similar to the findings in McEwan et al.
(2006) though their equation was written for slow standing modes
(see their Eq. (24)). However, observers have not reported
harmonics for slow waves whereas reports on higher harmonics for
kink modes are in abundance.
km s-1 are 400 s, 200 s, and 133 s,
respectively while for a 300 Mm loop these periods will be in a
ratio
600/300/200. If the length is fixed at 200 Mm and let
the kink speed to be 1100 km s-1 the periods of the first
three modes will be
364/182/121. It should be pointed out that
Eq. (25) is similar to the findings in McEwan et al.
(2006) though their equation was written for slow standing modes
(see their Eq. (24)). However, observers have not reported
harmonics for slow waves whereas reports on higher harmonics for
kink modes are in abundance.
In the light of these relations, the inverse Laplace transform of,
e.g. the first term in Eq. (24) will be of the form
 |
(26) |
Applying a term-by-term inversion to the function 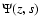 given by Eq. (24) we obtain
given by Eq. (24) we obtain
The solution of the nonhomogeneous Klein-Gordon equation given by
Eq. (27) can be simplified once the forms of the
functions u1 and u2 are known. In what follows we will
discuss a few particular cases and will investigate the
possibility of generating oscillations in coronal loops triggered
by an incident wave modelling the coronal global EIT wave.
The simplest particular case is when we have zero initial
conditions, i.e.
u1(z)=u2(z)=0, and
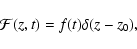 |
(28) |
where 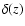 is the Dirac-delta function. In this case
the solution of the inhomogeneous KG equation is given by
is the Dirac-delta function. In this case
the solution of the inhomogeneous KG equation is given by
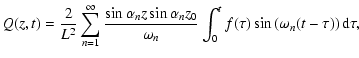 |
|
|
(29) |
where we used the property that
When deriving Eq. (29) we took into account that the
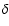 -function has a dimension of L-1 and a variable
change of the form
-function has a dimension of L-1 and a variable
change of the form
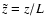 and
and
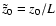 is
needed. The extra L in the denominator of Eq. (29)
arises after we apply the property that
is
needed. The extra L in the denominator of Eq. (29)
arises after we apply the property that
![$\delta[L({\tilde
z}-{\tilde z_0})]=L^{-1}\delta({\tilde z}-{\tilde z_0})$](/articles/aa/full/2008/36/aa09833-08/img91.gif) .
If we
further assume that
.
If we
further assume that
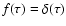 (i.e. the source
consists of an impulse acting at z=z0) the solutions describing
the oscillations in a fixed-ends loop is given by
(i.e. the source
consists of an impulse acting at z=z0) the solutions describing
the oscillations in a fixed-ends loop is given by
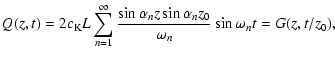 |
|
|
(30) |
which constitute the Green function for the coronal loop modelled
as a straight structure fixed at z=0,L. Once the Green function
is known, the solution of the inhomogeneous KG equation for an
arbitrary external action
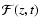 can be written as
can be written as
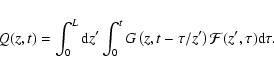 |
(31) |
The present analysis does not include any information about the
radius of the tube geometrical or the internal structure of the
tube and external magnetic field, factors which could be
important. However, it is easy to estimate the magnitude of the
external force required to induce oscillations in the tube. The
magnetic tension force in the tube with constant circular
cross-section is
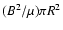 where R is the constant
radius of the tube. The external force must be at least as
large as the tension of the tube. Writing a simple force
equilibrium equation in transversal direction to the axis fo the
tube we obtain that the external force acting on the tube in a
point z0 along the tube has to be larger than
where R is the constant
radius of the tube. The external force must be at least as
large as the tension of the tube. Writing a simple force
equilibrium equation in transversal direction to the axis fo the
tube we obtain that the external force acting on the tube in a
point z0 along the tube has to be larger than
where
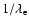 is the maximum displacement of the tube and is
given by (see, e.g. Edwin & Roberts 1983)
is the maximum displacement of the tube and is
given by (see, e.g. Edwin & Roberts 1983)
with
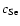 being the sound speed in the magnetic free region
outside the coronal loop and
being the sound speed in the magnetic free region
outside the coronal loop and 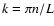 is the longitudinal
wavenumber. For a loop length of 200 Mm and
is the longitudinal
wavenumber. For a loop length of 200 Mm and
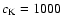 km s-1,
km s-1,
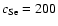 km s-1 we obtain a maximum
displacement of the fundamental mode of 12.9 Mm.
km s-1 we obtain a maximum
displacement of the fundamental mode of 12.9 Mm.
In the following section we are going to discuss a few particular
cases referring to the nature of the driver and find the equation
giving the transversal displacement of the loop as given by Eq.
(27).
The discussion of these separate particular cases is needed as the
true nature of EIT waves is not known. As specified before, the
force on the right hand side of Eq. (14) is the force
which acts on the coronal loop and represents the effect of the
incident EIT wave on the coronal loop. Obviously it is difficult
to estimate the value (or the direction) of this force, however,
some estimations can be made (see also the end of the previous
section). If we suppose that the entire energy of the EIT wave
(
 )
is converted into inducing oscillations of the loop,
the energy of the EIT wave will work toward displacing the loop.
Therefore we can write that
)
is converted into inducing oscillations of the loop,
the energy of the EIT wave will work toward displacing the loop.
Therefore we can write that
Obviously the energy of EIT waves is quantity which cannot be
directly measured however, previous indirect estimations (Ballai
2007) show that these energies are in the range of
1016-1019 J.
Let us suppose that the EIT wave is a wave and its action of the
coronal loop is described by a force of the form
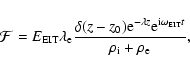 |
(32) |
where
 is the frequency of EIT waves. This form of
the externally acting force is inserted back into Eq.
(27), yielding
is the frequency of EIT waves. This form of
the externally acting force is inserted back into Eq.
(27), yielding
The presence of the
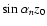 in the expression Q(z,t)simply means that the amplitude of generated oscillations will
depend on the height (along the loop) where the EIT wave interacts
with the loop. The maximum amplitude of oscillations (in the case
of modes with odd n) will be reached when the EIT wave hits the
top of the loop, i.e. the interaction occurs at z0=L/2. In this
case there will be no modes generated corresponding to an even n(for instance for an interaction of this type we will not have
first harmonics present in the loop). This statement supports the
conclusions drawn by Ballai (2007) where a list with possible
factors which can influence the characteristics of loop
oscillations was given. The singularity in the denominator of Eq. (33) is just apparent, its effect is balanced by the
numerator. If we concentrate only on the real part of Eq. (33), it is also obvious that the resulting signal will
not have a well defined standing mode pattern, instead the
oscillations will be a superposition of different oscillations.
The real part of Eq. (33) is numerically represented in
Fig. 2 (in all subsequent figures we will always use the real
part). The period of the driver EIT wave is left to vary between
50 and 800 s.
in the expression Q(z,t)simply means that the amplitude of generated oscillations will
depend on the height (along the loop) where the EIT wave interacts
with the loop. The maximum amplitude of oscillations (in the case
of modes with odd n) will be reached when the EIT wave hits the
top of the loop, i.e. the interaction occurs at z0=L/2. In this
case there will be no modes generated corresponding to an even n(for instance for an interaction of this type we will not have
first harmonics present in the loop). This statement supports the
conclusions drawn by Ballai (2007) where a list with possible
factors which can influence the characteristics of loop
oscillations was given. The singularity in the denominator of Eq. (33) is just apparent, its effect is balanced by the
numerator. If we concentrate only on the real part of Eq. (33), it is also obvious that the resulting signal will
not have a well defined standing mode pattern, instead the
oscillations will be a superposition of different oscillations.
The real part of Eq. (33) is numerically represented in
Fig. 2 (in all subsequent figures we will always use the real
part). The period of the driver EIT wave is left to vary between
50 and 800 s.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{9833fig2.eps}\end{figure}](/articles/aa/full/2008/36/aa09833-08/Timg110.gif) |
Figure 2:
The periods of oscillations generated by an EIT wave acting at z=z0. The period of the driver is changed in the interval 50 to 800 s. The horizontal lines represent the natural
periods of the loop, i.e.
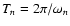 .
The inclined line corresponds to the periods of the EIT wave, the driver of the oscillations in the coronal loop. .
The inclined line corresponds to the periods of the EIT wave, the driver of the oscillations in the coronal loop. |
| Open with DEXTER |
The pattern of oscillations which can be generated in the coronal
loop depends on the characteristics of the driver. For each period
of the driver (in between 50 and 800 s) a wavelet analysis has
been carried out for the temporal part of Eq. (33). The
power of the signal has been summed up inside the cone of
influence set at a confidence level of 95% and the results are
shown in Fig. 2 which is color-coded, the red color corresponds
to the highest power, while the black color represents the lowest
power. Depending on the period of the EIT wave, various
oscillation modes can be excited. For the example shown in Fig. 2, the loop has a length of 200 Mm and a kink speed of 1000 km
s-1. The natural periods corresponding to these values are in
a ratio of
400/200/133, values represented by the horizontal
lines.
Let us consider a driver which has a period larger than 600 s.
In this case, the modes which can be excited will be the
fundamental mode (corresponding to 400 s) and the first harmonic
but with a very low power. The oscillation pattern of the driver
is still present but much weaker than the oscillation of the
fundamental mode. As the period of the driver becomes smaller,
other harmonics can be excited. For a period between 200 and
400 s the pattern of the driver is preserved (see the inclined
bright direction) but a considerable amount of the fundamental
mode and first harmonic can be generated. Higher harmonics are
also present but their power is very small. For a period of less
than 200 s the dominant oscillations will be the first and
second harmonics, while the fundamental mode is extremely weak.
The red regions correspond to the cases when the period of the
driver matches (or is very close) to one of the natural periods of
the loop. In that case there is a resonance between the driver and
the coronal loop.
In reality, however, if the EIT wave is an oscillating front
colliding with the coronal loop, then the interaction occurs not
only in one point, but in two, symmetrically situated from the
ends of the loop. Let us suppose now that the driver is a front
which interacts with the loop at the same time in two
points, at z0 and at L-z0. In this case, the driver will
have the form
For this expression the resulting oscillations will be described
by a similar function as given by Eq. (33) but now the
spatial dependence will contain in the numerator the expression
This situation can be achieved if the front of the EIT wave is
perfectly perpendicular to the coronal loop. For this particular
driver the corresponding period-diagram is shown in Fig. 3.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{9833fig3.eps} \end{figure}](/articles/aa/full/2008/36/aa09833-08/Timg113.gif) |
Figure 3:
The same as in Fig. 2 but now the oscillations are generated by an
EIT wave interacting with the coronal loop at z=z0 and z=L-z0. |
| Open with DEXTER |
According to expectations, in this case no modes corresponding to
an even n will be excited. In contrast to the first case, for
driver's period larger than the period corresponding to the first
natural period (400 s) the EIT wave will excite modes which will
carry predominantly the characteristic of the driver and in a
smaller quantity the properties of the fundamental mode. No first
harmonic can be generated, instead for a narrow range of the
driver's period, (a small interval around 200 s) the
oscillations will comprise addition from the fundamental mode and
the second harmonic.
In reality it is more likely that the front of the incident EIT
wave is not completely perpendicular to the axis of the loop, now
the two interaction points between the loop and EIT wave will
separated by a delay time, i.e. the time required for the front to
reach the other half of the loop. The delay time can be easily
calculated (see for details Ballai 2007) and depends on the length
of the loop, the speed of propagation of the EIT wave and the
attack angle, i.e. the angle the front of the EIT wave makes with
the vertical plane of the coronal loop. In this case, the acting
force will have a spatial and temporal dependence of the form
where 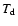 is the delay time and H(t) is the Heaviside step
function. After inserting this form back into Eq. (27)
we obtain that the modified transversal displacement of the
coronal loop is of the form
is the delay time and H(t) is the Heaviside step
function. After inserting this form back into Eq. (27)
we obtain that the modified transversal displacement of the
coronal loop is of the form
As a particular case we have chosen the situation when the delay
time corresponds to an integer number of EIT wave's period. In the
case of two external forces acting in phase upon the coronal loop
the possible modes appearing in the coronal loop are shown in
Fig. 4.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{9833fig4.eps}\end{figure}](/articles/aa/full/2008/36/aa09833-08/Timg119.gif) |
Figure 4:
The same as in Fig. 3 but now the oscillations are generated by an EIT
wave acting at z=z0 and z=L-z0 and the second interaction is delayed by a time corresponding to the double of EIT waves' period. |
| Open with DEXTER |
It is obvious that the period of generated oscillations will
contain the period of the EIT wave as the strongest component. For
periods larger than the natural period of the fundamental mode the
generated oscillation will be dominated by the period of the
fundamental mode with a weaker signal resembling the
characteristics of the driver and a very weak period corresponding
to the first harmonic. For periods of the driver situated between
the natural periods of the loop, the possibility of mode
generation goes parallel with the case explained in the case of a
single driver. It can be easily shown that the distribution of
possible periods in the coronal loop is similar even when the
delay time is not an integer number of EIT waves' period.
EIT waves have also been explained in terms of a non-wave feature
(i.e. not having a harmonic behaviour). In this context we could
list the models proposed by, e.g. Delanée (2000) and Attrill
et al. (2007) where EIT waves were associated with deformations and
evolutions of magnetic fields resulted after the release of the
CME. In order to include this possible explanation of EIT waves,
let us suppose an external force acting on the coronal loop of the
form
![\begin{displaymath}{\cal
F}=E_{\rm EIT}\lambda_{\rm e}\frac{{\rm e}^{-\lambda_z}...
...)-H(z-z_0^\prime)\right]}{\rho_{\rm i}+\rho_{\rm e}}\delta(t),
\end{displaymath}](/articles/aa/full/2008/36/aa09833-08/img120.gif) |
(35) |
which means that the external driving force is represented by a
finite width (
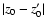 )
front which has no temporal
component other than a Dirac-delta function. If the form of
external force given by Eq. (35) is inserted back into
Eq. (27), we obtain that the temporal part of the
transversal displacement of the magnetic tube modelling a coronal
loop is given by
)
front which has no temporal
component other than a Dirac-delta function. If the form of
external force given by Eq. (35) is inserted back into
Eq. (27), we obtain that the temporal part of the
transversal displacement of the magnetic tube modelling a coronal
loop is given by
which means that this form of the EIT wave (a single finite width
front) will produce oscillations in the coronal loop at the
natural frequency of the loop only.
It is possible that the two forms of the external driver (the
harmonic and non-harmonic) treated here coexist in the sense that
they are the manifestation of the same phenomenon but at different
distance from the source, therefore a more careful analysis will
be needed in the future.
The generation and propagation of oscillations in coronal loops
modelled by a straight magnetic cylinder with fixed ends is
studied when the coronal loop is under the effect of an EIT wave, as
a driver. We found that if all forces acting on the flux tube are taken into
account, the governing equation describing the propagation of
standing transversal (kink) waves is described by an inhomogeneous
Klein-Gordon-type equation and the inhomogeneous part of the
equation is represented by the force (over a unit volume)
by EIT waves. The evolutionary equation contains information
about the propagation speed of waves (here the kink speed) and
the cut-off frequency of kink modes. The cut-off value is
determined by the densities inside/outside the loop and the
Alfvén speed (i.e. magnetic field).
Using the combined Laplace and Fourier sine transform techniques, the governing
equation is solved, such that the solution takes into
account general initial and boundary conditions.
Particular solutions have been found in the case of an EIT wave
considered first as a wave with a frequency
 ,
and later
as a shock wave with finite front thickness (a non-harmonic
driver). The results show that in case of a non-harmonic driver
the periods of generated modes always belong to the natural periods of the loop.
On the other hand, in the case of a periodic driver - for
an arbitrary period of the driver - there will be a mixture of standing modes which
could explain on the observed period ratio. The
analysis carried out here for different type of drivers show
that the generated oscillations will carry predominantly
information about the driver rather than the loop itself.
,
and later
as a shock wave with finite front thickness (a non-harmonic
driver). The results show that in case of a non-harmonic driver
the periods of generated modes always belong to the natural periods of the loop.
On the other hand, in the case of a periodic driver - for
an arbitrary period of the driver - there will be a mixture of standing modes which
could explain on the observed period ratio. The
analysis carried out here for different type of drivers show
that the generated oscillations will carry predominantly
information about the driver rather than the loop itself.
The oscillations described in this paper were all modelled in the
framework of ideal MHD. In reality coronal loop oscillations are
observed to decay relatively rapidly and several mechanisms have
been proposed to explain this damping (Ruderman & Roberts 2005;
Terradas et al. 2005, 2007; Selwa et al. 2007).
The inclusion of a
dissipative (or energy lost) mechanism in the present model will
be addressed in a future study. It could be possible that in the
case of a loop oscillating as a whole in the kink mode, the friction with the
environment could be also an important factor whose inclusion in
the model could result in a possible explanation of the damping
of these oscillations.
The present study can be further extended to the case when the
external EIT wave acts not only on a single magnetic loop but on
a system of adjacent loops. In this case the primary displacement of the first coronal loop
(generated by the incoming EIT wave) will be the driver for the
oscillations in the second loop (and so on), leading to coupled loop oscillations.
In order to describe a realistic loop, the present
model is going to be expanded to consider the effect of an
external magnetic field. It is expected that the presence of this
field will generate an additional force which will tend to suppress
the oscillation of the tube.
Acknowledgements
I.B. acknowledges the financial support by
NFS Hungary (OTKA, K67746). I.B. and A.M. were supported by The
National University Research Council Romania
(CNCSIS-PN-II/531/2007). M.D. acknowledges the support from STFC.
- Arregui, I.,
Terradas, J., Oliver, R., & Ballester, J. L. 2008, ApJ, 674,
1179 [NASA ADS] [CrossRef]
(In the text)
-
Aschwanden, M. J., Fletcher, L., Schrijver, C. J., & Alexander,
D. 1999, ApJ, 520, 880 [NASA ADS] [CrossRef]
(In the text)
- Attrill, G.
D. R., Harra, L. K., van Driel-Gesztelyi, L., Démoulin, P.,
& Wüsler, J.-P. 2007a, Astron. Nachr., 328, 760 [NASA ADS] [CrossRef]
(In the text)
- Attrill, G.
D. R., Harra, L. K., van Driel-Gesztelyi, L., & Démoulin,
P. 2007b, ApJ, 656, L101 [NASA ADS] [CrossRef]
- Ballai, I.
2007, Sol. Phys., 247, 177 [NASA ADS] [CrossRef]
(In the text)
- Ballai, I.,
Erdélyi, R., & Pintér, B. 2005, ApJ, 633, L145 [NASA ADS] [CrossRef]
(In the text)
- Ballai, I.,
Erdélyi, R., & Hargreaves, J. 2006, Phys. Plasmas, 13,
042108 [NASA ADS] [CrossRef]
(In the text)
- Banerjee,
D., Erdélyi, R., Ramon, O., & O'Shea, E. 2007, Sol. Phys.,
246, 3 [NASA ADS] [CrossRef]
(In the text)
- Delanée,
C. 2000, ApJ, 545, 512 [NASA ADS] [CrossRef]
(In the text)
- Edwin, P., &
Roberts, B. 1983, Sol. Phys., 88, 179 [NASA ADS] [CrossRef]
(In the text)
- Erdélyi,
R., & Hargreaves, J. 2008, A&A (in press)
(In the text)
- Hargreaves, J. 2008, Ph. D. Thesis,
University of Sheffield, 84
- Hasan, S. S.,
& Kalkofen, W. 1999, ApJ, 519, 899 [NASA ADS] [CrossRef]
(In the text)
- Hindman, B.
W., & Jain, R. 2008, ApJ, 677, 899 [CrossRef]
(In the text)
- Kalkofen,
W., Rossi, P., Bodo, G., & Massaglia, S. 1994, A&A, 284,
976 [NASA ADS]
(In the text)
- Lamb,H. 1932,
Hydrodynamics (Cambridge University Press), 138 [NASA ADS]
(In the text)
- Long, D. M.,
Gallagher, P. T., McAteer, R. T. J., & Bloomfield, D. S. 2008,
ApJ, 680, 81 [NASA ADS] [CrossRef]
(In the text)
- McEwan, M. P.,
Donnelly, G. R., Diaz, A. J., & Roberts, B. 2006, A&A, 460,
893 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Musielak,
Z. E., & Ulmschneider, P. 2001, A&A, 370, 541 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Musielak,
Z. E., & Ulmschneider, P. 2003, A&A, 400, 1057 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
-
Nakariakov, V. M., Ofman, L., DeLuca, E. E., Roberts, B., &
Davila, J. M. 1999, Science, 285, 862 [NASA ADS] [CrossRef]
- Rae, I. C., &
Roberts, B. 1982, ApJ, 256, 761 [NASA ADS] [CrossRef]
(In the text)
- Roberts, B.
2004, in Waves, oscillations and small-scale transient events in
the solar atmosphere: a joint view from SOHO and TRACE, ESA SP-547,
1
(In the text)
- Roberts, B.,
& Webb, A. R. 1978, Sol. Phys., 56, 5 [NASA ADS] [CrossRef]
(In the text)
- Roberts, B.,
Edwin, P. M., & Benz, A. O. 1984, ApJ, 279, 857 [NASA ADS] [CrossRef]
(In the text)
- Ruderman,
M. S., & Roberts, B. 2002, ApJ, 577, 475 [NASA ADS] [CrossRef]
- Selwa, M.,
Murawski, K., Solanki, S. K., & Wang, T. J. 2007, A&A, 462,
1127 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Spruit, H.C
1981, A&A, 98, 155 [NASA ADS]
(In the text)
- Sutmann, G.,
Musielak, Z. E., & Ulmschneider, P. 1998, A&A, 340,
556 [NASA ADS]
(In the text)
- Terradas,
J., Oliver, R., & Ballester, J. L. 2005, A&A, 441, 371 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Terradas,
J., Andries, J., & Goossens, M. 2007, Sol. Phys., 246, 231 [NASA ADS] [CrossRef]
(In the text)
- Thompson,
B. J., Gurman, J. B., Neupert, W. M., et al. 1999, ApJ, 517,
151 [NASA ADS] [CrossRef]
(In the text)
- Verth, G., &
Erdélyi, R. 2008, A&A, 486, 1015 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Verth, G., van
Doorselaere, T., Erdélyi, R., & Goossens, M. 2007,
A&A, 457, 341 [NASA ADS] [CrossRef]
(In the text)
-
Verwichte, E., Nakariakov, V. M., Ofman, L., & Deluca, E. E.
2004, Sol. Phys., 233, 77 [NASA ADS] [CrossRef]
(In the text)
-
Wills-Davey, M. J., & Thompson, B. J. 1999, Sol. Phys., 190,
467 [NASA ADS] [CrossRef]
(In the text)
Copyright ESO 2008
![]() and
and ![]() to be oriented along the loop
and in a transversal direction. We assume that the EIT wave is
acting with a force
to be oriented along the loop
and in a transversal direction. We assume that the EIT wave is
acting with a force ![]() (per unit volume) on the tube and the direction of
this force is directed along the x-axis. For the sake of
simplicity all dissipative effects are neglected. A schematic representation of
the model is shown in Fig. 1.
(per unit volume) on the tube and the direction of
this force is directed along the x-axis. For the sake of
simplicity all dissipative effects are neglected. A schematic representation of
the model is shown in Fig. 1.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9833fig1.eps}\end{figure}](/articles/aa/full/2008/36/aa09833-08/Timg5.gif)
![]() can be decomposed with respect to the
parallel and perpendicular direction of the tube such as
can be decomposed with respect to the
parallel and perpendicular direction of the tube such as
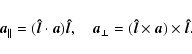
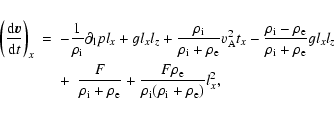
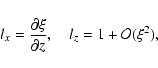
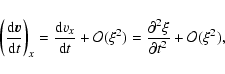
![]() and we choose the value of
the parameter
and we choose the value of
the parameter ![]() such that all first derivatives with
respect to z vanish. After a straightforward calculation we
obtain that when
such that all first derivatives with
respect to z vanish. After a straightforward calculation we
obtain that when
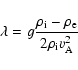
![]() )
for
the homogeneous part of Eq. (18), the dispersion
relation of these linear waves is given as
)
for
the homogeneous part of Eq. (18), the dispersion
relation of these linear waves is given as
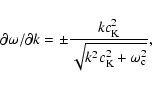
![]() followed by a wake
oscillating with the frequency
followed by a wake
oscillating with the frequency
![]() .
.
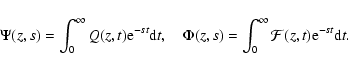
![\begin{displaymath}F_s[f(x)]=\frac{1}{L}\int_0^Lf(x)\sin\alpha_nx\;{\rm d}x,
\end{displaymath}](/articles/aa/full/2008/36/aa09833-08/img67.gif)
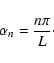
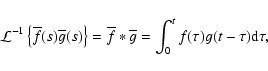
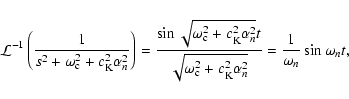
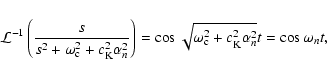
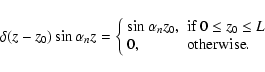
![\begin{displaymath}\frac{B^2}{\mu}\pi
R^2\left[\frac{1}{(1+\lambda_{\rm e}^2z_0^2)^{1/2}}+\frac{1}{(1+\lambda_{\rm e}^2(L-z_0)^2)^{1/2}}\right],
\end{displaymath}](/articles/aa/full/2008/36/aa09833-08/img96.gif)
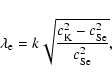
![]() )
is converted into inducing oscillations of the loop,
the energy of the EIT wave will work toward displacing the loop.
Therefore we can write that
)
is converted into inducing oscillations of the loop,
the energy of the EIT wave will work toward displacing the loop.
Therefore we can write that
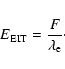
![\begin{figure}
\par\includegraphics[width=9cm,clip]{9833fig2.eps}\end{figure}](/articles/aa/full/2008/36/aa09833-08/Timg110.gif)
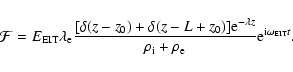
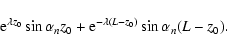
![\begin{figure}
\par\includegraphics[width=9cm,clip]{9833fig3.eps} \end{figure}](/articles/aa/full/2008/36/aa09833-08/Timg113.gif)
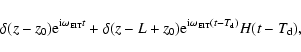
![\begin{figure}
\par\includegraphics[width=9cm,clip]{9833fig4.eps}\end{figure}](/articles/aa/full/2008/36/aa09833-08/Timg119.gif)
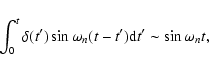
![]() ,
and later
as a shock wave with finite front thickness (a non-harmonic
driver). The results show that in case of a non-harmonic driver
the periods of generated modes always belong to the natural periods of the loop.
On the other hand, in the case of a periodic driver - for
an arbitrary period of the driver - there will be a mixture of standing modes which
could explain on the observed period ratio. The
analysis carried out here for different type of drivers show
that the generated oscillations will carry predominantly
information about the driver rather than the loop itself.
,
and later
as a shock wave with finite front thickness (a non-harmonic
driver). The results show that in case of a non-harmonic driver
the periods of generated modes always belong to the natural periods of the loop.
On the other hand, in the case of a periodic driver - for
an arbitrary period of the driver - there will be a mixture of standing modes which
could explain on the observed period ratio. The
analysis carried out here for different type of drivers show
that the generated oscillations will carry predominantly
information about the driver rather than the loop itself.