A&A 488, 1133-1147 (2008)
DOI: 10.1051/0004-6361:200809822
T. C. Hinse1,2 - R. Michelsen1 - U. G. Jørgensen1 - K. Gozdziewski3 - S. Mikkola4
1 - Niels Bohr Institute, University of Copenhagen, Juliane Maries Vej
30, 2100 Ø, Denmark
2 -
Armagh Observatory, College Hill, BT61 9DG Armagh, Northern Ireland, UK
3 -
Nicolaus Copernicus University, Torun Centre for Astronomy, Gagarin Str. 11, 87-100 Torun, Poland
4 -
Turku University Observatory, Väisäläntie 20, Piikkiö, Finland
Received 20 March 2008 / Accepted 3 June 2008
Abstract
Aims. We study gravitational perturbation effects of observed giant extrasolar planets on hypothetical Earth-like planets in the context of the three-body problem. This paper considers a large parameter survey of different orbital configuration of two extrasolar giant planets (HD 70642b and HD 4208b) and compares their dynamical effect on Earth-mass planetary orbits initially located within the respective habitable terrestrial region. We are interested in determining giant-planet orbit (and mass) parameters that favor the condition to render an Earth-mass planet to remain on a stable and bounded orbit within the continuous habitable zone.
Methods. We applied symplectic numerical integration techniques to studying the short and long term time evolution of hypothetical Earth-mass planets that are treated as particles. In addition, we adopt the MEGNO technique to obtain a complete dynamical picture of the terrestrial phase space environment. Both multi-particle and single-particle simulations were performed to follow an Earth-mass planet in the habitable region and its subsequent long term evolution.
Results. Our numerical simulations show that giant planets should be on circular orbits to minimize the perturbative effect on terrestrial orbits. The orbit eccentricity (and hence proximity) is the most important orbital parameter of dynamical significance. The most promising candidate for maintaining an Earth-mass planet on a stable and bounded orbit well-confined to the continuous habitable zone is HD 70642b. Even the large planetary mass of HD 70642b renders an Earth-mass planet habitable during the complete lifetime of the host star. The results allow us to extrapolate similar observed systems and points the necessity further constraining the uncertainty range in giant planet orbital eccentricity by future follow-up observations.
Key words: chaos - methods: N-body simulations - celestial mechanics - astrobiology
This paper considers dynamical aspects and orbital stability properties of telluric (Earth-like) planets within the circumstellar habitable zone (HZ) of two selected single-planet extrasolar systems HD 4208 and HD 70642. The ability of a planet to support life is based on our knowledge of life on Earth and Earth's location within the solar system. The concept of the HZ, or the radial distance around a star in which a telluric planet's atmosphere might be able to maintain liquid water to eventual initiate and support life, has been presented and discussed in the scientific literature for many years (Huang 1959; Hart 1979; Kasting et al. 1993; Kasting & Catling 2003). For liquid water to exist, the average surface temperature must remain between 273 K and 373 K at 1 atm. atmospheric pressure.
The discovery of the first extrasolar giant (Jupiter-like) planet (Mayor & Queloz 1995) raises the natural question of whether Earth-like planets exist within known extrasolar planetary systems. Most of the known extrasolar planets (in orbit around a main-sequence host star) were detected by ground-based radial velocity observations. This technique favors the detection of a massive planet in a close orbit. Detecting Earth-mass planets around solar like host stars is just outside the current detection capability of the radial velocity technique.
In addition to the formation of observed Jupiter-like planets, terrestrial
planets are expected to be formed by accretion processes within the
inner region of a circumstellar protoplanetary disk (Agnor et al. 1999; O'Brian et al. 2006; Quintana et al. 2007; Raymond et al. 2004; Quintana & Lissauer 2006; Wetherill 1996; Chambers 2001; Chambers & Wetherill 1998; Kokubo & Ida 2000; Chambers 2003; Thébault et al. 2002). Today,
major observational efforts focus on the detection of an Earth-like extrasolar
planet by various techniques. Recently, the terrestrial planet formation
theory is supported by both microlensing and radial velocity observations:
Beaulieu et al. (2006) demonstrate the microlensing detection of a 5.5
Earth-mass planet at 2.6 AU orbital distance from the host star. In addition,
Udry et al. (2007) report on the detection of an almost equally small mass
planet close to or in the habitable region in orbit around an M-dwarf star. The
currently on going satellite mission COROT![]() will possibly detect Earth-mass planets by the transit method. Other future
satellite missions sheduled for launch include
TPF
will possibly detect Earth-mass planets by the transit method. Other future
satellite missions sheduled for launch include
TPF![]() ,
KEPLER
,
KEPLER![]() , and
SIM
, and
SIM![]() - all capable
of detecting extrasolar Earth-mass planets orbiting main sequence host stars.
- all capable
of detecting extrasolar Earth-mass planets orbiting main sequence host stars.
This motivates us to conduct numerical experiments to study dynamics and stability properties of hypothetical telluric planetary orbits within observed extrasolar planetary systems. This subject is very interesting and has already been investigated by a few groups (Menou & Tabachnik 2003; Jones et al. 2001; Noble et al. 2002; Sándor et al. 2007; Asghari et al. 2004; Jones et al. 2005; Süli et al. 2007). In particular, we are interested in the orbital stability properties of a telluric planet considering giant planet perturbations. It is reasonable to expect that the requirement of long term orbit confinement of a telluric planet within the habitable zone is a necessary condition for the development of biological activity. The question is what orbit configurations of the giant planet are preferred to maintain a stable telluric planet that initially was assumed to be formed in the habitable zone. To answer this question, we chose to investigate and compare two systems containing a giant planet with different orbital properties. The difference in these two systems is mainly in the size of the derived semi-major axis. This work relies heavily on merging two approaches - the fast indicator mappings to resolve the overall phase space structure with longterm secular time scale integrations to understand individual orbits of Earth-like planets. In Sect. 2 we present orbital parameters inferred from radial velocity observations of the two systems HD 70642 (this system is a close analogue to the Sun) and HD 4208. In Sect. 3 we derive the zonal boundaries of the habitable region for each system. Sections 4 and 5 describes the applied numerical methods and adopted initial conditions for the parameter survey. Section 6 presents the results and the presented work is summarized with conclusions in Sect. 7.
A planet, HD 70642b, in orbit around the star HD 70642 has been announced by
Carter et al. (2003) based on radial velocity observations. Data aquisition has
been ongoing during a 5-year time period within the Anglo-Australian Planet
Search Program. As a result of the long observing baseline and constant
precision measurements, HD 70642b marks the onset of the emergence of planets in
long-period near circular orbits. Orbital parameters of the planet are listed
in Table 1. The star HD 70642 is a chromosphericlly
inactive nearby solar-like G5 dwarf. Physical properties were obtained by
photometrical and spectroscopic observations. The mass of HD 70642 is
![]() and its age is estimated to be
and its age is estimated to be
![]() yrs with
surface temperature
yrs with
surface temperature
![]() K. The metallicity of HD 70642 is
consistent with the majority of observed host stars harboring planets.
K. The metallicity of HD 70642 is
consistent with the majority of observed host stars harboring planets.
The existence of a single planet, HD4208b, in orbit around HD 4208 has been
presented by Vogt et al. (2001) based on radial velocity observations obtained
within the Keck planet search program. Orbital parameters, as determined from
1-planet Kepler fits, are listed in Table 1. Physical
information on host star properties are based on Strømgren photometry,
Hipparcos astrometric, and Keck spectral observations. HD 4208 is a Sun-like
star of spectral type G5V with an estimated mass of
![]() and
surface temperature
and
surface temperature
![]() K. This estimate agrees with
independent published results obtained within the Geneva-Copenhagen star
survey program (Nordström et al. 2004). However, no estimate of the stellar age
has been published yet in the literature. Preliminary calculations using stellar
evolution models indicate an age of
K. This estimate agrees with
independent published results obtained within the Geneva-Copenhagen star
survey program (Nordström et al. 2004). However, no estimate of the stellar age
has been published yet in the literature. Preliminary calculations using stellar
evolution models indicate an age of
![]() Gyr (Southworth 2005,
private communication). In the case of HD 4208, the process of isochrone
fitting age determination is not reliable due to too large an uncertainty
range in observed stellar parameters. In this paper, we assume an age of 4.5 Gyr for HD 4208.
Gyr (Southworth 2005,
private communication). In the case of HD 4208, the process of isochrone
fitting age determination is not reliable due to too large an uncertainty
range in observed stellar parameters. In this paper, we assume an age of 4.5 Gyr for HD 4208.
Table 1: Derived orbital parameters for HD 4208b and HD 70642b from synthetic 1-planet Kepler fits to observed radial velocity data.
In this paper, we adopt numerical estimates for the HZ from one-dimensional radiative-equilibrium atmosphere model calculations presented in Kasting et al. (1993).
![\begin{figure}
\par\includegraphics[width=7cm, height=5cm]
{9822Fig1a.eps}\includegraphics[width=7cm, height=5cm]
{9822Fig1b.eps}\end{figure}](/articles/aa/full/2008/36/aa09822-08/Timg61.gif) |
Figure 1:
Zonal boundaries of the habitable zone for the planetary systems
around HD 4208 ( left panel) and HD 70642 ( right panel). ZAMS HZ refers to
zero-age main sequence boundaries (initial boundaries) and CHZ refers to the
continuous habitable zone (inner triangular region). In geometrical
(x,y)-space, the contour lines represent circles of radius
|
| Open with DEXTER | |
Their work provides a good estimate of the position and extent of the HZ of an
Earth-like planet, although crucial parameters obviously have to be ignored,
which will have additional climatic effects on the location of
actual habitability of a planet from the host star. However, for all of these
advanced models, we obviously have to keep in mind that essential input for the
models are unknown in real life, such as the actual composition of the
exoplanetary atmosphere, the planetary albedo, and the question of whether
water actually exists on the planets. We disregard these additional
uncertainties in the following and adopt the boundary estimate of the HZ from
Kasting et al. (1993). Following their lead the HZ is determined by
applying several theoretical criteria to define the inner and outer boundaries.
The general strategy to find these criteria is to state environmental
conditions for a terrestrial-like planet in order to maintain surface water in
its liquid form during a substantial part of thehost star's main-sequence
period. In the model calculations, an Earth-like planet is assumed to have a 1
atm.
![]() atmosphere.
atmosphere.
Kasting et al. provide three criterions. We adopt the intermediate
criterion on the zonal boundaries in this work. This estimate of the inner and
outer boundaries of the HZ is referred to as the runaway greenhouse and
maximum greenhouse limit. The inner boundary is defined by the onset of water
evaporation. Water vapor enhances the greenhouse effect and therefore promotes
surface warming. Eventually at a critical point all surface water starts to
evaporate into the atmosphere and subsequently (in a runaway manner) is lost
from the upper atmosphere by hydrogen escape. The outer boundary is defined as
the maximum distance at which a surface temperature of 273 K can be maintained
by a cloud-free
![]() atmosphere (i.e. the point where there
would be enough
atmosphere (i.e. the point where there
would be enough
![]() and water in the planet's atmosphere to
raise surface temperatures to 273 K).
and water in the planet's atmosphere to
raise surface temperatures to 273 K).
The continous HZ (CHZ) is introduced to account for the gradual change in
stellar luminosity. According to stellar evolution models, the stellar
luminosity and surface temperature are a function of time, resulting in an
outward shift of the zonal boundaries. Adopting the intermediate criterion
Kasting et al. (1993) provides estimates of the time evolution of the HZ
boundaries for different stellar masses. This is necessary, since the habitable
zone for both HD 4208 (with assumed an age of
![]() yrs) and
HD 70642 is substantially evolved away from the initial ZAMS location. We
define the overlap region between the initial and present HZ annulus as the
continuous HZ (CHZ). In this paper, the zonal range of habitability for
both stars is determined by linear interpolation between the
yrs) and
HD 70642 is substantially evolved away from the initial ZAMS location. We
define the overlap region between the initial and present HZ annulus as the
continuous HZ (CHZ). In this paper, the zonal range of habitability for
both stars is determined by linear interpolation between the
![]() and
and
![]() boundary evolution lines shown in
Kasting et al. (1993, Fig. 14).
boundary evolution lines shown in
Kasting et al. (1993, Fig. 14).
This approach to adopting the zonal habitable boundaries is similar to previous work (Jones et al. 2001; Jones & Sleep 2002) that considers exoplanetary host stars of different spectral types. The time evolution of the HZ boundaries has been further developed by Jones et al. (2005) in combining the Kasting et al. model with modern stellar evolution models. A slightly different choice in the criterion for the boundary limits is made in Noble et al. (2002). A more advanced geodynamical model was developed to determine the HZ within the Solar system (Franck et al. 2000). Application of this model to the 47 UMa system is found in Cuntz et al. (2003).
For a planet to maintain habitability (and eventually initiate biological activity) during the host star's entire main-sequence life time, the telluric planet's orbit needs to remain confined to within the CHZ. The fulfillment of this requirement is not obvious, if external gravitational perturbations are applied.
The following outline is a simple attempt to impose geometrical constrains on (a,e) orbit parameters implying habitability. This method reflects a new approach to assessing a qualitative test of the orbit confinement in (a,e)-space of the telluric planet and differs from previous work within dynamical analysis work of habitable telluric planets.
The confinement of a telluric planet's orbit to a given annulus (i.e. the
CHZ), imposes certain constraints on orbital parameters (a,e). If
![]() and
and
![]() denotes the inner and outer boundary distance of a given annulus
from the central host star, then the constraint condition on the orbital
pericenter and apocenter distances is
denotes the inner and outer boundary distance of a given annulus
from the central host star, then the constraint condition on the orbital
pericenter and apocenter distances is
| (1) |
The underlying model used to study orbital stability properties of a telluric
planet adopts point-mass Newtonian mechanics considering gravitational
perturbations within the full and restricted three-body problem on different
time scales. In the stellarcentric frame, the planetary problem ((n+1)-body
problem; with n=2 being the number of planets) to be solved is given by the
equations of motion (Morbidelli 2002)
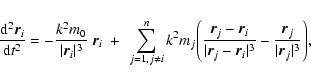 |
(2) |
To solve the equations of motion we used the symplectic (hybrid-MVS) and extrapolation (Radau) algorithms as implemented in the MERCURY package (Chambers & Migliorini 1997; Chambers 1999). We split our numerical analysis into three sections: i) computation of MEGNO maps (to be discussed in more detail in Sect. 4.2); ii) multi-particle test simulations over intermediate time scales, and iii) single-massive-planet simulations on long time scales.
In dynamical theory, orbital instability is usually associated with chaotic
dynamics. A powerful numerical method of quantitatively differentiating between
quasi-periodic and chaotic dynamics is the MEGNO (Mean Exponenial Growth
factor of Nearby Orbits) technique introduced by Cincotta & Simó (2000); Cincotta et al. (2003). Calculating the MEGNO factor
![]() (sometimes also referred to as the MEGNO indicator) for a given set of initial
conditions provides a measure of chaoticity of the system evolution over the
time span T. The MEGNO indicator is closely related to the Lyapunov
characteristic number (LCN or maximum Lyapunov exponent), which quantitatively
measures exponential divergence of nearby orbits (Morbidelli 2002) and
belongs to the class known as fast indicators. This technique is very
effective in exploring a multi-parameter, dynamical system. In order to
explore the global dynamics of a perturbed telluric planet, we numerically
computed the MEGNO indicator to construct phase space stability (instability)
maps. This technique is computationally efficient and allows one to explore a
large phase space in relatively short times. Detailed theoretical and
computational aspects of MEGNO and its applications to planet dynamics work are
given in Gozdziewski (2001). The MEGNO technique has been successfully
applied in a variety of dynamical analysis studies
(Breiter et al. 2005; Gozdziewski 2004,2003; Gozdziewski & Maciejewski 2001), including
stability studies of a telluric planet within 47 UMa (Gozdziewski 2002).
In the following we briefly review important properties of the MEGNO indicator.
(sometimes also referred to as the MEGNO indicator) for a given set of initial
conditions provides a measure of chaoticity of the system evolution over the
time span T. The MEGNO indicator is closely related to the Lyapunov
characteristic number (LCN or maximum Lyapunov exponent), which quantitatively
measures exponential divergence of nearby orbits (Morbidelli 2002) and
belongs to the class known as fast indicators. This technique is very
effective in exploring a multi-parameter, dynamical system. In order to
explore the global dynamics of a perturbed telluric planet, we numerically
computed the MEGNO indicator to construct phase space stability (instability)
maps. This technique is computationally efficient and allows one to explore a
large phase space in relatively short times. Detailed theoretical and
computational aspects of MEGNO and its applications to planet dynamics work are
given in Gozdziewski (2001). The MEGNO technique has been successfully
applied in a variety of dynamical analysis studies
(Breiter et al. 2005; Gozdziewski 2004,2003; Gozdziewski & Maciejewski 2001), including
stability studies of a telluric planet within 47 UMa (Gozdziewski 2002).
In the following we briefly review important properties of the MEGNO indicator.
The numerical calculation of the MEGNO indicator is based on the ODEX package
using the Gragg-Bulirsch-Stoer (GBS) extrapolation method of Hairer et al. (1993)
solving the variational equations (using the technique outlined in Mikkola &
Innanen 1999) within the framework of the n-body problem. The
variational equations describe the dynamical propagation of a small change in
initial conditions. Finding a solution to the system of variational equations
allows computation of the time-averaged MEGNO indicator. Because in the
chaotic system the variations can grow without bounds, during the course of the
integration of the system, it is necessary to renormalize the variational
vector after a certain time ![]() .
The renormalization procedure was
originally introduced by Benettin et al. (1976) ensuring the prevention of
numerical overflow and saturation. In practice, renormalization is a simple
numerical operation due to the linear nature of the variational equations.
Tancredi et al. (2001) points out that numerical errors are introduced at
renormalisation time steps in weak chaotic domains of phase space resulting in
a false computation of the LCN. However, this is only true for the 2-particle
shadow method (Benettin et al. 1976) in which two adjacent orbits are integrated
separately in phase space. Applying periodic renormalization in the framework of
the variational equations does not lead to spurious numercial artifacts in the
computation of the LCN as derived from the MEGNO technique. However, this
statement is only partially true. In Sect. 4.3, we demonstrate
the numerical effect of applying a renormalization time step in our effort to
find a solution of the variational equations when computing the MEGNO factor
and the derived LCN.
.
The renormalization procedure was
originally introduced by Benettin et al. (1976) ensuring the prevention of
numerical overflow and saturation. In practice, renormalization is a simple
numerical operation due to the linear nature of the variational equations.
Tancredi et al. (2001) points out that numerical errors are introduced at
renormalisation time steps in weak chaotic domains of phase space resulting in
a false computation of the LCN. However, this is only true for the 2-particle
shadow method (Benettin et al. 1976) in which two adjacent orbits are integrated
separately in phase space. Applying periodic renormalization in the framework of
the variational equations does not lead to spurious numercial artifacts in the
computation of the LCN as derived from the MEGNO technique. However, this
statement is only partially true. In Sect. 4.3, we demonstrate
the numerical effect of applying a renormalization time step in our effort to
find a solution of the variational equations when computing the MEGNO factor
and the derived LCN.
Following Cincotta & Simó (2000), Cincotta et al. (2003) and
Gozdziewski (2001), if the phase space trajectory is a regular or quasi-periodic solution (characterized by linear divergence of nearby orbits), then asymptotically
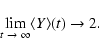 |
(3) |
In the literature, rigorous tests and accuracy checks have been performed in the
calculation of the MEGNO indicator to ensure numerical stability of results,
and possible caveats of this technique have been discussed
(Gozdziewski 2001). In the following, we report on an additional test
supplementing Gozdziewski's accuracy checks for the reliable computation of
![]() .
This test concerns the choice of the renormalization
time step
.
This test concerns the choice of the renormalization
time step ![]() :
a too long
:
a too long ![]() allows the separation vector to grow long
enough to introduce numerical errors. Hence,
allows the separation vector to grow long
enough to introduce numerical errors. Hence, ![]() should be kept small enough
to maintain numerical accuracy. The Lyapunov characterstic number can be
approximately recovered from the time-running evolution law
should be kept small enough
to maintain numerical accuracy. The Lyapunov characterstic number can be
approximately recovered from the time-running evolution law
![]() (Cincotta & Simó 2000; see Eq. (4)). The goal
of this test is to numerically reproduce the Lyapunov time (i.e.
(Cincotta & Simó 2000; see Eq. (4)). The goal
of this test is to numerically reproduce the Lyapunov time (i.e.
![]() )
for a particle perturbed by Jupiter for a range of renormalization
time steps. Wisdom (1983) provides the initial conditions for numerically
modeling asteroid dynamics within the 3:1 mean-motion
resonance
)
for a particle perturbed by Jupiter for a range of renormalization
time steps. Wisdom (1983) provides the initial conditions for numerically
modeling asteroid dynamics within the 3:1 mean-motion
resonance![]() . In this particular case, Wisdom consistently derived
. In this particular case, Wisdom consistently derived
![]() or
or
![]() yrs. Figure 2 shows the time
evolution of the LCN, as computed from the MEGNO, in the classical
yrs. Figure 2 shows the time
evolution of the LCN, as computed from the MEGNO, in the classical
![]() -graph for various choices of the renormalization time
step
-graph for various choices of the renormalization time
step
![]() ,
where
,
where
![]() is Jupiters orbital
period. Each numerical integration invokes identical initial conditions for
the test particle. The graphs are derived from the
is Jupiters orbital
period. Each numerical integration invokes identical initial conditions for
the test particle. The graphs are derived from the
![]() evolution law. The range for the variable renormalization time step is from
evolution law. The range for the variable renormalization time step is from
![]() to
to
![]() as indicated in the figure
legend. From Fig. 2 one observes a random scatter of
as indicated in the figure
legend. From Fig. 2 one observes a random scatter of
![]() for
for
![]() ,
showing no systematics in the final
,
showing no systematics in the final ![]() as a
function of
as a
function of ![]() (see the inset figure in Fig. 2). A systematic
trend is first observed for
(see the inset figure in Fig. 2). A systematic
trend is first observed for
![]() ,
clearly showing a significant
deviation of
,
clearly showing a significant
deviation of ![]() from the value published in Wisdom (1983).
Furthermore, Fig. 2 suggests that rescaling the variational
equations should be done on the order of
from the value published in Wisdom (1983).
Furthermore, Fig. 2 suggests that rescaling the variational
equations should be done on the order of
![]() or less. For
or less. For
![]() ,
the algorithm is no longer stable, yielding false
Lyapunov times.This test concludes that the Lyapunov time of an asteroid can be
determined from the time evolution of the MEGNO factor and the renormalization
time should be a few tens of Jupiter's orbital period. The experiment shows
the importance of choosing a proper renormalization time to obtain reliable
results. Too large
,
the algorithm is no longer stable, yielding false
Lyapunov times.This test concludes that the Lyapunov time of an asteroid can be
determined from the time evolution of the MEGNO factor and the renormalization
time should be a few tens of Jupiter's orbital period. The experiment shows
the importance of choosing a proper renormalization time to obtain reliable
results. Too large ![]() would allow the dynamical system to have enough time
between any two renormalizations of the variational vector to produce numerical
overflow due to exponential behavior of the orbit (or variational vector).
However, it must be mentioned that no ready-made description exists of how to
choose the correct renormalization step size and generally extrapolating the
results obtained in this test to other problems is not guaranteed, so numerical
tests are always encouraged. In general, the proper choice of the
renormalization time depends on the nature of the dynamical problem under
study. Intuitively, systems which involve strong perturbations generally
require a small renormalisztion step size, since large deviations in the
variational vector are expected on short time scales. A possibly universal
approach to determining a proper renormalization step size would be to
constantly monitor the norm of the variational vector in time and impose some
constraint of a maximum allowed length in phase space. Whenever this maximum is
reached, the algorithm applies the renormalization of the variational vector
at a given time, after which the monitoring process is repeated. Within the
present work, we were guided by our test and adopted a renormalization step
size equivalent to the orbital period of the outer giant planet. Our choice of
the renormalisation time proves adequate when comparing the obtained results
with previously published independent data.
would allow the dynamical system to have enough time
between any two renormalizations of the variational vector to produce numerical
overflow due to exponential behavior of the orbit (or variational vector).
However, it must be mentioned that no ready-made description exists of how to
choose the correct renormalization step size and generally extrapolating the
results obtained in this test to other problems is not guaranteed, so numerical
tests are always encouraged. In general, the proper choice of the
renormalization time depends on the nature of the dynamical problem under
study. Intuitively, systems which involve strong perturbations generally
require a small renormalisztion step size, since large deviations in the
variational vector are expected on short time scales. A possibly universal
approach to determining a proper renormalization step size would be to
constantly monitor the norm of the variational vector in time and impose some
constraint of a maximum allowed length in phase space. Whenever this maximum is
reached, the algorithm applies the renormalization of the variational vector
at a given time, after which the monitoring process is repeated. Within the
present work, we were guided by our test and adopted a renormalization step
size equivalent to the orbital period of the outer giant planet. Our choice of
the renormalisation time proves adequate when comparing the obtained results
with previously published independent data.
![\begin{figure}
\par\includegraphics[width=9cm,height=6cm,clip]{9822Fig2.eps}\end{figure}](/articles/aa/full/2008/36/aa09822-08/Timg88.gif) |
Figure 2:
Parameter survey of the renormalization time step |
| Open with DEXTER | |
The use of MEGNO maps is an efficient way to explore the system's phase space
structure, thereby providing a global picture of interesting dynamical features
associated to resonance phenomena. In this work we apply the MEGNO technique to
studying the orbital stability (instability) properties of a telluric planet
within initial
![]() parameter space (or any other 2D phase
space section with a different choice in initial conditions,
Gozdziewski (2003), where
parameter space (or any other 2D phase
space section with a different choice in initial conditions,
Gozdziewski (2003), where
![]() denotes the semi-major axis of the
hypothetical telluric (test particle) planet and
denotes the semi-major axis of the
hypothetical telluric (test particle) planet and
![]() the eccentricity
of the perturbing giant planet. Results are shown in
Figs. 4a, b and 5. In the
following we outline the general construction of MEGNO maps. For a given range
in eccentricity and semi-major axis, the grid of initial conditions is given by
the eccentricity
of the perturbing giant planet. Results are shown in
Figs. 4a, b and 5. In the
following we outline the general construction of MEGNO maps. For a given range
in eccentricity and semi-major axis, the grid of initial conditions is given by
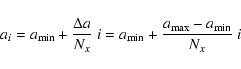 |
(5) |
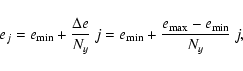 |
(6) |
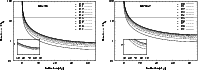 |
Figure 3:
Graphical representation of Eq. (7) showing the
dependence of the planet mass on the line-of-sight inclination for different
orbit eccentricities for the giant planets HD 4208b ( left panel) and HD 70642b
( right panel). Numerical values for K and P within the mass function are
taken from Table 1 for each system. The inset in
each plot represents the
|
| Open with DEXTER | |
Accuracy checks were performed in all numerical simulations presented in this
work. To capture the correct physics (near the pericenter passage), we
monitored the relative energy error dE/E (most sensitive) to probe numerical
accuracy. Convergence tests were carried out to determine the minimum accuracy
of the conservation of relative energy. Two accuracy parameters are necessary
for a GBS-integration, which needs to be specified for a given accuracy
requirement. To conserve energy on the order of d
![]() during a
given integration, the absolute
during a
given integration, the absolute ![]() and relative
and relative
![]() error
tolerance parameters are both set to
error
tolerance parameters are both set to
![]() using double
precision arithmetic. In general, the error in relative energy is
characterized by a random walk. This is explained by stochastic accumulation
of rounding errors during numerical computations. In Radau integrations, the
local error accuracy parameter for step size adjustment is set to 10-14resulting in
using double
precision arithmetic. In general, the error in relative energy is
characterized by a random walk. This is explained by stochastic accumulation
of rounding errors during numerical computations. In Radau integrations, the
local error accuracy parameter for step size adjustment is set to 10-14resulting in
![]() .
.
Writing the equations of motion in the stellar-centric frame, the three-body
problem has 12 dynamical variables (6 degrees of freedom). In addition,
including the masses as free parameters, we then have 15 free parameters to be
determined as initial conditions for the numerical integration. Assuming
coplanar orbits (eliminating four dynamical variables or two d.o.f.), we are
left with
![]() for each planet, where a the semi-major axis,
e the eccentricity,
for each planet, where a the semi-major axis,
e the eccentricity, ![]() is the longitude of pericenter, and Mdenotes the mean anomaly of the orbit. The mass of the host star is held
constant during the integration and its nominal value is adopted from the
literature (cf. Sects. 2.1 and 2.2). Our parameter
survey was done within the observed uncertainty range of the giant planet orbit
eccentricity e and giant planet mass
is the longitude of pericenter, and Mdenotes the mean anomaly of the orbit. The mass of the host star is held
constant during the integration and its nominal value is adopted from the
literature (cf. Sects. 2.1 and 2.2). Our parameter
survey was done within the observed uncertainty range of the giant planet orbit
eccentricity e and giant planet mass
![]() .
These quantities are
dynamically interesting. The giant planet mass, orbital element
uncertainty range, and nominal values are listed in
Table 1.
.
These quantities are
dynamically interesting. The giant planet mass, orbital element
uncertainty range, and nominal values are listed in
Table 1.
In constructing MEGNO stability maps, the telluric planet was started on a
circular orbit with mean longitude
![]() .
The planar three-body
problem was considered, and we set the mass of the telluric planet to be
.
The planar three-body
problem was considered, and we set the mass of the telluric planet to be
![]() .
The survey range in the telluric planets semi-major
axis was set to
.
The survey range in the telluric planets semi-major
axis was set to
![]() (HD 70642)
and
(HD 70642)
and
![]() (HD 4208). For these
experiments the observed giant planet's eccentricity was surveyed within the
observed uncertainty range as shown in Table 1. The
remaining orbital elements were set to their nominal published values and the
mean anomaly of the giant planet set to
(HD 4208). For these
experiments the observed giant planet's eccentricity was surveyed within the
observed uncertainty range as shown in Table 1. The
remaining orbital elements were set to their nominal published values and the
mean anomaly of the giant planet set to
![]() in all
numerical experiments.
in all
numerical experiments.
In multi-particle simulations, we adopt the co-planar restricted three-body
model and numerically follow 2000 non-interacting test-particles (i.e without
self-gravitation). Initially and for both systems, all particles are started
on circular orbits with
![]() randomly distributed
within the whole range of the HZ.
randomly distributed
within the whole range of the HZ.
The derived giant planet mass is a minimum mass (corresponding to an orbit
viewed edge-on). An upper limit in this quantity is unknown as long as the
angle between the line-of-sight and the normal to the orbit is undetermined.
This indeterminacy justifies a i-parameter survey, which directly translates
to a survey in the mass parameter. The functional dependence of a planet's real
mass on the line-of-sight inclination i and orbit eccentricity e, is
obtained by considering the mass-function (Hilditch 2001). The significance
of the e-dependency on the planetary mass is unknown and needs some
attention in the following.
![\begin{figure}
\par\includegraphics[width=17.3cm]{Fig4online.eps}\end{figure}](/articles/aa/full/2008/36/aa09822-08/Timg121.gif) |
Figure 4:
MEGNO maps of a telluric planet within the dynamical
habitable zone for HD 4208 and HD 70642. The MEGNO indicator is color-coded
with white (
|
| Open with DEXTER | |
If
![]() measures the giant planet mass, we have the following analytic
expression for the minimum mass of the planet companion as a function of
orbit eccentricity
measures the giant planet mass, we have the following analytic
expression for the minimum mass of the planet companion as a function of
orbit eccentricity
Based on a statistical analysis on observed minimum masses
Zucker & Mazeh (2001) estimates that 5% of solar-type G stars in the solar
neighborhood have planets in the range 1-10
![]() .
A similar result was
obtained by Tabachnik & Tremaine (2002). We decided to consider a giant
planet mass survey in the range
.
A similar result was
obtained by Tabachnik & Tremaine (2002). We decided to consider a giant
planet mass survey in the range
![]() for
HD 4208b and HD 70642b, respectively.
for
HD 4208b and HD 70642b, respectively.
In the following, we present results in the form of MEGNO maps
considering
![]() sections within the phase space of HD 70642
and HD 4208. In all maps, we superimpose the contour lines of the extent
of the habitable zone boundaries within the terrestrial region of each system.
The inner triangular region represents the continuous habitable zone.
We chose to color-code quasi-periodic motion by white. Initial conditions
resulting in quasi-periodic motion have
sections within the phase space of HD 70642
and HD 4208. In all maps, we superimpose the contour lines of the extent
of the habitable zone boundaries within the terrestrial region of each system.
The inner triangular region represents the continuous habitable zone.
We chose to color-code quasi-periodic motion by white. Initial conditions
resulting in quasi-periodic motion have
![]() at the end of the integration. Initial conditions resulting in chaotic
orbits of the telluric planet differ from the white color.
at the end of the integration. Initial conditions resulting in chaotic
orbits of the telluric planet differ from the white color.
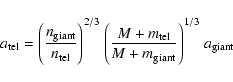 |
(8) |
For HD 4208, Fig. 4a shows the results of MEGNO scans within
the HD 4208b parameter space. Four selective scans corresponding to giant
planet masses
![]() are shown. From
Fig. 4a the dynamical effect of increasing the outer giant
planet's mass is evidently observed. For
are shown. From
Fig. 4a the dynamical effect of increasing the outer giant
planet's mass is evidently observed. For
![]() in
Fig. 4a, a general instability region occurs on the right side
of semi-major axis
in
Fig. 4a, a general instability region occurs on the right side
of semi-major axis
![]() and only dynamically
active for high giant-planet eccentricities. This instability region starts to
move inward towards the center of the continuous habitable zone for higher
masses of the observed giant planet. An interesting feature to note is the
decrease in the stability ``island'' at
and only dynamically
active for high giant-planet eccentricities. This instability region starts to
move inward towards the center of the continuous habitable zone for higher
masses of the observed giant planet. An interesting feature to note is the
decrease in the stability ``island'' at
![]() extending over a giant planet eccentricity range
extending over a giant planet eccentricity range
![]() .
Mean-motion resonances are observed and indicated with an arrow in
each MEGNO map within the figure panels of Fig. 4a. Of
particular interest is the 2:1 mean-motion resonance located at
.
Mean-motion resonances are observed and indicated with an arrow in
each MEGNO map within the figure panels of Fig. 4a. Of
particular interest is the 2:1 mean-motion resonance located at
![]() for
for
![]() .
The 2:1 resonance is ``active''
for almost all eccentricities of the outer giant planet. With increasing
giant-planet mass, the continuous habitable zone becomes dominated by the 3:1, 5:2,
and 2:1 mean-motion resonances. This is clearly evident for
.
The 2:1 resonance is ``active''
for almost all eccentricities of the outer giant planet. With increasing
giant-planet mass, the continuous habitable zone becomes dominated by the 3:1, 5:2,
and 2:1 mean-motion resonances. This is clearly evident for
![]() in Fig. 4a. The dynamical structure of the
terrestrial region in HD 4208 has also been studied by Asghari et al. (2004).
They present a stability map analysis of hypothetical telluric planets using
the Kolmogorov entropy as a quantitative measure to detect and differentiate
chaotic/quasi-periodic dynamics. They complement their analysis with (MEM)
maximum eccentricity maps. The results in Fig. 4a show an
almost one-to-one correlation of the MEGNO technique with the Kolmogorov
entropy method. Almost every feature from global (general) chaos to the
presence of mean-motion resonances are reproduced by two independent
techniques. However, Asghari et al. (2004) did not undertake a mass-parameter
survey for the giant planet HD 4208b. The results presented here in the form
of MEGNO stability maps considered various masses of the giant planet in
HD 4208.
in Fig. 4a. The dynamical structure of the
terrestrial region in HD 4208 has also been studied by Asghari et al. (2004).
They present a stability map analysis of hypothetical telluric planets using
the Kolmogorov entropy as a quantitative measure to detect and differentiate
chaotic/quasi-periodic dynamics. They complement their analysis with (MEM)
maximum eccentricity maps. The results in Fig. 4a show an
almost one-to-one correlation of the MEGNO technique with the Kolmogorov
entropy method. Almost every feature from global (general) chaos to the
presence of mean-motion resonances are reproduced by two independent
techniques. However, Asghari et al. (2004) did not undertake a mass-parameter
survey for the giant planet HD 4208b. The results presented here in the form
of MEGNO stability maps considered various masses of the giant planet in
HD 4208.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{09822f5.eps}\end{figure}](/articles/aa/full/2008/36/aa09822-08/Timg146.gif) |
Figure 5:
High-resolution MEGNO maps showing the phase-space finestructure of
several (high-order) mean-motion resonances within the habitable zone of
HD 4208. The mass of HD 4208b is
|
| Open with DEXTER | |
An interesting follow up is to study the phase-space finestructure of mean-motion resonances. Figure 5 (top panel) shows the finestructure of the 2:1 mean-motion resonance within HD 4208. This resonance resembles a wedge-like structure with a well-defined transition region from chaotic to quasi-periodic motions. The pecular V-shape structure is explained by resonance perturbation theory (Murray & Dermott 1999). The time evolution of the telluric semi-major axis captured within the 2:1 mean-motion resonance will exhibit oscillations determined by the resonance libration width.
The lower panel in Fig. 5, shows the
finestructure in the region
![]() AU. The high-resolution
MEGNO scan shows a magnification of three prominent mean-motion resonances. In
particular they correspond to the 9:5
AU. The high-resolution
MEGNO scan shows a magnification of three prominent mean-motion resonances. In
particular they correspond to the 9:5
![]() ,
5:3
,
5:3
![]() ,
and 8:5
,
and 8:5
![]() commensurabilities. Each resonance is located at the outer edge of the
continuous, habitable zone and dynamically active for near-circular orbits of
the giant perturber. The characteristic form of each resonance is V-shaped
and reflects the dependence of the libration width as a function of
giant-planet eccentricity. In both high-resolution scans several high-order,
mean-motion resonances are identified between the discussed resonances. It is
interesting to note the quasi-periodic region in the 5:3 mean-motion resonance
(lower panel of Fig. 5). This region
corresponds to regular motion in the libration zone of the 5:3 mean-motion
resonance and is characteristic of all mean-motion resonances. However, the
exact dynamical nature (quasi-periodic or chaotic) of a given mean-motion
resonance depends on the choice of initial conditions. A more detailed study
of resonance finestructure will be conducted in the future.
commensurabilities. Each resonance is located at the outer edge of the
continuous, habitable zone and dynamically active for near-circular orbits of
the giant perturber. The characteristic form of each resonance is V-shaped
and reflects the dependence of the libration width as a function of
giant-planet eccentricity. In both high-resolution scans several high-order,
mean-motion resonances are identified between the discussed resonances. It is
interesting to note the quasi-periodic region in the 5:3 mean-motion resonance
(lower panel of Fig. 5). This region
corresponds to regular motion in the libration zone of the 5:3 mean-motion
resonance and is characteristic of all mean-motion resonances. However, the
exact dynamical nature (quasi-periodic or chaotic) of a given mean-motion
resonance depends on the choice of initial conditions. A more detailed study
of resonance finestructure will be conducted in the future.
MEGNO stability maps only represent a portion of the total system's phase space.
No direct information on the time evolution of the telluric planet's
eccentricity and/or semi-major axis is provided by MEGNO maps. In the
following, we study the effect of giant planet (repeated) perturbations on
telluric planet orbital parameters. This is done by numerically following
![]() particles and studying their time evolution within (a,e)space. Since orbital energy and angular momentum are related to semi-major
axis and orbit eccentricity, this approach should give some detailed
understanding of the effect of resonance perturbations. Each particle is
assumed to model a telluric planet initially formed within the HZ.
In Figs. 8a, b and 7a, b, we show selected results in the form of
(a,e)-snapshots of multi-particle simulations for HD 4208 and HD 70642. The
particles were randomly distributed within
particles and studying their time evolution within (a,e)space. Since orbital energy and angular momentum are related to semi-major
axis and orbit eccentricity, this approach should give some detailed
understanding of the effect of resonance perturbations. Each particle is
assumed to model a telluric planet initially formed within the HZ.
In Figs. 8a, b and 7a, b, we show selected results in the form of
(a,e)-snapshots of multi-particle simulations for HD 4208 and HD 70642. The
particles were randomly distributed within
![]() (HD 70642) and
(HD 70642) and
![]() (HD 4208). The HZ boundaries are superimposed in each
snapshot and the CHZ is the inner triangular region. In particular, we focus
our discussion on particle dynamics with the CHZ. Each figure shows
simulation snapshots for two choices in initial parameters. The total
integration time is 106 years. Snapshot times were chosen so as to
demonstrate the most prominent dynamical transitions and features. Learning
from results obtained by MEGNO stability analysis, a total of four giant
planet masses were considered
(HD 4208). The HZ boundaries are superimposed in each
snapshot and the CHZ is the inner triangular region. In particular, we focus
our discussion on particle dynamics with the CHZ. Each figure shows
simulation snapshots for two choices in initial parameters. The total
integration time is 106 years. Snapshot times were chosen so as to
demonstrate the most prominent dynamical transitions and features. Learning
from results obtained by MEGNO stability analysis, a total of four giant
planet masses were considered
![]() .
Each
mass parameter was then paired with either two values in the orbit eccentricity
.
Each
mass parameter was then paired with either two values in the orbit eccentricity
![]() corresponding to the minimum and maximum values of
the observed eccentricity uncertainty range.
corresponding to the minimum and maximum values of
the observed eccentricity uncertainty range.
![\begin{figure}
\par\includegraphics[width=18cm,clip]{09822f6.eps}\end{figure}](/articles/aa/full/2008/36/aa09822-08/Timg155.gif) |
Figure 6:
Simulation snapshots for particles (telluric planets) within HD 70642
considering different giant planet parameters. For each panel the time is
indicated within each snapshot. A total of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=18cm,clip]{09822f7.eps}\end{figure}](/articles/aa/full/2008/36/aa09822-08/Timg157.gif) |
Figure 7:
Same as Fig. 6, but for different
choices of
|
| Open with DEXTER | |
For HD 70642 we present simulation snapshots of a swarm of particles under the
perturbation of different giant planet parameters. In general, within
Figs. 6 and 7, we
observe the development of oscillations in particle eccentricities induced by
giant-planet perturbations. The main dynamics are observed within a temporal
change in orbit eccentricity at a constant semi-major axis. This is best seen
by examining single-particle dynamics, to be discussed later. This dynamical
behavior is best demonstrated for the giant planet parameters shown in
Figs. 6b and 7b. Initially the particle swarm is excited in
eccentricity giving rise to a eccentricity gradient throughout the HZ after a
fast relaxation time (104 to 105 yrs). This e-excitement is greater
for particles in the proximity of the giant planet. The e-oscillations of
neighboring telluric orbits are phased at the beginning of each simulation
except at mean-motion resonance locations. These resonance perturbations
quickly introduce dephasing of orbit eccentricity oscillations. Comparing
Fig. 6b with MEGNO stability maps for HD 70642
(the
![]() case), we identified the prominent 3:1 (at
case), we identified the prominent 3:1 (at
![]() )
mean-motion resonances. Furthermore, the simulations in
Figs. 6a, b and
Figs. 7a, b shows that the oscillation
amplitude at a given semi-major axis is constant (except at mean-motion
resonances). However, the oscillation frequency increases with time, and
high-frequency oscillations are observed for particles close to the giant
perturber at the beginning. Animated MPEG simulation movies can be obtained
upon request.
Progressing in time, these frequencies increase and the e-oscillations begin
to narrow. In addition, we observe that telluric planets in general are
confined to within the CHZ for a low-
)
mean-motion resonances. Furthermore, the simulations in
Figs. 6a, b and
Figs. 7a, b shows that the oscillation
amplitude at a given semi-major axis is constant (except at mean-motion
resonances). However, the oscillation frequency increases with time, and
high-frequency oscillations are observed for particles close to the giant
perturber at the beginning. Animated MPEG simulation movies can be obtained
upon request.
Progressing in time, these frequencies increase and the e-oscillations begin
to narrow. In addition, we observe that telluric planets in general are
confined to within the CHZ for a low-
![]() giant planet orbit. This is
also true if HD 70642b is a massive
giant planet orbit. This is
also true if HD 70642b is a massive
![]() giant planet on
a circular orbit. Increasing the giant planet eccentricity results in a
migration of the periastron distance closer to the HZ region, introducing strong
concurrent perturbations on a telluric planet and resulting in large
oscillatory eccentricity excitations. Considering the case
giant planet on
a circular orbit. Increasing the giant planet eccentricity results in a
migration of the periastron distance closer to the HZ region, introducing strong
concurrent perturbations on a telluric planet and resulting in large
oscillatory eccentricity excitations. Considering the case
![]() ,
we observe that nearly all particles exceed the CH boundaries. Only a telluric
planet initially formed and located at
,
we observe that nearly all particles exceed the CH boundaries. Only a telluric
planet initially formed and located at
![]() will marginally stay within the CHZ. This result is nearly independent of
giant-planet mass (compare b-panel in Figs. 6
and 7).
will marginally stay within the CHZ. This result is nearly independent of
giant-planet mass (compare b-panel in Figs. 6
and 7).
![\begin{figure}
\par\includegraphics[width=18cm,clip]{09822f8.eps}\end{figure}](/articles/aa/full/2008/36/aa09822-08/Timg162.gif) |
Figure 8:
Simulation snapshots for particles (telluric planets) orbiting HD 4208
considering different giant planet parameters. For each panel the time is
indicated within each snapshot. A total of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=18cm,clip]{09822f9.eps}\end{figure}](/articles/aa/full/2008/36/aa09822-08/Timg163.gif) |
Figure 9:
Same as Fig. 8, but for different
choices of
|
| Open with DEXTER | |
Similar dynamical simulations were carried out for HD 4208.
In Figs. 8a, 8b, we observe telluric
e-excitations at
![]() and
and
![]() ,
corresponding to the 2:1 and 4:3 mean-motion
commensurabilities. Particles within the 2:1 resonance are observed to be
excited in eccentricity up to
,
corresponding to the 2:1 and 4:3 mean-motion
commensurabilities. Particles within the 2:1 resonance are observed to be
excited in eccentricity up to
![]() within the CHZ. Again the dynamics
are mainly oscillatory in eccentricity taken at the same semi-major axis.
Particles initially located with
within the CHZ. Again the dynamics
are mainly oscillatory in eccentricity taken at the same semi-major axis.
Particles initially located with
![]() are all on
low-e orbits during the integration time span and confined to within the
CHZ. In Fig. 8b the dynamical picture is more
dramatic when considering HD 4208b in a high-e orbit. First, we observe a quick
excitation of particle eccentricity at simulation start. The e-oscillations are
characterized by large amplitudes with an initial transient phasing of nearby
orbits. With time the frequency increases and e-oscillations tend to become
narrower leading to a crossing of nearby orbits. This observation is useful
when considering relative particle velocities and related accretion
possibilities within the terrestrial region. This is discussed in more
detail later. At mean-motion resonances, particle orbits are out of phase
nearly instantly. Particles initially located within a narrow band
are all on
low-e orbits during the integration time span and confined to within the
CHZ. In Fig. 8b the dynamical picture is more
dramatic when considering HD 4208b in a high-e orbit. First, we observe a quick
excitation of particle eccentricity at simulation start. The e-oscillations are
characterized by large amplitudes with an initial transient phasing of nearby
orbits. With time the frequency increases and e-oscillations tend to become
narrower leading to a crossing of nearby orbits. This observation is useful
when considering relative particle velocities and related accretion
possibilities within the terrestrial region. This is discussed in more
detail later. At mean-motion resonances, particle orbits are out of phase
nearly instantly. Particles initially located within a narrow band
![]() centered on
centered on
![]() (corresponds to 12% of the total range of the CHZ) have orbital
eccentricities well confined within the CHZ exhibiting e-oscillations
between
(corresponds to 12% of the total range of the CHZ) have orbital
eccentricities well confined within the CHZ exhibiting e-oscillations
between
![]() and
and
![]() .
For
.
For
![]() ,
particles are removed from the system by ejection (or
accreted onto the giant planet). At the end of the 106 year integration,
the formation of a gap is observed with a cleared region within
,
particles are removed from the system by ejection (or
accreted onto the giant planet). At the end of the 106 year integration,
the formation of a gap is observed with a cleared region within
![]() and
and
![]() .
From the
MEGNO stability map (Fig. 4a), we observe that this region is
dominated by chaotic particle motion resulting in orbital radial mixing with
subsequent ejection or accretion. The survival of a few particles at
.
From the
MEGNO stability map (Fig. 4a), we observe that this region is
dominated by chaotic particle motion resulting in orbital radial mixing with
subsequent ejection or accretion. The survival of a few particles at
![]() (3:2 mean-motion resonance) exhibits regular motion
(oscillatory in eccentricity), and this location is indicated as being
quasi-periodic within the corresponding MEGNO map
(cf. Fig. 4a). In Figs. 9a, b
we show additional simulation snapshots for various combinations in
giant-planet parameters. The dynamics as shown in
Fig. 9a are characterized by the 3:1
mean-motion resonance around
(3:2 mean-motion resonance) exhibits regular motion
(oscillatory in eccentricity), and this location is indicated as being
quasi-periodic within the corresponding MEGNO map
(cf. Fig. 4a). In Figs. 9a, b
we show additional simulation snapshots for various combinations in
giant-planet parameters. The dynamics as shown in
Fig. 9a are characterized by the 3:1
mean-motion resonance around
![]() and the
removal of particles with initial
and the
removal of particles with initial
![]() .
At
.
At
![]() we observe a large e-excitation of particles.
This excitation is best explained by the close proximity of the giant planet.
Furthermore, it is interesting to note the ``missing effect'' of the 5:2
mean-motion resonance at
we observe a large e-excitation of particles.
This excitation is best explained by the close proximity of the giant planet.
Furthermore, it is interesting to note the ``missing effect'' of the 5:2
mean-motion resonance at
![]() .
The corresponding
MEGNO stability map (Fig. 4a) indicates the presence of this
resonance. However, its effect is at most only at the 10%-level in
eccentricity excitation and less effective when compared with the dynamical
effect of the 3:1 mean-motion resonance. Finally, in
Fig. 9b, we show the worst-case scenario in
possible orbital parameters for HD 4208b considering
.
The corresponding
MEGNO stability map (Fig. 4a) indicates the presence of this
resonance. However, its effect is at most only at the 10%-level in
eccentricity excitation and less effective when compared with the dynamical
effect of the 3:1 mean-motion resonance. Finally, in
Fig. 9b, we show the worst-case scenario in
possible orbital parameters for HD 4208b considering
![]() .
In this case, almost all particles (with a > 0.9 AU) have been
removed from the CHZ after 106 years and roughly 10-15% of the total
initial population of test particles survived. In summary the dynamical picture
within the HZ of HD 4208 is characterized by mean-motion
resonances and large-scale chaos leading to particle removal by either
ejection or collision. This behavior is mainly explained by the proximity of
the giant planet to the terrestrial habitable region for either eccentric
giant planet orbits and/or high giant-planet mass.
.
In this case, almost all particles (with a > 0.9 AU) have been
removed from the CHZ after 106 years and roughly 10-15% of the total
initial population of test particles survived. In summary the dynamical picture
within the HZ of HD 4208 is characterized by mean-motion
resonances and large-scale chaos leading to particle removal by either
ejection or collision. This behavior is mainly explained by the proximity of
the giant planet to the terrestrial habitable region for either eccentric
giant planet orbits and/or high giant-planet mass.
Short-term multi-particle integrations allowed us to perform a large parameter survey of various initial conditions, providing a dynamical picture of the short-term topology of the habitable phase space region. In general, nothing can be concluded on the subsequent evolution of single-particle orbital elements. In the three-body problem stable and confined orbits are only proven up to the integration time. It is possible that particles apparently exhibiting quasi-periodic regular motion (confined within the CHZ in orbit eccentricity, Figs. 6a, 7a) within the first 106 years may suddenly undergo dynamical changes with large excursions in orbital parameters (sticky orbits). In order to learn more about the long term stability of the system, we are left with the question of the subsequent dynamical evolution of the particles. Since it is computationally time-consuming to probe each and every particle over billions of years, we integrated a few spot-test-objects over a time period of 1 billion years. For such a long time scale, it is no longer valid to model the telluric planet as a test particle. In the following we assign the telluric planet one Earth mass.
![\begin{figure}
\par\includegraphics[width=17.8cm,clip]{09822f10.eps}\end{figure}](/articles/aa/full/2008/36/aa09822-08/Timg181.gif) |
Figure 10:
Long-term integrations of an Earth mass planet under the gravitational
perturbation of HD 70642b for three locations in the HZ. The mass of
the giant planet is
|
| Open with DEXTER | |
![\begin{figure}
\mbox
{
\subfigure[$(e,\omega)$ -correlation for a telluric plane...
...tions
shown in a) and b).]
{\includegraphics{9822Fig11cNew.eps} }
}
\end{figure}](/articles/aa/full/2008/36/aa09822-08/Timg182.gif) |
Figure 11:
Demonstrating
|
| Open with DEXTER | |
We selected three initial conditions for the semi-major axis of a telluric
planet. Comparing Fig. 6 with
Fig. 7, it is seen that the maximum
eccentricity excitation of a telluric planet (at a given semi-major axis) is
only weakly dependent on the mass of HD 70642b, but strongly depends on the
orbit eccentricity of the perturbing giant planet. In the following we adopt
![]() and e=0.16 for HD 70642b and refer to this setup as the
``worst-case-scenario'' to probe quasi-periodic motion (cf.
Fig. 7b) during a 1 billion year integration.
Considering this parameter setup will enable us to judge the long term
dynamical evolution of a telluric planet perturbed by a giant planet on a
low-eccentric orbit. For giant planet circular orbits, the accumulation of
giant planet perturbations are expected to be less over time. If
quasi-periodic motion is demonstrated for the worst-case-scenario setup, then
it would provide a high degree of confidence in the conclusion that the bulk
of particles in the terrestrial habitable region are rendered quasi-periodic
(at least) when extrapolated to consider low-eccentric giant planet
perturbations. In contrast, if the worst-case-scenario exhibits erratic
and/or unbounded motion of the telluric planet, then we are left with the
tedious (and almost impossible) task of checking the long-term dynamical
evolution of individual planets initially started in the (C)HZ. In
Fig. 10 we show the time evolution of orbital Kepler
elements for three telluric planets orbiting HD 70642. The planets are
followed over a total integration time of 109 years using the 14th-order
Radau algorithm as implemented in the MERCURY package. Comparing with the
Burlisch-Stoer algorithm, we performed numerical tests indicating that Radau
reduces the relative energy error
and e=0.16 for HD 70642b and refer to this setup as the
``worst-case-scenario'' to probe quasi-periodic motion (cf.
Fig. 7b) during a 1 billion year integration.
Considering this parameter setup will enable us to judge the long term
dynamical evolution of a telluric planet perturbed by a giant planet on a
low-eccentric orbit. For giant planet circular orbits, the accumulation of
giant planet perturbations are expected to be less over time. If
quasi-periodic motion is demonstrated for the worst-case-scenario setup, then
it would provide a high degree of confidence in the conclusion that the bulk
of particles in the terrestrial habitable region are rendered quasi-periodic
(at least) when extrapolated to consider low-eccentric giant planet
perturbations. In contrast, if the worst-case-scenario exhibits erratic
and/or unbounded motion of the telluric planet, then we are left with the
tedious (and almost impossible) task of checking the long-term dynamical
evolution of individual planets initially started in the (C)HZ. In
Fig. 10 we show the time evolution of orbital Kepler
elements for three telluric planets orbiting HD 70642. The planets are
followed over a total integration time of 109 years using the 14th-order
Radau algorithm as implemented in the MERCURY package. Comparing with the
Burlisch-Stoer algorithm, we performed numerical tests indicating that Radau
reduces the relative energy error![]() by 1-2 orders of magnitudes with only
little expense of extra CPU time.
by 1-2 orders of magnitudes with only
little expense of extra CPU time.
All three telluric planets were initially started on a circular orbit at three
different initial locations in the HZ. Figure 10 shows the
time evolution of a,e along with the polar representation
![]() for each integration. Here
for each integration. Here
![]() denotes the argument of pericenter (or apsidal
longitude) of the tellus and the giant planet, respectively. For all three
cases, it is demonstrated that the telluric orbit is bounded and
exhibits quasi-periodic motion during the 109 years, and we can conclude
that a hypothetical telluric planet remains on a stable orbit out to a
semi-major axis of at least a = 1.25 AU. This result allows us to conclude
with high confidence the following. If a telluric planet was formed in the HZ
of HD 70642, it would remain on a stable orbit for at least one billion years,
as long as the giant-planet orbit eccentricity and mass remain lower than
the worst-case scenario parameter setup. However, how likely terrestrial
planets form by accretion processes under strong giant planet perturbations is
not addressed in this work. Also we demonstrate instability. In an additional
integration with
denotes the argument of pericenter (or apsidal
longitude) of the tellus and the giant planet, respectively. For all three
cases, it is demonstrated that the telluric orbit is bounded and
exhibits quasi-periodic motion during the 109 years, and we can conclude
that a hypothetical telluric planet remains on a stable orbit out to a
semi-major axis of at least a = 1.25 AU. This result allows us to conclude
with high confidence the following. If a telluric planet was formed in the HZ
of HD 70642, it would remain on a stable orbit for at least one billion years,
as long as the giant-planet orbit eccentricity and mass remain lower than
the worst-case scenario parameter setup. However, how likely terrestrial
planets form by accretion processes under strong giant planet perturbations is
not addressed in this work. Also we demonstrate instability. In an additional
integration with
![]() AU the telluric planet collided with the
host star after
AU the telluric planet collided with the
host star after
![]() years.
years.
In the following, we discuss the time evolution of the telluric planets
eccentricity on short time scales outside and inside (next subsection) a
mean-motion resonance. Figure 11a shows the time evolution
of the eccentricity for a massive telluric planet initially started with
a0 = 1.045 AU over a 8000-year period. Data points are shown every 36
days. In the same figure, we overplot the time variation of the argument of
periastron of the telluric planet at the same sampling rate. The figure
not only shows a 2000-year period in the eccentricity variation, but also
demonstrates a correlation between the apsidal line and eccentricity variation.
In Fig. 11a the horizontal line indicates the initial
argument of pericenter![]() of
HD 70642b and is equal to 277 degrees. From the figure we observe that,
whenever the apsidal difference of the two planets is
of
HD 70642b and is equal to 277 degrees. From the figure we observe that,
whenever the apsidal difference of the two planets is
![]() (moment of apsidal alignment), the telluric
orbit takes on its most elongated form
(moment of apsidal alignment), the telluric
orbit takes on its most elongated form
![]() .
In
Fig. 11a this is indicated by the crossing of the saw-tooth
(blue) curve with the horizontal line. In addition, whenever the orbit is close
to circular, the apsidal line of the telluric planet is unlocked and free to
rotate (precess) for a short period of time and the apsidal difference is at
maximum with
.
In
Fig. 11a this is indicated by the crossing of the saw-tooth
(blue) curve with the horizontal line. In addition, whenever the orbit is close
to circular, the apsidal line of the telluric planet is unlocked and free to
rotate (precess) for a short period of time and the apsidal difference is at
maximum with
![]() .
To confirm this
result, we repeated the simulations with the same initial conditions using the
SWIFT (BS + RMVS) algorithms.
It is important to stress that the apsidal alignment geometry between the two
planets is not causing chaotic evolution or resulting in global orbital
instability of the telluric planets orbit. The orbit in
Fig. 11a is characterized by a quasi-periodic time
evolution as indicated by the MEGNO factor (dashed line) in
Fig. 11c. After having noticed this
.
To confirm this
result, we repeated the simulations with the same initial conditions using the
SWIFT (BS + RMVS) algorithms.
It is important to stress that the apsidal alignment geometry between the two
planets is not causing chaotic evolution or resulting in global orbital
instability of the telluric planets orbit. The orbit in
Fig. 11a is characterized by a quasi-periodic time
evolution as indicated by the MEGNO factor (dashed line) in
Fig. 11c. After having noticed this
![]() -correlation, we studied the nature of this correlation for
different initial argument of pericenters (all other elements are similar to
the simulation presented in Fig. 11a) of the giant planet
HD 70642b. In particular, we looked at 3 additional, different values of
-correlation, we studied the nature of this correlation for
different initial argument of pericenters (all other elements are similar to
the simulation presented in Fig. 11a) of the giant planet
HD 70642b. In particular, we looked at 3 additional, different values of
![]() degrees. In all three cases (results can be obtained
upon request), the maximum eccentricity of the telluric planet occurred
whenever the apses of the two planets were aligned for a short period of time.
In addition, we repeated the simulation of Fig. 11a, but
changed the initial eccentricity of the telluric planet to e = 0.15 and also
changed the initial argument of pericenter of HD 70642b to
degrees. In all three cases (results can be obtained
upon request), the maximum eccentricity of the telluric planet occurred
whenever the apses of the two planets were aligned for a short period of time.
In addition, we repeated the simulation of Fig. 11a, but
changed the initial eccentricity of the telluric planet to e = 0.15 and also
changed the initial argument of pericenter of HD 70642b to
![]() degrees. The time evolution of the telluric planet's eccentricity and argument
of periastron is shown in Fig. 12. Again, we observe that, when the
apses of the planets are aligned (at 75 degrees), the eccentricity of the
telluric (massive) planet is at maximum. In addition, we also observe that the
minimum eccentricity of tellus occurs whenever the apse difference is 180
degrees. This event occurs in Fig. 12 when the argument of pariastron
of tellus intersects the upper horizontal line (75 deg + 180 deg = 255 degrees).
degrees. The time evolution of the telluric planet's eccentricity and argument
of periastron is shown in Fig. 12. Again, we observe that, when the
apses of the planets are aligned (at 75 degrees), the eccentricity of the
telluric (massive) planet is at maximum. In addition, we also observe that the
minimum eccentricity of tellus occurs whenever the apse difference is 180
degrees. This event occurs in Fig. 12 when the argument of pariastron
of tellus intersects the upper horizontal line (75 deg + 180 deg = 255 degrees).
The dynamical picture is changed when the two planets are in mean-motion
resonance. In the following, we consider the5:1 mean-motion resonance of a
massive telluric planet with HD 70642b. For now, we postpone any detailed
dynamical analysis of the mean-motion dynamics and focus on the long term
evolution inside this resonance. Initial conditions are similar to
Fig. 11a, except that the telluric planet is started with
semi-major axis
a0 = 1.123 AU, which corresponds to the 5:1 mean-motion
resonance. The result of a 8000-year integration (15th order Radau) is shown in
Fig. 11b. Compared to the dynamical behavior of the
eccentricity in Fig. 11a, we now observe a more erratic
time evolution of this element when the two planets participate in the 5:1
commensurability. Also, we observe an increase in eccentricity to
![]() of the telluric orbit. We explain this increase in eccentricity because
of the more frequent mutual planetary encounters at periapse alignment.
However, the erratic zig-zag behavior of the eccentricity is a clear hint of
chaotic time evolution, and it is mostly related to motion near the separatrix
separating phase space in quasi-periodic (regular) and chaotic dynamics.
Interestingly, and despite being chaotic, the initial conditions have been
integrated for 109 years (not shown in this work, but similar to
Fig. 10), and during this period, the system remains
bounded and hence dynamically stable. However, it should be noted that the
of the telluric orbit. We explain this increase in eccentricity because
of the more frequent mutual planetary encounters at periapse alignment.
However, the erratic zig-zag behavior of the eccentricity is a clear hint of
chaotic time evolution, and it is mostly related to motion near the separatrix
separating phase space in quasi-periodic (regular) and chaotic dynamics.
Interestingly, and despite being chaotic, the initial conditions have been
integrated for 109 years (not shown in this work, but similar to
Fig. 10), and during this period, the system remains
bounded and hence dynamically stable. However, it should be noted that the
![]() -correlation is a well known dynamical phenomenon in solar-system,
secular asteroid dynamics at mean-motion resonance (Lecar et al. 2001, p. 588).
Here, we demonstrate that the same mechanism also applies to gravitationally
interacting planets. In a later study, we plan to study the details of the
various mean-motion resonances of this system by considering the time evolution
of the corresponding critical angle around mean-motion resonances.
-correlation is a well known dynamical phenomenon in solar-system,
secular asteroid dynamics at mean-motion resonance (Lecar et al. 2001, p. 588).
Here, we demonstrate that the same mechanism also applies to gravitationally
interacting planets. In a later study, we plan to study the details of the
various mean-motion resonances of this system by considering the time evolution
of the corresponding critical angle around mean-motion resonances.
![\begin{figure}
\par\includegraphics[width=9cm, height=6cm]{9822Fig12New.eps}\end{figure}](/articles/aa/full/2008/36/aa09822-08/Timg197.gif) |
Figure 12:
Time evolution of eccentricity (sine curve) and argument of periastron
of tellus with identical initial condition as given in
Fig. 11a, except that the telluric planet was initially
started on an orbit with
e0=0.15 and
|
| Open with DEXTER | |
Results from the calculation of the MEGNO factor are in close
agreement with previous results (Asghari et al. 2004) published independently
and obtained by the Kolmogorov entropy method of quantifying chaotic dynamics.
This is the first time a direct comparison with a different fast-indicator
technique has been done establishing some confidence in their use.
Combining the calculation of MEGNO maps with direct particle simulations
enabled us to correlate dynamical features in the MEGNO maps with eccentricity
excitations of particle orbits within the habitable zone. Most of these
features are identified as corresponding to the location of orbital mean-motion
resonances with
![]() .
The main dynamical effect of a
mean-motion resonance is additional pumping of orbital eccentricities and the
perturbation effects at resonances generally starts to operate at high
giant-planet orbit eccentricity and mass.
The identification of chaotic regions within a MEGNO map implies not
necessarily dynamically unstable orbits for a given set of initial
conditions. By dynamical instability, we mean the event of large
excursions of the orbit eventually resulting in orbit crossing and/or
close encounters (one object entering the Hill sphere of another object) with
other planets. Based on the results of this work, we would not interpret every
chaotic feature observed in a MEGNO map as indicative of or synonymous with
being dynamically unstable. The problem is that no direct link exists
between the degree of instability and
.
The main dynamical effect of a
mean-motion resonance is additional pumping of orbital eccentricities and the
perturbation effects at resonances generally starts to operate at high
giant-planet orbit eccentricity and mass.
The identification of chaotic regions within a MEGNO map implies not
necessarily dynamically unstable orbits for a given set of initial
conditions. By dynamical instability, we mean the event of large
excursions of the orbit eventually resulting in orbit crossing and/or
close encounters (one object entering the Hill sphere of another object) with
other planets. Based on the results of this work, we would not interpret every
chaotic feature observed in a MEGNO map as indicative of or synonymous with
being dynamically unstable. The problem is that no direct link exists
between the degree of instability and
![]() ,
which is related to
the Lyapunov time. As an example, the solar system's Lyapunov time is
estimated as 5 Myr, indicating that it is chaotic, but still all planetary
orbits are dynamically stable over a period of at least 4 Gyr
(Lecar et al. 2001) - a property of the system termed stable chaos
(Milani et al. 1997; Milani & Nobili 1992) to indicate a chaotic system (short
Lyapunov time) exhibiting stable motion on long time scales.
From theory, a dynamical system has a spectrum of Lyapunov exponents
(possibly complex eigenvalues) each associated to a given
eigenvector of the system. Each Lyapunov exponent describes the rate of
change of its corresponding eigenvector in time, and the number of positive
(vanishing) Lyapunov exponents indicates the number of independent directions
in phase space along which the orbit exhibits chaotic (quasi-periodic)
behavior (Morbidelli 2002). In the general case, the time evolution
of a Kepler element is given by a linear combination of all Lyapunov exponents.
To probe whether an initial condition is in a chaotic region of phase
space, it has proven sufficient to only determine the largest
(maximum) Lyapunov exponent (MLE) in the spectrum of eigenvalues. The MEGNO
factor provides an estimate of the MLE characterizing the rate of exponential
divergence in the system. However, from the MEGNO factor alone, it is not
obvious which Kepler element of the telluric planets orbit will
exhibit chaotic behavior and the present work (co-planar orbits) suggests
that the typical chaotic variation is mainly found in the time variation of the
eccentricity and apsidal line. Hence a stability analysis should include a
discussion of these parameters. It is important to note that the apparent
chaotic variation in the semi-major axis in Fig. 10 is an
artificial effect due to the sampling frequency of data output.
After pointing out these remarks, the construction of MEGNO maps is a powerful
way to obtain a quick overview of dynamically interesting features indicating
chaotic motion of a given phase space region. However, we recommend that a
MEGNO map should always be supplemented with additional dynamical information
showing the change in other orbital quantities (i.e. semi-major axis,
eccentricity and apsidal line variation) for a given problem to enhance the
physical information contained in
,
which is related to
the Lyapunov time. As an example, the solar system's Lyapunov time is
estimated as 5 Myr, indicating that it is chaotic, but still all planetary
orbits are dynamically stable over a period of at least 4 Gyr
(Lecar et al. 2001) - a property of the system termed stable chaos
(Milani et al. 1997; Milani & Nobili 1992) to indicate a chaotic system (short
Lyapunov time) exhibiting stable motion on long time scales.
From theory, a dynamical system has a spectrum of Lyapunov exponents
(possibly complex eigenvalues) each associated to a given
eigenvector of the system. Each Lyapunov exponent describes the rate of
change of its corresponding eigenvector in time, and the number of positive
(vanishing) Lyapunov exponents indicates the number of independent directions
in phase space along which the orbit exhibits chaotic (quasi-periodic)
behavior (Morbidelli 2002). In the general case, the time evolution
of a Kepler element is given by a linear combination of all Lyapunov exponents.
To probe whether an initial condition is in a chaotic region of phase
space, it has proven sufficient to only determine the largest
(maximum) Lyapunov exponent (MLE) in the spectrum of eigenvalues. The MEGNO
factor provides an estimate of the MLE characterizing the rate of exponential
divergence in the system. However, from the MEGNO factor alone, it is not
obvious which Kepler element of the telluric planets orbit will
exhibit chaotic behavior and the present work (co-planar orbits) suggests
that the typical chaotic variation is mainly found in the time variation of the
eccentricity and apsidal line. Hence a stability analysis should include a
discussion of these parameters. It is important to note that the apparent
chaotic variation in the semi-major axis in Fig. 10 is an
artificial effect due to the sampling frequency of data output.
After pointing out these remarks, the construction of MEGNO maps is a powerful
way to obtain a quick overview of dynamically interesting features indicating
chaotic motion of a given phase space region. However, we recommend that a
MEGNO map should always be supplemented with additional dynamical information
showing the change in other orbital quantities (i.e. semi-major axis,
eccentricity and apsidal line variation) for a given problem to enhance the
physical information contained in
![]() on the orbital time
evolution.
on the orbital time
evolution.
We conclude the following about the stability of telluric planets in the
habitable region of HD 70642. We demonstrated the long term (109 years)
stability of 3 telluric orbits with different initial semi-major axis. The
stability was probed by adopting the ``worst-case-scenario'' combination of
observed giant planet orbit parameters. However, it was found that the
telluric planet's orbit eccentricity exhibits large variations on a 2000-year
period, and it is speculative at this point whether a telluric planet would be
able to develop some form of biology under such dynamical variations. From the
long term simulations we then concluded that global stability in the habitable
region is obtained for HD 70642b on a circular orbit. In the case of a
telluric planet in the CHZ, the mutual distance between the orbits of the
planets is only 2.26 AU, and we observed only small variations in the telluric
orbit eccentricity. Furthermore, it was found that the giant-planet mass is
the last important parameter when studying its dynamical influence on the
terrestrial region (when circular orbits were considered). Even a mass of
![]() orbiting the host star on a circular orbit (at distance
3.3 AU) would render the habitable region stable.
orbiting the host star on a circular orbit (at distance
3.3 AU) would render the habitable region stable.
The dynamical picture of the terrestrial region in HD 4208 is completely
different. Because of the giant planets' close proximity to the habitable zone,
stronger gravitational perturbations are introduced when compared to HD 70642.
Simulations suggest that the only permissable parameter combination for
HD 4208b is a minimum mass giant planet in a low-e orbit. This dynamical
setup still introduces a strong mean-motion resonance operating well inside the
CHZ (Fig. 8a) at
![]() AU. However,
the mass of HD 4208b seems to be dynamically significant now. Retaining the
giant planet on a circular orbit, but increasing the mass by an order of
magnitude has the effect of particle removal with
AU. However,
the mass of HD 4208b seems to be dynamically significant now. Retaining the
giant planet on a circular orbit, but increasing the mass by an order of
magnitude has the effect of particle removal with
![]() AU and
onwards. Considering the dramatic cases in which HD 4208b is on an eccentric
orbit with mass parameters either
AU and
onwards. Considering the dramatic cases in which HD 4208b is on an eccentric
orbit with mass parameters either
![]() or
or
![]() ,
shows
that telluric planets crosses the CHZ inner and outer boundaries. For the
high-mass range, no telluric planet survives over 106 years
(Fig. 9b).
Numerical simulations performed in this work suggest that extrasolar giant
planets should be on circular orbits with a semi-major axis that not much
smaller than a = 3.3 AU. If no additional perturbations are present, such a
dynamical configuration would cause a terrestrial Earth-mass planet to remain
on a stable and bounded orbit within the CHZ. At the time of writing, half a
dozen of the 230 exoplanetary systems have a > 3.3 AU with moderate-to-high
orbital eccentricities spanning the range e = 0.16 to 0.70. In view of this
work, these systems seem to be hostile to the dynamical environment covering
the habitable terrestrial region. We suggest that future observations of
already known exoplanets should aim to further constrain and minimize the
uncertainty range of the orbital eccentricity. This parameter seems to have
the most dynamical significance when considering the dynamical stability
properties of telluric planets in the habitable terrestrial region.
,
shows
that telluric planets crosses the CHZ inner and outer boundaries. For the
high-mass range, no telluric planet survives over 106 years
(Fig. 9b).
Numerical simulations performed in this work suggest that extrasolar giant
planets should be on circular orbits with a semi-major axis that not much
smaller than a = 3.3 AU. If no additional perturbations are present, such a
dynamical configuration would cause a terrestrial Earth-mass planet to remain
on a stable and bounded orbit within the CHZ. At the time of writing, half a
dozen of the 230 exoplanetary systems have a > 3.3 AU with moderate-to-high
orbital eccentricities spanning the range e = 0.16 to 0.70. In view of this
work, these systems seem to be hostile to the dynamical environment covering
the habitable terrestrial region. We suggest that future observations of
already known exoplanets should aim to further constrain and minimize the
uncertainty range of the orbital eccentricity. This parameter seems to have
the most dynamical significance when considering the dynamical stability
properties of telluric planets in the habitable terrestrial region.
Acknowledgements
This work benefited greatly from suggestions by the referee who pointed out and clarified important misleading aspects in the original submitted manuscript! This research project was supported by the Danish Natural Science Research Council, FNU. Numerical simulations were performed at the supercomputing facility at the University of Copenhagen (DCSC-KU) run on behalf of the Danish Center for Scientific Computing. T.C.H. would like to acknowledge Åke Nordlund for providing access to DCSC. K.G. is supported by the Polish Ministry of Science, Grant 1P03D 021 29.