A&A 488, 1093-1100 (2008)
DOI: 10.1051/0004-6361:200809634

Study of the solar anisotropy of cosmic ray primaries of about 200 GeV energy with the L3+C muon detector

The L3 collaboration[*]


1 - III. Physikalisches Institut, RWTH, 52056 Aachen, Germany55
2 - NIKHEF, and University of Amsterdam, 1009 DB Amsterdam, The Netherlands
3 - University of Michigan, Ann Arbor, MI 48109, USA
4 - LAPP, IN2P3-CNRS, BP 110, 74941 Annecy-le-Vieux Cedex, France
5 - Institute of Physics, University of Basel, 4056 Basel, Switzerland
6 - Louisiana State University, Baton Rouge, LA 70803, USA
7 - Institute of High Energy Physics, IHEP, 100039 Beijing, PR China60
8 - ITP, Academia Sinica, 100039 Beijing, PR China
9 - Humboldt University, 10115 Berlin, Germany
10 - University of Bologna and INFN-Sezione di Bologna, 40126 Bologna, Italy
11 - Tata Institute of Fundamental Research, Mumbai (Bombay) 400 005, India
12 - Northeastern University, Boston, MA 02115, USA
13 - Institute of Atomic Physics and University of Bucharest, 76900 Bucharest, Romania
14 - Central Research Institute for Physics of the Hungarian Academy of Sciences, 1525 Budapest 114, Hungary56
15 - Massachusetts Institute of Technology, Cambridge, MA 02139, USA
16 - Panjab University, Chandigarh 160 014, India
17 - KLTE-ATOMKI, 4010 Debrecen, Hungary57
18 - UCD School of Physics, University College Dublin, Belfield, Dublin 4, Ireland
19 - University of Florence and INFN, Sezione di Firenze, 50019 Sesto Fiorentino, Italy
20 - European Laboratory for Particle Physics, CERN, 1211 Geneva 23, Switzerland
21 - World Laboratory, FBLJA Project, 1211 Geneva 23, Switzerland
22 - University of Geneva, 1211 Geneva 4, Switzerland
23 - University of Hamburg, 22761 Hamburg, Germany
24 - Chinese University of Science and Technology, USTC, Hefei, Anhui 230 029, PR China60
25 - University of Lausanne, 1015 Lausanne, Switzerland
26 - Institut de Physique Nucléaire de Lyon, IN2P3-CNRS, Université Claude Bernard, 69622 Villeurbanne, France
27 - Centro de Investigaciones Energéticas, Medioambientales y Tecnológicas, CIEMAT, 28040 Madrid, Spain58
28 - Florida Institute of Technology, Melbourne, FL 32901, USA
29 - INFN-Sezione di Milano, 20133 Milan, Italy
30 - Institute of Theoretical and Experimental Physics, ITEP, Moscow, Russia
31 - INFN-Sezione di Napoli and University of Naples, 80125 Naples, Italy
32 - Department of Physics, University of Cyprus, Nicosia, Cyprus
33 - Radboud University and NIKHEF, 6525 ED Nijmegen, The Netherlands
34 - Osaka City University, Osaka 558-8585, Japan
35 - California Institute of Technology, Pasadena, CA 91125, USA
36 - INFN-Sezione di Perugia and Università Degli Studi di Perugia, 06100 Perugia, Italy
37 - Nuclear Physics Institute, St. Petersburg, Russia
38 - Carnegie Mellon University, Pittsburgh, PA 15213, USA
39 - INFN-Sezione di Napoli and University of Potenza, 85100 Potenza, Italy
40 - Princeton University, Princeton, NJ 08544, USA
41 - University of California, Riverside, CA 92521, USA
42 - INFN-Sezione di Roma and University of Rome, ``La Sapienza'', 00185 Rome, Italy
43 - University and INFN, Salerno, 84100 Salerno, Italy
44 - University of California, San Diego, CA 92093, USA
45 - University of Santiago de Compostela, 15706 Santiago, Spain
46 - Bulgarian Academy of Sciences, Central Lab. of Mechatronics and Instrumentation, 1113 Sofia, Bulgaria
47 - The Center for High Energy Physics, Kyungpook National University, 702-701 Taegu, Republic of Korea
48 - National Central University, Chung-Li, Taiwan, China
49 - Department of Physics, National Tsing Hua University, Taiwan, China
50 - Purdue University, West Lafayette, IN 47907, USA
51 - Paul Scherrer Institut, PSI, 5232 Villigen, Switzerland
52 - DESY, 15738 Zeuthen, Germany
53 - Eidgenössische Technische Hochschule, ETH Zürich, 8093 Zürich, Switzerland
54 - Supported by the German Bundesministerium für Bildung, Wissenschaft, Forschung und Technologie
55 - Supported by the Hungarian OTKA fund under contract numbers T019181, F023259 and T037350
56 - Also supported by the Hungarian OTKA fund under contract number T026178
57 - Supported also by the Comisión Interministerial de Ciencia y Tecnología
58 - Also supported by CONICET and Universidad Nacional de La Plata, CC 67, 1900 La Plata, Argentina
59 - Supported by the National Natural Science Foundation of China
60 - On leave from the Moscow Physical Engineering Institute (MePhl)
61 - On leave from JINR, 141980 Dubna, Russia
62 - Deceased

CERN, 1211 Geneva, Switzerland

Received 22 February 2008 / Accepted 3 June 2008

Abstract
Context. Primary cosmic rays experience multiple deflections in the non-uniform galactic and heliospheric magnetic fields which may generate anisotropies.
Aims. A study of anisotropies in the energy range between 100 and 500 GeV is performed. This energy range is not yet well explored.
Methods. The L3 detector at the CERN electron-positron collider, LEP, is used for a study of the angular distribution of atmospheric muons with energies above 20 GeV. This distribution is used to investigate the isotropy of the time-dependent intensity of the primary cosmic-ray flux with a Fourier analysis.
Results. A small deviation from isotropy at energies around 200 GeV is observed for the second harmonics at the solar frequency. No sidereal anisotropy is found at a level above 10-4. The measurements were performed in the years 1999 and 2000.

Key words: plasmas - sun: magnetic fields - Sun: solar wind - interplanetary medium - ISM: cosmic rays

1 Introduction

Cosmic rays of GeV-TeV-PeV energies are galactic in nature and very probably are produced mainly by the shocks generated by supernova explosions. Some of these particles reach the Solar System after experiencing multiple deflections in the non-uniform galactic magnetic field, particularly in the neighborhood of the Sun. This generates a structure (Amenomori et al. 2005; Erlykin & Wolfendale 2006) in the arrival direction of the particles, and the variation of the intensity of primary cosmic rays as a function of the equatorial coordinates $\alpha$ (right ascension) and $\delta $ (declination) is known as the sidereal anisotropy. Thus a detector located on the Earth observes a modulation of the cosmic-ray flux with a period of one sidereal day due to the Earth's rotation. The magnetic field within the heliosphere, whose structure is strongly influenced by the solar wind and the Sun's activity, plays a role in the propagation of galactic cosmic rays with energies of the order of 10 TeV and below. At these energies, the general large-scale structure of the heliomagnetic field may induce structures in the sidereal anisotropy. At lower energies, structures mainly may be due to the Solar wind plasma. Additional cosmic-ray intensity variations may depend on the arrival direction with respect to the Sun. These would appear as an intensity modulation with a period of one Solar day, known commonly as the solar anisotropy. In addition, the orbital motion of the Earth is expected to produce a signal modulated with this frequency. This effect, called the Compton-Getting effect, is well understood and can be corrected for (Compton & Getting 1935). Possible observations of a modulation in the cosmic-ray flux should be carefully analysed to account for changes in the muon production rate and energy loss in the atmosphere due to meteorological effects, such as diurnal and seasonal variations of temperature and pressure.

The presently available data on the anisotropy may be summarized as follows. Except for the very recent observation of an anisotropy on the most energetic cosmic-rays above 60 EeV by the AUGER collaboration (Abraham et al. 2007), no anisotropy at primary energies above 300 TeV has been observed (Amenomori et al. 2006; Maier et al. 2003). No effect due to the heliosphere nor to the galactic Compton-Getting effect due to the solar system orbiting around the center of the galaxy has been detected. For primary energies between 4 and 50 TeV a clear sidereal anisotropy is present (Amenomori et al. 2006). The GRAND collaboration observed a very significant solar anisotropy, expressed as the sum of the first two harmonics, around 10 GeV (Poirier et al. 2001).

The energy range for primaries between 100 and 500 GeV has not yet been fully explored. This is the domain the L3+C detector is sensitive to, and is the subject of this analysis. The anisotropy of primary cosmic rays is studied indirectly through the observation of muons which result from the decay of the secondary particles produced in the Earth's atmosphere. The median primary energy corresponding to a given muon energy threshold is about 10 times larger than the muon energies (Gaisser 1990). For a muon energy above 20 GeV the muon direction approximates, within $\rm 3^{\circ}$, the direction of the primary (Heck et al. 1998).

The analysis of the experimental data for studies on anisotropy is based on the expansion in spherical harmonics of the anisotropy function, defined as (Kiraly et al. 1979)

 \begin{displaymath}\Delta^{\rm dir}(\alpha, \delta) ~ = ~ \frac{I(\alpha, \delta) ~ - ~ \langle I \rangle} {\langle I \rangle} \end{displaymath} (1)

where $I(\alpha,\delta)$ is the intensity as a function of the right ascension $\alpha$ and declination $\delta $ and $\langle I \rangle$ is the mean intensity.

Anisotropy measurements at a level of 10-4 and better can be achieved by scanning a band with fixed declination range in the right ascension direction (Ramelli 2002; Achar et al. 2006)[*]. In this analysis the anisotropy function is reduced to a quantity independent of the declination, and is defined for the particular declination distribution given by the L3+C direction-dependent acceptance. Information about the anisotropy on large scales is estimated from the first few terms of the Fourier expansion of  $\Delta(\alpha)$:

 \begin{displaymath}\Delta (\alpha) ~ = ~ \sum_{m=1}^{\infty} \xi_{m} ~ \cos~(m(\alpha ~ - ~ \phi_{m})) \end{displaymath} (2)

where $\xi _{m}$ and $\phi _{m}$ are the corresponding amplitudes and phases of the mth harmonics respectively.

2 The L3+C detector and the event selection

The L3 detector (Adeva et al. 1990) operated at the LEP accelerator at CERN (near Geneva, Switzerland). It was located 30 m under ground, at 450 m above sea level, at a longitude of $6.02^{\circ}$ E and a latitude of $46.25^{\circ}$ N. It was designed to accurately measure muons, electrons and photons produced in $\rm e^{+} e^{-}$ collisions. The momentum distribution of atmospheric muons is measured with an upgraded setup known as L3+C (Adriani et al. 2002). The parts of the detector used in this analysis are sketched in Fig. 1.

After passing through the stratified rock overburden, called ``molasse'' (sedimentary rocks), the arrival time t0 of a muon is measured with a resolution of 1.7 ns by a 202 m2 scintillator array placed on top of the detector. The array is composed of 34 modules, each read out by two photomultipliers in coincidence to reduce noise. Inside a volume of about 1000 m3, with a magnetic field of 0.5 T, the coordinates and slopes of a muon track are measured in up to six drift chambers in the bending plane and up to eight times in the non-bending plane. These chambers are arranged concentrically around the LEP beam in line on two ferris wheels of eight octants, each containing three layers of drift cells. By subtracting the t0 time from the arrival times of the drift electrons at the sense wires, a track position in each chamber can be reconstructed with a precision of about 60 $\mu$m in the bending plane and 1 mm in the non-bending plane.

Only three points are needed to determine the radius of the track in the magnetic field, therefore the momentum of a muon traversing two octants can be measured twice. This redundancy is used to evaluate the detector efficiencies and the resolution of the apparatus. The best resolution is obtained when fitting the six points together over the full track length of 11 m. The multiple scattering and energy loss inside the L3 inner detectors, as well as the effect of the inhomogeneous magnetic field are taken into account in the event reconstruction (Innocente & Nagy 1993). For vertically incident muons, the mean energy loss in the molasse and the magnet is 19 GeV at low momenta and reaches 57 GeV at 1 TeV.

The detector achieved excellent muon momentum resolutions, 4.6% at 45 GeV and an angular resolution of better than 0.3$^{\circ}$ at 100 GeV (Achard et al. 2004, 2005).

L3+C recorded $\rm 1.2 \times 10^{10}$ muon triggers during its operation from mid July to November 1999 and April to November 2000.


  \begin{figure} \par\includegraphics*[width=9cm,clip]{9634fig1.eps} \end{figure} Figure 1: Schematic view of the experimental setup.
Open with DEXTER

This analysis is restricted to events that satisfy two criteria: muon tracks must be reconstructed from at least three chambers in any octant and a hit in the scintillators; exactly one track must be successfully reconstructed as coming from the surface. A selection of the time intervals of data taking is applied in order to assure stability in the detection efficiency. To account for muon rate variations due to meteorological effects and efficiency fluctuations a running average of the detection rate is calculated for each selected run over an interval of time lasting 12 h before the run to 12 h after the run. When filling the histogram corresponding to the live-time distribution, the contents are weighted by a factor proportional to this running average (Cutler & Groom 1991; Gerasimova et al. 2001). The Compton-Getting effect is taken care of by applying a weight factor to each event, according to the muon arrival direction and the Earth orbital velocity.

The analysed data correspond to a total live-time of 150.63 days, evenly distributed over the full data taking period. Muon samples were selected according to four different lower energy cuts in order to detect a possible energy dependence of the anisotropy: 20, 30, 50 and 100 GeV.


  \begin{figure} \par\includegraphics*[width=7.cm,clip]{9634fig2.eps} \end{figure} Figure 2: Distributions of the analyzed events as a function of the declination $\delta $ for different lower energy cuts. The distributions are normalized to 1.
Open with DEXTER

3 Data analysis

The anisotropy of primary cosmic rays is studied based on the idea that a fixed detector scans the sky in the right ascension direction ($\alpha$), thanks to the Earth rotation. Figure 2 shows distributions in declination of the events selected for four muon energy thresholds. The detector acceptance is energy dependent because of different material thicknesses crossed by the muons. For example, the structure observed for the lowest energy threshold around $\rm 55^{\circ}$ is caused by the access shaft to the detector underground cavern.

The analysis method searches for time variations of the muon detection rates with a period of one day, regardless of the arrival direction of the muons.

This study introduces a method that takes into account the directional information, $\alpha$, available from the reconstruction of the muon tracks (Ramelli 2002). For the sidereal anisotropy, the expected distribution $N_{\mu}^{\rm exp}(\alpha)$ of muon events as a function of $\alpha$ in the case of an isotropic primary cosmic ray flux is calculated by folding the observed event distribution as a function of the negative hour angle, - h.a., with the live-time distribution of the sidereal time $t_{\rm s}$. Typical distributions of these two quantities are shown in Fig. 3. $N_{\mu}^{\rm exp}(\alpha)$ is then compared with the actual measured distribution $N_{\mu}^{\rm meas}(\alpha)$ and $\Delta(\alpha)$ is calculated as:

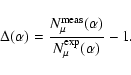\begin{displaymath}\Delta(\alpha)=\frac{N_{\mu}^{\rm meas}(\alpha)}{N_{\mu}^{\rm exp}(\alpha)}-1. \end{displaymath} (3)


  \begin{figure} \par\includegraphics*[width=7.cm,clip]{9634fig3a.eps}\par\includegraphics*[width=7.cm,clip]{9634fig3b.eps}\end{figure} Figure 3: Distributions of the event negative hour angle and (below) livetime for muons with a surface energy above 30 GeV obtained from data acquired on one day (1st of August 1999). The selection of good-quality data capture conditions is responsible for the live-time fluctuations. The convolution of the two distributions gives the expected distribution,under the assumption of isotropy.
Open with DEXTER

Figure 4 compares the measured event distribution with the expected distribution for muons above 30 GeV. As an example, only data for one day are displayed. On such a time scale the statistical fluctuations of the measured distribution around the smooth curve of the expected distribution are visible. Figure 5 represents the corresponding result of Eq. (3).

A harmonic analysis of the result is performed to extract the first three harmonics of $\Delta(\alpha)$ at the sidereal frequency.

If frequencies $\nu$, other than the sidereal frequency $\nu_\star$, are considered, then the pseudo-right ascension $\tilde{\alpha}_\nu$ is used instead of $\alpha$. It is defined as


\begin{displaymath}\tilde{\alpha}_\nu = \left[\phi_\nu - h.a. \right]_{\rm mod 24~h} \end{displaymath} (4)

where the phase $\phi_\nu$ is defined as


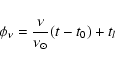\begin{displaymath}\phi_\nu = \frac{\nu}{\nu_\odot}(t-t_0)+t_l \end{displaymath} (5)

and where $\nu_\odot$ is the solar frequency (1/24 h), t is the time of the observation, t0 is a conventional time point which defines when $\tilde{\alpha}_\nu$ is equal for all frequencies and tl is a free phase shift parameter.

We choose t0 to be the time near the autumn equinox when in the year 2000 the mean local solar time and the local sidereal time are the same and are equal to tl. Thus for the solar frequency, the Sun is always located approximately at $\tilde{\alpha}_{\nu_\odot}= 12$ h. In addition to the solar frequency $\rm\nu_{\odot}$, three other frequencies are interesting: the sidereal frequency $\rm\nu_{*}$; the anti-sidereal frequency, which is a side lobe of the same size at the sidereal frequency if a real effect at the solar frequency is modulated with an annual frequency; and the extended sidereal frequency. Another 86 frequencies are analysed to check the uncertainties on the measurement. The combined statistical and systematic uncertainties are obtained by considering the distribution of the amplitudes $\xi$ of the 86 frequencies, which should obey the Rayleigh distribution R normalized to 1:

 
$\displaystyle R(\xi, \sigma) ~ = ~ \frac{1}{\sigma^{2}} ~ \xi ~ {\rm e}^{- \frac{\xi^2}{2 ~ \sigma^2}}. \rule{0mm}{8mm}$     (6)

The data are fitted to this function for the first three harmonics, and the four energy thresholds. The fitted value of $\rm\sigma$ is compared to the expected statistical uncertainty and good agreement is found, leading to the conclusion that systematic uncertainties are negligible compared to the statistical uncertainty.

The amplitude distributions for all 86 frequencies are displayed in Figs. 6 and 7 for the 1st and 2nd harmonics.


  \begin{figure} \par\includegraphics*[width=7.cm,clip]{9634fig4.eps} \end{figure} Figure 4: Measured (binned data) and expected (black line) event distribution in right ascension for muons with a surface energy larger than 30 GeV detected on one day (1st of August 1999). The structures are due to the live-time distribution presented in Fig. 3.
Open with DEXTER


  \begin{figure} \par\includegraphics*[width=8.cm,clip]{9634fig5.eps}\end{figure} Figure 5: The computed ratio between the two distributions shown in Fig. 4, according to Eq. (3).
Open with DEXTER

4 Results

No significant anisotropy is observed at the sidereal frequency for any of the first three harmonics. Figure 8 presents the case for the first harmonic. The results obtained with a muon energy cut at 100 GeV corresponding to primary protons of 1 TeV are compatible with the experimental result of Cutler and Groom (Cutler & Groom 1991), derived from muon data collected from 1978 to 1983 with a threshold of 100 GeV.

For a 200 GeV primary energy threshold, the observation of the first harmonic does not follow the ``tail-in'' and ``loss-cone'' model, NFJ, by Nagashima et al. (1998), which predicts a deficit of galactic origin at $\alpha = 12$ h, the so-called heliospheric effect. The GRAPES experiment, with a primary energy threshold of 60 GeV, collected data between 2000 and 2004, at the end of the period where the magnetic field of the sun changed its polarity and which followed our own data acquisition period. This collaboration observed the NFJ effect only partly, detecting only the ``tail-in'' part (Kojima et al. 2005).


  \begin{figure} \par\includegraphics*[width=7.cm,clip]{9634fig6.eps} \end{figure} Figure 6: Histogram showing the amplitude distribution $\xi _{m}$for the 86 frequencies of the spectrum presented in Figure 9, after excluding the 4 physically interesting ones. The histogram is fitted with the Raleighdistribution ( $\chi^{2}/ndf~ = 13.7/14$).
Open with DEXTER


  \begin{figure} \par\includegraphics*[width=7.cm,clip]{9634fig7.eps} \end{figure} Figure 7: Histogram showing the amplitude distribution $\xi _{m}$for the 86 frequencies of the spectrum presented in Fig. 10, after excluding the 4 physically interesting ones. The histogram is fitted with the Raleigh distribution ( $\chi^{2}/ndf~ = 15.01/15$).
Open with DEXTER


  \begin{figure} \par\includegraphics*[width=8.cm,clip]{9634fig8.eps} \end{figure} Figure 8: Dial plots showing the amplitude and the phase of the first harmonic of the anisotropy function at the sidereal frequency for four different energy cuts. The axes correspond to the right ascensions 0 h, 6 h, 12 h, and 18 h, the radii to the amplitudes whose graduation can be read on the axis. The circles represent the 68.5% confidence level regions for the 4 muon momentum thresholds. The dashed circle is the result of Cutler and Groom (Cutler 1991).
Open with DEXTER

Figures 9 and 10 show the amplitude $\xi _{m}$ as a function of the frequency for the first and the second harmonic respectively. The muon energy-threshold is set to 20 GeV. The largest amplitude is found for the second harmonic at the solar frequency. Figure 11 presents the energy dependence. An anisotropy is observed for a muon energy-threshold up to 50 GeV, corresponding to primaries up to 500 GeV. The largest significance is observed for a muon energy-threshold of 20 GeV, where the amplitude is 4.5$\sigma$ away from 0. In a Rayleigh distribution the probability of finding an amplitude higher than that is only $4 \times 10^{-5}$.

Figure 12 presents this anisotropy for a muon energy-threshold of 20 GeV. The $\chi^2$ of the fit amounts to 6.6 for 7 degrees of freedom (ndf). (A flat distribution provides a $\chi^2$ equal to 28.3 for ndf = 11. In this case the probability of finding a value greater or equal to 28.3 is $2.9 \times 10^{-3}$.)

The fact that for the first three energy thresholds the phase is different from the one at 100 GeV is also an interesting feature, in the sense that it indicates (although with a small significance) an energy dependence of the anisotropy. But as discussed above and by inspecting Fig. 11, a real significance is for a muon energy-threshold of 20, and eventually 30 GeV. At 50 and 100 GeV the uncertainties are too large to draw conclusions.


  \begin{figure} \par\mbox{\includegraphics*[bb=24 197 527 696, clip,width=8.3cm]{9634fig9.eps} }\end{figure} Figure 9: Amplitude $\xi _{m}$ for the first harmonic of the relative muon intensity variation as a function of $\tilde{\alpha}$ for frequencies near $\rm 1~ ~ day^{-1}$ and for a surface energy threshold of 20 GeV. Vertical lines indicate from left to right the anti-sidereal, the solar and the sidereal frequency.
Open with DEXTER


  \begin{figure} \par\includegraphics*[width=8.3cm,clip]{9634fig10.eps} \end{figure} Figure 10: Amplitude $\xi _{m}$ for the second harmonic of the relative muon intensity variation as a function of $\tilde{\alpha}$ for frequencies near $\rm 2~ ~ day^{-1}$ and for a surface energy threshold of 20 GeV. Vertical lines indicate from left to right the double anti-sidereal, the double solar and the double sidereal frequency.
Open with DEXTER


  \begin{figure} \par\includegraphics*[width=6.5cm,clip]{9634fig11.eps} \end{figure} Figure 11: Dial plots showing the amplitude and the phase of the second harmonic of the anisotropy function at the Solar frequency for four different muon energy-cuts. The circles represent the 68.5% confidence level region.
Open with DEXTER


  \begin{figure} \par\includegraphics*[width=8.cm,clip]{9634fig12.eps}\end{figure} Figure 12: Anisotropy distribution $\rm\Delta $ [per mil] in pseudo-right ascension, $\tilde{\alpha}$, for muons with energy greater than 20 GeV. The continuous line represents the fit to the data with the sum of the first two harmonics ( $ \chi^2 = 6.6/7 ~ ndf$). The vertical bars represent the statisticaluncertainties; the systematic uncertainties are negligible.
Open with DEXTER

The structure of the anisotropy function for the 2nd harmonic found is very similar in shape, but five times smaller in amplitude, to what has been reported by the GRAND experiment. This experiment measured the sum of the 1st and 2nd harmonic and was located at 41.7$^{\circ}$ N and 86.2$^{\circ}$ W. It had a 0.1 GeV muon threshold energy and collected data between 1997 and 2000 (Poirier et al. 2001). The observed diurnal peak in solar time was explained according to Hall et al. (1996, 1997) with the fact that cosmic rays are partially affected by the solar wind.

For muon energies above 100 GeV the effect was reported in 2003 by the MACRO collaboration (Ambrosio et al. 2003; Becherini et al. 2005).

No anisotropy is found from the analysis of the 3rd harmonic for any of the four muon threshold-energies.

A summary of the results of the spectral analysis for the solar frequency is given in Table 1.

The analyses of multi-muon events with multiplicities greater than 3, compared to the single muon events discussed above, show no significant deviation from isotropy. This result can be compared to earlier studies claiming an increase of the anisotropy for heavy primaries, producing higher muon multiplicities (Bressi et al. 1990).

Table 1: Amplitudes, $\xi _{m}$, and phases, $\phi _{m}$, of the first three harmonics obtained from the spectral analysis of the anisotropy function for the solar frequency for different muon energy thresholds.

5 Conclusions

Indirect measurements of the anisotropy of primary cosmic rays with energies around 200 GeV do not show any sidereal anisotropy at a level above 10-4. The largest deviation from isotropy is found for the second harmonics at solar frequency for muons above an energy threshold of 20 GeV, corresponding to primaries with energies of about 200 GeV. The amplitude is 4.5$\sigma$ away from 0. In explaining this effect, e.g. as a manifestation of the interaction of cosmic rays with the Solar wind plasma, one has to take into account the complexity and variability of the solar magnetic field during the time of data collection that occurred near the maximum of solar activity. In addition one should consider that the effect is certainly energy dependent, and that uncertainties exist about the magnetic field in the neighbourhood of the Sun.

Acknowledgements
The L3 collaboration would like to thank CERN for the support given to this experiment, and express in particular its gratitude to the crew operating at LEP point 2 for the successful installation of the additional hardware needed for L3+C.

References

 
Copyright ESO 2008