![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{0356fig1.eps} \end{figure}](/articles/aa/full/2008/34/aa10356-08/Timg6.gif) |
Figure 1: Self-coherent camera principle schematics. |
| Open with DEXTER | |
A&A 488, L9-L12 (2008)
DOI: 10.1051/0004-6361:200810356
LETTER TO THE EDITOR
R. Galicher1,2 - P. Baudoz1,2 - G. Rousset1,2
1 - LESIA, Observatoire de Paris, CNRS and University Denis Diderot Paris 7, 5 place Jules Janssen, 92195 Meudon, France
2 -
Groupement d'Intérêt Scientifique Partenariat Haute Résolution Angulaire Sol Espace (PHASE) between ONERA, Observatoire de Paris, CNRS and University Denis Diderot Paris 7, France
Received 9 June 2008 / Accepted 6 July 2008
Abstract
Context. In the context of exoplanet detection, the performance of coronagraphs is limited by wavefront errors.
Aims. To remove efficiently the effects of these aberrations using a deformable mirror, the aberrations themselves must be measured in the science image to extremely high accuracy.
Methods. The self-coherent camera which is based on the principle of light incoherence between star and its environment can estimate these wavefront errors. This estimation is derived directly from the encoded speckles in the science image, avoiding differential errors due to beam separation and non common optics.
Results. Earth-like planet detection is modeled by numerical simulations with realistic assumptions for a space telescope.
Conclusions. The self-coherent camera is an attractive technique for future space telescopes. It is also one of the techniques under investigation for the E-ELT planet finder the so-called EPICS.
Key words: instrumentation: adaptive optics - instrumentation: high angular resolution - instrumentation: interferometers - techniques: high angular resolution - techniques: image processing
Very high contrast imaging is mandatory for the direct detection of exoplanets, which are typically a factor of between 107 and 1010 fainter than their host and often located within a fraction of an arcsecond of their star. First of all, coronagraphs are required to suppress the overwhelming flux of the star but they are limited by wavefront errors in the upstream beam, which creates residual speckles in the science image. Adaptive optics must be used to correct for the effect of most of these aberrations. Some remain uncorrected generating quasi-static residual speckles (Cavarroc et al. 2006). Interferential techniques take advantage of the incoherence between companion and stellar lights to measure these wavefront errors in the science image to high accuracy (Codona & Angel 2004; Guyon 2004). In this letter, we describe such a technique called a self-coherent camera (Baudoz et al. 2006). Residual speckles in the science image, also called interferential image hereafter, are spatially encoded by fringes so that we can derive an estimation of wavefront errors to be corrected by a Deformable Mirror (DM). Since the number of DM actuators is finite, this correction leaves residual speckles. Thus, after reaching the DM limit correction, we apply an image post-processing algorithm (Galicher & Baudoz 2007) to achieve Earth-like planet imaging. Hereafter, we detail the SCC principle. Then, we describe the wavefront error estimator that we use. Finally, we present expected performances from space.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{0356fig1.eps} \end{figure}](/articles/aa/full/2008/34/aa10356-08/Timg6.gif) |
Figure 1: Self-coherent camera principle schematics. |
| Open with DEXTER | |
The beam from the telescope is reflected onto the DM and is split into two beams (Fig. 1). The image channel (shown in red in electronic edition) propagates through a coronagraph. It contains companion light and residual stellar light due to wavefront errors. Its complex amplitude is
![]() ,
where
,
where ![]() is the pupil coordinate.
is the pupil coordinate.
![]() and
and
![]() represent the stellar and companion complex amplitudes of the field in the pupil plane respectively, just after the D diameter Lyot stop. The second beam, called the reference channel, is filtered spatially in a focal plane using a pinhole of radius smaller than
represent the stellar and companion complex amplitudes of the field in the pupil plane respectively, just after the D diameter Lyot stop. The second beam, called the reference channel, is filtered spatially in a focal plane using a pinhole of radius smaller than ![]() .
Almost all companion light is stopped since it is not centered on the pinhole. In the pupil plane just after the diaphragm (DR), the reference complex amplitude is called
.
Almost all companion light is stopped since it is not centered on the pinhole. In the pupil plane just after the diaphragm (DR), the reference complex amplitude is called
![]() .
The pinhole reduces the impact of wavefront errors on
.
The pinhole reduces the impact of wavefront errors on
![]() since it acts as a spatial frequency filter. An optic recombines the two channels, separated by
since it acts as a spatial frequency filter. An optic recombines the two channels, separated by ![]() in the pupil plane, and creates a Fizeau fringed pattern in the focal plane. Residual speckles are therefore spatially encoded unlike companions. The mean intensity of residual speckles of the image channel is almost spatially flat and attenuated by the coronagraph. To optimize the fringe contrast, we have to match the intensity distributions and fluxes of image and reference channels. We use a
DR < D diameter diaphragm to obtain an almost flat reference intensity in the focal plane. This diaphragm reduces the impact of aberrations on
in the pupil plane, and creates a Fizeau fringed pattern in the focal plane. Residual speckles are therefore spatially encoded unlike companions. The mean intensity of residual speckles of the image channel is almost spatially flat and attenuated by the coronagraph. To optimize the fringe contrast, we have to match the intensity distributions and fluxes of image and reference channels. We use a
DR < D diameter diaphragm to obtain an almost flat reference intensity in the focal plane. This diaphragm reduces the impact of aberrations on
![]() ,
since only a fraction of the diffraction peak of size
,
since only a fraction of the diffraction peak of size
![]() is detected in the image (image b in Fig. 2). This implies that the reference channel is quite insensitive to aberrations and can be calibrated before the interference recording (Galicher & Baudoz 2007). Fluxes are equalized using a variable neutral density in the reference channel before the pinhole (Sect. 3). In Fig. 2, we present, on the same spatial scale, (a) the image formed after the sole coronagraph for a pupil of diameter D (the sole image channel) showing residual speckles; (b) the image corresponding to the sole reference channel for a pupil of diameter DR and (c) the interferential image, where the residual speckles are spatially encoded by fringes.
is detected in the image (image b in Fig. 2). This implies that the reference channel is quite insensitive to aberrations and can be calibrated before the interference recording (Galicher & Baudoz 2007). Fluxes are equalized using a variable neutral density in the reference channel before the pinhole (Sect. 3). In Fig. 2, we present, on the same spatial scale, (a) the image formed after the sole coronagraph for a pupil of diameter D (the sole image channel) showing residual speckles; (b) the image corresponding to the sole reference channel for a pupil of diameter DR and (c) the interferential image, where the residual speckles are spatially encoded by fringes.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{0356fig2.eps} \end{figure}](/articles/aa/full/2008/34/aa10356-08/Timg16.gif) |
Figure 2: a) Image formed after the sole coronagraph for a pupil of diameter D (sole image channel) showing the residual speckles. b) Image of the sole reference channel for a pupil of diameter DR. c) Interferential image (science image) where the speckles are spatially encoded by fringes. The spatial scale is the same for all the images. |
| Open with DEXTER | |
In polychromatic light, the intensity ![]() of the interferential image on the detector is
of the interferential image on the detector is
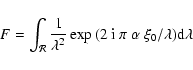 |
(5) |
As a second assumption, we consider that wavefront errors ![]() we are attempting to measure are small and we can write the star field
we are attempting to measure are small and we can write the star field
![]() in the pupil plane upstream from the coronagraph as
in the pupil plane upstream from the coronagraph as
In a third step, we assume a perfectly achromatic coronagraph (Cavarroc et al. 2006), which allows us to remove the coherent part of the energy ![]() to
to
![]()
We note that we require SCC sampling sufficient to detect the fringes that encode the residual speckles. The sampling is then larger than the classical sampling used in earlier techniques proposed by Guyon (2004) and Codona & Angel (2004). However, the SCC needs a single image to estimate wavefront errors, whereas the other two techniques require at least two images since they use an on-axis recombining as in a Michelson scheme and either temporal or spatial phase shifting arrangements. Finally, instead of spreading the incoming light into several images, the SCC spreads the light into fringes.
We consider an SCC device operating in visible light (
![]() ,
,
![]() ,
,
![]() ,
Sect. 2). We assume a perfectly achromatic coronagraph. The beamsplitter injects
,
Sect. 2). We assume a perfectly achromatic coronagraph. The beamsplitter injects ![]() of the incoming energy into the image channel. The filtering pinhole radius is
of the incoming energy into the image channel. The filtering pinhole radius is
![]() and D equals
25 DR. To be more realistic, we assume a calibration of the reference channel with a non-aberrated incoming wavefront and enter this value into the expression for the estimator in Eq. (8). We consider a
and D equals
25 DR. To be more realistic, we assume a calibration of the reference channel with a non-aberrated incoming wavefront and enter this value into the expression for the estimator in Eq. (8). We consider a
![]() DM. The nth-actuator influence function is
DM. The nth-actuator influence function is
![]() ,
where
,
where ![]() is the center of the nth-actuator. We call
is the center of the nth-actuator. We call
![]() the
the
![]() corrected area which is centered on-axis. We chose
corrected area which is centered on-axis. We chose
![]() to ensure that the correlation peaks of
to ensure that the correlation peaks of
![]() did not overlap, which corresponds to about 1.5 interfringes per
did not overlap, which corresponds to about 1.5 interfringes per ![]() .
We use
.
We use
![]() pixel interferential images with 4 pixels for the smallest interfringe over
pixel interferential images with 4 pixels for the smallest interfringe over
![]() (Shannon criteria). Compared to the classical sampling used in Guyon's and Codona's devices of 2 pixels per
(Shannon criteria). Compared to the classical sampling used in Guyon's and Codona's devices of 2 pixels per ![]() ,
the SCC image is 6/2=3 times oversampled, which reduces the field of view a priori. However, if the read out noise is not a limitation, this oversampling is not a problem since the interesting area
,
the SCC image is 6/2=3 times oversampled, which reduces the field of view a priori. However, if the read out noise is not a limitation, this oversampling is not a problem since the interesting area
![]() is given by the number of actuators of the DM. We consider static aberrations in the instrument upstream of the coronagraph. We adopt a 20 nm rms amplitude with a spectral power density varying as f-3, where f is the spatial frequency, which corresponds to typical VLT optic aberrations (Bordé & Traub 2006). We simulate an 8 m-diameter space telescope with a
is given by the number of actuators of the DM. We consider static aberrations in the instrument upstream of the coronagraph. We adopt a 20 nm rms amplitude with a spectral power density varying as f-3, where f is the spatial frequency, which corresponds to typical VLT optic aberrations (Bordé & Traub 2006). We simulate an 8 m-diameter space telescope with a ![]() throughput pointing a G2 star at 10 parsec. The quantum efficiency of the detector is
throughput pointing a G2 star at 10 parsec. The quantum efficiency of the detector is ![]() .
We consider photon noise, set the read out noise to 5e- per pixel, and consider the zodiacal light to be a uniform background at 22.5 mag arcsec-2. We have not used any linear approximation to simulate the focal plane images.
.
We consider photon noise, set the read out noise to 5e- per pixel, and consider the zodiacal light to be a uniform background at 22.5 mag arcsec-2. We have not used any linear approximation to simulate the focal plane images.
By correcting the wavefront errors, we improve the coronographic rejection and the reference intensity IR becomes dominant in the science image I (Eq. (1)). We adjust the calibrated neutral density in the reference channel at each step. To determine the value of the neutral density, we estimate the ratio r of the incoming energies from the image and reference channels in the center of the image to be
![]() where
where
![]() represents the
represents the
![]() centered on-axis area, and optimize fringe contrast for the next step. The neutral density transmission is 1 at step 0 and
centered on-axis area, and optimize fringe contrast for the next step. The neutral density transmission is 1 at step 0 and
![]() at step 3. At
at step 3. At
![]() ,
the average number of photons per pixel is about 1.3 and 50 for the reference channel, and 150 and 115 for the image one, respectively at steps 0 and 3. Finally, the intensity of
,
the average number of photons per pixel is about 1.3 and 50 for the reference channel, and 150 and 115 for the image one, respectively at steps 0 and 3. Finally, the intensity of
![]() decreases as the coronagraphic rejection increases. At each step, we adjust the exposure time to optimize the signal-to-noise ratio in the 16-bit dynamic range of the detector.
decreases as the coronagraphic rejection increases. At each step, we adjust the exposure time to optimize the signal-to-noise ratio in the 16-bit dynamic range of the detector.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0356fig3.eps} \end{figure}](/articles/aa/full/2008/34/aa10356-08/Timg64.gif) |
Figure 3:
|
| Open with DEXTER | |
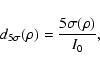 |
(9) |
![\begin{figure}
\par\includegraphics[width=6.4cm,clip]{0356fig4.eps} \end{figure}](/articles/aa/full/2008/34/aa10356-08/Timg71.gif) |
Figure 4:
SCC post-processed image of the final iteration image corresponding to a total exposure time of |
| Open with DEXTER | |
Similar results for high contrast imaging were demonstrated by Trauger & Traub (2007) in a laboratory experiment. They achieved a high contrast of 10-9 in polychromatic light (
![]() ), corresponding to a
), corresponding to a ![]() detection of
detection of
![]() .
.
SCC is one of the techniques under investigation for the E-ELT planet finder so-called EPICS. For this reason, we propose to consider the impact of different parameters, such as amplitude errors and turbulence residuals on the SCC performance. We will also test the compensation for amplitude errors proposed by Bordé & Traub (2006). A preliminary study, which assumes a more realistic coronagraph (achromatic Four Quadrant Phase Mask), indicates that our algorithm converges but more slowly than with a perfect coronagraph. The quality of the reference beam should not be important for SCC because of the filtering by the pinhole and the reduction in the beam diameter (DR), which induces a wide diffraction pattern in the focal plane. Experimental validations of the SCC technique are also planned soon.
We thank Pascal Bordé and Anthony Boccaletti for useful discussions.