A&A 487, 1147-1153 (2008)
DOI: 10.1051/0004-6361:20079323
Multi-wavelength spatially resolved analysis of quasi-periodic pulsations in a solar flare
A. R. Inglis1 - V. M. Nakariakov1 - V. F. Melnikov2
1 - Centre for Fusion, Space and Astrophysics, Physics Department, University of Warwick, Coventry, CV4 7AL, UK
2 - Radiophysical Research Institute (NIRFI), Nizhny Novgorod 603950, Russia
Received 23 December 2007 / Accepted 12 June 2008
Abstract
Aims. We aim to perform a spatially resolved analysis of a quasi-periodic pulsation event from 8th May 1998 using microwave data from the Nobeyama Radioheliograph and Radiopolarimeter, and X-ray data from the Yohkoh satellite.
Methods. Time spectra of the signals integrated over the emission source are constructed with the use of the Lomb-Scargle periodogram method, revealing the presence of a pronounced 16 s periodicity. The Pixon image reconstruction algorithm and Hanaoka algorithm are used to reconstruct images from the hard X-ray data from Yohkoh/HXT and Nobeyama Radioheliograph respectively. The phase relationship of the microwave emission was analysed with the use of cross-correlation techniques.
Results. The flaring loop was resolved in the microwave band. The hard X-ray sources are found to be located near the footpoint and at the loop apex determined by the soft X-ray image. The apex source is much fainter than footpoint one. In microwave, all parts of the loop are seen to oscillate with the same period and almost in phase. It was not possible to determine the spatial structure of the oscillation in the hard X-ray band. The period and the coherent spatial structure of the oscillation are indicative of the presence of either an MHD sausage mode or a periodic regime of magnetic reconnection.
Key words: Sun: flares - Sun: oscillations - waves - Sun: corona - magnetohydrodynamics (MHD)
Quasi-periodic pulsations (QPP) have been seen in emission from
solar flares for several decades (Nakariakov 2007). The emission
intensity from a solar flare is observed to oscillate with a
characteristic period, sometimes stably for several minutes, other
times in short bursts. The oscillation periods have been observed to
vary from a few seconds up to several minutes. In some cases
oscillations with more than one characteristic period occur
simultaneously (Melnikov et al. 2005). Presently, the interest in flaring
QPP is connected mainly with the development of coronal
seismological techniques for determination of physical
conditions and processes operating in flaring active regions. Also,
the understanding of flaring QPP in the solar corona will open up
very interesting perspectives for the diagnostics of stellar coronae
(Mathioudakis et al. 2003; Mitra-Kraev et al. 2005). In the
stellar context, coronal seismological methods are able to give
additional constraints on the physical parameters, compensating for the
lack of spatial resolution (Nakariakov 2007).
Various suggestions have been made regarding possible causes of QPP
in solar flares. One possible mechanism is the modulation of
physical parameters of the emitting plasma by magnetohydrodynamic
(MHD) modes of the flaring plasma structure. All four kinds of MHD
modes can produce modulation: torsional
(Tapping 1983), longitudinal
(Nakariakov & Melnikov 2006), kink (Grechnev et al. 2003) and
sausage (Nakariakov et al. 2003). In addition, sausage modes can
modulate the precipitation rate of the non-thermal electrons
accelerated by the flare via periodic change of the magnetic mirror
ratio (Zaitsev & Stepanov 1982). Also, recently (Nakariakov et al. 2006),
it has been suggested that QPP in a solar flare might be caused
by MHD oscillations in another loop situated near the flare site
but magnetically disconnected from the flaring region. The fast
waves leaking from the oscillating loop can reach the flaring site
and periodically trigger the process of magnetic reconnection. This
mechanism can explain the observed periodic variation of the flaring
emission in terms of the periodic acceleration of non-thermal
electrons. The mechanisms connected with the modulation of the
precipitation rate and the periodic triggering of reconnection can
explain the observed correlation in time of hard X-ray and microwave QPP.
It has already been emphasized that the correct identification of
the mechanism responsible for QPP should be based upon spatially
resolved analysis (Grechnev et al. 2003) and
(Nakariakov et al. 2003). This analysis includes examination of
amplitudes and phase relationships of oscillations in different parts
of the flaring loop. In particular, the presence of several
different MHD modes with different spatial structure and periods was
established in Melnikov et al. (2005). The leading instrument used in these
studies is the Nobeyama Radioheliograph (NoRH), which allows one to
detect the spatial distribution of the microwave emission of
non-thermal electrons, caused by the gyrosynchrotron mechanism,
along the flaring loop. In addition, hard X-ray instruments which
have comparable spatial and temporal resolution allow one to observe
the footpoints of the flaring loop or arcade and sometimes the
region above the loop apex.
The aim of this paper is to study QPP in a spatially resolved
flaring event, observed simultaneously in microwave and hard X-rays,
and to gain insight into the mechanism for the periodic modulation
of the emission. The flare discussed here is an M-class event which
occurred on the 8th May 1998 on the solar limb. It was observed by
the Nobeyama Radioheliograph and the Nobeyama Radiopolarimeter, and
by the Yohkoh, SOHO and GOES satellites. This event was first
analysed by Stepanov et al. (2004), who found a 16 s periodicity
and suggested that it was caused by an MHD ballooning mode. Here,
detailed analysis and an alternative interpretation of this event
are presented.
The time profile of the microwave flux integrated over the whole
flaring region (the light curve), recorded by NoRH at 17 GHz, is shown in Fig. 1. The signal is
averaged over 1 s. The time profile shows that this was a single
burst event beginning at 01:57 UT. Quasi-harmonic oscillations of
large modulation depth are evident immediately after the beginning
of the flare. These oscillations do not appear in 34 GHz due
to the low signal-to-noise ratio.
![\begin{figure}
\par\includegraphics[width=8cm]{9323fig1.ps}\end{figure}](/articles/aa/full/2008/33/aa9323-07/Timg1.gif) |
Figure 1:
a) Integrated flux time profile of microwave emission at 17 GHz for the solar flare of 8th May 1998, as observed by NoRH. Overlayed with the dashed line is the background emission profile obtained via 20 s smoothing of the integrated flux signal. b) The signal after subtraction of the background profile from the integrated flux. c) Solar flux time profiles of microwave emission at 9.4 GHz (dot-dashed line), 17 GHz (solid line) and 3.75 GHz (dotted line), obtained by the Nobeyama Radiopolarimeters. |
| Open with DEXTER |
The presence of the pronounced periodicity is also seen in the lower
frequency channels observed by the Nobeyama Radiopolarimeter (see
Fig. 1). The oscillations in different channels are seen
to be coincident.
![\begin{figure}
\par\includegraphics[width=8cm]{9323fig2.ps}\end{figure}](/articles/aa/full/2008/33/aa9323-07/Timg2.gif) |
Figure 2:
Hard X-ray light curves from the Yohkoh satellite, observing the solar flare of 8th May 1998. a) X-ray counts in the L (13-23 keV) range, b) X-ray counts in the M1 (23-33 keV) range, c) X-ray counts in the M2 (33-53 keV) range, d) X-ray counts in the H (53-93 keV) range. |
| Open with DEXTER |
The high quality of the observed oscillation is confirmed by the
spectrum of the analysed signal. Subtracting the running mean
smoothed by 20 s from the signal recorded at 17 GHz by NoRH, and
applying the periodogram technique described by Scargle (1982) and
Horne & Baliunas (1986), we obtain the power spectrum with the
pronounced peak of 16 s (Fig. 3). The smoothing is equivalent to the removal
of the low frequency component of the signal in the spectral domain, which is connected with the long period trend.
The observed period concurs with the findings of Stepanov et al. (2004). The peak is
found to be well above the 99% confidence level calculated
according to Horne & Baliunas (1986). The main spectral peak is surrounded by secondary peaks.
To check whether the secondary peaks appeared because of the finite duration of the sample, we calculated the
spectra of the smoothed signals multiplied by window
functions (see Fig. 3). This increases the amplitude resolution of the spectrum on the expense of the frequency resolution.
According to the figure, the use of a window function clearly suppresses the
spectral sidelobes of the peak, indicating that they may be
artificial rather than real in nature.
![\begin{figure}
\par\includegraphics[width=8cm]{9323fig3a.ps}\par\includegraphics[width=8cm]{9323fig3b.ps}\end{figure}](/articles/aa/full/2008/33/aa9323-07/Timg3.gif) |
Figure 3:
Top panel: Lomb-Scargle periodogram (Scargle 1982) of the 17 GHz
modulation depth from the Nobeyama Radioheliograph. Dashed
line: periodogram without a window function; dotted line:
periodogram using a Hann window function; solid line:
periodogram using a Blackman-Harris window function. The periodogram
reveals a oscillation period of 16 s, above the 99% confidence
level. Bottom panel: Lomb-Scargle periodogram of the M1 (23-33 keV) X-ray modulation observed by the Yohkoh satellite. |
| Open with DEXTER |
The impulsive burst of emission was also detected by the
Hard X-ray Telescope (HXT) on board Yohkoh. Hard X-ray light curves
corresponding to different energies are shown in
Fig. 2.
There is clear evidence of oscillations in the L, M1 and M2
channels. A periodogram analysis on the modulation depth in hard
X-rays reveals a period matching that of the microwave emission
above the 90% confidence level in both the L and M1 energy
channels. The Scargle periodogram of the oscillation in the M1 channel is shown
in Fig. 3. The count rate in the M2 band is too low for a reliable detection, while
the H channel observes little above the background level, consistent
with an M-class flaring event.
Both the NoRH and HXT allow for spatial resolution of the microwave
and hard X-ray emission sources, respectively. The location of the
various types of emission from a flare have implications for the
flare model. According to the standard flare model, magnetic
reconnection is supposed to take place above the loop top. Hard
X-ray emission is expected at the two footpoints of the flaring loop
as a result of the interaction of non-thermal electrons accelerated
in the flare with dense plasmas. A third source may also be present
above the loop top (Masuda et al. 1994). The source of the microwave emission
generated by non-thermal electrons by the gyrosynchrotron mechanism
is usually situated at a segment of the loop. Soft X-rays
from solar flares are due to thermal emission from the hot plasma
which fills the flaring loop. Consequently, soft X-ray images can
provide information about the geometry of the flaring region.
A soft X-ray image of the flare provided by the Yohkoh satellite is
shown in Fig. 4 with the 17 GHz microwave
emission source from the same time overlayed.
The microwave emission is seen to take the form of a single source.
This source coincides with the maximum emission of the soft X-ray
loop, near the southern footpoint. Figure 5 shows the
soft X-ray images with the hard X-ray emission sources from the L
(13-23 keV), M1 (23-33 kev), and M2 (33-53 kev) channels
overlayed. The images indicate that the flare is located on the
solar limb. This concurs with the observations made by the Extreme
Ultraviolet Imaging Telescope (EIT) on board SOHO, shown in Fig. 6.
![\begin{figure}
\par\includegraphics[width=8cm]{9323fig4.ps}\end{figure}](/articles/aa/full/2008/33/aa9323-07/Timg4.gif) |
Figure 4:
Image: Soft X-ray image from the Yohkoh satellite of the
flare of 8th May 1998. Contour: microwave emission source for the
same flare, observed by the Nobeyama Radioheliograph at 17 GHz. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8cm]{9323fig5a.ps}\vspace*{1.5mm}
\inc...
...23fig5b.ps}\vspace*{1.5mm}
\includegraphics[width=8cm]{9323fig5c.ps}\end{figure}](/articles/aa/full/2008/33/aa9323-07/Timg5.gif) |
Figure 5:
Contour maps of hard X-ray emission overlayed on a soft
X-ray image of the flaring loop at 01:57:50 UT, during the oscillatory phase. Top: the L (13-23 keV) channel, centre: the M1 (23-33 keV) channel, bottom: the M2 (33-53 keV) channel. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8cm]{9323fig6.ps}\end{figure}](/articles/aa/full/2008/33/aa9323-07/Timg6.gif) |
Figure 6:
Image: SOHO/EIT image of the flare of 8th May 1998. Contour: soft X-ray loop emission, obtained from the Yohkoh SXT. |
| Open with DEXTER |
The sources of different hard X-ray channels have different
structures. The low energy channel emission is similar to the soft
X-ray structure and is centred around a single maximum near and a
little above the centre of the soft X-ray loop, indicating that this
emission is thermal in nature. The higher energy channels however
reveal the presence of multiple emission sources. The M1 and M2
channels both show a southern footpoint located at (920,-270)
arcseconds. The presence of the second (northern) footpoint is also
expected from the standard flare model. Although emission from the
northern loop footpoint is tentatively observed in the M2 - and
sometimes in the M1 - channel, centred at (920, -220) arcsec,
this emission is weak and not confidently observed. The reason for
the weakness of the source may be explained by the main northern
emission site being hidden behind the solar limb. Both high energy
channels are also indicative of an emission source coming from above
the loop top. This source may be associated with the Masuda source.
The identification of the observed mode requires the analysis of the
spatial structure of the oscillation. An important characteristic
of the mode is the phase relationship between the oscillation at
different parts of the loop.
The application of the periodmapping technique (Nakariakov & King 2007)
allows us to determine the distribution of the
dominating periods of time oscillations in the spectra of the
individual pixels. As in this study we are interested in the mode
with the period of about 16 s found in Sect. 2.1, we smooth the time signal of each
pixel by 50 frames, which corresponds to 5 s, suppressing the high
frequency noise, and then subtract the signal smoothed by 500 frames, which corresponds to 50 s. The latter operation removes the low frequency trend from the data. The periodmap of the data cube
obtained in 17 GHz is shown in Fig. 7. In the map,
the colour of a pixel corresponds to the period of the highest peak
in the spectrum of the time signal of the pixel, provided the
spectral power of the peak is 5 times greater than the power
averaged over the spectrum. Otherwise, the pixel colour is white. In
addition, The pixels with the signals integrated over time, lower
than
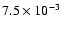 of the integrated signal from the
``strongest'' pixel, are left blank. This operation allows us to
subtract the spatial interference pattern which is the artefact of
the image synthesis.
of the integrated signal from the
``strongest'' pixel, are left blank. This operation allows us to
subtract the spatial interference pattern which is the artefact of
the image synthesis.
![\begin{figure}
\par\includegraphics[width=8cm]{9323fig7.ps}\end{figure}](/articles/aa/full/2008/33/aa9323-07/Timg8.gif) |
Figure 7:
Periodmap of the microwave emission at 17 GHz, obtained by
the Nobeyama Radioheliograph during the pulsating regime of the limb
flare of 8th May 1998. The bar shows the colour coding of the
frequencies in Hz. |
| Open with DEXTER |
The periodmap shows that the period of about 16 s dominates in
almost all pixels with time integrated signals stronger than the
set threshold. Some pixels near the edge of the region of 16 s
oscillations show the presence of higher periodicity. Thus, almost
all segments of the flaring loop oscillate with the same period of
about 16 s.
To investigate the spatial structure of phase of the oscillations, a
cross-correlation analysis was used. First, a pixel with the master
(reference) signal was selected, which we shall refer to as the ``master'' pixel.
There is however more than one possible selection criterion for the master pixel. For example,
the master pixel can be the pixel with the highest time variance of the signal. Alternatively
it may be the pixel with the highest time-integrated intensity. Once the master pixel is selected,
for each pixel of the image we calculate the correlation coefficient between the time signal of this pixel and the
time signal of the master pixel for different time lags between
these signals. The correlation coefficient is given by:
![\begin{displaymath}P_{xy}(L)=
\left\{\begin{array}{ll}
\frac{\sum_{k=0}^{N-L-1} ...
...\right] }} & \textrm{for L $\geq$\space 0},
\end{array}\right.
\end{displaymath}](/articles/aa/full/2008/33/aa9323-07/img9.gif) |
(1) |
where x and y are the two datasets, and L is the time lag.
Visualising the results obtained with this approach, one can make,
e.g., either a map showing the spatial distribution of the
correlation coefficient value calculated at a specified time lag, or
a map showing the time lags corresponding to the highest values of
the correlation coefficient for each pixel.
The top panel of Fig. 8 is a correlation power map of microwave
emission, calculated with zero time lag - Pxy(0). As the
master pixel we choose the pixel with the maximum value of the time
integrated intensity, found near the centre of the loop emission.
Here, for clarity, we have restricted our attention to areas showing
a correlation coefficient power of 0.5 or greater. Pixels with
Pxy less than 0.5 are blank. The strong correlation
throughout the emitting region is evident. The map also reveals some
evidence of a loop-like structure.
![\begin{figure}
\par\includegraphics[width=7.8cm]{9323fig8a.ps}\par\includegraphics[width=7.8cm]{9323fig8b.ps}\end{figure}](/articles/aa/full/2008/33/aa9323-07/Timg10.gif) |
Figure 8:
Top: cross-correlation coefficient map for background subtracted
microwave emission at 17 GHz, obtained by the Nobeyama
Radioheliograph during the pulsating regime of the limb flare of 8th
May 1998. The correlation coefficient is calculated with zero time lag. The master pixel is the pixel with the highest
time-integrated intensity of the signal. The bar shows the colour
coding of the correlation coefficient.
Bottom: correlation time-lag map for microwave emission. The bar shows the colour coding of the time lag in seconds. In both panels the central white point corresponds to the master pixel. |
| Open with DEXTER |
The bottom panel of Fig. 8 shows the spatial distribution of time lags
between the time signal from the master pixel and other pixels,
which correspond to maximum correlation coefficients. The emitting
region appears to be strongly correlated in time, with a maximum
shift in time of about 2 s occurring towards the edge of the region.
A cross-correlation analysis of the hard X-ray sources did not succeed
in either the M1 or M2 bands. The northern footpoint source is too weak to be meaningfully analysed.
This is unfortunate as we would expect the two footpoints to be well
correlated in time.
It is also possible to use the hard X-ray data to investigate the
evolution of the flare emission.
![\begin{figure}
\par\includegraphics[width=8.3cm]{9323fig9a.ps} \includegraphics[width=8.3cm]{9323fig9b.ps} \includegraphics[width=8.3cm]{9323fig9c.ps}\end{figure}](/articles/aa/full/2008/33/aa9323-07/Timg11.gif) |
Figure 9:
Hard X-ray contours from the M1 (23-33 kev) channel overlayed on an SXT image, at 01:57:11, 01:57:49 and 01:58:28 respectively. |
| Open with DEXTER |
The presence of a stable hard X-ray footpoint throughout the
impulsive phase of the flaring emission is clearly illustrated by
Fig. 9. The emission from the loop top is
observed to shift in location and become more complex in structure
over the same period. After the end of the impulsive phase - at
01:59 - the southern footpoint disappears, leaving only the loop top
emission. This emission decays slowly over time, much like the
thermal emission in the L (13-23 kev) energy channel.
Magnetograms of the active region prior to this event indicate the
presence of a single sunspot, suggesting this event began with flux
emergence leading to magnetic reconnection. Yohkoh SXT images also
show a slight but steady outward expansion of the flaring loop over
time, consistent with this interpretation.
Quasi-periodic pulsations were clearly observed in both microwaves
and hard X-rays for this event. It was also possible to spatially
resolve at least two different hard X-ray sources in the higher
energy bands of the HXT, located at the southern loop footpoint and
the loop top respectively. There is also some evidence of a hard
X-ray source at the primary flare's northern footpoint. This is weak
and only present at the onset of the impulsive phase. According to
the standard flare model two footpoint sources are typical. We
postulate therefore that the main emission site for the northern
footpoint is hidden behind the limb of the sun.
In Stepanov et al. (2004) this event was considered as an MHD ballooning
mode. However, more detailed analysis presented here does not
support this interpretation. Periodmapping and the cross-correlation
analysis of the microwave emission shows that well correlated
oscillations with a period of about 16 s are distributed over the
bulk of the loop. Also, the evidence of the characteristic
ballooning mode ``tongues'' was not found in either X-ray or
microwave emission. Thus, we conclude that the observed oscillation
is caused by another reason.
We also exclude the interpretation of the observed quasi-periodic pulsations in terms of flare-induced slow magnetoacoustic
waves (see, e.g. McAteer et al. (2005)). The observed emission is clearly connected with the non-thermal electrons. It is not clear
how a slow wave which is mainly acoustic in nature could affect the dynamics
of the non-thermal electrons and hence their precipitation rate.
Slow waves can produce the variations of the microwave emission by modulation of the
ratio of the plasma frequency to the electron gyro-frequency (see
Nakariakov & Melnikov 2006). However there are no known mechanisms which would link the modulation
of the hard X-ray emission with slow waves. A similar problem takes place with interpretation of the
observed oscillations of the hard X-ray emission in terms of a kink or torsional mode; they do not significantly affect
the non-thermal electron dynamics.
On the other hand, the sausage mode can produce modulation of the microwave (Nakariakov et al. 2003) and
hard X-ray (Zaitsev & Stepanov 1982) emission. The period of the sausage mode is determined by the
loop length.
The loop length was estimated to be between 40-80 Mm.
Unfortunately, due to the position of the flare on the limb
measurement of the line-of-sight angle is difficult. Soft X-ray and
EUV images indicate that there may be more than one loop in this
region. In particular, there is some evidence of a second, cool loop
above the primary loop. The northern footpoint of this is often
visible at about (930,-200) arcseconds, although it is not generally
a source of hard X-ray emission. Additionally, magnetograms of the
active region in the days preceding this event show only a single
sunspot, suggesting that this flaring event was an emergent
phenomenon. As a result a sunspot pair cannot be used as an
alternative length estimate. However, the characteristic period of
the oscillations, 16 s, together with this rough length estimate, is
consistent with the sausage mode interpretation (see
Nakariakov et al. 2003). As the period of the global
sausage mode - with the wavelength equal to double the loop length -
is determined by ratio of the wavelength to the Alfvén speed
outside the loop, this interpretation yields the estimation of the
external Alfvén speed in the range from 5 to 10 Mm/s.
An alternative interpretation of the observed quasi-periodic pulsations
could be a periodic regime of magnetic reconnection. In this case, the acceleration of
non-thermal electrons is periodically modulated, causing the periodic variation of the non-thermal
electron density, and hence the periodic modulation of the microwave and hard X-ray emission.
However, it is not clear what would determine
the period of the oscillations in this case. One possibility is the periodic triggering of magnetic
reconnection by an external oscillating loop (Nakariakov et al. 2006).
The theory of this phenomenon needs to be developed.
Hence, we cannot exclude this mechanism from consideration.
Useful additional information could be provided by spectroscopic instruments.
Unfortunately, the spectral information available for this event is very limited.
As mentioned previously, the Nobeyama Radioheliograph registers
little above background noise at 34 GHz. Similarly, useful data is
only available from the Nobeyama Radiopolarimeters at 3.75, 9, and
17 GHz. The strongest emission is in the 9 GHz band, indicating that
the gyrosynchotron turnover frequency is somewhere in this region.
Hard X-ray spectral information is equally limited, as the Yohkoh
satellite observes in only four energy bands, the highest of which
observes little above background levels. Therefore, no meaningful
spectral analysis is possible.
A spatially resolved analysis of the solar flare of 8th May 1998
shows that it may be considered as a Masuda-type event, as evidenced
by a hard X-ray emission source above the loop top. In high energy
bands a strong southern footpoint is also observed. The absence of a noticeable northern
footpoint in hard X-ray emission is attributed to the footpoint
being obscured behind the solar limb. Magnetograms from the SOHO
satellite provide evidence that this event was an emergent
phenomenon leading to magnetic reconnection. Yohkoh SXT images also
show an expansion of the loop over time.
The analysed flare has perhaps the most pronounced flaring
QPP since the famous 8 s period oscillatory event observed on the
7th of June, 1980 (Kane et al. 1983) with ISEE-3 in X-rays and with the Nobeyama Radiopolarimeter in
microwaves. In the event analysed here, the high quality 16 s
periodicity is seen to be very stable during the flare, and was
found to be present in the data with more than 99% confidence. In
contrast with the event on 7th of June, 1980, this time spatial
information is available, allowing us to determine the MHD mode
responsible for the oscillation.
The observed period of 16 s together with an estimate of the loop
length is consistent with the interpretation of the QPP in terms of
the sausage mode which periodically changes the loop cross-section
and the magnetic field. In this case the microwave emission is
modulated by the periodic variation of the magnetic field in the
emitting plasma. The periodic modulation of the hard X-ray emission
is caused by the periodic modulation of the mirror ratiobecause of
the variation of the loop cross-section. An alternative
interpretation is the periodic modulation of the flaring energy
release (either a periodic regime of magnetic reconnection, or periodic
triggering of reconnection by an external waves), and hence the particle acceleration by some external
oscillation. However, no evidence of such an oscillation was found in this event.
The observed period of 16 s is perhaps a typical period for the global sausage oscillations in flaring regions (e.g. with a similar value obtained in Nakariakov et al. 2003). This period
is significantly shorter than the periods of quasi-periodic pulsations associated with slow magnetoacoustic
modes (Mitra-Kraev et al. 2005; McAteer et al. 2005) and those possibly triggered by an external kink oscillation
(Foullon et al. 2005). Confident discrimination between the flaring oscillations caused by global
sausage modes and by oscillatory regimes of magnetic reconnection is impossible until the theory of the latter is understood.
Acknowledgements
The authors acknowledge helpful discussions with E. Verwichte, and
are very grateful to V. Grechnev for the help with the preliminary
analysis of this event. The work was supported by the Royal Society
British-Russian Research Collaboration grant. ARI acknowledges the
support of an STFC PhD studentship. VFM acknowledges the support of
RFBR grants 06-02-39029, 06-02-16295, 07-02-01066.
- Foullon, C.,
Verwichte, E., Nakariakov, V. M., & Fletcher, L. 2005,
A&A, 440, L59 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Grechnev, V. V.,
White, S. M., & Kundu, M. R. 2003, ApJ, 588,
1163 [NASA ADS] [CrossRef]
(In the text)
-
Horne, J. H., & Baliunas, S. L. 1986, ApJ, 302,
757 [NASA ADS] [CrossRef]
(In the text)
- Kane, S. R., Kai,
K., Kosugi, T., et al. 1983, ApJ, 271, 376 [NASA ADS] [CrossRef]
(In the text)
- Masuda, S., Kosugi, T.,
Hara, H., Tsuneta, S., & Ogawara, Y. 1994, Nature, 371,
495 [NASA ADS] [CrossRef]
(In the text)
- Mathioudakis, M.,
Seiradakis, J. H., Williams, D. R., et al. 2003,
A&A, 403, 1101 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- McAteer,
R. T. J., Gallagher, P. T., Brown, D. S.,
et al. 2005, ApJ, 620, 1101 [NASA ADS] [CrossRef]
(In the text)
- Melnikov,
V. F., Reznikova, V. E., Shibasaki, K., & Nakariakov,
V. M. 2005, A&A, 439, 727 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Mitra-Kraev, U.,
Harra, L. K., Williams, D. R., & Kraev, E. 2005,
A&A, 436, 1041 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Nakariakov, V. M.
2007, Adv. Space Res., 39, 1804 [NASA ADS] [CrossRef]
(In the text)
- Nakariakov,
V. M., & King, D. B. 2007, Sol. Phys., 241,
397 [NASA ADS] [CrossRef]
(In the text)
- Nakariakov,
V. M., & Melnikov, V. F. 2006, A&A, 446,
1151 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Nakariakov,
V. M., Melnikov, V. F., & Reznikova, V. E. 2003,
A&A, 412, L7 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Nakariakov,
V. M., Foullon, C., Verwichte, E., & Young, N. P.
2006, A&A, 452, 343 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Scargle, J. D.
1982, ApJ, 263, 835 [NASA ADS] [CrossRef]
(In the text)
- Stepanov,
A. V., Kopylova, Y. G., Tsap, Y. T., et al.
2004, Astron. Lett., 30, 480 [NASA ADS] [CrossRef]
(In the text)
- Tapping, K. F.
1983, Sol. Phys., 87, 177 [NASA ADS] [CrossRef]
(In the text)
- Zaitsev, V. V.,
& Stepanov, A. V. 1982, Soviet Astron. Lett., 8, 132 [NASA ADS]
(In the text)
Copyright ESO 2008
![\begin{figure}
\par\includegraphics[width=8cm]{9323fig1.ps}\end{figure}](/articles/aa/full/2008/33/aa9323-07/Timg1.gif)
![\begin{figure}
\par\includegraphics[width=8cm]{9323fig2.ps}\end{figure}](/articles/aa/full/2008/33/aa9323-07/Timg2.gif)
![\begin{figure}
\par\includegraphics[width=8cm]{9323fig3a.ps}\par\includegraphics[width=8cm]{9323fig3b.ps}\end{figure}](/articles/aa/full/2008/33/aa9323-07/Timg3.gif)
![\begin{figure}
\par\includegraphics[width=8cm]{9323fig4.ps}\end{figure}](/articles/aa/full/2008/33/aa9323-07/Timg4.gif)
![\begin{figure}
\par\includegraphics[width=8cm]{9323fig5a.ps}\vspace*{1.5mm}
\inc...
...23fig5b.ps}\vspace*{1.5mm}
\includegraphics[width=8cm]{9323fig5c.ps}\end{figure}](/articles/aa/full/2008/33/aa9323-07/Timg5.gif)
![\begin{figure}
\par\includegraphics[width=8cm]{9323fig6.ps}\end{figure}](/articles/aa/full/2008/33/aa9323-07/Timg6.gif)
![\begin{figure}
\par\includegraphics[width=8cm]{9323fig7.ps}\end{figure}](/articles/aa/full/2008/33/aa9323-07/Timg8.gif)
![\begin{displaymath}P_{xy}(L)=
\left\{\begin{array}{ll}
\frac{\sum_{k=0}^{N-L-1} ...
...\right] }} & \textrm{for L $\geq$\space 0},
\end{array}\right.
\end{displaymath}](/articles/aa/full/2008/33/aa9323-07/img9.gif)
![\begin{figure}
\par\includegraphics[width=7.8cm]{9323fig8a.ps}\par\includegraphics[width=7.8cm]{9323fig8b.ps}\end{figure}](/articles/aa/full/2008/33/aa9323-07/Timg10.gif)
![\begin{figure}
\par\includegraphics[width=8.3cm]{9323fig9a.ps} \includegraphics[width=8.3cm]{9323fig9b.ps} \includegraphics[width=8.3cm]{9323fig9c.ps}\end{figure}](/articles/aa/full/2008/33/aa9323-07/Timg11.gif)