A&A 487, 951-963 (2008)
DOI: 10.1051/0004-6361:20079240
Global properties of the H I distribution in the outer Milky Way
Planar and extra-planar gas
P. M. W. Kalberla - L. Dedes
Argelander-Institut für Astronomie, Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
Received 13 December 2007 / Accepted 31 March 2008
Abstract
Context. The determination of the global structure of the planar and extra-planar Milky Way H I disk depends critically on a reliable database but also on reasonable assumptions about the shape of the Milky Way rotation curve.
Aims. We derive the 3D H I volume density distribution for the Galactic disk out to 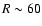 kpc.
kpc.
Methods. Our analysis is based on parameters for the warp and rotation curve derived previously. The data are taken from the Leiden/Argentine/Bonn all sky 21 cm line survey.
Results. The Milky Way H I disk is significantly warped but shows a coherent structure out to 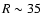 kpc. The radial surface density distribution, the densities in the middle of the warped plane, and the H I scale heights all follow exponential relations. The radial scale length for the surface density distribution of the H I disk is 3.75 kpc. Gas at the outskirts for
kpc. The radial surface density distribution, the densities in the middle of the warped plane, and the H I scale heights all follow exponential relations. The radial scale length for the surface density distribution of the H I disk is 3.75 kpc. Gas at the outskirts for
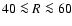 kpc is described best by a distribution with an exponential radial scale length of 7.5 kpc and a velocity dispersion of 74 km s-1. Such a highly turbulent medium fits also well with the average shape of the high velocity profile wings observed at high latitudes. The turbulent pressure gradient of such extra-planar gas is on average in balance with the gravitational forces. About 10% of the Milky Way H I gas is in this state. The large scale H I distribution is lopsided; for
kpc is described best by a distribution with an exponential radial scale length of 7.5 kpc and a velocity dispersion of 74 km s-1. Such a highly turbulent medium fits also well with the average shape of the high velocity profile wings observed at high latitudes. The turbulent pressure gradient of such extra-planar gas is on average in balance with the gravitational forces. About 10% of the Milky Way H I gas is in this state. The large scale H I distribution is lopsided; for 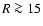 kpc there is more gas in the south. The H I flaring indicates that this asymmetry is caused by a dark matter wake, located at
kpc there is more gas in the south. The H I flaring indicates that this asymmetry is caused by a dark matter wake, located at 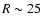 kpc in direction of the Magellanic System.
kpc in direction of the Magellanic System.
Conclusions. The H I disk is made up of two major components. Most prominent is the normal H I disk which can be traced to 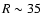 kpc. This is surrounded by a patchy distribution of highly turbulent gas reaching large scale heights but also large radial distances. At the position of the Sun the exponential scale height in the z direction is 3.9 kpc. This component resembles the anomalous gas discovered previously in some galaxies.
kpc. This is surrounded by a patchy distribution of highly turbulent gas reaching large scale heights but also large radial distances. At the position of the Sun the exponential scale height in the z direction is 3.9 kpc. This component resembles the anomalous gas discovered previously in some galaxies.
Key words: Galaxy: disk - Galaxy: halo - Galaxy: structure - Galaxy: kinematics and dynamics - ISM: structure
The gaseous content of galaxies is a crucial counterpart to the stellar
population but has the additional advantage that it can be traced far beyond
the stellar population, radially but also perpendicular to the disk. Stars are
born out of gas condensations and their deaths affect the three-dimensional
evolution of the Galactic disc. The gas traces such activities. Here we are
interested in the steady state situation caused by dynamical processes as
described e.g. by de Avillez (2000). The 21 cm line traces these
processes, in particular the diffuse part of the interstellar medium (ISM). A
thin disk is expected in the plane, overlaid by a thick H I disk which is
associated with an ionized layer. Depending on the supernova rate in the
underlying disc a more or less established disc-halo interface is expected.
Most prominent, comparing the gaseous content of galaxies with the stellar
distribution, is the large radial extent of the gaseous disk. The outer part
is only slightly affected by the stellar disk but traces environmental
influences such as influences from the intergalactic medium. We
explore global parameters for layers above the disk and gas at the outskirts
of the Milky Way. For such an analysis we need to determine the properties of
the dominant part of the H I distribution first, i.e. the H I disk which
co-rotates with the stellar disk. Knowing the properties of the gas within the
disk we may proceed to determine the nature of the gas around this disk.
In Sect. 2 we briefly introduce the database and the conversion of brightness
temperatures
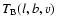 to densities
to densities
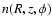 .
The observer's location
inside the Galactic disk causes some ambiguities and constraints that need to
be discussed. In Sect. 3 we derive radial dependencies of the average surface
density distribution within the disk. This is followed in Sect. 4 by a
discussion of average properties of the mid-plane volume densities. We find
that the gas distribution within the Milky Way H I disk is approximately
exponential for a large part of the disk. The gas properties at
.
The observer's location
inside the Galactic disk causes some ambiguities and constraints that need to
be discussed. In Sect. 3 we derive radial dependencies of the average surface
density distribution within the disk. This is followed in Sect. 4 by a
discussion of average properties of the mid-plane volume densities. We find
that the gas distribution within the Milky Way H I disk is approximately
exponential for a large part of the disk. The gas properties at 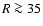 kpc
differ significantly; this is studied in Sect. 5. At the outskirts we find
that the H I distribution needs to be described as a highly turbulent phase.
In Sect. 6 we consider the H I distribution at the polar caps. We require hydrostatic equilibrium and derive a velocity dispersion of
kpc
differ significantly; this is studied in Sect. 5. At the outskirts we find
that the H I distribution needs to be described as a highly turbulent phase.
In Sect. 6 we consider the H I distribution at the polar caps. We require hydrostatic equilibrium and derive a velocity dispersion of
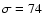 km s-1 for the halo gas phase. Such a phase explains not only the H I distribution at the outskirts but also the average local emission high above the disk. About 10% of the H I is in this phase and we demonstrate that the Milky Way would look very similar to NGC 891 or NGC 2403 if it were observed edge-on at large distances. Section 7 contains a summary.
km s-1 for the halo gas phase. Such a phase explains not only the H I distribution at the outskirts but also the average local emission high above the disk. About 10% of the H I is in this phase and we demonstrate that the Milky Way would look very similar to NGC 891 or NGC 2403 if it were observed edge-on at large distances. Section 7 contains a summary.
Our analysis is based on the Leiden/Argentine/Bonn (LAB) H I line survey
(Kalberla et al. 2005). This survey combines the southern sky survey of the
Instituto Argentino de Radioastronomía (IAR) (Bajaja et al. 2005) with an
improved version of the Leiden/Dwingeloo Survey (LDS) (Hartman & Burton 1997). Currently, this is the most sensitive Milky Way H I line survey with the most extensive coverage both spatially and kinematically. The line profiles have been corrected for spurious sidelobe emission; we expect therefore that profile wings, most critical for our investigations, are only mildly contaminated by instrumental problems.
![\begin{figure}
\par\mbox{\includegraphics[angle=-90,width=8.7cm]{9240f01a.eps} \...
...0f01g.eps} \includegraphics[angle=-90,width=8.7cm]{9240f01h.eps} }
\end{figure}](/articles/aa/full/2008/33/aa9240-07/Timg29.gif) |
Figure 1:
Derived volume density distribution at R = 10, 12.5, 15, 17.5, 20, 22.5, 25, 30 kpc ( top to bottom). Locations affected by local emission with
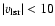 km s-1 are flagged dark. We display densities n < 0.5 cm-3. A logarithmic transfer function was chosen to emphasize low densities. The thin white lines indicate the average flaring at a km s-1 are flagged dark. We display densities n < 0.5 cm-3. A logarithmic transfer function was chosen to emphasize low densities. The thin white lines indicate the average flaring at a 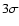 level and enclose the warped disk. The thick white lines indicate latitudes
level and enclose the warped disk. The thick white lines indicate latitudes
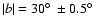 . . |
| Open with DEXTER |
All the individual steps necessary to convert the observed brightness
temperature distribution
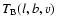 as a function of galactic longitude,
latitude and LSR velocity to densities
as a function of galactic longitude,
latitude and LSR velocity to densities
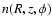 have been described by
Kalberla et al. (2007). We use cylindrical coordinates
have been described by
Kalberla et al. (2007). We use cylindrical coordinates
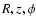 to describe the Milky Way disk;
to describe the Milky Way disk; 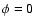 is in direction l = 0. We use the IAU
recommendations for the galactic constants;
is in direction l = 0. We use the IAU
recommendations for the galactic constants;
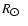 = 8.5 kpc and
= 8.5 kpc and
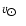 = 220 km s-1.
= 220 km s-1.
Figure 1 shows several global properties of the Galactic H I
density distribution. We have chosen a common logarithmic transfer function to
cover the high dynamic range of the density fluctuations within the Galactic
disk. The average extension of the flaring disk layer is indicated. The thin
white lines indicate the thickness of the disk at a 3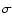 level of the
second moment fitted by Kalberla et al. (2007). The warp is obvious for
level of the
second moment fitted by Kalberla et al. (2007). The warp is obvious for 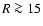 kpc as a sine-wave pattern. With increasing distance, the southern part of
the disk, -
kpc as a sine-wave pattern. With increasing distance, the southern part of
the disk, -
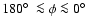 ,
returns to
,
returns to
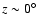 while the
northern part,
while the
northern part,
 ,
bends up strongly and becomes
increasingly disrupted. Within the galactic plane several shells are
detectable; some of them have very low central densities. All kind of spurs,
arcs, filaments, and chimneys are visible, indicating violent interactions for
most parts of the disk, most pronounced for
,
bends up strongly and becomes
increasingly disrupted. Within the galactic plane several shells are
detectable; some of them have very low central densities. All kind of spurs,
arcs, filaments, and chimneys are visible, indicating violent interactions for
most parts of the disk, most pronounced for 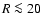 kpc.
kpc.
We do not discuss details visible in Fig. 1 but a few comments
concerning the
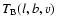 to
to
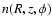 conversion are necessary. The
shape of the Milky Way rotation curve, but also the location of the Sun within
the Galactic plane, causes complex geometrical transformations. A white line
is plotted in Fig. 1 at latitudes
conversion are necessary. The
shape of the Milky Way rotation curve, but also the location of the Sun within
the Galactic plane, causes complex geometrical transformations. A white line
is plotted in Fig. 1 at latitudes
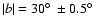 for visualization. Some ambiguities are discussed next.
for visualization. Some ambiguities are discussed next.
Local gas at low velocities may cause spurious features in the density
distribution, most serious for
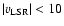 km s-1. These regions have
been disregarded, indicated by the black color in
Fig. 1. Figure 2 displays the velocity field at
mid-plane. The central green region, enclosed by isophotes, corresponds to
km s-1. These regions have
been disregarded, indicated by the black color in
Fig. 1. Figure 2 displays the velocity field at
mid-plane. The central green region, enclosed by isophotes, corresponds to
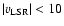 km s-1. There are some more regions with unreliable
kinematic distances. In the direction of the Galactic center, we discarded
data originating from |R| < 3.5 kpc. This region, approximately the extent
of the bar, is affected by ambiguities due to large velocity dispersions of
the emission lines (Weiner & Sellwood 1999, Fig. 8). Low dv/dR values, predominantly at
km s-1. There are some more regions with unreliable
kinematic distances. In the direction of the Galactic center, we discarded
data originating from |R| < 3.5 kpc. This region, approximately the extent
of the bar, is affected by ambiguities due to large velocity dispersions of
the emission lines (Weiner & Sellwood 1999, Fig. 8). Low dv/dR values, predominantly at
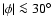 ,
,
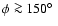 ,
and
,
and
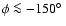 introduce additional distance uncertainties. We strictly exclude these regions from further analysis and use for the northern part of the Galactic plane the range
introduce additional distance uncertainties. We strictly exclude these regions from further analysis and use for the northern part of the Galactic plane the range
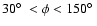 and
and
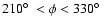 for the southern part.
for the southern part.
A fraction of the observed H I gas distribution is presumably not associated with the disk. Intermediate and high velocity clouds (IVCs and HVCs, respectively) are most probably located above the disk (van Woerden et al. 2004). One might think that such features should be excluded from the database prior to the determination of
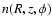 for the H I disk. We emphasize that no such
filtering was applied to the observations.
for the H I disk. We emphasize that no such
filtering was applied to the observations.
The scale height of the H I disk and the mid-plane density was determined by
adaptive filtering of the volume density distribution. The basic underlying
assumption is that the disk can be characterized as a homogeneous gas layer in
circular rotations, for details we refer to Kalberla et al. (2007). The thin
white lines in Fig. 1 characterize the extension of the gas in
the Galactic plane. We display the 3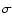 level of the second moment
fitted by Kalberla (2007) to the flaring gas layer. The 3
level of the second moment
fitted by Kalberla (2007) to the flaring gas layer. The 3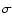 limit
is somewhat arbitrary, a different measure might be chosen to distinguish
between disk and extra-planar gas. Whatever criteria might be applied, Fig. 1 shows that most of the H I gas settles down in a thin disk phase while there remains an extra-planar contribution, either diffuse or filamentary, but in most cases unambiguously associated with the disk. This extra-planar part was excluded when calculating disk scale heights and the
mid-plane densities, but was left in the database for the rest of the analysis. There is direct evidence that on average 5% of the H I gas is located outside the disk (Fig. 12). As discussed later, this is a lower limit only.
limit
is somewhat arbitrary, a different measure might be chosen to distinguish
between disk and extra-planar gas. Whatever criteria might be applied, Fig. 1 shows that most of the H I gas settles down in a thin disk phase while there remains an extra-planar contribution, either diffuse or filamentary, but in most cases unambiguously associated with the disk. This extra-planar part was excluded when calculating disk scale heights and the
mid-plane densities, but was left in the database for the rest of the analysis. There is direct evidence that on average 5% of the H I gas is located outside the disk (Fig. 12). As discussed later, this is a lower limit only.
Inside the solar circle the translation between distance and velocity is
ambiguous because there are two positions along the line of sight that have
the same velocity. These positions, however, may have different z distances,
so their densities may differ accordingly. We modeled the expected flaring of
the H I distribution and weighted the derived quantities correspondingly. Our
method is comparable to that of Nakanishi & Sofue (2003), except that they use a
sech2 approach (Spitzer 1942) in place of our more detailed model. Our
model matches well with the observed flaring; for a verification of the model
we refer to Kalberla et al. (2007, Fig. 14).
For a description of the global properties of the Galactic H I disk we discuss
in the next sections the first three moments of the
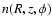 distribution; the surface density,
distribution; the surface density,
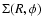 ,
the first moment
,
the first moment
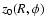 ,
representing the mid-plane, and the second moment
,
representing the mid-plane, and the second moment
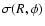 ,
representing the scale height of the gas. In addition we derived
characteristic mid-plane volume densities
,
representing the scale height of the gas. In addition we derived
characteristic mid-plane volume densities
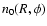 for positions
for positions
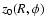 ,
averaging over
,
averaging over
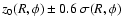 .
.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{9240f02.eps}\end{figure}](/articles/aa/full/2008/33/aa9240-07/Timg48.gif) |
Figure 2:
Milky Way velocity field at mid-plane for the mass distribution derived by Kalberla et al. (2007). The isophotes indicate velocities -190
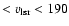 km s-1 in steps of 10 km s-1. The thick lines are at km s-1 in steps of 10 km s-1. The thick lines are at
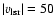 ,
100 and 150 km s-1. ,
100 and 150 km s-1. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{9240f03.eps} \end{figure}](/articles/aa/full/2008/33/aa9240-07/Timg49.gif) |
Figure 3:
Derived mean surface densities of the H I gas perpendicular to the
disk (red). The dotted blue line gives
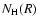 in the northern, the
dotted green line in the southern part of the Milky Way. The dashed black
line reproduces the distribution published by Binney & Merrifield (1998, BM98) in
Fig. 9.19. Wolfire et al. (2003) (thick black line) used partial data from Wouterloot et al. (1990, W90).
in the northern, the
dotted green line in the southern part of the Milky Way. The dashed black
line reproduces the distribution published by Binney & Merrifield (1998, BM98) in
Fig. 9.19. Wolfire et al. (2003) (thick black line) used partial data from Wouterloot et al. (1990, W90). |
| Open with DEXTER |
Figure 3 displays average surface densities determined for the
total disk, but also for azimuth
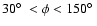 (north) and
(north) and
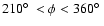 (south) separately. There are some deviations
between north and south, we therefore derived the detailed surface density
distribution across the disk in individual sectors of
(south) separately. There are some deviations
between north and south, we therefore derived the detailed surface density
distribution across the disk in individual sectors of
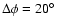 .
Figure 4 displays the results separately for both parts
of the disk. Strong fluctuations, typically within a factor of two, with a
correlation length of a few kpc are common. Some of the modulations are
caused by a spiral structure (Levine et al. 2006a,b; Kalberla et al. 2007).
.
Figure 4 displays the results separately for both parts
of the disk. Strong fluctuations, typically within a factor of two, with a
correlation length of a few kpc are common. Some of the modulations are
caused by a spiral structure (Levine et al. 2006a,b; Kalberla et al. 2007).
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{9240f04a.eps}
\includegraphics[angle=-90,width=9cm,clip]{9240f04b.eps} \end{figure}](/articles/aa/full/2008/33/aa9240-07/Timg52.gif) |
Figure 4:
Systematic variations of the average H I surface density distribution determined in
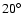 wide sectors for
wide sectors for
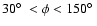 (north) and
(north) and
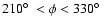 (south). For comparison with Fig. 3 the fit (black) and total averages for north
and south (blue and green respectively) are given.
(south). For comparison with Fig. 3 the fit (black) and total averages for north
and south (blue and green respectively) are given. |
| Open with DEXTER |
Figure 4 confirms the general systematic differences
between north and south. Most striking, however, are two regions with
exceptional low fluctuations; in the north for
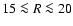 kpc and in
the south for
kpc and in
the south for
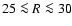 kpc. A comparison with the mass model and the
flaring data from Kalberla et al. (2007, Figs. 18 and 19) indicates that these regions are located at the outer edge of the dark matter ring structures that were needed to explain the observed gaseous flaring. These structures have
different locations in the northern (
kpc. A comparison with the mass model and the
flaring data from Kalberla et al. (2007, Figs. 18 and 19) indicates that these regions are located at the outer edge of the dark matter ring structures that were needed to explain the observed gaseous flaring. These structures have
different locations in the northern (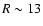 kpc) and southern part (
kpc) and southern part (
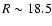 kpc) of the Galactic disk but extend in azimuth over at least 120
kpc) of the Galactic disk but extend in azimuth over at least 120 .
.
Despite all the scatter, the global radial surface density distribution
appears to follow an exponential law over a broad radial range. We
approximate the mean surface density distribution by
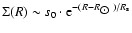 with s0 = 30
with s0 = 30
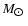 pc-2 and
pc-2 and
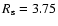 kpc. The exponential disk approximation is reasonable for
kpc. The exponential disk approximation is reasonable for
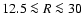 kpc. For
kpc. For
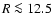 kpc the surface densities saturate
at approximately
kpc the surface densities saturate
at approximately
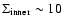
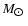 pc-2. This result is in
clear conflict with the contemporary knowledge from reviews (Dickey & Lockman 1990), and text books; we reproduce in Fig. 3 the distribution of Binney & Merrifield (1998, Fig. 9.19). Dickey and Lockman give
pc-2. This result is in
clear conflict with the contemporary knowledge from reviews (Dickey & Lockman 1990), and text books; we reproduce in Fig. 3 the distribution of Binney & Merrifield (1998, Fig. 9.19). Dickey and Lockman give
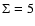
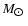 pc-2,
the average surface densities for
pc-2,
the average surface densities for 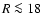 kpc according to Binney & Merrifield (1998) is
even less. For
kpc according to Binney & Merrifield (1998) is
even less. For 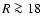 kpc our data agree with Binney & Merrifield (1998, Fig. 9.19), a general scale error cannot explain the problem.
kpc our data agree with Binney & Merrifield (1998, Fig. 9.19), a general scale error cannot explain the problem.
Discrepancies in Fig. 3 need a detailed discussion, fortunately
this is simplified greatly by a recent review (Lockman 2002a, Sect. 4.3). Figure 9.19 of Benny & Merrifield (1998) dates back to Dame (1993) who used data provided by
Lockman (1988). Lockman studied two cases, a surface density distribution
for a flat rotation curve and alternatively the case of a curve that is flat
for R <
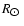 ,
rising at a rate
,
rising at a rate
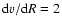 km s-1 kpc -1 up to 2
km s-1 kpc -1 up to 2
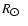 and staying flat afterwards. In both cases it was assumed that the scale-height of the H I layer is constant. Some unspecified data were ``arbitrary scaled by a factor of 2'' by Dame to match other results. The case of a rising rotation curve was then adopted by Binney & Merrifield (1998, Fig. 9.19) as characteristic for the Milky Way.
and staying flat afterwards. In both cases it was assumed that the scale-height of the H I layer is constant. Some unspecified data were ``arbitrary scaled by a factor of 2'' by Dame to match other results. The case of a rising rotation curve was then adopted by Binney & Merrifield (1998, Fig. 9.19) as characteristic for the Milky Way.
A slightly different surface density distribution, also plotted in Fig. 3, was used by Wolfire et al. (2003), we refer to their detailed discussion. These authors match
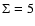
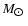 pc-2 according to Dickey & Lockman (1990) with surface densities derived by Wouterloot et al. (1990). Their curve rises for
pc-2 according to Dickey & Lockman (1990) with surface densities derived by Wouterloot et al. (1990). Their curve rises for 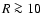 kpc. At
kpc. At
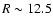 kpc it matches our average surface density distribution and at larger distances our results agree well with Wouterloot et al. (1990), their data are also plotted in Fig. 3. In general we have for
kpc it matches our average surface density distribution and at larger distances our results agree well with Wouterloot et al. (1990), their data are also plotted in Fig. 3. In general we have for 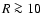 kpc a good agreement with Henderson et al. (1982); Kulkarni et al. (1982); Diplas & Savage (1991); Voskes (1999); Levine et al. (2006a,b).
kpc a good agreement with Henderson et al. (1982); Kulkarni et al. (1982); Diplas & Savage (1991); Voskes (1999); Levine et al. (2006a,b).
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{9240f05.eps} \end{figure}](/articles/aa/full/2008/33/aa9240-07/Timg70.gif) |
Figure 5:
Derived average mid-plane volume density of the H I gas (red). The
dotted blue line gives n(R) in the north (
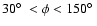 ), the dotted green line in the southern part of the Milky Way ( ), the dotted green line in the southern part of the Milky Way (
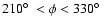 ). The black line represents an exponential fit with a radial scale length of 3.15 kpc. ). The black line represents an exponential fit with a radial scale length of 3.15 kpc. |
| Open with DEXTER |
Attempting to explain the discrepancies for 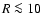 kpc, the determination
of H I surface densities close to
kpc, the determination
of H I surface densities close to
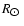 may be subject to serious
uncertainties, this was discussed in Sect. 2. In addition we found large
biases caused by the assumption that the H I gas at |z| > 0 kpc is strictly
co-rotating with gas at the mid-plane (Kalberla et al. 2007, see Figs. 3 and 5 for the flaring). Such biases may depend on the methods used. For a
co-rotation we derive a 10% lower surface density for
may be subject to serious
uncertainties, this was discussed in Sect. 2. In addition we found large
biases caused by the assumption that the H I gas at |z| > 0 kpc is strictly
co-rotating with gas at the mid-plane (Kalberla et al. 2007, see Figs. 3 and 5 for the flaring). Such biases may depend on the methods used. For a
co-rotation we derive a 10% lower surface density for
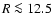 kpc, at
the same time the exponential scale length increases from
kpc, at
the same time the exponential scale length increases from
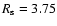 kpc to
kpc to
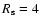 kpc. The slope is consistent with previous results
(Henderson et al. 1982; Diplas & Savage 1991; Voskes 1999; Levine et al. 2006a,b) but the
average surface density for
kpc. The slope is consistent with previous results
(Henderson et al. 1982; Diplas & Savage 1991; Voskes 1999; Levine et al. 2006a,b) but the
average surface density for
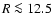 kpc is still discrepant. We tested
the case of a rising rotation curve as proposed by de Boer et al. (2005) with a
peak rotational velocity of 250 km s-1 but found no significant changes of the
local surface density. This most probably is caused by the fact that locally
this rotation curve is flat. We question whether a rotation curve with a local
rate
kpc is still discrepant. We tested
the case of a rising rotation curve as proposed by de Boer et al. (2005) with a
peak rotational velocity of 250 km s-1 but found no significant changes of the
local surface density. This most probably is caused by the fact that locally
this rotation curve is flat. We question whether a rotation curve with a local
rate
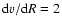 km s-1 kpc -1 is realistic for the Milky Way.
km s-1 kpc -1 is realistic for the Milky Way.
Figure 5 displays the average mid-plane volume density
distribution n(R,z0) for the total disk, for
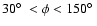 (north), and
(north), and
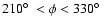 (south). Figure 6 shows how the volume densities depend on azimuth; these plots reproduce for
(south). Figure 6 shows how the volume densities depend on azimuth; these plots reproduce for
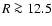 kpc the same trends as seen before in the surface densities (Fig. 4).
kpc the same trends as seen before in the surface densities (Fig. 4).
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{9240f06a.eps}
\includegraphics[angle=-90,width=9cm,clip]{9240f06b.eps} \end{figure}](/articles/aa/full/2008/33/aa9240-07/Timg75.gif) |
Figure 6:
Systematic variations of the average H I volume density distribution determined in
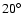 wide sectors for
wide sectors for
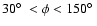 (north) and
(north) and
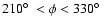 (south). For comparison with Fig. 5 the fit (black) and total averages for north and south (blue and green respectively) are given.
(south). For comparison with Fig. 5 the fit (black) and total averages for north and south (blue and green respectively) are given. |
| Open with DEXTER |
For
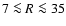 kpc the average mid-plane volume density follows
approximately an exponential distribution,
kpc the average mid-plane volume density follows
approximately an exponential distribution,
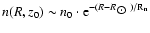 with n0 = 0.9 cm-3 and
Rn = 3.15 kpc. This line is drawn in Figs. 5 and 6.
with n0 = 0.9 cm-3 and
Rn = 3.15 kpc. This line is drawn in Figs. 5 and 6.
The surface density is essentially a product of mid-plane volume density and
the corresponding flaring. The fact that surface density as well as mid-plane
volume density can be approximated by an exponential function implies that
the flaring also needs to be described well by an exponential function. We
confirm this as the fit
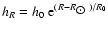 kpc with
h0 =
0.15 kpc and R0 = 9.8 kpc for the half width at half maximum provides a
good approximation to the observed flaring (Kalberla 2007, Fig. 6) for
kpc with
h0 =
0.15 kpc and R0 = 9.8 kpc for the half width at half maximum provides a
good approximation to the observed flaring (Kalberla 2007, Fig. 6) for
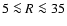 kpc. For
kpc. For 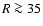 kpc, data and fit diverge
rapidly. Figure 7 re-plots for comparison the flaring derived in
Kalberla et al. (2007).
kpc, data and fit diverge
rapidly. Figure 7 re-plots for comparison the flaring derived in
Kalberla et al. (2007).
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{9240f07.eps} \end{figure}](/articles/aa/full/2008/33/aa9240-07/Timg80.gif) |
Figure 7:
Derived mean flaring of the H I gas (red). The dotted blue line
holds for the northern, the dotted green line for the southern part of
the Milky Way. For comparison an exponential fit for R < 35 kpc is
plotted (long dashed), also the flaring according to the model by
Kalberla et al. (2007). |
| Open with DEXTER |
The finding that surface density, mid-plane density, and flaring can be
represented by exponential functions does not reflect a general property of
galactic disks but is closely related to the rotation curve used, hence it
depends on the Galactic mass distribution. In particular, the divergence of
the exponential fit from the observed flaring for 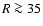 kpc is caused by
the shape of the gravitational potential which is oblate for small radii but
changes to prolate in the outer part. The transition region, the location
where we have a potential similar to the spherical case, is at
kpc is caused by
the shape of the gravitational potential which is oblate for small radii but
changes to prolate in the outer part. The transition region, the location
where we have a potential similar to the spherical case, is at 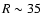 kpc
(for a more detailed discussion see Kalberla 2003, Sects. 5.2.2 and 5.2.3). This radius defines the ``edge'' of the disk.
kpc
(for a more detailed discussion see Kalberla 2003, Sects. 5.2.2 and 5.2.3). This radius defines the ``edge'' of the disk.
Common to the average surface density and the average mid-plane density is
that they both do not indicate a boundary of the Milky Way disk with a
truncation of the observable H I distribution. Beyond a radius of 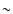 35 kpc the gas appears to have a more shallow distribution. We study this behavior in more detail.
35 kpc the gas appears to have a more shallow distribution. We study this behavior in more detail.
The Galactic warp was shown by Kalberla et al. (2007, Figs. 16 and 17) to be
well defined for 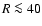 kpc. Three basic modes exist with slowly variable
phases. The outermost part of the warp for
kpc. Three basic modes exist with slowly variable
phases. The outermost part of the warp for 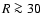 kpc contains higher
Fourier modes, thus the disk is scalloping. We determine these modes by
subtracting the basic warp modes 0 to 2 from the derived mid-plane
positions. For the residuals we use a least square fitting algorithm to search
for oscillations with higher frequencies. We determine simultaneously
amplitude, frequency, and phase. For various initial estimates in frequencies,
corresponding to modes 3 to 20, we demand that the fit stays stable in
frequency. As a result, we find oscillations with scalloping modes 10 to 20. The significance of these higher warp modes is low for
kpc contains higher
Fourier modes, thus the disk is scalloping. We determine these modes by
subtracting the basic warp modes 0 to 2 from the derived mid-plane
positions. For the residuals we use a least square fitting algorithm to search
for oscillations with higher frequencies. We determine simultaneously
amplitude, frequency, and phase. For various initial estimates in frequencies,
corresponding to modes 3 to 20, we demand that the fit stays stable in
frequency. As a result, we find oscillations with scalloping modes 10 to 20. The significance of these higher warp modes is low for 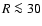 kpc. The
associated power, defined by the squares of the amplitudes, is below 0.6% of
the total warp power in this range. For
kpc. The
associated power, defined by the squares of the amplitudes, is below 0.6% of
the total warp power in this range. For 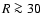 kpc we find a significant
contribution; the preferred modes are 10 and 13. The relative strength of the
scalloping increases linearly up to
kpc we find a significant
contribution; the preferred modes are 10 and 13. The relative strength of the
scalloping increases linearly up to 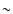 2.5% of the total warp power at R
= 40 kpc. This is shown in Fig. 11 (magenta). The warp can be
traced further with the scalloping power increasing to larger distances but
the significance of the warp is highly questionable there.
2.5% of the total warp power at R
= 40 kpc. This is shown in Fig. 11 (magenta). The warp can be
traced further with the scalloping power increasing to larger distances but
the significance of the warp is highly questionable there.
Our analysis is complementary to Levine et al. (2006a) who used Morlet wavelet transforms for an analysis of the warp out to R = 30 kpc. They concluded
that the m=10 and 15 scalloping modes are well above the noise, but localized;
this suggests that the scalloping in this range does not pervade the whole
disk, but only local regions. We applied a straightforward sine wave analysis
which is insensitive to local oscillations and found some coherent grouping of
higher mode oscillations, spreading out over several annuli, although
insignificant for fits at individual radii. Only for 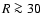 kpc does
scalloping become powerful enough to be significant in each case. This result
supports Saha & Jog (2006) who concluded that scalloping at high modes has to be restricted to the outermost part of a galaxy.
kpc does
scalloping become powerful enough to be significant in each case. This result
supports Saha & Jog (2006) who concluded that scalloping at high modes has to be restricted to the outermost part of a galaxy.
Figure 8 plots average mid-plane volume densities for
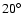 wide sectors as used before. Comparing the distributions with the
exponential fit from Fig. 5 we find a shallower decrease for
wide sectors as used before. Comparing the distributions with the
exponential fit from Fig. 5 we find a shallower decrease for 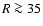 kpc. Average surface densities displayed in Fig. 9
show the same trend. Both plots suggest that the H I gas in the outskirts
differs significantly from the H I gas in the Galactic disk, which was fitted
before by an exponential law.
kpc. Average surface densities displayed in Fig. 9
show the same trend. Both plots suggest that the H I gas in the outskirts
differs significantly from the H I gas in the Galactic disk, which was fitted
before by an exponential law.
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm]{9240f08.eps} \end{figure}](/articles/aa/full/2008/33/aa9240-07/Timg85.gif) |
Figure 8:
Average mid-plane volume densities for
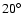 wide
radial sectors in the Milky Way. For comparison the fitted distribution
of the HVD gas is given (red solid lines).
wide
radial sectors in the Milky Way. For comparison the fitted distribution
of the HVD gas is given (red solid lines). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm]{9240f09.eps}\end{figure}](/articles/aa/full/2008/33/aa9240-07/Timg86.gif) |
Figure 9:
Average mid-plane surface densities for
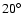 wide
radial sectors in the Milky Way. For comparison the fitted distribution
of the HVD gas is given (red solid lines).
wide
radial sectors in the Milky Way. For comparison the fitted distribution
of the HVD gas is given (red solid lines). |
| Open with DEXTER |
![\begin{figure}
\par\mbox{\includegraphics[angle=-90,width=9cm]{9240f10a.eps} \in...
...240f10c.eps} \includegraphics[angle=-90,width=9cm]{9240f10d.eps} }
\end{figure}](/articles/aa/full/2008/33/aa9240-07/Timg87.gif) |
Figure 10:
Position-velocity diagrams for the Milky Way H I brightness
termerature at latitudes -10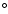 ,
-5 ,
-5 ( left) and 10
( left) and 10 ,
5 ,
5 ( right). The white isophotes display HVD emission from the model (10% to
90% in steps of 10%), the red isophote marks an average disk emission
of 100 mK. A logarithmic transfer function was used for
( right). The white isophotes display HVD emission from the model (10% to
90% in steps of 10%), the red isophote marks an average disk emission
of 100 mK. A logarithmic transfer function was used for
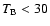 K. K. |
| Open with DEXTER |
Tracing the shallow H I volume density distribution at large distances back to
the observed brightness temperature distribution we find that these belong to
weak emission profile wings. The wings cannot be explained by emission from
the cold or the warm neutral medium (CNM and WNM, respectively). Similar wings
have been found in the Leiden/Dwingeloo Survey (Hartmann & Burton 1997) at high latitudes and Kalberla et al. (1998, Fig. 1) argued that the wings can be traced to low latitudes; this implies large distances. The LDS profile wings could be fitted well by a pervasive emission component with a high velocity dispersion (HVD) of 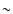 60 km s-1.
60 km s-1.
It is tempting to associate the shallow density distribution, visible in
Figs. 8 and 9, with such an HVD
component. The proof, however, is not straightforward. The observed profile
wings must originate from a diffuse distribution of unresolved H I clumps and
it is a priori not obvious how these wings translate into the corresponding
volume density distribution. We therefore modeled the H I emission for an HVD
component with a radial scale length of
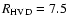 kpc
(Kalberla 2003). Synthetic emission lines were calculated for a
dispersion of
kpc
(Kalberla 2003). Synthetic emission lines were calculated for a
dispersion of
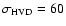 km s-1 and
km s-1 and
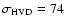 km s-1
(differences will be discussed in Sect. 6.1). Next we derived the surface
density and volume density distribution for the synthetic HVD distribution by
applying the same procedures as used before for the analysis of the LAB
observations. Figures 8 and 9 show the
result. The HVD component is weak in comparison to the disk emission at low
radii but dominates the H I distribution at the outskirts for
km s-1
(differences will be discussed in Sect. 6.1). Next we derived the surface
density and volume density distribution for the synthetic HVD distribution by
applying the same procedures as used before for the analysis of the LAB
observations. Figures 8 and 9 show the
result. The HVD component is weak in comparison to the disk emission at low
radii but dominates the H I distribution at the outskirts for 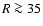 kpc.
kpc.
The assumption of a pervasive extended HVD H I component agrees well with the
data (Figs. 8 and 9). The HVD model with
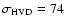 km s-1 fits slightly better. As discussed before for the
disk gas, there are systematic differences between north and south. Where is
the HVD emission located in the observed
km s-1 fits slightly better. As discussed before for the
disk gas, there are systematic differences between north and south. Where is
the HVD emission located in the observed
 distribution?
distribution?
In the Galactic outskirts the HVD gas becomes noticeable for 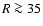 kpc
and the range
kpc
and the range
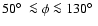 and
and
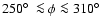 is useful for its analysis. The translation between
is useful for its analysis. The translation between
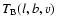 and
and
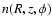 ,
discussed in Sect. 2, is such that this gas must appear at high
negative velocities for longitudes
,
discussed in Sect. 2, is such that this gas must appear at high
negative velocities for longitudes
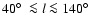 and at high
positive velocities for
and at high
positive velocities for
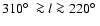 .
Figure 10 gives a few examples for the observed H I brightness temperature distribution, l-v slices at latitudes
.
Figure 10 gives a few examples for the observed H I brightness temperature distribution, l-v slices at latitudes
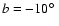 ,
-
,
-
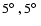 ,
and
,
and
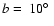 .
.
Extra-planar H I gas has a low volume filling factor. Correspondingly, a
patchy low level emission is expected in the region of interest. A second
property is the high velocity dispersion for this clumpy medium. This shows up
as extensions (stripes) in the v direction. Figure 10 shows
a rather complicated pattern. A part of the emission may originate from large
distances but the warp makes it difficult to determine whether individual
filaments belong to the disk (having a low velocity dispersion) or not. For a
clearer picture we calculated the expected average disk emission and plotted
the positions where this emission should reach a level of 100 mK (red
isophotes). Then we include the average emission according to the
HVD model in Fig. 9 (white isophotes).
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{9240f11.eps} \end{figure}](/articles/aa/full/2008/33/aa9240-07/Timg98.gif) |
Figure 11:
Asymmetry of mid-plane volume densities, surface densities, and
scale heights characterized by their south/north ratios S/N. In addition
the warp scalloping power in % is given. |
| Open with DEXTER |
In the inner Galaxy the HVD emission is clear in Fig. 10 with
high velocities against the disk emission at longitudes
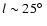 and
and
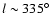 .
The region at
.
The region at
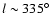 is currently studied by Alyson
Ford with the Parkes telescope. The region
is currently studied by Alyson
Ford with the Parkes telescope. The region
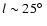 was investigated in
detail by Lockman (2002b, 2004). Numerous small clumps can be traced with the GBT up to distances of several hundred pc above the mid-plane. These clumps are usually unresolved in the LAB survey but contribute to the observed surface densities.
was investigated in
detail by Lockman (2002b, 2004). Numerous small clumps can be traced with the GBT up to distances of several hundred pc above the mid-plane. These clumps are usually unresolved in the LAB survey but contribute to the observed surface densities.
Comparing the HVD model emission with observations, we find for some regions significant deviations from the expected distribution. This reflects the fact that HVCs and IVCs are grouped in complexes, while there are also regions with little extra-planar H I gas.
Figures 3 to 9 show a pronounced asymmetry of the gas distribution for 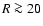 kpc. For a more quantitative comparison we calculate the
south/north ratios (S/N) for mid-plane volume densities, surface densities and
for the scale heights. Figure 11 demonstrates that the asymmetry is
strongest for mid-plane volume densities.
kpc. For a more quantitative comparison we calculate the
south/north ratios (S/N) for mid-plane volume densities, surface densities and
for the scale heights. Figure 11 demonstrates that the asymmetry is
strongest for mid-plane volume densities.
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{9240f12.eps}\end{figure}](/articles/aa/full/2008/33/aa9240-07/Timg102.gif) |
Figure 12:
Fraction of extra-planar gas observed outside the disk for -
15 < z < 20 kpc. |
| Open with DEXTER |
We argued in Sect. 4 that the H I gas in the Milky Way behaves on average as
expected for an exponential gaseous disk; the surface density is correlated
with the product of the mid-plane density and the scale height. This balance,
however, does not apply for the asymmetries visible in Fig. 11;
there is more gas in the south than in the north. The south/north asymmetry is
even more pronounced if we compare the extra-planar gas fraction for 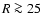 kpc (Fig. 12). The northern part of the extra-planar gas appears abruptly torn away to the south for
kpc (Fig. 12). The northern part of the extra-planar gas appears abruptly torn away to the south for 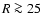 kpc, in the direction of the Magellanic System.
kpc, in the direction of the Magellanic System.
The distribution of planar and extra-planar gas is locally affected by
dynamical processes. Here we consider a steady state that is dictated by the
necessity of a global balance between gas pressure and gravitational
forces. We discuss first how a pressure balance can be achieved by a multi-phase
medium, next we use H I line data to verify the derived model. We also compare
the extra-planar H I gas in the Milky Way with the anomalous gas phase
observed in a few galaxies.
For a multi-phase medium, forces acting on the gas due to the pressure
gradient
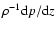 need to balance the gravity kz(e.g. Boulares & Cox 1990) and we may use this property to fit the
parameters of the gas distribution. We use the mass distribution provided by
Kalberla et al. (2007) to calculate kz at R = 8.5 kpc up to z = 10 kpc (Fig. 13). The volume density of the extra-planar gas phase is
three orders of magnitude below the density of the other material in the
disk. Correspondingly, kz is unaffected by the halo gas (at the peak,
need to balance the gravity kz(e.g. Boulares & Cox 1990) and we may use this property to fit the
parameters of the gas distribution. We use the mass distribution provided by
Kalberla et al. (2007) to calculate kz at R = 8.5 kpc up to z = 10 kpc (Fig. 13). The volume density of the extra-planar gas phase is
three orders of magnitude below the density of the other material in the
disk. Correspondingly, kz is unaffected by the halo gas (at the peak, 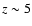 kpc, the influence is
kpc, the influence is 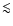 0.3%); the extra-planar gas is a genuine
tracer of the Galactic potential.
0.3%); the extra-planar gas is a genuine
tracer of the Galactic potential.
We fit
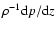 for a multi-component gas to match kz and obtain agreement with a mean error of 0.6%. In Fig. 13,
for a multi-component gas to match kz and obtain agreement with a mean error of 0.6%. In Fig. 13,
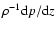 is over-plotted on kz; the gas pressure is corrected for a helium abundance of 9% of the hydrogen by number. Essentially, both curves are
identical, with differences hardly visible. Table 1 lists the different phases,
densities
is over-plotted on kz; the gas pressure is corrected for a helium abundance of 9% of the hydrogen by number. Essentially, both curves are
identical, with differences hardly visible. Table 1 lists the different phases,
densities
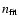 and velocity dispersions
and velocity dispersions
 used to balance
the gas pressure gradient against the gravitational field. For comparison we
give
used to balance
the gas pressure gradient against the gravitational field. For comparison we
give
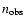 and
and
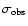 ,
derived previously by fitting the gas
distribution in the Solar neighborhood (Kalberla 2003, Table 1). These
parameters agree well. The most significant deviation is found for the
velocity dispersion of the HVD component. This is a sensitive parameter in
fitting the pressure gradient, but is less well determined when fitting observed
profile wings. In Sect. 5.2 we used both solutions for comparison.
,
derived previously by fitting the gas
distribution in the Solar neighborhood (Kalberla 2003, Table 1). These
parameters agree well. The most significant deviation is found for the
velocity dispersion of the HVD component. This is a sensitive parameter in
fitting the pressure gradient, but is less well determined when fitting observed
profile wings. In Sect. 5.2 we used both solutions for comparison.
Table 1:
Local multi-component gas parameters used for Fig. 13 in comparison to parameters derived from observations (Kalberla et al. 2003).
The shape of kz for
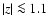 kpc is dominated by the stellar
distribution, see Kuijen & Gilmore (1989). We plot their kz relation for reference. At large z distances we find differences; the dark matter distribution dominates the shape of the kz function and the gravitational forces become model dependent. The model assumptions by Kuijken & Gilmore (1989) lead to ever-rising forces which are physically implausible. The forces have to decrease at large z distances (Rohlfs 1977). Such a solution was provided by Dehnen & Binney (1998, Galactic Model 2) and we plot their kz for reference. This model is currently favored for ISM research (Cox 2005 Sect. 2.2) and the downward bending of kz is interpreted as a shaping provided by the non-planar geometry in the Dehnen & Binney model. In the model of Kalberla (2007) the decrease of the forces at large z distances is caused by the mass associated with the disk. The three
kz curves are discrepant for
kpc is dominated by the stellar
distribution, see Kuijen & Gilmore (1989). We plot their kz relation for reference. At large z distances we find differences; the dark matter distribution dominates the shape of the kz function and the gravitational forces become model dependent. The model assumptions by Kuijken & Gilmore (1989) lead to ever-rising forces which are physically implausible. The forces have to decrease at large z distances (Rohlfs 1977). Such a solution was provided by Dehnen & Binney (1998, Galactic Model 2) and we plot their kz for reference. This model is currently favored for ISM research (Cox 2005 Sect. 2.2) and the downward bending of kz is interpreted as a shaping provided by the non-planar geometry in the Dehnen & Binney model. In the model of Kalberla (2007) the decrease of the forces at large z distances is caused by the mass associated with the disk. The three
kz curves are discrepant for
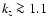 kpc. Stars cannot be used to decide between the models but we may use the gas distribution for this purpose.
kpc. Stars cannot be used to decide between the models but we may use the gas distribution for this purpose.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.4cm]{9240f13.eps} \end{figure}](/articles/aa/full/2008/33/aa9240-07/Timg112.gif) |
Figure 13:
Gravitational acceleration kz at
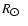 = 8.5 kpc, (solid red line) and gas pressure balance = 8.5 kpc, (solid red line) and gas pressure balance
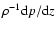 (dotted green). For comparison we plot kz according to Kuijken & Gilmore (1989) (dashed, blue) and Dehnen & Binney (1998, Galactic Model 2). The lower dotted line gives
(dotted green). For comparison we plot kz according to Kuijken & Gilmore (1989) (dashed, blue) and Dehnen & Binney (1998, Galactic Model 2). The lower dotted line gives
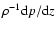 for a multi-phase gas without halo components.
for a multi-phase gas without halo components. |
| Open with DEXTER |
Attempting to fit the gas phase to match kz from Dehnen & Binney (1998, Galactic Model 2), we need only 80% of the observed density for the hot halo
phase, but 5.5 times the observed density for the neutral halo phase. This,
clearly, does not match the observations. We conclude that the observed
extra-planar gas phase can be used to constrain dark matter models. Our
approach is consistent with the extra-planar gas as observed in the local
vicinity. However, some caution is needed. It is not expected that parameters
derived at the position of the Sun agree exactly with model parameters
for
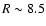 kpc, since results are dependent on local influences,
predominantly caused by the local hot bubble. A hydrostatic model can predict
only global properties.
kpc, since results are dependent on local influences,
predominantly caused by the local hot bubble. A hydrostatic model can predict
only global properties.
Current ISM models (e.g. Cox 2005, Sect. 2.1) do not include a hot or
neutral halo phase. For comparison, we plot
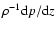 for the fitted
parameters from Table 1, but without a hot or neutral halo phase. This makes a huge difference. For a global pressure balance at large z distances a halo
gas phase is unambiguously needed. Preliminary evidence for such a phase from
interstellar absorption lines was given by
Münch & Zirin (1961). Lockman & Gehman (1991) have shown that more than two H I components are needed to explain the average local H I emission. In the next
section we discuss the observational evidence for a multiphase H I component
in more detail. We show H I emission resulting from a neutral halo gas phase
and demonstrate how the observations compare with the model given in Table 1.
for the fitted
parameters from Table 1, but without a hot or neutral halo phase. This makes a huge difference. For a global pressure balance at large z distances a halo
gas phase is unambiguously needed. Preliminary evidence for such a phase from
interstellar absorption lines was given by
Münch & Zirin (1961). Lockman & Gehman (1991) have shown that more than two H I components are needed to explain the average local H I emission. In the next
section we discuss the observational evidence for a multiphase H I component
in more detail. We show H I emission resulting from a neutral halo gas phase
and demonstrate how the observations compare with the model given in Table 1.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.2cm]{9240f14.eps}\end{figure}](/articles/aa/full/2008/33/aa9240-07/Timg114.gif) |
Figure 14:
Average H I emission to logarithmic scale for latitudes
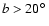 .
The data are from the Bell Labs telescope (thick black line) and from the LAB survey (red). The step function shows the weights for each channel in dB. The thin red dotted line represents broad Gaussian components indicating baseline problems. .
The data are from the Bell Labs telescope (thick black line) and from the LAB survey (red). The step function shows the weights for each channel in dB. The thin red dotted line represents broad Gaussian components indicating baseline problems. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.2cm]{9240f15.eps}\end{figure}](/articles/aa/full/2008/33/aa9240-07/Timg115.gif) |
Figure 15:
Average H I emission in logarithmic scale for latitudes
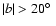 from the LAB survey. The red line is for the north polar
cap, the dashed green line for the southern part. The thin dotted
black line represents the model according to Table 1.
from the LAB survey. The red line is for the north polar
cap, the dashed green line for the southern part. The thin dotted
black line represents the model according to Table 1. |
| Open with DEXTER |
Figure 14 displays the average H I emission measured at the north
polar cap for
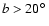 .
We use
.
We use
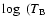 )
to compress the huge dynamic
range of the H I emission. We compare data from the Bell labs survey
(Stark 1992, Fig. 10) with data from the LAB survey
(Kalberla et al. 2005). Both agree well, except for the wings at high
velocities. Observational shortcomings cause the discrepancy. The bandwidth of
the Bell labs filter bank was too small to cover the necessary velocity range
completely; it needed to be shifted in velocity to obtain the main H I
emission. The outer two channels of the filter bank were defined to be zero
for all spectra. The weights (in dB, dashed line) show how this affects the
mean Bell labs emission spectrum. As the weights decrease, the average Bell
labs profile becomes incomplete and biased.
)
to compress the huge dynamic
range of the H I emission. We compare data from the Bell labs survey
(Stark 1992, Fig. 10) with data from the LAB survey
(Kalberla et al. 2005). Both agree well, except for the wings at high
velocities. Observational shortcomings cause the discrepancy. The bandwidth of
the Bell labs filter bank was too small to cover the necessary velocity range
completely; it needed to be shifted in velocity to obtain the main H I
emission. The outer two channels of the filter bank were defined to be zero
for all spectra. The weights (in dB, dashed line) show how this affects the
mean Bell labs emission spectrum. As the weights decrease, the average Bell
labs profile becomes incomplete and biased.
The LAB survey may be influenced by systematic errors, too. The lower
red dotted curve in Fig. 14 shows the mean of all broad LAB
Gaussians, most probably representing baseline defects in the LAB survey
(Haud & Kalberla 2006). This is two orders of magnitude below the mean
emission; the weak profile wings are significant.
Figure 15 compares the LAB data for the northern and southern
polar caps. We also plot the model distribution according to our best fit mass
model, using the fitted parameters for the H I components from Table 1. Note
that the fit was to match
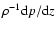 with kz, but no fit was
applied to the plotted profile in Fig. 15, and to the wings
in Figs. 8 and 9. All profiles in
Fig. 15 show extended wings, but with some systematic
differences. The enhanced emission for
with kz, but no fit was
applied to the plotted profile in Fig. 15, and to the wings
in Figs. 8 and 9. All profiles in
Fig. 15 show extended wings, but with some systematic
differences. The enhanced emission for
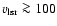 km s-1 at the southern
polar cap is due to the Magellanic Stream. We find enhancements at
km s-1 at the southern
polar cap is due to the Magellanic Stream. We find enhancements at
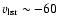 km s-1, caused by distinct IVCs and at
km s-1, caused by distinct IVCs and at
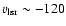 km s-1,
caused by HVCs.
km s-1,
caused by HVCs.
The broad wing underlying the CNM and WNM emission in Fig. 15
is caused by extra-planar gas, the HVD component. Numerous clumps, filaments,
and spurs, located above the CNM and WNM disk, contribute to a signal which
can be well represented by a weak component with a large velocity dispersion.
We conclude that the local observed extra-planar H I gas distribution,
forced to be on average in pressure balance
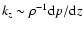 (Fig. 13), is consistent with the gas component that was proposed
in Sect. 5.2 to explain the gas distribution at the outskirts of the
Galaxy. Systematic differences are caused by a warped and asymmetric gas
distribution. Gas in the southern part of the outer Milky Way appears to be
enhanced. This is consistent with the enhanced positive velocity wing in
Fig. 15 for
(Fig. 13), is consistent with the gas component that was proposed
in Sect. 5.2 to explain the gas distribution at the outskirts of the
Galaxy. Systematic differences are caused by a warped and asymmetric gas
distribution. Gas in the southern part of the outer Milky Way appears to be
enhanced. This is consistent with the enhanced positive velocity wing in
Fig. 15 for
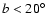 .
The negative profile wing is enhanced for
.
The negative profile wing is enhanced for
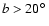 due to the warp that bends up to the north.
due to the warp that bends up to the north.
During our analysis we distinguished disk emission and extra-planar gas. For a
safe determination of the first moments of the stationary disk gas we masked
and excluded outliers of the H I volume density distribution which are most
probably not associated with the disk. This part of the
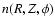 distribution has radial velocities that are incompatible with a circular
rotation of the disk gas around the Galactic center. Individual features show
up as sheets and filaments in the
distribution has radial velocities that are incompatible with a circular
rotation of the disk gas around the Galactic center. Individual features show
up as sheets and filaments in the
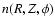 distribution (see
Fig. 1 or Kalberla et al. 2007, Sects. 2.2 and 3). The
corresponding clouds, visible in the
distribution (see
Fig. 1 or Kalberla et al. 2007, Sects. 2.2 and 3). The
corresponding clouds, visible in the
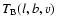 distribution
(Fig. 10), are usually classified as HVCs and IVCs. In general
it is assumed that IVCs are located in the lower Galactic halo while HVCs are
at larger distances (Albert & Danly 2004).
distribution
(Fig. 10), are usually classified as HVCs and IVCs. In general
it is assumed that IVCs are located in the lower Galactic halo while HVCs are
at larger distances (Albert & Danly 2004).
For a determination of the extra-planar gas fraction we use a range where the
properties of the Galactic disk are well defined,
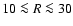 kpc. On
average we find there direct evidence that about 5% of the H I is not
associated with the disk (Fig. 12). This estimate is independent
of the mass model used. Using parameters from Table 1, integrating for
kpc. On
average we find there direct evidence that about 5% of the H I is not
associated with the disk (Fig. 12). This estimate is independent
of the mass model used. Using parameters from Table 1, integrating for 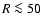 kpc, we derive that the HVD component amounts in total to 10% of the gas.
This discrepancy is explained by the fact that most of the HVD gas phase in
the Milky Way cannot be distinguished from the CNM/WNM gas phase. Only gas at
the wings of the HVD distribution is counted and we estimate that about 50% of
this gas remains undetected by our filter and revise the extra-planar gas
fraction to be 10%, consistent with the HVD model.
kpc, we derive that the HVD component amounts in total to 10% of the gas.
This discrepancy is explained by the fact that most of the HVD gas phase in
the Milky Way cannot be distinguished from the CNM/WNM gas phase. Only gas at
the wings of the HVD distribution is counted and we estimate that about 50% of
this gas remains undetected by our filter and revise the extra-planar gas
fraction to be 10%, consistent with the HVD model.
To compare the Milky Way with sensitive observations of other galaxies, we
take the viewpoint of an external observer. The H I emission is synthesized
accordingly. We use a flat disk without warp at an inclination of
 and calculate the total emission along the line of sight. The contours in
Fig. 16 represent observable column densities, normalized and
plotted in steps of 2 dB. We consider observations with a limited dynamic
range of 30 dB; the lowest contour is at -30 dB.
and calculate the total emission along the line of sight. The contours in
Fig. 16 represent observable column densities, normalized and
plotted in steps of 2 dB. We consider observations with a limited dynamic
range of 30 dB; the lowest contour is at -30 dB.
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm]{9240f16.eps} \end{figure}](/articles/aa/full/2008/33/aa9240-07/Timg125.gif) |
Figure 16:
Position velocity diagram along the major axis, observable for a
galaxy like the Milky Way with an inclination of
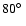 .
The thin
contours represent normalized column densities in steps of 2 dB; the
lowest contour is at -30 dB. The green dashed lines gives the rotation
curve at z =0 kpc, the solid red line the mean rotation for the H I in
the halo. .
The thin
contours represent normalized column densities in steps of 2 dB; the
lowest contour is at -30 dB. The green dashed lines gives the rotation
curve at z =0 kpc, the solid red line the mean rotation for the H I in
the halo. |
| Open with DEXTER |
The simulated position velocity diagram shows that the velocity at the peak of
the line emission is identical with the rotation curve from the model. The
average observable rotation velocity for the halo gas phase alone, determined
from the peak emission of the halo gas phase lags behind. The total column
density distribution is symmetric at large column densities, but as a
consequence of the lagging halo some asymmetries appear at low
levels. Projection effects cause extended regions with H I emission at lower
velocities. Such features at levels below -20 dB were first observed in NGC 891 (Swaters et al. 1997), the so-called beards (Fraternali et al. 2001). Close to
the center, the beards extend to forbidden velocities, mimicking an apparent
counter-rotation.
Beards and forbidden velocities in Fig. 16 have the same
origin. The line of sight passes through various layers of extra-planar gas
that rotate slower than the disk. The lag is approximately constant for
z/hz(R) with z distances normalized to scale heights
(Kalberla 2003, Fig. 11). For small radii, the densest part of the thick extra-planar gas disk close to the center becomes most prominent. The lag is most pronounced there.
Our model takes both the flaring and lagging halo into account. Both are
necessary to explain the observations. The beards in Fig. 16
originate from the same H I halo gas phase that causes the extended wings in
Figs. 14 and 15. At the end of this subsection we
point out that an external observer, with a telescope that is limited in
dynamic range to 30 dB, would see the Galactic H I disk out to 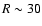 kpc only. At low levels it is far easier to find extended emission perpendicular to the disk as shown recently by Oosterloo et al. (2007) in the case of NGC 891. Reaching the outskirts at distances of
kpc only. At low levels it is far easier to find extended emission perpendicular to the disk as shown recently by Oosterloo et al. (2007) in the case of NGC 891. Reaching the outskirts at distances of 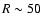 kpc, is a demanding task and needs a dynamic range of 40 dB or better. The HVD component at such radii is essentially invisible.
kpc, is a demanding task and needs a dynamic range of 40 dB or better. The HVD component at such radii is essentially invisible.
We used the LAB survey to derive the H I volume density distribution in the
Milky Way. The
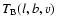 to
to
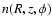 conversion depends on the
rotation curve; we have chosen an almost flat curve with lagging rotation for
gas above the mid-plane (Kalberla et al. 2007). The corresponding mass model implies that some of the dark matter is associated with a thick exponential disk.
conversion depends on the
rotation curve; we have chosen an almost flat curve with lagging rotation for
gas above the mid-plane (Kalberla et al. 2007). The corresponding mass model implies that some of the dark matter is associated with a thick exponential disk.
Our aim was to derive global properties for the H I gas distribution in the
Milky Way. We calculated the first moments to determine surface densities,
mid-plane positions, associated mid-plane densities, and scale-heights. Planar
and extra-planar gas was distinguished by applying adaptive filters. We
discuss mid-plane positions first.
The Galactic warp can be traced from
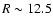 kpc out to
kpc out to 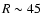 kpc
but the coherent structure is lost for
kpc
but the coherent structure is lost for 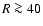 kpc. The scalloping power,
defined by the squares of the amplitudes from a sine wave fit, is below 0.6%
in the inner part of the disk. For
kpc. The scalloping power,
defined by the squares of the amplitudes from a sine wave fit, is below 0.6%
in the inner part of the disk. For
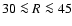 kpc we observe a linear
increase up to 3% of the total warp power.
kpc we observe a linear
increase up to 3% of the total warp power.
We derive average surface densities and, taking the warp into account, average
volume densities at mid-plane. In both cases we find significant fluctuations
and asymmetries between north and south which are correlated. Surface
densities and mid-plane volume densities are affected by spiral structure, but
differences between north and south need to be explained by an asymmetric disk
(Levine et al. 2006a,b; Kalberla 2007).
Average surface densities, mid-plane volume densities, and scale heights can
be approximated over a broad radial range by exponential relations. For the
surface density we find a scale length of 3.75 kpc within
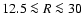 kpc. Mid-plane volume densities are well approximated with a scale length
of 3.15 kpc for
kpc. Mid-plane volume densities are well approximated with a scale length
of 3.15 kpc for
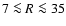 kpc. Both relations imply that the scale
heights also can be described well by an exponential relation, in this case
valid for
kpc. Both relations imply that the scale
heights also can be described well by an exponential relation, in this case
valid for
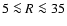 kpc.
kpc.
For
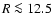 kpc we find approximately constant surface densities (
kpc we find approximately constant surface densities (
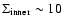
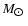 pc-2). This is also the inner part of the H I disk which is unaffected by the warp.
pc-2). This is also the inner part of the H I disk which is unaffected by the warp.
The exponential disk approximation for the disk gas breaks down in all
respects at radial distances 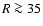 kpc. In the outer part we find a
shallower distribution which can be approximated by a gas phase with a radial
scale length of 7.5 kpc and a high velocity dispersion of 74 km s-1.
kpc. In the outer part we find a
shallower distribution which can be approximated by a gas phase with a radial
scale length of 7.5 kpc and a high velocity dispersion of 74 km s-1.
Our results are apparently in disagreement with Maloney (1993), who found
a sharp truncation of the neutral hydrogen distribution for the outer disk H I
gas in NGC 3198 at a surface density level
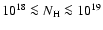 cm-2. This limit is attributed to the extragalactic radiation field. To study the origin of the HVD component at large distances we examined the data. At a distance of 60 kpc the telescope beam covers a typical area of 600 pc in diameter. Any emission within this area is smoothed out completely. Inspecting
the data cube visually, we find regions with peak densities of
cm-2. This limit is attributed to the extragalactic radiation field. To study the origin of the HVD component at large distances we examined the data. At a distance of 60 kpc the telescope beam covers a typical area of 600 pc in diameter. Any emission within this area is smoothed out completely. Inspecting
the data cube visually, we find regions with peak densities of
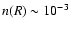 cm-3, surrounded by less dense envelopes. These unresolved
individual condensations may be well above the predicted cut-off limit.
cm-3, surrounded by less dense envelopes. These unresolved
individual condensations may be well above the predicted cut-off limit.
Maloney's interpretation was questioned recently by Oosterloo et al. (2007) who
found that a deeper mapping of NGC891 led predominantly to the detection of
unknown low level emission in the vertical direction, while the radial limits
remained. Such an asymmetry is unexpected for an isotropic radiation field.
Our analysis shows the same trend. At the outskirts of the disk the HVD
component becomes most extended in z direction. Mid plane volume densities
are dominated by the HVD component for 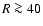 kpc, while surface densities
(integrated in z direction) show the same effect for
kpc, while surface densities
(integrated in z direction) show the same effect for 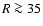 kpc (compare
Figs. 8 and 9).
kpc (compare
Figs. 8 and 9).
The H I gas distribution, averaged over all latitudes
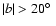 ,
probing approximately the local volume within a radius of 1 kpc, has broad
profile wings. These wings may be affected by stray radiation of the telescope,
but for the Bell Labs and the LAB survey they are not explainable by
instrumental problems. The same HVD component with a dispersion of 74 km s-1,
which was used to fit the gas distribution in the outskirts, is useful also to
explain this local component. A multi-phase medium containing this HVD
component is found to balance gravity by its pressure gradient,
,
probing approximately the local volume within a radius of 1 kpc, has broad
profile wings. These wings may be affected by stray radiation of the telescope,
but for the Bell Labs and the LAB survey they are not explainable by
instrumental problems. The same HVD component with a dispersion of 74 km s-1,
which was used to fit the gas distribution in the outskirts, is useful also to
explain this local component. A multi-phase medium containing this HVD
component is found to balance gravity by its pressure gradient,
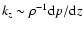 for the mass model proposed by Kalberla et al. (2007).
for the mass model proposed by Kalberla et al. (2007).
Evidence for a population of fast gas clouds with a velocity dispersion of
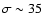 km s-1was found by Radhakrishnan & Srinivasan (1980); Kulkarni & Fich (1985); Lockman & Gehman (1991); Mohan et al. (2004). Kalberla et al. (1998), analyzing the Leiden/Dwingeloo Survey, proposed a more extreme dispersion of
km s-1was found by Radhakrishnan & Srinivasan (1980); Kulkarni & Fich (1985); Lockman & Gehman (1991); Mohan et al. (2004). Kalberla et al. (1998), analyzing the Leiden/Dwingeloo Survey, proposed a more extreme dispersion of
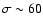 km s-1which is modified here to
km s-1which is modified here to
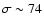 km s-1. Most remarkable, however, is the early prediction by Pikelner & Shklovsky (1958) who proposed a neutral halo gas phase with
km s-1. Most remarkable, however, is the early prediction by Pikelner & Shklovsky (1958) who proposed a neutral halo gas phase with
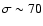 km s-1.
km s-1.
The HVD component analyzed here as a diffuse emission component with a
dispersion of
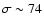 km s-1, is patchy. It is made up of a large
number of filaments and small H I clumps. These stand out from the normal disk
emission only if they reach large z distances or if they have high forbidden
velocities. Evidence for such clumps in the inner Galaxy was given by
Lockman (2002b). Stanimirovic (2006) found similar clumps in the anti-center direction. Clouds with high forbidden velocities in the inner Galaxy were detected by Stil et al. (2006) in the VLA Galactic Plane Survey. These authors estimate that this population of fast clouds has a radial scale length of 2.8 to 8 kpc, consistent with the scale length of 7.5 kpc derived by us.
km s-1, is patchy. It is made up of a large
number of filaments and small H I clumps. These stand out from the normal disk
emission only if they reach large z distances or if they have high forbidden
velocities. Evidence for such clumps in the inner Galaxy was given by
Lockman (2002b). Stanimirovic (2006) found similar clumps in the anti-center direction. Clouds with high forbidden velocities in the inner Galaxy were detected by Stil et al. (2006) in the VLA Galactic Plane Survey. These authors estimate that this population of fast clouds has a radial scale length of 2.8 to 8 kpc, consistent with the scale length of 7.5 kpc derived by us.
For our analysis we used adaptive filters to distinguish the stationary disk
component from extra-planar gas. Over the main body of the disk (
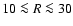 kpc) we measure that on average 5% of the gas is outside the disk
(Fig. 12). This is a lower limit only. Assuming that the
extra-planar gas can be characterized as an HVD component implies that a
significant fraction of this phase is hidden from direct observation since it
cannot be distinguished from disk gas. For our analysis we estimate that only
50% of the LVD gas can be discriminated, resulting in an extra-planar gas
fraction of 10%. This is consistent with a hydrostatic model (Sect. 6.1),
observations at the polar caps (Sect. 6.2) and also with the gas distribution
at the Galactic outskirts (Sect. 5.2). We conclude that all over the
Galactic H I disk the ``normal'' phase, the CNM and WNM, is associated by
an ``anomalous'' gas phase, described here as an HVD phase. For the inner
Galaxy (
kpc) we measure that on average 5% of the gas is outside the disk
(Fig. 12). This is a lower limit only. Assuming that the
extra-planar gas can be characterized as an HVD component implies that a
significant fraction of this phase is hidden from direct observation since it
cannot be distinguished from disk gas. For our analysis we estimate that only
50% of the LVD gas can be discriminated, resulting in an extra-planar gas
fraction of 10%. This is consistent with a hydrostatic model (Sect. 6.1),
observations at the polar caps (Sect. 6.2) and also with the gas distribution
at the Galactic outskirts (Sect. 5.2). We conclude that all over the
Galactic H I disk the ``normal'' phase, the CNM and WNM, is associated by
an ``anomalous'' gas phase, described here as an HVD phase. For the inner
Galaxy (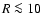 kpc) we observe an increase of the extra-planar gas
fraction of a few percent. This might be explained by fountain activities but,
as discussed in Sect. 2, estimates at such distances are highly uncertain.
kpc) we observe an increase of the extra-planar gas
fraction of a few percent. This might be explained by fountain activities but,
as discussed in Sect. 2, estimates at such distances are highly uncertain.
In this light, the general features of the extra-planar H I gas in NGC 891 and
NGC 2403 appear to be comparable (within a factor of 2) to what we see in the
Milky Way. This is confirmed by projecting the H I gas distribution of the
Milky Way to large distances. Simulating position-velocity diagrams, the HVD
component causes wings and beards close to the center. The gaseous outskirts,
however, would hardly be observable. The telescope sensitivity needs to be improved by a factor of 10 to observe this part, which is feasible with the SKA.
HVCs and IVCs are usually classified from observations according to their
velocities. One can distinguish between coherent complexes and isolated
compact objects. Their origin may be from fountain flow or accretion. Also,
metalicities are important but here we discuss H I properties only.
For our analysis of the global properties of the H I distribution we have
chosen different criteria. The primary goal was to derive the properties of
the main body, the H I disk. This has a well defined dynamically cool gas
distribution. There are two phases, CNM and WNM, both with velocity
dispersions perpendicular to the disk that are low compared to the rotation
velocity. The gas disk is flaring but the most prominent inner part of the H I
disk is highly flattened.
However, as proposed by Spitzer (1956) and much later established by
X-ray observations of the predominantly hot ISM of elliptical galaxies, the
hot Galactic ISM does not have to be so flat. The extra-planar H I is embedded
in the hot component. This arises the question of whether there might be a
quasi-static system near equilibrium as modeled by Spitzer or whether the
Milky Way halo is strongly affected by steadily changing conditions, e.g. due
to mass inflow or star bursts.
The star-formation-rate (SFR) in the solar neighborhood is remarkably constant
over the lifetime of the disk, infall of material appears also to be
approximately constant at one-half of the SFR (Twarog 1980). Ongoing
accretion may be derived from HVC complexes and also from the Magellanic
Stream but it is unclear whether irregularities in accretion rate and outflows
are strong enough to affect the global shape of the Galactic halo
significantly. Little is known about the impact of star bursts on the
structure and dynamics of the Milky Way halo. Supershells and chimneys may
reach z distances of several kpc but appear not to be able to shape a
significant fraction of the halo (McClure-Griffiths et al. 2006).
As a halo model therefore we have chosen the simple case of a quasi-static
system that can be approximated numerically by a hydrostatic distribution. We
are interested in global properties of the gas distribution, not in
details that are more important for individual components. A global model
makes sense when averaging the H I emission over several kpc as we obtain a
self-consistent solution. As discussed in Sects. 5 and 6, the same model
parameters apply to both polar caps and to the sectors
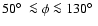 and
and
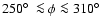 at
at
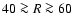 kpc. These
are the only regions available for an unambiguous separation of planar and
extra-planar gas in the Milky Way.
kpc. These
are the only regions available for an unambiguous separation of planar and
extra-planar gas in the Milky Way.
Figure 10, a l-v plot of measured brightness temperatures,
displays numerous IVCs and HVCs. These features appear partly to be organized
in complexes but are in general close to the disk. Projection effects cause a
complicated picture, in particular velocity crowding in some parts of the sky
makes it difficult to judge whether a particular feature belongs to the disk
or not. Deviation velocities between planar and extra-planar gas components
depend strongly on position.
The density distribution
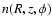 in Fig. 1 shows a
clearer picture. Extra-planar gas is offset from the Galactic disk but most of
it is clearly associated with the disk. Again we find large scale fluctuations
but there is a general trend that the extra-planar gas distribution increases
with decreasing mid-plane distance. This situation appears best to be described
as a ``thick disk'' having twice the radial scale length of the CNM/WNM gas
distribution. We use the model of a turbulent HVD distribution. Local
enhancements, or complexes, are considered as statistical fluctuations; they
become less dominant if one averages over larger areas, this is a typical
property of a turbulent medium. Figure 15, showing average
emission of the polar caps at latitudes
in Fig. 1 shows a
clearer picture. Extra-planar gas is offset from the Galactic disk but most of
it is clearly associated with the disk. Again we find large scale fluctuations
but there is a general trend that the extra-planar gas distribution increases
with decreasing mid-plane distance. This situation appears best to be described
as a ``thick disk'' having twice the radial scale length of the CNM/WNM gas
distribution. We use the model of a turbulent HVD distribution. Local
enhancements, or complexes, are considered as statistical fluctuations; they
become less dominant if one averages over larger areas, this is a typical
property of a turbulent medium. Figure 15, showing average
emission of the polar caps at latitudes
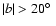 also includes IVCs,
HVCs, and the Magellanic stream. These local phenomena show up as minor
perturbations.
also includes IVCs,
HVCs, and the Magellanic stream. These local phenomena show up as minor
perturbations.
Comparing properties of the HVD component with global properties of the HVC
gas we find some interesting agreements. HVCs have a multi-phase structure and
are most probably confined by an external hot halo phase
(Kalberla & Haud 2006). HVCs have specific turbulent energy densities that are
an order of magnitude higher than that of comparable clumps in the Galactic
disk. The same conditions hold for the HVD component. Most surprising,
however, is that the integrated flux distribution for HVCs as function of
velocity Wakker (1991, Fig. 5) is a continuation of the gas
distribution in the broad wings of the HVD component to high velocities
(Fig. 15).
The HVD component is coupled to the disk but it is anomalous in the sense that
it represents a highly turbulent clumpy phase, best described as an extended
very thick disk. At the position of the Sun we determine an exponential scale
height of 3.9 kpc. The HVD component can be best characterized as an
extra-planar gas component; it expands the phase space occupied by the H I
disk predominantly perpendicular to the disk. IVCs are located in the lower
Galactic halo (Albert & Danly 2004). Their velocities as well as known z distances place them at the less distant part of the HVD phase
space. Distances for HVCs are less well known but according to their
velocities at least some of them may belong to the outer part of the HVD phase
space. The HVC velocity limit is
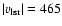 km s-1, roughly coincident
with the escape velocity of the Milky Way.
km s-1, roughly coincident
with the escape velocity of the Milky Way.
Individual extra-planar gas layers are extremely patchy and lag behind the
underlying rotating disk. These layers are affected by flaring and the lag
depends on the distance z/hz(R), normalized to the disk scale height. The
anomalous gas phase is rather extended. We could trace it up to 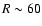 kpc.
kpc.
The gravitational potential at the outskirts of the Milky Way is very shallow.
The rotation of anomalous gas for 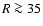 kpc is therefore essentially
unaffected by flaring. The fact that we observe an extended HVD gas phase at
kpc is therefore essentially
unaffected by flaring. The fact that we observe an extended HVD gas phase at
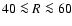 kpc implies accretion by a ``drizzle'' of low mass fragments. This gas cannot originate from fountain flows. Fountain events far outside R25 are highly improbable as the radial scale lengths for stars and HVD gas differ significantly.
kpc implies accretion by a ``drizzle'' of low mass fragments. This gas cannot originate from fountain flows. Fountain events far outside R25 are highly improbable as the radial scale lengths for stars and HVD gas differ significantly.
A continuous flow of material in galaxies from the disk into the halo was studied by Collins et al. (2002); Fraternali & Binney (2006; Heald et al. (2006a). Their models can explain the vertical gas distribution but fail to reproduce the apparent counter rotation and vertical velocity gradients. They also produce a general outflow, contrary to observations.
Our aim was to describe global features of the H I distribution that may be
representative of a steady state. Calculating radial distribution functions we
found in all cases significant systematic differences between the northern and
southern part of the Milky Way. The system is asymmetrical. Midplane volume
densities and surface densities are most discrepant at 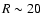 kpc.
Considering the H I flaring we found a systematic modulation that may be
explainable by a misaligned gravitational field originating from a misaligned
dark matter disk (Fig. 11). The flaring ratio peaks at
kpc.
Considering the H I flaring we found a systematic modulation that may be
explainable by a misaligned gravitational field originating from a misaligned
dark matter disk (Fig. 11). The flaring ratio peaks at 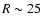 kpc are in excellent agreement with Weinberg (1998) who predicted that the interaction between Milky Way and Magellanic system causes a dark matter wake at this position.
kpc are in excellent agreement with Weinberg (1998) who predicted that the interaction between Milky Way and Magellanic system causes a dark matter wake at this position.
Our results depend on the rotation curve, hence on the mass model. We tested
several different possibilities and summarize briefly how much our conclusions
are affected by the mass model used (Kalberla et al. 2007).
The global surface density distribution, mid plane densities and also flaring
depend weakly on the rotation curve (Voskes 1999; Nakanishi & Sofue 2003; Levine et al. 2006a,b) but our results are
not altered significantly as long as a nearly flat rotation curve is used.
The radial exponential scale length of 3.75 kpc derived by us changes to 4 kpc
if one uses a constant rotation with a circular velocity of 220 km s-1. Our
conclusion that surface densities, mid plane densities and flaring can be
approximated by exponential relations remains valid, although the correlation
degrades somewhat if we use alternative rotation curves.
Deviations from axisymmetry depend on non-circular terms in the rotation
curve. We used the first order epicyclic streamline correction by
Levine et al. (2006a, Eqs. (1), (2)) which is a great improvement in overcoming discontinuities at large radial distances. This correction is empirical but the assumption that surface densities should not have azimuthal
discontinuities remains valid for all mass models. The correction is
consistent with an asymmetrical mass distribution and the results do not
depend significantly on the details of the mass model. The same holds for
asymmetries in the H I distribution.
The average H I emission at the polar caps (Sect. 6.2) has broad high velocity
wings. This is known from observations. Parameters for the underlying HVD
component are completely independent of any mass model. The parameter fitting,
assuming halo gas in global hydrostatic equilibrium with the gravitational
field, depends strongly on the mass model. A dependence on the mass model
exists also for HVD gas at the outskirts of the Milky Way. It is the shape of
the outer rotation curve that determines the distance of this component.
We argued that the thin H I disk, defined by the CNM & WNM gas, is
associated with a thick extended HVD gas disk. This model is self-consistent for
the mass model used but it necessarily has to break down for significant
changes of the mass model or the outer rotation curve.
Acknowledgements
This project was supported by Deutsche Forschungsgemeinschaft, grant KA1265/5-1. We thank J. Kerp and F. Kenn for discussions and a careful reading of the manuscript and the anonymous referee for constructive criticism.
- Albert, C. E.,
& Danly, L. 2004, ASSL: High Velocity Clouds, 312, 73 [NASA ADS]
(In the text)
- Bajaja, E.,
Arnal, E. M., Larrarte, J. J., et al. 2005, A&A, 440, 767 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Binney, J.,
& Merrifield, M. 1998 (Princeton, NJ: Princeton University
Press)
(In the text)
- Boulares,
A., & Cox, D. P. 1990, ApJ, 365, 544 [NASA ADS] [CrossRef]
(In the text)
- Collins, J.
A., Benjamin, R. A., & Rand, R. J. 2002, BAAS, 34, 709 [NASA ADS]
(In the text)
- Cox, D. P. 2005,
ARA&A, 43, 337 [NASA ADS] [CrossRef]
(In the text)
- Dame, T. M. 1993,
Back to the Galaxy, 278, 267 [NASA ADS]
(In the text)
- de
Avillez, M. A. 2000, MNRAS, 315, 479 [NASA ADS] [CrossRef]
(In the text)
- de Boer, W.,
Sander, C., Zhukov, V., Gladyshev, A. V., & Kazakov, D. I.
2005, A&A, 444, 51 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Dehnen, W., &
Binney, J. 1998, MNRAS, 294, 429 [NASA ADS] [CrossRef]
(In the text)
- Dickey, J. M.,
& Lockman, F. J. 1990, ARA&A, 28, 215 [NASA ADS] [CrossRef]
(In the text)
- Diplas, A.,
& Savage, B. D. 1991, ApJ, 377, 126 [NASA ADS] [CrossRef]
(In the text)
-
Fraternali, F., & Binney, J. J. 2006, MNRAS, 366, 449 [NASA ADS] [CrossRef]
(In the text)
-
Fraternali, F., Oosterloo, T., Sancisi, R., & van Moorsel, G.
2001, ApJ, 562, L47 [NASA ADS] [CrossRef]
(In the text)
-
Fraternali, F., Oosterloo, T., Boomsma, R., Swaters, R., &
Sancisi, R. 2004, IAU Symp., 217, 136 [NASA ADS]
- Hartmann,
D., & Burton, W. B. 1997, Atlas of Galactic Neutral Hydrogen
(Cambridge: Cambridge University Press)
(In the text)
- Haud, U., &
Kalberla, P. M. W. 2006, Baltic Astron., 15, 413 [NASA ADS]
(In the text)
- Heald, G. H.,
Rand, R. J., Benjamin, R. A., Collins, J. A., & Bland-Hawthorn,
J. 2006, ApJ, 636, 181 [NASA ADS] [CrossRef]
(In the text)
-
Henderson, A. P., Jackson, P. D., & Kerr, F. J. 1982, ApJ, 263,
116 [NASA ADS] [CrossRef]
(In the text)
- Kalberla,
P. M. W. 2003, ApJ, 588, 805 [NASA ADS] [CrossRef]
(In the text)
- Kalberla,
P. M. W., & Haud, U. 2006, A&A, 455, 481 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Kalberla, P. M.
W., Westphalen, G., Mebold, U., Hartmann, D., & Burton, W. B.
1998, A&A, 332, L61 [NASA ADS]
(In the text)
- Kalberla,
P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440,
775 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Kalberla,
P. M. W., Dedes, L., Kerp, J., & Haud, U. 2007, A&A, 469,
511 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Kuijken, K.,
& Gilmore, G. 1989b, MNRAS, 239, 651 [NASA ADS]
(In the text)
- Kulkarni,
S. R., & Fich, M. 1985, ApJ, 289, 792 [NASA ADS] [CrossRef]
(In the text)
- Kulkarni,
S. R., Heiles, C., & Blitz, L. 1982, ApJ, 259, L63 [NASA ADS] [CrossRef]
(In the text)
- Levine, E. S.,
Blitz, L., & Heiles, C. 2006a, ApJ, 643, 881 [NASA ADS] [CrossRef]
(In the text)
- Levine, E. S.,
Blitz, L., & Heiles, C. 2006b, Science, 312, 1773 [CrossRef]
(In the text)
- Lockman, F.
J. 1988, The Outer Galaxy, 306, 79 [NASA ADS]
(In the text)
- Lockman, F.
J. 2002a, Seeing Through the Dust: The Detection of HI and the
Exploration of the ISM in Galaxies, 276, 107 [NASA ADS]
(In the text)
- Lockman, F.
J. 2002b, ApJ, 580, L47 [NASA ADS] [CrossRef]
(In the text)
- Lockman, F.
J. 2004, Recycling Intergalactic and Interstellar Matter, 217,
130 [NASA ADS]
(In the text)
- Lockman, F. J.,
& Gehman, C. S. 1991, ApJ, 382, 182 [NASA ADS] [CrossRef]
(In the text)
- McClure-Griffiths, N. M., Ford,
A., Pisano, D. J., et al. 2006, ApJ, 638, 196 [NASA ADS] [CrossRef]
(In the text)
- Maloney, P.
1993, ApJ, 414, 41 [NASA ADS] [CrossRef]
- Mohan, R.,
Dwarakanath, K. S., & Srinivasan, G. 2004, J.A&A, 25,
185 [NASA ADS]
(In the text)
- Münch, G.,
& Zirin, H. 1961, ApJ, 133, 11 [NASA ADS] [CrossRef]
(In the text)
-
Nakanishi, H., & Sofue, Y. 2003, PASJ, 55, 191 [NASA ADS]
(In the text)
-
Oosterloo, T., Fraternali, F., & Sancisi, R. 2007, AJ, 134,
1019 [NASA ADS] [CrossRef]
(In the text)
- Lockman, F.
J., & Shields, J. C. 2007, ApJ, 656, 928 [NASA ADS] [CrossRef]
- Pikelner,
S. B., & Shklovsky, I. S. 1958, Rev. Mod. Phys., IAU Symp. 8,
30, 935
(In the text)
-
Radhakrishnan, V., & Srinivasan, G. 1980, A&A, 1, 47
(In the text)
- Rohlfs, K.
1977, Lect. Notes Phys. (Berlin: Springer Verlag), 69 [NASA ADS],
(In the text)
- Saha, K., &
Jog, C. J. 2006, MNRAS, 367, 1297 [NASA ADS] [CrossRef]
(In the text)
- Spitzer, L. 1942,
ApJ, 95, 329 [NASA ADS] [CrossRef]
(In the text)
- Spitzer, L.
J. 1956, ApJ, 124, 20 [NASA ADS] [CrossRef]
(In the text)
-
Stanimirovic, S., Putman, M., Heiles, C. P., Joshua, E. G., &
Goldsmith, P. F. 2006, ApJ, 653, 1210 [NASA ADS] [CrossRef]
(In the text)
- Stark, A. A.,
Gammie, C. F., Wilson, R. W., et al. 1992, ApJS, 79, 77 [NASA ADS] [CrossRef]
(In the text)
- Stil, J. M.,
Lockman, F. J., Taylor, A. R., et al. 2006, ApJ, 637, 366 [NASA ADS] [CrossRef]
(In the text)
- Swaters, R.
A., Sancisi, R., & van der Hulst, J. M. 1997, ApJ, 491,
140 [NASA ADS] [CrossRef]
(In the text)
- Twarog, B. A.
1980, ApJ, 242, 242 [NASA ADS] [CrossRef]
(In the text)
- van Woerden, H.,
Wakker, B. P., Schwarz, U. J., & de Boer, K. S. 2004a, High
Velocity Clouds, ASSL, 312
- Voskes, T.
1999, M.Sc. Thesis, University of Leiden,
[arXiv:astro-ph/0601653]
(In the text)
- Wakker, B. P.
1991, A&A, 250, 499 [NASA ADS]
(In the text)
- Weinberg,
M. D. 1998, MNRAS, 299, 499 [NASA ADS] [CrossRef]
(In the text)
- Weiner, B. J.,
& Sellwood, J. A. 1999, ApJ, 524, 112 [NASA ADS] [CrossRef]
(In the text)
- Wolfire, M.
G., McKee, C. F., Hollenbach, D., & Tielens, A. G. G. M. 2003,
ApJ, 587, 278 [NASA ADS] [CrossRef]
(In the text)
- Wouterloot,
J. G. A., Brand, J., Burton, W. B., & Kwee, K. K. 1990,
A&A, 230, 21 [NASA ADS]
(In the text)
Copyright ESO 2008
![\begin{figure}
\par\mbox{\includegraphics[angle=-90,width=8.7cm]{9240f01a.eps} \...
...0f01g.eps} \includegraphics[angle=-90,width=8.7cm]{9240f01h.eps} }
\end{figure}](/articles/aa/full/2008/33/aa9240-07/Timg29.gif)
![\begin{figure}
\par\includegraphics[width=9cm,clip]{9240f02.eps}\end{figure}](/articles/aa/full/2008/33/aa9240-07/Timg48.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{9240f03.eps} \end{figure}](/articles/aa/full/2008/33/aa9240-07/Timg49.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{9240f04a.eps}
\includegraphics[angle=-90,width=9cm,clip]{9240f04b.eps} \end{figure}](/articles/aa/full/2008/33/aa9240-07/Timg52.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{9240f05.eps} \end{figure}](/articles/aa/full/2008/33/aa9240-07/Timg70.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{9240f06a.eps}
\includegraphics[angle=-90,width=9cm,clip]{9240f06b.eps} \end{figure}](/articles/aa/full/2008/33/aa9240-07/Timg75.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{9240f07.eps} \end{figure}](/articles/aa/full/2008/33/aa9240-07/Timg80.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm]{9240f08.eps} \end{figure}](/articles/aa/full/2008/33/aa9240-07/Timg85.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm]{9240f09.eps}\end{figure}](/articles/aa/full/2008/33/aa9240-07/Timg86.gif)
![\begin{figure}
\par\mbox{\includegraphics[angle=-90,width=9cm]{9240f10a.eps} \in...
...240f10c.eps} \includegraphics[angle=-90,width=9cm]{9240f10d.eps} }
\end{figure}](/articles/aa/full/2008/33/aa9240-07/Timg87.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{9240f11.eps} \end{figure}](/articles/aa/full/2008/33/aa9240-07/Timg98.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{9240f12.eps}\end{figure}](/articles/aa/full/2008/33/aa9240-07/Timg102.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=8.4cm]{9240f13.eps} \end{figure}](/articles/aa/full/2008/33/aa9240-07/Timg112.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=8.2cm]{9240f14.eps}\end{figure}](/articles/aa/full/2008/33/aa9240-07/Timg114.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=8.2cm]{9240f15.eps}\end{figure}](/articles/aa/full/2008/33/aa9240-07/Timg115.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm]{9240f16.eps} \end{figure}](/articles/aa/full/2008/33/aa9240-07/Timg125.gif)