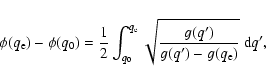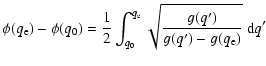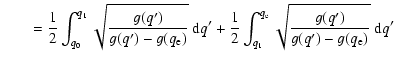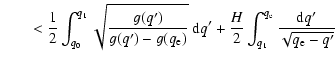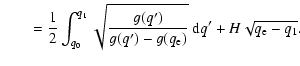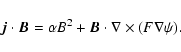A&A 487, 1163-1170 (2008)
DOI: 10.1051/0004-6361:200809753
Hot Jupiters and stellar magnetic activity
A. F. Lanza
INAF - Osservatorio Astrofisico di Catania, via S. Sofia 78,
95123 Catania, Italy
Received 10 March 2008 / Accepted 19 May 2008
Abstract
Context. Recent observations suggest that stellar magnetic activity may be influenced by the presence of a close-by giant planet. Specifically, chromospheric hot spots rotating in phase with the planet orbital motion have been observed during some seasons in a few stars harbouring hot Jupiters. The spot leads the subplanetary point by a typical amount of 
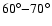 ,
with the extreme case of
,
with the extreme case of 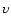 And where the angle is
And where the angle is 
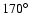 .
.
Aims. The interaction between the star and the planet is described considering the reconnection between the stellar coronal field and the magnetic field of the planet. Reconnection events produce energetic particles that, moving along magnetic field lines, impact onto the stellar chromosphere giving rise to a localized hot spot.
Methods. A simple magnetohydrostatic model is introduced to describe the coronal magnetic field of the star connecting its surface to the orbiting planet. The field is assumed to be axisymmetric around the rotation axis of the star and its configuration is more general than a linear force-free field.
Results. With a suitable choice of the free parameters, the model can explain the phase differences between the hot spots and the planets observed in HD 179949,  And, HD 189733, and
And, HD 189733, and 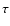 Bootis, as well as their visibility modulation on the orbital period and seasonal time scales. The possible presence of cool spots associated with the planets in
Bootis, as well as their visibility modulation on the orbital period and seasonal time scales. The possible presence of cool spots associated with the planets in 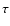 Boo and HD 192263 cannot be explained by the present model. However, we speculate about the possibility that reconnection events in the corona may influence subphotospheric dynamo action in those stars producing localized photospheric (and chromospheric) activity migrating in phase with their planets.
Boo and HD 192263 cannot be explained by the present model. However, we speculate about the possibility that reconnection events in the corona may influence subphotospheric dynamo action in those stars producing localized photospheric (and chromospheric) activity migrating in phase with their planets.
Key words: stars: planetary systems - stars: activity -
stars: late-type - stars: magnetic fields -
stars: general
About 300 extrasolar giant planets are presently
known![[*]](/icons/foot_motif.gif) ,
among which
,
among which  25 percent have a
projected orbital semi-major axis of less than 0.1 AU.
Such planets are expected
to interact significantly with their host stars, not only through tides, but possibly also
with other mechanisms. Recent investigations by Shkolnik et al. (2005,2008) show that
HD 179949 and
25 percent have a
projected orbital semi-major axis of less than 0.1 AU.
Such planets are expected
to interact significantly with their host stars, not only through tides, but possibly also
with other mechanisms. Recent investigations by Shkolnik et al. (2005,2008) show that
HD 179949 and 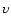 Andromedae have chromospheric hot spots that rotate
with the orbital period of their inner planets. The spots are not located at
the subplanetary point, but lead the
planet by
Andromedae have chromospheric hot spots that rotate
with the orbital period of their inner planets. The spots are not located at
the subplanetary point, but lead the
planet by 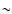
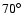 in the case of HD 179949 and by
in the case of HD 179949 and by
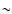
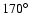 in the case of
in the case of 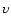 And. They are quite
persistent features, with lifetimes of the order of 350-400 days, although they are not detected in all observing seasons. Two other stars,
HD 189733 and
And. They are quite
persistent features, with lifetimes of the order of 350-400 days, although they are not detected in all observing seasons. Two other stars,
HD 189733 and 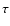 Bootis, show some evidence of an excess of chromospheric variability, probably due to flaring, that is modulated with the orbital periods of their respective planets.
Again, their active regions lead the subplanetary longitudes by
Bootis, show some evidence of an excess of chromospheric variability, probably due to flaring, that is modulated with the orbital periods of their respective planets.
Again, their active regions lead the subplanetary longitudes by
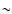
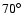 .
Wide-band optical photometry by MOST (the Microvariability and Oscillations of STar satellite; see, e.g., Walker et al. 2003) has given further support to the presence of an active region on
.
Wide-band optical photometry by MOST (the Microvariability and Oscillations of STar satellite; see, e.g., Walker et al. 2003) has given further support to the presence of an active region on 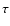 Boo leading the planet by
Boo leading the planet by
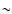
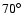 .
In 2004 it resembled a dark spot producing a light dip of about 0.001 mag, while in 2005 it varied between dark and bright (Walker et al. 2008).
.
In 2004 it resembled a dark spot producing a light dip of about 0.001 mag, while in 2005 it varied between dark and bright (Walker et al. 2008).
Further intriguing observational evidence concerns HD 192263, a K dwarf for which Santos et al. (2003)
convincingly demonstrated the presence of a close-by planet with an orbital period
of 24.35 days. Intermediate-band optical photometry by Henry et al. (2002) showed that the star, during two
observing seasons, presented a photospheric starspot that rotated with the orbital period of the planet
for at least three orbital cycles. The spot was not
located at the subplanetary longitude, but the planet was leading the
spot by about
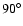 .
.
In all the above cases, an interpretation based on tidal effects can be
ruled out because there is only one signature per orbital cycle and not two.
Following the original suggestions by Cuntz et al. (2000) and Rubenstein & Schaefer (2000), the chromospheric
hot spot may be interpreted as an effect of the energy released by the reconnection
between the stellar
coronal magnetic field and the magnetic field of the planet that moves inside the star's Alfvén radius
(cf. Ip et al. 2004). To explain the phase lag between the planet and the hot spot,
McIvor et al. (2006) determined the
locations at which magnetic field lines that connect the planet to the star reach the stellar surface.
At those locations, electrons accelerated at the reconnection site hit the chromosphere
of the star producing the hot spot. Their model can account for the
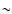
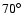 phase lag
observed in HD 179949 if the closed corona of the star extends out to the radius of the planet and the stellar
large scale dipole field is significantly tilted
with respect to the stellar rotation axis. However, the model cannot account for
the
phase lag
observed in HD 179949 if the closed corona of the star extends out to the radius of the planet and the stellar
large scale dipole field is significantly tilted
with respect to the stellar rotation axis. However, the model cannot account for
the 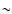
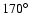 phase lag observed in
phase lag observed in 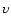 And by any choice of the free parameters.
And by any choice of the free parameters.
Table 1:
Stellar and planetary parameters for different cases of star-planet magnetic interaction.
A step towards a more realistic modelling of the star-planet magnetic interaction was made by
Cranmer & Saar (2007), who extrapolated observed maps of the photospheric magnetic field of the Sun to compute the coronal field at different phases of activity
cycle 22. The potential field source surface method was applied to derive the field assumed to become open at a distance of 2.5 solar radii from the centre of the Sun. By tracing magnetic flux tubes from the planet to the surface of the star, they were able to model the visibility of the hot spot along the stellar rotation and the orbital period of the planet. The cyclic variations of the solar field accounts for the long-term variations observed in the hot spot, while the inferred phase shifts between light curve maximum and planetary meridian passage range between -0.2 and 0.2.
Preusse et al. (2006)
considered a different model in which the hot spot is due to the dissipation of Alfvén waves produced by the
planet moving inside the outer stellar corona. The key difference is that Alfvén waves propagate along
characteristics that do not coincide with the magnetic field lines and that can intersect the stellar surface at almost any angle with respect to the direction of the planet, depending on the choice of the
model free parameters. Therefore,
their model is capable of accounting for both the phase lags observed in
HD 179949 and
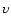 And.
However, the chromospheric flux in a hot spot can be considered comparable to that
of a typical solar active region, i.e.,
And.
However, the chromospheric flux in a hot spot can be considered comparable to that
of a typical solar active region, i.e.,
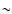
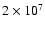 erg cm2 s-1 (Priest 1982), which, in the case of isotropic emission,
implies a very large Alfvén wave flux at the source, located close to the planet. In order to
have an energy flux at the source compatible with the estimates from the reconnection model
by Ip et al. (2004), a highly collimated emission of Alfvén waves is required, which is difficult to justify without a specific physical mechanism.
Another difficulty of the model by Preusse et al. (2006) is that it cannot explain the
observations of
erg cm2 s-1 (Priest 1982), which, in the case of isotropic emission,
implies a very large Alfvén wave flux at the source, located close to the planet. In order to
have an energy flux at the source compatible with the estimates from the reconnection model
by Ip et al. (2004), a highly collimated emission of Alfvén waves is required, which is difficult to justify without a specific physical mechanism.
Another difficulty of the model by Preusse et al. (2006) is that it cannot explain the
observations of 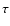 Boo and HD 192263 because Alfvén waves
cannot produce a cooling of the photosphere leading to the formation of dark spots.
In the light of such difficulties, in the present work we proceed as indicated by McIvor et al. (2006), investigating other geometries for the coronal field lines connecting the star to the planet and discuss the possible effects of coronal field reconnection on the dynamo action occurring in the convection zone of the star.
Boo and HD 192263 because Alfvén waves
cannot produce a cooling of the photosphere leading to the formation of dark spots.
In the light of such difficulties, in the present work we proceed as indicated by McIvor et al. (2006), investigating other geometries for the coronal field lines connecting the star to the planet and discuss the possible effects of coronal field reconnection on the dynamo action occurring in the convection zone of the star.
2 Model of the stellar coronal field
We focus on the interpretation of chromospheric spots moving synchronously with hot Jupiters.
In Table 1, we list the relevant stellar and planetary parameters, i.e., from the first to the eighth column, the name of the star, its spectral type, rotation period
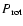 ,
radius R, semi-major axis of the planetary orbit (assumed to be circular) A0, orbital period
,
radius R, semi-major axis of the planetary orbit (assumed to be circular) A0, orbital period
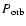 ,
ratio of the Alfvén velocity to the planet orbital velocity
,
ratio of the Alfvén velocity to the planet orbital velocity
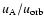 ,
calculated for a magnetic field of 0.15 G and a coronal density at the orbital distance of the planet of
,
calculated for a magnetic field of 0.15 G and a coronal density at the orbital distance of the planet of
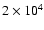 protons cm-3; and the references.
We assume that magnetic reconnection at the intersection between stellar and planetary magnetospheres accelerates electrons to supra-thermal energies. A fraction of those high-energy particles travels inward along magnetic field lines and
impacts onto the dense chromospheric layers of the star, producing a localized heating which gives rise to the hot spot.
protons cm-3; and the references.
We assume that magnetic reconnection at the intersection between stellar and planetary magnetospheres accelerates electrons to supra-thermal energies. A fraction of those high-energy particles travels inward along magnetic field lines and
impacts onto the dense chromospheric layers of the star, producing a localized heating which gives rise to the hot spot.
The position and the extension of the spot depend on the geometry of the stellar coronal field that conveys energetic particles to the chromosphere. We want to show that a coronal field geometry exists that can explain the observed phenomenology, although we will not investigate how it can be produced and maintained.
We assume that the orbital plane of the planet coincides with the stellar equatorial plane and that its orbit is circular. We consider a spherical polar reference frame with the origin at the centre of the star, the 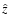 axis
along the stellar rotation axis and assume the radius R of the star as the unit of measure. We indicate the radial distance from the origin with r, the colatitude measured from the North pole with
axis
along the stellar rotation axis and assume the radius R of the star as the unit of measure. We indicate the radial distance from the origin with r, the colatitude measured from the North pole with 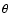 ,
and the azimuthal angle
with
,
and the azimuthal angle
with 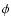 .
.
In the low-density environment of the stellar corona, the Alfvén velocity is at least one order of magnitude larger than the orbital velocity of the planet (cf. e.g., Ip et al. 2004, and Table 1), therefore we can assume that the corona is in a state of magnetostatic equilibrium. For simplicity, we consider a specific class of magnetostatic equilibria, i.e., that investigated by Neukirch (1995) which includes as a particular case the linear force-free equilibria in spherical geometry previously described by Chandrasekhar (1956) and Chandrasekhar & Kendall (1957).
Generalizing a previous approach by Low, Neukirch assumes that the current density in the corona has two components, one directed along the magnetic field, as in force-free models, and the other flowing in a direction perpendicular to the local gravitational acceleration.
Note that the gravitational field of the star dominates over the centrifugal force and the gravitational field of the planet over most of the stellar corona, because the star is rotating quite slowly
(the rotation period of HD 179949 is about 7 days, while that of 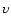 And is about 12 days; cf. Shkolnik et al. 2005,2008) and the mass of the planet is of the order of
10-3 stellar masses. Therefore, the spherical equilibria computed by Neukirch (1995) under the assumption of a purely radial stellar gravitational field are good approximations for our case.
And is about 12 days; cf. Shkolnik et al. 2005,2008) and the mass of the planet is of the order of
10-3 stellar masses. Therefore, the spherical equilibria computed by Neukirch (1995) under the assumption of a purely radial stellar gravitational field are good approximations for our case.
The plasma pressure, density and temperature in the corona are not derived consistently by solving the energy equation, rather they are determined
a posteriori to verify the magnetohydrostatic balance and the equation of state. Nevertheless, in view of our ignorance of the plasma heating function, this approach is acceptable to analytically investigate coronal field geometries of a wider class than linear force-free fields.
Non-axisymmetric coronal fields give rise to an additional modulation of the hot spot intensity with the rotation period of the star because magnetic field lines are rooted in the star. Therefore, we shall consider only axisymmetric configurations. Since the orbital radius of the planet is significantly greater than the stellar radius, the field component with the slowest decay as a function of the radial distance (i.e., the dipole-like component) is the one leading to the strongest interaction. For simplicity, we shall consider only that component assuming that it dominates over all the other components. This can be justified in the case of a solar-like 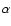 -
- dynamo, as the axisymmetric dynamo mode with dipole-like symmetry with respect to the equator is the one with the strongest excitation rate and dominates the global field geometry outside the star.
dynamo, as the axisymmetric dynamo mode with dipole-like symmetry with respect to the equator is the one with the strongest excitation rate and dominates the global field geometry outside the star.
Under these hypotheses, we consider the magnetic field configuration indicated as case II in Sect. 4 of Neukirch (1995), whose field components in the axisymmetric case (l=1, m=0) are:
where 2B0 is the surface magnetic field at the North pole of the star, 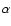 the helicity parameter of the corresponding linear force-free field, and the function g is defined as:
the helicity parameter of the corresponding linear force-free field, and the function g is defined as:
![\begin{displaymath}g (q) \equiv \frac{[b_{0} J_{-3/2}(q) + c_{0} J_{3/2}(q)]\!\s...
...[b_{0} J_{-3/2}(q_{0}) + c_{0} J_{3/2}(q_{0})]\!\sqrt{q_{0}}},
\end{displaymath}](/articles/aa/full/2008/33/aa09753-08/img37.gif) |
(2) |
where b0 and c0 are free constants, J-3/2 and J3/2 are Bessel functions of the first kind of order -3/2 and 3/2, respectively,
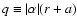 and
and
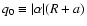 ,
with a a parameter measuring the deviation from the corresponding linear force-free field. The function g is a linear combination of the two independent solutions
,
with a a parameter measuring the deviation from the corresponding linear force-free field. The function g is a linear combination of the two independent solutions
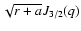 and
and
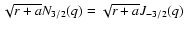 obtained by Neukirch for his case II
(see Eqs. (40)-(43) in Neukirch 1995)
obtained by Neukirch for his case II
(see Eqs. (40)-(43) in Neukirch 1995)![[*]](/icons/foot_motif.gif) .
When a=0 we recover the linear axisymmetric force-free solution of Chandrasekhar (1956) and Chandrasekhar & Kendall (1957) as given in, e.g., Flyer et al. (2004). The physical meaning of the parameter a can be understood by noting that the transformation
.
When a=0 we recover the linear axisymmetric force-free solution of Chandrasekhar (1956) and Chandrasekhar & Kendall (1957) as given in, e.g., Flyer et al. (2004). The physical meaning of the parameter a can be understood by noting that the transformation
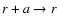 changes our field into a linear force-free field. Therefore, our field is a somewhat radially ``squeezed'' version of a linear force-free field, with the additional confining forces being the gravity and the pressure gradient and a measuring the amount of radial compression.
We introduce the absolute value of
changes our field into a linear force-free field. Therefore, our field is a somewhat radially ``squeezed'' version of a linear force-free field, with the additional confining forces being the gravity and the pressure gradient and a measuring the amount of radial compression.
We introduce the absolute value of 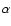 in the definition of the radial variable q, so Eq. (1) is valid for both positive and
negative
in the definition of the radial variable q, so Eq. (1) is valid for both positive and
negative 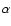 .
Changing the sign of
.
Changing the sign of 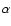 is equivalent to change the sign
of
is equivalent to change the sign
of 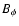 leaving Br and
leaving Br and
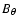 unaltered,
as can be deduced by comparing Eqs. (18) and (24) of Neukirch (1995).
unaltered,
as can be deduced by comparing Eqs. (18) and (24) of Neukirch (1995).
The magnetic field given by Eqs. (1) does not extend to infinity, but is confined to the region between r=R and
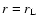 ,
where
,
where 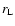 corresponds to the first zero of g (see Chandrasekhar 1956, for a discussion of the boundary conditions at
corresponds to the first zero of g (see Chandrasekhar 1956, for a discussion of the boundary conditions at
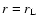 ). Therefore, it can be used to model the inner, closed corona of the star, but not the outer region where the field lines become radial and the stellar wind is accelerated. Schrijver et al. (2003) estimate that the extent of the closed corona is
). Therefore, it can be used to model the inner, closed corona of the star, but not the outer region where the field lines become radial and the stellar wind is accelerated. Schrijver et al. (2003) estimate that the extent of the closed corona is
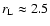 for the Sun and increases remarkably for more active stars, e.g.,
for the Sun and increases remarkably for more active stars, e.g.,
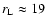 for a star having a surface magnetic flux density or a coronal X-ray flux 10 times greater than the Sun. Since the stars we are considering rotate faster and generally have higher X-ray fluxes than the Sun
(cf., e.g., Shkolnik et al. 2005,2008; Saar et al. 2007),
we estimate that our model can be extended up to a radial distance of
for a star having a surface magnetic flux density or a coronal X-ray flux 10 times greater than the Sun. Since the stars we are considering rotate faster and generally have higher X-ray fluxes than the Sun
(cf., e.g., Shkolnik et al. 2005,2008; Saar et al. 2007),
we estimate that our model can be extended up to a radial distance of
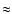 20-30 before becoming inadequate (cf. Sect. 3).
20-30 before becoming inadequate (cf. Sect. 3).
To derive the path of the magnetic field lines, we use the approach of Flyer et al. (2004), introducing a
flux function:
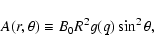 |
(3) |
so that the magnetic field is given by:
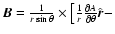
![$\left. \frac{\partial A}{\partial r} \hat{\vec \theta} + \alpha A \hat{\vec \phi} \right]$](/articles/aa/full/2008/33/aa09753-08/img53.gif) .
Magnetic field lines lie over surfaces of constant
.
Magnetic field lines lie over surfaces of constant
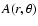 ,
as can be deduced by noting that
,
as can be deduced by noting that
 .
The variation of the azimuthal angle along a given field line can be derived from the equation:
.
The variation of the azimuthal angle along a given field line can be derived from the equation:
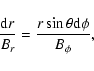 |
(4) |
where
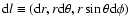 is the line element.
Substituting the expressions of the magnetic field components, it gives:
is the line element.
Substituting the expressions of the magnetic field components, it gives:
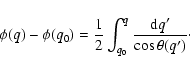 |
(5) |
Making use of Eq. (3), and indicating by 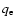 the value of q at which the field line reaches the equatorial plane, i.e.,
the value of q at which the field line reaches the equatorial plane, i.e.,
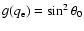 ,
where
,
where
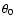 is the initial colatitude of the field line on the stellar surface, we find:
is the initial colatitude of the field line on the stellar surface, we find:
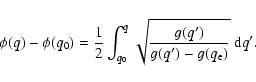 |
(6) |
Equation (6) is valid for a magnetic field line extending to the equatorial plane because the integral exists all along the closed
interval
![$[q_{0}, q_{\rm e}]$](/articles/aa/full/2008/33/aa09753-08/img63.gif) ,
as it is shown in Appendix A.
,
as it is shown in Appendix A.
3 Applications
The magnetic configuration connecting the chromospheric spot to the planet with the observed phase shift is not unique in the framework of our model, even in the force-free case.
A complete exploration of the parameter space would be long and complex, so we limit ourselves to present some possible configurations obtained by fixing
b0=-1.1, c0=1.0, and
a=1.4, and varying 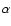 and
and
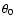 until the magnetic field lines reach the equatorial plane at the planet orbital radius
until the magnetic field lines reach the equatorial plane at the planet orbital radius 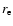 with an azimuthal angle difference
with an azimuthal angle difference
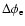 compatible with the observations.
Our choice of b0 and c0 is motivated by the need to have coronal field lines with an azimuthal angle
compatible with the observations.
Our choice of b0 and c0 is motivated by the need to have coronal field lines with an azimuthal angle
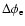 sufficient to account for the large phase gap observed in
sufficient to account for the large phase gap observed in 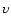 And. By carrying out some experiments with different values of those parameters, we selected some values out of the almost infinite possible choices for illustrative purposes.
In Table 2, for each star listed in the first column, we report the values of a,
And. By carrying out some experiments with different values of those parameters, we selected some values out of the almost infinite possible choices for illustrative purposes.
In Table 2, for each star listed in the first column, we report the values of a, 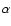 ,
,
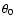 ,
,
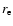 ,
,
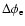 ,
and
,
and 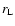 in the columns from the second to the seventh. Note that
in the columns from the second to the seventh. Note that
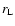 corresponds to the first zero of g at
corresponds to the first zero of g at
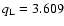 .
For HD 179949 and
.
For HD 179949 and 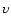 And we also list the parameters for two force-free models.
And we also list the parameters for two force-free models.
The best observed example of a star-planet interaction is provided by HD 179949, so we describe its models in some detail.
A meridional section of its magnetosphere computed for
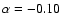 and a=1.4 is shown in Fig. 1. The
field lines at an initial colatitude
and a=1.4 is shown in Fig. 1. The
field lines at an initial colatitude
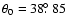 reach the planet on the equatorial plane at
reach the planet on the equatorial plane at
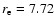 with
with
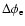 comparable with the observations
- note that typical uncertainties on the observed phase lags are
comparable with the observations
- note that typical uncertainties on the observed phase lags are
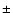
 .
The corresponding force-free field with
.
The corresponding force-free field with
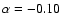 gives
gives
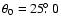 and
and
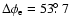 which is too small to explain the observations. Therefore, instead of changing b0 or c0, we decided to
vary
which is too small to explain the observations. Therefore, instead of changing b0 or c0, we decided to
vary 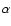 and find an acceptable solution
with
and find an acceptable solution
with
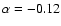 that is also shown in Fig. 1. In this case, the field lines reaching the planet have an initial colatitude of
that is also shown in Fig. 1. In this case, the field lines reaching the planet have an initial colatitude of
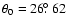 .
The angle
.
The angle
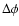 between the footpoint on the stellar surface and the point at
distance r along a field line connecting to the planet is plotted vs. the radial distance
in Fig. 2. At the orbital radius of the planet this corresponds to an angle of
between the footpoint on the stellar surface and the point at
distance r along a field line connecting to the planet is plotted vs. the radial distance
in Fig. 2. At the orbital radius of the planet this corresponds to an angle of
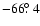 in the case of the field lines with
in the case of the field lines with
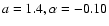 ,
giving a phase lag of
,
giving a phase lag of 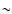 0.18 between the planet and the hot spot, or to an angle of
0.18 between the planet and the hot spot, or to an angle of
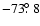 in the case of the force-free field lines with
in the case of the force-free field lines with
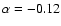 ,
giving a phase lag of
,
giving a phase lag of 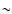 0.205.
0.205.
Table 2:
Model parameters for different cases of star-planet magnetic interaction.
![\begin{figure}
\par\includegraphics[width=8cm,height=12cm]{09753.f1} %\end{figure}](/articles/aa/full/2008/33/aa09753-08/Timg80.gif) |
Figure 1:
Projections of the magnetic field lines of the magnetosphere of HD 179949
on a meridional plane. Configurations are displayed
for Neukirch's models with two sets of parameters, i.e.,
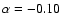 ,
a=1.4 (solid lines) and ,
a=1.4 (solid lines) and
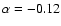 and a=0 (dotted lines). The distance z from the equatorial plane and the distance
and a=0 (dotted lines). The distance z from the equatorial plane and the distance
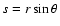 from the rotation axis are measured in units of the stellar radius R. The small green circle indicates the planet assumed to have a radius of 0.1. The dot-dashed line indicates a field line with initial colatitude
from the rotation axis are measured in units of the stellar radius R. The small green circle indicates the planet assumed to have a radius of 0.1. The dot-dashed line indicates a field line with initial colatitude
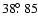 connecting the surface of the star to the planet for the model with
connecting the surface of the star to the planet for the model with
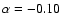 and a=1.4. The dashed line is the same for the force-free model (
and a=1.4. The dashed line is the same for the force-free model (
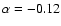 ,
a=0.0) and has an initial colatitude of ,
a=0.0) and has an initial colatitude of
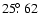 . . |
| Open with DEXTER |
The latitudinal extension of the hot spot on the surface of the star depends on the radius of the planetary magnetosphere, i.e., the distance from the planet at which magnetic reconnection occurs.
If we assume a magnetospheric radius
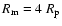 ,
where
,
where
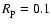 is the radius of the planet, then the radial boundaries of the magnetic reconnection region are
at 7.32 and 8.12, respectively. The colatitudes on the stellar surface of the magnetic field lines reaching the equatorial plane at those distances are
is the radius of the planet, then the radial boundaries of the magnetic reconnection region are
at 7.32 and 8.12, respectively. The colatitudes on the stellar surface of the magnetic field lines reaching the equatorial plane at those distances are
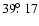 and
and
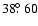 ,
respectively. On the other hand, the longitudinal extension of the region is approximately
,
respectively. On the other hand, the longitudinal extension of the region is approximately 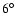 ,
as derived by the intersections of the surface of the star with the projections on the equatorial plane of the field lines tangent to the planet's magnetosphere. Therefore, the energy carried by high-energy electrons is focused onto a quite small region of the stellar chromosphere, producing a remarkable contrast to the background emission.
,
as derived by the intersections of the surface of the star with the projections on the equatorial plane of the field lines tangent to the planet's magnetosphere. Therefore, the energy carried by high-energy electrons is focused onto a quite small region of the stellar chromosphere, producing a remarkable contrast to the background emission.
![\begin{figure}
\par\includegraphics[width=8cm,height=6cm]{09753.f2} %\end{figure}](/articles/aa/full/2008/33/aa09753-08/Timg87.gif) |
Figure 2:
Variation of the azimuthal angle
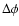 along a magnetic field line starting at the surface of HD 179949 as a function of the radial distance in units of the stellar radius. The solid line is for Neukirch's model with
along a magnetic field line starting at the surface of HD 179949 as a function of the radial distance in units of the stellar radius. The solid line is for Neukirch's model with
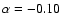 ,
a=1.4, and an initial colatitude ,
a=1.4, and an initial colatitude
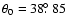 ;
the dotted line is for ;
the dotted line is for
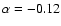 ,
a=0, and ,
a=0, and
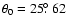 .
The vertical dot-dashed line indicates the orbital radius of the planet of HD 179949. .
The vertical dot-dashed line indicates the orbital radius of the planet of HD 179949. |
| Open with DEXTER |
The hot spot on HD 179949 stays in view for about 0.5 of an orbital cycle (see Fig. 6 in Shkolnik et al. 2008), which suggests that the inclination of the stellar rotation axis on the line of sight is quite high and the latitude of the spot quite low. Therefore, the magnetic
configuration with a=1.4 is favoured over the force-free configuration because it gives a spot at a lower latitude (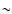
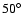 vs.
vs. 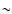
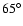 ).
However, the non-force-free magnetic configuration is associated with significant perturbations of the thermal equilibrium of the stellar corona. Their relative amplitudes depend not only on the intensity and geometry of the field, but also on the background pressure and density distributions
which are largely unknown (cf. Eqs. (28) and (30) of Neukirch 1995). An example is shown in Fig. 3 where the relative variations of the temperature, pressure and density in a meridional plane are plotted for a background isothermal corona with a field having the geometry computed for HD 179949. The background pressure and density are proportional to
).
However, the non-force-free magnetic configuration is associated with significant perturbations of the thermal equilibrium of the stellar corona. Their relative amplitudes depend not only on the intensity and geometry of the field, but also on the background pressure and density distributions
which are largely unknown (cf. Eqs. (28) and (30) of Neukirch 1995). An example is shown in Fig. 3 where the relative variations of the temperature, pressure and density in a meridional plane are plotted for a background isothermal corona with a field having the geometry computed for HD 179949. The background pressure and density are proportional to
![$\exp~[\Lambda (1/r -1/R)]$](/articles/aa/full/2008/33/aa09753-08/img90.gif) ,
with
,
with
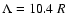 ,
and the ratio of the plasma pressure to the magnetic pressure at the base of the corona
,
and the ratio of the plasma pressure to the magnetic pressure at the base of the corona
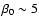 ,
while the unperturbed background temperature is
,
while the unperturbed background temperature is
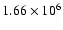 K. The largest temperature and density perturbations are localized at high latitudes and quite close to the star. There the decrease of the plasma pressure provides a force that pushes the magnetic field lines toward the poles and the surface of the star, thus accounting for the squeezing characteristic of the considered non-force-free configurations compared to the corresponding force-free models with a=0, as discussed above.
K. The largest temperature and density perturbations are localized at high latitudes and quite close to the star. There the decrease of the plasma pressure provides a force that pushes the magnetic field lines toward the poles and the surface of the star, thus accounting for the squeezing characteristic of the considered non-force-free configurations compared to the corresponding force-free models with a=0, as discussed above.
![\begin{figure}
\par\includegraphics[width=8cm,height=16cm,angle=90]{09753.f3} %\end{figure}](/articles/aa/full/2008/33/aa09753-08/Timg94.gif) |
Figure 3:
Relative temperature ( left panel), logarithm of the relative pressure ( middle panel) and of the relative density ( right panel) for an illustrative coronal model computed for HD 179949 (see text for details). |
| Open with DEXTER |
If the magnetic field of the planet is a dipole aligned with the planet's rotation axis and that axis is perpendicular to the orbital plane, then the planet's field is directed in the meridional plane close to the equator and reconnection occurs mainly with the stellar
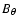 component. If the star has a solar-like magnetic cycle characterized by cyclic inversions of the sign of
component. If the star has a solar-like magnetic cycle characterized by cyclic inversions of the sign of
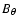 ,
then reconnection delivers most of the energy when
,
then reconnection delivers most of the energy when
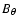 is opposite to the planet's field. This implies that the mean energy of the accelerated electrons is a function
of the cycle phase of the star, with a significantly lower value when the two field components have the same sign. This may explain the on/off character of the star-planet magnetic interaction reported by Shkolnik et al. (2008). Recent observations of the evolution of the surface magnetic field in
is opposite to the planet's field. This implies that the mean energy of the accelerated electrons is a function
of the cycle phase of the star, with a significantly lower value when the two field components have the same sign. This may explain the on/off character of the star-planet magnetic interaction reported by Shkolnik et al. (2008). Recent observations of the evolution of the surface magnetic field in 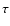 Boo support the hypothesis that magnetic cycles in F-type dwarfs may be significantly shorter than the solar cycle (Donati et al. 2008).
Boo support the hypothesis that magnetic cycles in F-type dwarfs may be significantly shorter than the solar cycle (Donati et al. 2008).
Models similar to that presented for HD 179949 can be computed for 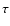 Boo and
HD 189733 for which the hot spots lead the respective planets by
Boo and
HD 189733 for which the hot spots lead the respective planets by
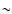
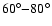 .
On the other hand,
in the case of
.
On the other hand,
in the case of 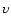 And, we need a higher value of
And, we need a higher value of 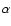 to account for the larger phase shift. In Fig. 4, we show meridional sections of the magnetosphere of the star computed for a model with a=1.4 and a force-free model, respectively. Note the lower latitudes of the footpoints of the field lines connecting to the planet in comparison to the case of HD 179949.
In Fig. 5, we plot the variation of the azimuthal angle along magnetic field lines for
the models shown in Fig. 4.
to account for the larger phase shift. In Fig. 4, we show meridional sections of the magnetosphere of the star computed for a model with a=1.4 and a force-free model, respectively. Note the lower latitudes of the footpoints of the field lines connecting to the planet in comparison to the case of HD 179949.
In Fig. 5, we plot the variation of the azimuthal angle along magnetic field lines for
the models shown in Fig. 4.
In the case of HD 192263, we may assume that chromospheric plages are associated with the photospheric spots lagging the planet by 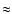
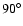 .
The former can be explained by the present model by assuming a positive
.
The former can be explained by the present model by assuming a positive 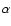 ,
whereas in all the other cases the sign of
,
whereas in all the other cases the sign of 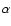 is negative (cf. Table 2).
Magnetic configurations with opposite values of
is negative (cf. Table 2).
Magnetic configurations with opposite values of 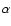 have the same energy and opposite magnetic helicity, so there is no preference for a particular sign
of
have the same energy and opposite magnetic helicity, so there is no preference for a particular sign
of 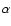 from the point of view of the energy balance or field stability. Note that a linear force-free configuration with a given value of
from the point of view of the energy balance or field stability. Note that a linear force-free configuration with a given value of
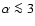 is stable provided that its magnetic helicity exceeds a certain value (cf., e.g., Berger 1985).
is stable provided that its magnetic helicity exceeds a certain value (cf., e.g., Berger 1985).
We suggest that the sign of 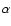 may be related to the conservation of angular momentum in radial plasma motion along field lines. In other words, if there is a mass flow along the field lines, it tends to bend the lines toward negative
may be related to the conservation of angular momentum in radial plasma motion along field lines. In other words, if there is a mass flow along the field lines, it tends to bend the lines toward negative
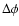 (i.e.,
(i.e.,
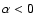 )
when rotation is in the same sense as the orbital motion of the planet, or toward positive
)
when rotation is in the same sense as the orbital motion of the planet, or toward positive
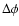 (i.e.,
(i.e.,
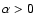 )
when it is in the opposite sense.
The selection of the sign of
)
when it is in the opposite sense.
The selection of the sign of 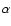 takes place close to the stellar surface since plasma motion cannot affect the field geometry in the low-
takes place close to the stellar surface since plasma motion cannot affect the field geometry in the low-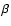 environment of the outer corona.
This effect cannot be described in detail in the framework our magnetohydrostatic approach, but it could be incorporated in more general models.
environment of the outer corona.
This effect cannot be described in detail in the framework our magnetohydrostatic approach, but it could be incorporated in more general models.
In the case of HD 192263, the absolute value of 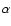 is 4-5 times smaller than in the other cases, because the relative orbital radius of the planet is correspondingly larger. As a consequence, the relative radius of the closed corona turns out to be 4-5 times larger than in the other cases. However, it can be significantly reduced by making a different choice
for the free parameters b0 and c0 in the definition of the function g, in order to have its first zero at a value smaller than
is 4-5 times smaller than in the other cases, because the relative orbital radius of the planet is correspondingly larger. As a consequence, the relative radius of the closed corona turns out to be 4-5 times larger than in the other cases. However, it can be significantly reduced by making a different choice
for the free parameters b0 and c0 in the definition of the function g, in order to have its first zero at a value smaller than
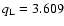 .
.
![\begin{figure}
\par\includegraphics[width=8cm,height=12cm]{09753.f4} %\end{figure}](/articles/aa/full/2008/33/aa09753-08/Timg102.gif) |
Figure 4:
Projections of the magnetic field lines of the magnetosphere of
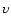 And
on a meridional plane. Configurations are displayed
for Neukirch's models with two sets of parameters, i.e., And
on a meridional plane. Configurations are displayed
for Neukirch's models with two sets of parameters, i.e.,
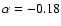 ,
a=1.4 (solid lines) and ,
a=1.4 (solid lines) and
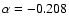 and a=0 (dotted lines). The distance z from the equatorial plane and the distance
and a=0 (dotted lines). The distance z from the equatorial plane and the distance
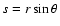 from the rotation axis are measured in units of the stellar radius R. The small green circle indicates the planet assumed to have a radius of 0.1. The dot-dashed line indicates a field line with initial colatitude
from the rotation axis are measured in units of the stellar radius R. The small green circle indicates the planet assumed to have a radius of 0.1. The dot-dashed line indicates a field line with initial colatitude
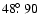 connecting the surface of the star to the planet for the model with
connecting the surface of the star to the planet for the model with
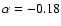 and a=1.4. The dashed line is the same for the force-free model (
and a=1.4. The dashed line is the same for the force-free model (
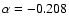 ,
a=0.0) and has an initial colatitude
of ,
a=0.0) and has an initial colatitude
of
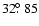 . . |
| Open with DEXTER |
The model presented in Sect. 2 can explain phase gaps up to
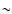
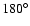 ,
which is not possible in the framework of the previous model by McIvor et al. (2006). Our model accounts for chromospheric hot spots, but it
cannot account for cool dark spots moving in phase with the planet, as suggested by MOST observations of
,
which is not possible in the framework of the previous model by McIvor et al. (2006). Our model accounts for chromospheric hot spots, but it
cannot account for cool dark spots moving in phase with the planet, as suggested by MOST observations of 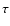 Boo in 2004 or in the case of HD 192263. Therefore, we speculate about the possibility that the magnetic reconnection in the stellar corona may perturb some process responsible for the dynamo action inside the star. Specifically, the effect leading to regeneration of the poloidal field from the toroidal field in a solar-like dynamo, i.e., the
Boo in 2004 or in the case of HD 192263. Therefore, we speculate about the possibility that the magnetic reconnection in the stellar corona may perturb some process responsible for the dynamo action inside the star. Specifically, the effect leading to regeneration of the poloidal field from the toroidal field in a solar-like dynamo, i.e., the
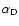 -effect
-effect![[*]](/icons/foot_motif.gif) , may be perturbed by magnetic helicity losses at the reconnection sites in the corona (Brandenburg & Subramanian 2005; Blackman & Brandenburg 2003). In Appendix B we propose some preliminary ideas about a mechanism that may couple coronal reconnection
with the
, may be perturbed by magnetic helicity losses at the reconnection sites in the corona (Brandenburg & Subramanian 2005; Blackman & Brandenburg 2003). In Appendix B we propose some preliminary ideas about a mechanism that may couple coronal reconnection
with the
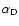 -effect in the convective layers immediately below the surface.
If a significant dynamo action takes place in those subsurface layers, as suggested by
Brandenburg (2007,2005), this may give rise to a local amplification of the magnetic field that will manifest in localized photospheric (and chromospheric) activity,
including cool spots.
Models with a longitude-dependent
-effect in the convective layers immediately below the surface.
If a significant dynamo action takes place in those subsurface layers, as suggested by
Brandenburg (2007,2005), this may give rise to a local amplification of the magnetic field that will manifest in localized photospheric (and chromospheric) activity,
including cool spots.
Models with a longitude-dependent
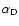 effect have been explored by, e.g., Moss et al. (2002) and show that the maximum magnetic field strength usually falls within
effect have been explored by, e.g., Moss et al. (2002) and show that the maximum magnetic field strength usually falls within 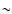
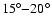 of the maximum of the
of the maximum of the
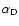 effect. Differential rotation tends to wipe out non-axisymmetric components of the magnetic field, but active longitudes may survive at latitudes of minimal shear as discussed by, e.g., Bigazzi & Ruzmaikin (2004).
effect. Differential rotation tends to wipe out non-axisymmetric components of the magnetic field, but active longitudes may survive at latitudes of minimal shear as discussed by, e.g., Bigazzi & Ruzmaikin (2004).
If this scenario is correct, we expect to find not only hot chromospheric spots but also cool photospheric spots at the longitudes where magnetic field lines connecting the planet with the star intersect the stellar surface. The phase lags observed in 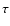 Boo and
HD 192263 may be explained in the framework of the coronal field model described in Sect. 3.
Boo and
HD 192263 may be explained in the framework of the coronal field model described in Sect. 3.
![\begin{figure}
\par\includegraphics[width=8cm,height=6cm]{09753.f5} %\end{figure}](/articles/aa/full/2008/33/aa09753-08/Timg108.gif) |
Figure 5:
Variation of the azimuthal angle
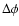 along a magnetic field line starting at the surface of
along a magnetic field line starting at the surface of 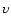 And as a function of the radial distance in units of the stellar radius. The solid line is for Neukirch's model with And as a function of the radial distance in units of the stellar radius. The solid line is for Neukirch's model with
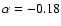 ,
a=1.4, and an initial colatitude ,
a=1.4, and an initial colatitude
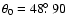 ;
the dotted line is for ;
the dotted line is for
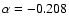 ,
a=0, and ,
a=0, and
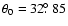 .
The vertical dot-dashed line indicates the orbital radius of the planet
of .
The vertical dot-dashed line indicates the orbital radius of the planet
of  And. And. |
| Open with DEXTER |
In the case of the Sun, it is well known that new active regions have a marked preference to form close to existing active regions giving rise to complexes of activity with lifetimes up to 5-6 months
(e.g., Harvey & Zwaan 1993). We conjecture that a possible cause of this increased probability of new magnetic flux emergence may be a localized enhancement of the subphotospheric dynamo action promoted by helicity losses in the coronal part of an already existing active region. However, the correlation between the rate of coronal mass ejection and the rate of flux emergence in a complex of activity needs to be studied in detail to test this conjecture.
5 Conclusions
We extended the model proposed by McIvor et al. (2006) considering a non-potential magnetic field configuration for the closed corona of a star accompanied by a hot Jupiter. We showed that a tilt of the axis of symmetry of the magnetic field with respect to the rotation axis of the star is not needed to reproduce the observed phase lags between the hot spots and the planets in HD 179949,
 And,
And, 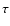 Boo, and HD 189733. This agrees with mean-field dynamo models that predict that the large-scale stellar dipole-like field is aligned with the rotation axis when differential rotation is significant, as was recently found in the case of
Boo, and HD 189733. This agrees with mean-field dynamo models that predict that the large-scale stellar dipole-like field is aligned with the rotation axis when differential rotation is significant, as was recently found in the case of 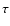 Boo (Donati et al. 2008; Catala et al. 2007). The novelty of the present model is that it can easily account for a phase gap as large as that observed in
Boo (Donati et al. 2008; Catala et al. 2007). The novelty of the present model is that it can easily account for a phase gap as large as that observed in 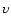 And, which is not possible with previous approaches (Cranmer & Saar 2007; McIvor et al. 2006).
And, which is not possible with previous approaches (Cranmer & Saar 2007; McIvor et al. 2006).
We also found that coronal linear force-free fields tend to give hot spots at quite high latitudes, making it difficult to explain the observed modulation of their visibility. Non-force-free equilibria, such as those computed by Neukirch (1995), give a significantly lower spot latitude for an appropriate choice of the parameter a, allowing us to fit the observations without assuming a high inclination for the stellar rotation axis and the orbital plane of the planet.
The on/off nature of the star-planet interaction suggested by Shkolnik et al. (2008) can also be explained in the framework of our model as a consequence of stellar activity cycles
(see Cranmer & Saar 2007, for a model based on observed solar cycle variations of the magnetic field).
We speculate about the role of magnetic helicity losses due to reconnection events in the stellar corona induced by the planet and suggest that this may give rise to a longitude dependent
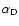 -effect in the stellar dynamo process.
Note that the mechanism we suggest may provide a physical basis for the
-effect in the stellar dynamo process.
Note that the mechanism we suggest may provide a physical basis for the
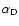 -effect perturbation model originally proposed by Cuntz et al. (2000). Therefore, it is worthwhile to investigate dynamo models with an
-effect perturbation model originally proposed by Cuntz et al. (2000). Therefore, it is worthwhile to investigate dynamo models with an
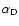 -effect varying in phase with the longitude of the planet to see whether they can reproduce the observations. This kind of model could provide an explanation for a modulation of the photospheric activity in phase with the planet that cannot be interpreted by means of the chromospheric heating model.
-effect varying in phase with the longitude of the planet to see whether they can reproduce the observations. This kind of model could provide an explanation for a modulation of the photospheric activity in phase with the planet that cannot be interpreted by means of the chromospheric heating model.
Zeeman Doppler Imaging (ZDI) techniques are of great interest to map the magnetic fields in the photospheres of planet-harbouring stars, thus providing boundary conditions for an extrapolation to their coronal fields (Donati et al. 2008; Moutou et al. 2007). Although non-potential configurations for assigned boundary conditions may not be unique, including ZDI information in our approach may in principle give the possibility of a self-consistent model of the stellar coronal field to study its interaction with the planet's magnetosphere (cf. e.g., Wiegelmann et al. 2007).
Acknowledgements
The author wishes to thank the anonymous Referee for a careful reading of the manuscript and valuable comments that greatly helped to improve the present work.
A.F.L. is grateful to Drs. P. Barge, C. Moutou and I. Pagano for drawing his attention to the interesting problem of star-planet magnetic interaction. This work has been partially supported by the Italian Space Agency (ASI) under contract ASI/INAF I/015/07/0,
work package 3170. Active star research and exoplanetary studies at INAF-Catania Astrophysical Observatory and the Department of Physics
and Astronomy of Catania University is funded by MUR (Ministero dell'Università e Ricerca), and by Regione Siciliana, whose financial support is gratefully
acknowledged.
This research has made use of the ADS-CDS databases, operated at the CDS, Strasbourg, France.
Appendix A: On the integrability of the function in Eq. (6)
We prove that the integral appearing in:
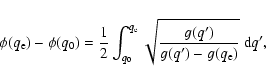 |
(A.1) |
is finite, in spite of the denominator of the integrand vanishing at
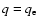 .
Let us select a point
.
Let us select a point
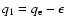 ,
where
,
where 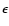 is a small positive number. Applying Lagrange's formula, we can write the denominator of the integrand as:
is a small positive number. Applying Lagrange's formula, we can write the denominator of the integrand as:
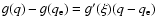 ,
where
,
where
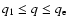 ,
,
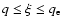 ,
and
,
and
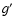 is the derivative of g.
If
is the derivative of g.
If
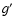 has no zeros in the interval
has no zeros in the interval
![$[q_{1}, q_{\rm e}]$](/articles/aa/full/2008/33/aa09753-08/img117.gif) ,
the function
,
the function
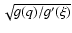 is continuous and limited in the same interval. Indicating its upper bound with H, we have:
is continuous and limited in the same interval. Indicating its upper bound with H, we have:
This formula can be applied to estimate an upper bound for the error made when the numerical integration is truncated at a value
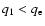 .
Specifically, in the case of the values listed in Table 2, we have fixed q1 by requiring that
.
Specifically, in the case of the values listed in Table 2, we have fixed q1 by requiring that
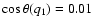 ,
thus finding an error smaller
than
,
thus finding an error smaller
than
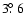 for
for
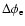 .
.
Appendix B: A mechanism to perturb stellar dynamo action
The value of the parameter
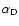 of the dynamo process depends, among others, on the mean value of the current helicity density
of the dynamo process depends, among others, on the mean value of the current helicity density
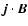 (cf. e.g., Eq. (9.58) of Brandenburg & Subramanian 2005).
Therefore, a perturbation of
(cf. e.g., Eq. (9.58) of Brandenburg & Subramanian 2005).
Therefore, a perturbation of
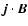 in the subsurface layers may produce a corresponding perturbation of
in the subsurface layers may produce a corresponding perturbation of
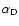 .
The current density in Neukirch's model
(cf. Eq. (7) in Neukirch 1995) is:
.
The current density in Neukirch's model
(cf. Eq. (7) in Neukirch 1995) is:
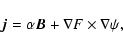 |
(B.1) |
where 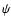 is the gravitational potential and
is the gravitational potential and
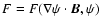 a suitable scalar function defined in Neukirch (1995). Since
a suitable scalar function defined in Neukirch (1995). Since
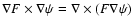 ,
taking the divergence of Eq. (B.1) we find that
,
taking the divergence of Eq. (B.1) we find that
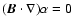 ,
i.e.,
,
i.e., 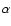 is constant along a given magnetic field line. The current helicity at the surface of the star
is given by:
is constant along a given magnetic field line. The current helicity at the surface of the star
is given by:
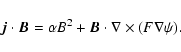 |
(B.2) |
If the perturbations of the coronal magnetic field due to reconnection events do not directly affect the field at the surface, B2 and
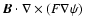 are not modified by the motion of the planet. However, reconnection events induced by the planet will change the value of
are not modified by the motion of the planet. However, reconnection events induced by the planet will change the value of 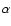 in the corona and such changes will be conducted on the Alfvén travel time to the stellar surface where they change
in the corona and such changes will be conducted on the Alfvén travel time to the stellar surface where they change
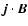 .
Since the magnetic field at the surface is mainly radial,
.
Since the magnetic field at the surface is mainly radial,
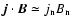 ,
where
,
where 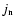 and
and 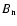 are the components of
are the components of 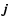 and
and 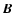 normal to the surface bounding the star. The perturbation of
normal to the surface bounding the star. The perturbation of
 is then conducted into the subsurface layers because
is then conducted into the subsurface layers because 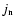 and
and 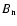 are continuous across the bounding surface.
are continuous across the bounding surface.
According to this scenario, a localized subphotospheric perturbation of
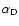 is produced that moves in phase with the planet. A corresponding localized increase in the mean field gradient may promote a magnetic buoyancy instability that leads to the formation of an active region. Note that magnetic buoyancy instability is a threshold process (Acheson 1979), therefore a small increase of the field gradient may be sufficient to trigger the emergence of the magnetic field
already amplified by the stellar dynamo.
is produced that moves in phase with the planet. A corresponding localized increase in the mean field gradient may promote a magnetic buoyancy instability that leads to the formation of an active region. Note that magnetic buoyancy instability is a threshold process (Acheson 1979), therefore a small increase of the field gradient may be sufficient to trigger the emergence of the magnetic field
already amplified by the stellar dynamo.
The active region will rotate with the orbital period of the planet,
although the finite Alfvén travel time across the corona and the finite time scale of magnetic flux emergence may introduce an additional phase lag between the planet and the spot.
- Acheson, D. J.
1979, Sol. Phys., 62, 23 [NASA ADS] [CrossRef]
(In the text)
- Berger, M. A. 1985,
ApJS, 59, 433 [NASA ADS] [CrossRef]
(In the text)
-
Bigazzi, A., & Ruzmaikin, A. 2004, ApJ, 604, 944 [NASA ADS] [CrossRef]
(In the text)
-
Blackman, E. G., & Brandenburg, A. 2003, ApJ, 584, L99 [NASA ADS] [CrossRef]
-
Brandenburg, A. 2005, ApJ, 625, 539 [NASA ADS] [CrossRef]
-
Brandenburg, A. 2007, in Convection in Astrophysics, ed.
F. Kupka, I. Roxburg, & K. L. Chan,
IAU Symp., 239, 457
-
Brandenburg, A., & Subramanian, K. 2005, Phys. Rep., 417,
1 [NASA ADS] [CrossRef]
- Catala, C.,
Donati, J.-F., Shkolnik, E., Bohlender, D., & Alecian, E. 2007,
MNRAS, 374, L42 [NASA ADS]
-
Chandrasekhar, S. 1956, Proc. Natl. Acad. Sci. USA, 42, 1 [NASA ADS] [CrossRef]
(In the text)
- Chandrasekhar, S., &
Kendall, P. C. 1957, ApJ, 126, 457 [NASA ADS] [CrossRef]
(In the text)
- Cranmer,
S. R., & Saar, S. H. 2007
[arXiv:astro-ph/0702530v1
(In the text)
- Cuntz, M.,
Saar, S. H., & Musielak, Z. E. 2000, ApJ, 533, L151 [NASA ADS] [CrossRef]
(In the text)
- Donati,
J.-F., Moutou, C., Farés, R., et al. 2008, MNRAS, 385,
1179 [NASA ADS] [CrossRef]
(In the text)
- Flyer, N.,
Fornberg, B., Thomas, S., & Low, B. C. 2004, ApJ, 606,
1210 [NASA ADS] [CrossRef]
(In the text)
- Harvey,
K. L., & Zwaan, C. 1993, Sol. Phys., 148, 85 [NASA ADS] [CrossRef]
(In the text)
- Henry, G. W.,
Donahue, R. A., & Baliunas, S. L. 2002, ApJ, 577, L111 [NASA ADS] [CrossRef]
(In the text)
- Ip, W.-H., Kopp,
A., & Hu, J.-H. 2004, ApJ, 602, L53 [NASA ADS] [CrossRef]
(In the text)
- McIvor, T.,
Jardine, M., & Holzwarth, V. 2006, MNRAS, 367, L1 [NASA ADS] [CrossRef]
(In the text)
- Moss, D.,
Piskunov, N., & Sokoloff, D. 2002, A&A, 396, 885 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Moutou, C.,
Donati, J.-F., Savalle, R., et al. 2007, A&A, 473,
651 [NASA ADS] [CrossRef] [EDP Sciences]
- Neukirch, T.
1995, A&A, 301, 628 [NASA ADS]
(In the text)
- Preusse,
S., Kopp, A., Büchner, J., & Motschmann, U. 2006, A&A,
460, 317 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Priest, E. R. 1982,
Solar magnetohydrodynamics (Dordrecht: D. Reidel Publ. Co.),
Chap. 6
(In the text)
- Rubenstein,
E. P., & Schaefer, B. E. 2000, ApJ, 529, 1031 [NASA ADS] [CrossRef]
(In the text)
- Saar, S. H.,
Cuntz, M., Kashyap, V. L., & Hall, J. C. 2007
[arXiv:0712.3270v2]
- Santos, N.
C., Udry, S., Mayor, M., et al. 2003, A&A, 406, 373 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
-
Schrijver, C. J., DeRosa, M. L., & Title, A. M. 2003, ApJ, 590,
493 [NASA ADS] [CrossRef]
(In the text)
-
Shkolnik, E., Walker, G. A. H., Bohlender, D. A., Gu, P.-G., &
Kürster, M. 2005, ApJ, 622, 1075 [NASA ADS] [CrossRef]
-
Shkolnik, E., Bohlender, D. A., Walker, G. A. H., & Collier
Cameron, A. 2008, ApJ, 676, 628 [NASA ADS] [CrossRef]
- Smirnov, V. I.
1964, A course of higher mathematics, Vol. III, part II,
Sect. 148 (Oxford: Pergamon Press), 553
- Walker, G.
A. H., Croll, B., Matthews, J. M., et al. 2008, A&A, 482,
691 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Walker, G.
A. H., Matthews, J. M., Kuschnig, R., et al. 2003, PASP, 115,
1023 [NASA ADS] [CrossRef]
(In the text)
-
Wieglmann, T., Neukirch, T., Ruan, P., & Inhester, B. 2007,
A&A, 475, 701 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
Copyright ESO 2008
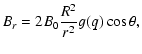
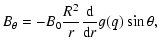
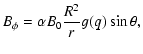
![\begin{displaymath}g (q) \equiv \frac{[b_{0} J_{-3/2}(q) + c_{0} J_{3/2}(q)]\!\s...
...[b_{0} J_{-3/2}(q_{0}) + c_{0} J_{3/2}(q_{0})]\!\sqrt{q_{0}}},
\end{displaymath}](/articles/aa/full/2008/33/aa09753-08/img37.gif)
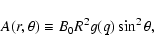
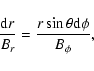
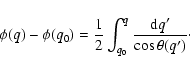
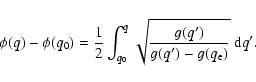
![\begin{figure}
\par\includegraphics[width=8cm,height=12cm]{09753.f1} %\end{figure}](/articles/aa/full/2008/33/aa09753-08/Timg80.gif)
![\begin{figure}
\par\includegraphics[width=8cm,height=6cm]{09753.f2} %\end{figure}](/articles/aa/full/2008/33/aa09753-08/Timg87.gif)
![\begin{figure}
\par\includegraphics[width=8cm,height=16cm,angle=90]{09753.f3} %\end{figure}](/articles/aa/full/2008/33/aa09753-08/Timg94.gif)
![\begin{figure}
\par\includegraphics[width=8cm,height=12cm]{09753.f4} %\end{figure}](/articles/aa/full/2008/33/aa09753-08/Timg102.gif)
![\begin{figure}
\par\includegraphics[width=8cm,height=6cm]{09753.f5} %\end{figure}](/articles/aa/full/2008/33/aa09753-08/Timg108.gif)