A&A 487, 815-830 (2008)
DOI: 10.1051/0004-6361:200809720
T. Pechácek1 - V. Karas1 - B. Czerny2
1 - Astronomical Institute, Academy of Sciences, Bocní II 1401, 14131 Prague, Czech Republic
2 -
Copernicus Astronomical Center, Bartycka 18, 00716 Warsaw, Poland
Received 4 March 2008 / Accepted 19 June 2008
Abstract
Aims. Theory of random processes provides an attractive mathematical tool to describe the fluctuating signal from accreting sources, such as active galactic nuclei and Galactic black holes observed in X-rays. These objects exhibit featureless variability on different timescales, probably originating from an accretion disc.
Methods. We study the basic features of the power spectra in terms of a general framework, which permits semi-analytical determination of the power spectral density (PSD) of the resulting light curve. We consider the expected signal generated by an ensemble of spots randomly created on the accretion disc surface. Spot generation is governed by Poisson or by Hawkes processes. The latter one represents an avalanche mechanism and seems to be suggested by the observed form of the power spectrum. We include general relativity effects shaping the signal on its propagation to a distant observer.
Results. We analyse the PSD of a spotted disc light curve and show the accuracy of our semi-analytical approach by comparing the obtained PSD with the results of Monte Carlo simulations. The asymptotic slopes of PSD are 0 at low frequencies and they drop to -2 at high frequencies, usually with a single frequency break. More complex two-peak solutions also occur. The amplitude of the peaks and their frequency difference depend on the inherent timescales of the model, i.e., the intrinsic lifetime of the spots and the typical duration of avalanches.
Conclusions. At intermediate frequencies, the intrinsic PSD is influenced by the individual light curve profile as well as by the type of the underlying process. However, even in cases when two Lorentzians seem to dominate the PSD, it does not necessarily imply that two single oscillation mechanisms operate simultaneously. Instead, it may well be the manifestation of the avalanche mechanism. The main advantage of our approach is an insight in the model functioning and the fast evaluation of the PSD.
Key words: accretion, accretion disks - black hole physics - galaxies: active - X-rays: binaries
It is widely accepted that massive black holes with accretion discs
reside in cores of active galactic nuclei, where most activity
originates and X-rays are produced (e.g.,
Blandford et al. 1990). The
observed light curves,
![]() ,
show irregular, featureless
fluctuations with a very complex behaviour, practically at every studied
frequency (Gaskell et al. 2006). Variability has been
traditionally analysed by the Fourier method
(Feigelson & Babu 1992). Remarkably, a number of similarities
appear between the properties of massive black holes in galactic nuclei
and those in X-ray binaries, suggesting that some kind of universal
rescaling operates according to central masses of these systems
(Mirabel & Rodríguez 1998). This concerns also the X-ray power spectra
(e.g., Markowitz et al. 2003;
McHardy et al. 2006).
,
show irregular, featureless
fluctuations with a very complex behaviour, practically at every studied
frequency (Gaskell et al. 2006). Variability has been
traditionally analysed by the Fourier method
(Feigelson & Babu 1992). Remarkably, a number of similarities
appear between the properties of massive black holes in galactic nuclei
and those in X-ray binaries, suggesting that some kind of universal
rescaling operates according to central masses of these systems
(Mirabel & Rodríguez 1998). This concerns also the X-ray power spectra
(e.g., Markowitz et al. 2003;
McHardy et al. 2006).
Light curves can be characterised by an appropriate estimator of the
source variability which, in the mathematical sense, is a functional:
![]() .
We accept the idea that the
signal resulting from a spotted accretion disc is intrinsically
stochastic, likely originating from turbulence. Hence,
.
We accept the idea that the
signal resulting from a spotted accretion disc is intrinsically
stochastic, likely originating from turbulence. Hence,
![]() is a random value. It can be a number (for
example, the ``rms'' characteristic), function of a single variable (for
example, the power-spectral density - PSD) or of many variables (e.g.,
poly-spectra, rms-flux relation, etc.). The appropriate choice depends
on the type of information we seek and the quality of data available.
The PSD is a traditional and widely utilised method to examine variable
signals, and the AGN light curves are no exception. A typical signal can be
represented by a broad band PSD with the tendency towards flattening at
low frequency
(Lawrence & Papadakis 1993; Lawrence et al. 1987; Mushotzky et al. 1993; McHardy & Czerny 1987; Uttley et al. 2002).
is a random value. It can be a number (for
example, the ``rms'' characteristic), function of a single variable (for
example, the power-spectral density - PSD) or of many variables (e.g.,
poly-spectra, rms-flux relation, etc.). The appropriate choice depends
on the type of information we seek and the quality of data available.
The PSD is a traditional and widely utilised method to examine variable
signals, and the AGN light curves are no exception. A typical signal can be
represented by a broad band PSD with the tendency towards flattening at
low frequency
(Lawrence & Papadakis 1993; Lawrence et al. 1987; Mushotzky et al. 1993; McHardy & Czerny 1987; Uttley et al. 2002).
There is an ongoing debate about the overall shape of the PSD and the occurrence of the break frequency or, possibly, two break frequencies at which the slope of the PSD can change (Markowitz et al. 2003; Nowak et al. 1999). In the case of a widely-studied Seyfert galaxy, MCG-6-30-15, McHardy et al. (2005) have closely examined the slope of PSD, namely its bending, with RXTE and XMM-Newton data. It is worth noticing that the accurate fits to the X-ray sources seem to exhibit a multi-Lorentzian structure rather than a simple power law. The same is true for the best studied example, the Seyfert 1 galaxy Akn 564 (McHardy et al. 2007).
It was proposed (Abramowicz et al. 1991; Wiita et al. 1992; Zhang & Bao 1991) that hot spots contribute to the variability of the AGN variability, or that they could even be the dominant process shaping the variability pattern. These spots should occur on the disc surface following its intermittent irradiation by localised coronal flares (Merloni & Fabian 2001; Galeev et al. 1979; Czerny et al. 2004). Here, the ``spots'' represent a somewhat generic designation for non-axisymmetric features evolving on the disc surface in connection with flares. They share the bulk orbital motion with the underlying disc. The observed signal is thus modulated by relativistic effects as photons propagate towards a distant observer.
Various schemes have been discussed in which the fluctuations of the disc emissivity at different points of space and time are mutually interconnected in some way. In particular, the avalanche model (Poutanen & Fabian 1999; Zycki & Niedzwiecki 2005; Zycki 2002) seems to be physically substantiated within the framework of magnetically-triggered flares and spots. It is also a promising model capable to reproduce, for example, the broken power-law PSD profiles. Notice, however, that other promising ideas were proposed (e.g., Mineshige et al. 1994; Lyubarskii 1997), provoking the question of whether a common mathematical basis could reflect the entire range of models and provide us with general constraints, independent of (largely unknown) model details.
We add to this model by applying the method of random point processes (Cox & Miller 1965). Interestingly enough, a rather formal approach can provide useful analytical formulae defining the basic form of the expected power spectrum. Apart from this practical aspect, we suggest that the concept discussed here offers much better insight into various influences that shape the expected form the power spectrum. These are very attractive features especially with respect to avalanche models, which may have different flavours, typically with a vast parameter space, thus proving very demanding to examine in a systematic manner.
Even more important is that the adopted formalism provides a very general tool and allows for a broader perspective on different mechanisms of variability (Pechácek & Karas 2007). We develop the idea in a systematic way and give the explicit correspondence between our approach and some of the above-mentioned and widely-known scenarios (Poutanen & Fabian 1999; Abramowicz et al. 1991). This description provides semi-analytical solutions, convenient to search through a broad parameter space. Our results can help to identify how the intrinsic properties of individual flares and the relativistic effects influence the overall PSD. In particular, we can identify those situations in which a doubly-broken power law occurs.
We consider stochastic processes (e.g.,
Feller 1971;
Gardiner 1994)
in the framework appropriate for modelling the accretion disc
variability. In particular, in Sect. 2 we consider
a simple model of a spotted accretion disc
constrained by the following three assumptions about the creation and
evolution of spots: (i) each spot is described by its time and place of
birth (tj, rj and ![]() )
in the plain of the disc; (ii) every
new occurrence starts instantaneously; afterwards, the emissivity decays
gradually to zero (the total radiated energy is of course finite); and
(iii) the intrinsic emissivity is fully determined by a finite set of
parameters which form a vector,
)
in the plain of the disc; (ii) every
new occurrence starts instantaneously; afterwards, the emissivity decays
gradually to zero (the total radiated energy is of course finite); and
(iii) the intrinsic emissivity is fully determined by a finite set of
parameters which form a vector,
![]() ,
defining the
light curve profile. Later on, we will consider the modulation of the
intrinsic emission by the orbital motion and relativistic lensing. The
disc itself has a passive role in our considerations; we will treat it
as a geometrically thin, optically thick layer lying in the equatorial
plane.
,
defining the
light curve profile. Later on, we will consider the modulation of the
intrinsic emission by the orbital motion and relativistic lensing. The
disc itself has a passive role in our considerations; we will treat it
as a geometrically thin, optically thick layer lying in the equatorial
plane.
Because of the apparently random nature of the variability, we adopt a stochastic model in which the creation of spots is governed by a random process. The assumption that spots are mutually statistically independent seems to be a reasonable (first) approximation, however, we find that we do need to introduce some kind of relationship between them. This connection is discussed in Sect. 3. The statistical dependence among spots can be introduced in several ways. In Sect. 4, we explore in detail the specific models of interrelated spots using the formalism of Hawkes-type processes. Conclusions are summarised in Sect. 5. Finally, in the Appendix we provide some mathematical prerequisites, which the reader may find useful to understand the general background of the paper, and we also summarise the mathematical notation.
We will apply our investigations to models where the signal is produced
by point-like orbiting spots (circular Keplerian motion along the
azimuthal ![]() direction). The intrinsic emission, produced in the
local co-orbiting frame of the spot, is influenced by the Doppler effect and
gravitational lensing, which cannot be ignored at typical distances
of several units or tens of gravitational radii. Photons emitted at
different moments and positions experience different light-travel time
on the way towards the observer, so the observed timing properties
should reflect this specific modulation. We adopt the Schwarzschild
metric for the gravitational field and employ the method of transfer
function (Pechácek et al. 2006,2005) to describe the
light amplification (or dilution);
direction). The intrinsic emission, produced in the
local co-orbiting frame of the spot, is influenced by the Doppler effect and
gravitational lensing, which cannot be ignored at typical distances
of several units or tens of gravitational radii. Photons emitted at
different moments and positions experience different light-travel time
on the way towards the observer, so the observed timing properties
should reflect this specific modulation. We adopt the Schwarzschild
metric for the gravitational field and employ the method of transfer
function (Pechácek et al. 2006,2005) to describe the
light amplification (or dilution);
![]() is inclination angle
of the observer (
is inclination angle
of the observer (
![]() deg corresponds the edge-on view of
the disc plane). The periodical modulation of the observed signal is
included in the transfer function
deg corresponds the edge-on view of
the disc plane). The periodical modulation of the observed signal is
included in the transfer function
![]() .
An implicit relation holds for the phase,
.
An implicit relation holds for the phase,
| (1) |
In the case of an infinitesimal surface element with intrinsically
constant and isotropic emissivity I, orbiting with Keplerian orbital
frequency ![]() ,
the flux measured by a distant observer varies
just as F changes along the orbit.
,
the flux measured by a distant observer varies
just as F changes along the orbit.
We remind the reader that the mass of central black holes in galactic
nuclei is in the range of ![]()
![]() Mass
of the accretion disc is at least three orders of magnitude smaller than
the black hole mass, so we neglect it in our calculations (the accretion
disc self-gravity may be important for its intrinsic structure, but the
direct gravitational effect on light is quite small;
Karas et al. 1995). Hence,
the gravitational field can indeed be described by a vacuum black-hole
spacetime (Misner et al. 1973). We use geometrical units with
c=G=1. Transformation to physical scales can be achieved when the mass
of the central black hole is specified because Keplerian frequency
scales inversely with the gravitational radius. The gravitational radius
of a massive black hole is
Mass
of the accretion disc is at least three orders of magnitude smaller than
the black hole mass, so we neglect it in our calculations (the accretion
disc self-gravity may be important for its intrinsic structure, but the
direct gravitational effect on light is quite small;
Karas et al. 1995). Hence,
the gravitational field can indeed be described by a vacuum black-hole
spacetime (Misner et al. 1973). We use geometrical units with
c=G=1. Transformation to physical scales can be achieved when the mass
of the central black hole is specified because Keplerian frequency
scales inversely with the gravitational radius. The gravitational radius
of a massive black hole is
![]() pc, and the corresponding
characteristic time-scale is
pc, and the corresponding
characteristic time-scale is
![]() s, where the mass
s, where the mass
![]() .
All lengths and times can be made dimensionless by
expressing them in units of M, so they can be easily scaled to
different masses. For example, for the Keplerian orbital period we
obtain
.
All lengths and times can be made dimensionless by
expressing them in units of M, so they can be easily scaled to
different masses. For example, for the Keplerian orbital period we
obtain
![]() ,
where the radius
is expressed in units of
,
where the radius
is expressed in units of ![]() and
and
![]() is given in
seconds.
is given in
seconds.
Let us note that the intrinsic timescales of the spot evolution and of avalanches (both timescales will be discussed below) need not to be directly connected with the Keplerian orbital period. This internal freedom of the model can help to bring the predicted frequency of the breaks of the PSD profile in agreement with the data.
Now we will describe the process of the creation of spots from the
statistics point of view. Let us consider a signal of the form
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9720fig1}\end{figure}](/articles/aa/full/2008/33/aa09720-08/Timg64.gif) |
Figure 1:
Illustrating
the correspondence between the ignition moments of the elementary
events and the resulting light curve. The model is fully determined by a
set of points in ( |
| Open with DEXTER | |
Quantities
![]() ,
tj, rj,
,
tj, rj,
![]() and
and
![]() are random values. The vector
are random values. The vector
![]() determines the duration and shape of each event (tj is time of
ignition; parameter
determines the duration and shape of each event (tj is time of
ignition; parameter
![]() determines the initial phase of the
periodical modulation of the jth event; and
determines the initial phase of the
periodical modulation of the jth event; and
![]() is the
corresponding initial time-offset). These assumptions bring the
formulation of the problem close to the framework studied by Brémaud
et al. (2002, 2005). We will
calculate the power spectrum of this process directly from
Eq. (A.10) in the Appendix.
is the
corresponding initial time-offset). These assumptions bring the
formulation of the problem close to the framework studied by Brémaud
et al. (2002, 2005). We will
calculate the power spectrum of this process directly from
Eq. (A.10) in the Appendix.
We remark that for the amplitudes of individual events we assume the identical values (at each given radius). This restriction is imposed only for the sake of definiteness of our examples; the formalism can deal with a distribution of amplitudes. Indeed, we do not impose any serious constraint on the model because the information about the level of the fluctuating signal can be adjusted by setting the frequency of the events (Lehto 1989). A simple demonstration of this concept is shown in Fig. 1. This plot illustrates how the model light curve arises from the elementary components. Naturally, we can approach such decomposition from another angle, by investigating how the total light curve can be expressed in terms of some basic profile. It is important to realise that, for the purposes of our present paper, light curves are of secondary importance. Instead, our calculations allow us to proceed from the distribution of the onset times and the characteristics of individual flares directly to the power spectral density, which stands as the primary characteristic of the source signal.
Equation (2) represents a very general class of random
processes. By applying the Fourier transform, we find
= \frac{2\sin(T\omega)}{\omega...
...{F}\big[I(t-{\delta_j},~\vec{\xi}_j)
\;F(t-\delta_{{\rm p}j},r_j)\big](\omega),$](/articles/aa/full/2008/33/aa09720-08/img67.gif) |
(3) |
| (4) |
Knowing the incomplete Fourier transform of f(t), we can calculate
its squared absolute value and perform the averaging over all
realisations of the process. This can be simplified by assuming
that every single event quickly decays. In principle, between -T and Tthe process is influenced by all events ignited during the whole
interval
![]() ,
however, because of
the fast decay of the events, the interval can be restricted to
,
however, because of
the fast decay of the events, the interval can be restricted to
![]() ,
where C is a sufficiently large positive
constant. In other words, every realisation of the process f(t) on
,
where C is a sufficiently large positive
constant. In other words, every realisation of the process f(t) on
![]() can be described by a set of points in
(k+4)-dimensional space
can be described by a set of points in
(k+4)-dimensional space
![]() with
with
![]() .
.
Values of the initial time delay and phase are functions of initial
position of each spot, i.e.
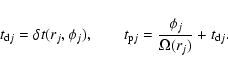 |
(5) |
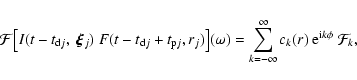 |
(6) |
Defining the function
\big\vert^2
=\Big\vert\sum\limits_j s(t_j,~\phi_j,~r_j, ~\vec{\xi}_j;~\omega)\Big\vert^2.
\end{displaymath}](/articles/aa/full/2008/33/aa09720-08/img82.gif) |
(8) |
| (10) |
To start with a simple example, we assume mutually independent events
with uniformly distributed ignition times. In other words, in this
subsection we assume that there is no relationship among different spots
- neither in their position nor in the time of birth (spots are
statistically-independent). The intensity and the second-order measure
are
Let us consider box-shaped events with exponentially-distributed
life-times, i.e.,
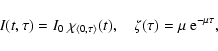 |
(15) |
Coefficients ck(r) are given by the relation
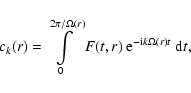 |
(17) |
| |
= | 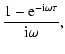 |
(18) |
| = | 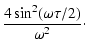 |
(19) |
| |
= | \Big\vert^2$](/articles/aa/full/2008/33/aa09720-08/img109.gif) |
|
| (20) |
The assumption that spots are statistically independent seems to be a reasonable (first) approximation. However, the actual ignition times and spot parameters should probably depend on the history of a real system. The statistical dependence among spots can be introduced in several ways. In this section we discuss different models where an existing spot gives, with a certain probability, birth to new spots. In this way a single spot at the beginning can trigger a whole avalanche of its offsprings. This avalanche can be in principle of arbitrary length, although, to obtain an infinitely long avalanche with non-diverging rate of new spots one would have to fine-tune the parameters. In order to avoid the unlikely fine-tuning and to obtain a stationary process, we will assume the occurrence of many spontaneous spots distributed by the Poisson process that keeps triggering new avalanches of finite duration.
The first example can be called ``Chinese process''. By definition, an
existing spot gives birth to exactly one new spot with probability
![]() .
In other words, every event produces at most one
offspring. The spot of the kth generation is always ignited later than
the spot of the (k-1)th generation. As mentioned above, spontaneous
spots arise randomly, according to Poissonian process. In the simplest
version of this model, delays between the parent spot and its lineal
descendant are random values obeying the probability density p(t).
.
In other words, every event produces at most one
offspring. The spot of the kth generation is always ignited later than
the spot of the (k-1)th generation. As mentioned above, spontaneous
spots arise randomly, according to Poissonian process. In the simplest
version of this model, delays between the parent spot and its lineal
descendant are random values obeying the probability density p(t).
| |
Figure 2: Distinguishing between the Chinese process a) and the Hawkes processes b). In both panels, points represent ignition times of the spots. Each sequence starts with a spontaneously generated parent spot (open circles) and it continues with subsequent secondary ones (filled circles). Arrows symbolise the parent-daughter relation. The difference between the two scenarios is described in Sects. 4.1 and 4.2, respectively. Within the schematic level of this graph, the pulse avalanche process (see Sect. 4.3) belongs also to case b). |
| Open with DEXTER | |
More generally, every spot can deliver n new spots, where
n is a random value with Poisson distribution and the mean ![]() .
We
describe this situation in terms of (i) standard Hawkes' process; and
(ii) the pulse avalanche model. The temporal distribution of new spots
is now governed either by the function
.
We
describe this situation in terms of (i) standard Hawkes' process; and
(ii) the pulse avalanche model. The temporal distribution of new spots
is now governed either by the function ![]() of the Hawkes' process
(Hawkes 1971), or
of the Hawkes' process
(Hawkes 1971), or
![]() in the case of avalanches
(Poutanen & Fabian 1999). Spots of different generations can appear
at the same time.
in the case of avalanches
(Poutanen & Fabian 1999). Spots of different generations can appear
at the same time.
The difference between the Chinese process and the latter two processes is schematically sketched in Fig. 2. Mathematically, all three examples belong to the class of cluster processes.
Point processes are characterised by the generating functional,
![]() ,
which is defined by its action (Daley & Vere-Jones 2003)
,
which is defined by its action (Daley & Vere-Jones 2003)
The functional
![]() satisfies various relations which can be derived
in close analogy with the theory of generating functions of random variables.
For our purposes it will be useful to expand
satisfies various relations which can be derived
in close analogy with the theory of generating functions of random variables.
For our purposes it will be useful to expand
![]() into a series in terms
of factorial measures,
into a series in terms
of factorial measures,
Let
![]() be the generating functional of a cluster
with the center at y,
be the generating functional of a cluster
with the center at y,
![\begin{displaymath}\mathcal{G}\big[h(x)\big]={\rm E}\Big[\int\limits_{\mathcal{X}}
\mathcal{G}\big[h(x)~\vert~y\big]~N_{\rm c}({\rm d}y)\Big].
\end{displaymath}](/articles/aa/full/2008/33/aa09720-08/img122.gif) |
(23) |
| (29) |
![\begin{displaymath}\breve{m}_{[2]}(u)=\lambda\int\limits_\mathcal{X}m_{[2]}(y,y+u~\vert~0)~{\rm d}y + m^2_1.
\end{displaymath}](/articles/aa/full/2008/33/aa09720-08/img132.gif) |
(30) |
The second-order measure of a marked cluster process is
![\begin{displaymath}S_{\rm P}(\omega)=\lambda~\tilde{m}_{[2]}(\omega,-\omega~\vert~0),
\end{displaymath}](/articles/aa/full/2008/33/aa09720-08/img141.gif) |
(35) |
![\begin{displaymath}\tilde{m}_{[2]}
(\omega,\omega'~\vert~0)
=\int\limits_{{\math...
...x_2\omega')}
m_{[2]}(x_1,\ x_2~\vert~0)~{\rm d}x_1~{\rm d}x_2.
\end{displaymath}](/articles/aa/full/2008/33/aa09720-08/img142.gif) |
(36) |
Until now the variability patterns have been restricted only by very
general properties of the assumed process. This means that the model is
kept in a very general form. However, formulae (14) and (33) are too general for any practical use. Their main value
is after defining special cases. Then these formulae can be readily
applied to derive the analytical form of the PSD. Such special cases are
conveniently defined by means of marks. We discuss possible choices of
the mark distribution,
![]() .
.
We can simplify the situation by assuming axial symmetry. Therefore, all
statistical properties should depend only on the radius (the azimuthal
part of G is constant). The distribution of marks has now the form
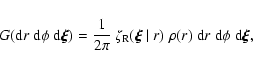 |
(37) |
Let n(r) be an average number of spots at radius r, each of them
shining with the average intensity
![]() for
average duration
for
average duration
![]() .
Let us further assume that
these characteristics scale with the radius as power laws:
.
Let us further assume that
these characteristics scale with the radius as power laws:
| (40) |
| (44) |
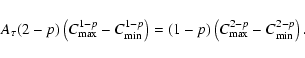 |
(45) |
| (46) |
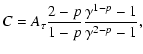 |
(47) | ||
| (48) |
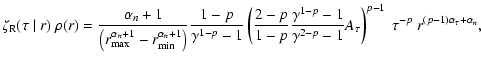 |
(49) |
| (50) |
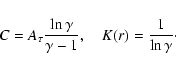 |
(51) |
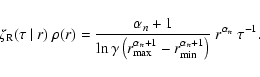 |
(52) |
![\begin{displaymath}d_n(r)=\frac{1}{2\pi}\int\limits_0^{2\pi}
{\rm e}^{{\rm i}n[\phi+\Omega(r)\delta t(r,~\phi)]}~
{\rm d}\phi,
\end{displaymath}](/articles/aa/full/2008/33/aa09720-08/img170.gif) |
(53) |
Let us denote ![]() the probability that an existing spot generates a
new one, and qk the probability that a family of spots consists of
exactly k members. The value qk obeys the geometrical distribution,
the probability that an existing spot generates a
new one, and qk the probability that a family of spots consists of
exactly k members. The value qk obeys the geometrical distribution,
![]() .
.
We interpret probability density p(t) of the delay between successive
spots as a mean number of first-generation spots that occur at the
ignition time t>0, where t=0 is a moment of ignition of the parent
spot. Analogically,
![]() is the mean number of
second-generation spots. For a sequence of k spots, we obtain the
intensity measure
is the mean number of
second-generation spots. For a sequence of k spots, we obtain the
intensity measure
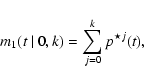 |
(56) |
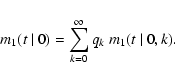 |
(57) |
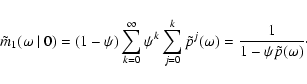 |
(58) |
Calculation of the quadratic measure is a less intuitive procedure. We
start from the generating functional (21) of the
process,
![\begin{displaymath}\mathcal{G}\left[h(t)~\vert~0\right]=\sum\limits_{l=0}^\infty q_l~ h(0)~\mathcal{G}_l[h(t)],
\end{displaymath}](/articles/aa/full/2008/33/aa09720-08/img187.gif) |
(61) |
Substituting
![]() in the expansion (22), we
obtain the Fourier image
in the expansion (22), we
obtain the Fourier image
![\begin{displaymath}\tilde{m}_{[2]}(\omega,\omega'~\vert~0)\!
=\!\frac{\psi\big[\...
...}(\omega')\big]\big[1-\psi\tilde{p}(\omega+\omega')\big]}\cdot
\end{displaymath}](/articles/aa/full/2008/33/aa09720-08/img190.gif) |
(62) |
![\begin{figure}
\par\includegraphics[width=14.5cm,clip]{9720fig3.eps}\end{figure}](/articles/aa/full/2008/33/aa09720-08/Timg195.gif) |
Figure 3:
Power spectra from the spot model in which the birth
and duration of spots are governed by the market Hawkes process with
the exponential infectivity (76). Values of |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14.5cm,clip]{9720fig4.eps}\end{figure}](/articles/aa/full/2008/33/aa09720-08/Timg197.gif) |
Figure 4:
Graphs of the model PSD as in the previous figure, but for
the case of Hawkes process with the power law infectivity (80).
Parameter values |
| Open with DEXTER | |
Hawkes' process (Brémaud & Massoulié 2002; Hawkes 1971) is more complicated
than the previous example because it consists of two types of events.
First, new spots are generated by the Poisson process operating with
intensity ![]() (let us denote t0 the moment of ignition).
Second, an existing spot can give birth to new one at a later time, t,
according to the Poisson process with varying intensity
(let us denote t0 the moment of ignition).
Second, an existing spot can give birth to new one at a later time, t,
according to the Poisson process with varying intensity
![]()
![]() .
.
The mean number of events is
The generating functional of the cluster of the Hawkes process fulfils
the integral equation,
![\begin{displaymath}\mathcal{G}\big[h(x)~\vert~0\big]
=h(0)\exp\Big\{\!-\!\int\li...
...hcal{G}\left[h(x)~\vert~y\right]\right)~\mu(y)~{\rm d}y\Big\}.
\end{displaymath}](/articles/aa/full/2008/33/aa09720-08/img205.gif) |
(69) |
| |
= | 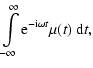 |
(72) |
| = | ![$\displaystyle \int\limits_{-\infty}^{\infty} {\rm e}^{ -{\rm i}\omega t}m_{[1]}(t~\vert~0)~{\rm d}t
=\frac{1}{1-\tilde{\mu}(\omega)}\cdot$](/articles/aa/full/2008/33/aa09720-08/img213.gif) |
(73) |
![\begin{displaymath}\tilde{m}_{[2]}(\omega,\omega'~\vert~0)
=\frac{\tilde{m}_{[1]...
...ilde{m}_{[1]}(\omega'~\vert~0)-1}
{1-\mu(\omega+\omega')}\cdot
\end{displaymath}](/articles/aa/full/2008/33/aa09720-08/img214.gif) |
(74) |
![\begin{displaymath}S_{\rm\! P}(\omega)=\lambda~\frac{\vert\tilde{m}_{[1]}(\omega~\vert~0)\vert^2-1}{1-\nu}\cdot
\end{displaymath}](/articles/aa/full/2008/33/aa09720-08/img215.gif) |
(75) |
For the exponential form of infectivity measure,
Figure 3 shows the resulting PSD of this model in a logarithmic
plot of
![]() versus
versus ![]() .
Here we can study the occurrence
of break frequency where the PSD slope changes depending on the model
parameters.
Light curve profiles of individual spots were chosen as exponentials,
.
Here we can study the occurrence
of break frequency where the PSD slope changes depending on the model
parameters.
Light curve profiles of individual spots were chosen as exponentials,
![]() ,
where
,
where
![]() is random value with probability density
is random value with probability density
![]() and the
mean
and the
mean
![]() .
The
characteristic time of infectivity,
.
The
characteristic time of infectivity,
![]() ,
is set to be
,
is set to be
![]() .
In general, we can identify two
characteristic frequencies in the PSD. The first one corresponds to the
characteristic frequency of the profile I(t) (in our case this
frequency is given by
.
In general, we can identify two
characteristic frequencies in the PSD. The first one corresponds to the
characteristic frequency of the profile I(t) (in our case this
frequency is given by
![]() ), the second one is given by
the characteristic frequency of the avalanches (
), the second one is given by
the characteristic frequency of the avalanches (
![]() ).
).
We remind the reader that this plot (as well as the subsequent Figs. 4-6) does not include general relativity
effects; they will be recovered later in the paper. This is merely to
simplify calculations - the relativistic effects complicate the
derivation of the analytical formula for the PSD and it is somewhat
difficult to distinguish them from the intrinsic properties of the
signal.
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{9720fig5.eps}\end{figure}](/articles/aa/full/2008/33/aa09720-08/Timg229.gif) |
Figure 5:
Decomposition
of the total PSD curve,
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14.5cm,clip]{9720fig6.eps}\end{figure}](/articles/aa/full/2008/33/aa09720-08/Timg231.gif) |
Figure 6:
The pulse avalanche model for the uniform probability density
|
| Open with DEXTER | |
Another natural choice of infectivity is a power-law function of the form
We note that the characteristic times ![]() and
and ![]() ,
as defined in Eq. (67), diverge for the
infectivity (80) and
,
as defined in Eq. (67), diverge for the
infectivity (80) and
![]() .
In this case,
.
In this case, ![]() does not exist. Again, we derive an analytical form of the PSD for the
adopted infectivity function. The procedure is entirely analogical as
above, but we do not give the explicit form of
does not exist. Again, we derive an analytical form of the PSD for the
adopted infectivity function. The procedure is entirely analogical as
above, but we do not give the explicit form of
![]() because the final formula is rather complicated.
The resulting PSD curves with the power-law infectivity
are plotted in Fig. 4.
because the final formula is rather complicated.
The resulting PSD curves with the power-law infectivity
are plotted in Fig. 4.
It is also interesting to note at this point, how the peaks of the PSD
move when the model parameters are shifted. For example, see the panel
![]() of Fig. 3. Although in this case the two timescales
are equal to each other, changing the other parameter,
of Fig. 3. Although in this case the two timescales
are equal to each other, changing the other parameter, ![]() ,
from 0.1 to 0.99 brings the peak over two orders of magnitude. In other
words, the maximum of the PSD can appear at a frequency lower than the
inverse of the spot decay time. The frequency shift of the peaks
is again given by factor
,
from 0.1 to 0.99 brings the peak over two orders of magnitude. In other
words, the maximum of the PSD can appear at a frequency lower than the
inverse of the spot decay time. The frequency shift of the peaks
is again given by factor
![]() ,
as explained in
Eq. (79).
,
as explained in
Eq. (79).
In order to understand better the behaviour of the PSD peaks, we rewrite
Eq. (33) in the form
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{9720fig7.eps}\end{figure}](/articles/aa/full/2008/33/aa09720-08/Timg250.gif) |
Figure 7:
Upper panels: power spectra from the Poisson-driven spot model,
calculated for a thin accretion disc extending between radii r=6 M and
r=100 M (in geometrical units), for three inclinations
|
| Open with DEXTER | |
The pulse avalanche model was discussed in the context of various astronomical objects whose light curves exhibit signs of stochastic behaviour. They are, namely, gamma-ray bursting sources (Stern & Svensson 1996). As a framework to describe the timing characteristics of accreting black holes, the model was studied by Poutanen & Fabian (1999). Details of the process are different in those two papers and our description is closer to the latter one.
The basic properties of the pulse avalanche model can be summarised as
follows. (i) The observed signal consists of pulses of the form
![]() ,
where
,
where ![]() is their
characteristic duration. (ii) Each pulse gives birth to b baby pulses;
the number of baby pulses varies, obeying the Poisson distribution
is their
characteristic duration. (ii) Each pulse gives birth to b baby pulses;
the number of baby pulses varies, obeying the Poisson distribution
![]() with the mean value
with the mean value ![]() .
(iii) The baby
pulses are delayed with respect to the parent ones by
.
(iii) The baby
pulses are delayed with respect to the parent ones by ![]() ,
which
is a random value with exponential distribution,
,
which
is a random value with exponential distribution,
![]() .
(iv) Some pulses
occur spontaneously, according to the Poisson process operating at the
mean rate
.
(iv) Some pulses
occur spontaneously, according to the Poisson process operating at the
mean rate ![]() .
Finally, (v) temporal constants,
.
Finally, (v) temporal constants, ![]() ,
for all
pulses are mutually independent and drawn from the same distribution
function,
,
for all
pulses are mutually independent and drawn from the same distribution
function,
![]() .
Such a process is clearly of the form (2).
.
Such a process is clearly of the form (2).
The underlying point process is a cluster process operating on the set
![]() with properties similar to the Hawkes process. (In fact, we will see below that
the Hawkes process can be considered as a special case of the pulse avalanche
process.) The center process is the Poissonian one, and its intensity is
with properties similar to the Hawkes process. (In fact, we will see below that
the Hawkes process can be considered as a special case of the pulse avalanche
process.) The center process is the Poissonian one, and its intensity is
![]() .
The clusters are driven by the
Poissonian branching process (Cox & Miller 1965) with the parameter measure
.
The clusters are driven by the
Poissonian branching process (Cox & Miller 1965) with the parameter measure
| |
= | 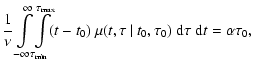 |
|
| = | 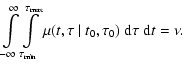 |
(85) |
The resulting functions
![]() and
and
![]() are
complicated and their inverse Fourier transforms can be directly found
only in very special cases, e.g. by assuming
are
complicated and their inverse Fourier transforms can be directly found
only in very special cases, e.g. by assuming
![]() .
In that case the pulse avalanche model is transformed into the Hawkes process
with the exponential infectivity measure.
.
In that case the pulse avalanche model is transformed into the Hawkes process
with the exponential infectivity measure.
Fortunately, we do not need the explicit form of the moments to find the
final formula for the PSD. This result is provided by
Eq. (33) with
| (87) |
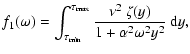 |
(88) | ||
![$\displaystyle f_2(\omega)=\Big[1-\int_{\tau_{\rm min}}^{\tau_{\rm max}}\frac{\nu\zeta(y)}{1+{\rm i}\alpha\omega y}~{\rm d}y\Big]^{-1}.$](/articles/aa/full/2008/33/aa09720-08/img268.gif) |
(89) |
![\begin{figure}
\par\includegraphics[width=16.7cm,clip]{9720fig8.eps}\end{figure}](/articles/aa/full/2008/33/aa09720-08/Timg270.gif) |
Figure 8:
The analytical curves of the PSD profiles are plotted, with
relativistic effects included. In order to allow comparison with
previous figures, we selected appropriate combinations of the model
parameters: the infectivity |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{9720fig9.eps}\end{figure}](/articles/aa/full/2008/33/aa09720-08/Timg271.gif) |
Figure 9:
The ratio
|
| Open with DEXTER | |
Relativistic effects influence the photon energy in the course of light propagation through the curved spacetime, towards a distant observer. In this paper we consider only the energy-integrated light curves, but even those are affected because the energy shifts modify the observed flux level. Furthermore, light rays are bent as they pass near the black hole, causing the light-focusing effect. In consequence the observed light curves differ from their intrinsic profiles produced at the point of emission, and this further complicates the decomposition of the PSD spectrum into elementary components. Therefore, in general the power spectrum cannot be rigorously expressed as a combination of Lorentzians. However, in most circumstances the relativistic effects are not very prominent - only a small fraction of rays passing very close to the black hole horizon and those crossing the caustics are affected. One expects that they cannot be ignored if the accretion disc extends down to the innermost stable orbit or if some non-negligible emission arises below that orbit. Also, high-inclination objects are affected more because in those cases the disc is seen edge-on and the intrinsic fluctuations of the emission are considerably amplified.
Exemplary power spectra, including the relativistic effects are modelled
in Fig. 7 where the numerical simulation is compared with
the analytical result. The upper panels assume that orbiting spots are
generated by Poissonian process; the lower ones show the PSD derived
from Eq. (33). The assumed radial distribution of the spots
was
![]() ,
where
,
where ![]() is
normalisation constant. It turns out that the relativistic effects
influence the final PSD especially at high frequencies
and high inclinations.
is
normalisation constant. It turns out that the relativistic effects
influence the final PSD especially at high frequencies
and high inclinations.
We remind the reader that frequencies in these plots are given in
geometrical units (in physical units frequencies scale inversely with
the mass of the black hole). We notice that a high-frequency part of the
spectrum decays as
![]() ,
whereas the
break occurs towards lower frequencies. These plots
provide us with graphical comparisons between the analytical form and
the corresponding results of numerical simulations. We note that
the adopted approximation of relativistic effects
(Pechácek et al. 2005) holds for moderate inclination
(
,
whereas the
break occurs towards lower frequencies. These plots
provide us with graphical comparisons between the analytical form and
the corresponding results of numerical simulations. We note that
the adopted approximation of relativistic effects
(Pechácek et al. 2005) holds for moderate inclination
(![]() 70 deg). It loses accuracy when the view angle becomes almost
edge-on, although the main trend of the PSD remains unchanged.
70 deg). It loses accuracy when the view angle becomes almost
edge-on, although the main trend of the PSD remains unchanged.
The main advantage of the analytical method is, obviously, in the possibility of obtaining a general form of the PSD, including the relativistic effects. We are ale to search systematically through the vast parameter space of different models for which the model PSD can be explored across a wide range of frequencies. We take the advantage of this approach and plot variety of profiles in Fig. 8. Here, we omit the numerically-simulated curves of the previous figure, so the entire graph is constructed very efficiently. We assumed that spots are generated by the Hawkes mechanism.
Basic trends of the PSD shape are readily recognised. In particular,
the curves have either one or two maxima, prominence and position of
which changes with parameters. Notice, for example, the bottom right
panel in which the PSD is almost flat over several decades of frequency,
well below the typical orbital frequency in the disc (vertical lines
denote the Keplerian frequencies at the edges of the assumed spot
distribution). The flattish part of the spectrum can be extended further,
to lower frequencies, by enlarging the ![]() parameter towards unity,
i.e., by protracting the sequence of avalanches. Next, for large
inclinations we notice that relativistic effects produce a
prominent bump. This feature occurs near the orbital frequency of the
inner disc. Relativistic effects are the main cause of differences
between this figure and Fig. 3, in which those effects were
neglected.
parameter towards unity,
i.e., by protracting the sequence of avalanches. Next, for large
inclinations we notice that relativistic effects produce a
prominent bump. This feature occurs near the orbital frequency of the
inner disc. Relativistic effects are the main cause of differences
between this figure and Fig. 3, in which those effects were
neglected.
As already mentioned, general relativity affects mainly the
high-frequency domain of the PSD, around the orbital frequency of the
inner disc, where it adds power to the observed PSD. In physical units
the relevant frequency generated at radius r is
![]() [Hz]. On
the other hand, it does not influence the middle part of the spectrum,
i.e. at frequency
[Hz]. On
the other hand, it does not influence the middle part of the spectrum,
i.e. at frequency ![]()
![]() ,
neither it changes the asymptotical form at far ends of the frequency
range (where the PSD decays as power law). It has been argued that the
additional signal is actually not present in the data of MCG-6-30-15
(Zycki & Niedzwiecki 2005), although the light curve from the long
observation should reveal some excess. However, the situation here is
more complex because of the avalanches contributing power to lower
frequencies. In fact, our model predicts rather weak enhancement near
the inner edge orbital frequency - unless the inclination is almost
edge-on (which is unlikely). More power is therefore typically expected
at moderate frequencies, lower than the inner-edge orbital frequency.
,
neither it changes the asymptotical form at far ends of the frequency
range (where the PSD decays as power law). It has been argued that the
additional signal is actually not present in the data of MCG-6-30-15
(Zycki & Niedzwiecki 2005), although the light curve from the long
observation should reveal some excess. However, the situation here is
more complex because of the avalanches contributing power to lower
frequencies. In fact, our model predicts rather weak enhancement near
the inner edge orbital frequency - unless the inclination is almost
edge-on (which is unlikely). More power is therefore typically expected
at moderate frequencies, lower than the inner-edge orbital frequency.
In order to see at which frequencies the relativistic effects are
most important, we construct the ratio
![]() of
the PSD calculated with (denoted by superscript ``gr'') and without
(``cl'') these effects taken into account:
of
the PSD calculated with (denoted by superscript ``gr'') and without
(``cl'') these effects taken into account:
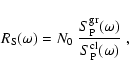 |
(90) |
We adopted the viewpoint that the variability pattern is determined by the interplay among the bulk orbital motion, relativistic effects, and the intrinsic changes of the inner accretion disc. We concentrated our attention solely on the PSD characteristics. The spots have a certain kind of memory in our model.
We gave several examples in which the PSD changes the slope and certain break frequencies. The frequency of the break depends on the interplay of model properties, i.e., the intrinsic form of the spot light curves, which determine the individual contributions to the total signal together with the avalanche mechanism. The location of spots on the disc and the inclination of the source define the importance of relativistic effects.
In some cases, a double break occurs and the overall PSD profile is then approximated by a broken power law. This is a promising feature in view of applications to real sources with accreting black holes. The broken power-law profile either resembles a combination of the Lorentzians or, in some cases, an intermediate power law develops and connects the two peaks across the middle frequencies. The change of the PSD slope is clearly visible and well-defined in some cases, though under most circumstances it appears rather blurry. The low-frequency limit of the PSD slope is a constant; the-high frequency behaviour depends mainly on the shape of the spot emission profile, including the general relativity effects. In our calculations the emissivity was decaying exponentially and the slope of the PSD was equal to -2 at high frequencies. In between those two limits the intrinsic PSD is influenced by both the individual light curve profile and the underlying process.
It is interesting to notice that the doubly-broken power law occurs only for certain assumptions about the intrinsic light curves of the individual spots or avalanches - their onset and the decay; in other cases the break frequencies are not well defined, or the broken power-law PSD is not preferred at all. We stress that if two Lorentzian seem to dominate the PSD (i.e., two peaks show up), it still does not necessarily mean that two single oscillation mechanisms operate simultaneously. Instead, it may well be the manifestation of the avalanche mechanism.
We employed a general statistical approach to the variability of a black hole accretion disc with orbiting spots that continuously arise and decay. The origin and evolution of spots were described by Poissonian and Hawkes' processes, the latter one representing a category of avalanche models. We derived analytical formulae for the PSD, Eqs. (14) and (33), and we discussed their limitations and accuracy. The main advantage of the analytical form is the insight into the properties and the fast evaluation that captures the main trends of the PSD shape.
It is worth noting that the PSD does not maintain all information about the light curves that can be studied by Fourier methods (Vio et al. 1992). Extensions have been discussed and compared with real data (Vaughan & Uttley 2008; Krolik et al. 1993; Karas 1997; Nowak et al. 1999), but this would go beyond the scope of our present work.
Our approach allows us to investigate the influence of the assumed mechanism, which describes the creation of parent spots and of subsequent cascades of daughter spots. In particular, we can discuss the PSD slope at different frequency ranges and locate the break frequencies depending on the model parameters. The relationship between the mathematical nature of the process and the PSD of the resulting signal is an interesting consequence of this investigation, as it provides a way to grasp and rigorously constrain the physical models of the source. Therefore we believe that the method that we described is very helpful for identifying the underlying mechanisms that shape the PSD in black hole accreting sources.
Acknowledgements
We thank Dr. L. Subr for helpful comments. We appreciate the continued support from research grants of the Academy of Sciences (ref. 300030510) and of the Czech Science Foundation (ref. 202/06/0041). Part of this work was supported via the ESA Plan for European Cooperating States (98040). V.K. is a member of the Center for Theoretical Astrophysics in Prague, LC06014.
In this Appendix, we briefly introduce the formal mathematical approach and
notation used throughout the paper. We employ the concept of random
values on probability space,
![]() (Kolmogorov 1950; Cox & Miller 1965), where
(Kolmogorov 1950; Cox & Miller 1965), where ![]() is the sample space
(i.e., the set of all possible outcomes of an experiment),
is the sample space
(i.e., the set of all possible outcomes of an experiment), ![]() denotes the
denotes the ![]() -algebra on
-algebra on ![]() ,
and P is non-negative,
,
and P is non-negative,
![]() -additive measure satisfying conditions
-additive measure satisfying conditions
![]() ,
,
![]() .
It is usually assumed on physical grounds that real
signals satisfy all mathematical prerequisites.
.
It is usually assumed on physical grounds that real
signals satisfy all mathematical prerequisites.
A real random value is a map X from ![]() to real numbers,
to real numbers,
![]() .
The distribution function F(x) and the probability density function
f(x) are then defined by
.
The distribution function F(x) and the probability density function
f(x) are then defined by
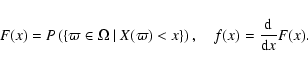 |
(A.1) |
![\begin{displaymath}{\rm E}\big[g(X)\big]=\int\limits_{\mathbb{R}}g(x)~F({\rm d}x)
=\int\limits_{\mathbb{R}}g(x)~f(x)~{\rm d}x.
\end{displaymath}](/articles/aa/full/2008/33/aa09720-08/img289.gif) |
(A.2) |
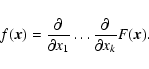 |
(A.3) |
Most important for applications are the first and the second moments,
which receive their own designation:
![]() ,
and
,
and
![]() ,
respectively. The meaning of Rij is the correlation matrix.
Finally, it is useful to introduce the covariance matrix,
,
respectively. The meaning of Rij is the correlation matrix.
Finally, it is useful to introduce the covariance matrix,
![\begin{displaymath}C_{ij}={\rm E}\big[X_i~X_j\big]-{\rm E}\big[X_i\big]\;{\rm E}\big[X_j\big]
=R_{ij}-\mu_i~\mu_j.
\end{displaymath}](/articles/aa/full/2008/33/aa09720-08/img299.gif) |
(A.5) |
It can be proven that statistically independent random values are always uncorrelated, in which case Cij is a diagonal matrix.
The random process can be interpreted as a function of two variables,
![]() .
For a fixed value of some
.
For a fixed value of some
![]() ,
,
![]() is a function of time, called the trajectory or
the realisation of the random process. For a fixed value of
is a function of time, called the trajectory or
the realisation of the random process. For a fixed value of
![]() ,
the function
,
the function
![]() is a real
random value. A process is
called stationary if
is a real
random value. A process is
called stationary if
![]() for every
for every
![]() .
This implies that all moments of X(t) are independent of
time,
.
This implies that all moments of X(t) are independent of
time,
![\begin{displaymath}{\rm E}\big[X^k(t)\big]={\rm E}\big[X^k(t+r)\big]={\cal M}_k,
\end{displaymath}](/articles/aa/full/2008/33/aa09720-08/img314.gif) |
(A.6) |
for all r and t. A weaker form of this condition is often used: a random process is called a weak-sense stationary if
![\begin{displaymath}{\rm E}\big[X(t)\big]={\rm E}\big[X(t+r)\big],\quad
{\rm E}\big[X^2(t)\big]={\rm E}\big[X^2(t+r)\big].
\end{displaymath}](/articles/aa/full/2008/33/aa09720-08/img315.gif) |
(A.7) |
A stationary random process does not change its nature with time.
However, in general there is no way to calculate the statistical
characteristics of such a process knowing only a single realisation. For
this purpose, a stronger assumption has to be made: a random process is
called an ergodic one if for all fixed
![]() and a real
function h(x)
and a real
function h(x)
![\begin{displaymath}{\rm E}\big[h\left(X(r)\right)\big]=
\lim\limits_{T\rightarrow\infty}\frac{1}{T}\int\limits_0^T h\left(X(t)\right)
{\rm d}t.
\end{displaymath}](/articles/aa/full/2008/33/aa09720-08/img316.gif) |
(A.8) |
It is commonly assumed that real processes satisfy this condition.
Stationary processes can be characterised by autocorrelation R(t)and autocovariance C(t) functions,
![\begin{displaymath}R(t)={\rm E}\big[X(r)~X(r+t)\big],\quad
C(t)=R(t)-\mu^2,
\end{displaymath}](/articles/aa/full/2008/33/aa09720-08/img317.gif) |
(A.9) |
which, according to stationarity, are independent of r. By setting r=-t we find that R(t)=R(-t).
Another way of characterising processes is by their spectral properties,
which are also our main interest in this paper.
Power spectral function of a stationary stochastic process X(t) is
The concept of point processes was originally developed to describe
random configurations of points in space (Daley & Vere-Jones 2003; Cox & Miller 1965). One
way to characterise such random configurations in some
topological space
![]() is by means of
the counting measure, N(A). For every
is by means of
the counting measure, N(A). For every
![]() ,
the counting measure gives the number of
points lying in A.
,
the counting measure gives the number of
points lying in A.
Similar to random processes, a random point process can be characterised
by its mean value and moments. The first-order moment is called
the intensity measure,
![\begin{displaymath}M_1(A)={\rm E}\big[N(A)\big].
\end{displaymath}](/articles/aa/full/2008/33/aa09720-08/img323.gif) |
(A.12) |
The random measure
![]() represents the ground process of
the marked process N. If the dynamics of the process is governed
only by the ground process and the marks are mutually independent and
random values with the distribution functions
represents the ground process of
the marked process N. If the dynamics of the process is governed
only by the ground process and the marks are mutually independent and
random values with the distribution functions
![]() ,
then the measure of the marked process fulfils
,
then the measure of the marked process fulfils