A&A 487, 431-443 (2008)
DOI: 10.1051/0004-6361:20079154

Galaxy-cluster gas-density distributions of the representative XMM-Newton cluster structure survey (REXCESS)

J. H. Croston¹ - G. W. Pratt² - H. Böhringer² - M. Arnaud³ - E. Pointecouteau⁴ - T. J. Ponman⁵ - A. J. R. Sanderson⁵ - R. F. Temple⁵ - R. G. Bower⁶ - M. Donahue⁷

1 - Centre for Astrophysics Research, Science and Technology Research Institute, University of Hertfordshire, Hatfield, AL10 9AB, UK
2 - MPE Garching, Giessenbachstrasse, 85748 Garching, Germany
3 - Laboratoire AIM, DAPNIA/Service d'Astrophysique - CEA/DSM - CNRS - Université Paris Diderot, Bât. 709, CEA-Saclay, 91191 Gif-sur-Yvette Cedex, France
4 - CESR, 9 Av. du colonel Roche, BP4346, 31028 Toulouse Cedex 4, France
5 - School of Physics and Astronomy, University of Birmingham, Edgbaston, Birmingham, B15 2TT, UK
6 - Institute for Computational Cosmology, University of Durham, Durham, DH1 3LE, UK
7 - Physics and Astronomy Department, Michigan State University, East Lansing, MI 48824-2320, USA

Received 27 November 2007 / Accepted 21 January 2008

Abstract
We present a study of the structural and scaling properties of the gas distributions in the intracluster medium (ICM) of 31 nearby (z < 0.2) clusters observed with XMM-Newton, which together comprise the Representative XMM-Newton Cluster Structure Survey (REXCESS). In contrast to previous studies, this sample is unbiased with respect to X-ray surface brightness and cluster dynamical state, and it fully samples the cluster X-ray luminosity function. The clusters cover a temperature range of 2.0-8.5 keV and possess a variety of morphologies. The sampling strategy allows us to compare clusters with a wide range of central cooling times on an equal footing. We applied a recently developed technique for the deprojection and PSF-deconvolution of X-ray surface brightness profiles to obtain non-parametric gas-density profiles out to distances ranging between 0.8 R₅₀₀ and 1.5 R₅₀₀. We scaled the gas density distributions to allow for the systems' differing masses and redshifts. The central gas densities differ greatly from system to system, with no clear correlation with system temperature. At intermediate radii ($\sim$ 0.3 R₅₀₀), the scaled density profiles show much less scatter, with a clear dependence on system temperature. We find that the density at this radius scales proportionally to the square root of temperature, consistent with the presence of an entropy excess as suggested in previous literature. However, at larger scaled radii this dependence becomes weaker: clusters with kT > 3 keV scale self-similarly, with no temperature dependence of gas-density normalisation. The REXCESS sample allows us to investigate the correlations between cluster properties and dynamical state. We find no evidence of correlations between cluster dynamical state and either the gas density slope in the inner regions or temperature, but do find some evidence of a correlation between dynamical state and outer gas density slope. We also find a weak correlation between dynamical state and both central gas normalisation and inner cooling times, but this is only significant at the 10% level. We conclude that, for the X-ray cluster population as a whole, both the central gas properties and the angle-averaged, large-scale gas properties are linked to the cluster dynamical state. We also investigate the central cooling times of the clusters. While the cooling times span a wide range, we find no evidence of a significant bimodality in the distributions of central density, density gradient, or cooling time. Finally, we present the gas mass-temperature relation for the REXCESS sample, finding that $h(z)M_{\rm gas} \propto T^{1.99\pm0.11}$, which is consistent with the expectation of self-similar scaling modified by the presence of an entropy excess in the inner regions of the cluster and consistent with earlier work on relaxed cluster samples. We measure a logarithmic intrinsic scatter in this relation of $\sim$$10\%$, which should be a good measure of the intrinsic scatter in the $M_{\rm gas}$-T relation for the cluster population as a whole.

Key words: galaxies: clusters: general - galaxies: intergalactic medium - cosmology: large-scale structure of Universe

1 Introduction

The X-ray emitting gas in galaxy clusters contains the signatures of important evolutionary processes such as mergers, AGN activity, galaxy interactions and tidal stripping. The impact of gas physical processes on the observable X-ray properties of galaxy clusters must be fully understood in order to use galaxy clusters to test the predictions of structure formation models, and to understand the relationship between AGN activity, galaxy evolution and the evolution of large-scale structure. The global scaling relations between cluster observables such as X-ray luminosity/temperature and cluster mass must be well constrained in the local Universe so that cluster evolution to high redshifts can be investigated; this is not possible without a good understanding of the processes that lead to the observed scatter in these relationships.

Since the first evidence that the gas and dark matter content of galaxy clusters does not scale according to the simplest self-similar predictions (e.g. Edge & Stewart 1991; Arnaud & Evrard 1999), non-gravitational heating processes have been thought to play an important role in determining the X-ray properties of galaxy clusters. Recent results have shown that the dark matter component of galaxy clusters does scale self-similarly, in good agreement with theoretical predictions (e.g. Pointecouteau et al. 2005; Vikhlinin et al. 2006). It has also been shown that the departure of the observed $L_{\rm X}/T_{\rm X}$ relation from theoretical predictions is due to increased entropy in cluster gas (e.g. Ponman et al. 2003; Pratt et al. 2006). A combination of radiative cooling and feedback processes associated with galaxy formation, either from galaxy winds or AGN activity associated with central supermassive black holes, is the most widely accepted explanation for these results (e.g. Voit 2005). Cluster mergers are also expected to have an important effect on their observed X-ray properties: for example, simulations have shown that cluster merger processes are likely to have an important effect on the $L_{\rm X}/T_{\rm X}$ relation (Rowley et al. 2004), although cooling and heating processes in the inner regions may be the dominant source of scatter (O'Hara et al. 2006).

Radial surface brightness profiles and gas density profiles have been the key means of obtaining information about the structure and scaling properties of the intracluster medium (ICM) since the advent of X-ray imaging of clusters, providing an essential tool to enable study of three-dimensional gas distributions, and, together with temperature, the study of the gas entropy distributions and the total mass profiles via the assumption of hydrostatic equilibrium. ROSAT studies (e.g. Neumann & Arnaud 1999) suggested that a $\beta$ model was an adequate parametrization of the X-ray surface brightness distribution outside the core region in galaxy clusters, with clear evidence for self-similarity, but a large dispersion in the central regions. The core regions of clusters are now much better resolved with XMM-Newton and Chandra, and more complex models are required to fit their surface brightness profiles (e.g. Pratt & Arnaud 2002; Pointecouteau et al. 2004; Vikhlinin et al. 2006). There is also some evidence that the slope of the gas density profile may steepen at large radii in some clusters (e.g. Viklinin et al. 1999; Neumann 2005; Vikhlinin et al. 2006). Constraints on the radial distribution of hot gas in the galaxy cluster population are crucial both for accurate estimation of total cluster masses and for studies of gas entropy. Spherically symmetric methods for constraining the gas distributions of galaxy clusters have obvious limitations when applied to samples that are not selected for regularity; however, as a straightforward method that is easy to apply to both observations and simulations, they remain an essential tool for studying cluster properties in three dimensions.

Table 1: Cluster properties. Columns: (1) Cluster ID, (2) redshift, (3) column density in 10²⁰ cm^-2, (4) X-ray temperature from a mekal fit in the [0.15-0.75] R₅₀₀ region in keV, (5) X-ray temperature from a mekal fit in the [0.15-1] R₅₀₀ region in keV, (6) abundance obtained from a mekal fit in the [0.15-1] R₅₀₀ region, in units of solar abundance, (7) R₅₀₀ in kpc, iteratively determined from the $M_{500}-Y_{\rm X}$ relation of Arnaud et al. (2007) as described in the text, (8) logarithm of gas mass to R₅₀₀ determined as described in the text in $M_{\odot }$, (9) inner slope of the gas density profile determined in the region with r < 0.05 R₅₀₀, (10) outer slope of the gas density profile determined in the region [0.3-0.8] R₅₀₀ as defined in the text.

In this paper we examine the gas distributions in 31 clusters drawn from the Representative XMM-Newton Cluster Structure Survey (REXCESS). Full details of the sample selection function can be found in Böhringer et al. (2007). To achieve a statistically well-defined sample which fully samples the X-ray luminosity function and is unbiased with respect to dynamical state, a sample of 33 clusters was constructed from the REFLEX catalogue (Böhringer et al. 2004) based on the following criteria: redshift z < 0.2; close to homogeneous coverage of luminosity space; kT > 2.0 keV; detectable with XMM-Newton to a radius of $\sim$R₅₀₀; and distances selected to optimise the extent of the cluster within the XMM-Newton field-of-view. In addition, a firm detection of more than 30 photons in the original RASS detection, and a low column density towards the source were also required. Observations of the full sample of 31 clusters plus 2 archive observations have now been completed. The analysis presented here consists of the 31 clusters for which it is reasonable to carry out a 1-dimensional analysis. We exclude the clusters RXC J2152-1942 (Abell 2384B) and RXC J0956-1004 (Abell 901/902) which are highly irregular/multiple cluster systems and hence cannot be analysed in this way.

Throughout this paper we adopt a $\Lambda$CDM cosmology with H₀ = 70 km s^-1 Mpc^-1, $\Omega_{\rm M} = 0.3$ and $\Omega_{\Lambda} = 0.7$.

2 Data analysis

2.1 Data preparation

Table 1 lists the global properties of the cluster sample and the details of the XMM-Newton observations. Observations were retrieved and reprocessed with the XMM-Newton Science Analysis System (SAS) version 7.0, ensuring up to date calibration across the sample. Data sets were cleaned for flares, PATTERN-selected and corrected for vignetting as described in Pratt et al. (2007). The background used for the present analysis consists of custom event files generated from data taken in Filter Wheel Closed (FWC) mode, which correspond to an accurate representation of the particle and instrumental background present in XMM-Newton observations. These background data sets were cleaned, PATTERN-selected and vignetting corrected as above, then recast to have the same aspect as the observation data files. The background event lists were rescaled to the source quiescent count rate in the [10-12] and [12-14] keV range for EMOS and EPN cameras, respectively, by adjusting the WEIGHT column in each background event file.

Sources other than the target object were detected in a broad band ([0.3-10.0] keV) coadded EPIC image using the SAS wavelet detection task ewavdetect, with a detection threshold set at $5 \sigma$. After visual screening, detected sources were excluded from the event file for all subsequent analysis.

   
2.2 Surface brightness and gas density profiles

Vignetting-corrected surface brightness profiles were extracted for each camera in the 0.3-2.0 keV band from source and scaled background event files in $3\hbox{$.\!\!^{\prime\prime}$ }3$ bins out to a radius of 15$^\prime$. The profiles were centred on the peak in X-ray surface brightness. The background surface brightness profiles were then subtracted, and the background subtracted profiles from the three cameras co-added. No weighting for camera response was applied at this stage. We then applied the second stage of background subtraction to account for the X-ray background. As the REXCESS sample was chosen with specific field-of-view criteria, all of the observations include an outer region which can be used to measure accurately the cosmic X-ray background (CXB) component. The residual background level due to the CXB in the co-added, background subtracted surface brightness profile was determined by a careful visual analysis of the region where the profile flattens due to background domination; the mean level in this region was then calculated and subtracted, and the resulting profile rebinned to a significance of $3\sigma$ per bin.

Deprojected, PSF-corrected emission measure profiles were obtained from the surface brightness profiles using the non-parametric method described in Croston et al. (2006). The response matrices used were obtained using the Ghizzardi et al. (2001) parametrisation of the XMM-Newton PSF, weighted by the contribution of each camera to the combined profile. The profiles were then converted to gas density by calculating a global conversion factor for each profile in XSPEC using the global temperatures listed in Table 1, which are spectroscopic temperatures estimated in the [0.15 < R < 1] R₅₀₀aperture. A correction factor to take into account radial variations of temperature and abundance was calculated for each radial bin using a parameterisation of the projected temperature and abundance profiles, as detailed in Pratt & Arnaud (2003). The surface brightness profiles and corresponding gas density profiles for each cluster are presented in the Appendix. The gas density profiles in tabular form are included in the electronic version of this paper.

Figure 1: Gas density profiles for the entire sample. Top left: unscaled profiles; top right: profiles of unscaled density with scaled radius; middle left: profiles of density scaled for redshift evolution; middle right: profiles of density scaled according to T0.525 as implied by modified self-similar S-T scaling; bottom left: density profiles with a representation of the 1-sigma scatter of the sample; bottom right: the relative dispersion ( $\sigma/\langle n_{\rm e} \rangle$) as a function of radius for the cluster sample with profiles scaled according to expected evolution with redshift (black) and by T0.525 (red).

Open with DEXTER

3 Results

3.1 Global properties of cluster gas density profiles

Figure 1 shows the 31 cluster gas density profiles superposed to allow an investigation of their global properties. The individual surface brightness profiles (in the energy range 0.3-2.0 keV) and gas density profiles are given in the Appendix. There is a considerable amount of scatter in the unscaled profiles (top left panel), which is unsurprising. Structure formation models predict that the mean cluster density scales with $\rho_{\rm c} (z)$ and so according to h(z)² and predict a universal profile shape when the radial coordinate is scaled according to the cluster mass. We use a scaling radius of R₅₀₀, defined as the radius enclosing a mean overdensity of 500 times the critical density. We therefore expect that gas density profiles scaled by h(z)^-2, and in radial units of r/R₅₀₀ should coincide.

The physical distances were converted to scaled radius using the values of R₅₀₀ given in Table 1, which were determined iteratively as described by Kravtsov et al. (2006), based on the $M_{500}-Y_{\rm X}$ relation of Arnaud et al. (2007) (see also Maughan et al. 2007). Here $Y_{\rm X}$ is the product of the gas mass within R₅₀₀ and the temperature in the [0.15-1] R₅₀₀ region. This approach allows us to determine R₅₀₀ directly from the data without first fitting total mass profiles. For self-consistency, we prefer to use a scaling relation determined from XMM-Newton results, rather than relying on results determined from lensing masses, which have large individual uncertainties and are only applicable to the high mass regime, or from simulations that do not yet reproduce all of the observed properties of the cluster population. A comparison between the empirical relation of Arnaud et al. (2007) and the simulated relation of Nagai et al. (2007) shows only a small normalisation offset (<$8\%$), so that the only difference to our results if the simulated relation were used would be to shift all the profiles in the direction of smaller radii. It would therefore have no effect on any of our conclusions, which are all based on the relative profiles.

The total gas mass to a radius of R₅₀₀ was determined for the sample by integrating over the gas density profiles. For profiles where the data does not extend to R₅₀₀ (9/31 clusters) we extrapolated the profiles from the outer bin of the density profile (never less than 0.8 R₅₀₀) assuming a power law slope in log space, determined by a fit to the outer four bins. The errors on gas mass were determined by combining in quadrature the errors obtained from Monte Carlo simulation over the statistical errors in the surface brightness profiles and the errors due to the temperature uncertainties.

The scatter in gas density at 0.3 R₅₀₀ is $\sigma/\langle n_{\rm e} \rangle = 0.265$. We then scaled the gas densities according to their expected evolution with redshift: $n_{\rm e} \propto n_{0} h(z)^{2}$(shown in the middle left panel of Fig. 1), which reduced the scatter at 0.3 R₅₀₀ to $\sigma/ \langle n_{\rm e} \rangle = 0.236$. The bottom right panel of Fig. 1 shows the relative dispersion as a function of radius for this scaling (in red), which drops from $\sim$$100\%$ in the inner regions to a minimum of $\sim$$15\%$ at 0.6 R₅₀₀, before increasing slightly in the outer regions.

   
3.2 Dependence of gas density on temperature

Figure 2 shows the evolution-corrected gas density profiles colour-coded by cluster temperature. At the smallest radii probed by this data, the dispersion in profiles is uncorrelated with temperature (e.g. left hand panel of Fig. 3). We investigate the origin of this scatter in Sect. 4.3. At intermediate radii ($\sim$ 0.3 R₅₀₀), there is a clear systematic bias with system temperature, although this trend becomes weaker again at the maximum radii probed by the data. Figure 3 also quantifies the relationship between gas density normalisation at a radius of 0.3 R₅₀₀ and at 0.7 R₅₀₀. Results are shown for the redshift-scaled gas density profiles; however, using the unscaled profiles does not significantly alter the result. There is evidence for a correlation in both cases, although the trend is weaker at 0.7 R₅₀₀. We obtained a null hypothesis probability <0.0001 on a Spearman rank test for the comparison at 0.3 R₅₀₀ and a higher null hypothesis probability of 0.004 at 0.7 R₅₀₀. We carried out orthogonal linear regression, finding a slope of 0.50 $\pm$ 0.08 for the relationship between $n_{\rm e} (0.3~R_{500})$ and T.

The departure of the density from the simple scaling is best discussed in terms of the radial entropy profiles of the systems. To be consistent with previous work, we define entropy as $S = T / n_{\rm e}^{2/3}$. The observed departure from simple scaling of the entropy-temperature relation for clusters (e.g. Finoguenov et al. 2002; Ponman et al. 2003) implies a temperature dependence of the gas density normalisation such that $n_{\rm e} \propto T^{0.525}$. This is in excellent agreement with the trend we see at 0.3 R₅₀₀. However, at 0.7 R₅₀₀, the correlation is weaker and we find a flatter slope of 0.25 $\pm$ 0.06. It is apparent from the righthand panel of Fig. 3 that the correlation at 0.7 R₅₀₀ is mainly due to lower densities in the systems below $kT \sim 3.0$ keV; at higher temperatures the relation appears to be flat. This suggests that the ``entropy excess'' may extend to larger scaled radii in cooler systems, consistent with the expectation that non-gravitational processes have a greater effect at the low mass end of the cluster population.

	Figure 2: Gas density distributed scaled according to expected evolution with redshift, and coded by temperature so that blue corresponds to a temperature of $\sim$2.0 keV and red a temperature of $\sim$8 keV.
Open with DEXTER

	Figure 3: Plots of gas density normalisation vs. cluster temperature at 0.03 R500 ( left), 0.3 R500 ( middle) and at 0.7 R500 ( right), for the redshift-scaled density profiles. For the latter two cases, lines of best fit obtained as described in the text are overplotted.
Open with DEXTER

We then scaled the density profiles by T^0.525 (in addition to the redshift scaling discussed above), as shown in the middle right panel of Fig. 1. As shown in the bottom right panel, the relative dispersion decreases for this scaling (shown in red) out to a radius of $\sim$ 0.5 R₅₀₀, reaching a minimum of $\sigma/\langle n_{\rm e} \rangle = 0.133$ at 0.5 R₅₀₀. Beyond $\sim$ 0.5 R₅₀₀ the relative dispersion for this scaling is slightly higher than for the redshift-evolution-only profiles. This result is consistent with the weaker correlation between gas density and temperature at 0.7 R₅₀₀, supporting the conclusion that an entropy excess is likely to be significant in the cluster inner regions only.

3.3 Radial dependence of density profile slope

We investigated the radial dependence of the density profile slope, defined as the logarithmic gradient of density with radius, and determined from the deprojected profiles, with a binning chosen to correspond to a typical temperature profile for the sample. In Fig. 4, we present the superposed plots of ${\rm d} \log(n_{\rm e}) / {\rm d} \log(r)$ for the cluster sample, colour-coded by temperature in the same way as for Fig. 2. There is a large scatter at all radii of the profiles, which in many cases are not very smooth. The scatter at a radius of 0.3 R₅₀₀ is $\sigma/ \langle \alpha \rangle = 0.20$. It is evident from Fig. 4 that in most cases $\alpha$ appears still to be increasing in the outermost regions (e.g. at a distance of $\sim$ 0.8-1.0 R₅₀₀) in contrast to the power-law behaviour expected for a $\beta$-model profile. This is in agreement with earlier work (e.g. Vikhlinin et al. 1999; Neumann 2005), and has important implications for cluster mass estimates obtained using analytical models. We have fully taken into account systematic uncertainties in the background level in determining the outer slopes: the systematic uncertainty in the background level is typically $\sim$$2{-}3\%$, leading to an uncertainty in outer slope that is negligible compared to the statistical uncertainties on surface brightness. In one case, RXC J2234.5-3744, the background uncertainty is $\sim$$14\%$ due to residual flare contamination, which leads to a $\sim$$3\%$ error in the [0.3-0.8] R₅₀₀ slope. In Fig. 4, the mean slope is shown only out to 0.9 R₅₀₀, where the effects of systematic uncertainty in the background level are negligible. Our conclusions relating to the gas density gradient are therefore robust.

	Figure 4: Profiles of $\alpha$, the density profile slope for the entire cluster sample, colour-coded by cluster temperature as in Fig. 2. Thick red line indicates the mean profile.
Open with DEXTER

   
3.4 Parametrization of cluster structure

In order to further investigate the distribution of cluster structure and the dependence of cluster structure on other properties such as gas temperature and dynamical state, we first considered the outer logarithmic slope of the gas density profiles. We chose to use the region of [0.3-0.8] R₅₀₀, since, as shown in Figs. 1 and 4, all of the profiles have steepened from their inner slopes by 0.3 R₅₀₀, and all extend to at least 0.8 R₅₀₀. The use of a fixed outer radius minimizes the possibility of bias due to brighter, and hence higher temperature, clusters extending to larger radii. We express the slope as a $\beta$ value, where $\beta$ is defined as 1/3 times the slope, for comparison with other works using analytical models. The outer slope in the region [0.3-0.8] R₅₀₀ is hereafter referred to as $\alpha _{0.3-0.8}$, or $\beta _{0.3-0.8}$ when expressed as a $\beta$ value. We also measured the inner logarithmic slope within 0.05 R₅₀₀, before any of the profiles have begun to steepen significantly, which is hereafter referred to as $\alpha _{<0.05}$. Both $\alpha _{0.3-0.8}$ and $\alpha _{<0.05}$ were measured by a simple linear least-squares fit in log space over the relevant region. As discussed above, the effects of systematic uncertainties in the background level have been fully taken into account and are less than the statistical uncertainties in nearly all cases.

In Fig. 5 (top) we plot the distribution of $\beta _{0.3-0.8}$and $\alpha _{<0.05}$ for the gas density profiles scaled according to expected evolution with redshift. The mean value for $\alpha _{<0.05}$is -0.5 $\pm$ 0.3, with the large scatter reflecting the range from clusters with central cores to those that are highly peaked (using a fixed inner boundary in scaled radius does not reduce the scatter or significantly alter the mean slope). We are confident that the values of $\alpha _{0.3-0.8}$ are unaffected by PSF-correction or resolution issues: in Croston et al. (2006) we showed that the PSF correction is very accurate beyond $\sim$0.05 arcmin, and we find that $\alpha _{0.3-0.8}$ is uncorrelated with redshift or angular scale. The mean value of $\alpha _{0.3-0.8}$ is -1.80 $\pm$ 0.28 (corresponding to $\beta_{0.3-0.8} = 0.60$ $\pm$ 0.10), which is consistent with other studies, e.g. Neumann & Arnaud (1999), Ota & Mitsuda (2004), Vikhlinin et al. (2006). The scatter in $\alpha _{0.3-0.8}$ is considerably smaller than for $\alpha _{<0.05}$; however, a few clusters are exceptionally flat in their outer regions (three clusters have $\beta < 0.5$). There is no evidence for bimodality in $\alpha _{<0.05}$. We also investigated whether $\alpha _{<0.05}$ and $\alpha _{0.3-0.8}$, the inner and outer slopes, are correlated. As shown in Fig. 6, no such correlation appears to exist, indicating that in general the dynamical evolution of the angle-averaged gas distribution in the central and outer regions of the clusters are not closely connected.

The REXCESS sample includes clusters with evidence for irregularity, and in some cases the choice of the centre for the profiles is very dependent on the radius used for centroiding (see Sect. 4.2). We therefore examined the effect of this uncertainty on the structural parameters of the density profiles by considering three of the most irregular clusters, RXC J2048-1750, RXC J2129-5048 and RXC J1516-0056. For each of these clusters, surface brightness profiles were extracted using centroid positions obtained within radii of 0.3, 0.5 and 1.0 times R₅₀₀, which were deprojected in the same way as for the original profiles. We found that the choice of centroid unsurprisingly has an important effect on the measured value of $\alpha _{<0.05}$, introducing a scatter of between 40-67 percent; however, the results for the inner two choices of centroiding region, more appropriate for studying the slope in the inner regions, were in reasonable agreement. The choice of centroid does not appear to introduce significant uncertainty in $\alpha _{0.3-0.8}$: the dispersion between the three cases ranged from 2-6 percent in these ``worst-case'' clusters. We comment below on the effect of centroid choice on other results.

	Figure 5: Histograms of the distribution of inner logarithmic slope ( $\alpha _{<0.05}$) and outer slope ( $\beta _{0.3-0.8}$) for the density profiles scaled according to their expected evolution with redshift.
Open with DEXTER

	Figure 6: Comparison of the inner and outer slopes of the density profile ( $\alpha _{<0.05}$ and $\alpha _{0.3-0.8}$, respectively) for each cluster.
Open with DEXTER

   
3.5 Dependence of cluster structure on temperature

In Fig. 7 we plot the inner and outer density slopes ( $\alpha _{<0.05}$ and $\beta _{0.3-0.8}$) against the cluster temperature in the region [0.15-1] R₅₀₀. $\beta _{0.3-0.8}$appears to correlate with global temperature. Based on a Spearman rank test, we find a $\sim$2 percent probability that such a correlation could occur by chance. There is no significant correlation between $\alpha _{<0.05}$ and the global cluster temperature. It is clear from Fig. 4 that the slope does not depend on temperature over most of the radial range. It is only at radii beyond $\sim$ 0.3 R₅₀₀ that the slopes of the cooler profiles are preferentially below the mean, with hotter profiles mainly above the mean.

4 Discussion

4.1 Total gas mass and the M_gas-T relation

Figure 8 shows the relationship between gas mass and global temperature for the REXCESS sample. Here we use temperature in the [0.15-0.75] R₅₀₀ region to enable direct comparisons with previous work. We fitted a scaling relation of the form $h(z)M_{\rm gas} = C [T_{\rm X}/5~{\rm keV}]^{\gamma}$ using two linear regression methods, a weighted least squares method that incorporates an intrinsic scatter term in the errors (WLSS), and BCES, which is an orthogonal method that does not take into account the statistical errors. These methods are discussed in more detail in Pratt et al. (2006). The results of the fits are given in Table 2. The slopes and normalisations obtained with the two methods are consistent, and are also in good agreement with those obtained for a smaller sample of relaxed clusters by Arnaud et al. (2007). The results of our fits and the Arnaud et al. relaxed cluster relation are shown in Fig. 8. As shown in Table 2, the intrinsic logarithmic scatter for the REXCESS sample is a factor of 2.5 times higher than for the Arnaud et al. (2007) relaxed cluster sample. This is likely to arise as a result of the wider range of cluster morphologies in our sample, although the sample appears to include clusters with both higher and lower gas mass for their temperature.

	Figure 7: Plots of the inner ( left) and outer ( right) slopes ( $\alpha _{<0.05}$ and $\beta _{0.3-0.8}$), respectively, versus the global cluster temperature, $T_{\rm X}$.
Open with DEXTER

Table 2: Results of linear regression analysis for the $M_{\rm gas}$-T relation. $\gamma$ is the slope in log-log space, C the normalisation, and $\sigma _{\rm raw}$ and $\sigma _{\rm intrins}$ the raw and intrinsic logarithmic scatter about the relation, respectively.

We investigated the effect of choice of cluster centre on the gas mass measurements and found that for the three most disturbed systems the gas masses obtained varied by between 7 and 12% for centroiding using regions of radius 0.1, 0.3 and 0.5 $\times$ R₅₀₀. As the cluster dynamical state appears to be relatively independent of temperature (see Sect. 4.2), we do not expect this systematic uncertainty to affect our conclusions about the scaling of gas mass and temperature. As, in addition, our sample selection strategy is unbiased with respect to cluster dynamical state, the $\sim$$9 \%$scatter about the $M_{\rm gas}$-T relation we measure for this sample should be a good measure of the intrinsic scatter in the relation for the cluster population as a whole.

The steep relation between gas mass and temperature implies a decrease in the total gas mass content of cooler clusters relative to higher mass systems, when compared with standard predictions. This is clearly connected with the excess of entropy seen at intermediate radii in cooler systems and their relatively flat outer slopes. All of these factors suggest that significant non-gravitational heating is likely to have occurred, raising the gas entropy and lifting material beyond R₅₀₀. Energetically it is most appealing if this energy injection occurred prior to cluster collapse (e.g., McCarthy et al. 2007), but a single level of ``preheating'' is unable to explain the full range of observed properties, both as a function of cluster temperature and as a function of the variations within in a temperture band. We will explore the theoretical models that can account for the observed trends in a future paper.

	Figure 8: Cluster gas mass vs. global temperature. Solid line is the best fitting relation to this sample obtained using WLSS, dashed line is the results obtained with BCES, and the dotted line is the best-fitting relation for the sample of regular clusters discussed in Arnaud et al. (2007).
Open with DEXTER

   
4.2 Dependence of cluster structure on dynamical state

The radial gas distribution in galaxy clusters is likely to be strongly affected by the cluster dynamical state, since mergers are expected to disrupt the gas structure significantly. We used two different quantitative measures of substructure in the 2D surface brightness distribution as means of characterising the cluster dynamical state: the power ratio method of Buote & Tsai (1995) and centre shifts (e.g. Mohr et al. 1995; Poole et al. 2006).

The power ratio method used here is described in more detail in Pratt et al. (2007). Here, we make use of power ratio measurements for the entire REXCESS sample (to be discussed in a forthcoming paper), determined in an aperture of radius R₅₀₀. We examined the dependence of cluster structure on the three lowest order power ratios of relevance for this work: P₂/P₀, which corresponds to a measure of ellipticity, P₃/P₀, which is the best measure of further substructure, and P₄/P₀, which also measures deviation from a relaxed dynamical state. As some of the P₃/P₀values are formally upper limits, we used the generalized Kendall's $\tau$ test for censored data, as implemented in the ASURV package. We did not find a correlation with inner gas density slope ( $\alpha _{<0.05}$); however, there is evidence for a correlation between P₃/P₀ and $\beta _{0.3-0.8}$, with a null hypothesis probability of $\sim$$0.1\%$ on the generalized Kendall's $\tau$ test. There is weak evidence for a correlation between P₃/P₀ and temperature, with a null hypothesis probability of $\sim$$10\%$ on a generalized Kendall's $\tau$ test. This correlation likely arises as a result of the correlation between $\beta$ and temperature, as discussion in Sect. 3.5. The relations between gas structure and P₃/P₀ are shown in Fig. 9.

	Figure 9: The relationship between cluster dynamical state as parametrised by power ratios and centre shifts and gas properties. Top: P3/P0, bottom: $\langle w \rangle$. Left to right: inner slope of gas density ( $\alpha _{<0.05}$), outer slope of gas density ( $\beta _{0.3-0.8}$), temperature.
Open with DEXTER

	Figure 10: Cooling time profiles for the cluster sample. Left: unscaled profiles in physical units; middle: unscaled gas density in units of scaled radius (corresponding to the top left panel of Fig. 1); right: profiles obtained from the redshift-scaled gas density profiles (corresponding to the middle left panel of Fig. 1).
Open with DEXTER

Centre shifts were determined for the entire REXCESS sample. Centroids were obtained for regions of n $\times$ 0.1 $\times$ R₅₀₀ with n=1..10 (i.e. the region with r < 0.1 R₅₀₀ was not included, so that the centre shifts are not affected by the large scatter in central gas properties). The results of this analysis will be presented in more detail in a forthcoming paper; however, for the purposes of a comparison with gas structural properties we used $\langle w \rangle$, defined as the standard deviation of the projected separations between the X-ray peak and centroid at each radius (e.g. Maughan et al. 2007) in the region between 0.1 $\times$ R₅₀₀ and R₅₀₀. We found that the exclusion of the central region, possibly affected by a cooling core, did not significantly affect the measured $\langle w \rangle$ values, except in the cases where $\langle w \rangle$ is very small. In Fig. 9 we plot $\langle w \rangle$ against inner and outer gas density slopes ( $\alpha _{<0.05}$ and $\beta _{0.3-0.8}$). On a Spearman rank test, we find no strong evidence for a significant correlation with $\alpha _{<0.05}$, but find evidence for a correlation between $\langle w \rangle$ and $\beta _{0.3-0.8}$, with a null hypothesis probabilty of $0.08\%$ on a Spearman rank test. $\langle w \rangle$ is also uncorrelated with temperature. The lack of correlation with inner density slope suggests that cluster substructure and central cooling behaviour are independent.

	Figure 11: Histograms of central gas density and central cooling time (at 0.03 R500, the innermost radius at which both density and temperature data is available for all clusters), showing that there is no strong evidence for bimodality in their cooling properties.
Open with DEXTER

4.3 Cooling times

Cooling time profiles were determined from the gas density and temperature profiles for each cluster, where the cooling time, $t_{\rm cool}$ is defined as:

$$% t_{\rm cool} (r) = \frac{\frac{3}{2} \rho_{\rm gas} (r) k T (r) V}{L_{\rm X} (r)}$$ (1)

where $L_{\rm X}(r)$ is the X-ray luminosity at radius r determined using the appropriate mekal model parameters at each radius in XSPEC. Figure 10 shows the cooling time profiles for all 31 clusters in physical and scaled units in the radial range where the temperature profile is well constrained for each cluster. As the temperature profiles we use here are not deprojected, we compared the cooling time profiles obtained using projected and deprojected temperature profiles for the cluster with the steepest central temperature drop. We conclude that the use of projected temperatures introduces an uncertainty of at most $\sim$$15\%$ at radii less then 0.02 R₅₀₀ and has negligible effects at larger radii.

The lower envelope of the cooling time profile distribution for REXCESS is in good agreement with previous work (e.g. Sanderson et al. 2006; Bauer et al. 2005); however, the dispersion in the inner regions of this sample is higher than seen in other samples, particularly those dominated by cooling core clusters (e.g. Voigt & Fabian 2004; Sanderson et al. 2006), with a value of $\sigma/\langle t_{\rm cool} \rangle = 0.85$ at 0.03 R₅₀₀ (as the cooling time profiles are dominated by the behaviour of the gas density profiles, the scatter as a function of radius is similar to that shown in Fig. 1). We find a mean slope in the region [0.2-0.8] R₅₀₀ of 1.4 $\pm$ 0.3, which is consistent with the results of Bauer et al. (2005). In the region [0.05-0.2] R₅₀₀ the mean slope for our sample is $\sim$0.9 $\pm$ 0.3, somewhat flatter than that seen over a similar range in scaled radius by Sanderson et al. (2006), due to the larger scatter towards higher cooling times in our sample. The spatial resolution of our temperature profiles in the inner regions limits our ability to draw strong conclusions about the central cooling properties of this sample; however, the large dispersion in central cooling properties suggests that there are more clusters with high central cooling times in this sample compared to other studies. Nevertheless, $t_{\rm cool}$ drops below the Hubble time at a radius of $\sim$50-200 kpc for virtually all of the clusters in the sample.

Traditionally, clusters have been divided into two classes according to their central cooling times: ``cool-core'' systems with short central cooling times and high central densities and ``non-cool-core systems'' with cooling times comparable to the Hubble time. Because of their higher surface brightness, cool-core systems have tended to be over represented in previous deep observations of clusters, leading to the perception that the distribution of system cooling times is bimodal. However, as shown in Fig. 11, the distributions of gas densities and cooling times for the REXCESS sample at the innermost radius appear to be well represented by a broad single peaked distribution, and any division of this sample based on the central cooling time would be arbitrary. We note, however, that our cooling time profiles do not extend to very small radii, and so we cannot rule out bimodality in the cooling time profiles on smaller scales. In particular there does appear to be a subset of profiles which continue to have a steep gradient in cooling time at small radii, which corresponds primarily to those profiles with $t_{\rm cool} (0.03~R_{500}) < 1$ Gyr. The mean slope for profiles with inner cooling times higher than 1 Gyr is significantly flatter, with several profiles that are asymptotically flat in the central regions. Hence our data do not rule out models in which conduction can stabilize the cores of clusters with high central cooling times (e.g. Donahue et al. 2005). As noted in Sect. 3.5, the distribution of inner gas density slope ( $\alpha _{<0.05}$) also shows no strong evidence for bimodality. These conclusions are independent of the choice of radius and gas density scaling.

Finally, we investigated the connection between central gas properties and cluster dynamical state by comparing the inner cooling times and gas densities with $\langle w \rangle$ and P₃/P₀. Although it is widely anticipated that clusters with long central cooling times result from cluster mergers, recent papers have suggested that central density cusps are unlikely to be destroyed in the merger event (e.g., McCarthy et al. 2004; Borgani et al. 2004; Poole et al. 2006). It is therefore of considerable interest to investigate the connection between central gas properties and cluster dynamical state by comparing the inner cooling times and gas densities with $\langle w \rangle$ and P₃/P₀. Figure 12 illustrates that correlations are present, in the sense that clusters with lower central densities, and higher central cooling times, tend to show more evidence for disturbance. However, the trend is driven by a few systems with the highest level of disturbance, and the null hypothesis that there is no correlation can only be rejected at the $\sim$$85{-}97\%$ level using the Spearman rank correlation test (for $\langle w \rangle$) or the generalized Kendall's $\tau$ test (for P₃/P₀). While there is therefore weak evidence that merger activity can affect cluster central densities and cooling times, it does not appear to affect the slope of the density profile (Sect. 4.2) in the inner regions. Clearly these issues need to be addressed by careful comparison with cosmological simulations.

	Figure 12: Comparisons between central gas properties and dynamical state. Left: P3/P0 vs. $n_{\rm e} (0.007~R_{500}$) ( top) and $t_{\rm cool} (0.03~R_{500})$ ( bottom); right: $\langle w \rangle$ vs. $n_{\rm e} (0.007~R_{500}$) ( top) and $t_{\rm cool} (0.03~R_{500})$ ( bottom).
Open with DEXTER

	Figure 13: Comparison of the observed gas density profiles (1$\sigma$ dispersion in red) and simulated profiles of Borgani et al. (2004) (dashed lines) scaled by $\rho _{\rm vir}$.
Open with DEXTER

4.4 Comparison with simulations

We compared the observed gas density profiles with the simulated profiles of all clusters with kT > 2 keV from Borgani et al. (2004), in which the SPH code GADGET-2 (Springel 2005) was used to simulate a concordance $\Lambda$CDM model ( $\Omega_{\rm M} = 0.3$, $\Omega_{\Lambda} = 0.7$, $\sigma_{8} = 0.8$, h = 0.7) within a box of 192 h^-1 Mpc on a side, using 480³ dark matter particles and an equal number of gas particles. The simulation included radiative cooling, star formation and galactic ejecta powered by supernova feedback. Figure 13 shows in red the $1\sigma$ dispersion of the entire sample of observed profiles as in the bottom left panel of Fig. 1, with the simulated profiles as dashed lines. Observed profiles were scaled by $\rho _{\rm vir}$, defined as $100~\rho_{\rm crit,0}$. The agreement is very good in the radial range [0.02-0.3] R₅₀₀; however at larger radii the observed profiles are slightly flatter than the simulated profiles. We found that the simulated profiles have a mean slope in the radial range [0.3-0.8] R₅₀₀ of -1.97 $\pm$ 0.25, which is consistent within the errors with our measured mean slope of -1.80 $\pm$ 0.28, but is slightly higher. For the purpose of this comparison we used the ``true'' R₅₀₀ values from the simulations. The small difference between the slope of the observed and simulated profiles at large radius may be due to differences in the definition of R₅₀₀. We cannot apply our method for determining R₅₀₀ based on the observed $Y_{\rm X}-M_{500}$ relation directly to the simulations, because spectroscopic-like temperature measurements that exclude the central regions of the cluster are not available. The relative dispersion in the simulated profiles at 0.3 R₅₀₀ is $\sigma/\langle n_{\rm e} \rangle = 0.13$, which is significantly lower than the value of $\sim$0.22 for the redshift-scaled observed profiles.

Nagai et al. (2007) carried out a similar comparison of the gas distributions in simulated and observed clusters, using an observed sample consisting of the z=0 relaxed cluster sample of Vikhlinin et al. (2006). They found slightly better agreement in the outer regions between the Chandra profiles and their simulations that included cooling and star formation. Their slightly better agreement between observations and simulations may be a result of comparing with a sample including only relaxed clusters. Differences in the numerical treatments and implementations of cooling and star formation in the simulations may also be relevant.

	Figure 14: The gas density normalisation (at 0.3 R500) vs. temperature distribution for the simulated cluster sample using both the spectroscopic-like temperature ( left) and the emission-weighted temperature ( right). No significant correlation is seen.
Open with DEXTER

	Figure 15: The outer slope ( $\beta _{0.3-0.8}$) vs. temperature distribution for the observed and simulated cluster samples using both the spectroscopic-like temperature ( left) and the emission-weighted temperature ( right) for the simulated sample.
Open with DEXTER

We also investigated whether the temperature-dependence of gas density normalisation seen in the REXCESS clusters (see Sect. 3.2) is also present in the simulations. Figure 14 shows the relationship between gas density normalisation and temperature (shown for both the emission-weighted and spectroscopic-like temperatures) for the simulations. There is no significant temperature-dependence of gas density normalisation for the simulated cluster sample.

Finally we compared the outer slope with gas temperature, using both the emission-weighted temperatures within R₅₀₀ and the spectroscopic-like temperatures defined in Rasia et al. (2005). Figure 15 shows that the correlation between gas density slope ( $\beta _{0.3-0.8}$) and temperature observed in the REXCESS sample is not present in the simulated data (on a Spearman rank test we find null hypothesis probabilities of $35\%$ and $75\%$ for $T_{\rm sl}$ and $T_{\rm ew}$, respectively, compared with <$1\%$ for the observed sample) - there are clearly a number of simulated clusters in the low T, steep $\beta$ region of Fig. 15, which is not populated by the observed sample. However, the temperature measurements for the simulated sample do not exclude the central region which makes it difficult to draw firm conclusions. It is also clear from Fig. 15 that the temperature distribution in the simulated sample is different to that of the observed sample, with fewer high temperature clusters.

These differences hint that the simulations may not match the true thermal history of the intracluster medium. In particular, the heat input appears too centrally concentrated so that the excess entropy seen in the lower temperature clusters at intermediate radii is not reproduced. A more detailed comparison with simulations will form part of a later paper.

5 Conclusions

We have presented the first detailed study of the structural properties of cluster gas in a large, representative sample of nearby galaxy clusters. As the sample was selected by X-ray luminosity, it includes clusters of all dynamical states, allowing us to investigate the effect that the inclusion of less regular systems has on results obtained with previous studies of regular clusters. We found the following results:

• The 1D gas density profiles scale self-similarly, with a scatter ranging from $\sim$$100\%$ in the inner regions to $\sim$$20\%$ at a radius of 0.3 R₅₀₀ when expected evolution with redshift is taken into account.

• Gas density normalisation at 0.3 R₅₀₀ is correlated with global cluster temperature, with a scaling of $n_{\rm e} (0.3~R_{500}) \propto T_{\rm X}^{0.5}$, consistent with the expectation of modified entropy-temperature scaling models. Using this scaling reduced the scatter in the gas density profiles at 0.3 R₅₀₀ to $\sim$$15\%$; however, the scatter at larger radii is slightly increased, which indicates that the entropy excess is much less significant beyond $\sim$ 0.5 R₅₀₀.

• The gas density slope continues to increase with radius in the region 0.5 R₅₀₀-R₅₀₀, as found by others, which is of importance for cluster mass estimates.

• The outer gas density slope is correlated with X-ray temperature, primarily due to a lack of hot clusters with flat gas distributions. The flatter slope in lower temperature systems, combined with the entropy excess at intermediate radii and the steep slope of the $M_{\rm gas}$-T relation suggests that gas has been displaced from the centres of the lower temperature systems to larger radii.

• Based on a characterisation of the cluster dynamical state using power ratios and centre shifts, there is evidence of a correlation between cluster dynamical state and outer gas density slope, and no correlation with inner gas density slope. There is also evidence for a correlation between dynamical state and the central gas properties (gas density normalisation at 0.007 R₅₀₀ and cooling time at 0.03 R₅₀₀).

• There is no evidence for bimodality in the central gas density, gas density slope or cooling times for this sample, suggesting that X-ray clusters form a single population with a continuous distribution of central gas properties.

• The gas-mass temperature relation for the REXCESS sample is in good agreement with predictions of self-similar scaling modified by the presence of an entropy excess, and with previous work on samples of regular clusters; however, the intrinsic scatter is a factor of $\sim$2.5 times higher than for the relaxed cluster population.

• The scaling properties of the gas density profiles appear to be in broad agreement with those of simulated cluster samples (Borgani et al. 2004) at intermediate radius, with a slightly flatter slope in the outer regions. However, in contrast to the observational data there is no correlation between gas density normalisation and temperature in the simulated sample, or between the outer slope and temperature. These discrepancies suggest that the non-gravitational heating of the intra-cluster medium may be too centrally concentrated in these models.

Acknowledgements

We are grateful for helpful comments and discussion with members of the REXCESS collaboration, particularly Stefano Borgani, Chris Collins, Alexis Finoguenov, Thomas Reiprich, and Kathy Romer. We thank the referee for helpful suggestions.

References

• Arnaud, M., & Evrard, A. E. 1999, MNRAS, 305, 631 [NASA ADS] [CrossRef] (In the text)
• Arnaud, M., Pointecouteau, E., & Pratt, G. W. 2007, A&A, 474, 37 [NASA ADS] [CrossRef] (In the text)
• Bauer, F. E., Fabian, A. C., Sanders, J. S., Allen, S. W., & Johnstone, R. M. 2005, MNRAS, 359, 1481 [NASA ADS] [CrossRef] (In the text)
• Böhringer, H., Schuecker, P., Guzzo, L., et al., 2004, A&A, 425, 367 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Böhringer, H., Schuecker, P., Pratt, G. W., et al. 2007, A&A, 469, 363 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Borgani, S., Murante, G., Springel, V., et al. 2004, MNRAS, 348, 1078 [NASA ADS] [CrossRef] (In the text)
• Buote, D. A., & Tsai, J. C. 1995, ApJ, 452, 522 [NASA ADS] [CrossRef] (In the text)
• Croston, J. H., Arnaud, M., Pointecouteau, E., & Pratt, G. W. 2006, A&A, 459, 1007 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Donahue, M., Voit, G. M., O'Dea, C. P., Baum, S. A., & Sparks, W. B. 2005, ApJ, 630, L13 [NASA ADS] [CrossRef] (In the text)
• Edge, A. C., & Stewart, G. C. 1991, MNRAS, 252, 428 [NASA ADS] (In the text)
• Finoguenov, A., Jones, C., Böhringer, H., & Ponman, T. J. 2002, ApJ, 578, 74 [NASA ADS] [CrossRef] (In the text)
• Feigelson, E. D., & Babu, G. J. 1992, ApJ, 397, 55 [NASA ADS] [CrossRef]
• Kravtsov, A. V., Vikhlinin, A., & Nagai, D. 2006, ApJ, 650, 128 [NASA ADS] [CrossRef] (In the text)
• McCarthy, I. G., Balogh, M. L., Babul, A., Poole, G. B., & Horner, D. J. 2004, ApJ, 613, 811 [NASA ADS] [CrossRef] (In the text)
• McCarthy, I. G., Babul, A., Bower, R. G., & Balogh, M. L. 2007, MNRAS, submitted [arXiv:0706.2768] (In the text)
• Maughan, B. J., Jones, C., Forman, W., & Van Speybroeck, L. 2007, ApJ, in press [arXiv:astro-ph/0703156] (In the text)
• Mohr, J. J., Evrard, A. E., Fabricant, D. G., & Geller, M. J. 1995, ApJ, 447, 8 [NASA ADS] [CrossRef] (In the text)
• Nagai, D., Vikhlinin, A., & Kravtsov, A. V. 2007, ApJ, 655, 98 [NASA ADS] [CrossRef] (In the text)
• Neumann, D. M. 2005, A&A, 439, 465 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Neumann, D. M., & Arnaud, M. 1999, A&A, 348, 711 [NASA ADS] (In the text)
• O'Hara, T. B., Mohr, J. J., Bialek, J. J., & Evrard, A. E. 2006, ApJ, 639, 64 [NASA ADS] [CrossRef] (In the text)
• Ota, N., & Mitsuda, K. 2004, A&A, 428, 757 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Pointecouteau, E., Arnaud, M., Kaastra, J., & de Plaa, J. 2004, A&A, 423, 33 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Pointecouteau, E., Arnaud, M., & Pratt, G. W. 2005, A&A, 435, 1 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Ponman, T. J., Sanderson, A. J. R., & Finoguenov, A. 2003, MNRAS, 343, 331 [NASA ADS] [CrossRef] (In the text)
• Poole, G. B., Fardal, M. A., Babul, A., et al. 2006, 373, 881 (In the text)
• Pratt, G. W., & Arnaud, M. 2002, A&A, 394, 375 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Pratt, G. W., & Arnaud, M. 2003, A&A, 408, 1 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Pratt, G. W., Arnaud, M., & Pointecouteau, E. 2006, A&A, 446, 429 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Pratt, G. W., Böhringer, H., Croston, J. H., et al. 2007, A&A, 461, 71 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Rasia, E., Mazzotta, P., Borgani, S., et al. 2005, ApJ, 618, L1 [NASA ADS] [CrossRef] (In the text)
• Rowley, D. R., Thomas, P. A., & Kay, S. T. 2004, MNRAS, 352, 181 [CrossRef] (In the text)
• Sanderson, A. J. R. S., Ponman, T. J., & O'Sullivan, E. 2006, MNRAS, 372, 1496 [NASA ADS] [CrossRef] (In the text)
• Springel, V. 2005, MNRAS, 364, 1105 [NASA ADS] [CrossRef] (In the text)
• Vikhlinin, A., Forman, W., & Jones, C. 1999, ApJ, 525, 47 [NASA ADS] [CrossRef] (In the text)
• Vikhlinin, A., Kravtsov, A., Froman, W., et al. 2006, ApJ, 640, 691 [NASA ADS] [CrossRef] (In the text)
• Voit, G. M. 2005, RevMP, 77, 207 [NASA ADS] (In the text)
• Voigt, L., & Fabian, A. C. 2004, MNRAS, 347, 1130 [NASA ADS] [CrossRef] (In the text)

 

  
Online Material

Appendix A: Surface brightness and density profiles

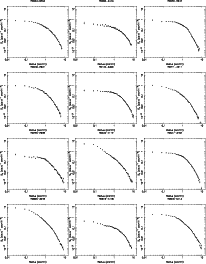	Figure A.1: Co-added MOS1, MOS2 and pn surface brightness profiles for the entire sample in the energy band 0.3-2.0 keV.
Open with DEXTER

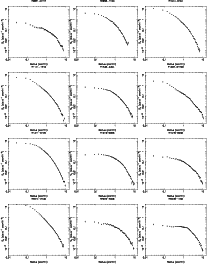	Figure A.1: continued.
Open with DEXTER

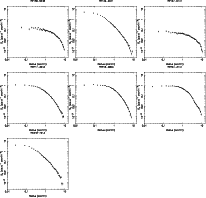	Figure A.1: continued.
Open with DEXTER

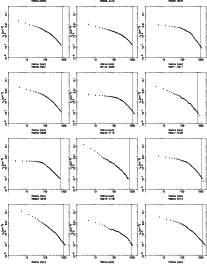	Figure A.2: Individual gas density profiles for the entire sample. Vertical lines indicate R500 for each cluster.
Open with DEXTER

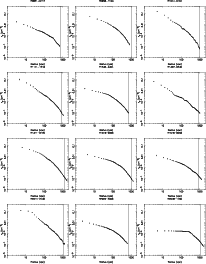	Figure A.2: continued.
Open with DEXTER

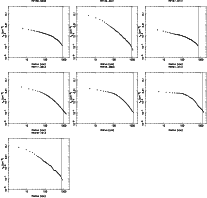	Figure A.2: continued.
Open with DEXTER

Appendix B: Gas density profiles in tabular form

Table B.1: Deprojected, PSF-corrected gas density profile for R0003.8+ 0203. Central co-ordinates are 0.957193, +2.065736 deg.

Table B.2: Deprojected, PSF-corrected gas density profile for R0006.0- 3443. Central co-ordinates are 1.501494, -34.722416 deg.

Table B.3: Deprojected, PSF-corrected gas density profile for R0020.7- 2542. Central co-ordinates are 5.175512, -25.708040 deg.

Table B.4: Deprojected, PSF-corrected gas density profile for R0049.4- 2931. Central co-ordinates are 12.345959, -29.520634 deg.

Table B.5: Deprojected, PSF-corrected gas density profile for R0145.0- 5300. Central co-ordinates are 26.243294, -53.020847 deg.

Table B.6: Deprojected, PSF-corrected gas density profile for R0211.4- 4017. Central co-ordinates are 32.852787, -40.291523 deg.

Table B.7: Deprojected, PSF-corrected gas density profile for R0225.1- 2928. Central co-ordinates are 36.287731, -29.477345 deg.

Table B.8: Deprojected, PSF-corrected gas density profile for R0345.7- 4112. Central co-ordinates are 56.442833, -41.20423 deg.

Table B.9: Deprojected, PSF-corrected gas density profile for R0547.6- 3152. Central co-ordinates are 86.908127, -31.872705 deg.

Table B.10: Deprojected, PSF-corrected gas density profile for R0605.8- 3518. Central co-ordinates are 91.475204, -35.302299 deg.

Table B.11: Deprojected, PSF-corrected gas density profile for R0616.8- 4748. Central co-ordinates are 94.215797, -47.794964 deg.

Table B.12: Deprojected, PSF-corrected gas density profile for R0645.4- 5413. Central co-ordinates are 101.371223, -54.227322 deg.

Table B.13: Deprojected, PSF-corrected gas density profile for R0821.8+ 0112. Central co-ordinates are 125.461357, +1.196681 deg.

Table B.14: Deprojected, PSF-corrected gas density profile for R0958.3- 1103. Central co-ordinates are 149.592957, -11.064354 deg.

Table B.15: Deprojected, PSF-corrected gas density profile for R1044.5- 0704. Central co-ordinates are 161.137039, -7.068715 deg.

Table B.16: Deprojected, PSF-corrected gas density profile for R1141.4- 1216. Central co-ordinates are 175.351334, -12.277625 deg.

Table B.17: Deprojected, PSF-corrected gas density profile for R1236.7- 3354. Central co-ordinates are 189.171173, -33.925987 deg.

Table B.18: Deprojected, PSF-corrected gas density profile for R1302.8- 0230. Central co-ordinates are 195.721649, -2.516951 deg.

Table B.19: Deprojected, PSF-corrected gas density profile for R1311.4- 0120. Central co-ordinates are 197.872711, -1.341458 deg.

Table B.20: Deprojected, PSF-corrected gas density profile for R1516.3+ 0005. Central co-ordinates are 229.074707, +0.089344 deg.

Table B.21: Deprojected, PSF-corrected gas density profile for R1516.5- 0056. Central co-ordinates are 229.184189, -0.969569 deg.

Table B.22: Deprojected, PSF-corrected gas density profile for R2014.8- 2430. Central co-ordinates are 303.715393, -24.505901 deg.

Table B.23: Deprojected, PSF-corrected gas density profile for R2023.0- 2056. Central co-ordinates are 305.744995, -20.948496 deg.

Table B.24: Deprojected, PSF-corrected gas density profile for R2048.1- 1750. Central co-ordinates are 312.041901, -17.841291 deg.

Table B.25: Deprojected, PSF-corrected gas density profile for R2129.8- 5048. Central co-ordinates are 322.427062, -50.816654 deg.

Table B.26: Deprojected, PSF-corrected gas density profile for R2149.1- 3041. Central co-ordinates are 327.281677, -30.701303 deg.

Table B.27: Deprojected, PSF-corrected gas density profile for R2157.4- 0747. Central co-ordinates are 329.367279, -7.804555 deg.

Table B.28: Deprojected, PSF-corrected gas density profile for R2217.7- 3543. Central co-ordinates are 334.440002, -35.726048 deg.

Table B.29: Deprojected, PSF-corrected gas density profile for R2218.6- 3853. Central co-ordinates are 334.667725, -38.901772 deg.

Table B.30: Deprojected, PSF-corrected gas density profile for R2234.5- 3744. Central co-ordinates are 338.612549, -37.736019 deg.

Table B.31: Deprojected, PSF-corrected gas density profile for R2319.6- 7313. Central co-ordinates are 349.916748, -73.227684 deg.