A&A 487, 671-687 (2008)
DOI: 10.1051/0004-6361:200809953
Simulations of eccentric disks in close binary systems
W. Kley1 -
J. C. B. Papaloizou2 -
G. I. Ogilvie2
1 - Institut für Astronomie & Astrophysik,
Universität Tübingen,
Auf der Morgenstelle 10, 72076 Tübingen, Germany
2 -
Department of Applied Mathematics and Theoretical Physics,
University of Cambridge,
Centre for Mathematical Sciences,
Wilberforce Road,
Cambridge, CB3 0WA, UK
Received 11 April 2008 / Accepted 23 June 2008
Abstract
Context. Eccentric accretion disks in superoutbursting cataclysmic and other binary systems.
Aims. We study the development of finite eccentricity in accretion disks in close binary systems using a grid-based numerical scheme. We perform detailed parameter studies to explore the dependence on viscosity, disk aspect ratio, the inclusion of a mass-transfer stream and the role of the boundary conditions.
Methods. Using a two-dimensional grid-based scheme we study the instability of accretion disks in close binary systems that causes them to attain a quasi-steady state with finite eccentricity. Mass ratios
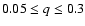 appropriate to superoutbursting cataclysmic binary systems are considered.
appropriate to superoutbursting cataclysmic binary systems are considered.
Results. Our grid-based scheme enables us to study the development of eccentric disks for disk aspect ratio h in the range
0.01-0.06 and dimensionless kinematic viscosity 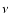 in the range
in the range
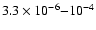 .
Previous studies using particle-based methods were limited to the largest values for these parameters on account of their diffusive nature. Instability to the formation of a precessing eccentric disk that attains a quasi-steady state with mean eccentricity in the range 0.3-0.5 occurs readily. The shortest growth times are
.
Previous studies using particle-based methods were limited to the largest values for these parameters on account of their diffusive nature. Instability to the formation of a precessing eccentric disk that attains a quasi-steady state with mean eccentricity in the range 0.3-0.5 occurs readily. The shortest growth times are  15 binary orbits for the largest viscosities and the instability mechanism is for the most part consistent with the mode-coupling mechanism associated with the 3:1 resonance proposed by Lubow. However, the results are sensitive to the treatment of the inner boundary and to the incorporation of the mass-transfer stream. In the presence of a stream we found a critical viscosity below which the disk remains circular.
15 binary orbits for the largest viscosities and the instability mechanism is for the most part consistent with the mode-coupling mechanism associated with the 3:1 resonance proposed by Lubow. However, the results are sensitive to the treatment of the inner boundary and to the incorporation of the mass-transfer stream. In the presence of a stream we found a critical viscosity below which the disk remains circular.
Conclusions. Eccentric disks readily develop in close binary systems with
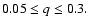 Incorporation of a mass-transfer stream tends to impart stability for small enough viscosity (or, equivalently, mass-transfer rate through the disk) and to assist in obtaining a prograde precession rate that is in agreement with observations. For the larger q the location of the 3:1 resonance is pushed outwards towards the Roche lobe where higher-order mode couplings and nonlinearity occur. It is likely that three-dimensional simulations that properly resolve the disk's vertical structure are required to make significant progress in this case.
Incorporation of a mass-transfer stream tends to impart stability for small enough viscosity (or, equivalently, mass-transfer rate through the disk) and to assist in obtaining a prograde precession rate that is in agreement with observations. For the larger q the location of the 3:1 resonance is pushed outwards towards the Roche lobe where higher-order mode couplings and nonlinearity occur. It is likely that three-dimensional simulations that properly resolve the disk's vertical structure are required to make significant progress in this case.
Key words: accretion, accretion disks - stars: binaries: close - novae, cataclysmic variables
1 Introduction
SU Ursae Majoris systems are a class of cataclysmic variable that
in addition to undergoing ordinary outbursts undergo less frequent
larger superoutbursts. During these, their light curves show superhumps which
have a period generally slightly longer than the orbital period
(for a discussion of relevant observations see for example Patterson et al. 2005; Ak et al. 2002).
A natural explanation of this phenomenon is that it is associated
with a rigidly precessing eccentric accretion disk.
Superoutbursts and superhumps are found to be limited to cataclysmic binaries
with mass ratio q < 0.35.Assuming that the difference between the superhump period and the orbital period
represents the solid body precession of an eccentric disk, Patterson et al. (2005)
discuss the establishment of
the expected correlation of this period with q.
Studies of the light curve and effects on it associated with the mass-transfer stream
impacting the disk
have enabled an eccentricity of
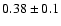 to be found for the disk in
OY Car by
Hessman et al. (1992), who also argue that the
normal superhumps are produced by tidal stresses after the maximally extended disk edge
approaches the companion.
Similar results for
IY UMa, which has a similar mass
ratio, were obtained by
Rolfe et al. (2001).
These authors also noted the potential importance of the impacting accretion
or mass-transfer stream
on the eccentric disk with its varying outer radius for understanding the late superhump light.
to be found for the disk in
OY Car by
Hessman et al. (1992), who also argue that the
normal superhumps are produced by tidal stresses after the maximally extended disk edge
approaches the companion.
Similar results for
IY UMa, which has a similar mass
ratio, were obtained by
Rolfe et al. (2001).
These authors also noted the potential importance of the impacting accretion
or mass-transfer stream
on the eccentric disk with its varying outer radius for understanding the late superhump light.
These observations motivate an interest in developing
good numerical schemes for simulating accretion disks undergoing tidal
interaction with a secondary binary component.
Although, starting with Whitehurst (1988), there have been many simulations of eccentric disks
using particle-based methods
(e.g. Smith et al. 2007; Kunze et al. 1997; Murray 1998, and references therein)
there has been almost no grid-based work
to date that is applicable to close binary systems,
even though such an approach, apart from constituting a check,
is promising in the context of being able to gain access to a wider region
of parameter space that may be difficult to access with particle-based methods.
Heemskerk (1994) performed grid-based simulations, but without
including disk viscosity and was only able to
obtain an eccentric disk when only the m=3 component
of the companion's tidal potential was retained.
Subsequent grid-based simulations by Stehle (1999) and Kornet & Rozyczka (2000)
also did not show clear evidence for the onset of an eccentric instability.
Papaloizou (2005) solved the linearized equations for the
m=1 mode of a free disk
without a binary companion and considered the possible development of
a parametric instability when the vertical structure was incorporated.
A study of eccentric disks also has application to other areas of astrophysics
where disks and orbiting companions interact.
Thus Kley & Dirksen (2006) have studied eccentric disks
in the context of the very small mass ratios appropriate to disk-planet interactions
where their existence may have important consequences for theories
of planet formation.
Motivated by these considerations, the aim of this paper is
to make an extensive study of the dynamics of two-dimensional disks that lie
in the orbital plane of a binary system, which consists of a primary star and a
lower-mass secondary star in a circular orbit.
The disk is centred on the primary star in a binary system with mass ratio in the range
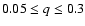 thought to be
relevant for superoutbursting cataclysmic binaries.
We perform grid-based simulations of disks
that are initialised with circular motion, in order to study
the onset of an eccentric instability
and the properties of the resulting quasi-stationary eccentric disk.
Use of a grid-based rather than a particle-based
method enables consideration of disks with a wider range of viscosities
and more realistic aspect ratios in the range
0.01-0.05 that are
presently difficult to access for particle-based methods such as SPH
due to their inherently diffusive nature (but see Schäfer et al. 2004).
We establish numerical convergence and
explore the dependence of the results on the physical parameters of the disk.
We also consider variations of the inner
boundary conditions and the presence of a mass-transfer stream.
Due to the global nature of the eccentric disk mode, results are found to be sensitive
to these.
When a stream is present we are able to find a transition to stability when the
viscosity is reduced below a critical value. We also find that incorporation
of a mass-transfer stream is important for obtaining values for the
disk precession frequency that are compatible with observations.
thought to be
relevant for superoutbursting cataclysmic binaries.
We perform grid-based simulations of disks
that are initialised with circular motion, in order to study
the onset of an eccentric instability
and the properties of the resulting quasi-stationary eccentric disk.
Use of a grid-based rather than a particle-based
method enables consideration of disks with a wider range of viscosities
and more realistic aspect ratios in the range
0.01-0.05 that are
presently difficult to access for particle-based methods such as SPH
due to their inherently diffusive nature (but see Schäfer et al. 2004).
We establish numerical convergence and
explore the dependence of the results on the physical parameters of the disk.
We also consider variations of the inner
boundary conditions and the presence of a mass-transfer stream.
Due to the global nature of the eccentric disk mode, results are found to be sensitive
to these.
When a stream is present we are able to find a transition to stability when the
viscosity is reduced below a critical value. We also find that incorporation
of a mass-transfer stream is important for obtaining values for the
disk precession frequency that are compatible with observations.
The plan of the paper is as follows. In Sect. 2 we describe the hydrodynamic model.
We then go on to describe the numerical methods we use in Sect. 2.2.
Numerical simulations showing the growth of eccentricity
for a typical disk model are then presented in Sect. 3.
It is found that a quasi-stationary eccentric disk with mean eccentricity in the range
0.3-0.5 is often produced.
We explore the dependence of this phenomenon on
disk viscosity,
aspect ratio and the inner boundary condition in Sect. 4,
showing that the development of an eccentric disk
is favoured at high viscosity but, because it is a global phenomenon,
it is sensitive to the treatment of the disk inner boundary.
The quasi-stationary eccentric disk is found to precess
as a rigid body. In this section we also study
the dependence of the disk precession rate
on the disk aspect ratio and boundary conditions showing that
the precession rate is prograde for cool enough disks.
We then investigate the dependence of the tendency of the
disk to become eccentric on the binary mass ratio in
Sect. 5 and discuss numerical resolution demonstrating
the numerical convergence of our results in Sect. 6.
In Sect. 7 we explore the instability
mechanism and establish the importance of the m=3 component
of the tidal potential for causing the instability
through the mode-coupling mechanism proposed by Lubow (1991a).
Comparison with a linear analysis of eccentric modes is made in Sect. 8.
We go on to investigate the effect of a
mass-transfer stream in Sect. 9.
This is shown to make an important contribution to the disk precession rate
and also to cause the disk to become stable to developing
eccentricity for sufficiently small viscosity.
Finally in Sect. 10 we summarize and discuss our results.
2 Hydrodynamical model
To model a flat two-dimensional disk we generally use a cylindrical (
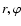 )
coordinate system centred
on the primary star that corotates with the binary.
The latter is assumed to have a circular orbit and thus to rotate uniformly.
This coordinate system is
convenient because the positions
of the two stars remain fixed during the simulations.
We have checked that the same results
are obtained when simulations are run in the inertial frame.
The disk material is treated as a viscous fluid with a constant kinematic shear viscosity and
(except where noted below) vanishing bulk viscosity.
)
coordinate system centred
on the primary star that corotates with the binary.
The latter is assumed to have a circular orbit and thus to rotate uniformly.
This coordinate system is
convenient because the positions
of the two stars remain fixed during the simulations.
We have checked that the same results
are obtained when simulations are run in the inertial frame.
The disk material is treated as a viscous fluid with a constant kinematic shear viscosity and
(except where noted below) vanishing bulk viscosity.
For a flat disk located
in the orbital plane z=0, the
velocity components are
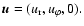 Thus
Thus
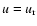 is the radial velocity
and the local disk angular velocity is
is the radial velocity
and the local disk angular velocity is
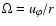 as measured in the corotating frame which rotates with the constant angular
velocity,
as measured in the corotating frame which rotates with the constant angular
velocity, 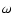 ,
of the binary.
,
of the binary.
The vertically integrated continuity equation is
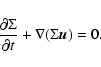 |
(1) |
The vertically integrated radial component of the equation of motion is
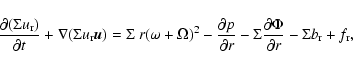 |
(2) |
and the azimuthal component can be written in the form
![\begin{displaymath}\frac{\partial [\Sigma r^2 (\omega + \Omega)]}{\partial t}
...
...artial \varphi}
- r \Sigma b_{\rm\varphi} + r f_{\rm\varphi}.
\end{displaymath}](/articles/aa/full/2008/32/aa09953-08/img41.gif) |
(3) |
Here 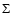 denotes the surface density
denotes the surface density
where 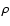 is the density, p the
vertically integrated (two-dimensional) pressure. The
gravitational potential
is the density, p the
vertically integrated (two-dimensional) pressure. The
gravitational potential 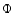 is due the primary
with mass M1 and the secondary having mass M2 and is given by
is due the primary
with mass M1 and the secondary having mass M2 and is given by
where G is the gravitational constant and 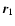 and
and
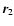 are the position vectors of M1 and M2, respectively.
Since the mass of the disk in cataclysmic variables is only about
are the position vectors of M1 and M2, respectively.
Since the mass of the disk in cataclysmic variables is only about
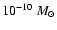 we can safely neglect the self-gravity of the disk
as well as its influence on the binary orbit.
The additional terms
we can safely neglect the self-gravity of the disk
as well as its influence on the binary orbit.
The additional terms
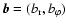 take into account the
acceleration of the origin of the coordinate system.
Rotation of the coordinate axes
is taken account of through the terms involving
take into account the
acceleration of the origin of the coordinate system.
Rotation of the coordinate axes
is taken account of through the terms involving 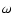 .
The viscous force per unit area is
.
The viscous force per unit area is
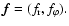 The explicit form of the components of
The explicit form of the components of 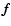 is given in Kley (1999).
is given in Kley (1999).
For simplicity we use a locally isothermal equation of state
where the vertically integrated
pressure p is related to the surface density and
sound speed through
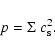 |
(4) |
The local isothermal sound speed 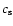 is taken to have
a fixed dependence on radius
and is given
by
is taken to have
a fixed dependence on radius
and is given
by
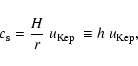 |
(5) |
where
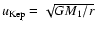 denotes the Keplerian orbital velocity
of the unperturbed disk that would exist in the absence of the binary companion.
Equation (5) follows from vertical hydrostatic equilibrium.
The constant ratio h of the vertical height H to the
radial distance to the primary, r, is taken as a fixed input parameter.
Here we adopt a
standard value of
denotes the Keplerian orbital velocity
of the unperturbed disk that would exist in the absence of the binary companion.
Equation (5) follows from vertical hydrostatic equilibrium.
The constant ratio h of the vertical height H to the
radial distance to the primary, r, is taken as a fixed input parameter.
Here we adopt a
standard value of
This is somewhat large when compared to values expected for
disks in cataclysmic binary systems (Smith et al. 2007),
but smaller values are also considered below.
We adopt a system of units for which
the unit of length is taken to be the orbital separation of the
binary,
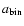 .
The unit of time, t0, is taken to be
the reciprocal of the orbital angular frequency
.
The unit of time, t0, is taken to be
the reciprocal of the orbital angular frequency 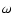 of the binary. Thus
of the binary. Thus
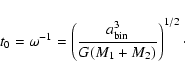 |
(7) |
The orbital period of the binary is then given by
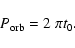 |
(8) |
The results of calculations
will usually be expressed as a function of the evolution time
in units of
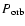 .
The unit of velocity is
given by
.
The unit of velocity is
given by
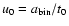 .
Setting the gravitational constant G to be unity,
Eq. (7) can be also viewed as specifying the unit of mass
to be the total mass of the system
M = M1 + M2.The surface density can be scaled by any constant value
.
Setting the gravitational constant G to be unity,
Eq. (7) can be also viewed as specifying the unit of mass
to be the total mass of the system
M = M1 + M2.The surface density can be scaled by any constant value
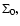 because this drops out of the governing equations. Accordingly
the surface density may be scaled to make the total disk mass
be any specified value.
The kinematic viscosity coefficient,
because this drops out of the governing equations. Accordingly
the surface density may be scaled to make the total disk mass
be any specified value.
The kinematic viscosity coefficient, 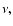 is expressed in units of
is expressed in units of
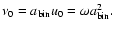
2.2 Numerical methods
The governing Eqs. (1)-(3) determining the
evolution of 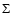 ,
u and
,
u and 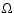 are
solved using an Eulerian finite-difference scheme.
The computational domain
are
solved using an Eulerian finite-difference scheme.
The computational domain
![$[r_{\rm min}, r_{\rm max}] \times
[\varphi_{\rm min}, \varphi_{\rm max}]$](/articles/aa/full/2008/32/aa09953-08/img66.gif) is subdivided into
is subdivided into
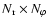 grid cells that are equally spaced in each coordinate direction.
For typical runs we use
grid cells that are equally spaced in each coordinate direction.
For typical runs we use
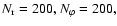 though many have been checked at the higher resolution
though many have been checked at the higher resolution
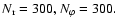
The numerical method utilises a staggered mesh,
where scalar quantities are located at cell centres and vector quantities
at cell interfaces. We adopt an
operator-split scheme for which advection is based on the
spatially 2nd order monotonic transport algorithm of van Leer (1977), and
the viscosity can be treated either explicitly or implicitly.
The basic features of the two-dimensional code RH2D
that we use have been described
in more detail in Kley (1989). The
use of the code in cylindrical
 coordinates has been described
in Kley (1999).
coordinates has been described
in Kley (1999).
Implementation in a rotating coordinate system
requires special treatment of the Coriolis terms
to ensure angular momentum conservation
(Kley 1998).
To prevent possible instabilities due to shocks, that could
for example be generated by the
tidal perturbation of the
secondary, we use
an artificial bulk viscosity as described in Kley (1999).
This is in addition to the physical shear viscosity  We note, that an excellent test of the correct implementation of viscosity in
numerical simulations of accretion disks is the study of non-axisymmetric instabilities
in the viscously spreading ring problem (Speith & Kley 2003).
We note, that an excellent test of the correct implementation of viscosity in
numerical simulations of accretion disks is the study of non-axisymmetric instabilities
in the viscously spreading ring problem (Speith & Kley 2003).
In addition, to prevent numerical instabilities due to very low densities (or very steep density
gradients) near the outer boundary of the disk, where it is tidally
truncated by the secondary,
we introduce a ``density floor'',
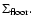 This is applied such that
whenever evolution causes the density at any location
to fall below
This is applied such that
whenever evolution causes the density at any location
to fall below
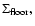 it is reset to this value.
Formally, this implementation
does not conserve mass exactly, but for sufficiently low values it does not produce
any influence on the dynamics.
In all simulations we use a value of
it is reset to this value.
Formally, this implementation
does not conserve mass exactly, but for sufficiently low values it does not produce
any influence on the dynamics.
In all simulations we use a value of
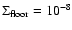 expressed in units such that the initial value of
expressed in units such that the initial value of
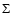 at
at
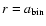 would be unity in the absence of tidal truncation (i.e. in units of
would be unity in the absence of tidal truncation (i.e. in units of 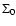 defined in Eq. (10) below).
We test the dynamical influence of the floor
in Sect. 4.3 below.
defined in Eq. (10) below).
We test the dynamical influence of the floor
in Sect. 4.3 below.
Since this is an explicit code, the timestep limitation is given by the Courant condition
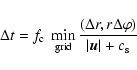 |
(9) |
where the Courant number 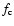 has to be smaller than one, and we typically use
has to be smaller than one, and we typically use
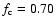 .
After a few test simulations it soon became clear that, due to the large
range in radius with
.
After a few test simulations it soon became clear that, due to the large
range in radius with
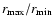 typically larger than 10,
the required computational times become excessive because of the stringent timestep limitation
arising from the inner boundary. This occurs because the Keplerian
angular velocity increases rapidly as the primary star is approached according to
typically larger than 10,
the required computational times become excessive because of the stringent timestep limitation
arising from the inner boundary. This occurs because the Keplerian
angular velocity increases rapidly as the primary star is approached according to
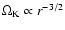 .
This results in approximately
25 000 timesteps being required for one binary orbit with our standard resolution.
As typically a few hundred orbital times need to be calculated per run, this necessitates
about 10 million timesteps for each run.
Exploration of a large parameter space would be prohibitive.
For that purpose we implemented the FARGO algorithm
(Masset 2000) into our RH2D code.
In this algorithm, for each annular grid ring,
the mean angular velocity
.
This results in approximately
25 000 timesteps being required for one binary orbit with our standard resolution.
As typically a few hundred orbital times need to be calculated per run, this necessitates
about 10 million timesteps for each run.
Exploration of a large parameter space would be prohibitive.
For that purpose we implemented the FARGO algorithm
(Masset 2000) into our RH2D code.
In this algorithm, for each annular grid ring,
the mean angular velocity
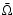 is calculated
and all variables are simply shifted by an integer number of grid cells, corresponding
to an advection velocity as close as possible to
is calculated
and all variables are simply shifted by an integer number of grid cells, corresponding
to an advection velocity as close as possible to
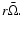 Advection is then only performed using the residual velocity, leading to a substantially
increased timestep.
This method leads,
for our standard parameters using an equidistant grid, to a speed-up by a factor of about 5.
Advection is then only performed using the residual velocity, leading to a substantially
increased timestep.
This method leads,
for our standard parameters using an equidistant grid, to a speed-up by a factor of about 5.
Additional test simulations have shown that for cases that do not use the
FARGO algorithm, numerical instabilities due to very small
densities are likely to occur in the outer region. These could only be avoided
by further reducing the timestep or adopting an implicit treatment of viscosity, both of which
result in additional computational cost.
A higher density floor also helps to reduce these instabilities but to avoid them
entirely (and still use a large timestep) one would need unreasonably large values that
possibly influence the dynamics; see the discussion on boundary conditions in Sect. 4.3
below.
Here, the use of the faster advection algorithm enhances the
stability properties, allowing an explicit treatment of viscosity.
A few comparison simulations that do not use FARGO, but allowed a reduced
timestep, were performed
to check the accuracy of our method
using the NIRVANA code (Ziegler 1998).
Finally, we note that the order of the applied numerical scheme matters in obtaining the eccentric state
of the disk. Switching to a simple first order upwind scheme does not result in eccentric
disks no matter how fine the grid resolution is chosen. For the 2nd order upwind scheme the
different choices of the slope-limiter all yield very similar results.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{9953f01.eps} \end{figure}](/articles/aa/full/2008/32/aa09953-08/Timg84.gif) |
Figure 1:
The grid structure used in the computations. The radial domain is
![$[r_{\rm min}, r_{\rm max}] = [0.05, 0.70]$](/articles/aa/full/2008/32/aa09953-08/img1.gif) and the
and the 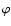 domain
is the whole annulus
domain
is the whole annulus
![$[0, 2\pi ].$](/articles/aa/full/2008/32/aa09953-08/img3.gif) For our standard case this is covered with For our standard case this is covered with
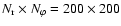 grid cells that are equally spaced in each direction. The Roche lobe of the primary, for
our standard mass ratio
q = M2/M1 = 0.1, is
defined by the additional solid (red) line. The primary and secondary star are located at
( grid cells that are equally spaced in each direction. The Roche lobe of the primary, for
our standard mass ratio
q = M2/M1 = 0.1, is
defined by the additional solid (red) line. The primary and secondary star are located at
(
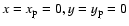 )
and ( )
and (
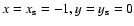 )
respectively.
Note that in this figure, for illustrative purposes,
we display a low-resolution )
respectively.
Note that in this figure, for illustrative purposes,
we display a low-resolution
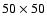 grid. grid.
|
| Open with DEXTER |
2.3 Setup and boundary conditions
The coordinate system is centred on the primary star and, because it
corotates with the binary system, the position of the secondary in Cartesian coordinates is
fixed at x=-1, y=0 (see Fig. 1).
For the radial domain we adopt
![$[r_{\rm min}, r_{\rm max}]$](/articles/aa/full/2008/32/aa09953-08/img85.gif) where
where
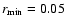 and
and
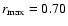 for all models
in units where the binary separation is unity.
The azimuthal domain is taken to be
for all models
in units where the binary separation is unity.
The azimuthal domain is taken to be
![$[0, 2\pi ].$](/articles/aa/full/2008/32/aa09953-08/img3.gif)
For the initial surface density profile, for r <0.4in dimensionless units, we adopt a power law of the form
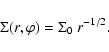 |
(10) |
For r>0.4, 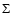 is reduced smoothly towards
a minimum value of
is reduced smoothly towards
a minimum value of
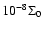 .
The initial velocity is taken to be pure Keplerian rotation around the primary star
as would be measured in an inertial frame
(
.
The initial velocity is taken to be pure Keplerian rotation around the primary star
as would be measured in an inertial frame
(
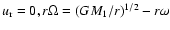 ). No correction is made
for pressure effects or the non-axisymmetric binary potential. The
presence of the secondary star is allowed to cause the surface density
distribution to evolve away from the initial
profile on a dynamical timescale.
This normally causes a rapid adjustment of the
outer profile through tidal truncation of the disk.
The fixed temperature stratification is always given by
). No correction is made
for pressure effects or the non-axisymmetric binary potential. The
presence of the secondary star is allowed to cause the surface density
distribution to evolve away from the initial
profile on a dynamical timescale.
This normally causes a rapid adjustment of the
outer profile through tidal truncation of the disk.
The fixed temperature stratification is always given by
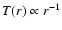 which follows from the assumed constant aspect ratio
which follows from the assumed constant aspect ratio
In the azimuthal ( )
direction, periodic boundary conditions
for all variables are imposed. At the outer radial boundary of the grid
which extends somewhat beyond the Roche lobe of the primary
(see Fig. 1) we use standard outflow
boundary conditions. This imposes
zero gradient conditions on all variables apart from the radial velocity, i.e. the values in the ambient ghost cells
have the same values as the last active grid point.
The radial velocity at the ambient ghost cell
is set equal to the value at
)
direction, periodic boundary conditions
for all variables are imposed. At the outer radial boundary of the grid
which extends somewhat beyond the Roche lobe of the primary
(see Fig. 1) we use standard outflow
boundary conditions. This imposes
zero gradient conditions on all variables apart from the radial velocity, i.e. the values in the ambient ghost cells
have the same values as the last active grid point.
The radial velocity at the ambient ghost cell
is set equal to the value at
 if the flow direction is outward (zero gradient condition) and zero otherwise.
This outflow condition allows material to leave the system but inflow is
not permitted.
if the flow direction is outward (zero gradient condition) and zero otherwise.
This outflow condition allows material to leave the system but inflow is
not permitted.
As we found that the form of the boundary condition applied at the inner boundary
may play an important role in determining the characteristics of the
flow, we implemented four different boundary conditions at
 :
:
We found from our numerical simulations that
the form of the inner boundary condition can make quite a difference
in the results concerning the eccentricity and precession rate of the disk.
3 Standard model
To study the effect of varying the physical and numerical
parameters defining the simulations, we first consider in detail a standard model
for use
as a reference for the extensive parameter studies we have performed.
The parameters defining this model are summarized in Table 1.
Table 1:
Parameters of the standard model. Values are quoted in dimensionless
units.
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{9953f02.eps}
\end{figure}](/articles/aa/full/2008/32/aa09953-08/Timg100.gif) |
Figure 2:
Greyscale plot of the surface density of the disk for the
standard model after 1 binary orbit.
The solid (red) curve indicates the Roche lobe of the primary star (central red dot). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9953f03.eps} \end{figure}](/articles/aa/full/2008/32/aa09953-08/Timg101.gif) |
Figure 3:
Greyscale plot of the surface density of the disk for the
standard model at
100, 150, 175 and 200 orbital periods. The solid (red) curve
indicates the Roche lobe of the primary star (central red dot).
|
| Open with DEXTER |
We now describe the characteristic behaviour of the standard model.
Due to the strong gravitational perturbation induced by the secondary,
the initial axisymmetry of the disk is rapidly destroyed and a strong two-armed spiral density
response is formed. This is shown in Fig. 2 where the surface density
is displayed after the system has evolved for one orbital period of the binary.
The two-armed spiral which is strongest in the
outer disk region but extends all the way through the disk down to the primary star
is clearly visible.
The surface density shows some evidence for a non-axisymmetric pattern
near the inner boundary of the disk, confined to the innermost
two radial gridcells. Such a feature (here a m=6 mode) is generated
typically in grid-based simulations with reflecting inner boundary conditions, and is
not a consequence of using the FARGO-algorithm.
It can be reduced or minimised by using special,
non-reflecting or damping, boundary conditions.
After the onset of the eccentric instability this feature dissapears in the simulation.
In the subsequent evolution the disk slowly becomes eccentric. This is indicated
in Fig. 3 where we display
the two-dimensional surface density structure at four different times.
The distortion of the disk is evident at later times. While in the first snapshot
taken after 100 orbits there is only a slight indication of disk eccentricity, the subsequent panels
demonstrate a growing eccentric disk mode and one can infer the presence
of an apsidal line joining
the locations of minimum and maximum displacements from the primary. Additionally there is
indication for precession of this apsidal line.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9953f04.eps} \end{figure}](/articles/aa/full/2008/32/aa09953-08/Timg102.gif) |
Figure 4:
Radial distribution of the azimuthally averaged surface density 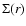 at different times. The solid black curve indicates the tapered initial
profile. at different times. The solid black curve indicates the tapered initial
profile.
|
| Open with DEXTER |
The tidal torques induced by the secondary also lead to a truncation of the disk
and a rearrangement of the (mean) radial surface density profile. This
is demonstrated in Fig. 4 where the azimuthally averaged
density is shown at 5 different times. The solid black curve indicates
the initial (axisymmetric) profile,
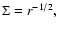 with
a taper applied for r>0.4. Clearly, the disk becomes truncated at a radius around
with
a taper applied for r>0.4. Clearly, the disk becomes truncated at a radius around
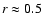 where the surface density starts to drop much more steeply. After about 250 orbits
the average surface density distribution attains a new quasi-stationary profile (see below).
where the surface density starts to drop much more steeply. After about 250 orbits
the average surface density distribution attains a new quasi-stationary profile (see below).
![\begin{figure}
\par\includegraphics[width=4cm,clip]{9953f05a.eps}\hspace*{4mm}
\...
....eps}\hspace*{4mm}
\includegraphics[width=3.8cm,clip]{9953f05d.eps} \end{figure}](/articles/aa/full/2008/32/aa09953-08/Timg105.gif) |
Figure 5:
Evolution of various global disk properties of the standard model as functions of time. The total mass in the computational domain, or equivalently the
disk mass, is shown in the upper left panel. The disk radius, defined as the
radius containing 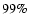 of the mass, is shown in the upper right panel.
The disk eccentricity is shown in the lower left panel and the
m=1 and m=2 Fourier amplitudes are shown in the lower right panel.
of the mass, is shown in the upper right panel.
The disk eccentricity is shown in the lower left panel and the
m=1 and m=2 Fourier amplitudes are shown in the lower right panel. |
| Open with DEXTER |
In Fig. 5 we display the time-evolution of several global disk
quantities (in dimensionless units).
The total mass in the computational domain is seen to drop off rapidly within the first 2 orbits due to the initial mass loss
through the outer boundary induced by the tidal perturbation of the secondary
(see also Fig. 2).
After this initial
burst of mass loss, the disk is tidally truncated, such that
as seen in Fig. 5, the disk radius, defined to be the radius
containing 99% of the mass, is reduced from 0.61 to 0.48. This is then smaller
than the Roche lobe. The mass subsequently remains constant until
 The disk radius reaches a minimum at around
The disk radius reaches a minimum at around
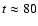 ,
and increases slowly thereafter.
This increase of the radius of the disk is coupled with an increase in the
mean eccentricity
,
and increases slowly thereafter.
This increase of the radius of the disk is coupled with an increase in the
mean eccentricity 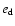 of the disk which is displayed in the bottom left panel of Fig. 5.
The quantity
of the disk which is displayed in the bottom left panel of Fig. 5.
The quantity 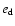 is determined by first calculating the eccentricity
for each individual gridcell assuming that it is in an unperturbed orbit around
the central star, with the position and velocity given by the actual grid values
averaged to the cell centres. To obtain the global value
is determined by first calculating the eccentricity
for each individual gridcell assuming that it is in an unperturbed orbit around
the central star, with the position and velocity given by the actual grid values
averaged to the cell centres. To obtain the global value 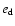 we then
perform a mass-weighted average over the individual cell values.
The longitude of the disk's periastron
we then
perform a mass-weighted average over the individual cell values.
The longitude of the disk's periastron
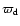 is calculated in
the same way. The explicit formulae are given for example in Murray & Dermott (1999).
is calculated in
the same way. The explicit formulae are given for example in Murray & Dermott (1999).
As seen in Fig. 5, 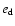 begins to exponentiate after
begins to exponentiate after
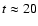 with
an e-folding time of about 80 orbits. After about 250 orbits the eccentricity
has settled to a final value of
with
an e-folding time of about 80 orbits. After about 250 orbits the eccentricity
has settled to a final value of
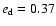 with an average
outer disk radius
with an average
outer disk radius
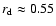 .
The increase in
.
The increase in 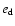 is
also associated with a further decrease in the disk mass.
Beyond
is
also associated with a further decrease in the disk mass.
Beyond
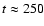 mass spills over the Roche lobe and is lost from the system.
This mass loss does not affect the dynamics of the system (i.e. it
does not change the
equilibrium values of
mass spills over the Roche lobe and is lost from the system.
This mass loss does not affect the dynamics of the system (i.e. it
does not change the
equilibrium values of 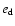 and
and 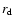 )
because the absolute value of the
mass density scales out of the evolution equations.
This feature has been confirmed numerically
in additional test calculations where the total mass in the system is kept constant by rescaling
the density of all grid cells at each timestep in order
to account for the lost mass.
In the bottom right panel of Fig. 5 the time-evolution
of the m=1 and m=2 surface density Fourier amplitudes
calculated at a single
disk radius (r=0.37) are displayed.
The m=1 mode associated with the eccentricity
increases exponentially from the beginning of the run up to
)
because the absolute value of the
mass density scales out of the evolution equations.
This feature has been confirmed numerically
in additional test calculations where the total mass in the system is kept constant by rescaling
the density of all grid cells at each timestep in order
to account for the lost mass.
In the bottom right panel of Fig. 5 the time-evolution
of the m=1 and m=2 surface density Fourier amplitudes
calculated at a single
disk radius (r=0.37) are displayed.
The m=1 mode associated with the eccentricity
increases exponentially from the beginning of the run up to
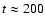 after
which induced additional mass loss leads to a reduction
in the amplitude. To show the evolution more clearly we have plotted here
only the first 200 orbits.
The only other Fourier amplitude that plays a significant role is
that associated with m=2, which at early times (when
the spiral arm feature dominates the disk) is much larger than the m=1amplitude, but it becomes weaker
at later times. In the final stages
it increases again, saturating eventually at a value still
smaller than the m=1 amplitude.
after
which induced additional mass loss leads to a reduction
in the amplitude. To show the evolution more clearly we have plotted here
only the first 200 orbits.
The only other Fourier amplitude that plays a significant role is
that associated with m=2, which at early times (when
the spiral arm feature dominates the disk) is much larger than the m=1amplitude, but it becomes weaker
at later times. In the final stages
it increases again, saturating eventually at a value still
smaller than the m=1 amplitude.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9953f06.eps} \end{figure}](/articles/aa/full/2008/32/aa09953-08/Timg114.gif) |
Figure 6:
Time-evolution of the longitude of pericentre (periastron) of the disk.
The solid darker (red) curve is the mass-weighted mean pericentre over the whole disk, calculated
as described in the text. The lighter dashed (green) curve corresponds to a phase of the
m=1 Fourier mode at the single radius r=0.37. Note that the phases are calculated in the
inertial frame.
|
| Open with DEXTER |
As mentioned above, Fig. 3 indicates
global precession of the eccentric disk.
This is quantified in Fig. 6 where the solid
(red) curve corresponds to the time-evolution of the longitude of pericentre
(periastron) of the disk,
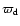 ,
calculated in the same manner as
,
calculated in the same manner as 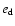 .
Obviously the disk precesses as a whole at a constant rate, a feature that is supported by the additional
light (green) curve which corresponds to the phase of the m=1 Fourier component at
one given radius r=0.37. Both angles precess at the same rate,
confirming our interpretation. The periodic disturbances
in
.
Obviously the disk precesses as a whole at a constant rate, a feature that is supported by the additional
light (green) curve which corresponds to the phase of the m=1 Fourier component at
one given radius r=0.37. Both angles precess at the same rate,
confirming our interpretation. The periodic disturbances
in
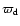 coincide with the times when the disk's apocentre
is closest to the
secondary star. In this case the outer parts of the eccentric disk are strongly disturbed
which renders the calculation of
coincide with the times when the disk's apocentre
is closest to the
secondary star. In this case the outer parts of the eccentric disk are strongly disturbed
which renders the calculation of
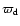 more inaccurate.
From the plot, which shows the phases in the inertial frame, we conclude that the disk
experiences a slow retrograde precession with a period
more inaccurate.
From the plot, which shows the phases in the inertial frame, we conclude that the disk
experiences a slow retrograde precession with a period
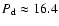 orbits.
orbits.
![\begin{figure}
\par\includegraphics[width=4cm,clip]{9953f07a.eps}\hspace*{4mm}
\includegraphics[width=4cm,clip]{9953f07b.eps} \end{figure}](/articles/aa/full/2008/32/aa09953-08/Timg116.gif) |
Figure 7:
Radial variation of the eccentricity and longitude of pericentre of the
disk at various times (quoted in binary orbits).
|
| Open with DEXTER |
To study the internal structure of the disk we show in Fig. 7 the disk's
radial distribution of eccentricity and the longitude of pericentre
at different times (indicated by the
legend) which lie within the time interval plotted in Fig. 6.
The distribution of eccentricity within the disk does not vary much with
the binary orbital phase and drops
smoothly towards zero in the centre of the disk, due to the rigid boundary at the inner radius.
In the main part of the
disk the eccentricity lies around e=0.4 which is consistent with two-dimensional
surface plots of the density (see the snapshot at t=200 in Fig. 3).
The radial variation of the pericentre indicates a small twist within the
innermost parts of the disk,
which is larger when the disk's apocentre is closest to the secondary star
(at times 351 and 352) when it can reach about 45 degrees.
In addition, the fact that the curves
at different times appear vertically shifted indicates again the
precession of the disk as a single entity.
4 Dependence on viscosity, temperature and the inner boundary condition
4.1 Viscosity
The first parameter we investigate is the kinematic viscosity 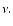 To study dependence of the results on the magnitude of the kinematic
viscosity we started from our standard model (
To study dependence of the results on the magnitude of the kinematic
viscosity we started from our standard model (
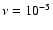 )
and varied
only the value of
)
and varied
only the value of 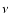 keeping all other parameters unchanged.
keeping all other parameters unchanged.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{9953f08.eps} \end{figure}](/articles/aa/full/2008/32/aa09953-08/Timg118.gif) |
Figure 8:
Time-evolution of the mean eccentricity of the disk
(natural logarithm) for
different kinematic viscosities (in dimensionless units).
|
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=4cm,clip]{9953f09a.eps}\hspace*{4mm}
\...
...9c.eps}\hspace*{4mm}
\includegraphics[width=4cm,clip]{9953f09d.eps} \end{figure}](/articles/aa/full/2008/32/aa09953-08/Timg121.gif) |
Figure 9:
Dependence of various global disk parameters on the magnitude of the viscosity.
upper left panel: growth rate of the eccentricity of the disk; upper right
panel: the radius,
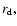 within
which 99% of the mass of the disk is contained; lower left panel: the mass-weighted
mean eccentricity of the disk
within
which 99% of the mass of the disk is contained; lower left panel: the mass-weighted
mean eccentricity of the disk 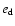 ;
lower right panel: precession rate of the disk ;
lower right panel: precession rate of the disk
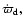 negative values indicating retrograde precession. The values for negative values indicating retrograde precession. The values for 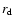 , ,
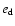 and
and
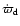 are
determined at a time at which the system reaches its final quasi-steady state.
are
determined at a time at which the system reaches its final quasi-steady state.
|
| Open with DEXTER |
The variation of the mean disk eccentricity
with time is displayed for different kinematic
viscosities in Fig. 8, where the middle (green) curve refers
to the standard model which (for reference) has been displayed already in
Fig. 5 at early times.
The growth rate of the eccentricity depends strongly on the magnitude
of the viscosity: increasing the viscosity shortens the growth time substantially,
while for smaller viscosities it takes much longer for the disk to become eccentric.
For the lowest-viscosity model (
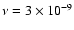 ), which corresponds essentially
to an inviscid calculation, the disk does not attain significant eccentricity
in a run time of 1000 orbits. However, there is an indication
that there may be a very long-term eccentricity growth produced by numerical effects. From the upper left
panel of Fig. 9 a simple extrapolation indicates a limiting
value of
), which corresponds essentially
to an inviscid calculation, the disk does not attain significant eccentricity
in a run time of 1000 orbits. However, there is an indication
that there may be a very long-term eccentricity growth produced by numerical effects. From the upper left
panel of Fig. 9 a simple extrapolation indicates a limiting
value of 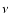 for which the disk becomes eccentric of
for which the disk becomes eccentric of
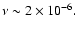 Already the growth time for
Already the growth time for
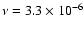 is
is 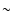 162 orbits.
In general the models settle to a quasi-stationary state with a constant eccentricity, which
decreases as the viscosity decreases. However, quasi-steady states with mean
eccentricities below e =0.36 do not seem to be reached for this
model by decreasing the viscosity alone. But then a longer time is
required for this value to be attained.
162 orbits.
In general the models settle to a quasi-stationary state with a constant eccentricity, which
decreases as the viscosity decreases. However, quasi-steady states with mean
eccentricities below e =0.36 do not seem to be reached for this
model by decreasing the viscosity alone. But then a longer time is
required for this value to be attained.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{9953f10.eps} \end{figure}](/articles/aa/full/2008/32/aa09953-08/Timg125.gif) |
Figure 10:
Four snapshots of the disk surface density contours during
one orbital period as viewed in the non-rotating frame.
Time increases from top to bottom and left to right
The solid (red) curve
indicates the Roche lobe of the primary star.
The viscosity is 10-4, the mass ratio is 0.1 and
H/r =0.05. As the companion has a close approach to the disk outer
edge a tidal tail is pulled out ( top right). This subsequently rejoins the
disk ( bottom left) which remains relatively unperturbed until the
next close approach.
|
| Open with DEXTER |
Clearly the initial growth of 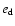 in these models is exponential
and growth rates,
in these models is exponential
and growth rates,
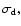 defined through
defined through
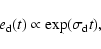 |
(12) |
can be determined by fitting simulation data to the above relation.
The results are plotted in the upper left panel of Fig. 9
where the variation of
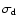 with viscosity is plotted.
In the remaining 3 panels we plot the
equilibrium values of the radius
with viscosity is plotted.
In the remaining 3 panels we plot the
equilibrium values of the radius 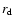 ,
the eccentricity
,
the eccentricity 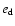 and the
precession rate
and the
precession rate
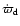 of the disk. Each of the quantities (
of the disk. Each of the quantities (
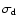 ,
,
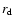 ,
,
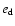 )
shows a strikingly similar dependence on
)
shows a strikingly similar dependence on 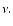 This behaviour can be understood in terms of the diffusive influence of viscosity.
For larger viscosity the disk material will tend to spread outwards at a faster rate
with more material being
pushed to the outer regions of the disk where it feels a stronger
(eccentricity enhancing) tidal perturbation due to the secondary. Hence
the increase of the growth rate with viscosity. For the very same
reason, the equilibrium value of the radius
This behaviour can be understood in terms of the diffusive influence of viscosity.
For larger viscosity the disk material will tend to spread outwards at a faster rate
with more material being
pushed to the outer regions of the disk where it feels a stronger
(eccentricity enhancing) tidal perturbation due to the secondary. Hence
the increase of the growth rate with viscosity. For the very same
reason, the equilibrium value of the radius 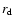 as well as the final eccentricity will increase with
as well as the final eccentricity will increase with 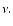 The fact that all
these quantities respond similarly to variations of
The fact that all
these quantities respond similarly to variations of 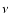 indicates that
they respond in a similar manner to the outward expansion of the disk.
On the contrary, the disk precession rate
indicates that
they respond in a similar manner to the outward expansion of the disk.
On the contrary, the disk precession rate
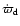 depends only weakly on the
viscosity (for
depends only weakly on the
viscosity (for
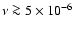 ).
From the lower two panels (
).
From the lower two panels (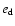 ,
,
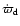 )
there is an indication that for
)
there is an indication that for
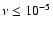 the disk shrinks rapidly
causing corresponding changes to the precession rate while the eccentricity levels off.
However, we did not consider simulations with
the disk shrinks rapidly
causing corresponding changes to the precession rate while the eccentricity levels off.
However, we did not consider simulations with
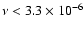 as it is likely
that at this stage they become resolution-limited
such that the numerical viscosity cannot be neglected.
as it is likely
that at this stage they become resolution-limited
such that the numerical viscosity cannot be neglected.
Finally we illustrate the behaviour of the eccentric disk
once it has attained its final quasi-steady state for the
case with
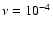 in Fig. 10. Cases with other values
of
in Fig. 10. Cases with other values
of 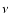 show similar behaviour. In Fig. 10 we show the
surface density contours during
one orbital period as viewed in the non-rotating frame.
In this frame the secondary (moving counter clock wise) has a close approach to the
slowly precessing disk's apocentre approximately once every orbit.
As the companion approaches the disk's outer
edge a tidal tail is pulled out. This subsequently rejoins the
disk which remains relatively unperturbed until the
next close approach. As even at apocentre, the disk matter rotates
faster than the binary, so the tidal tail leads the secondary and
is clearly responsible for angular momentum transfer to the orbit.
This must also be associated with enhanced tidal dissipation.
As the disk appears relatively unperturbed away from these closest approaches,
most of the tidal angular momentum transfer may occur as a result of these
close approaches.
show similar behaviour. In Fig. 10 we show the
surface density contours during
one orbital period as viewed in the non-rotating frame.
In this frame the secondary (moving counter clock wise) has a close approach to the
slowly precessing disk's apocentre approximately once every orbit.
As the companion approaches the disk's outer
edge a tidal tail is pulled out. This subsequently rejoins the
disk which remains relatively unperturbed until the
next close approach. As even at apocentre, the disk matter rotates
faster than the binary, so the tidal tail leads the secondary and
is clearly responsible for angular momentum transfer to the orbit.
This must also be associated with enhanced tidal dissipation.
As the disk appears relatively unperturbed away from these closest approaches,
most of the tidal angular momentum transfer may occur as a result of these
close approaches.
![\begin{figure}
\par\includegraphics[width=4cm,clip]{9953f11a.eps}\hspace*{4mm}\includegraphics[width=4cm,clip]{9953f11b.eps} \end{figure}](/articles/aa/full/2008/32/aa09953-08/Timg131.gif) |
Figure 11:
Mean disk eccentricity 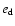 and disk radius
and disk radius 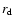 as functions of time
for the standard model (red curve),
the same case but with an added explicit bulk viscosity
as functions of time
for the standard model (red curve),
the same case but with an added explicit bulk viscosity
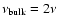 (green curve) and a case
with standard parameters, but
for which the initial disk radius is taken to be
(green curve) and a case
with standard parameters, but
for which the initial disk radius is taken to be
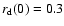 (blue curve).
(blue curve).
|
| Open with DEXTER |
The imposed kinematic viscosity, 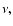 is intended to represent the effects of
some form of disk turbulence, probably arising from the
magnetorotational instability (Balbus & Hawley 1998). It is possible that an effective bulk viscosity
may also result which could also act as a stabilizing mechanism.
In addition, in typical SPH simulations on this problem an explicit bulk viscosity
is included; see for example the recent study by Smith et al. (2007).
In order to investigate its effects, we performed runs for which
an explicit bulk viscosity
is intended to represent the effects of
some form of disk turbulence, probably arising from the
magnetorotational instability (Balbus & Hawley 1998). It is possible that an effective bulk viscosity
may also result which could also act as a stabilizing mechanism.
In addition, in typical SPH simulations on this problem an explicit bulk viscosity
is included; see for example the recent study by Smith et al. (2007).
In order to investigate its effects, we performed runs for which
an explicit bulk viscosity
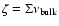 was added.
In this study we used a constant
was added.
In this study we used a constant
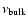 and present in Fig. 11
results for the case when the bulk viscosity coefficient
is twice as large as the shear viscosity coefficient:
and present in Fig. 11
results for the case when the bulk viscosity coefficient
is twice as large as the shear viscosity coefficient:
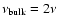 .
The influence of the added bulk viscosity on the simulations is very small:
the only effect is a slightly increased damping, as indicated for example
by the longer growth time. Otherwise an added bulk viscosity has no dynamical
influence. This indicates that
the direct effect of viscosity on the eccentric mode is unimportant
and implies that mechanisms such as viscous overstability cannot be
responsible for the eccentric instability seen here.
We also plot the evolution for a case where the initial disk
radius
.
The influence of the added bulk viscosity on the simulations is very small:
the only effect is a slightly increased damping, as indicated for example
by the longer growth time. Otherwise an added bulk viscosity has no dynamical
influence. This indicates that
the direct effect of viscosity on the eccentric mode is unimportant
and implies that mechanisms such as viscous overstability cannot be
responsible for the eccentric instability seen here.
We also plot the evolution for a case where the initial disk
radius
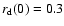 ,
rather than the usual
,
rather than the usual
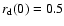 ,
in Fig. 11.
As expected the initial growth
is slowed down due to the small outer disk radius which remains around
,
in Fig. 11.
As expected the initial growth
is slowed down due to the small outer disk radius which remains around
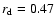 until
t=150. Only when the eccentric instability, which appears to grow (though more slowly)
even for this small disk, has developed sufficiently does the radius of the disk
increase again. (It should be noted that, owing to the way in which it is defined, an increase of
until
t=150. Only when the eccentric instability, which appears to grow (though more slowly)
even for this small disk, has developed sufficiently does the radius of the disk
increase again. (It should be noted that, owing to the way in which it is defined, an increase of 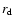 may be associated purely with a growth of the eccentricity of the disk rather than an increase of the semimajor axis at which the disk is tidally truncated.) At later times the behaviour is in fact identical to the standard
model. Hence, different initial conditions lead to the same outcome, as one might expect
for viscous flows.
may be associated purely with a growth of the eccentricity of the disk rather than an increase of the semimajor axis at which the disk is tidally truncated.) At later times the behaviour is in fact identical to the standard
model. Hence, different initial conditions lead to the same outcome, as one might expect
for viscous flows.
4.2 Temperature
In this section we study the effect of variations of the disk temperature or, equivalently, the relative scaleheight h=H/r of the
disk.
Starting again from the standard model we vary h from 0.01 to 0.06.The variation of
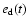 is displayed in Fig. 12, where the
thick (coloured) lines refer to different values of h, and the dashed lines are
eyeball fits made during the initial growth period. The growth timescale
depends on the disk temperature and it is found to be shorter for cooler disks.
The final disk eccentricities do not depend on the value of h as long as
is displayed in Fig. 12, where the
thick (coloured) lines refer to different values of h, and the dashed lines are
eyeball fits made during the initial growth period. The growth timescale
depends on the disk temperature and it is found to be shorter for cooler disks.
The final disk eccentricities do not depend on the value of h as long as
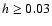 .
For the smallest value displayed here, h=0.02, the standard grid resolution
(
.
For the smallest value displayed here, h=0.02, the standard grid resolution
(
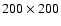 )
is not sufficient. In additional simulations we found that
runs (for h=0.02) with higher resolution yield larger values of
)
is not sufficient. In additional simulations we found that
runs (for h=0.02) with higher resolution yield larger values of
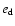 more consistent with the other runs.
The final radius of the disk,
more consistent with the other runs.
The final radius of the disk, 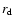 ,
also does not depend on the disk aspect ratio
for h > 0.02. All runs yield an outer disk radius
,
also does not depend on the disk aspect ratio
for h > 0.02. All runs yield an outer disk radius
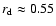 ,
with a slight tendency for larger disks to be associated with larger h.
,
with a slight tendency for larger disks to be associated with larger h.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9953f12.eps} \end{figure}](/articles/aa/full/2008/32/aa09953-08/Timg138.gif) |
Figure 12:
Time-evolution of the mean eccentricity of the disk for
different disk aspect ratios
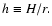 |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=3.9cm,clip]{9953f13a.eps}\hspace*{4mm}
\includegraphics[width=4cm,clip]{9953f13b.eps} \end{figure}](/articles/aa/full/2008/32/aa09953-08/Timg139.gif) |
Figure 13:
Left: dependence of the growth time (
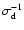 )
of disk
eccentricity on h=H/r. Quoted is the time (in orbital periods) to increase the
eccentricity by a factor of e; Right: the equilibrium surface density profile of the disk normalized to the
central value for different h. )
of disk
eccentricity on h=H/r. Quoted is the time (in orbital periods) to increase the
eccentricity by a factor of e; Right: the equilibrium surface density profile of the disk normalized to the
central value for different h. |
| Open with DEXTER |
The inferred growth times as a function of h=H/r are plotted in the left panel
of Fig. 13. The growth is fastest for cooler disks and the growth time
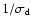 increases linearly with increasing h. For the thinnest disks we study with
h = 0.02, the e-folding time is around 10 orbits (for the standard
viscosity).
In the right panel of Fig. 13 the equilibrium surface densities are
displayed for various h. Obviously the value of h does not play a role
in determining the equilibrium structure. At higher resolution, the surface
density profile of the
cool h=0.02 disk is in better agreement with the others as well.
increases linearly with increasing h. For the thinnest disks we study with
h = 0.02, the e-folding time is around 10 orbits (for the standard
viscosity).
In the right panel of Fig. 13 the equilibrium surface densities are
displayed for various h. Obviously the value of h does not play a role
in determining the equilibrium structure. At higher resolution, the surface
density profile of the
cool h=0.02 disk is in better agreement with the others as well.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9953f14.eps} \end{figure}](/articles/aa/full/2008/32/aa09953-08/Timg141.gif) |
Figure 14:
Dependence of the equilibrium disk precession rate
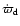 on
disk temperature. The two separate lines with the triangles refer to two different
grid resolutions, the upper to the standard case and the lower to
on
disk temperature. The two separate lines with the triangles refer to two different
grid resolutions, the upper to the standard case and the lower to
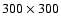 .
The additional curves with the small open and solid diamonds are approximate parabolic
fits to the data points. Values obtained by solving the linear eigenvalue
problem using the azimuthally averaged surface density profiles
are also indicated by the filled circles. The open triangles are obtained from models
where the disk is impacted by a mass-transfer stream (see Sect. 9 below). .
The additional curves with the small open and solid diamonds are approximate parabolic
fits to the data points. Values obtained by solving the linear eigenvalue
problem using the azimuthally averaged surface density profiles
are also indicated by the filled circles. The open triangles are obtained from models
where the disk is impacted by a mass-transfer stream (see Sect. 9 below).
|
| Open with DEXTER |
We plot the equilibrium precession rate of the disk
as a function of h in Fig. 14.
The inverse of this quantity gives the period of one
complete turn of the disk (in the inertial frame).
Values obtained by solving the linear
free m=1 mode eigenvalue problem using the
mean surface density distributions shown in Fig. 13
and assuming a free outer boundary
are also plotted
(for a discussion of this approach see Papaloizou 2005; or Goodchild & Ogilvie 2006).
These are in good agreement with the results derived from the nonlinear
simulations.
For very cool disks,
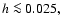 the precession rate is positive while for hotter disks the disk precesses
in a retrograde sense.
The precession period at the transition is infinite,
corresponding to the disk
being stationary in the inertial frame.
In general the precession rate is determined by a combination of different effects.
There is a contribution,
the precession rate is positive while for hotter disks the disk precesses
in a retrograde sense.
The precession period at the transition is infinite,
corresponding to the disk
being stationary in the inertial frame.
In general the precession rate is determined by a combination of different effects.
There is a contribution,
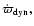 due to the axisymmetric component of the binary potential, and there is also a pressure contribution,
due to the axisymmetric component of the binary potential, and there is also a pressure contribution,
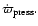 The
first part
The
first part
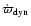 is positive, giving a prograde contribution, while the
latter part
is positive, giving a prograde contribution, while the
latter part
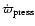 is negative, tending to produce retrograde precession.
Our results confirm the existence of these
contributions and indicate a parabolic
dependence of
is negative, tending to produce retrograde precession.
Our results confirm the existence of these
contributions and indicate a parabolic
dependence of
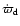 on h for locally isothermal disks.
The influence of the viscosity on the precession rate is negligible as we have indicated above.
on h for locally isothermal disks.
The influence of the viscosity on the precession rate is negligible as we have indicated above.
A change of the direction of precession sometimes occurs during the
earlier growth phases of the simulations and is illustrated
in Fig. 15 where we plot the time-evolution of the apsidal line
of the disk
for h=0.03. Initially, during the period of eccentricity growth, the disk precesses
in a prograde sense and at time
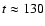 ,
as it settles into a quasi-stationary state,
it turns around and undergoes
retrograde precession. Thus this value of h lies close to the borderline separating these two possibilities for the final state.
,
as it settles into a quasi-stationary state,
it turns around and undergoes
retrograde precession. Thus this value of h lies close to the borderline separating these two possibilities for the final state.
We also remark that the precession rate is sensitive to the mass distribution
in the outer regions of the disk and it can be changed from retrograde to prograde
by supplying matter from the secondary through the L1 point
(see Fig. 14 and Sect. 9 below).
4.3 Effect of the inner boundary condition
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9953f15.eps} \end{figure}](/articles/aa/full/2008/32/aa09953-08/Timg148.gif) |
Figure 15:
Time-evolution of the pericentre (in the inertial frame)
of the disk,
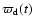 ,
for
a model with an intermediate H/r=0.03. ,
for
a model with an intermediate H/r=0.03.
|
| Open with DEXTER |
We here discuss the effects of the different
kinds of boundary conditions
that we have implemented
as described in Sect. 2.3,
and discuss briefly the influence of a higher density floor.
The evolution of the mean eccentricity of the disk for the
different inner boundary conditions for a kinematic viscosity of
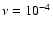 is shown in Fig. 16.
is shown in Fig. 16.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9953f16.eps} \end{figure}](/articles/aa/full/2008/32/aa09953-08/Timg149.gif) |
Figure 16:
Time-evolution of the mean eccentricity of the disk for
different inner boundary conditions for a kinematic viscosity of
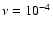 (ten times the standard value). (ten times the standard value).
|
| Open with DEXTER |
The results shown in Fig. 16 indicate that the adoption of an inner boundary condition
with damping properties (such as the damping boundary conditions and the outflow condition)
lead to configurations that differ from the standard case. Both the growth rate and
the mean equilibrium eccentricity of the disk are strongly affected.
Increased damping yields smaller growth rates and smaller final
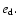 The outer disk radius shows similar tendency but it varies within a much smaller range
from
The outer disk radius shows similar tendency but it varies within a much smaller range
from
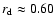 for the damping boundary condition to
for the damping boundary condition to
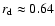 for the viscous
outflow condition (see Table 2).
The viscous outflow condition and the standard reflecting condition behave very
similarly because both have strong reflective
properties.
The most pronounced influence of the boundary is on the precession rate of the disk,
as is indicated in Table 2.
For the free outflow condition we find
a very slow positive, i.e. prograde, precession of the disk.
However, as is indicated in Fig. 17, a very pronounced
eccentric inner hole forms in the centre of the disk which does not happen in cases
where the inner boundary is forced to be axisymmetric.
When an open boundary condition is used, material on an eccentric orbit can leave the system freely and is not ``reflected back'' into the computational domain.
A side-effect of the use of the open boundary condition
(and also the damping condition)
is a reduction in the overall eccentricity of the disk.
Clearly, the treatment of the inner boundary condition is an important
issue that needs to be considered in more detail.
In the case of a central compact stellar object,
such as a white dwarf or neutron star, which has a
very small pressure scaleheight in its upper layers, it might behave
approximately as a rigid wall with typical reflecting wall conditions
for the normal velocity
and a no-slip boundary condition for the tangential velocity.
This is the situation of the boundary layer problem in the theory of accretion disks
which has an associated radial lengthscale that is too small to make inclusion
tractable in a simulation of the type considered here.
However, it appears that the overall disk properties may be significantly affected by the
behaviour of this small innermost region of the disk.
The final line in Table 2 refers to a model with a reflecting inner boundary
and a high density floor of 10-3 (instead of 10-8). While the final values of the
disk's eccentricity and radius are not changed much, there is a significant difference in
the precession rate. The higher density in the outer parts of the primary's Roche lobe
slows down the precession by a factor of about 2.8. Hence, to accurately determine the
important rate of disk precession a small floor value is clearly required.
for the viscous
outflow condition (see Table 2).
The viscous outflow condition and the standard reflecting condition behave very
similarly because both have strong reflective
properties.
The most pronounced influence of the boundary is on the precession rate of the disk,
as is indicated in Table 2.
For the free outflow condition we find
a very slow positive, i.e. prograde, precession of the disk.
However, as is indicated in Fig. 17, a very pronounced
eccentric inner hole forms in the centre of the disk which does not happen in cases
where the inner boundary is forced to be axisymmetric.
When an open boundary condition is used, material on an eccentric orbit can leave the system freely and is not ``reflected back'' into the computational domain.
A side-effect of the use of the open boundary condition
(and also the damping condition)
is a reduction in the overall eccentricity of the disk.
Clearly, the treatment of the inner boundary condition is an important
issue that needs to be considered in more detail.
In the case of a central compact stellar object,
such as a white dwarf or neutron star, which has a
very small pressure scaleheight in its upper layers, it might behave
approximately as a rigid wall with typical reflecting wall conditions
for the normal velocity
and a no-slip boundary condition for the tangential velocity.
This is the situation of the boundary layer problem in the theory of accretion disks
which has an associated radial lengthscale that is too small to make inclusion
tractable in a simulation of the type considered here.
However, it appears that the overall disk properties may be significantly affected by the
behaviour of this small innermost region of the disk.
The final line in Table 2 refers to a model with a reflecting inner boundary
and a high density floor of 10-3 (instead of 10-8). While the final values of the
disk's eccentricity and radius are not changed much, there is a significant difference in
the precession rate. The higher density in the outer parts of the primary's Roche lobe
slows down the precession by a factor of about 2.8. Hence, to accurately determine the
important rate of disk precession a small floor value is clearly required.
Table 2:
Results obtained using the different inner
boundary conditions and density floor.
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{9953f17.eps} \end{figure}](/articles/aa/full/2008/32/aa09953-08/Timg154.gif) |
Figure 17:
Two-dimensional surface density structure for the model with the open outflow
inner boundary condition after 250 orbital periods.
|
| Open with DEXTER |
5 Mass ratio
We now investigate the influence of the mass ratio
q = M2/M1 on the
disk dynamics.
To speed up the simulations all of the runs in this section have been performed
with
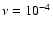 which is ten times larger than adopted for the standard simulation
(see Table 1).
which is ten times larger than adopted for the standard simulation
(see Table 1).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9953f18.eps} \end{figure}](/articles/aa/full/2008/32/aa09953-08/Timg155.gif) |
Figure 18:
Time-evolution of the mean eccentricity of the disk (logarithmic) for
different mass ratios q=M2/M1 of the binary for a kinematic viscosity of
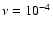 (ten times the standard value). The thinner black dashed lines indicate approximate linear
fits. (ten times the standard value). The thinner black dashed lines indicate approximate linear
fits.
|
| Open with DEXTER |
The eccentricity as a function of time is shown in Fig. 18
for different q with over-plotted straight-line fits indicating exponential growth.
For larger mass ratios q the growth is strongly enhanced, but all models settle to
approximately the same final eccentricity 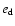 .
For the smallest mass ratio (q=0.05) there
is no direct indication of an exponential growth phase and we have drawn an
approximate straight-line fit applicable to the middle of the growth phase.
The extracted growth rates are plotted as a function of mass ratio in
the left panel of Fig. 19. For small q the growth rate
increases linearly with q but it slows down at the largest value q=0.3plotted.
We have performed explorative runs for larger q and find eccentricity growth all the
way to q=1 with fastest grow occuring at
.
For the smallest mass ratio (q=0.05) there
is no direct indication of an exponential growth phase and we have drawn an
approximate straight-line fit applicable to the middle of the growth phase.
The extracted growth rates are plotted as a function of mass ratio in
the left panel of Fig. 19. For small q the growth rate
increases linearly with q but it slows down at the largest value q=0.3plotted.
We have performed explorative runs for larger q and find eccentricity growth all the
way to q=1 with fastest grow occuring at
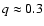 (see Fig. 19).
Below it is argued that this behaviour may be related to higher order non-linear mode coupling
which becomes more important for larger q, but in this work we do not elaborate on this issue
any further.
(see Fig. 19).
Below it is argued that this behaviour may be related to higher order non-linear mode coupling
which becomes more important for larger q, but in this work we do not elaborate on this issue
any further.
The variation of the disk radius with time (right panel of Fig. 19)
shows a sharp drop in 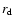 just after the start of the simulations due to the tidal
effect of the secondary which is stronger for larger q.
After attaining a minimum value, as low as 0.46 for the largest q, the disk expands
again on the eccentricity
growth timescale. The quasi-stationary disk radius is
smaller for larger q due to the enhanced tidal effects.
Note that for the q=0.05 case we have used a larger outer boundary radius
just after the start of the simulations due to the tidal
effect of the secondary which is stronger for larger q.
After attaining a minimum value, as low as 0.46 for the largest q, the disk expands
again on the eccentricity
growth timescale. The quasi-stationary disk radius is
smaller for larger q due to the enhanced tidal effects.
Note that for the q=0.05 case we have used a larger outer boundary radius
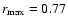 .
.
![\begin{figure}
\par\includegraphics[width=4cm,clip]{9953f19a.eps}\hspace*{4mm}
\includegraphics[width=3.9cm,clip]{9953f19b.eps} \end{figure}](/articles/aa/full/2008/32/aa09953-08/Timg158.gif) |
Figure 19:
Left: dependence of the growth rate (
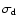 )
of the disk
eccentricity on the mass ratio q.
Right: the disk radius )
of the disk
eccentricity on the mass ratio q.
Right: the disk radius 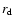 as a function of time for different q. The curves
are smoothed.
as a function of time for different q. The curves
are smoothed.
|
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=4cm,clip]{9953f20a.eps}\hspace*{4mm}
\includegraphics[width=3.9cm,clip]{9953f20b.eps} \end{figure}](/articles/aa/full/2008/32/aa09953-08/Timg159.gif) |
Figure 20:
Left: dependence of the growth rate (
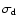 )
of the disk
eccentricity on the numerical resolution. The two-dimensional grid always has an equal
number of
grid points in each direction. Thus in the standard case 200
corresponds to )
of the disk
eccentricity on the numerical resolution. The two-dimensional grid always has an equal
number of
grid points in each direction. Thus in the standard case 200
corresponds to
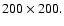 Right: the precession rate of the disk as a function of resolution.
Right: the precession rate of the disk as a function of resolution. |
| Open with DEXTER |
6 Numerical resolution
An important issue in (multi-dimensional) simulations is the question of numerical
resolution. To study its effect we have varied the grid resolution
in our standard model from
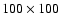 up to
up to
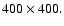 The grids we use are always uniform.
The models are typically started at t=0 to study the whole
growth phase of the evolution. In some cases
higher-resolution simulations have been started using
results obtained from coarser grids to provide initial data
with the object of investigating the quasi-stationary state.
Our main results are contained in Fig. 20 where the dependence of the
growth and precession rates of the disk are indicated for different grid resolutions.
The physical parameters used are those of the standard model.
At low resolution, the growth rate increases approximately as a linear
function of the number
of grid cells. Beyond
The grids we use are always uniform.
The models are typically started at t=0 to study the whole
growth phase of the evolution. In some cases
higher-resolution simulations have been started using
results obtained from coarser grids to provide initial data
with the object of investigating the quasi-stationary state.
Our main results are contained in Fig. 20 where the dependence of the
growth and precession rates of the disk are indicated for different grid resolutions.
The physical parameters used are those of the standard model.
At low resolution, the growth rate increases approximately as a linear
function of the number
of grid cells. Beyond
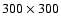 it levels off which indicates
that we have reached numerical convergence. This finding is corroborated
by the fact that the precession rate apparently levels off at the same resolution
(right panel).
The converged growth rate
it levels off which indicates
that we have reached numerical convergence. This finding is corroborated
by the fact that the precession rate apparently levels off at the same resolution
(right panel).
The converged growth rate
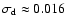 differs from the value for our standard resolution (
differs from the value for our standard resolution (
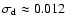 )
by
approximately
)
by
approximately 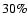 ;
similarly the value of
;
similarly the value of
 differs by about
differs by about 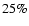 .
While the absolute values for the growth and precession rate change, the qualitative behaviour
of the disk, in particular the prograde slow precession in this case, does not change.
.
While the absolute values for the growth and precession rate change, the qualitative behaviour
of the disk, in particular the prograde slow precession in this case, does not change.
7 Instability mechanism
In this section we investigate the mechanism of
excitation of the disk eccentricity.
A mechanism responsible for this
that involves the coupling
of velocity (or surface density) perturbations with different azimuthal mode numbers through
the companion's tidal potential has been described
by Lubow (1991a).
This was later confirmed by Lubow (1991b) by carrying out and analysing
appropriate SPH simulations.
Although incorporating the slow precession of the disk
as viewed in the inertial frame
in the discussion below would introduce minor adjustments, for simplicity
we neglect it.
Then when viewed from this frame,
the eccentricity of the disk may be considered to be associated
with a stationary surface density perturbation with azimuthal mode number
m=1. A disk in which the gas orbits in circles about the primary
is subject to a tidal potential with components which vary as trigonometric functions
of
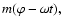
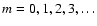 These produce corresponding responses in the state variables that
scale with the mass ratio, q.
These produce corresponding responses in the state variables that
scale with the mass ratio, q.
When the disk becomes
eccentric through the excitation of an m=1 mode that is approximately stationary in the inertial frame, nonlinear
coupling between the response to the tidal potential and this mode
produces an effective forcing which will be a sum of components
that are trigonometric functions of
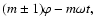
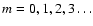 These will have amplitudes that scale as eq,e being the characteristic disk eccentricity.
More generally a coupling of order j produces effective forcing
These will have amplitudes that scale as eq,e being the characteristic disk eccentricity.
More generally a coupling of order j produces effective forcing
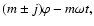
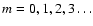 with
pattern speed
with
pattern speed
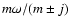 and amplitude scaling as
ej.
and amplitude scaling as
ej.
Each of these effective forcings produces a surface density
response that results in energy and angular momentum exchange with the
companion. This exchange may in some cases
produce a feedback causing the eccentricity
to grow. This works because a companion in fixed circular orbit
must undergo angular momentum changes, 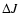 ,
and energy changes,
,
and energy changes,
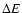 ,
such that
,
such that
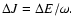 However, the angular momentum and energy changes associated with
a disturbance with pattern speed
However, the angular momentum and energy changes associated with
a disturbance with pattern speed
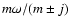 are such that
are such that
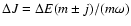 .
Thus for surface density disturbances with the - alternative, that rotate
faster than the companion and are thus expected to transfer orbital angular
momentum to it, too little
is transferred per unit of energy transferred.
The difference has to come from the disk orbits
which accordingly become eccentric.
Energy and angular momentum transfer to the companion
is expected to be especially effective if there is an associated
Lindblad resonance in the disk (Goldreich & Tremaine 1980).
.
Thus for surface density disturbances with the - alternative, that rotate
faster than the companion and are thus expected to transfer orbital angular
momentum to it, too little
is transferred per unit of energy transferred.
The difference has to come from the disk orbits
which accordingly become eccentric.
Energy and angular momentum transfer to the companion
is expected to be especially effective if there is an associated
Lindblad resonance in the disk (Goldreich & Tremaine 1980).
Similarly disturbances
with the + alternative, which rotate more slowly
than the companion and are expected to gain angular momentum,
may cause eccentricity growth. However, such disturbances
are less closely matched to the rotation of the disk
and in particular have no Lindblad resonances within it
(Goldreich & Tremaine 1979)
and are thus not expected to be significant.
Accordingly, disturbances rotating with pattern speeds
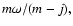 with m and
with m and 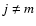 being integers,
may be associated with eccentricity growth
if there is an associated significant energy and angular momentum
transfer. The presence of a Lindblad resonance is expected to
enhance this. Although in principle any value of j might contribute to eccentricity growth, linear instability
could result only when j=1 (Lubow 1991a)
and the forcing as a result of coupling is linear in e.In that case the only value of m leading to a disturbance
with a Lindblad resonance within the disk is m=3.From the above discussion this disturbance has
azimuthal mode number
m-j = k = 2 and pattern speed
being integers,
may be associated with eccentricity growth
if there is an associated significant energy and angular momentum
transfer. The presence of a Lindblad resonance is expected to
enhance this. Although in principle any value of j might contribute to eccentricity growth, linear instability
could result only when j=1 (Lubow 1991a)
and the forcing as a result of coupling is linear in e.In that case the only value of m leading to a disturbance
with a Lindblad resonance within the disk is m=3.From the above discussion this disturbance has
azimuthal mode number
m-j = k = 2 and pattern speed
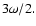 The associated Lindblad resonance corresponds to the 3:1 resonance
at which the disk orbital period is one third of that of the binary.
When this is present the mode coupling may lead to a linear
instability to eccentricity growth (Goodchild & Ogilvie 2006).
The associated Lindblad resonance corresponds to the 3:1 resonance
at which the disk orbital period is one third of that of the binary.
When this is present the mode coupling may lead to a linear
instability to eccentricity growth (Goodchild & Ogilvie 2006).
According to the above view of the mode coupling leading to eccentricity growth,
the surface density perturbation corresponding to the disk eccentricity
should grow together with a surface density perturbation
with k=2 and angular frequency 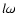 ,
with l=3.
This disturbance is derived from a coupling between the disk eccentricity
and the m=3 component of the tidal potential, which accordingly plays an important part
in the process.
,
with l=3.
This disturbance is derived from a coupling between the disk eccentricity
and the m=3 component of the tidal potential, which accordingly plays an important part
in the process.
Following Lubow (1991b), in order
to demonstrate the operation of this mechanism and the significance
of the m=3 component of the tidal potential,
we define the mode amplitude
associated with the pair (k,l) as
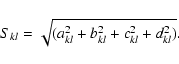 |
(13) |
In this expression
where the integration is over the surface area of the disk, A.Note that Skl also involves integration over the
domain
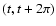 and is thus a function of the local time t.
and is thus a function of the local time t.
In order to test the predictions of the above mode-coupling
analysis, we evaluate the time-evolution of the mode amplitudes for the (k,l) pairs
(1,0),(1,3),(2,3),(3,3),(2,2),(3,2) for runs with q=0.1 and q=0.2.We describe below results obtained with the kinematic viscosity
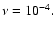 However, similar results are obtained for
However, similar results are obtained for
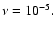 In order to establish the importance of the component
of the tidal potential with m=3,we consider cases for which the full tidal potential is used,
only the m=3 component of the tidal potential is used and finally for which the
full tidal potential with the m=3 component removed is used.
By studying the time-evolution of the mode amplitudes in these cases,
the importance of the m=3 component of the tidal potential
could be confirmed. Note that because the defined mode amplitudes
involve integrals over the disk radius, the significance
of their absolute values is unclear because of cancellation effects.
However, they may still be used to relate to the growth
rates of linear modes.
In order to establish the importance of the component
of the tidal potential with m=3,we consider cases for which the full tidal potential is used,
only the m=3 component of the tidal potential is used and finally for which the
full tidal potential with the m=3 component removed is used.
By studying the time-evolution of the mode amplitudes in these cases,
the importance of the m=3 component of the tidal potential
could be confirmed. Note that because the defined mode amplitudes
involve integrals over the disk radius, the significance
of their absolute values is unclear because of cancellation effects.
However, they may still be used to relate to the growth
rates of linear modes.
The time-evolution of the mode amplitudes Sk,l for
q=0.1 is plotted in
Fig. 21.
The upper panel gives results
for the case when only the component of the tidal potential with m=3 is
retained. The lower panel gives results corresponding to the case when the full tidal potential
is used. In both cases the mode with k=2 and l=3 grows at the same rate as the mode with
k=1 and l=0, the latter mode being responsible for the disk eccentricity.
Although it is difficult to demonstrate the causal nature of this connection, this behaviour would certainly be expected from the discussion of mode coupling given above.
We also find that the final state and magnitude of the eccentricity of the disk
is similar in all cases for which the disk is unstable to becoming eccentric.
However, the growth rate is measured to be smaller when the full potential is used.
Figure 22 gives similar plots to those
shown in in Fig. 21 but for q=0.2.Note that, as expected from the mode-coupling theory,
there is a very close correspondence between the mode with k=2 and l=3and the mode with k=1 and l=0 when only the m=3 component of the tidal potential is used
for this mass ratio.
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{9953f21.eps}\end{figure}](/articles/aa/full/2008/32/aa09953-08/Timg187.gif) |
Figure 21:
Time-evolution of the mode amplitudes Sk,l
(see Eq. (13)) for
q=0.1 with a kinematic viscosity
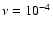 plotted on a logarithmic scale.
The upper panel gives results
for the case when only the component of the tidal potential with m=3 is
retained. The lower panel gives results corresponding to the case when the full tidal potential
is used. In both cases the mode with k=2 and l=3 grows at the same rate as the mode with
k=1 and l=0, the latter mode being responsible for the disk eccentricity.
The growth is slower when the full potential is used.
plotted on a logarithmic scale.
The upper panel gives results
for the case when only the component of the tidal potential with m=3 is
retained. The lower panel gives results corresponding to the case when the full tidal potential
is used. In both cases the mode with k=2 and l=3 grows at the same rate as the mode with
k=1 and l=0, the latter mode being responsible for the disk eccentricity.
The growth is slower when the full potential is used.
|
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{9953f22.eps} \end{figure}](/articles/aa/full/2008/32/aa09953-08/Timg188.gif) |
Figure 22:
As in Fig. 21 but for q=0.2.Note that there is a very close correspondence between S2,3 and S1,0when only the m=3 component of the tidal potential is used.
|
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{9953f23.eps} \end{figure}](/articles/aa/full/2008/32/aa09953-08/Timg189.gif) |
Figure 23:
Time-evolution of the mode amplitudes Sk,l,
plotted on a logarithmic scale, for
q=0.1 ( upper panel) and q=0.2 ( lower panel). For these cases, the tidal potential
with the m=3 component removed is used and
the kinematic viscosity
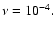 When q=0.1 little growth of the disk eccentricity
or S1,0 is seen. When q=0.2 some growth occurs but at a significantly slower rate than when
the full potential is used (see Fig. 22).
When q=0.1 little growth of the disk eccentricity
or S1,0 is seen. When q=0.2 some growth occurs but at a significantly slower rate than when
the full potential is used (see Fig. 22). |
| Open with DEXTER |
In order to determine whether the m=3 component of the tidal potential
is essential for producing eccentricity growth, we performed simulations using
the full tidal potential with the m=3 component removed.
The time-evolution of the mode amplitudes Sk,l is shown
in Fig. 23
for q=0.1 and q=0.2.When q=0.1 little growth of the disk eccentricity
is seen confirming the importance
of the m=3 component.
However, when q=0.2 some growth is seen but at a significantly slower rate than when
the full potential is used.
Although the results discussed above indicate the importance of the m=3component of the tidal potential, they also indicate that it is
not always needed. From Fig. 23 it
is apparent that although eccentricity growth is
very small when q=0.1, it is still present
but reduced when q=0.2. The time required to attain saturation
is increased from about 30 to 150 orbits in that case.
As in the other cases the mode with k=2 and l=3 grows at the same rate as the mode with
k=1 and l=0 indicating that this is still responsible for causing eccentricity growth.
Also a response with k=3 and l=3 is still present even though
it cannot be driven by the m=3 component of the potential.
The most natural explanation is that this response is produced
by a forcing originating from a coupling between the response to the dominant m=2 tide
and the m=1 tide. As before that can then couple to the S1,0 mode producing eccentricity growth.
Thus in this case one has replaced the
(3,3),(1,0) pairwise coupling by a
(2,2), (1,1),(1,0) triple coupling. In so doing the strength
is reduced by a factor q making the process less significant in the
smaller mass ratio case as is seen in the simulations.
This process thus contributes more effectively for larger q.On the other hand the 3:1 resonance which enables effective angular momentum
transport between disk and companion is pushed towards the Roche lobe
requiring further disk expansion and resulting in
the process becoming increasingly nonlinear.
8 Comparison with linear theory
In an attempt to understand the linear phase of the simulations, during which the eccentricity is small and grows exponentially in time, we analysed the full set of linear equations governing small perturbations, with azimuthal mode number m=1, of a steady, axisymmetric disk. (This is in addition to the approach mentioned in Sect. 4.2, in which approximations are made that are appropriate for slowly evolving global eccentric modes.) For the purposes of comparison with the standard model in which a reflecting inner boundary condition is used, the basic state of the linear calculation is a non-accreting solution with zero radial velocity.
This approach yields appropriate solutions corresponding to slowly precessing eccentric modes of the disk, of which the ``lowest-order'' mode with the simplest radial structure might be expected to be the most relevant. The precession rate can be positive or negative depending on the mass ratio of the binary, the value of H/r, the surface density profile and the boundary conditions. While it is possible, using this approach, to account for a number of aspects of the simulation results, the sensitivity of the precession rate to the exact surface density profile and the boundary conditions is a matter of concern.
Such modes also grow or decay slowly as a result of viscosity. It is known that shear viscosity can render modes unstable through the mechanism of viscous overstability (Kato 1978), in which some of the energy being drawn by viscous stresses from the differential rotation of the disk is diverted into growing oscillations. Viscous overstability has been identified as an important issue in the theory of eccentric disks (Ogilvie 2001).
A local analysis in the case of an isothermal two-dimensional disk with constant kinematic shear viscosity and no bulk viscosity indicates overstability for radial wavelengths  9H and a maximum local growth rate of approximately
9H and a maximum local growth rate of approximately
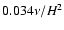 for a radial wavelength of approximately 13H (Latter & Ogilvie 2006). This behaviour is confirmed in our global linear calculations. For sufficiently thin disks, growing modes are obtained. However, for the standard model with H/r=0.05, the preferred local wavelength of the viscous overstability is as long as 0.66r and in fact we do not find overstable global modes. In addition, we confirm by this method that the inclusion of a bulk viscosity with
for a radial wavelength of approximately 13H (Latter & Ogilvie 2006). This behaviour is confirmed in our global linear calculations. For sufficiently thin disks, growing modes are obtained. However, for the standard model with H/r=0.05, the preferred local wavelength of the viscous overstability is as long as 0.66r and in fact we do not find overstable global modes. In addition, we confirm by this method that the inclusion of a bulk viscosity with
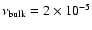 makes a negative contribution to the growth rate that is quite negligible in comparison with those found in the simulations. Therefore viscous overstability is not relevant to the standard model but might be an important issue when thinner disks are considered.
makes a negative contribution to the growth rate that is quite negligible in comparison with those found in the simulations. Therefore viscous overstability is not relevant to the standard model but might be an important issue when thinner disks are considered.
It is possible within this linear approach to model the nonlinear mode-coupling process by adding terms that correspond to a localised growth of the eccentric perturbations in the vicinity of the 3:1 resonance. Rather than localising the growth in the form of a delta function as done by Goodchild & Ogilvie (2006), this effect can be represented using a Gaussian or Lorentzian function of radius centred on the resonance and with a width appropriate to a Lindblad resonance broadened by pressure. Including these terms allows us to obtain growing eccentric modes with growth rates comparable to those obtained in the simulations. However, it is again found that a detailed comparison is difficult because of the sensitivity of the results to the exact surface density profile and the treatment of the resonance.
According to the angular momentum equation in the case of a uniform shear viscosity, the surface density in the non-accreting basic state should deviate from the initial r-1/2 profile only as a result of the tidal torque applied to the disc. Papaloizou & Pringle (1977) provide a method to calculate the tidal torque per unit radius, which gives a result proportional to the viscosity of the disk. When this is balanced with the viscous torque it predicts a surface density profile that is independent of the viscosity and depends only on the mass ratio q. Unfortunately this approach does not give accurate agreement with the surface density profile shown in Fig. 4, indicating that the angular momentum balance is nonlocal and involves propagating density waves not considered by Papaloizou & Pringle (1977). The standard model disk is therefore smaller than predicted by Papaloizou & Pringle (1977). We note that a two-dimensional isothermal disk may allow radial wave propagation to a greater extent than more realistic models. It may also be relevant that SPH simulations are less likely to allow these waves to propagate and may therefore produce larger disks that are more susceptible to eccentric instability. Clearly the tidal truncation of disks needs to be better understood in order to make accurate predictions of the growth and precession rates of eccentric modes.
9 Effect of a mass-transfer stream
To make better contact with possibly more realistic cases with mass overflow from the
secondary we have performed some studies where we modify the
outer boundary condition to allow for mass inflow through the L1 point.
The model parameters are dealt with in the same way as before. We adopt the
mass ratio q =0.1 which allows a scaling to be made such that
binary parameters match very closely those of OY Car which has
a primary of mass
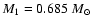 and
and
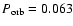 d. The
physical separation of the two stars is thus
d. The
physical separation of the two stars is thus
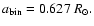 Mass is injected into the system at a constant rate.
Note that in the case of locally isothermal disk models with
constant kinematic viscosity as adopted here, the independence of the dynamics of the flow,
and in particular the final values of eccentricity and disk radius in a quasi-steady state,
to the surface density scale
means that the results are
independent of the magnitude of the inflow rate!
This may thus be scaled to a value appropriate for
cataclysmic variables, typically
Mass is injected into the system at a constant rate.
Note that in the case of locally isothermal disk models with
constant kinematic viscosity as adopted here, the independence of the dynamics of the flow,
and in particular the final values of eccentricity and disk radius in a quasi-steady state,
to the surface density scale
means that the results are
independent of the magnitude of the inflow rate!
This may thus be scaled to a value appropriate for
cataclysmic variables, typically
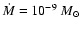 /yr.
However, in a more realistic disk model that includes
suitable radiation and energy transport mechanisms and allows for the possibility
of time-dependent outbursts, this
would not be the case.
/yr.
However, in a more realistic disk model that includes
suitable radiation and energy transport mechanisms and allows for the possibility
of time-dependent outbursts, this
would not be the case.
In the simulations presented here the Roche lobe of the primary is as empty as possible
initially, i.e. the
density is constant and equals the floor value.
![\begin{figure}
\par\includegraphics[width=4cm,clip]{9953f24a.eps}\hspace*{4mm}
\includegraphics[width=4cm,clip]{9953f24b.eps} \end{figure}](/articles/aa/full/2008/32/aa09953-08/Timg197.gif) |
Figure 24:
Mean disk eccentricity 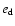 and disk radius
and disk radius 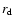 as functions of time
for models that include mass inflow through the L1 point and different inner boundary
conditions and viscosities. For the first two plots (green and red curves) the standard viscosity 10-5 has been used, while the third plot (blue curve) is for a model that has been
continued from the first at time
as functions of time
for models that include mass inflow through the L1 point and different inner boundary
conditions and viscosities. For the first two plots (green and red curves) the standard viscosity 10-5 has been used, while the third plot (blue curve) is for a model that has been
continued from the first at time
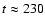 but with
but with
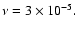 |
| Open with DEXTER |
The first set of simulations were performed with the standard viscosity
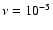 in
dimensionless units which would scale to a value of
in
dimensionless units which would scale to a value of
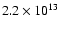 cm2/s for the OY Car
system. The inner boundary condition is open to allow for accretion
of mass onto the primary star and enable a steady state to be reached.
We have performed simulations with both the ``viscous outflow'' and the ``free outflow''
conditions as described in Sect. 2.3 above.
From Fig. 24 it is clear that the standard viscosity value
used does not result in an eccentric disk.
Even an increase of the viscosity by a factor of 3 does not produce an eccentric disk in the ``free outflow'' case
as the final (blue) curve in Fig. 24 indicates.
In this latter case the disk's radius is increased to
cm2/s for the OY Car
system. The inner boundary condition is open to allow for accretion
of mass onto the primary star and enable a steady state to be reached.
We have performed simulations with both the ``viscous outflow'' and the ``free outflow''
conditions as described in Sect. 2.3 above.
From Fig. 24 it is clear that the standard viscosity value
used does not result in an eccentric disk.
Even an increase of the viscosity by a factor of 3 does not produce an eccentric disk in the ``free outflow'' case
as the final (blue) curve in Fig. 24 indicates.
In this latter case the disk's radius is increased to
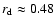 due to the spreading action of viscosity but the disk nevertheless does not switch
to an eccentric mode. The apparently large initial disk radii in these models are explained
by the fact that the disk is initially empty and the 99% radius is contributed to by the material
that is infalling from the L1 point.
due to the spreading action of viscosity but the disk nevertheless does not switch
to an eccentric mode. The apparently large initial disk radii in these models are explained
by the fact that the disk is initially empty and the 99% radius is contributed to by the material
that is infalling from the L1 point.
We then ran models with a larger viscosity
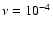 using the ``viscous outflow'' condition at the inner boundary.
The models were started from both an empty Roche lobe and a
standard initial disk as in the previous simulations.
In these cases the disk attained an eccentric mode.
In both cases an identical final state is reached, however much more quickly
for the model with
an initial disk.
The evolution of the total mass in the disk (within the primary's Roche lobe)
is displayed in the top left panel of Fig. 25.
The two cases show a complementary behaviour:
in the case with an initial disk the total mass drops towards the final
equilibrium (at around
using the ``viscous outflow'' condition at the inner boundary.
The models were started from both an empty Roche lobe and a
standard initial disk as in the previous simulations.
In these cases the disk attained an eccentric mode.
In both cases an identical final state is reached, however much more quickly
for the model with
an initial disk.
The evolution of the total mass in the disk (within the primary's Roche lobe)
is displayed in the top left panel of Fig. 25.
The two cases show a complementary behaviour:
in the case with an initial disk the total mass drops towards the final
equilibrium (at around
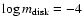 )
while for the empty case it rises initially,
overshoots the equilibrium point and settles to the equilibrium value roughly
100 orbits later.
Additional disk properties such as the disk radius, eccentricity and precession
rate are all independent of the initial condition as indicated by the other panels
in Fig. 25.
)
while for the empty case it rises initially,
overshoots the equilibrium point and settles to the equilibrium value roughly
100 orbits later.
Additional disk properties such as the disk radius, eccentricity and precession
rate are all independent of the initial condition as indicated by the other panels
in Fig. 25.
![\begin{figure}
\par\includegraphics[width=3.8cm,clip]{9953f25a.eps}\hspace*{4mm}...
...9cm}\includegraphics[width=4cm,clip]{9953f25c.eps}\hspace*{1.9cm}}
\end{figure}](/articles/aa/full/2008/32/aa09953-08/Timg201.gif) |
Figure 25:
Disk mass 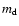 ,
radius ,
radius 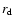 and eccentricity
and eccentricity 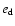 as functions of time
for models including mass inflow through the L1 point with different initial
conditions.
The first (red) curve corresponds to an initially empty Roche lobe of the primary,
while in the second (green) a standard initialized disk
is used. The ``viscous outflow'' condition and a viscosity as functions of time
for models including mass inflow through the L1 point with different initial
conditions.
The first (red) curve corresponds to an initially empty Roche lobe of the primary,
while in the second (green) a standard initialized disk
is used. The ``viscous outflow'' condition and a viscosity
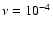 (ten times standard) are used.
(ten times standard) are used.
|
| Open with DEXTER |
The dynamical influence and importance of the stream inflow can now be studied (irrespective
of initial conditions) through a direct
comparison with the corresponding model without a stream; the results are summarized
in Table 3. The mean disk eccentricity 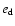 and the disk radius
and the disk radius 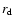 in the final equilibrium phase are very similar in both cases, with an expected
smaller disk radius and slightly smaller eccentricity due to the incoming relatively low angular
momentum disk material. The surprising difference lies in the
magnitude of the rate of disk precession. For the model without the stream the disk precesses
in a retrograde sense quite rapidly, performing a full revolution in about 17 binary orbits.
The impact of
the stream is such as to slow down the precession such that it takes
about 140 orbits to make a full revolution.
in the final equilibrium phase are very similar in both cases, with an expected
smaller disk radius and slightly smaller eccentricity due to the incoming relatively low angular
momentum disk material. The surprising difference lies in the
magnitude of the rate of disk precession. For the model without the stream the disk precesses
in a retrograde sense quite rapidly, performing a full revolution in about 17 binary orbits.
The impact of
the stream is such as to slow down the precession such that it takes
about 140 orbits to make a full revolution.
Table 3:
Comparison of two models with and without stream inflow, all other parameters being
identical. The viscosity is
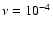 and at the inner boundary ``viscous outflow''
conditions are applied.
The model that has no stream corresponds to the second model in Table 2.
and at the inner boundary ``viscous outflow''
conditions are applied.
The model that has no stream corresponds to the second model in Table 2.
The surface density distribution of the model with stream inflow and an
initial disk is shown during the quasi-stationary
phase at 4 times separated by 10 binary orbits.
From Fig. 26 we can directly infer the slow retrograde precession
of the disk which is also confirmed independently
by a phase analysis of the m=1 Fourier mode at the specific radius r=0.37.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9953f26.eps}\end{figure}](/articles/aa/full/2008/32/aa09953-08/Timg202.gif) |
Figure 26:
Greyscale plot of the surface density of the disk for the model
with stream inflow that started with an initial disk at
210, 220, 230 and 240 orbital periods. The solid (red) curve
indicates the Roche lobe of the primary star (central red dot). The ``viscous outflow''
condition is used at the inner boundary.
|
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{9953f27.eps} \end{figure}](/articles/aa/full/2008/32/aa09953-08/Timg203.gif) |
Figure 27:
Longitude of the disk pericentre
(in the inertial frame) as a function of time. The solid (red) curve corresponds to
a disk in a quasi-steady state
with stream inflow (as displayed in the previous Fig. 26).
The light dashed (green) line corresponds to a model where the stream is switched off at t=240and the simulation is continued.
|
| Open with DEXTER |
The change of the precession rate by about
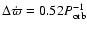 is also apparent from Fig. 27 where a quasi-stationary model with stream inflow
(from Fig. 26) is continued after the stream is switched off.
Clearly visible is the immediate transition to the state with no stream. The new
average precession rate corresponds closely to the case with no stream inflow.
Quite obviously, the disk precession rate is sensitive
to modifying conditions at the outer boundary
as well as at the inner boundary as we have seen above.
Additional runs with cooler disks (h=0.03 and 0.04) demonstrate that the transition from
prograde to retrograde disk precession occurs in the case with stream inflow for much larger
values around between h=0.04 and 0.05, see upward triangles in Fig. 14.
On the other hand the disk radius and eccentricity are more robust.
is also apparent from Fig. 27 where a quasi-stationary model with stream inflow
(from Fig. 26) is continued after the stream is switched off.
Clearly visible is the immediate transition to the state with no stream. The new
average precession rate corresponds closely to the case with no stream inflow.
Quite obviously, the disk precession rate is sensitive
to modifying conditions at the outer boundary
as well as at the inner boundary as we have seen above.
Additional runs with cooler disks (h=0.03 and 0.04) demonstrate that the transition from
prograde to retrograde disk precession occurs in the case with stream inflow for much larger
values around between h=0.04 and 0.05, see upward triangles in Fig. 14.
On the other hand the disk radius and eccentricity are more robust.
10 Conclusions
In this paper we have performed grid-based simulations of eccentric disks
in close binary systems. Adopting a grid-based rather than a particle-based
method enables consideration of a wider and more appropriate
range of physical parameters. We have been able to consider
disk aspect ratios in the range
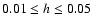 and dimensionless
viscosities in the range
and dimensionless
viscosities in the range
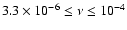 ,
whereas particle-based methods are limited to the upper limits of these ranges.
We note the relationship between
,
whereas particle-based methods are limited to the upper limits of these ranges.
We note the relationship between 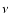 and the
and the 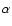 parameter
of Shakura & Sunyaev (1973)
parameter
of Shakura & Sunyaev (1973)
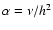 .
Thus
.
Thus
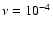 corresponds to
corresponds to
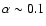 for h=0.03.
We have also considered the effects of different inner boundary conditions, the effects of a mass-transfer
stream and considered and demonstrated numerical convergence.
However, due to heavy computational demands the grid-based simulations carried out
in this first survey have been limited to two dimensions
and simply adopted a locally isothermal equation of state.
We summarize the main results of our simulations below.
for h=0.03.
We have also considered the effects of different inner boundary conditions, the effects of a mass-transfer
stream and considered and demonstrated numerical convergence.
However, due to heavy computational demands the grid-based simulations carried out
in this first survey have been limited to two dimensions
and simply adopted a locally isothermal equation of state.
We summarize the main results of our simulations below.
We find instability to the formation of an eccentric disk in the mass range
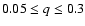 .
Explorative calculations have shown instability even for
larger mass ratios up to q=1 in these two-dimensional simulations, see
Fig. 19.
The most unstable cases are those with a reflecting
inner boundary, large viscosity, small aspect ratio and no mass-transfer stream.
An initially non-eccentric disk quickly enters
a linear phase of exponential growth of an unstable mode.
.
Explorative calculations have shown instability even for
larger mass ratios up to q=1 in these two-dimensional simulations, see
Fig. 19.
The most unstable cases are those with a reflecting
inner boundary, large viscosity, small aspect ratio and no mass-transfer stream.
An initially non-eccentric disk quickly enters
a linear phase of exponential growth of an unstable mode.
For
q=0.1 we found growth times ranging between 162 and 15binary orbits for 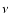 in the range
in the range
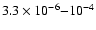 with h in the range
0.02-0.05.
A quasi-stationary precessing eccentric disk is attained in all cases
in about four growth times. In the most unstable cases (large
with h in the range
0.02-0.05.
A quasi-stationary precessing eccentric disk is attained in all cases
in about four growth times. In the most unstable cases (large 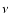 and small h)
this corresponds
to about 60 binary orbits or about 6 days for superoutbursting
cataclysmic binaries. This is consistent with reported superhump development times
of a few days.
and small h)
this corresponds
to about 60 binary orbits or about 6 days for superoutbursting
cataclysmic binaries. This is consistent with reported superhump development times
of a few days.
The mean eccentricities of the quasi-stationary disks
are typically in the range 0.3-0.6 when there is no mass-transfer
stream and an inner reflecting boundary. This is in the upper part of the range
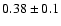 found for OY Car Hessman et al. (1992)
and for IY Ma by
Rolfe et al. (2001).
found for OY Car Hessman et al. (1992)
and for IY Ma by
Rolfe et al. (2001).
However, it is important to note that results are
sensitive to the inclusion of a mass-transfer stream and the treatment
of the inner boundary condition. For the largest
viscosities, use of an inner outflow condition rather than a reflecting
boundary condition reduces the final mean eccentricity from 0.5 to 0.3.
Incorporation of a mass-transfer stream does not affect the growth
of eccentricity for
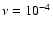 but we are able to see a transition to stability
to formation of an eccentric disk
at about
but we are able to see a transition to stability
to formation of an eccentric disk
at about
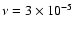 in this case independently of the inner boundary condition.
This is also consistent with the idea that the effective viscosity and consequently
the mass-transfer rate through the disk
is larger during the outburst phases of cataclysmic binaries
during which superhumps are reported (Patterson et al. 2005).
in this case independently of the inner boundary condition.
This is also consistent with the idea that the effective viscosity and consequently
the mass-transfer rate through the disk
is larger during the outburst phases of cataclysmic binaries
during which superhumps are reported (Patterson et al. 2005).
Once the simulated disks go through an instability that
results in them becoming eccentric, they typically attain a
characteristic quasi-steady state.
This was illustrated in Fig. 10.
Viewed from an inertial frame
the secondary has a close approach to the
slowly precessing disk apocentre approximately once every orbit,
pulling out a tidal tail. This later impacts back on the
disk which is not strongly affected by the secondary until
the next close approach. Thus almost the entire tidal dissipation may occur
as a result of these events. In this context we note that tidal
dissipation has been proposed as the source of the luminosity variations during the
main superhump phase while it has been proposed that effects due to modulation by the
mass-transfer stream become significant during the late superhump
phase
().
We have investigated the mechanism responsible for the excitation
of the disk eccentricity and found this to be basically
consistent with
the mode-coupling mechanism of Lubow (1991a).
Neglecting the slow precession of the disk, viewed from the inertial frame
the eccentricity of the disk may be considered to arise from a stationary surface density perturbation with azimuthal mode number
m=1. In addition the disk responds directly to the tidal potential
of the companion
producing a surface density response that corotates with it
and consists of a sum of Fourier components with
 with amplitudes that scale
with the mass ratio, q.
Nonlinear
coupling between the response to the tidal potential and the m=1 mode
causes the excitation of secondary density waves with pattern speeds
with amplitudes that scale
with the mass ratio, q.
Nonlinear
coupling between the response to the tidal potential and the m=1 mode
causes the excitation of secondary density waves with pattern speeds
 ,
,
 which exceed that of the binary
and are thus associated
with a tidal energy and angular momentum transfer to it. The
back reaction on the m=1 mode causes the eccentricity to grow.
To work effectively the secondary waves should be associated with
an inner Lindblad resonance. The most favourable case corresponds to m=3and the disk gas orbiting with
which exceed that of the binary
and are thus associated
with a tidal energy and angular momentum transfer to it. The
back reaction on the m=1 mode causes the eccentricity to grow.
To work effectively the secondary waves should be associated with
an inner Lindblad resonance. The most favourable case corresponds to m=3and the disk gas orbiting with
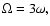 at a 3:1
commensurability. In this case the Fourier component of the tidal potential
with m=3 plays a key role.
at a 3:1
commensurability. In this case the Fourier component of the tidal potential
with m=3 plays a key role.
The results of simulations with q=0.1 supported this view with
growth being almost absent when the m=3 component was removed.
However, for q=0.2 growth still occurred in this situation albeit at a reduced rate.
This is apparently because higher-order couplings generated through
the other Fourier components result in an effective forcing with m=3.Being of higher order, this is more effective at larger q. But it should be noted
that as q increases, the 3:1 commensurability is driven towards the Roche lobe
thus becoming increasingly nonlinear and
affected by factors such as the outer boundary condition and any stream inflow.
As we indicate below, it is possible
that dissipative effects not included in our two-dimensional simulations play a
more important role. For these reasons we concentrated on the case q=0.1in this article.
The main determinants of the disk precession rate were found to be the
disk aspect ratio and the impact of a mass-transfer stream if present.
Results for
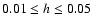 for q=0.1 are summarized in Fig. 14.
for q=0.1 are summarized in Fig. 14.
The quasi-steady disk precession rate
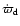 was found to decrease
from positive values at small h (prograde precession) to attain negative values
at larger h. This is because, as expected, the pressure contribution
tends to produce retrograde precession. When no mass-transfer stream was present the
transition from prograde to retrograde occurred for
was found to decrease
from positive values at small h (prograde precession) to attain negative values
at larger h. This is because, as expected, the pressure contribution
tends to produce retrograde precession. When no mass-transfer stream was present the
transition from prograde to retrograde occurred for
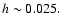 We also determined the precession rates by independently solving the linear mode problem
using the average surface density profile and in view of the strong nonlinearity
present obtained surprising agreement with h at the transition being
We also determined the precession rates by independently solving the linear mode problem
using the average surface density profile and in view of the strong nonlinearity
present obtained surprising agreement with h at the transition being 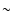 0.03.
0.03.
An approximate parabolic
fit to the data points for the case with
no mass-transfer stream was found to be
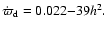 This indicates that
This indicates that
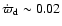 as indicated by observations (Patterson et al. 2005) only for
as indicated by observations (Patterson et al. 2005) only for
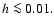 In view of the fact that values for h estimated from
accretion disk modelling fall in the range
In view of the fact that values for h estimated from
accretion disk modelling fall in the range
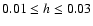 (), this is rather small.
Note that Goodchild & Ogilvie (2006) also obtained similarly small estimates from
their one-dimensional linear formalism.
(), this is rather small.
Note that Goodchild & Ogilvie (2006) also obtained similarly small estimates from
their one-dimensional linear formalism.
However, the simulations for which the disk was impacted by a mass-transfer stream
show the transition for
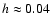 and indicate the possibility of obtaining
the observed precession rates for values of h estimated from accretion disk modelling.
Thus our results demonstrate the importance of the mass-transfer stream
in this context as well as in the context of obtaining a transition from
instability to stability at a reasonable value for the disk viscosity. On the other hand, it might be argued that the significance of the mass-transfer stream would
be reduced during a superoutburst, when the accretion rate through the disk exceeds the mass-transfer rate from the companion.
and indicate the possibility of obtaining
the observed precession rates for values of h estimated from accretion disk modelling.
Thus our results demonstrate the importance of the mass-transfer stream
in this context as well as in the context of obtaining a transition from
instability to stability at a reasonable value for the disk viscosity. On the other hand, it might be argued that the significance of the mass-transfer stream would
be reduced during a superoutburst, when the accretion rate through the disk exceeds the mass-transfer rate from the companion.
In addition we comment that there is sensitivity to the inner boundary
condition such that changing from a reflecting condition to a dissipative
or free outflow condition also acts to make the precession frequency
move in the prograde direction.
The most recent relevant SPH simulations have been
performed by Smith et al. (2007). Both two- and
three-dimensional simulations have been considered.
Several important issues should be noted.
Such simulations are inevitably highly diffusive
(
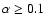 )
and thick (
)
and thick (
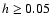 )
so that
parameter studies at smaller h and smaller
)
so that
parameter studies at smaller h and smaller 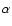 of the type considered here cannot be carried out.
Comparison has to be limited to cases with large
of the type considered here cannot be carried out.
Comparison has to be limited to cases with large 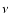 and h.The SPH simulations are performed with
and h.The SPH simulations are performed with  105 particles
and also with a mass-transfer stream. For a disk with h =0.05 one can estimate that there is only about one smoothing length per
scaleheight in a three-dimensional simulation so that the
vertical thickness is poorly resolved. The three-dimensional SPH simulations
tend to produce a weaker phenomenon than that reported here with almost no activity
for
105 particles
and also with a mass-transfer stream. For a disk with h =0.05 one can estimate that there is only about one smoothing length per
scaleheight in a three-dimensional simulation so that the
vertical thickness is poorly resolved. The three-dimensional SPH simulations
tend to produce a weaker phenomenon than that reported here with almost no activity
for
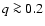 and
mean disk eccentricities
at the small end of the range implied by observation.
In addition very long growth times approaching thousands
of orbits are generally reported.
and
mean disk eccentricities
at the small end of the range implied by observation.
In addition very long growth times approaching thousands
of orbits are generally reported.
On the other hand Patterson et al. (2005)
indicate that the superhump phenomenon occurs for
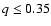 and that it is associated with high mass-transfer events during
superoutbursts and a short development time requiring growth times
and that it is associated with high mass-transfer events during
superoutbursts and a short development time requiring growth times  20 binary
orbits (see above). It may also occur in a quasi-steady manner in systems
such as nova-like variables which are also believed to have
a high mass-transfer rate which in this case is steady.
This is also consistent with our finding that
stability to eccentricity generation occurs at low viscosities and accordingly
low mass-transfer rates through the disk when a mass-transfer stream is present.
20 binary
orbits (see above). It may also occur in a quasi-steady manner in systems
such as nova-like variables which are also believed to have
a high mass-transfer rate which in this case is steady.
This is also consistent with our finding that
stability to eccentricity generation occurs at low viscosities and accordingly
low mass-transfer rates through the disk when a mass-transfer stream is present.
The reported two-dimensional SPH simulations are more in line with those
reported here. This suggests that the three-dimensional case
is more dissipative though the adequacy of the resolution in the vertical
direction should also be an issue.
It is likely that
inclusion of effects arising from the vertical structure of the disk
could result in processes leading to
additional dissipation (Papaloizou 2005)
but these would need to be simulated with adequate resolution.
The two-dimensional grid-based simulations reported here
are possibly too
unstable to forming eccentric disks, particularly at larger q.
However, in those cases, the 3:1 resonance driving the instability is pushed towards the
Roche lobe where higher-order mode couplings
and increasing nonlinearity occur and numerical studies should include
a treatment of the vertical direction if this region is to be correctly dealt with.
Therefore an important direction for future work will be to develop
three-dimensional grid-based simulations which resolve the disk
vertical structure and address the issue of the importance
of possible additional dissipation modes.
Acknowledgements
Very fruitful discussions with Aurelien Crida and Roland Speith are gratefully acknowledged.
W.K. acknowledges the very kind hospitality and support of DAMTP during his
visit to Cambridge in the spring of 2007.
- Ak, T., Ozkan,
M. T., & Mattei, J. A. 2002, A&A, 389, 478 [NASA ADS] [CrossRef] [EDP Sciences]
- Balbus, S. A.,
& Hawley, J. F. 1998, Rev. Mod. Phys., 70, 1 [NASA ADS] [CrossRef]
(In the text)
- de Val-Borro, M.,
Edgar, R. G., Artymowicz, P., et al. 2006, MNRAS, 370,
529 [NASA ADS]
(In the text)
- Goldreich, P., &
Tremaine, S. 1979, ApJ, 233, 857 [NASA ADS] [CrossRef]
(In the text)
- Goldreich, P., &
Tremaine, S. 1980, ApJ, 241, 425 [NASA ADS] [CrossRef]
(In the text)
- Goodchild, S., &
Ogilvie, G. 2006, MNRAS, 368, 1123 [NASA ADS] [CrossRef]
(In the text)
- Heemskerk,
M. H. M. 1994, A&A, 288, 807 [NASA ADS]
(In the text)
- Hessman, F. V.,
Mantel, K.-H., Barwig, H., & Schoembs, R. 1992, A&A, 263,
147 [NASA ADS]
(In the text)
- Kato, S. 1978, MNRAS,
185, 629 [NASA ADS]
(In the text)
- Kley, W. 1989,
A&A, 208, 98 [NASA ADS]
(In the text)
- Kley, W. 1998,
A&A, 338, L37 [NASA ADS]
(In the text)
- Kley, W. 1999, MNRAS,
303, 696 [NASA ADS] [CrossRef]
(In the text)
- Kley, W., &
Dirksen, G. 2006, A&A, 447, 369 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Kornet, K., &
Rozyczka, M. 2000, Acta Astron., 50, 163 [NASA ADS]
(In the text)
- Kunze, S., Speith, R.,
& Riffert, H. 1997, MNRAS, 289, 889 [NASA ADS]
- Latter, H. N.,
& Ogilvie, G. I. 2006, MNRAS, 372, 1829 [NASA ADS] [CrossRef]
(In the text)
- Lubow, S. H.
1991a, ApJ, 381, 259 [NASA ADS] [CrossRef]
(In the text)
- Lubow, S. H.
1991b, ApJ, 381, 268 [NASA ADS] [CrossRef]
(In the text)
- Masset, F. 2000,
A&AS, 141, 165 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Murray, C. D.,
& Dermott, S. F. 1999, Solar system dynamics (Cambridge
University Press)
(In the text)
- Murray, J. R.
1998, MNRAS, 297, 323 [NASA ADS] [CrossRef]
- Ogilvie, G. I.
2001, MNRAS, 325, 231 [NASA ADS] [CrossRef]
(In the text)
- Papaloizou, J., &
Pringle, J. E. 1977, MNRAS, 181, 441 [NASA ADS]
(In the text)
- Papaloizou,
J. C. B. 2005, A&A, 432, 757 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Patterson, J., Kemp,
J., Harvey, D. A., et al. 2005, PASP, 117, 1204 [NASA ADS] [CrossRef]
- Rolfe, D. J.,
Haswell, C. A., & Patterson, J. 2001, MNRAS, 324, 529 [NASA ADS] [CrossRef]
(In the text)
- Schäfer, C.,
Speith, R., Hipp, M., & Kley, W. 2004, A&A, 418, 325 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Shakura, N. I.,
& Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS]
(In the text)
- Smith, A. J.,
Haswell, C. A., Murray, J. R., Truss, M. R., &
Foulkes, S. B. 2007, MNRAS, 378, 785 [NASA ADS] [CrossRef]
- Speith, R., &
Kley, W. 2003, A&A, 399, 395 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Stehle, R. 1999,
MNRAS, 304, 687 [NASA ADS] [CrossRef]
(In the text)
- van Leer, B. 1977, J.
Comp. Phys., 23, 276 [NASA ADS] [CrossRef]
(In the text)
- Whitehurst, R. 1988,
MNRAS, 232, 35 [NASA ADS]
(In the text)
- Ziegler, U. 1998,
Comput. Phys. Commun., 109, 111 [NASA ADS] [CrossRef]
(In the text)
Copyright ESO 2008
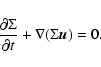
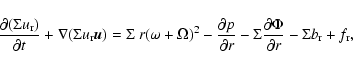
![\begin{displaymath}\frac{\partial [\Sigma r^2 (\omega + \Omega)]}{\partial t}
...
...artial \varphi}
- r \Sigma b_{\rm\varphi} + r f_{\rm\varphi}.
\end{displaymath}](/articles/aa/full/2008/32/aa09953-08/img41.gif)
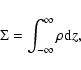
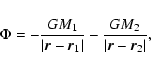
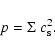
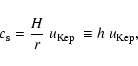
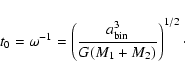
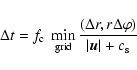
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{9953f01.eps} \end{figure}](/articles/aa/full/2008/32/aa09953-08/Timg84.gif)
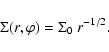
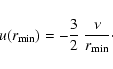
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{9953f02.eps}
\end{figure}](/articles/aa/full/2008/32/aa09953-08/Timg100.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9953f03.eps} \end{figure}](/articles/aa/full/2008/32/aa09953-08/Timg101.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9953f04.eps} \end{figure}](/articles/aa/full/2008/32/aa09953-08/Timg102.gif)
![\begin{figure}
\par\includegraphics[width=4cm,clip]{9953f05a.eps}\hspace*{4mm}
\...
....eps}\hspace*{4mm}
\includegraphics[width=3.8cm,clip]{9953f05d.eps} \end{figure}](/articles/aa/full/2008/32/aa09953-08/Timg105.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9953f06.eps} \end{figure}](/articles/aa/full/2008/32/aa09953-08/Timg114.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{9953f08.eps} \end{figure}](/articles/aa/full/2008/32/aa09953-08/Timg118.gif)
![\begin{figure}
\par\includegraphics[width=4cm,clip]{9953f09a.eps}\hspace*{4mm}
\...
...9c.eps}\hspace*{4mm}
\includegraphics[width=4cm,clip]{9953f09d.eps} \end{figure}](/articles/aa/full/2008/32/aa09953-08/Timg121.gif)
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{9953f10.eps} \end{figure}](/articles/aa/full/2008/32/aa09953-08/Timg125.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9953f12.eps} \end{figure}](/articles/aa/full/2008/32/aa09953-08/Timg138.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9953f14.eps} \end{figure}](/articles/aa/full/2008/32/aa09953-08/Timg141.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9953f15.eps} \end{figure}](/articles/aa/full/2008/32/aa09953-08/Timg148.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9953f16.eps} \end{figure}](/articles/aa/full/2008/32/aa09953-08/Timg149.gif)
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{9953f17.eps} \end{figure}](/articles/aa/full/2008/32/aa09953-08/Timg154.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9953f18.eps} \end{figure}](/articles/aa/full/2008/32/aa09953-08/Timg155.gif)
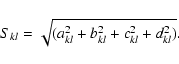
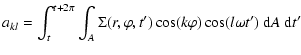
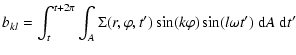
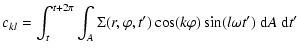
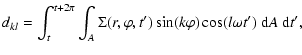
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{9953f21.eps}\end{figure}](/articles/aa/full/2008/32/aa09953-08/Timg187.gif)
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{9953f22.eps} \end{figure}](/articles/aa/full/2008/32/aa09953-08/Timg188.gif)
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{9953f23.eps} \end{figure}](/articles/aa/full/2008/32/aa09953-08/Timg189.gif)
![\begin{figure}
\par\includegraphics[width=3.8cm,clip]{9953f25a.eps}\hspace*{4mm}...
...9cm}\includegraphics[width=4cm,clip]{9953f25c.eps}\hspace*{1.9cm}}
\end{figure}](/articles/aa/full/2008/32/aa09953-08/Timg201.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9953f26.eps}\end{figure}](/articles/aa/full/2008/32/aa09953-08/Timg202.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{9953f27.eps} \end{figure}](/articles/aa/full/2008/32/aa09953-08/Timg203.gif)