A&A 487, 723-729 (2008)
DOI: 10.1051/0004-6361:200809950

A kinetic description of the dissipative quasi-parallel solar wind termination shock

D. Verscharen - H.-J. Fahr

Argelander Institute for Astronomy, University of Bonn, Auf dem Hügel 71, 53121 Bonn, Germany

Received 11 April 2008 / Accepted 28 May 2008

Abstract
Context. As a special case of astrophysical MHD shock waves, the solar wind termination shock is typically treated using the MHD jump conditions as they have been determined by Rankine and Hugoniot. A kinetic analysis becomes necessary for both a more detailed view of the governing processes and a deeper understanding of the plasma behaviour.
Aims. In the case of a parallel shock, only an electric field can be considered as the main process decelerating the solar wind ions. This field leads to a strong acceleration for the electrons due to the other sign of their charge and the much lower mass of the electrons than of the ions. This situation enforces a two-stream instability, which is considered to be compensated by wave-particle interactions with electrostatic plasma waves.
Methods. The kinetic approach leads to an equation in Fokker-Planck form, which can be solved by using Ito's calculus for stochastic differential equations.
Results. These two processes (electric field and wave-particle interaction) yield a decelerated subsonic solar wind on the downstream side of the termination shock, showing some new features in the ion distribution function, such as a double-hump structure and a comparatively large number of reflected ions. Within these considerations, we estimate of the spatial size of the shock region.

Key words: plasmas - solar wind - shock waves - magnetohydrodynamics (MHD)

1 Introduction

In the inner heliosphere the solar wind represents a supersonic quasineutral plasma flow with typical bulk velocities in the range of about 400 km s-1 for the slow solar wind type or 800 km s-1 for the fast solar wind. The solar wind density and the kinetic ram pressure of the plasma flow in this region systematically decrease with increasing solar distance. In order to be able to adapt to the local interstellar medium (LISM) with its finite pressure $P_{{\rm LISM}}$, the solar wind plasma thus has to undergo a shock, the so-called solar wind termination shock, where it transforms into a subsonic downstream plasma flow with downstream Mach numbers ${\rm Ma}_2\leq 1$ (Zank 1999; Fahr 2004; Lee 1997). This termination shock has to arrange the dissipative deceleration of a collisionless plasma flow. The specific structure of astrophysical magnetohydrodynamic (i.e. MHD) shocks is strongly characterised by the orientation of the local magnetic field $\vec{B}$ with respect to the shock surface normal $\vec{n}$. In this respect ``parallel'' means that the magnetic field upstream of the shock is parallel to the normal $\vec{n}$ of the shock surface, i.e. $\left[ \vec{B} \times \vec{n}\right] =0$, and ``perpendicular'' means that the scalar product $(\vec{B}\cdot \vec{n})$ upstream of the shock vanishes. In the ``parallel case'' there evidently is no magnetic Lorentz force component acting upon the plasma stream that can decelerate the plasma flow. This means that the bulk Lorentz force ($\propto$ $\vec{U}_n\times \vec{B}$) cannot contribute to the decrease in the bulk velocity $\vec{U}_n$ of the plasma in n-direction. Thus, the magnetic field at the first order does not play a dynamic role in the treatment of parallel MHD shock waves. Only by electromagnetic or hydromagnetic waves could it play an indirect role. Thus, at first glance, only one process remains that could enforce the neccessary plasma deceleration, namely the action of the selfconsistent shock-electric field. Ions are slowed down by running against this electric potential wall associated with this field $\vec{E}$, thereby reducing the bulk momentum of the plasma. If its selfconsistent form slows down the ions, it will also, however, simultaneously lead to an acceleration of the plasma electrons during the shock transit. Of course the electron mass $m_{{\rm e}}$ is much lower than the mass $m_{{\rm p}}$ of a proton, which is the most abundant ion in the solar wind plasma (i.e. $m_{{\rm p}}/m_{\rm e}\approx 1836$).

The first result of this electric field influence is a slowed-down ion flow and, in contrast, a strongly over-shooting fast electron flow. This situation creates electric space charges and represents a typical electrostatic two-stream instability. Thus, it cannot represent the final dynamical state of the downstream plasma flow for evident reasons: the plasma would constitute a non-neutral state due to different local densities of electrons and ions. Several different plasma micro-processes are consequently put in operation by this primarily unstable situation which tend to asymptotically bring both particle species to one identical subsonic bulk velocity and to an asymptotic quasineutral plasma condition. In this respect we investigate in detail in the present paper the collisionless wave-particle interaction with consistently excited electrostatic plasma waves (also called Langmuir waves) that are dynamically coupling ions and electrons.

This type of quasiparallel MHD shock envisaged in this paper in fact often appears in astrophysical reality, for example at different regions of the solar wind termination shock where the upstream frozen-in magnetic fields either systematically or temporarily attain small tilt angles with respect to the shock normal (e.g. see Li & Zank 2006; Chalov & Fahr 1996; Zank et al. 2004; Kóta & Jokipii 2006; Schwadron & McComas 2006). In some of the termination shock areas, the periodically changing magnetic field orientation at current sheet layers temporarily leads to parallel shock conditions. In addition, the parallel shock more or less is a permanent feature at high solar latitudes. Furthermore it is worth mentioning that nearly parallel shock conditions also permanently occur at the flanks of the earth's bow shock (Treumann & Scholer 2002). In all these cases typical nonstationarities and strong wave generation have been theoretically predicted as characteristic features of such quasiparallel shocks (Krasnoselskikh et al. 2002) and also observed by in-situ CLUSTER observations (Lobzin et al. 2007) or VOYAGER observations (Burlaga et al. 2006).

It has been clear from the very beginning that the physical details of the above-mentioned dissipative plasma-wave microprocesses are not embedded in the internal physics of the Rankine-Hugoniot conservation laws of magnetohydrodynamic shock theory, since microprocesses are not specified therein. Thus, a kinetic treatment of the shock transition definitely becomes necessary for the sake of a better physical understanding of the internal shock properties. For the situation of a perpendicular shock, analytic solutions of the ion distribution function have more recently been worked out from an adequately formulated Boltzmann-Vlasov equation (Fahr & Siewert 2006); however, up to now no analytic solutions could be provided for the parallel case due to the mathematically much less accessible and treatable form of the Boltzmann-Vlasov equation governing this case (see Siewert & Fahr 2008). In this paper we solve the adequate Boltzmann-Vlasov equation for the parallel case including stochastic, entropy-generating, wave-particle interaction processes. The numerical solution of this equation is obtained using the Ito-stochastic calculus transforming the governing second-order partial differential equation into a set of stochastic linear differential equations. This procedure has already been successfully applied for different space plasma problems in the past (e.g., Chalov et al. 1995; Chalov & Fahr 1998; Dworsky & Fahr 2000). With this solution method, we then obtain the ion distribution function on the downstream side of the parallel shock in dependence on specific values for the introduced shock parameters, such as the shock thickness, the upstream solar wind density, and solar wind bulk velocity. Some remarks on the observability of the phenomena predicted by our theoretical approach are given in the conclusions of this paper.

2 Theoretical approach

We assume a one-dimensional shock configuration where both the plasma bulk flow vector $\vec{U}$ and the upstream local magnetic field $\vec{B}$ are parallel to the shock normal $\vec{n}$. The one-dimensional steady-state Boltzmann-Vlasov equation for a collisionless medium moving along the normal space coordinate s can then be given in the form (see Fahr & Siewert 2006)

 \begin{displaymath} \frac{\partial f}{\partial s}=-\frac{1}{w_{\parallel }}\frac... ...lel }}\left( \frac{\delta f}{\delta t}\right) _{{\rm wp}}\cdot \end{displaymath} (1)

Here s is the line element counted along the shock normal, $w_{\parallel}$ the individual ion velocity in the same direction, i.e. parallel to $\vec{B}$, and  $F_{\parallel}$ represents the external force (in this case generated by the electric field $\vec{E}$). The distribution function $f=f(s,w_{\parallel },t)$ depends on the phase-space coordinates for space s, velocity $w_{\parallel}$, and time t. The last term on the right-hand side of Eq. (1) takes the place of the Boltzmann collision term describing stochastic processes. It does not correspond to a local time derivative, but represents temporal changes of the distribution function due to the wave particle interactions (indicated by the index wp) during shock transit.

2.1 Electric field

As described above, the source of deceleration of the solar wind ions is a space-charge-induced electric field $\vec{E}$. This field must be consistent with the requirements formulated by the Rankine-Hugoniot MHD shock relations.

2.1.1 Consistency with MHD

Thus it is at first necessary to find an expression that can describe an electric field consistent with the MHD shock conditions. As described before, the magnetic field can be omitted in these considerations. Therefore, one is left with the fairly simple Euler equation in connection with a force term that is the result of the electric field:

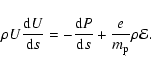\begin{displaymath}\rho U\frac{{\rm d}U}{{\rm d}s}=-\frac{{\rm d}P}{{\rm d}s}+\frac{e}{m_{{\rm p}}}\rho \mathcal{E}. \end{displaymath} (2)

In this formula U denotes the ion bulk velocity, P the pressure, and $\rho$ the mass density of the ions. Also, $\mathcal{E}$ represents the field component in the $\vec{n}$-direction of the electric field $\vec{E}$. Rearranging the terms of this equation yields the mandatory condition for the electric field

 \begin{displaymath} \mathcal{E}=\frac{m_{{\rm p}}}{e} \left[U\frac{{\rm d}U}{{\rm d}s} + \frac{1}{\rho}\frac{\rm d P}{\rm d s} \right]\cdot \end{displaymath} (3)

Using the pseudo-polytropic relation $C=P/\rho^{\gamma_{{\rm SA}}}={\rm const.}$ with the super-adiabatic heat capacity ratio $\gamma_{{\rm SA}} > 5/3$ to respect the super-adiabaticity and non-isentropicity of the shocked plasma yields

\begin{displaymath}\mathcal{E}=\frac{m_{{\rm p}}}{e}\left[U\frac{{\rm d}U}{{\rm ... ...^{\gamma_{{\rm SA}}-2}\frac{{\rm d}\rho}{{\rm d}s}\right]\cdot \end{displaymath} (4)

The super-adiabatic behaviour follows from the fact that during the shock transit kinetic energy from the flow is permanently converted into thermal energy, whereas the plasma cannot be described as if it was enclosed in a box. Incorporating the mass flux conservation $\mathcal{F}_{{\rm m}}=\rho U=\rho_1 U_1={\rm const.}$, where index 1 denotes the particular upstream parameter, leads to

\begin{displaymath}\mathcal{E}=\frac{m_{{\rm p}}}{e}U\frac{{\rm d}U}{{\rm d}s}\l... ...left(\frac{U_{1}}{U}\right)^{\gamma_{{\rm SA}} +1}\right]\cdot \end{displaymath} (5)

Here one can represent the bulk velocity in units of the upstream sound velocity $c_{{\rm s},1}=\sqrt{\gamma_{{\rm SA}} P_{1}/\rho _{1}}$ and introduce the Mach number ${\rm Ma}$ to find the expression

\begin{displaymath}\mathcal{E}=\frac{m_{{\rm p}}}{e}U\frac{{\rm d}U}{{\rm d}s}\l... ...\left(\frac{U_1}{U} \right)^{\gamma_{{\rm SA}}+1} \right]\cdot \end{displaymath} (6)

For a highly supersonic upstream flow ( ${\rm Ma}_{1}^{2}\gg 1$), one thus obtains as a first-guess solution

 \begin{displaymath} \mathcal{E} \approx \frac{m_{{\rm p}}}{e}U\frac{{\rm d}U}{{\rm d}s}=\frac{m_{{\rm p}}}{2e}\frac{{\rm d}U^2}{{\rm d}s} \end{displaymath} (7)

as an adequate and consistent condition for a first guess for the electric field (Siewert & Fahr 2007). As we show later, this initial field expression is changed, where the iteratively obtained solutions for ion bulk velocities and ion pressures can be taken into account as velocity moments of the ion distribution function described in Eq. (1).

2.1.2 Source of instability: over-shooting electrons

The field given in the form of Eq. (7) takes care of arranging the primarily MHD-desired behaviour to decelerate the ions. The conservation of energy then automatically leads to an expression for the electron bulk velocity $u_{{\rm e}}$. Thus, starting from

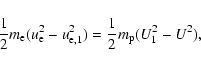\begin{displaymath}\frac{1}{2}m_{{\rm e}}(u_{{\rm e}}^{2}-u_{{\rm e},1}^{2})=\frac{1}{2}m_{{\rm p}}(U_{1}^{2}-U^{2}), \end{displaymath} (8)

with the assumption of identical upstream bulk velocities for ions and electrons ( $U_{1}=u_{{\rm e},1}$), one obtains the bulk velocity of the over-shooting electrons on the downstream side of the shock given by

 \begin{displaymath} u_{{\rm e}}^{{\rm el}}=\sqrt{\frac{m_{{\rm p}}}{m_{{\rm e}}}... ...}}{U^{2}}\left( 1+\frac{m_{{\rm e}}}{m_{{\rm p}}}\right) -1}. \end{displaymath} (9)

The upper index ${\rm el}$ indicates that there is no other interaction than the electric field considered for this value. To orient the reader, a typical compression ratio of a strong shock with a value of $\varkappa=U_{1}/U_{2,0}=4$ and an upstream bulk velocity of U1=400 km s-1 leads to a downstream electron bulk velocity of about $u_{{\rm e}}^{{\rm el}}\approx 66~400$ km s-1, whereas the ions just have a downstream bulk velocity of only U2,0=100 km s-1.

2.2 Wave-particle interaction

The quasilinear theory of Landau damping is used to obtain the temporal change of the ion distribution function due to the interaction between particles and electrostatic plasma waves. Considering in the frame of the ions the electrons that are in resonance with the excited plasma waves $\vec{k}\cdot\vec{v}\approx \omega _{{\rm p}}$ (k = wavenumber, $\omega_{{\rm p}} $ = electron plasma frequency, $\vec{v}=\vec{u}_{{\rm e}}-\vec{w}$ = ion velocity in electron bulk frame), one obtains as an expression for the change of the ion distribution function the general Fokker-Planck term in the form

 \begin{displaymath}\left( \frac{\delta f}{\delta t}\right) _{{\rm wp}}=\frac{\pa... ...llel }}D_{{\rm wp}}\frac{\partial f}{\partial w_{\parallel }}, \end{displaymath} (10)

where $D_{{\rm wp}}$ denotes the quasilinear diffusion coefficient (for quasilinear theory see for example Lifshitz & Pitaevskii 1981; Kadomtsev 1965; Davidson et al. 1970), which is given by

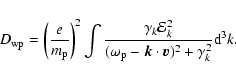\begin{displaymath}D_{{\rm wp}}=\left( \frac{e}{m_{{\rm p}}}\right) ^{2}\int \fr... ...{\rm p}}-\vec{k}\cdot \vec{v})^2+\gamma _{k}^{2}}{\rm d}^{3}k. \end{displaymath} (11)

In this expression $\gamma _{k}$ is the well known Landau damping rate, which in the above expression indicates a nonlinear increment of the ion velocity in the electron bulk frame. Recalling the one-dimensionality and changing to the shock frame then leads to

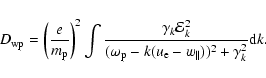\begin{displaymath}D_{{\rm wp}}=\left( \frac{e}{m_{{\rm p}}}\right) ^{2}\int \fr... ... p}}-k(u_{{\rm e}}-w_{\parallel}))^2+\gamma _{k}^{2}}{\rm d}k. \end{displaymath} (12)

Most of the interacting electrons have much higher particular velocities than the ions, meaning that $u_{{\rm e}}\gg w_{\parallel }$. Therefore, the diffusion coefficient can be simplified to

 \begin{displaymath}D_{{\rm wp}}(u_{{\rm e}})\approx \left( \frac{e}{m_{{\rm p}}}... ...}{(\omega _{{\rm p}}-ku_{{\rm e}})^2+\gamma _{k}^{2}}{\rm d}k, \end{displaymath} (13)

which in this form is independent of $w_{\parallel}$ and permits a simplification of Eq. (10) by

 \begin{displaymath} \left(\frac{\delta f}{\delta t}\right)_{{\rm wp}} \approx D_... ...u_{{\rm e}})\frac{\partial^2 f}{\partial w_{\parallel}^2}\cdot \end{displaymath} (14)

The diffusion coefficient can be simplified, if only the resonant particles ( $ku_{{\rm e}}=\omega _{{\rm p}}$) are taken into account, as mentioned before, as an upper limit for the resonance. Then only the maximum Landau damping rate needs to be considered, which is given by

\begin{displaymath}\gamma _{{\rm max}}=\frac{\sqrt{3}}{2}\omega _{{\rm p}}\sqrt[3]{\frac{m_{{\rm e}}}{4m_{{\rm p}}}}\cdot \end{displaymath} (15)

In this case, then the diffusion coefficient is finally obtained in the form

 \begin{displaymath} D_{{\rm wp}}(u_{{\rm e}})\approx \left( \frac{e}{m_{{\rm p}}... ...athcal{E}_{k_{{\rm max}}}^{2}\delta (k-k_{{\rm max}}){\rm d}k \end{displaymath} (16)

(Davidson et al. 1970). The integration over the conjugate square of the turbulent electric field is carried out under the assumption of a quasi-equilibrium interpreted between the differential electron kinetic energy and the energy density contained in the self-excited turbulent electric field. Under equipartition conditions, the latter energy density should be in balance with the kinetic energy density of the overshooting electrons in the ion rest frame (see also Vedenov 1963), so the following estimation may be reasonable:

 \begin{displaymath} 2 \int \frac{\mathcal{E}_{k_{{\rm max}}}^{2}}{8\pi}\delta (k... ...k\approx \frac{1}{2}m_{{\rm e}}n_{{\rm e}}(u_{{\rm e}}-U)^{2}. \end{displaymath} (17)

Factor 2 on the left-hand side indicates that both of the linearly independent wave propagation directions are taken into account. Hence, the final form of the diffusion coefficient is then given by

\begin{displaymath}D_{{\rm wp}}\approx D_{\parallel }=\frac{\sqrt[3]{\frac{4m_{{... ...{m_{{\rm p}}}\right) ^{2}\omega _{{\rm p}}(u_{{\rm e}}-U)^{2}. \end{displaymath} (18)

In the following $D_{{\rm wp}}$ is denoted as $D_{\parallel}$ to clarify its difference from the more general form of the diffusion coefficient. In the formula above it can be easily seen that the turbulent interaction works more efficiently at high velocity differences between electrons and ions and evidently vanishes for equal bulk velocities.

2.3 Ito-Stochastic differential equation

Now with the terms derived above the adequate Boltzmann-Vlasov equation attains the form

 \begin{displaymath} \frac{\partial f}{\partial s}=-\frac{1}{2}\frac{{\rm d}U^2}{... ..._{\parallel}\frac{\partial^2 f}{\partial w_{\parallel}^2}\cdot \end{displaymath} (19)

To bring this equation into a typical Fokker-Planck form, the differential particle current $N=w_{\parallel }f$ can be introduced. With this substitution, Eq. (19) reads as

 \begin{displaymath} \frac{\partial N}{\partial s}=-\frac{\partial }{\partial w_{... ...el }^{2}}\left(\frac{2D_{\parallel }}{w_{\parallel }}N\right). \end{displaymath} (20)

This Fokker-Planck equation contains a velocity drift term

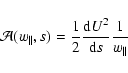\begin{displaymath}\mathcal{A}(w_{\parallel },s)=\frac{1}{2}\frac{{\rm d}U^{2}}{{\rm d}s}\frac{1}{w_{\parallel }} \end{displaymath} (21)

and a velocity diffusion term

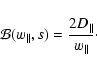\begin{displaymath}\mathcal{B}(w_{\parallel },s)=\frac{2D_{\parallel }}{w_{\parallel }}\cdot \end{displaymath} (22)

The Ito-calculus for stochastic differential equations can be applied with the help of these expressions. The basic underlying method is appropriately described in Gardiner (1994). This calculus describes the motion of one single particle under the influence of drift and diffusion. Therefore, it must include both the deterministic behaviour due to the drift term and the stochastic behaviour due to the diffusion term. Leading to a simple integrable equation for the motion of one particle (the so-called Langevin equation), this approach constitutes an easier method from the numerical point of view to solve a Fokker-Planck equation than other possible methods. Additionally, the physical interpretation of both acting processes becomes clearer because one can follow one particle on every step during its shock transit. In contrast to that method, the actual differential equation could also be solved numerically by using a finite-difference method based on splitting the physical processes, where the explicit counterflow scheme is applied for the convective part and for the diffusive part of the equation the implicit scheme with Newton's method used to solve the nonlinear system of equations. The problem here is, however, to reach convergence of the numerical solutions (see Chalov et al. 2004). As a parabolic partial differential equation the Fokker-Planck Eq. (20) will probably need a more complicated classical PDE treatment (as an initial/boundary-value problem) to avoid singularities in the solution (see for example Evans 1998).

The associated Langevin equation for the general case is given by

 \begin{displaymath}\frac{{\rm d}w_{\parallel }}{{\rm d}s}=\mathcal{A}(w_{\parallel },s)+\sqrt{\mathcal{B}(w_{\parallel },s)}\xi (s). \end{displaymath} (23)

In this differential equation the quantity $\xi (s)$ is a rapidly varying stochastic term (i.e. $\langle \xi (s)\xi (s^{\prime })\rangle=\delta (s-s^{\prime })$). In the special case of our problem here the integration of the corresponding Langevin equation is achieved by means of the Ito stochastic equation

 \begin{displaymath}{\rm d}w_{\parallel }=\frac{1}{2}\frac{{\rm d}U^{2}}{{\rm d}s... ...arallel }}{\left\vert w_{\parallel }\right\vert }}{\rm d}W_{s} \end{displaymath} (24)

with ${\rm d s}=w_{\parallel} {\rm d t}$.

From this, ${\rm d}W_{s}$ is the increment of the Wiener process given by

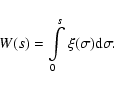\begin{displaymath}W(s)=\int \limits _0^s \xi(\sigma){\rm d}\sigma. \end{displaymath} (25)

It can be obtained from its probability distribution

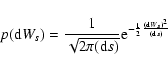\begin{displaymath}p({\rm d}W_s)=\frac{1}{\sqrt{2\pi({\rm d}s)}}{\rm e}^{-\frac{1}{2}\frac{({\rm d}W_s)^2}{({\rm d}s)}} \end{displaymath} (26)

for a stochastic step of width ${\rm d}W_{s}$ within the distance ${\rm d}s$.

Looking at Eq. (24), the splitting of the two acting processes becomes apparent. The effect of the decelerating electric field is described by the first term (the drift term) and the stochastic effect of the wave-particle interaction appears within the second term (i.e. the diffusion term).

To continue at this point, the specification of a bulk velocity profile U=U(s) is necessary. In our case here we represent the velocity step over the shock by a ``$\tanh$''-profile (compare with Lee et al. 1986) in the form

 \begin{displaymath} U(s)=\frac{U_{1}+U_{\rm 2,i}}{2}-\frac{U_{1}-U_{\rm 2,i}}{2}\cdot \tanh \left( \frac{s}{\lambda }\right), \end{displaymath} (27)

which brings the ion bulk velocity U(s) from its higher upstream value U1 down to the downstream value $U_{\rm 2,i}$ within a characteristic length scale $\lambda $. The ion pressure profile behaves similarly and is hence described by a profile, which ignores the upstream pressure:

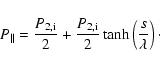\begin{displaymath}P_{\parallel}=\frac{P_{\rm 2,i}}{2}+\frac{P_{\rm 2,i}}{2}\tanh\left(\frac{s}{\lambda}\right)\cdot \end{displaymath} (28)

For the first guess, $U_{\rm 2,i}$ is considered to be given by $U_{2,0}=U_1/\varkappa$. During the iteration its value changes, which leads to a change in the velocity profile and, hence, to a change in the electric field according to Eq. (7). The electron velocity profile contains two ingredients: one is the initial velocity over-shoot from Eq. (9), and the other is due to turbulent kinetic energy loss:

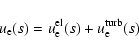\begin{displaymath}u_{{\rm e}}(s)=u_{{\rm e}}^{{\rm el}}(s)+u_{{\rm e}}^{{\rm turb}}(s) \end{displaymath} (29)

where the last quantity is given by

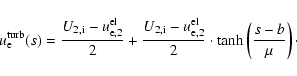\begin{displaymath}u_{{\rm e}}^{{\rm turb}}(s)=\frac{U_{\rm 2,i}-u_{{\rm e},2}^{... ...^{{\rm el}}}{2}\cdot \tanh \left( \frac{s-b}{\mu }\right)\cdot \end{displaymath} (30)

As a result, the electron bulk velocity first shoots up to $u_{{\rm e},2}^{{\rm el}}$, but then is systematically driven down to $U_{\rm 2,i}$ by the action of the dynamic coupling between electrons and ions. The characteristic length scale of the electrostatic turbulent wave-particle interaction depends on the parameters b and $\mu$.

Each integration of Eq. (24) corresponds to the phasespace propagation of one selected ion over the shock structure influenced by drift and diffusion (MacKinnon & Craig 1991). Thus, such integrations must be carried out with a statistically relevant sample of ions (in this case for 30 000 ions) to reach statistical significance. Counting the individual ions on the downstream side in their different velocity space intervals thus finally yields the ion distribution function $f_{2}(w_{\parallel })$. As the most important velocity moments of $f_{2}(w_{\parallel })$, the resulting downstream bulk velocity

 \begin{displaymath} U^{\prime}_{2}=\frac{1}{n_2}\int\limits_{-\infty }^{+\infty }w_{\parallel}f_{2}(w_{\parallel }){\rm d}w_{\parallel } \end{displaymath} (31)

and the temperature of the ions

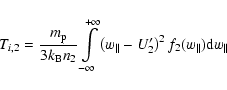\begin{displaymath}T_{{i},2}=\frac{m_{{\rm p}}}{3k_{{\rm B}}n_{2}}\int\limits_{-... ...rime}_{2}\right)^{2}f_{2}(w_{\parallel }){\rm d}w_{\parallel } \end{displaymath} (32)

are calculated. This quantity, together with n2, also delivers the ion pressure

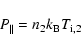\begin{displaymath}P_{\parallel}=n_2 k_{\rm B} T_{\rm i,2} \end{displaymath} (33)

and, thus, allows us to iteratively update the electric field taken from Eq. (3).

From arguments of energy conservation the electron temperature $T_{{\rm e},2}$ can also then indirectly be achieved. For the further iteration of Eq. (24), the downstream bulk velocity in Eq. (27) now is set equal to the newly found value $U^{\prime}_{2}$. Hence, one only obtains the asymptotic, ``real'' value of the resulting downstream bulk velocity $U_{\rm 2,i}$ after several iterations after it results from the action of the processes.

3 Results

3.1 Thickness of the shock

To estimate the size $\lambda $ of the space charge region where the electric field $\mathcal{E}$ dominates, an approximative solution of Poisson's equation in the following form can be used,

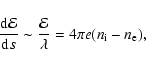\begin{displaymath}\frac{{\rm d}\mathcal{E}}{{\rm d}s}\sim \frac{\mathcal{E}}{\lambda }=4\pi e(n_{{\rm i}}-n_{{\rm e}}), \end{displaymath} (34)

since such stationary electric fields at the shock transition are always the result of a charge density distribution in a plasma.

To form a rather simple estimate, the densities are derived from the particle flux conservation $\mathcal{F}=n_{{\rm i}}U=n_{\rm e}u_{\rm e}={\rm const.}$ Then, the above estimation leads to

 \begin{displaymath}\lambda \sim \sqrt{\frac{m_{{\rm p}}}{8\pi e^{2}n_{1}}\frac{\... ...{{\rm e},2}^{{\rm el}}}\right) }}\sim 5\times 10^{5}~{\rm cm}. \end{displaymath} (35)

As described by Davidson et al. (1970) the characteristic time for wave-particle interaction is given by a few maximum growth periods

\begin{displaymath}\tau \approx \frac{1}{\gamma_{{\rm max}}}=\frac{2}{\sqrt{3}}\... ...mega_{{\rm p}}}\sqrt[3]{\frac{4m_{{\rm p}}}{m_{{\rm e}}}}\cdot \end{displaymath} (36)

The plasma frequency $\omega_{{\rm p}}=\sqrt{4\pi n_{{\rm e}}e^{2}/m_{{\rm e}}}$ on the downstream side of the termination shock (at about 90 AU) can be calculated for a typical value for the downstream electron number density of $n_{{\rm e}}=1.2\times 10^{-3}~{\rm cm}^{-3}$. Therefore, one can estimate the region of turbulent wave-particle interaction to have a most probable size of a few multiples of

 \begin{displaymath} \sigma \approx U_{2,0}\tau \simeq 1\times 10^{6}~{\rm cm}. \end{displaymath} (37)

This evaluation is needed to find appropriate estimates for the parameters b and $\mu$ that characterise the turbulence region.

3.2 Properties of the downstream distribution function

Using standard parameters (good compilations are given by Scherer et al. 2000; or can be found in the review of Zank 1999; and measurments from space probes can be found at Gazis et al. 1994) for the quiet solar periods; i.e., like $U_{1}=4\times 10^{7}~{\rm cm/s}$, $n_{\rm {i},1}=n_{{\rm e},1}=5\times 10^{-4}~{\rm cm}^{-3}$, $T_{\rm {i},1}=1.0\times 10^{4}~{\rm K}$, $\varkappa=U_{1}/U_{2,0}=4$, the resulting ion distribution function $f_{2}(w_{\parallel })$ can be calculated and plotted. The tilde sign on top of velocities indicates that these values are normalised by U1 for a better numerical handling; i.e., velocities are given in units of the upstream bulk velocity (e.g., $\tilde{w}_{\parallel }=w_{\parallel }/U_{1}$) and length scales in units of $\lambda $, which is set to the estimated value of $5\times 10^{5}~{\rm cm}$. The shock extent is discretised into 10 000 steps over the range of $-20\leq \tilde{s}\leq +20$. The initial ion velocities are taken from an upstream distribution function $f_{1}(w_{\parallel })$ taken as a Maxwell-Boltzmann distribution with $T=T_{\rm {i},1}$. The parameter b is set to $2\times 10^{6}~{\rm cm}$, whereas $\mu$ is always chosen so that the ratio $b{:}\mu$ amounts to 4:1. This assures that the electron bulk velocity profile decreases continuously from its overshoot value to its asymptotic value $\tilde{U}_{2}$. Calculations with different values for this ratio do not show any severe dependence on $\mu$. The distribution function is plotted in Fig. 1.


  \begin{figure} \par\includegraphics[width=7.8cm,clip]{9950fig1.eps}\end{figure} Figure 1: Normalised ion distribution function on the downstream side of the termination shock. The underlying parameters are described in the text. The sample consists of 30 000 particles. Two humps have been developed in the distribution with one reflected and one continuing beam. The dotted curves are the fit results described in Sect. 3.4.
Open with DEXTER

The real bulk velocity on the downstream side as calculated by Eq. (31) has a value of $U_{\rm 2,i}\simeq 1.6\times 10^{7}~{\rm cm/s}$, which leads to a true compression ratio of $r =U_{1}/\tilde{U}_{2}\simeq 2.5$. The ion temperature amounts to $T_{{i},2}\simeq 2.27\times 10^{6}~{\rm K}$, the electron temperature to  $T_{{\rm e},2}\simeq 3.13\times 10^{6}~{\rm K}$. Thus, the downstream sound velocity takes a value of

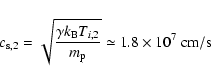\begin{displaymath}c_{{\rm s},2}=\sqrt{\frac{\gamma k_{{\rm B}}T_{{i},2}}{m_{{\rm p}}}}\simeq 1.8\times 10^{7}~{\rm cm/s} \end{displaymath} (38)

and is higher than $U_{\rm 2,i}$. For this reason the shock in fact decelerates the ions from an initially supersonic to a subsonic bulk velocity.

In view of Fig. 1 one recognises that partial ion reflection obviously occurs at the termination shock. The hump on the left-hand side of the downstream ion distribution function $f_{2}(w_{\parallel })$ is developed due to ion scattering at electrostatic turbulences and represents ions that have attained negative particular velocity with respect to the shock rest frame. The amount of these ions is determined by the parameters $\lambda $ and b. For smaller shock size parameters, the fraction of these ions decreases and vice versa. Within the usual ranges the other parameters have only a very weak influence on the plasma stream properties. Even a change in the classical compression ratio $\varkappa$ does not change the downstream bulk velocity $U^{\prime}_{2}$, since the turbulent interaction is so dominant that it superposes the classical velocity profile. This holds for $\varkappa >2$, whereas it is usually assumed to be approximately 4.

The energy densities contained in the electric field and in the wave field can be derived from the bulk velocity behaviour. The electric field energy $e\Phi \approx e\mathcal E \lambda$ leads to the change in the ion velocity and, therefore, the mean field from a global view is given by

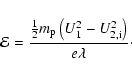\begin{displaymath}\mathcal E=\frac {\frac{1}{2}m_{\rm p} \left(U_1^2-U_{\rm 2,i}^2\right)}{e \lambda}\cdot \end{displaymath} (39)

Using $\lambda $ from Eq. (35) this yields

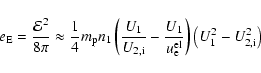\begin{displaymath}e_{\rm E}=\frac{\mathcal E^2}{8\pi} \approx \frac{1}{4}m_{\rm... ..._{\rm e}^{{\rm el}}} \right) \left(U_1^2-U_{\rm 2,i}^2 \right) \end{displaymath} (40)

as an expression for the electric energy density. The condition of equipartition in Eq. (17) reveals a wave field energy density of

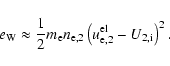\begin{displaymath}e_{\rm W} \approx \frac{1}{2}m_{\rm e}n_{\rm e,2} \left(u_{\rm e,2}^{{\rm el}}-U_{\rm 2,i} \right)^2. \end{displaymath} (41)

For the given compression of $\varkappa=4$ at the beginning, this leads to a ratio of $e_{\rm E}/e_{\rm W}\approx 80$. For the resulting true compression of r=2.5, this ratio changes for the benefit of the electric field to $e_{\rm E}/e_{\rm W} \approx 240$ as expected because the bulk velocity change and the over-shooting is smaller than in the first view so that much less turbulent waves are excited.

3.3 The shock thickness dependence

At this point the interest in the two most important parameters $\lambda $ and b arises. A set of calculations of the downstream distribution function $f_{2}(w_{\parallel })$ is carried out by us for different parameters and the moments $U^{\prime}_{2}$ and T2 (temperature both for ions and electrons) are calculated. The dependence on $\lambda $ is shown in Fig. 2. The real value of b does not change during the iterations, thus $\tilde{b}=b/\lambda$ must change because of the rescaling by units of $\lambda $.


  \begin{figure} \par\includegraphics[width=7.8cm,clip]{9950fig2.eps}\end{figure} Figure 2: Dependence of the moments on parameter $\protect\lambda$. The ordinate for units of velocities is on the left, for the temperatures on the right. Velocities are scaled in units of U1, and b has a value of $2\times 10^{6}~{\rm cm}$.
Open with DEXTER

In addition to the above-mentioned moments, the sound velocity $\tilde{c}_{{\rm s},2}$ on the downstream side of the shock is plotted into the diagram in the same scaled units as $\tilde{U}_{2}$. Thus, it is possible to see which cases have no physical meaning, i.e. where the downstream bulk velocity is higher than the speed of sound. In these cases the solar wind would not be shocked down to a subsonic flow. This situation is given for $\lambda \ga 6\times 10^{5}~{\rm cm}$ and, therefore, an upper limit is obtained from the numerical simulation. This result is in very good agreement with the above approximative value of $\lambda =5\times 10^{5}~{\rm cm}$. The parameter $\lambda $ obviously has an effect on both the deceleration and the change in the temperature.

The other important parameter for the calculation is the size of the interaction region, which is determined by b. In Fig. 3 we show the behaviour of the moments of the ion distribution function in dependence on b.


  \begin{figure} \par\includegraphics[width=7.8cm,clip]{9950fig3.eps}\end{figure} Figure 3: Dependence of the moments on parameter b. The ordinate for units of velocities is on the left, for the temperatures on the right. Velocities are scaled in units of U1, $\tilde b$ is scaled as $\tilde b=b/\protect\lambda$. $\protect\lambda$ is chosen to be $5\times 10^{5}~{\rm cm}$.
Open with DEXTER

Essentially, this parameter only has an influence on the temperature that is identically represented by the width of the distribution function. The downstream bulk velocity does not show a pronounced relationship with the size of the region where wave-particle interaction occurs. Because of the energy conservation, increasing ion temperature at constant bulk velocity means decreasing electron temperature, and the other way around. However, there is one point where isothermal conditions appear. At $b=\tilde{b}\lambda =5\times 5\times 10^{5}~{\rm cm}=2.5\times 10^{6}~{\rm cm}$ the ion and the electron temperatures turn out to be equal. A further transfer of thermal energy from electrons to ions during the ongoing of the propagation further downstream should be forbidden by the second law of thermodynamics (anti-entropic behaviour!). On the other side, the same argument as above holds for $\tilde{b}\la 3$, namely that the downstream velocity is higher there than the sound velocity. Hence, the possible range for $\tilde b$ can be restricted to $3\la \tilde{b}\la 5$, which means that, in rescaled units, b takes a value between $1.5\times 10^{6}~{\rm cm}$ and $2.5\times 10^{6}~{\rm cm}$. This strong restriction shows that the estimated size of $2\times 10^{6}~{\rm cm}$ is a good choice for the size of the interaction region.

3.4 Possible observations of the double-hump feature of the ion distribution 

In the more recent past some observational indications for the occurrence of MHD plasma waves at the solar wind termination shock were obtained from VOYAGER measurements (see Burlaga et al. 2006). In addition, the plasma wave subsystems (PWS) onboard the VOYAGER-1 probe have received radio waves in the kHz region, which are interpreted as the result of electrostatic plasma oscillations at the termination shock as converted into electromagnetic turbulence by several authors (Gurnett & Kurth 1996). Although these emissions seemed to be singular events connected with preceding solar outbursts propagating in the solar wind, this nevertheless is a direct indication of the occurrence of plasma waves. The observed radiation suggests a plasma frequency of about $900~{\rm Hz}$, whereas in our case the plasma frequency of the downstream plasma is at about $\nu _{{\rm p}}\approx 320~{\rm Hz}$. The observed higher frequency, however, can be the result of the different solar wind properties after a particle outburst.

A better chance to confirm the results of the kinetic shock model presented here is perhaps given through the spectral observation of energetic neutral atoms (ENAs). The interstellar boundary explorer (IBEX) satellite will soon (scheduled launch in August 2008!) present the opportunity to detect spectral intensities of ENA fluxes of shock-generated ENAs from a vantage point near the earth (McComas et al. 2005). From these measurements the ion distribution function at the termination shock can be reconstructed (Gruntman et al. 2001). For this reason it appears to be adviced to offer an analytical fit result for the numerically obtained ion distribution function of this paper here. Therefore, the superposition of two Gaussians of the form

 \begin{displaymath} \bar f(\tilde{w}_{\parallel })=a\cdot \exp \left( -b\left( \tilde{w}_{\parallel}-c\right) ^{2}\right) \end{displaymath} (42)

is selected as a best fit to the numerically obtained normalised distribution function $\bar f_{2}(\tilde{w}_{\parallel })$. The fit function is plotted additionally into Fig. 1, the fit parameters are listed in Table 1.

Table 1: Result of the fit according to Eq. (42).

The small errors indicate the quality of the fit result. Integrating both Gaussians and summing up yields 1.01, which emphasises this result (i.e., the distribution function is normalised to 1).

4 Conclusions

The ion distribution function $f_{2}(w_{\parallel })$ shows two beams, both of which are well-fitted by a Gaussian profile. One of these beams represents ions that are reflected at the shock. The number of these reflected ions are determined by the shock size parameters $\lambda $ and b. From classical MHD theory, this detailed double-hump behaviour cannot be obtained. The MHD shock treatment only relates several global quantities to one another and does not present the kinetic details. In our model global assumptions are partially taken from MHD. On the other hand, the moments of the numerically calculated distribution function determine the MHD shock characterisation. Thus, our results are in good agreement with the magnetohydrodynamic theory; however, they show several additional details.

The predominant quantities for downstream bulk velocity and temperature are the parameters that characterise the shock extent. The others do not change the plasma properties on the downstream side appreciably, if they are chosen within the typical range. Connecting the differently gained results leads to the solar wind termination shock having a small shock thickness of about $2\times 10^{6}~{\rm cm}$ in comparison with other considerations. For example, Siewert & Fahr (2007) find a shock thickness of about $\lambda _{\parallel }\ga 2\times 10^{10}~{\rm cm}$ for similar conditions for the parallel case (using a typical magnetic field of $B=5\times 10^{-7}~{\rm G}$). They consider Whistler waves as the process that compensates for the two-stream instability. It is, however, obvious from basic considerations in this paper that electrostatic plasma waves couple the electron and ion bulk velocities much more efficiently.

For the typically chosen parameters, the real compression ratio turns out to be r=2.5. A comparison with measured data is hard to do because of the very poor data basis. Different data from the shock passage of VOYAGER-1 leads to a derivation of the compression ratio of r=2.6-0.2+0.4 (Stone et al. 2005), which interestingly enough lies in perfect accordance with our value here. However, this result must be handled with caution, because VOYAGER-1 is supposed to have observed in a termination shock region with a quasi-perpendicular shock situation. On the other hand, this space probe is the only instrument to now that has been able to achieve in-situ measurements of this parameter.

Our calculations in addition show a higher temperature for the electrons than for the ions, except for the situation where isothermal conditions can be reached at $T_{2}\simeq 2.8\times 10^{6}~{\rm K}$ as described before. For most of the MHD simulations, this is not the typical result, and even multifluid simulations in contrast indicate a lower downstream temperature for the electrons (e.g., Zank 1999).

The true size of the shock layer is the crucial factor in our model; hence, one should study the possibility of a simultaneous kinetic treatment of the involved electrons. This could yield the ability to find a self-consistent plasma description, wherein the shock extent does not need to be a given parameter but a quantity that results from the calculation itself. Due to the fact that - after the again singular VOYAGER-2 passage - no more in-situ measurements can be expected in the very near future, remote sensing by satellites like IBEX represents the best capability for an observational study of our results with a high statistic significance. Within the energy bands of IBEX, the conspicuous double-hump structure should be observable.

Our model shows that the connection of classical MHD with kinetic methods is a good way to obtain detailed results for the behaviour of shocked space plasmas. The very complex closed solution of the full Boltzmann equation becomes unnecessary using this approach.

Acknowledgements
We are grateful for financial support to the DFG within the frame of the DFG-Project Fa 97/31-2. In addition, we express our gratitude to A. Dworsky for his help in applying the Ito-stochastic calculus.

References

 
Copyright ESO 2008