A&A 487, 697-707 (2008)
DOI: 10.1051/0004-6361:200809779
From B[e] to A[e]
On the peculiar variations of the SMC supergiant LHA 115-S 23 (AzV 172)
M. Kraus1 - M. Borges Fernandes2,3 - J. Kubát1 - F. X. de Araújo4
1 - Astronomický ústav, Akademie ved Ceské republiky, Fricova 298, 251 65 Ondrejov, Czech Republic
2 -
Royal Observatory of Belgium, Ringlaan 3, 1180 Brussels, Belgium
3 -
UMR 6525 H. Fizeau, Univ. Nice Sophia Antipolis, CNRS, Observatoire de la Côte d'Azur, Av. Copernic, 06130 Grasse, France
4 - Observatório Nacional, Rua General José Cristino 77, 20921-400 São Cristovão, Rio de Janeiro, Brazil
Received 14 March 2008 / Accepted 1 June 2008
Abstract
Context. Optical observations from 1989 of the Small Magellanic Cloud (SMC) B[e] supergiant star LHA 115-S 23 (in short: S 23) revealed the presence of photospheric He I absorption lines, classifying S 23 as a B8 supergiant. In our high-resolution optical spectra from 2000, however, we could not identify any He I line. Instead, the spectral appearance of S 23 is more consistent with the classification as an A1 supergiant, maintaining the so-called B[e] phenomenon.
Aims. The observed changes in spectral behaviour of S 23 lead to different spectral classifications at different observing epochs. The aim of this research is, therefore, to find and discuss possible scenarios that might cause a disappearance of the photospheric He I absorption lines within a period of only 11 years.
Methods. From our high-resolution optical spectra, we perform a detailed investigation of the different spectral appearances of S 23 based on modern and revised classification schemes. In particular, we derive the contributions caused by the interstellar as well as the circumstellar extinction self-consistently. The latter is due to a partly optically thick wind. We further determine the projected rotational velocities of S 23 in the two epochs of spectroscopic observations.
Results. Based on its spectral appearance in 2000, we classify S 23 as A1 Ib star with an effective temperature of about 9000 K. This classification is supported by the additional analysis of the photometric UBV data. An interstellar extinction value of
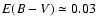 is derived. This is considerably lower than the previously published value, which means that, if the circumstellar extinction due to the stellar wind is neglected, the interstellar extinction, and hence the luminosity of the star, are overestimated. We further derive a rotation velocity of
is derived. This is considerably lower than the previously published value, which means that, if the circumstellar extinction due to the stellar wind is neglected, the interstellar extinction, and hence the luminosity of the star, are overestimated. We further derive a rotation velocity of
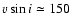 km s-1, which means that S 23 is rotating with about 75% of its critical speed. The object S 23 is thus the fourth B[e] supergiant with confirmed high projected rotational velocity. The most striking result is the apparent cooling of S 23 by more than 1500 K with a simultaneous increase of its rotation speed by about 35% within only 11 years. Since such a behaviour is excluded by stellar evolution theories, we discuss possible scenarios for the observed peculiar variations in S 23.
km s-1, which means that S 23 is rotating with about 75% of its critical speed. The object S 23 is thus the fourth B[e] supergiant with confirmed high projected rotational velocity. The most striking result is the apparent cooling of S 23 by more than 1500 K with a simultaneous increase of its rotation speed by about 35% within only 11 years. Since such a behaviour is excluded by stellar evolution theories, we discuss possible scenarios for the observed peculiar variations in S 23.
Key words: stars: fundamental parameters - stars: winds, outflows - supergiants - stars: individual: LHA 115-S 23 (AzV 172)
B[e] stars belong to one of the puzzling phenomena in modern astrophysics.
While many of their members have been known for decades, the number of new
detections of B[e] stars is growing tremendously (see, e.g., Kraus &
Miroshnichenko 2006). The classification by Lamers et al. (1998)
of B[e] stars according to their evolutionary phase made clear that B[e] stars
occur in the pre- as well as in the post-main sequence phase, and the most
popular class is formed by the B[e] supergiants with confirmed members
predominantly in the Magellanic Clouds (see the recent review by Zickgraf
2006).
The derivation of stellar parameters of B[e] stars is complicated because in
most cases the stellar photospheres are hidden inside the dense and optically-thick winds. Thus, the spectra are contaminated with wind continuum emission in
the form of free-free and free-bound emission as well as with an enormous
amount of emission lines that are generated in the circumstellar wind material,
which is usually non-spherically symmetric. Evidence for non-sphericity thereby
comes from polarimetric observations, e.g., by Magalhães (1992),
Magalhães et al. (2006), and Melgarejo et al.
(2001), in rare cases even from optical imaging with the
Hubble Space Telescope, as was the case for the galactic B[e] star Hen 2-90
(Sahai et al. 2002; Kraus et al. 2005), and from
interferometric observations with, e.g., the VLTI/AMBER and VLTI/MIDI
instruments (e.g., Domiciano de Souza et al. 2007). An observed
strong infrared (IR) excess emission due to warm and hot circumstellar dust
(e.g., Zickgraf et al. 1985, 1986, 1989,
1992; Gummersbach et al. 1995, Borges Fernandes et al.
2007) indicates the presence of a high-density disk. This disk must
further be the location of the neutral material like O I (Kraus et al.
2007) and the molecular gas, expressed by CO first-overtone bands
(McGregor et al. 1988a, 1988b, 1989; Morris et al. 1996; Kraus et al. 2000) and TiO band emission (Zickgraf et al. 1989). The proposed scenario for B[e] supergiants thus
suggests that their circumstellar material consists of a disk-like structure
formed by a high density equatorial wind with low outflow velocity, and a
normal B-type line-driven wind of high velocity and much lower density in polar
directions (Zickgraf et al. 1985; Zickgraf 2006). A
possible mechanism for the formation of outflowing high density disks might be
rapid rotation of the central star (see, e.g., Bjorkman & Cassinelli
1993; Curé 2004; Curé et al. 2005). In
addition, if the star is rotating rapidly, the wind material in the equatorial
plane recombines in hydrogen in the vicinity of the stellar surface, as has
recently been shown by Kraus (2006). And for at least three B[e]
supergiants projected rotational velocities at a significant fraction of their
critical speed have indeed been found (Gummersbach et al. 1995;
Zickgraf 2000, 2006), hinting to the possible
connection between the presence of a circumstellar disk and stellar rotation.
For the Small Magellanic Cloud (SMC) star LHA 115-S 23 (AzV 172, 2MASS
J00555380-7208596, in the following refered to as S 23) that is investigated in
this paper, no rotational velocity has been derived yet. In addition, not much is
known about the orientation of the system, although it has been suggested to be
seen more or less edge-on, based on the low expansion velocity derived from the
Balmer lines (Zickgraf et al. 1992, referred to as ZSW in the
following). This object was first classified by Azzopardi & Vigneau (1982) as a B8 supergiant, and the detection of several photospheric
He I absorption lines in the optical mid-resolution spectrograms of ZSW is
in agreement with the classification of S 23 as a late B-type supergiant.
These authors further fixed the interstellar extinction at
E(B-V) = 0.10,
derived an effective temperature of
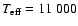 K, and a surface
gravity of
K, and a surface
gravity of
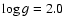 .
This led to
.
This led to
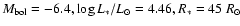 ,
and the assignment of the luminosity class Ib.
The spectra of ZSW showed further strong Balmer line emission, [O I]
emission, as well as many Fe II and [Fe II] emission lines. In
combination with the pronounced infrared excess in the photometric data, which
can be ascribed to warm or hot circumstellar dust, ZSW assigned S 23 to the
group of B[e] supergiants.
,
and the assignment of the luminosity class Ib.
The spectra of ZSW showed further strong Balmer line emission, [O I]
emission, as well as many Fe II and [Fe II] emission lines. In
combination with the pronounced infrared excess in the photometric data, which
can be ascribed to warm or hot circumstellar dust, ZSW assigned S 23 to the
group of B[e] supergiants.
About eleven years later, during our observing mission of Magellanic Cloud B[e]
supergiants, we observed S 23 using a high-resolution optical spectrograph.
Our spectra confirm the presence of the strong Balmer emission lines as well as
of the [O I], [Fe II], and Fe II emission lines. But
interestingly, even with a more than 10 times higher resolution, our spectra do
not display any He I line either in absorption nor in emission. The
absence of the He I lines speaks more in favour of a cooler central
object than a late B supergiant. This paper is therefore aimed to investigate
in detail the spectral appearances of S 23 at the two epochs of observations
and to discuss possible scenarios that might cause the observed peculiar
variations of S 23.
The paper is structured as follows: our observations are described in
Sect. 2. Then, we perform the spectral classification of S 23 for the
two different observing epochs, using modern, improved classification schemes
(Sect. 3) and determine the contributions of both, interstellar
and circumstellar extinctions (Sect. 4). From the detected
photospheric Mg II absorption lines, we next derive the projected
rotation velocity of S 23 at the two epochs of observations
(Sect. 5). In Sect. 6, we discuss possible scenarios
that might explain the observed peculiarities, before we summarise our major
results in Sect. 7.
2 Observations
![\begin{figure}
\par\includegraphics[width=9cm,clip]{9779fi1a.eps}\par\vspace*{4.5mm}
\includegraphics[width=8.54cm,clip]{9779fi1b.eps}\end{figure}](/articles/aa/full/2008/32/aa09779-08/Timg9.gif) |
Figure 1:
Parts of the rectified FEROS spectrum (dashed lines) showing the regions around several expected He I lines. For better visualization, we convolved the FEROS data to a resolution of R = 4900 as was used by ZSW (solid lines). |
| Open with DEXTER |
We obtained the optical spectra with the 1.52-m telescope at the European Southern Observatory in La Silla (Chile) using the high resolution Fiber-fed Extended Range Optical Spectrograph (FEROS). FEROS is a bench-mounted Echelle spectrograph with fibers, which covers a sky
area of 2
 of diameter, with a wavelength coverage from 3600 Å to
9200 Å and a spectral resolution of
R = 55 000 (in the region around 6000 Å). We adopted its complete automatic on-line reduction.
The high-resolution spectrum of S 23 was taken on October 14, 2000, with an
exposure time of 3600 s. The S/N ratio in the 5500 Å region is
approximately 40. Since within the same night we were able to take two
consecutive spectra of the star, which do not show significant differences,
we added them up for a better S/N ratio achievment.
of diameter, with a wavelength coverage from 3600 Å to
9200 Å and a spectral resolution of
R = 55 000 (in the region around 6000 Å). We adopted its complete automatic on-line reduction.
The high-resolution spectrum of S 23 was taken on October 14, 2000, with an
exposure time of 3600 s. The S/N ratio in the 5500 Å region is
approximately 40. Since within the same night we were able to take two
consecutive spectra of the star, which do not show significant differences,
we added them up for a better S/N ratio achievment.
In Fig. 1, we display parts of the rectified high-resolution FEROS
spectra. The first three panels show the regions around the positions of
several He I lines, which were identified by ZSW in their 1989
low-resolution (i.e. R=4900) observations (see Fig. 4 of ZSW), with the
He I  4472 line being the strongest one with almost equal
equivalent width to the adjacent Mg II
4472 line being the strongest one with almost equal
equivalent width to the adjacent Mg II  4481 line. This He I line is clearly absent in our FEROS spectrum (or at least below the detection limit) as well as the other two He I lines at
4481 line. This He I line is clearly absent in our FEROS spectrum (or at least below the detection limit) as well as the other two He I lines at
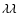 4388, 4438, whose detection was previously reported. The fourth panel of Fig. 1 displays the region around the He I
4388, 4438, whose detection was previously reported. The fourth panel of Fig. 1 displays the region around the He I  5876 line. If He I is present in a stellar spectrum, then this line is usually quite strong. But obviously, it is also absent from our FEROS spectrum. We checked the complete FEROS spectrum, but we could not identify a single He I line.
5876 line. If He I is present in a stellar spectrum, then this line is usually quite strong. But obviously, it is also absent from our FEROS spectrum. We checked the complete FEROS spectrum, but we could not identify a single He I line.
Due to our rather low S/N ratio and the fact that
the photospheric He I absorption lines are expected to be broad and
shallow, the high-resolution spectrum might not be able to display these lines
properly. Instead, for these lines a (much) lower spectral resolution might be
advantageous as has been shown by Verschueren (1991). We therefore
convolved our data to the same resolution as the ZSW spectrum and overplotted
the low-resolution spectrum in Fig. 1. However, even with the
low-resolution data, the He I lines do not show up.
While other known B[e] supergiants do not display even a single
photospheric absorption line in their optical spectra due to their high
density and therefore optically thick winds, S 23 displays at least one
clearly detectable line, namely the Mg II doublet at  4481. And
also the higher Balmer lines (H
4481. And
also the higher Balmer lines (H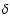 ,
H
,
H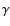 ,
see Fig. 2),
as already mentioned by ZSW, show indications for a photospheric absorption
component on which P Cygni profiles seem to be superimposed. Some other lines
in our spectra also display absorption components, like Fe II,
Ti II, and Si II (see Fig. 1). These absorption components
are, however, much narrower than the Mg II line, indicating that they
are circumstellar in origin.
,
see Fig. 2),
as already mentioned by ZSW, show indications for a photospheric absorption
component on which P Cygni profiles seem to be superimposed. Some other lines
in our spectra also display absorption components, like Fe II,
Ti II, and Si II (see Fig. 1). These absorption components
are, however, much narrower than the Mg II line, indicating that they
are circumstellar in origin.
We measure the heliocentric radial velocity for several lines in our spectra:
from the narrow pure emission lines of the forbidden transitions (like
[O I], [Fe II], see Fig. 1), from the narrow absorption
components observed for most of the permitted transitions (like Fe II, and
two lines of Si II and Cr II), and from the narrow absorption
components of the Balmer lines![[*]](/icons/foot_motif.gif) .
For each element we derive mean values, which are listed in
Table 1. For comparison, we also included in this table the
values obtained by ZSW. While our metal lines all deliver values in the range
.
For each element we derive mean values, which are listed in
Table 1. For comparison, we also included in this table the
values obtained by ZSW. While our metal lines all deliver values in the range
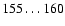 km s-1, the values of ZSW indicate a much larger
scatter between the radial velocities of the forbidden and the pemitted lines,
which had been interpreted by these authors as a slow outflow component.
In fact, the narrow absorption components of the permitted lines, often
overlaid on broader emission components, are not of pure atmospheric origin.
Instead, they are generated due to absorption by the circumstellar material.
The same holds also for the narrow absorption components seen in the Balmer
lines. For a proper radial velocity determination we therefore rely on
forbidden lines, which display narrow but symmetrical line profiles.
From these lines, we thus obtain a mean radial velocity of
km s-1, the values of ZSW indicate a much larger
scatter between the radial velocities of the forbidden and the pemitted lines,
which had been interpreted by these authors as a slow outflow component.
In fact, the narrow absorption components of the permitted lines, often
overlaid on broader emission components, are not of pure atmospheric origin.
Instead, they are generated due to absorption by the circumstellar material.
The same holds also for the narrow absorption components seen in the Balmer
lines. For a proper radial velocity determination we therefore rely on
forbidden lines, which display narrow but symmetrical line profiles.
From these lines, we thus obtain a mean radial velocity of
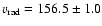 km s-1, which we will use here.
It is slightly lower than the value found by ZSW from their [O I]
lines, but this might be a spectral resolution effect rather than a stellar
effect.
km s-1, which we will use here.
It is slightly lower than the value found by ZSW from their [O I]
lines, but this might be a spectral resolution effect rather than a stellar
effect.
Table 1:
Mean heliocentric radial velocities derived from different ions
compared to those derived by ZSW.
The largest difference between the ZSW and our data is reached by the two
emission peaks of the H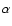 line. Here, a clear shift in velocities is
present. This shift is about 40 km s-1 for the blue peak, while it is
only 10-15 km s-1 for the red peak. We tested the influence of the
different resolutions by smearing our H
line. Here, a clear shift in velocities is
present. This shift is about 40 km s-1 for the blue peak, while it is
only 10-15 km s-1 for the red peak. We tested the influence of the
different resolutions by smearing our H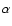 line to the same resolution as
ZSW. The measured radial velocities are in much better agreement with the
ZSW values, so that we can conclude that the differences in the appearance of
the H
line to the same resolution as
ZSW. The measured radial velocities are in much better agreement with the
ZSW values, so that we can conclude that the differences in the appearance of
the H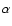 line in ZSW and in our spectrum are most probably caused by the
different spectral resolutions.
line in ZSW and in our spectrum are most probably caused by the
different spectral resolutions.
3 Spectral classification of S 23
3.1 Temperature classification
The determination of the spectral type and luminosity class of stars with
metallicities different from the galactic one has been found to be a difficult
task in the past. The reason for this is the fact that with decreasing
metallicity the metal lines in the spectra become very weak and hard to
detect. The proper determination of the spectral type is rather complicated,
especially for B-type stars which do not or only very weakly show He II
lines in their spectra. For these objects, the classification has to be
performed with the help of
the metal lines and is, for galactic objects, normally based on the line
strengths of silicon and magnesium, usually in comparison to helium. As shown,
e.g., by Lennon et al. (1993) for galactic B supergiants, the
equivalent widths of many spectral lines show a typical behaviour with spectral
type, i.e. effective temperature. And later on, Lennon (1997)
suggested determining the spectral classes of B-type supergiants in the SMC
according to line ratios in such a way that the same trend in line ratios
with spectral type is achieved as for solar metallicity (Lennon et al.
1992). His classification scheme (see Table 1 of Lennon 1997), which has been extended to G-type stars by Evans et al.
(2004), is used by many authors to classify B-type supergiants in many
galaxies with abundances similar to the SMC value (e.g., Evans & Howarth
2003; Bresolin et al. 2006; Bresolin et al.
2007).
The spectral type of S 23 has been determined by Azzopardi & Vigneau
(1987) as B8, and later on, ZSW, derived an effective temperature of
about 11 000 K based on comparison of the observed
spectral energy distribution to Kurucz (1979) model atmospheres.
Inspection of their mid-resolution spectrum indicates the presence
of the He I  4472 and Mg II
4472 and Mg II  4481 lines, with
the Mg II line being slightly stronger than the He I line.
Lennon et al. (1993) already mentioned the sharp decrease in
He I equivalent width from early to late B-type supergiants, and the
simultaneous strong increase in Mg II
4481 lines, with
the Mg II line being slightly stronger than the He I line.
Lennon et al. (1993) already mentioned the sharp decrease in
He I equivalent width from early to late B-type supergiants, and the
simultaneous strong increase in Mg II  4481 equivalent width.
The relative strength of these two lines is therefore one of the main
classification characteristics of especially late B-type supergiants
(e.g., Bresolin et al. 2006; Lennon 1997).
According to the classification scheme of Lennon (1997), the line
ratio as inferred from the ZSW spectrum would thus suggest a spectral type
between B8 and B9 of S 23 in the year 1989.
4481 equivalent width.
The relative strength of these two lines is therefore one of the main
classification characteristics of especially late B-type supergiants
(e.g., Bresolin et al. 2006; Lennon 1997).
According to the classification scheme of Lennon (1997), the line
ratio as inferred from the ZSW spectrum would thus suggest a spectral type
between B8 and B9 of S 23 in the year 1989.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{9779fig3.eps}\end{figure}](/articles/aa/full/2008/32/aa09779-08/Timg29.gif) |
Figure 3:
Effective temperature dependence of the line ratio Mg II  4481 over He I 4481 over He I  4472 calculated from model stellar atmospheres with 4472 calculated from model stellar atmospheres with
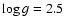 at solar abundances. The behaviour between spectral type and effective temperature taken from Evans & Howarth (2003) is indicated in the bottom label for solar abundance, and in the top label for SMC abundance. The two boxes indicate the observed ratios with their errors for the ZSW spectrum taken in 1989 and our spectrum taken in 2000, respectively.
at solar abundances. The behaviour between spectral type and effective temperature taken from Evans & Howarth (2003) is indicated in the bottom label for solar abundance, and in the top label for SMC abundance. The two boxes indicate the observed ratios with their errors for the ZSW spectrum taken in 1989 and our spectrum taken in 2000, respectively. |
| Open with DEXTER |
Our own high-resolution spectra display only the Mg II  4481 line
while the adjacent He I
4481 line
while the adjacent He I  4472 line is definitely below the
detection limit. This would speak more in favour of a star with spectral type
A0 or later. To quantify these classifications and to constrain the possible
range in effective temperature at the two observing epochs, it is necessary to
calculate theoretical line ratios of Mg II
4472 line is definitely below the
detection limit. This would speak more in favour of a star with spectral type
A0 or later. To quantify these classifications and to constrain the possible
range in effective temperature at the two observing epochs, it is necessary to
calculate theoretical line ratios of Mg II  4481 over He I
4481 over He I
 4472. This is done by using the code SYNSPEC (see Hubeny & Lanz
2000) to compute line identification tables based on Kurucz
(1979) model atmospheres in local thermodynamical equilibrium (LTE)
and Kurucz (1993) line lists. These calculations have been performed
for effective temperatures ranging from 8000 K up to 15 000 K and solar
abundances. With these line identification tables that contain information
about the expected line equivalent widths, we then calculated the Mg II
4472. This is done by using the code SYNSPEC (see Hubeny & Lanz
2000) to compute line identification tables based on Kurucz
(1979) model atmospheres in local thermodynamical equilibrium (LTE)
and Kurucz (1993) line lists. These calculations have been performed
for effective temperatures ranging from 8000 K up to 15 000 K and solar
abundances. With these line identification tables that contain information
about the expected line equivalent widths, we then calculated the Mg II
 4481 over He I
4481 over He I  4472 line ratios. The results are shown
as the dashed line in Fig. 3. To convert the effective temperature
scale into a spectral type, we made use of the recent classification of Evans
& Howarth (2003), who redefined effective temperatures for
galactic (indicated along the bottom axis of Fig. 3) and SMC
supergiants (indicated along the top axis). In addition, we follow the approach
of Lennon (1997), who suggested that the same line ratio mirrors the
same spectral type. We find that the transition from a line ratio smaller than
one to a ratio larger than one happens at an effective temperature of about
12 000 K for solar abundances, which corresponds to a spectral type between
B8 and B9, in agreement with what has been claimed by Lennon (1997).
4472 line ratios. The results are shown
as the dashed line in Fig. 3. To convert the effective temperature
scale into a spectral type, we made use of the recent classification of Evans
& Howarth (2003), who redefined effective temperatures for
galactic (indicated along the bottom axis of Fig. 3) and SMC
supergiants (indicated along the top axis). In addition, we follow the approach
of Lennon (1997), who suggested that the same line ratio mirrors the
same spectral type. We find that the transition from a line ratio smaller than
one to a ratio larger than one happens at an effective temperature of about
12 000 K for solar abundances, which corresponds to a spectral type between
B8 and B9, in agreement with what has been claimed by Lennon (1997).
Table 2:
Photometric data of S 23 (in mag) collected from the literature
and sorted by their year(s) of observation.
Concerning the measured line ratios of S 23 we could derive a value of
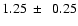 from the low-resolution spectrum of ZSW
from the low-resolution spectrum of ZSW![[*]](/icons/foot_motif.gif) . This value, with
its error, is included in Fig. 3. Its location in the diagram
indicates that in 1989 the spectrum of S 23 was that of a B8.5-B9 star with
effective temperature
. This value, with
its error, is included in Fig. 3. Its location in the diagram
indicates that in 1989 the spectrum of S 23 was that of a B8.5-B9 star with
effective temperature
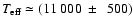 K. This
classification is in fair agreement with the one derived by ZSW.
K. This
classification is in fair agreement with the one derived by ZSW.
From our own spectrum taken in 2000, we derive a line ratio of
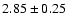 .
This ratio has to be considered as a lower limit since we used, for the
equivalent width of the He I
.
This ratio has to be considered as a lower limit since we used, for the
equivalent width of the He I  4472 line, the value we consider
the detection limit. With this line ratio, we therefore determine an upper
limit to the effective temperature that is mirrored by this line ratio.
We find, for S 23, a spectral type later than A0 and an effective temperature
4472 line, the value we consider
the detection limit. With this line ratio, we therefore determine an upper
limit to the effective temperature that is mirrored by this line ratio.
We find, for S 23, a spectral type later than A0 and an effective temperature
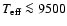 K. If the spectral appearance of S 23 at the two
observing epochs is indeed determined by the temperature of the central star,
then the change in line ratio suggests that the star must have cooled by at
least 1500 K within a period of 11 years only, a scenario that is
definitely excluded by stellar evolution theory (see Sect. 6.1).
In the following, we will therefore refer to this behaviour as an apparent cooling of the star.
K. If the spectral appearance of S 23 at the two
observing epochs is indeed determined by the temperature of the central star,
then the change in line ratio suggests that the star must have cooled by at
least 1500 K within a period of 11 years only, a scenario that is
definitely excluded by stellar evolution theory (see Sect. 6.1).
In the following, we will therefore refer to this behaviour as an apparent cooling of the star.
3.2 Luminosity class
For the SMC, great effort has been undertaken for a proper luminosity
classification of the supergiant population. In principle, several methods for
the determination of the stellar luminosity exist and have been successfully
applied in the literature. For O-type to early B-type supergiants, the He I/He II line ratios are good and, especially, metallicity-independent luminosity indicators (e.g.,
Walborn 1983). For B and later type supergiants, the H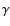 equivalent width is an ideal and metallicity-independent tool for the
luminosity class determination, as shown by Azzopardi (1987), while the use of metal
lines as suggested by Massey et al. (1995) delivers unreliable
results when applied to stars in low-metal content galaxies like the SMC (see
the discussion in Lennon 1997).
equivalent width is an ideal and metallicity-independent tool for the
luminosity class determination, as shown by Azzopardi (1987), while the use of metal
lines as suggested by Massey et al. (1995) delivers unreliable
results when applied to stars in low-metal content galaxies like the SMC (see
the discussion in Lennon 1997).
For S 23, the luminosity class determination is complicated due to fact
that its H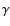 line shows an additional emission component (see
Fig. 2). In this case, the equivalent width method of Azzopardi
(1987) is not applicable.
line shows an additional emission component (see
Fig. 2). In this case, the equivalent width method of Azzopardi
(1987) is not applicable.
ZSW had derived the luminosity class Ib from determining E(B-V) based on the
photometric B and V data of S 23 from Azzopardi & Vigneau (1982).
Using the intrinsic colors for a B8 supergiant from Schmidt-Kaler (1982),
they found a value of
E(B-V) = 0.10. However, as we will show in
Sect. 4, this extinction determination is based on assumptions
that are not reliable for typical B[e] stars, and consequently, the E(B-V)
value derived by ZSW overestimates the real amount of interstellar
extinction and, therefore, the luminosity of S 23.
From our FEROS spectrum alone, we are not able to make any estimates about the
stellar luminosity. We therefore searched the literature for complementary
photometric data. These data, which have usually errors on the order of
0.01 mag, are summarised in Table 2, and the 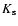 band belongs
to the 2MASS observations. Inspection of this table delivers the following
important information:
band belongs
to the 2MASS observations. Inspection of this table delivers the following
important information:
- the UBV data of S 23 have changed substantially between the
observations taken in 1972-74 and those taken in 1999, while the near-IR
photometry appears constant in the measurements taken in 1988 and in 1998;
- the UBV data of Azzopardi & Vigneau (1982) were taken
14-16 years before ZSW took their near-IR data. With the knowledge of
a possible variation/cooling of the central star as discussed above,
the combination of these two datasets for the construction of the spectral
energy distribution is therefore most certainly unreliable;
- in 1999, the star appears to be more luminous in the UBV bands than
it was during the 1972-74 observing period;
- the UBV data of Massey (2002) were taken only one year
earlier than our FEROS spectra, and we use them as complementary data to our
optical spectra for a tentative luminosity determination.
From the photometry of Massey (2002) we can estimate the luminosity
class of S 23 in the year 1999, if we completely neglect the interstellar
extinction towards S 23 for the moment. From the distance modulus of
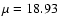 (Keller & Wood 2006), we thus find a first-guess absolute
visual magnitude of
MV = -5.62, assigning to S 23 the luminosity class Ib.
(Keller & Wood 2006), we thus find a first-guess absolute
visual magnitude of
MV = -5.62, assigning to S 23 the luminosity class Ib.
4 Interstellar and circumstellar extinction
In the previous section, we determined the luminosity class of S 23 as Ib. For
this, we ignored the presence of any interstellar extinction value, knowing
that this delivers only a lower limit to the real stellar luminosity. In this
section, we therefore intend to derive the values of the interstellar and
possible circumstellar extinction. This is necessary for a proper dereddening
of the photometric data and a reliable stellar luminosity determination.
To derive E(B-V) from the color index of a star, one should not only rely on
the B-V color index, but also check, if possible, the result by using a
different color index, e.g. U-B. The observed colors from Azzopardi &
Vigneau (1982) given in Table 2 serve as an example. According
to the classification of S 23 as B8 Ib, ZSW derived a value of
E(B-V) = 0.10
from (B-V). Using as well the color index (U-B), and the intrinsic color
of Johnson (1966), we find an extinction of
E(B-V) = 0.49. For the
calculation of this value, we used the relation
E(B-V) = E(U-B) / 0.77, which
has been found from observations by Leitherer & Wolf (1984). The
value found from the U-B color index thus seems to indicate an extinction
five times higher.
One might argue that, since the star seems to be somehow variable, the spectral
type derived from the optical data of ZSW cannot be applied to the UBV data
taken about 14 years earlier. Therefore, we checked the possible interstellar
extinction values derived from the more recent set of UBV data from Massey
(2002), using the spectral classification derived from our optical
spectra that have a time offset of about one year, only.
From Fig. 3, we found the spectral type of S 23 as A0 or later,
and in the following we will deal with two stellar scenarios, namely an A0 Ib
star with
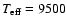 K, and an A1 Ib star with
K, and an A1 Ib star with
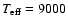 K. Using the tables with intrinsic colors from Johnson (1966),
we find the following extinction values:
K. Using the tables with intrinsic colors from Johnson (1966),
we find the following extinction values:
and
Again, both methods (even considering an error in the UBV band fluxes
of about 0.01 mag) deliver results that differ by a factor 2-3. This
discrepancy in extinction implies that, obviously, the interstellar reddening
is not the only extinction source acting on the observed UBV data. Instead,
circumstellar material along the line of sight is causing an extinction of the
stellar flux as well.
Possible circumstellar extinction sources might be, on the one hand,
circumstellar dust with a wavelength dependent extinction behaviour different
from the global interstellar one. On the other hand, since B[e] stars are known
to have high mass loss rates, the circumstellar extinction might be caused by
the high density wind that drops partly optically thick at optical and/or UV
wavelengths.
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{9779fig4.eps}\end{figure}](/articles/aa/full/2008/32/aa09779-08/Timg42.gif) |
Figure 4:
Fitting process of the Mg II  4481 line with a pure
rotation profile ( left panel), a pure Gaussian profile ( mid panel), and
our best fit model ( right panel) with a profile consisting mainly of stellar
rotation plus some macro-turbulence. 4481 line with a pure
rotation profile ( left panel), a pure Gaussian profile ( mid panel), and
our best fit model ( right panel) with a profile consisting mainly of stellar
rotation plus some macro-turbulence. |
| Open with DEXTER |
To test which circumstellar extinction source might be acting on the UBV
fluxes of S 23, we performed some simple test calculations for both scenarios.
For the circumstellar dust scenario, we adopted a grain size distribution
according to Mathis et al. (1977) for either silicates or amorphous
carbon grains
with SMC abundances of Si and C taken from Venn (1999). The optical
depths of the circumstellar grains, resulting in a wavelength dependent dust
extinction, are then calculated for the scenarios of an A0 Ib and an A1 Ib
star. Interestingly, we found that neither the silicates nor the carbon grains
(nor any combination of both) can account for the circumstellar extinction of
S 23. We therefore conclude that circumstellar dust is most probably not the
(major) source of the extra extinction. The location of the circumstellar dust
around S 23, whose presence might be inferred from the IR photometry, should
thus be out of the line of sight.
The situation is more complicated when the extinction is caused by the stellar
wind. In this case, the wind not only absorbs and scatters the stellar light,
instead it contributes with additional emission even at optical and UV
wavelengths, as has recently been shown by Kraus et al. (2008b) for
classical OB supergiants, and by Kraus et al. (2007) for the LMC B[e]
supergiant R 126.
We test the influence of the wind to the UBV band fluxes by assuming for
simplicity (and since nothing is known about the real structure and geometry of
the wind around S 23) a spherically symmetric isothermal wind, and calculate
the wind contribution with the model of Kraus et al. (2008b). For the
terminal wind velocity we use the escape velocity, which was found from
observations of late B-type and early A-type supergiants by Lamers et al.
(1995) to be a reasonable approximation. The only free
parameter in the wind calculations is thus the mass loss rate, 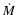 ,
which is varied over a certain range to calculate the wind extinction
and emission in the UBV bands.
,
which is varied over a certain range to calculate the wind extinction
and emission in the UBV bands.
Interestingly, we could not constrain the circumstellar extinction for the
scenario of an A0 Ib star, while the scenario of an A1 Ib star delivered
reasonable values for both the mass loss rate, with
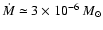 yr-1, and the interstellar extinction, with
yr-1, and the interstellar extinction, with
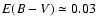 ,
constraining the classification of S 23 more towards an A1 star rather than an A0 star.
,
constraining the classification of S 23 more towards an A1 star rather than an A0 star.
Compared to the value found from the observed B-V color index, our value is
slightly lower, indicating that the neglect of the wind influence to the
emergent flux from the atmosphere leads to an overestimation of the real
interstellar extinction. Such behaviour has also recently been found for
classical B-type supergiants (Kraus et al. 2008a).
With the tentative classification of S 23 as A1 Ib star with an effective
temperature of roughly 9000 K, and with the derived interstellar extinction of
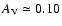 ,
we find the following set of stellar parameters:
,
we find the following set of stellar parameters:
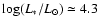 ,
,
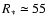 -
-
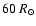 ,
and, from
the comparison with stellar evolutionary tracks calculated for SMC stars by
Charbonnel et al. (1993), an initial mass of
,
and, from
the comparison with stellar evolutionary tracks calculated for SMC stars by
Charbonnel et al. (1993), an initial mass of
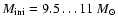 .
.
Finally, the small interstellar extinction value confirms the luminosity class
adjustment of Ib, meaning that S 23 belongs to the group of low-luminosity B[e] supergiants, which has members in the LMC (Gummersbach et al. 1995) as well as in the Milky Way (Borges Fernandes et al. 2007), and which should probably be extended at least to early A-type stars.
5 Stellar rotation
With the classification of S 23 as an early A-type supergiant at the time of
our observation, we next intend to determine its stellar rotation speed given
by the parameter
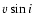 .
For late B-type and early A-type stars and
supergiants, the most reliable photospheric line for the stellar rotation
determination is the Mg II
.
For late B-type and early A-type stars and
supergiants, the most reliable photospheric line for the stellar rotation
determination is the Mg II  4481 doublet (e.g., Royer 2005;
Royer et al. 2002), which is also the only clearly detectable
photospheric line in our spectra.
4481 doublet (e.g., Royer 2005;
Royer et al. 2002), which is also the only clearly detectable
photospheric line in our spectra.
It has recently been shown that the Fourier analysis provides an excellent
tool for the rotation velocity determination even for hot stars (see Royer
2005; Simón-Díaz & Herrero 2007). However, for the
Fourier analysis to work properly, it is necessary to have data with extremely
good S/N ratio because otherwise the noise level is too high to allow the zero
points caused by the rotation profile to show up in the Fourier transform of
the spectral data (Simón-Díaz & Herrero 2007). With the rather
low S/N ratio of our FEROS data of the faint object S 23, the powerful Fourier
analysis is thus not applicable. Instead, we have to rely on the less accurate
full-width at half-maximum (FWHM) method to extract the possible stellar
rotation of the star, i.e., we fit
synthetic line profiles to the observed, normalised Mg II line. The
stellar rotation profile is described in the usual way (see, e.g., Gray
1976) with a limb-darkening coefficient of
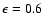 .
.
The line profile of the Mg II  4481 line appears to be asymmetric
(see Fig. 4). However, this asymmetry is probably not real,
but an artefact due to noise since only one of our spectra shows this
asymmetry, while the other spectrum shows a symmetric line profile. For a
proper FWHM determination we therefore rely on the blue part of the line,
only. Given the low S/N ratio, we derive a FWHM of the observed Mg II
4481 line appears to be asymmetric
(see Fig. 4). However, this asymmetry is probably not real,
but an artefact due to noise since only one of our spectra shows this
asymmetry, while the other spectrum shows a symmetric line profile. For a
proper FWHM determination we therefore rely on the blue part of the line,
only. Given the low S/N ratio, we derive a FWHM of the observed Mg II
 4481 line of
4481 line of
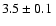 Å. If we assume either a pure Gaussian
profile or a pure rotation profile, we thus obtain maximum velocity
values of
Å. If we assume either a pure Gaussian
profile or a pure rotation profile, we thus obtain maximum velocity
values of
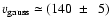 km s-1 and
km s-1 and
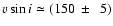 km s-1, respectively. However, both possibilities,
i.e., either a pure Gaussian or a pure rotation profile, do not deliver
satisfactory fits to the observed line profile (see left and middle panel of
Fig. 4). While the edges are too sharp in the case of pure stellar
rotation, the wings of the pure Gaussian are way too broad. Instead, a
combination of both might be a good solution. But how can we estimate the
individual amounts of the Gaussian and the rotational components?
km s-1, respectively. However, both possibilities,
i.e., either a pure Gaussian or a pure rotation profile, do not deliver
satisfactory fits to the observed line profile (see left and middle panel of
Fig. 4). While the edges are too sharp in the case of pure stellar
rotation, the wings of the pure Gaussian are way too broad. Instead, a
combination of both might be a good solution. But how can we estimate the
individual amounts of the Gaussian and the rotational components?
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{9779fig5.eps}\end{figure}](/articles/aa/full/2008/32/aa09779-08/Timg55.gif) |
Figure 5:
Maximum velocity caused by macro-turbulence to the Mg II
 4481 line for a sample of B-type supergiants. The data are taken from Ryans et al. (2002). 4481 line for a sample of B-type supergiants. The data are taken from Ryans et al. (2002). |
| Open with DEXTER |
It has been known for a long time that within the atmospheres of OBA
supergiants some macroscopic line broadening occurs that is of no rotational origin. This broadening component can be described with a Gaussian profile and is usually referred to as (macro-)turbulence (see, e.g., Howarth 2004). This
``extra'' broadening of the photospheric lines is thereby not restricted to
hydrogen and helium lines, but also appears in metal lines. The
physical understanding and interpretation of this component is, however, still
missing. In an attempt to determine the contribution of this macro-turbulence
to line broadening, Ryans et al. (2002) investigated a sample of
B-type supergiants trying to disentangle the contributions of rotation
and macro-turbulence with high precision. One of the key lines in their
investigation was the Mg II  4481 line. Inspection of their
Table 3 reveals that there is an obvious trend between the maximum possible
turbulent velocity and the effective temperature of the star. This is shown in
Fig. 5, where we plotted the maximum turbulent velocity
found for the sample supergiants of Ryans et al. (2002) versus
spectral type of the stars. While for the early-type supergiants maximum
macro-turbulence as high as 70 km s-1 might be present, it rapidly
decreases towards the late type stars to about 30-35 km s-1 only.
If this trend continues for the A-type supergiants, we might expect
a maximum macro-turbulence of about 30 km s-1 acting on the photospheric
lines of S 23.
4481 line. Inspection of their
Table 3 reveals that there is an obvious trend between the maximum possible
turbulent velocity and the effective temperature of the star. This is shown in
Fig. 5, where we plotted the maximum turbulent velocity
found for the sample supergiants of Ryans et al. (2002) versus
spectral type of the stars. While for the early-type supergiants maximum
macro-turbulence as high as 70 km s-1 might be present, it rapidly
decreases towards the late type stars to about 30-35 km s-1 only.
If this trend continues for the A-type supergiants, we might expect
a maximum macro-turbulence of about 30 km s-1 acting on the photospheric
lines of S 23.
We use this value of 30 km s-1 for the Gaussian profile and calculate
the Mg II  4481 line profile by adjusting the rotational velocity
such that the observed FWHM is reproduced. Since the Gaussian velocity
contribution is rather small, it does not significantly influence the total
line width, which is still purely rotationally dominated with about the same
value of
4481 line profile by adjusting the rotational velocity
such that the observed FWHM is reproduced. Since the Gaussian velocity
contribution is rather small, it does not significantly influence the total
line width, which is still purely rotationally dominated with about the same
value of
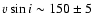 km s-1 as without macro-turbulence.
The only influence of the Gaussian component concerns the line wings (see
right panel of Fig. 4). Overall, this combination of rotation
plus macro-turbulence gives a reasonably good fit to the observed line profile.
km s-1 as without macro-turbulence.
The only influence of the Gaussian component concerns the line wings (see
right panel of Fig. 4). Overall, this combination of rotation
plus macro-turbulence gives a reasonably good fit to the observed line profile.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{9779fig6.eps}\end{figure}](/articles/aa/full/2008/32/aa09779-08/Timg57.gif) |
Figure 6:
Distribution of projected rotational velocities with spectral type
of a sample of galactic (Abt et al. 2002; Verdugo et al. 1999)
and SMC (Hunter et al. 2008; Venn 1999) supergiants. The big
spot with errorbars is the value of S 23 derived from our analysis. |
| Open with DEXTER |
The value of
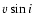 found from our fitting is high when compared
to the projected rotation velocities of normal galactic B and A-type
supergiants, for which a tendency of decreasing rotation velocity with
effective temperature is reported. This can be seen in Fig. 6,
where we plot the results for four samples: (i) galactic B-type supergiants
from Abt et al. (2002); (ii) galactic A-type supergiants from Verdugo et al. (1999); (iii) SMC B-type supergiants from Hunter et al. (2008); and (iv) SMC A-type supergiants from Venn (1999).
The SMC stars turn out to have even smaller velocities
than their galactic counterparts, but this effect might arise simply from
small number statistics. Compared to the mean rotational velocity of the
galactic and SMC late B-type and early A-type supergiants, the value derived
for S 23 is clearly a factor of three higher.
found from our fitting is high when compared
to the projected rotation velocities of normal galactic B and A-type
supergiants, for which a tendency of decreasing rotation velocity with
effective temperature is reported. This can be seen in Fig. 6,
where we plot the results for four samples: (i) galactic B-type supergiants
from Abt et al. (2002); (ii) galactic A-type supergiants from Verdugo et al. (1999); (iii) SMC B-type supergiants from Hunter et al. (2008); and (iv) SMC A-type supergiants from Venn (1999).
The SMC stars turn out to have even smaller velocities
than their galactic counterparts, but this effect might arise simply from
small number statistics. Compared to the mean rotational velocity of the
galactic and SMC late B-type and early A-type supergiants, the value derived
for S 23 is clearly a factor of three higher.
However, as discussed already in the introduction, the B[e] phenomenon seems to
be linked to rapid stellar rotation. For the class of the B[e] supergiants,
only for three stars the value of
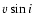 could be derived so far.
These are the LMC B[e] supergiants Hen S93 with
could be derived so far.
These are the LMC B[e] supergiants Hen S93 with
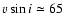 km s-1 (Gummersbach et al. 1995) and R 66
with
km s-1 (Gummersbach et al. 1995) and R 66
with
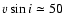 km s-1 (Zickgraf 2006),
and the SMC B[e] supergiant R 50 with
km s-1 (Zickgraf 2006),
and the SMC B[e] supergiant R 50 with
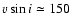 km s-1 (Zickgraf 2000). The latter
one has a projected rotation speed on the same order as S 23, which is now
the fourth B[e] supergiant with confirmed high projected rotational velocity.
From our derived set of stellar parameters we can further estimate the critical
velocity of the star, which turns out to be on the order of 200 km s-1.
This means, that S 23 is rotating with at least 75% of its critical velocity.
km s-1 (Zickgraf 2000). The latter
one has a projected rotation speed on the same order as S 23, which is now
the fourth B[e] supergiant with confirmed high projected rotational velocity.
From our derived set of stellar parameters we can further estimate the critical
velocity of the star, which turns out to be on the order of 200 km s-1.
This means, that S 23 is rotating with at least 75% of its critical velocity.
Interestingly, the optical spectrum of ZSW indicates that the Mg II
 4481 line is less broad during the 1989 observations. A tentative
derivation of its FWHM delivers a value of (
4481 line is less broad during the 1989 observations. A tentative
derivation of its FWHM delivers a value of (
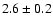 ) Å. Neglecting
any other broadening mechanism, this FWHM value results in a maximum
rotational velocity of
) Å. Neglecting
any other broadening mechanism, this FWHM value results in a maximum
rotational velocity of
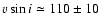 km s-1. This
result is surprising, because it indicates that S 23 might not only have
cooled, but at the same time also increased its projected rotational velocity
by at least 35%.
km s-1. This
result is surprising, because it indicates that S 23 might not only have
cooled, but at the same time also increased its projected rotational velocity
by at least 35%.
6 Discussion
The investigation of our high-resolution optical spectra in combination with
the photometric data of Massey (2002) resulted in the tentative
classification of S 23 as a rapidly rotating A1 Ib star. On the other hand,
our evaluation of the Mg II/He I line ratio derived (even though
with large error bars) from the spectra of ZSW, delivered a spectral
classification more consistent with a star of roughly spectral type
B9 Ib. The most striking differences are thus an apparent temperature
decrease by about 1500 K, based on the spectral type versus effective
temperature calibration of Evans & Howarth (2003), and
shown in Fig. 3; and, even more curious, an increase in projected
rotational velocity by about 35% (see previous section) within a time interval
of only 11 years. In this section, we therefore investigate different scenarios
that might explain this peculiar behaviour. For this, we first consider some
natural possibilities like stellar evolution (Sect. 6.1) and mass
ejection occulting the star in form of a shell phase as is often observed for
the classical Be stars (Sect. 6.2). Since both attempts fail to
explain the observed peculiar variations in S 23, we present and discuss in
Sect. 6.3 further scenarios, which are more speculative. Of course,
the amount and quality of our available data is definitely not sufficient for a
proper analysis, which could lead to a discrimination between the different
scenarios. Instead, we want to discuss qualitatively the expected observable
effects for those scenarios that seem to be at least likely and worth further
investigation.
6.1 Stellar evolution
The apparent cooling of the star in combination with a simultaneous speed-up
of the rotation velocity is unexpected and surprising. The first scenario
we might think of is stellar evolution. However, stellar evolution theories
predict that when the star expands, i.e., cools, it can only decrease
its rotation velocity. An increase in rotation speed during the post-main
sequence evolution of a rapidly rotating star at SMC metallicity and with an
initial mass of about
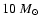 can only occur during the blue loop, i.e.,
while the star contracts and heats up again (Maeder & Meynet 2001).
In addition, the timescales for such a star to cool from about 11 000 K to
less than 9500 K is on the order of 5000 yr (Meynet, private communication).
This is definitely longer than the one decade we found. The changes in the
spectral appearance of S 23 can thus definitely not be explained by current
theories of stellar evolution.
can only occur during the blue loop, i.e.,
while the star contracts and heats up again (Maeder & Meynet 2001).
In addition, the timescales for such a star to cool from about 11 000 K to
less than 9500 K is on the order of 5000 yr (Meynet, private communication).
This is definitely longer than the one decade we found. The changes in the
spectral appearance of S 23 can thus definitely not be explained by current
theories of stellar evolution.
6.2 Comparison with shell formations of classical Be stars
A different interpretation of the apparent cooling might be given by the
assumption of material ejection, e.g., in form of a ring or shell, leading to
an (partly) occultation of the central star. Such phenomenon are known, e.g.,
from Be stars that can undergo a so-called shell phase (see, e.g., Hanuschik
1996; Porter & Rivinius 2003). The shell, ejected from
the central star, thereby acts as an extinction source.
Derivation of the stellar parameters from absorption lines created within
such a shell can, therefore, result in much lower apparent effective
temperature values than the real stellar one derived during a non-shell
phase. Such a behaviour has been reported, e.g., for the Be shell star 4 Herculis, for which an apparent drop in effective temperature by 3000 K during
the shell phase was found by Koubský et al. (1997).
However, contrary to our target S 23, but in agreement with expected physical
behaviour, the rotation velocity derived from the shell absorption line
decreased as well. A shell phase of S 23, mimicking a temperature decrease,
thus has severe problems in explaining our observations, even if the
presence of some ``shell-lines'' (like the Fe II and Si II lines)
in our spectra hint towards the existence of a large amount of circumstellar
material.
6.3 Possible (speculative) scenarios for S 23
Since neither stellar evolution, nor a high-density mass ejection in the form of
a ring or shell can explain the peculiarities observed for S 23, we need to
think of different mechanisms. In this section, we therefore present three
alternative scenarios that might be worth further detailed investigation.
These are (i) a high precession rate, (ii) an eclipsing binary, and (iii)
surface He abundance and/or temperature inhomogeneities. All three are able to
explain the peculiarities of S 23, and all three can be tested by future
observations. But we want to stress again that these scenarios can only
be considered as simplified models, given the quality of the available data.
One possible explanation for the apparent cooling with increasing rotation
velocity might be a precession of the star with respect to the line of sight.
Since we know that S 23 is rapidly rotating, the classification of the star
strongly depends on the inclination angle under which it is observed.
The effects of rapid stellar rotation are manifold. Rapid rotation leads to a
deformation of the stellar surface in the form of flattening. Thus, the polar
regions become much hotter than the equatorial region, which is usually
referred to as gravity darkening. Depending on the fraction of the rotation
velocity to the critical velocity, the difference between polar and equatorial
effective temperature can exceed a factor of two. The same holds also for the
other stellar parameters like the surface gravity, stellar flux,
mass flux, and escape velocity.
From the differences in observed rotation velocity,
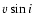 ,
we may
conclude that the inclination of the system has increased between ZSW
and our observations, which means, that the system was observed more edge-on
in 2000 than in 1989. To quantify this, we take the values of
,
we may
conclude that the inclination of the system has increased between ZSW
and our observations, which means, that the system was observed more edge-on
in 2000 than in 1989. To quantify this, we take the values of
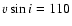 km s-1 in 1989, and
km s-1 in 1989, and
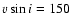 km s-1 in 2000.
Then, the difference in inclination follows to
km s-1 in 2000.
Then, the difference in inclination follows to
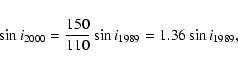 |
(1) |
which means that the inclination angle has increased by almost 40%. Assuming
that the star was seen more or less edge-on (i.e., inclination angle of
 )
in 2000, it must thus have been seen under an inclination angle of
about
)
in 2000, it must thus have been seen under an inclination angle of
about
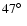 in 1989. This conclusion is, however, only strictly valid,
as long as the inclination did not cross the equatorial plane yet.
in 1989. This conclusion is, however, only strictly valid,
as long as the inclination did not cross the equatorial plane yet.
A lower limit to the inclination angle in 2000 is given by the critical
rotation of the star,
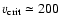 km s-1.
Assuming that the star is rotating at its critical speed, it delivers
a minimum inclination angle of
km s-1.
Assuming that the star is rotating at its critical speed, it delivers
a minimum inclination angle of
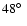 in 2000, and of
in 2000, and of
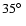 in 1989.
in 1989.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{9779fig7.eps}\end{figure}](/articles/aa/full/2008/32/aa09779-08/Timg71.gif) |
Figure 7:
Shape of S 23 rotating with 75% of its critical velocity. Also
included are the assumed positions of the observers with respect to the
rotation axis of the star in the two periods of optical observations. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{9779fig8.eps}\end{figure}](/articles/aa/full/2008/32/aa09779-08/Timg72.gif) |
Figure 8:
Distribution of the surface parameters (effective temperature, escape velocity, hydrogen density, and mass flux) with co-latitude, 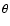 ,
normalised to their polar values. All parameters are found to drop from pole to equator (for details on their calculation see Kraus 2006). ,
normalised to their polar values. All parameters are found to drop from pole to equator (for details on their calculation see Kraus 2006). |
| Open with DEXTER |
To get a rough idea of the influence of the rapid rotation in combination
with the postulated precession on the observable mean effective temperature,
we consider the following scenario for S 23 (which need not be correct, but
which is only meant to show the basic idea of this toy model).
Since rotation at the critical limit is not very realistic, we assume in the
following that the star was seen more or less edge-on in 2000 so that S 23
rotates with 75% of its critical speed, i.e.,
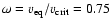 .
Such an edge-on scenario is not in contradiction
with our results from Sect. 4, where we found that the dust is most
probably not located along the line of sight. In fact, for rapidly rotating
stars the mass loss happens much stronger via the poles than via the equatorial
region, and to date models like, e.g., the wind-compressed disk (Bjorkman &
Cassinelli 1993) failed in confining the material within the
equatorial plane. In addition, spectropolarimetric observations of Bjorkman et al. (1998) for the galactic B[e] star HD 50138 have shown that the
polarisation is mainly caused by scattering within an almost edge-on seen pure
gaseous disk, while the huge amount of dust observed from this system seems not
to be connected with the disk at all.
.
Such an edge-on scenario is not in contradiction
with our results from Sect. 4, where we found that the dust is most
probably not located along the line of sight. In fact, for rapidly rotating
stars the mass loss happens much stronger via the poles than via the equatorial
region, and to date models like, e.g., the wind-compressed disk (Bjorkman &
Cassinelli 1993) failed in confining the material within the
equatorial plane. In addition, spectropolarimetric observations of Bjorkman et al. (1998) for the galactic B[e] star HD 50138 have shown that the
polarisation is mainly caused by scattering within an almost edge-on seen pure
gaseous disk, while the huge amount of dust observed from this system seems not
to be connected with the disk at all.
Following Kraus (2006), we compute the surface structure of the star
rotating with
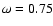 (shown in Fig. 7). For the adopted
rotation speed, a deformation (i.e., flattening) of the stellar surface is
obvious. Also included in this plot are the inclination angles under which the
star might have been observed in 1989 and in 2000. While in 2000 most of the
observed flux was emitted from the equatorial region with some minor
contributions from higher altitudes, the flux observed in 1989 was emitted from
an intermediate altitude, with contributions from both, the polar and the
equatorial region.
(shown in Fig. 7). For the adopted
rotation speed, a deformation (i.e., flattening) of the stellar surface is
obvious. Also included in this plot are the inclination angles under which the
star might have been observed in 1989 and in 2000. While in 2000 most of the
observed flux was emitted from the equatorial region with some minor
contributions from higher altitudes, the flux observed in 1989 was emitted from
an intermediate altitude, with contributions from both, the polar and the
equatorial region.
To obtain an idea about the expected differences in the observed stellar
spectra, we further calculate the surface distribution of the latitude
dependent stellar parameters like effective temperature
 ,
escape velocity
,
escape velocity
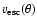 ,
mass flux
,
mass flux
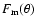 ,
and
hydrogen desity
,
and
hydrogen desity
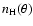 for a star rotating with
for a star rotating with
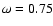 .
These parameters are shown in Fig. 8 as a function of the
co-latitude
.
These parameters are shown in Fig. 8 as a function of the
co-latitude 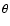 (i.e.,
(i.e.,
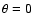 at the pole), normalised to their polar
values. They are all found to decrease by non-negligible amounts from the
pole to the equator.
at the pole), normalised to their polar
values. They are all found to decrease by non-negligible amounts from the
pole to the equator.
In particular, we find from Fig. 8 the following behaviour of the
effective temperature:
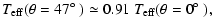 |
|
|
(2) |
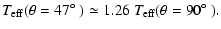 |
|
|
(3) |
Since for an inclination of
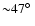 the stellar emission contains
contributions from the hotter as well as from the cooler regions, we might
assume that the effective temperature at
the stellar emission contains
contributions from the hotter as well as from the cooler regions, we might
assume that the effective temperature at
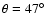 is reflecting
quite well the real observed spectrum. This means, that we can calculate
the polar as well as the equatorial value of the effective temperature,
resulting in
is reflecting
quite well the real observed spectrum. This means, that we can calculate
the polar as well as the equatorial value of the effective temperature,
resulting in
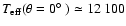 K, and
K, and
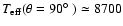 K. The equatorial value is
somewhat lower than our effective temperature of 9 000 K derived from the
FEROS spectrum. This is, however, no contradiction, because the real
``observable'' mean effective temperature under an edge-on inclination of the
star will certainly be somewhat higher than the pure value at
K. The equatorial value is
somewhat lower than our effective temperature of 9 000 K derived from the
FEROS spectrum. This is, however, no contradiction, because the real
``observable'' mean effective temperature under an edge-on inclination of the
star will certainly be somewhat higher than the pure value at
 ,
due to some contributions from higher altitudes. In addition, the
temperature calibration of Evans & Howarth (2003) is certainly
too coarse for a detailed temperature assignment.
,
due to some contributions from higher altitudes. In addition, the
temperature calibration of Evans & Howarth (2003) is certainly
too coarse for a detailed temperature assignment.
In summary, the precession scenario might explain both, the apparent cooling
with an increase in rotation velocity, just from an increase of the inclination
axis of a rapidly rotating star from about
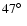 to about
to about
 .
Whether such a strong precession will indeed occur, and what might be the
reason for such rapid precession movement, is, however, not known.
.
Whether such a strong precession will indeed occur, and what might be the
reason for such rapid precession movement, is, however, not known.
To test the precession scenario, we would need to monitor the star over a
period of several years to see whether the He I lines re-appear
(i.e., the star ``heats up'' again) with a simultaneous decrease of the projected
rotation velocity measured from the Mg II lines.
A second possible scenario to explain the strong variations observed in S 23
might be that of an eclipsing binary system, in which one component is
perhaps a B9 Ib star and the other one perhaps a A1 Ib star. The
disappearance of the He I lines in our spectra might then be
interpreted with the A1 Ib star occulting more or less the hotter B9 Ib
component, while the spectra of ZSW, in which the He I lines were
present and strong, indicate that the hotter component was dominating the
spectral appearance of the system.
To test the hypothesis of S 23 being an eclipsing binary, it
is certainly useful to perform a high S/N monitoring of its few available
photospheric lines, (i.e., the He I lines and the Mg II line).
A further test for the eclipsing binary scenario would be the monitoring of its
light curve. Since the hotter component is also expected to be the more
luminous one, the system must appear fainter when the B9 star is eclipsed than
when the A1 star is eclipsed.
A third quite interesting scenario is based on the assumption that S 23 might
have a patchy surface abundance in He. The existence of such inhomogeneous or
spotty surface patterns are known especially for some so-called chemically
peculiar (CP) stars (see, e.g., Smith 1996; Briquet et al.
2001,2004; Lehmann et al. 2006; Krticka et al. 2007). These objects at or close to the main-sequence are supposed
to be rigidly rotating, and the variations observed in their He I line
profiles are interpreted as abundance inhomogeneities in the form of large stellar
spots that appear within and again disappear from the line of sight as the star
revolves. In addition, these stars are found to possess longitudinal magnetic
fields (e.g., Khokhlova et al. 2000; Briquet et al. 2007), and there seems to be evidence that variations in the magnetic field might be the cause for the abundance inhomogeneities.
Furthermore, the stellar surfaces of some of the CP stars seem to have
temperature inhomogeneities (see, e.g., Böhm-Vitense & van Dyk 1987;
Lehmann et al. 2006), and even the need of a co-existence of
abundance and temperature inhomogeneities has recently been claimed by
Lehmann et al. (2007), even though the physical processes
resulting in such patchy surface structures are not understood at all.
S 23 is definitely not a main-sequence star, and to our knowledge, no such
abundance or temperature inhomogeneities have been reported for a supergiant
so far. In addition, nothing is known about a possible magnetic field on the
surface of S 23. Nevertheless, such a surface inhomogeneity seems to be an
interesting scenario, at least to explain the variations in the He I
lines. Whether this inhomogeneity can also explain the different observed values of
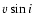 ,
needs to be investigated in more detail. At least the classical stellar rotation profile used in Sect. 5 to derive
,
needs to be investigated in more detail. At least the classical stellar rotation profile used in Sect. 5 to derive
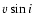 from the FWHM will in such a scenario certainly not be valid anymore.
from the FWHM will in such a scenario certainly not be valid anymore.
If S 23 possesses He spots, the variation of the He I lines must be
correlated to the rotation period of the star. Assuming that S 23 is seen
edge-on, the derived value of
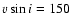 km s-1 delivers the
equatorial rotation velocity. With a radius of roughly 60
km s-1 delivers the
equatorial rotation velocity. With a radius of roughly 60 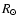 ,
this
results in a period of about 20 days. To prove or disprove the scenario of
surface inhomogeneities in either He abundance, or temperature, or even both,
one would need to monitor the He I and Mg II lines in the spectrum of
S 23 over at least one rotational period.
,
this
results in a period of about 20 days. To prove or disprove the scenario of
surface inhomogeneities in either He abundance, or temperature, or even both,
one would need to monitor the He I and Mg II lines in the spectrum of
S 23 over at least one rotational period.
7 Conclusions
We investigated the SMC star S 23, which was formerly classified by ZSW as a
B8 Ib star, belonging to the class of B[e] supergiants. Our optical spectra
show clear differences to the previously published one. These differences
especially concern the absence of all photospheric He I absorption lines.
Our spectra are therefore consistent more with a spectral classification of S 23
as A1 Ib supergiant. This classification is further supported by our analysis
of the photometric UBV data. During this analysis, we could derive
self-consistently the contributions of the interstellar extinction, and of the
circumstellar extinction caused by the stellar wind. A circumstellar extinction
caused predominantly by dust could be excluded.
We further determined the projected rotation velocity of S 23 from an
analysis of its photospheric Mg II line. We found a value of
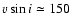 km s-1, which claims that S 23 is rotating
with at least 75% of its critical velocity. Consequently, S 23 is the fourth
member of the B[e] supergiant star group with confirmed high projected
rotational velocity.
km s-1, which claims that S 23 is rotating
with at least 75% of its critical velocity. Consequently, S 23 is the fourth
member of the B[e] supergiant star group with confirmed high projected
rotational velocity.
The most puzzling result is the fact that within a period of only 11
years, between the two sets of spectroscopic observations, the star seems to
have cooled by more than 1500 K, and at the same time increased its rotation
speed by about 35%. Such behaviour is definitely ruled out by any stellar
evolution scenario. And also the scenario of a shell phase, as is often
reported for classical Be stars, has severe difficulties in explaining all the
observed peculiarities in S 23. Therefore, we presented and discussed several
other alternatives: a rapidly rotating star undergoing a high precession, the
scenario of an eclipsing binary, and the idea of He abundance and/or
temperature inhomogeneities on the stellar surface, as they have been reported
from CP stars. All these suggestions can explain most of the curiosities
of S 23. However, the question, which of these scenarios is the correct one,
or whether even all scenarios have to be discarded, could not be solved.
Nevertheless, we suggested observational tests that can be performed
to distinguish or discard the different scenarios. Definitely more observations
with a much better time resolution are needed to disentangle the
mystery of the peculiar variations in S 23.
Acknowledgements
We are greateful to Herman Hensberge and Georges Meynet for many fruitful
discussions concerning the peculiarities of S 23, and to the anonymous referee
for the helpful comments and suggestions.
This research made use of the NASA Astrophysics Data System (ADS) and of the
SIMBAD and 2MASS databases. M.K. acknowledges financial support from GA AV
CR number KJB300030701, and M.K. and J.K. from GA CR number
205/08/0003. M.B.F. acknowledges financial support from the Belgian Federal
Science Policy Office (Research Fellowship for non-EU Postdocs) and CNRS for
the post-doctoral grant.
- Abt, H. A., Levato, H.,
& Grosso, M. 2002, ApJ, 573, 359 [NASA ADS] [CrossRef]
(In the text)
- Azzopardi, M.
1987, A&AS, 69, 421 [NASA ADS]
(In the text)
- Azzopardi, M., &
Vigneau, J. 1982, A&AS, 50, 291 [NASA ADS]
(In the text)
- Bjorkman, J.
E., & Cassinelli, J. P. 1993, ApJ, 409, 429 [NASA ADS] [CrossRef]
(In the text)
- Bjorkman, K. S.,
Miroshnichenko, A. S., Bjorkman, J. E., et al. 1998, ApJ, 509,
904 [NASA ADS] [CrossRef]
- Böhm-Vitense, E.,
& van Dyk, S. D. 1987, AJ, 93, 1527 [NASA ADS] [CrossRef]
(In the text)
- Borges Fernandes,
M., Kraus, M., Lorenz Martins, S., & de Araújo, F. X.
2007, MNRAS, 377, 1343 [NASA ADS] [CrossRef]
(In the text)
- Bresolin, F.,
Pietrzynski, G., Urbaneja, M. A., et al. 2006, ApJ, 648, 1007 [NASA ADS] [CrossRef]
(In the text)
- Bresolin, F.,
Urbaneja, M. A., Gieren, W., Pietrzynski, G., & Kudritzki,
R.-P. 2007, ApJ, 671, 2028 [NASA ADS] [CrossRef]
(In the text)
- Briquet, M., De
Cat, P., Aerts, C., & Scuflaire, R. 2001, A&A, 380,
177 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Briquet, M.,
Aerts, C., Lüftinger, T., et al. 2004, A&A, 413, 273 [NASA ADS] [CrossRef] [EDP Sciences]
- Briquet, M.,
Hubrig, S., Schöller, M., & De Cat, P. 2007, Astron.
Nachr., 328, 41 [NASA ADS] [CrossRef]
(In the text)
- Charbonnel,
C., Meynet, G., Maeder, A., et al. 1993, A&AS, 101, 415 [NASA ADS]
(In the text)
- Curé, M. 2004,
ApJ, 614, 929 [NASA ADS] [CrossRef]
(In the text)
- Curé, M., Rial, D.
F., & Cidale, L. 2005, A&A, 437, 929 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Domiciano de
Souza, A., Driebe, T., Chesneau, O., et al. 2007, A&A, 464,
81 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Evans,
C. J., & Howarth, I. D. 2003, MNRAS, 345, 1223 [NASA ADS] [CrossRef]
(In the text)
- Evans, C. J.,
Howarth, I. D., Irwin, M. J., Burnley, A. W., & Harries, T. J.
2004, MNRAS, 353, 601 [NASA ADS] [CrossRef]
(In the text)
- Gray, D. F. 1976, The
observation and analysis of stellar photospheres (New York:
Wiley)
(In the text)
-
Gummersbach, C. A., Zickgraf, F.-J., & Wolf, B. 1995, A&A,
302, 409 [NASA ADS]
(In the text)
- Hanuschik, R.
W. 1996, A&A, 308, 170 [NASA ADS]
(In the text)
- Howarth, I. D.
2004, in Stellar Rotation, ed. A. Maeder, & P. Eenens (San
Francisco: ASP), IAU Symp., 215, 33
(In the text)
- Hubeny, I., &
Lanz, T. 2000, SYNSPEC - A User's Guide
(In the text)
- Hunter, I., Lennon,
D. J., Dufton, P. L., et al. 2008, A&A, 479, 541 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Johnson, H. L.
1966, ARA&A, 4, 193 [NASA ADS] [CrossRef]
(In the text)
- Keller, S. C., &
Wood, P. R. 2006, ApJ, 642, 834 [NASA ADS] [CrossRef]
(In the text)
- Khokhlova, V.
L., Vasilchenko, D. V., Stepanov, V. V., & Romanyuk, I. I.
2000, Astron. Lett., 26, 177 [NASA ADS] [CrossRef]
(In the text)
- Koubský, P.,
Harmanec, P., Kubát, J., et al. 1997, A&A, 328, 551 [NASA ADS]
(In the text)
- Kraus, M. 2006,
A&A, 456, 151 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Kraus, M., &
Miroshnichenko, A. S. 2006, Stars with the B[e] phenomenon, ASP
Conf. Ser., 355 (San Francisco: ASP)
(In the text)
- Kraus, M., Krügel, E.,
Thum, C., & Geballe, T. R. 2000, A&A, 362, 158 [NASA ADS]
- Kraus, M., Borges
Fernandes, M., de Araújo, F. X., & Lamers, H. J. G. L. M.
2005, A&A, 441, 289 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Kraus, M., Borges
Fernandes, M., & de Araújo, F. X. 2007, A&A, 463,
627 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Kraus, M., Borges
Fernandes, M., & Kubát, J. 2008a, A&A, submitted
(In the text)
- Kraus, M.,
Kubát, J., & Krticka, J. 2008b, A&A, 481, 499 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Krticka, J.,
Mikulásek, Z., Zverko, J., & Ziznovský, J. 2007,
A&A, 470, 1089 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Kurucz, R. L. 1979,
ApJS, 40, 1 [NASA ADS] [CrossRef]
(In the text)
- Kurucz, R. L. 1993,
Atomic Data for Opacity Calculations, Kurucz CD-ROM No. 1
(In the text)
- Lamers, H. J. G. L.
M., Snow, T. P., & Lindholm, D. M. 1995, ApJ, 455, 269 [NASA ADS] [CrossRef]
(In the text)
- Lamers, H. J. G. L.
M., Zickgraf, F.-J., de Winter, D., et al. 1998, A&A, 340,
117 [NASA ADS]
(In the text)
- Lehmann, H.,
Tsymbal, V., Mkrtichian, D. E., & Fraga, L. 2006, A&A, 457,
1033 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Lehmann, H.,
Tkachenko, A., Fraga, L., Tsymbal, V., & Mkrtichian, D. E.
2006, A&A, 471, 941 [NASA ADS] [CrossRef]
(In the text)
- Leitherer, C.,
& Wolf, B. 1984, A&A, 132, 151 [NASA ADS]
(In the text)
- Lennon, D. J. 1997,
A&A, 317, 871 [NASA ADS]
(In the text)
- Lennon, D. J.,
Dufton, P. L., & Fitzsimmons, A. 1992, A&AS, 94, 569 [NASA ADS]
(In the text)
- Lennon, D. J.,
Dufton, P. L., & Fitzsimmons, A. 1993, A&AS, 97, 559 [NASA ADS]
(In the text)
- Maeder, A., &
Meynet, G. 2001, A&A, 373, 555 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
-
Magalhães, A. M. 1992, ApJ, 398, 286 [NASA ADS] [CrossRef]
(In the text)
-
Magalhães, A. M., Melgarejo, R., Pereyra, A., & Carciofi,
A. C. 2006, in Stars with the B[e] Phenomenon, ed. M. Kraus, &
A. S. Miroshnichenko (San Francisco: ASP), ASP Conf. Ser., 355,
147
(In the text)
- Massey, P. 2002,
ApJS, 141, 81 [NASA ADS] [CrossRef]
(In the text)
- Massey, P., Lang,
C. C., DeGioia-Eastwood, K., & Garmany, C. D. 1995, ApJ, 438,
188 [NASA ADS] [CrossRef]
(In the text)
- Mathis, J. S.,
Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [NASA ADS] [CrossRef]
(In the text)
- McGregor,
P. J., Hillier, D. J., & Hyland, A. R. 1988a, ApJ, 334,
639 [NASA ADS] [CrossRef]
(In the text)
- McGregor,
P. J., Hyland, A. R., & Hillier, D. J. 1988b, ApJ, 324,
1071 [NASA ADS] [CrossRef]
(In the text)
- McGregor,
P. J., Hyland, A. R., & McGinn, M. T. 1989, A&A, 223,
237 [NASA ADS]
(In the text)
-
Melgarejo, R., Magalhães, A. M., Carciofi, A. C., &
Rodrigues, C. V. 2001, A&A, 377, 581 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Morris, P. W.,
Eenens, P. R. J., Hanson, M. M., Conti, P. S., & Blum, R. D.
1996, ApJ, 470, 597 [NASA ADS] [CrossRef]
(In the text)
- Porter, J. M.,
& Rivinius, Th. 2003, PASP, 115, 1153 [NASA ADS] [CrossRef]
(In the text)
- Prévot, M.
L., Lequeux, J., Maurice, E., et al. 1984, A&A, 132, 389 [NASA ADS]
- Royer, F. 2005,
Mem. S. A. It. Suppl. 8, 124
(In the text)
- Royer,
F., Grenier, S., Baylac, M.-O., Gómez, A. E., & Zorec, J.
2002, A&A, 393, 897 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Ryans, R. S. I.,
Dufton, P. L., Rolleston, W. R. J., et al. 2002, MNRAS, 336,
577 [NASA ADS] [CrossRef]
(In the text)
- Sahai, R., Brillant,
S., Livio, M., et al. 2002, ApJ, 573 [CrossRef], L 123
(In the text)
- Schmidt-Kaler, Th.
1982, in Landolt-Börnstein, New Series, Group IV, Vol. 2b, ed.
K. Schaifers, & H. H. Voigt (Berlin: Springer, 1)
(In the text)
-
Simón-Díaz, S., & Herrero, A. 2007, A&A, 468,
1063 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
-
Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131,
1163 [NASA ADS] [CrossRef]
- Smith, K. C.
1996, Ap&SS, 237, 77 [NASA ADS] [CrossRef]
(In the text)
- Venn, K. A. 1999,
ApJ, 518, 405 [NASA ADS] [CrossRef]
(In the text)
- Verdugo, E.,
Talavera, A., & Gómez de Castro, A. I. 1999, A&A, 346,
819 [NASA ADS]
(In the text)
- Verschueren, W.
1991, Ph.D. Thesis, Free University of Brussels, Belgium
(In the text)
- Walborn, N.
R. 1983, ApJ, 265, 716 [NASA ADS] [CrossRef]
(In the text)
- Zickgraf,
F.-J. 2000, in The Be Phenomenon in early-type stars, ed. M. A.
Smith, H. F. Henrichs, & J. Fabregat (San Francisco: ASP), ASP
Conf. Ser., 214, 26
(In the text)
- Zickgraf,
F.-J. 2006, in Stars with the B[e] Phenomenon, ed. M. Kraus, &
A. S. Miroshnichenko (San Francisco: ASP), ASP Conf. Ser., 355,
135
(In the text)
- Zickgraf, F.-J., Wolf,
B., Stahl, O., Leitherer, C., & Klare, G. 1985, A&A, 143,
421 [NASA ADS]
(In the text)
- Zickgraf,
F.-J., Wolf, B., Stahl, O., Leitherer, C., & Appenzeller, I.
1986, A&A, 163, 119 [NASA ADS]
(In the text)
- Zickgraf,
F.-J., Wolf, B., Stahl, O., & Humphreys, R. M. 1989, A&A,
220, 206 [NASA ADS]
(In the text)
- Zickgraf, F.-J., Stahl,
O., & Wolf, B. 1992, A&A, 260, 205 [NASA ADS] (ZSW)
(In the text)
Copyright ESO 2008
![\begin{figure}
\par\includegraphics[width=9cm,clip]{9779fi1a.eps}\par\vspace*{4.5mm}
\includegraphics[width=8.54cm,clip]{9779fi1b.eps}\end{figure}](/articles/aa/full/2008/32/aa09779-08/Timg9.gif)
![\begin{figure}
\par\includegraphics[width=9cm,clip]{9779fig2.eps}\end{figure}](/articles/aa/full/2008/32/aa09779-08/Timg12.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{9779fig3.eps}\end{figure}](/articles/aa/full/2008/32/aa09779-08/Timg29.gif)
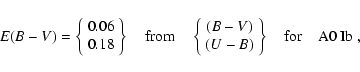
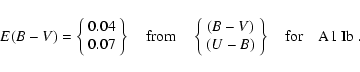
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{9779fig4.eps}\end{figure}](/articles/aa/full/2008/32/aa09779-08/Timg42.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{9779fig5.eps}\end{figure}](/articles/aa/full/2008/32/aa09779-08/Timg55.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{9779fig6.eps}\end{figure}](/articles/aa/full/2008/32/aa09779-08/Timg57.gif)
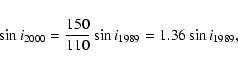
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{9779fig7.eps}\end{figure}](/articles/aa/full/2008/32/aa09779-08/Timg71.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{9779fig8.eps}\end{figure}](/articles/aa/full/2008/32/aa09779-08/Timg72.gif)