A&A 487, 345-355 (2008)
DOI: 10.1051/0004-6361:20078686
P. A. Dybczynski1 - G. Leto2 - M. Jakubík3 - T. Paulech4 - L. Neslusan3
1 - Astronomical Observatory of the A. Mickiewicz University,
S![]() oneczna 36, 60-286 Poznan, Poland
oneczna 36, 60-286 Poznan, Poland
2 - Catania Astrophysical Observatory, via Santa Sofia 78,
95123 Catania, Italy
3 - Astronomical Institute of the Slovak Academy of Sciences,
05960 Tatranská Lomnica, Slovakia
4 - Astronomical Institute of the Slovak Academy of Sciences,
Dúbravská cesta 9, 84504 Bratislava, Slovakia
Received 17 September 2007 / Accepted 4 April 2008
Abstract
Aims. Considering a model of an initial disk of planetesimals that consists of 10 038 test particles, we simulate the formation of distant-comet reservoirs for the first 1 Gyr. Since only the outer part of the Oort cloud can be formed within this period, we analyse the efficiency of the formation process and describe approximately the structure of the part formed.
Methods. The dynamical evolution of the particles is followed by numerical integration of their orbits. We consider the perturbations by four giant planets on their current orbits and with their current masses, in addition to perturbations by the Galactic tide and passing stars.
Results. In our simulation, the population size of the outer Oort cloud reaches its maximum value at about 210 Myr. After a subsequent, rapid decrease, it becomes almost stable (with only a moderate decrease) from about 500 Myr. At 1 Gyr, the population size decreases to about ![]() of its maximum value. The efficiency of the formation is low. Only about
of its maximum value. The efficiency of the formation is low. Only about ![]() of the particles studied still reside in the outer Oort cloud after 1 Gyr. The space density of particles in the comet cloud, beyond the heliocentric distance, r, of 25 000 AU is proportional to r-s, where
of the particles studied still reside in the outer Oort cloud after 1 Gyr. The space density of particles in the comet cloud, beyond the heliocentric distance, r, of 25 000 AU is proportional to r-s, where
![]() .
From about 50 Myr to the end of the simulation, the orbits of the Oort cloud comets are not distributed randomly, but high galactic inclinations of the orbital planes are strongly dominant. Among all of the outer perturbers considered, this is most likely caused by the dominant, disk component of the Galactic tide.
.
From about 50 Myr to the end of the simulation, the orbits of the Oort cloud comets are not distributed randomly, but high galactic inclinations of the orbital planes are strongly dominant. Among all of the outer perturbers considered, this is most likely caused by the dominant, disk component of the Galactic tide.
Key words: comets: general - Oort cloud - solar system: formation
In the past centuries, many attempts have been made to determine the origin of comets. The modern era of these studies started in the middle of 20th century, when Oort (1950) provided support to the concept of a distant cometary reservoir that was gravitationally-bound to the Solar System. At the same time, he suggested that cometary nuclei formed in the proto-planetary disk (PPD, hereinafter), and that many were ejected to large heliocentric distances, because of gravitational scattering by giant planets.
Ejection from the planetary region was further studied by Safronov (1972) and Fernández (1985), who proposed that cometary nuclei were delivered to the Oort cloud (OC) by Uranus and, mainly, Neptune. The internal giant planets, Jupiter and Saturn, were able to eject the nuclei into the interstellar space far more efficiently than into the distant cloud. The existence of a less distant, inner reservoir was suggested by Hills (1981), who proposed that this reservoir should be between zero and 100 times more populated than the outer cloud.
Using direct numerical integrations, the first simulation of OC formation, starting in the PPD region, was performed by Duncan et al. (1987, DQT87, hereinafter). Using computational equipment available at the time, they integrated the motion of comets on initially low-inclined, but already-highly-eccentric orbits. The integration scheme adopted was a generalization of that proposed by Stiefel & Schiefele (1971) for the restricted three-body problem with an additional conservative, perturbing-potential. Besides other results, they found that the density profile between 3000and 50 000 AU is roughly proportional to r-3.5 (where r is the heliocentric distance) and about 20% of comets, which survive inside the cloud after 4.5 Gyr, reside in the classical OC (semi-major axes, a > 20 000 AU). The directional distribution of the orbits appeared completely randomized after about 1 Gyr of orbital evolution, apart from the most-inner part of the cloud.
Another simulation of both OC and scattered-disk formation was
performed by Dones et al. (2005, DLDW,
hereinafter; see also Dones et al.
2004). They assumed more-realistic initial-conditions, starting the
integration of test comets on low-eccentric and low-inclined orbits in
the planetary region, from 4 to 40 AU. They assumed that the giant
planets already had their current masses and were on their current
orbits. They also assumed that the Solar System was situated in a
Galactic environment identical to that presently observed, that is they
assumed the current frequency value of stellar passages around the Solar
System and present density of Galactic matter in the solar neighbourhood,
![]() .
While DQT87 considered the value of
.
While DQT87 considered the value of
![]()
![]() pc-3 as determined by
Bahcall (1984), DLDW considered
pc-3 as determined by
Bahcall (1984), DLDW considered
![]()
![]() pc-3,
which is based on Hipparcos observations. Although DLDW confirmed the
overall features of the scenario described by DQT87, some quantitative
differences were found. They found a shallower slope in the density
profile with index
pc-3,
which is based on Hipparcos observations. Although DLDW confirmed the
overall features of the scenario described by DQT87, some quantitative
differences were found. They found a shallower slope in the density
profile with index
![]() (
(
![]() for the inner, and
for the inner, and
![]() for the outer OC). It corresponds to another result that
the ratio of the inner and outer cloud populations is about 1:1. In
disagreement with observations, they obtained a far larger simulated
population in the scattered disk, with respect to the population of
the OC, and an original mass in planetesimals, between 4 to 40 AU,
that exceeded between 2 and 8 times the mass of solids in the
minimum-mass solar nebula.
for the outer OC). It corresponds to another result that
the ratio of the inner and outer cloud populations is about 1:1. In
disagreement with observations, they obtained a far larger simulated
population in the scattered disk, with respect to the population of
the OC, and an original mass in planetesimals, between 4 to 40 AU,
that exceeded between 2 and 8 times the mass of solids in the
minimum-mass solar nebula.
The problem of too high a value of mass in the estimated cometary population was pointed out by Neslusan & Jakubík (2005), who derived the total mass of the distant cometary reservoir from observations of dynamically new comets in the zone of visibility. Even in the modern era, these problems have caused authors to search for alternative origins of comets. Clube & Napier (1982) and Napier & Staniucha (1982) proposed that comets formed in giant molecular clouds (GMCs) and were captured by the Solar System during mutual encounters. Another scenario was suggested by Neslusan (2000), who proposed that the comets were present in the proto-solar nebula, before its collapse into the proto-sun and its surrounding, nebular disk. These alternative theories were not widely accepted, because they did not provide strong evidence that cometary nuclei were formed in the thin environment of the interstellar clouds. These attempts highlight the problems, and their significances, that still exist in the understanding of cometary origins.
We present a new simulation of the formation of the outer Oort cloud. We perform an extended simulation that is similar to one performed by DLDW, apart from the fact that a larger number, 10 038, test particles (TPs), and different partial-assumptions, methods, and procedures, are used. Specifically, we use the RADAU integrator (Everhart 1985) within the MERCURY software package (Chambers 1999), in place of the RMVS3 integrator within the SWIFT package (Levison & Duncan 1994). Although we use a model of stellar passages near or through the Solar System that is based on the same observed frequency as DLDW (the frequency for various stellar types was published by García-Sánchez et al. 2001), we consider the individual radii of influence spheres for each stellar spectral type. Almost all of these radii are larger than the radius of the influence sphere considered by DLDW, which was 1 pc. In contrast to these authors, we do not investigate stellar perturbations by means of numerical integration, but use improved impulse approximation (Dybczynski 1994). We attempt to improve the description of outer-OC formation, and examine if and how these differences influence our results.
Concerning the content of our paper, we introduce the initial assumptions and methods used in Sect. 2. The regimes of numerical integration of test particles are described in Sect. 3. The results are given in Sect. 4 and discussed in Sect. 5.
At the start of our simulation, we assume the existence of a disk of planetesimals orbiting the Sun. We identify these planetesimals with massless TPs and study their orbital evolution.
The specific assumptions concerning the initial orbital elements of the TPs are the following. The TPs are distributed within almost circular and co-planar orbits, at heliocentric distances from 4 to 50 AU. Their average plane is identical to the invariable plane of four giant planets.
The radial distribution of their number density correlates with the
surface density of the solar nebula, ![]() ,
which was derived to depend
on the heliocentric distance r following
,
which was derived to depend
on the heliocentric distance r following
![]() (e.g. Morbidelli & Brown 2004). Since we assume almost circular
orbits, we can, approximately, identify the distance r with the orbital
semi-major axis of a TP, a. Therefore, the distribution law for
the semi-major axis is assumed to be
(e.g. Morbidelli & Brown 2004). Since we assume almost circular
orbits, we can, approximately, identify the distance r with the orbital
semi-major axis of a TP, a. Therefore, the distribution law for
the semi-major axis is assumed to be
The distributions of both eccentricity and inclination with respect
to the invariable plane of perturbing planets are Gaussian, centered on
zero, with a half-with given by
![]() and
and
![]() rad, respectively. We therefore model a ``cold''
disk that contains bodies that have already settled into the average
plane of disk.
rad, respectively. We therefore model a ``cold''
disk that contains bodies that have already settled into the average
plane of disk.
The argument of perihelion, ![]() ,
and the longitude of ascending
node,
,
and the longitude of ascending
node, ![]() ,
which are both related to the coordinate system that has
an xy-plane identical to the invariable plane of the considered planets,
in addition to the true anomaly, f, of the TPs are distributed randomly,
in the entire interval from 0 to
,
which are both related to the coordinate system that has
an xy-plane identical to the invariable plane of the considered planets,
in addition to the true anomaly, f, of the TPs are distributed randomly,
in the entire interval from 0 to ![]() rad.
rad.
The TPs, that reach the OC, can originate in various source regions.
To characterize the origin of TPs in the outer OC, we adopt the formal
distribution, corresponding to the initial semi-major axis, ![]() ,
of
the source regions, that is:
,
of
the source regions, that is:
![]() AU for the Jupiter region;
AU for the Jupiter region;
![]() AU for the Saturn region;
AU for the Saturn region;
![]() AU
for the Uranus region;
AU
for the Uranus region;
![]() AU for the Neptune region;
and
AU for the Neptune region;
and
![]() AU for the Kuiper-belt (KB) region. The
relative abundances of the TPs considered in these regions are
AU for the Kuiper-belt (KB) region. The
relative abundances of the TPs considered in these regions are ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
and
,
and ![]() ,
respectively.
,
respectively.
We assume that the TPs are perturbed by the four giant planets, from Jupiter to Neptune, in addition to other perturbers, described in the following subsections. We further assume that these planets maintain their currently-measured masses and revolve about the Sun in their present orbits (Astronomical Almanac for 2004, 2002). The planetary perturbations are calculated by numerical integration of the planets, and the TPs, using the RADAU integrator (Everhart 1985) that is included as part of MERCURY software package (Chambers 1999). A sophisticated optimization of the integration time-step in the RA15 subroutine reduces the total time needed to complete an integration to a level that is comparable with fast symplectic integrators. It is also efficient in the case of close encounters. The TPs that approach a massive body, the Sun or a planet, to a distance closer than the physical radius of the body are regarded as colliding with this body and are discarded from further integrations.
Over the entire period for which we study the orbital evolution of the TPs, we assume that the Solar System is situated in a Galactic environment similar to the current environment. We therefore assume the current density of the Galactic-disk matter in the solar neighbourhood, a similar frequency of stellar passages and abundance of individual stellar spectral types, and no massive interstellar clouds in the vicinity of the Solar System.
Therefore, the Galactic tide (GT) is the dominant outer perturber of
the comets at large heliocentric distances. The perturbation by the GT
was described well, for example by Heisler & Tremaine (1986). In the
modified heliocentric galactic-Ox'y'z'-coordinate-system, in which the
x'-axis is orientated outward from the Galactic centre and the z'-axis
is orientated toward the South Galactic pole, the vector of perturbing
force can be written as
![]() ,
where x', y', z' are the rectangular coordinates of the given TP in the
modified heliocentric galactic-coordinate-system, and
Kx = (A - B)(3A + B),
Ky = -(A - B)2, and
,
where x', y', z' are the rectangular coordinates of the given TP in the
modified heliocentric galactic-coordinate-system, and
Kx = (A - B)(3A + B),
Ky = -(A - B)2, and
![]() .
Symbols A and
B stand for the Oort constants,
.
Symbols A and
B stand for the Oort constants,
![]() for the mean density of mass
in the solar neighbourhood, and k for the Gauss gravitational constant.
In agreement with Levison et al. (2001), we adopt
for the mean density of mass
in the solar neighbourhood, and k for the Gauss gravitational constant.
In agreement with Levison et al. (2001), we adopt
![]()
![]() pc-3 and
pc-3 and
![]() ,
whereby
,
whereby
![]() km s-1 kpc-1. In this situation,
the second term in Kz component vanishes.
km s-1 kpc-1. In this situation,
the second term in Kz component vanishes.
The Ox'y'z' coordinate system rotates on the large timescale of our
simulation. For a numerical integration, it is more suitable to use a
strictly-inertial, non-rotating frame. In addition, we have the advantage
that, in such a non-rotating frame, a transit of the TPs from the planetary
to the OC region, and vice versa, is not problematic. The transformation
between the coordinates in the rotating and non-rotating frames was
explicitly given by Fouchard et al. (2005). With
the knowledge of the vector of force ![]() in the Ox'y'z' system,
the components of the acceleration in the non-rotating system Oxyz,
which we identify with Ox'y'z' at the start of the integration, are
in the Ox'y'z' system,
the components of the acceleration in the non-rotating system Oxyz,
which we identify with Ox'y'z' at the start of the integration, are
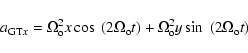 |
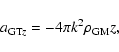 |
We consider the stellar perturbations, on comets, due to a set of stars, at large heliocentric distances. The star characteristics are modelled using the description of real stellar passages by García-Sánchez et al. (2001), who divide the stars into 13 characteristic spectral types. For each type, the frequency of passages, the velocity dispersion, and the peculiar velocity of the Sun relative to the corresponding local standard of rest, are all given.
Table 1: Some parameters of the considered model of stellar perturbations.
Based on the characteristics given by
García-Sánchez et al. (2001)
and the typical masses of the considered spectral types
(Gray 1992; Hansen & Kawaler 1994), we estimate a typical
``sphere of influence'',
![]() (in AU), for the ith spectral type (see
Table 1). We take into account the perturbation due to every star of
the ith type, which reaches a minimum distance from the Sun shorter
than
(in AU), for the ith spectral type (see
Table 1). We take into account the perturbation due to every star of
the ith type, which reaches a minimum distance from the Sun shorter
than
![]() .
Calculating the specific sphere of influence, we attempt,
at least roughly, to respect the fact that a perturbation of the cometary
nuclei in the OC, by a more massive star, from a larger distance, can
be comparable with a perturbation by a less massive star passing closer
to the OC. In other words, we should consider each star that provides
a significant perturbation to the orbits of each comet.
.
Calculating the specific sphere of influence, we attempt,
at least roughly, to respect the fact that a perturbation of the cometary
nuclei in the OC, by a more massive star, from a larger distance, can
be comparable with a perturbation by a less massive star passing closer
to the OC. In other words, we should consider each star that provides
a significant perturbation to the orbits of each comet.
Since we consider all comets out to a heliocentric distance of
![]() AU (Sect. 3), we suggest the criterion by which
each star changes the aphelion velocity of a comet on a highly-eccentric
orbit (with q = 1 AU and aphelion distance equal to
AU (Sect. 3), we suggest the criterion by which
each star changes the aphelion velocity of a comet on a highly-eccentric
orbit (with q = 1 AU and aphelion distance equal to
![]() ), on
average, by more than roughly about
), on
average, by more than roughly about ![]() (numerically, more than
0.02 m s-1). We estimate the typical velocity change,
(numerically, more than
0.02 m s-1). We estimate the typical velocity change,
![]() ,
using a procedure developed by
Rickman et al. (2004). In agreement with
these authors, we model a sample of test objects, randomly-distributed
on a sphere of radius
,
using a procedure developed by
Rickman et al. (2004). In agreement with
these authors, we model a sample of test objects, randomly-distributed
on a sphere of radius
![]() and, using the classical impulse
approximation, calculate the average impulses
and, using the classical impulse
approximation, calculate the average impulses
![]() for a
star of given type, with typical mass M*i (given in solar masses
in Table 1), which transverses the Solar System in a series of
heliocentric distances (from
for a
star of given type, with typical mass M*i (given in solar masses
in Table 1), which transverses the Solar System in a series of
heliocentric distances (from
![]() to
to
![]() AU,
step
AU,
step
![]() AU). The distance, that corresponds to a minimum
difference between
AU). The distance, that corresponds to a minimum
difference between
![]() and the chosen limit
and the chosen limit
![]() m s-1, is identified as
m s-1, is identified as
![]() .
.
The calculated numerical values of
![]() can be seen in Table 1.
The radius of the influence sphere for the most-massive B0-stars is
almost a factor of 10 larger than that of the least-massive M5-stars.
In Table 1, we also indicate the numbers of stars of a given spectral
type, N*i, that enter the corresponding influence sphere during a
period of 1 Gyr. All of these stars are considered as perturbing
stars in our simulation. We consider in total 18 250 perturbing
stars.
can be seen in Table 1.
The radius of the influence sphere for the most-massive B0-stars is
almost a factor of 10 larger than that of the least-massive M5-stars.
In Table 1, we also indicate the numbers of stars of a given spectral
type, N*i, that enter the corresponding influence sphere during a
period of 1 Gyr. All of these stars are considered as perturbing
stars in our simulation. We consider in total 18 250 perturbing
stars.
In our simulation of stellar perturbations, the closest approach to
the Sun is experienced by a 0.47 ![]() star, which reaches a
heliocentric distance of 13 320 AU. The strongest perturbation
corresponds to a 0.99
star, which reaches a
heliocentric distance of 13 320 AU. The strongest perturbation
corresponds to a 0.99 ![]() star that has the second closest
approach, 13 863 AU. Three very massive stars of spectral class B0
approach the Sun to within 1 pc: they are 9.85, 15.40, and
13.13
star that has the second closest
approach, 13 863 AU. Three very massive stars of spectral class B0
approach the Sun to within 1 pc: they are 9.85, 15.40, and
13.13 ![]() stars that approach to a heliocentric distance of
127 429, 167 354, and 182 432 AU, respectively.
stars that approach to a heliocentric distance of
127 429, 167 354, and 182 432 AU, respectively.
According to the first study of OC formation by DQT87, the OC was formed and the orbits of its comets were completely thermalized within 1 Gyr. Similarly, in the simulation performed by DLDW, the population of the outer OC reached its maximum value at a time of about 600 Myr, and the structure of the cloud at 4 Gyr remains almost similar (although the population has slightly declined) to that at 1 Gyr. We therefore focus our attention on the most important period of the outer-cloud formation and perform our first simulation for the period of 1 Gyr.
Output from the integration is recorded after every mega-year. Because
of rapid evolution during the first mega-year, we repeat the integration
for this period with the output that is made after every kilo-year period.
The full characteristics of all TPs that remain integrated are recorded
with the positions and velocities of the perturbing planets, in each
output. A continuous integration period begins at the start of each
mega-year, or at the onset of a stellar impulse and ends at the finish
of the mega-year or the onset of next stellar impulse. A given TPs is
checked, if it occurs beyond the limit of
![]() AU, or
collides with the Sun or planet. Each TP that occurs beyond
AU, or
collides with the Sun or planet. Each TP that occurs beyond
![]() AU is regarded as ejected. All ejected and colliding
TPs are discarded from further integrations. The lists of these discarded
TPs are written in each output record.
AU is regarded as ejected. All ejected and colliding
TPs are discarded from further integrations. The lists of these discarded
TPs are written in each output record.
The integration is performed using GRID computing (see acknowledgements). The input data of 10 038 TPs are divided into 240 parts. Each part is processed by a separate CPU in the GRID.
We adopt two conditions to classify a given TP, in our simulation,
as a member of the outer OC: its perihelion distance, q, must be
q > 45 AU (this condition was chosen by DLDW) and its semi-major
axis, a, must be
a > 25 000 AU. This limiting value is larger than
the conventional value of 20 000 AU established by Hills (1981)
and used often by other authors in the past. However, astronomers used
to consider the value
![]()
![]() pc-3 of the
Galactic-matter density, found by Bahcall (1984), in the period, when
the value of 20 000 AU started to be considered. Since there is a
reciprocal dependence between
pc-3 of the
Galactic-matter density, found by Bahcall (1984), in the period, when
the value of 20 000 AU started to be considered. Since there is a
reciprocal dependence between
![]() and the heliocentric distance
of the border between the inner and outer Oort clouds, and we consider
a lower value of the Galactic-matter density,
and the heliocentric distance
of the border between the inner and outer Oort clouds, and we consider
a lower value of the Galactic-matter density,
![]()
![]() pc-3, a larger distance of the border
appears to be necessary. Unless a strong stellar perturbation is in
action, no TPs with
pc-3, a larger distance of the border
appears to be necessary. Unless a strong stellar perturbation is in
action, no TPs with
![]() AU can overcome the Jupiter-Saturn
dynamical barrier and come to the zone of visibility within a single
orbital revolution (Dybczynski 2006).
AU can overcome the Jupiter-Saturn
dynamical barrier and come to the zone of visibility within a single
orbital revolution (Dybczynski 2006).
Table 2: The end-states of 10 038 considered TPs.
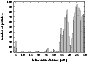 |
Figure 1: The survival of planetesimals in the Jupiter, Saturn, Uranus, Neptune, and Kuiper-belt regions of the PPD after 1 Gyr. The animations of the evolution of this dependence (as well as the dependencies plotted in Figs. 3, 5, 7, 9, and 10) are available at http//www.aanda.org. |
| Open with DEXTER | |
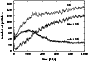 |
Figure 2: The evolution of the population of outer OC during the first giga-year. The evolution of the inner-OC as well as whole-OC population is demonstrated, too. |
| Open with DEXTER | |
All end states of 10 038 considered TPs at 1 Gyr are summarized in Table 2. We remind that the TPs were situated in various regions (the first column) of the PPD in the beginning of performed simulation. After 1 Gyr, the specific end-states are: (i) the TPs still have their perihelion q < 45 AU; (ii) they are moved into the outer (OOC); or (iii) inner (IOC) Oort cloud; (iv) they are ejected into the interstellar space; or (v) are destroyed at a collision with one of the considered massive bodies, mostly with the Sun. Almost all TPs were ejected from the Saturn's region, during the studied period (see also Fig. 1). A relatively-numerous population of Jupiter's Trojans is created a short time after the beginning the simulation and survives, most likely, the entire age of the Solar System. Relatively large sub-populations, that also survive, occur in the Neptune and KB regions. The population of the inner OC is larger than the population of the outer OC. (We regard a given TP as a member of the inner OC, if its q > 45 AU and 2000 < a < 25 000 AU.) The ratii of both populations are not high only for the TPs originating in the Jupiter and Saturn regions: 1.53 and 1.62, respectively. In particular, the population of the inner cloud appears to originate in the Uranus and Neptune regions. The corresponding ratii are 6.24 and 5.11, respectively. The ratio of inner- and outer-OC population sizes for the integrated Neptune+KB region is 4.60 at 1 Gyr.
The evolution of the outer OC population during the studied period of 1 Gyr is shown in Fig. 2. The population reaches its maximum size at a time of about 210 Myr after the beginning of our simulation. From about 500 Myr, only a minute decrease can be observed.
It appears that the efficiency of all perturbers to create the outer
OC is low and the population of this cloud at 1 Gyr consists of only
29 TPs, i.e. ![]() of the 10 038 considered TPs. The slow decrease
in the size of the population from about 500 Myr (Fig. 2) indicates
that this population is, almost, in a steady state and can be expected
to be not very different at present.
of the 10 038 considered TPs. The slow decrease
in the size of the population from about 500 Myr (Fig. 2) indicates
that this population is, almost, in a steady state and can be expected
to be not very different at present.
The formation efficiency is much lower than that obtained by DQT87 and DLDW in their simulations. The discrepancy between the DLDW formation efficiency and our own is caused obviously by one or more differences between our and their: (i) model of stellar perturbations; (ii) model of the initial PPD; (iii) choice of the border between the inner and outer OC; (iv) choice of the outer border of the studied region, and, perhaps; (v) numbers of considered TPs.
Concerning the first potential reason, our model includes the more distant passages of very massive stars, which can erode especially the outer OC. On the other-hand side, the random generation of an extremely low number of close passages produced an unusually-distant closest passage in the minimum-proximity distance of 13 320 AU. An absence of closer passages certainly weakens the formation efficiency we obtained.
The larger extent of our PPD (reason labelled as (ii), above), up to
50 AU (DLDW considered the PPD up to 40 AU) cannot account for the
diversity, because our efficiency decreases even more, when we omit the
TPs from the region between 40 and 50 AU. Initially, 8559 TPs are
situated in 4-40 AU region and 24 of them are in the outer OC
at 1 Gyr. It implies that the efficiency is ![]() for 4-40 AU PPD
(in contrast to
for 4-40 AU PPD
(in contrast to ![]() for 4-50 AU PPD).
for 4-50 AU PPD).
Between all of the above potential reasons, we can exclude the third,
also for our own and DQT87 results, when we re-define our border,
between the inner and outer OC, to 20 000 AU. At 1 Gyr, the number
of the TPs in the more inward, extended, outer OC is 39.8, (the average
number from simulation times 991, 992, 993,..., 1000 Myr),
i.e. ![]() .
DQT87 found that about
.
DQT87 found that about ![]() of the TPs considered were still
surviving, at the end of their simulation. As far as we noticed, they
did not make any restriction on the perihelion distance of the
surviving TPs, therefore we regard their values as possible maximum values of the
numbers of OC residents. About
of the TPs considered were still
surviving, at the end of their simulation. As far as we noticed, they
did not make any restriction on the perihelion distance of the
surviving TPs, therefore we regard their values as possible maximum values of the
numbers of OC residents. About ![]() of the survivors were in the outer
part of the cloud (
a > 20 000 AU). This implies that about
of the survivors were in the outer
part of the cloud (
a > 20 000 AU). This implies that about ![]() of
all considered TPs were in the outer OC at the end of simulation. DQT87
therefore achieved more than one order of magnitude (cf. DQT87's value
of
of
all considered TPs were in the outer OC at the end of simulation. DQT87
therefore achieved more than one order of magnitude (cf. DQT87's value
of ![]() to corresponding our value of
to corresponding our value of ![]() )
greater efficiency in
the outer-OC formation. DLDW considered 2000 TPs in a so-called
``cold'' run, and 1000 TPs in a ``hot'' run, and
)
greater efficiency in
the outer-OC formation. DLDW considered 2000 TPs in a so-called
``cold'' run, and 1000 TPs in a ``hot'' run, and ![]() and
and ![]() ,
respectively, of all TPs were found at the end of the simulation to be
in the outer OC. They obtained a lower efficiency than DQT87, but one
that was still considerably higher than our own.
,
respectively, of all TPs were found at the end of the simulation to be
in the outer OC. They obtained a lower efficiency than DQT87, but one
that was still considerably higher than our own.
The significantly-smaller sphere within which we monitor the motion
of the TPs (reason (iv) above) does not, of course, contain the TPs that
would be outside it, into the outermost region considered by DLDW. It
can also be responsible for a decrease in the efficiency of outer-OC
formation in our simulation, because the orbital aphelia of some TPs
that occur at distances larger than 100 000 AU can later decrease
to below this limit. It is, however, questionable which border should
be considered to provide the most appropriate description of reality.
The system of the closest stars, ![]() Centauri, is situated at a
distance of about 280 000 AU. Other nearby stars are not at
significantly-larger distances. Although the dominance of the solar
gravity diminishes halfway to the nearest stars, a strong perturbing
action is expected, when a given TP is at a far smaller heliocentric
distance, often even below the limit of 100 000 AU. Moreover, we
ignore the perturbations by the giant molecular clouds, which can
significantly erode the cloud, especially at the largest heliocentric
distances. Perhaps, a more realistic value would be a little larger
than 100 000 AU. In the observational data
(Marsden & Williams 2003), less than
Centauri, is situated at a
distance of about 280 000 AU. Other nearby stars are not at
significantly-larger distances. Although the dominance of the solar
gravity diminishes halfway to the nearest stars, a strong perturbing
action is expected, when a given TP is at a far smaller heliocentric
distance, often even below the limit of 100 000 AU. Moreover, we
ignore the perturbations by the giant molecular clouds, which can
significantly erode the cloud, especially at the largest heliocentric
distances. Perhaps, a more realistic value would be a little larger
than 100 000 AU. In the observational data
(Marsden & Williams 2003), less than ![]() of new comets had an
original semi-major axis that was larger than 50 000 AU, i.e. that
had the aphelia beyond 100 000 AU, in addition to another few
hyperbolic comets. Nevertheless, this does not imply that a large amount
of OC comets are beyond our limit, which could account for the
more-than-an-order-of-magnitude difference between the DLDW's and our
results.
of new comets had an
original semi-major axis that was larger than 50 000 AU, i.e. that
had the aphelia beyond 100 000 AU, in addition to another few
hyperbolic comets. Nevertheless, this does not imply that a large amount
of OC comets are beyond our limit, which could account for the
more-than-an-order-of-magnitude difference between the DLDW's and our
results.
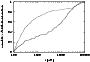 |
Figure 3: The cumulative radial distribution of planetesimals after 100 Myr (dotted curve) and 1 Gyr (solid curve). |
| Open with DEXTER | |
Another significant difference between our and DLDW results is the
relatively-early maximum, in ![]() 210 Myr, of the outer-OC population
in our simulation. It contrasts with the maximum at about 600 Myr, which
was found by DLDW. In Fig. 3, the cumulative radial distribution of comets
that have heliocentric distances larger than 100 AU, at 100 Myr
and 1 Gyr, is presented. Even at the end of the simulation, some
210 Myr, of the outer-OC population
in our simulation. It contrasts with the maximum at about 600 Myr, which
was found by DLDW. In Fig. 3, the cumulative radial distribution of comets
that have heliocentric distances larger than 100 AU, at 100 Myr
and 1 Gyr, is presented. Even at the end of the simulation, some ![]() of
the TPs reside within 10 000 AU, while in the DLDW simulation
only
of
the TPs reside within 10 000 AU, while in the DLDW simulation
only ![]() were closer than 10 000 AU, after 1 Gyr. This implies that
our results are more consistent with the DQT87 result, for which the
inner part of the cloud was far more populated than in the DLDW model.
There is also a significant difference in the median TP distance after
the first 100 Myrs: DLDW obtained 1800 AU, while in our results
this median distance is only about 340 AU. This may indicate that our
model produces a far slower eccentricity-evolution than obtained by DLDW.
were closer than 10 000 AU, after 1 Gyr. This implies that
our results are more consistent with the DQT87 result, for which the
inner part of the cloud was far more populated than in the DLDW model.
There is also a significant difference in the median TP distance after
the first 100 Myrs: DLDW obtained 1800 AU, while in our results
this median distance is only about 340 AU. This may indicate that our
model produces a far slower eccentricity-evolution than obtained by DLDW.
To reveal the actual cause of the differences between DLDW and our own scenarios of outer-OC formation, we would need to perform additional simulations with modified initial assumptions. Such simulations will be completed in the future. At the moment, we speculate only that a replenishment in the population after 210 Myr is too slow to compensate for the relatively-strong erosion due to stellar perturbations, which are more frequent and intensive in our model in comparison to those in the model used by DLDW. While DLDW considered the passages of 13 162 stars during 1 Gyr, on average, our model assumes 18 250 such passages. DLDW also limited the stellar influence to the sphere of radius of 1 pc while in our calculations there are many more distant encounters included.
We calculate the overall efficiency with which a given planet moves
the TPs into the outer OC, regardless of whether the TPs still reside in
this part of the cloud at the end of the simulation, or have been moved
away. We find that ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
and
,
and ![]() of the TPs moved into the outer OC from the Jupiter, Saturn, Uranus,
Neptune, and KB regions, respectively (see also Fig. 4). We do not record
the individual ejection events in our simulation, and we therefore are
unable to say which planet ejects a given TP. Such an efficiency was,
however, determined by Safronov (1972), who determined the ratio of the
mass that moved into the OC by the given giant planet and the total
delivered mass. It should be noted that, at that time, the OC structure
was known less accurately and the term OC was used to refer to a
structure now called the outer OC. According to Safronov (1972),
of the TPs moved into the outer OC from the Jupiter, Saturn, Uranus,
Neptune, and KB regions, respectively (see also Fig. 4). We do not record
the individual ejection events in our simulation, and we therefore are
unable to say which planet ejects a given TP. Such an efficiency was,
however, determined by Safronov (1972), who determined the ratio of the
mass that moved into the OC by the given giant planet and the total
delivered mass. It should be noted that, at that time, the OC structure
was known less accurately and the term OC was used to refer to a
structure now called the outer OC. According to Safronov (1972), ![]() ,
,
![]() ,
,
![]() ,
and
,
and ![]() of the comets should have been ejected by
Jupiter, Saturn, Uranus, and Neptune, respectively. It is clear that
the efficiencies with which Jupiter and Saturn could move the TPs into
the outer OC would be too low to explain our abundances, if the TPs do
not radially migrate. Many TPs originating in the Jupiter and Saturn
regions must have been placed in the outer OC by close encounters with
Uranus and Neptune, after initial orbit enlargements.
of the comets should have been ejected by
Jupiter, Saturn, Uranus, and Neptune, respectively. It is clear that
the efficiencies with which Jupiter and Saturn could move the TPs into
the outer OC would be too low to explain our abundances, if the TPs do
not radially migrate. Many TPs originating in the Jupiter and Saturn
regions must have been placed in the outer OC by close encounters with
Uranus and Neptune, after initial orbit enlargements.
In Fig. 4, we show the evolution of the outer-OC partial-populations
that originate in the Jupiter, Saturn, Uranus, Neptune, and KB regions.
At 1 Gyr, the outer OC is mostly populated from the Neptune and, at
a slightly lower rate, Uranus regions. The sub-populations that originate
in the other regions are, however, higher in number that had previously
believed. Specifically, the final (after 1 Gyr) relative abundances
of TPs that originate in the individual regions are ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
and
,
and ![]() ,
respectively. It is more or less a
constant rate in a given, equal-width interval of heliocentric distance,
as indicated by full bars in Fig. 5. Comparing the above figures with
those for TPs that occur in the outer OC for a limited time interval
within the investigated 1 Gyr period, it is obvious that Jupiter and
Saturn move some TPs to the outer-OC border-region, where orbits are
not very stable.
,
respectively. It is more or less a
constant rate in a given, equal-width interval of heliocentric distance,
as indicated by full bars in Fig. 5. Comparing the above figures with
those for TPs that occur in the outer OC for a limited time interval
within the investigated 1 Gyr period, it is obvious that Jupiter and
Saturn move some TPs to the outer-OC border-region, where orbits are
not very stable.
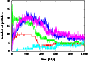 |
Figure 4: The evolution of the delivery of comets to the outer Oort cloud, which initially originated in the Jupiter, Saturn, Uranus, Neptune, and Kuiper-belt regions. The contributions from these regions are illustrated by red, green, dark blue, violet, and light blue curve, respectively. |
| Open with DEXTER | |
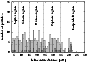 |
Figure 5: The numbers of TPs that moved into the outer OC from the Jupiter, Saturn, Uranus, Neptune, and Kuiper-belt regions. The full bars illustrate the numbers of TPs in 0.5 AU-wide intervals of the initial PPD, which reside in the outer OC at 1 Gyr. The empty bars indicate the TPs that exist, at least for a short period, in the outer OC. |
| Open with DEXTER | |
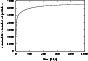 |
Figure 6: The evolution of the cumulative ejection of comets into the interstellar space. |
| Open with DEXTER | |
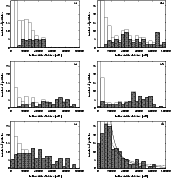 |
Figure 7: The distribution of the heliocentric distance of the OC comets (cross-hatched bars) for the times 1 (plot a)), 4 b), 16 c), 63 d), 250 e), and 1000 Myr f). The corresponding distributions of all comets, still bound to the Sun, are also shown (empty bars). In the region r < 10 000 AU, these distributions are outside of the chosen scale because of a better transparency of the first group of the distributions. If all comets in the given interval are in the OC, then the cross-hatched bar overlaps the empty bar, which is not visible, in this interval, then. In plot f), our fit of the behaviour in the interval from 25 000 to 100 000 AU, by the power-law with index s = -2.26, is shown with thick-solid curve and the corresponding fit by the power-law with DQT87's index s = -1.5 is shown with the thin-dotted curve. |
| Open with DEXTER | |
In Fig. 4, the contributions from the regions of Uranus (dark blue curve), and Neptune (violet) increase slowly, reach a maximum, and then decrease moderately after 500 Myr. On the other hand, the contributions from the Jupiter (red) and Saturn (green) regions increase sharply in the first mega-year and, from about 1 Myr, stagnate or decrease. The fact, that the sub-population from the Jupiter (Saturn) region is only about one third (one half) of that from Uranus or Neptune region, implies a non-negligible probability that an OC comet formed in the hotter, Jupiter (Saturn) region of the PPD. In the light of this knowledge, the composition of comet C/1999 S4 (LINEAR), which corresponds to the Jupiter-Saturn formation region (Mumma et al. 2001; Boehnhardt 2001), is no longer surprising.
Only the contribution to the outer OC from the KB region (light blue curve in Fig. 4) is, slowly, still increasing at the end of the simulation. From Fig. 5, we conclude that the fraction of TPs in the outer OC, at 1 Gyr, from the KB region, more exactly from its part beyond 40 AU, is relatively large. The perihelia of these TPs have obviously been reduced by the strong perturbation of Neptune, since the original orbits of the TPs are situated between the 3:2 and 5:3 mean-motion resonances with this planet. This region was found by Duncan et al. (1995) to be highly unstable. Subsequently, the TPs are ejected to large heliocentric distances. The depletion in the ring between about 40 and 42 AU is well observed in Fig. 1. It appears to be meaningful to choose the outer border of the initial PPD to be at 50 AU.
The cumulative number of the TPs ejected into the interstellar space is shown in Fig. 6. Regardless of whether the TPs, moved to the outer OC and ejected into the interstellar space, remain in position or are later moved, the ratii of these TPs are 0.035, 0.045, 0.065, 0.076, and 0.085, for TPs that originate in the Jupiter, Saturn, Uranus, Neptune, and KB regions, respectively, according to our simulation. For the integrated Neptune+KB region, the ratio equals 0.078. Fernández (1985) determined the ratii of the mass of comets, moved to the outer OC and ejected into the interstellar space by each giant planet, resulting in 0.03, 0.16, 1.3, and 2.6, for Jupiter, Saturn, Uranus, and Neptune, respectively. We must assume that the perihelia of TPs, which are initially in the Uranus and Neptune regions, are reduced, i.e. that radial migration occurs, to explain the disagreement in the two sequences of values.
A much lower efficiency is observed for ejecting TPs into the outer OC than into interstellar space. The relative ratii are magnified even more, when we consider the TPs that belong to the outer OC only at 1 Gyr. The ratii are then found to be 0.0022, 0.0022, 0.0048, 0.0059, and 0.014, respectively. The ratio for the integrated Neptune+KB region in this case is 0.0076.
The evolution of the distribution of heliocentric distance, r, of
the TPs, residing in the OC, is shown in Fig. 7. The plots provide the
distribution for several, selected times (cross-hatched bars), the last
time corresponding to the end of the integration at 1 Gyr. Some
distant TPs have a perihelion that is still in the planetary region,
and cannot be classified as the TPs that are the members of the OC. In
the same plots, we show the radial distribution of all TPs (as empty
bars), to be able to map the distribution of all TPs, regardless of
whether they are or are not in the OC. The number of low-q TPs is,
of course, extremely large in the region within 10 000 AU. To
emphasize the data for
r > 10 000 AU, we choose a 0-28 vertical
range, although with this choice the top of the empty bars, for
![]() AU, are located above the upper edge of the plot.
AU, are located above the upper edge of the plot.
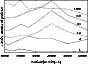 |
Figure 8: The evolution of the relative distribution of semi-major axis, a, of comets in the region of the Oort cloud beyond 10 000 AU. The curves labelled by 1, 4, 16, 63, 250, and 1000 illustrate the distributions for the corresponding time in Myr. |
| Open with DEXTER | |
The rapid evolution of the inner cloud, out to 25 000 AU, has not yet ended at 1 Gyr. We therefore do not analyse the structure of this region. In the region between the distances of 25 000 and 50 000 AU, the TPs from both inner and outer OC are situated, while beyond 50 000 AU, only the TPs from the outer OC, according to our definition, can be found. Unfortunately, the number of the TPs in the latter region is statistically small, therefore we cannot correctly describe its radial structure in an analytical form. We therefore describe the structure of the wider region instead, between the distances of 25 000 and 100 000 AU.
DQT87 approximated the space-density distribution of comets in the
entire OC using the power law
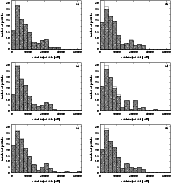 |
Figure 9: The distribution of the semi-major axis, a, of comets in the Oort cloud (cross-hatched bars). Plots a), b), c), d), e), and f) illustrate the distributions for the times of 900, 920, 940, 960, 980, and 1000 Myr. The corresponding distributions of all comets, still gravitationally-bound to the Sun, are also illustrated (empty bars). If all comets in the given interval are in the OC, then the cross-hatched bar overlaps the empty bar, which is not visible, then. |
| Open with DEXTER | |
In more detail, the structure of the OC can be characterized by the distributions of orbital elements of comets populating this reservoir. Unfortunately, the efficiency, with which all perturbers create the outer OC, is low, and the small final population of this cloud does not enable us to study a more detailed structure of the outer OC.
To determine, at least qualitatively, some features of the outer OC,
we show the evolution in the distributions of semi-major axis, a, in
Figs. 8 and 9. In Fig. 8, there are relative
a-distributions for 1, 4,
16, 63, 250, and 1000 Myr. In this figure, we can often see the peak
at about 40 000 AU. Another, lower peak occurs, from time to time,
at about 20 000 AU. All the structures are strongly variable. The
variability can be seen especially in the plots of Fig. 9, where the
a-distributions for the times of 900, 920, 940, 960, 980, and
1000 Myr are shown. The maximum at ![]() 40 000 AU
quasi-periodically appears and disappears. Two potential reasons
appear to explain the variability: a libration of the perihelion
distance due to the Galactic tide and stellar perturbations. Due to the
Galactic tide, the perihelia of some TPs are reduced below and enlarged
up to the defined perihelion border of the OC, at 45 AU. When the
perihelion is lifted above this limit, the given TP appears in the OC.
After the decrease in the perihelion, the TP is no longer regarded as
a resident in the comet cloud.
40 000 AU
quasi-periodically appears and disappears. Two potential reasons
appear to explain the variability: a libration of the perihelion
distance due to the Galactic tide and stellar perturbations. Due to the
Galactic tide, the perihelia of some TPs are reduced below and enlarged
up to the defined perihelion border of the OC, at 45 AU. When the
perihelion is lifted above this limit, the given TP appears in the OC.
After the decrease in the perihelion, the TP is no longer regarded as
a resident in the comet cloud.
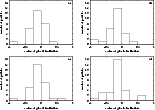 |
Figure 10:
The distribution of the cosine of inclination, |
| Open with DEXTER | |
However, we can discard this explanation of variability on the basis of the a-distributions shown in Fig. 9. The a-distributions of the TPs in the OC are drawn using cross-hatched bars and the corresponding distributions of all TPs, regardless of the position of their perihelion, are drawn using empty bars. We observe that only few TPs have perihelia below 45 AU (the height of the empty bar slightly exceeds the height of its cross-hatched counterpart). In the case of the perihelion libration of a significant number of TPs, the height of many more empty bars would have to exceed the height the cross-hatched bars. Moreover, only the height of the given cross-hatched bar could change, while the height of the corresponding empty bar would have to remain constant. Therefore, the changes in the distributions must be caused mainly by stellar perturbations, which thus appear to be relatively strong.
In the distributions of angular elements of TPs residing in the outer OC, we find a stable feature that is illustrated in Fig. 10: a peak in
the distribution of the cosine of galactic inclination on one side
(or both sides) of
![]() .
The feature appears at about
50 Myr after the beginning of the simulation, and survives until the
simulation end. The same qualitative feature can also be detected in the
corresponding distribution of TPs in the inner OC. It is obviously caused
by the action of the Galactic-tide disk-component. The comets in the
orbits with a very small perihelion distance (in planetary region) in
the minimum of the libration cycle of this element have, typically, a
characteristic galactic-inclination behaviour, which approaches, for a
long time, the value of
.
The feature appears at about
50 Myr after the beginning of the simulation, and survives until the
simulation end. The same qualitative feature can also be detected in the
corresponding distribution of TPs in the inner OC. It is obviously caused
by the action of the Galactic-tide disk-component. The comets in the
orbits with a very small perihelion distance (in planetary region) in
the minimum of the libration cycle of this element have, typically, a
characteristic galactic-inclination behaviour, which approaches, for a
long time, the value of
![]() ;
more exactly, it is slightly lower or
slightly higher than
;
more exactly, it is slightly lower or
slightly higher than
![]() .
(The behaviour of the angular orbital
elements of such a comet, during about two libration cycles of its
perihelion, is illustrated in Fig. 4b of Neslusan & Jakubík 2005.)
Since all considered TPs are ejected into the OC from the planetary
region, their minimum perihelion distance during the libration cycle
must be small and, thus, a high galactic inclination can be expected to
be retained for a long period. Some can, later, be moved to another
phase space region by stellar perturbations and the radial component of
the Galactic tide. The apparent existence of a peak in
.
(The behaviour of the angular orbital
elements of such a comet, during about two libration cycles of its
perihelion, is illustrated in Fig. 4b of Neslusan & Jakubík 2005.)
Since all considered TPs are ejected into the OC from the planetary
region, their minimum perihelion distance during the libration cycle
must be small and, thus, a high galactic inclination can be expected to
be retained for a long period. Some can, later, be moved to another
phase space region by stellar perturbations and the radial component of
the Galactic tide. The apparent existence of a peak in
![]() -distribution is proof of the dominance of the Galactic-tide
disk-component among the outer perturbers of the OC.
-distribution is proof of the dominance of the Galactic-tide
disk-component among the outer perturbers of the OC.
We have simulated the formation of the OC and the accompanying
dynamical evolution of the Kuiper belt, for the initial period of
1 Gyr. We considered a PPD model consisting of 10 038 TPs,
the perturbations of the four giant planets, moving in their
presently-observed orbits with their present masses, and perturbations
by the Galactic tide and passing stars![]() . The inner OC is
still found to be forming at 1 Gyr. The properties of the outer OC,
at this time, are given below.
. The inner OC is
still found to be forming at 1 Gyr. The properties of the outer OC,
at this time, are given below.
Its population strongly rises during the first mega-year due to ejections of TPs from the Jupiter-Saturn region (Fig. 4). However, it immediately decreases and, from few mega-years after the beginning, it stagnates until about 300 Myr, from when it slowly decreases. The sub-populations from the regions of Uranus and Neptune gradually rise until about 210 Myr, when they, as well as the entire population of the outer OC, reach their maximum sizes. Approximately the same number of the TPs from the regions of Uranus and Neptune reside in the outer OC in any time during the first giga-year. The sub-population from the KB region becomes significant in the outer OC after a few hundred mega-years. Surprisingly, it is comparable with the sub-population from the Jupiter or Saturn region at 1 Gyr. Because of its increasing trend, we expect that the outer OC is more populated with bodies from the KB region than the Jupiter or Saturn region at present, i.e. at 4.5 Gyr.
Although a majority of the bodies, residing in the outer OC at 1 Gyr, originates in the cool, Uranus-Neptune and, in part, KB region, the sub-population of bodies that originate in a hotter, Jupiter-Saturn and, possibly, sub-Jupiter region appears to be significant. In contrast with older estimates resulting in a negligible size of this sub-population, the amount of OC bodies from the Jupiter-Saturn region, according our result, is smaller only about a factor of three, in comparison with the amount of bodies originating in the Uranus-Neptune-KB region. The statement, that all (or almost all) OC comets formed in a cool region of the solar nebula, cannot be regarded precise any longer.
According to our simulation, only about ![]() of the bodies
considered in the 4-50 AU region of the PPD resided in the outer OC
at 1 Gyr. This unexpectedly-low formation rate of the outer OC and,
thus, small number of TPs in this cloud does not enable a detailed study
of its internal structure to be completed, even though the number of all
considered TPs is larger than for any previous study. Only a few details
can be discerned. The radial space-density distribution of TPs in the outer
part of the OC, beyond 25 000 AU, can be characterized by a power
law with a slope index
of the bodies
considered in the 4-50 AU region of the PPD resided in the outer OC
at 1 Gyr. This unexpectedly-low formation rate of the outer OC and,
thus, small number of TPs in this cloud does not enable a detailed study
of its internal structure to be completed, even though the number of all
considered TPs is larger than for any previous study. Only a few details
can be discerned. The radial space-density distribution of TPs in the outer
part of the OC, beyond 25 000 AU, can be characterized by a power
law with a slope index
![]() ,
during a short period just
before 1 Gyr. This implies that the outer OC is more
centrally-concentrated cloud than found by DQT87 (s = 3.5), and
roughly the same (within the determination uncertainty) radial
space-density distribution than found later by DLDW (s = 3.7).
,
during a short period just
before 1 Gyr. This implies that the outer OC is more
centrally-concentrated cloud than found by DQT87 (s = 3.5), and
roughly the same (within the determination uncertainty) radial
space-density distribution than found later by DLDW (s = 3.7).
The population of the outer OC in our simulation reaches its maximum size earlier (210 Myr) than that in the simulation of DLDW (600 Myr) and, moreover, the efficiency of the outer-OC formation is more than one order of magnitude lower in our simulation. Due to this discrepancy in particular, we cannot draw any definitive conclusions about the formation scenario of the outer OC. Other simulations are necessary to clarify which difference or differences in the initial assumptions could cause the formation-efficiency diversity. It is possible that the diversity can occur due to the model of stellar perturbations, which includes the influence of massive distant stars, but does not include extremely close stellar encounters with the Sun. Another possible reason could be that the model of the initial PPD has a larger number of TPs and a more distant outer border. We further considered a shorter range of heliocentric distances, in which the outer OC is situated, with a more distant inner and several times shorter outer border. The shorter, and probably more-realistic outer-border of the studied region can in particular reduce the formation efficiency.
Another typical feature of the internal outer-OC structure is the dominance of high galactic inclinations in the distribution of this orbital element. This proves that the disk component of the Galactic tide is the dominant outer-perturber of all considered.
In our work, we focused our attention on the cometary population coming to the OC after the giant-planet formation. Future simulations of OC formation should include an earlier phase of this process. During the first ten mega-years, the gas-particle interactions in the PPD and dense primordial stellar-environment could be important as proposed by Fernández & Brunini (2000) and Brasser et al. (2006,2007). At the same time, these future simulations should include the concept of a gradual rise in planetary masses and migration of the formed giant planets (Fernández & Ip 1984; Gomes et al. 2005). Unfortunately, a simulation including the interaction between the planetary embryos and massive TPs requires a large cluster of processors with a rapid connection enabling parallel computation. This technical requirement cannot yet be met by many research groups.
Acknowledgements
G.L. thanks the ``Trinacria Virtual Laboratory'' (http://www.trigrid.it/) for the computational resources and technical support. M.J., T.P., and L.N. thank the project ``Enabling Grids for E-sciencE II'' (http://www.eu-egee.org/) for the provided computational capacity and support in a development of the computer code, which was necessary for a management of tasks on the GRID. They also acknowledge the partial support of this work by VEGA - the Slovak Grant Agency for Science (grant No. 7047).
Read movie "fig01_movie.avi" with Media Players Classic
fig01_movie.avi
or if you don't have the pluging installed, you can download
the movie (animated mpeg)
fig01_movie_firstMyr.avi
(animated mpeg)
fig03_movie.avi
(animated mpeg)
fig03_movie_firstMyr.avi
(animated mpeg)
fig05_movie.avi
(animated mpeg)
fig05_movie_firstMyr.avi
(animated mpeg)
fig07_movie.avi
(animated mpeg)
fig07_movie_firstMyr.avi
(animated mpeg)
fig09_movie.avi
(animated mpeg)
fig09_movie_firstMyr.avi
(animated mpeg)
fig10_movie.avi
(animated mpeg)
fig10_movie_firstMyr.avi
(animated mpeg)