A&A 487, 63-74 (2008)
DOI: 10.1051/0004-6361:20077688
Constraining dark energy via baryon acoustic oscillations in the
(an)isotropic light-cone power spectrum
C. Wagner - V. Müller - M. Steinmetz
AIP - Astrophysikalisches Institut Potsdam, An der Sternwarte 16,
14482 Potsdam, Germany
Received 20 April 2007 / Accepted 15 May 2008
Abstract
Context. The measurement of the scale of the baryon acoustic oscillations (BAO) in the galaxy power spectrum as a function of redshift is a promising method to constrain the equation-of-state parameter of the dark energy w.
Aims. To measure the scale of the BAO precisely, a substantial volume of space must be surveyed. We test whether light-cone effects are important and whether the scaling relations used to compensate for an incorrect reference cosmology are in this case sufficiently accurate. We investigate the degeneracies in the cosmological parameters and the benefits of using the two-dimensional anisotropic power spectrum. Finally, we estimate the uncertainty with which w can be measured by proposed surveys at redshifts of about z=3 and z=1, respectively.
Methods. Our data is generated by cosmological N-body simulations of the standard 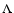 CDM scenario. We construct galaxy catalogs by ``observing'' the redshifts of different numbers of mock galaxies on a light cone at redshifts of about z=3 and z=1. From the ``observed'' redshifts, we calculate the distances, assuming a reference cosmology that depends on
CDM scenario. We construct galaxy catalogs by ``observing'' the redshifts of different numbers of mock galaxies on a light cone at redshifts of about z=3 and z=1. From the ``observed'' redshifts, we calculate the distances, assuming a reference cosmology that depends on
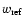 .
We do this for
.
We do this for
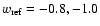 ,
and -1.2 holding the other cosmological parameters fixed. By fitting the corresponding (an)isotropic power spectra, we determine the apparent scale of the BAO and the corresponding w.
,
and -1.2 holding the other cosmological parameters fixed. By fitting the corresponding (an)isotropic power spectra, we determine the apparent scale of the BAO and the corresponding w.
Results. In the simulated survey we find that light-cone effects are small and that the simple scaling relations used to correct for the cosmological distortion work fairly well even for large survey volumes. The analysis of the two-dimensional anisotropic power spectra enables an independent determination to be made of the apparent scale of the BAO, perpendicular and parallel to the line of sight. This is essential for two-parameter w-models, such as the redshift-dependent dark energy model
w=w0+(1-a) wa. Using Planck priors for the matter and baryon density and
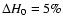 for the Hubble constant, we estimate that the BAO measurements of future surveys around z=3 and z=1 will be able to constrain, independently of other cosmological probes, a constant w to
for the Hubble constant, we estimate that the BAO measurements of future surveys around z=3 and z=1 will be able to constrain, independently of other cosmological probes, a constant w to 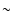
 and
and 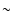
 (68% c.l.), respectively.
(68% c.l.), respectively.
Key words: cosmology: cosmological parameters - cosmology: large-scale
structure of Universe
There are two main observational indications of the existence of an unknown
energy component in the Universe, which is usually referred to as dark energy (DE). First,
observations of distant supernovae Ia (Perlmutter et al. 1999; Riess et al. 1998) favor an accelerating
expansion of the Universe and therefore imply an energy component of
negative pressure P. In particular, the parameter w of the equation of state
(EOS) 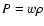 must obey w<-1/3. Second, measurements of the anisotropies
in the cosmic microwave background (CMB) (Spergel et al. 2007,2003) in combination with observations of
the large-scale structure of the Universe argue for a
spatially flat Universe. Matter (baryonic and dark) contributes however less
than 30% to the critical density. Hence, about 70% of the present-day
energy density of the Universe appears to be in an unknown form of energy.
The simplest way to account for this missing energy and the accelerating
expansion is to introduce a cosmological constant
must obey w<-1/3. Second, measurements of the anisotropies
in the cosmic microwave background (CMB) (Spergel et al. 2007,2003) in combination with observations of
the large-scale structure of the Universe argue for a
spatially flat Universe. Matter (baryonic and dark) contributes however less
than 30% to the critical density. Hence, about 70% of the present-day
energy density of the Universe appears to be in an unknown form of energy.
The simplest way to account for this missing energy and the accelerating
expansion is to introduce a cosmological constant 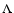 in Einstein's
equations, which has a redshift-independent EOS parameter w=-1. So far
all observations appear to agree with the model of a cosmological constant.
There is however at least one theoretical drawback. The observed value of
in Einstein's
equations, which has a redshift-independent EOS parameter w=-1. So far
all observations appear to agree with the model of a cosmological constant.
There is however at least one theoretical drawback. The observed value of
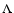 ,
which is interpreted as vacuum energy, is highly inconsistent with
current predictions by particle physics, a discrepancy commonly referred to as
the cosmological constant
problem (for a review, see Carroll 2001). This has motivated consideration
of more general dark energy models that have a redshift-dependent EOS
parameter w(z). The measurement of the parameter w can therefore
help to distinguish between not only a simple cosmological constant and other dark
energy models, but potentially also between these different models.
,
which is interpreted as vacuum energy, is highly inconsistent with
current predictions by particle physics, a discrepancy commonly referred to as
the cosmological constant
problem (for a review, see Carroll 2001). This has motivated consideration
of more general dark energy models that have a redshift-dependent EOS
parameter w(z). The measurement of the parameter w can therefore
help to distinguish between not only a simple cosmological constant and other dark
energy models, but potentially also between these different models.
Several possible methods to constrain the EOS parameter w are summarized by
the Dark Energy Task Force Report (Albrecht et al. 2006).
The method that we consider here uses the expansion history
of the Universe. To measure this precisely, we require a
standard candle or a standard ruler. For redshifts up to
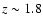 ,
supernovae Ia can be observed and calibrated to be standard candles, with which one can measure
the luminous distance
,
supernovae Ia can be observed and calibrated to be standard candles, with which one can measure
the luminous distance
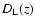 .
Eisenstein et al. (1999,1998)
proposed that the baryon acoustic oscillations (BAO) imprinted in the galaxy power
spectrum could be utilized as a standard ruler. The BAO have the same origin as the acoustic
peaks in the anisotropies of the CMB. Before recombination, baryons and photons
were tightly coupled. Gravitation and radiation pressure
produced acoustic oscillations in this hot plasma; during the expansion of the
Universe, the plasma then cooled and finally nuclei and electrons recombined. The released
photons propagated through the expanding Universe and are observed by
ourselves as
the highly redshifted radiation of the CMB; in contrast, the baryons followed
the clustering of the dark matter and eventually collapsed to form
galaxies. Since the dark matter did not participate
in the acoustic oscillations, the oscillatory feature in the galaxy power
spectrum is far less pronounced than for the CMB photons
(Bond & Efstathiou 1984; Holtzman 1989; Peebles & Yu 1970; Sunyaev & Zeldovich 1970; Eisenstein & Hu 1998; Hu & Sugiyama 1996).
.
Eisenstein et al. (1999,1998)
proposed that the baryon acoustic oscillations (BAO) imprinted in the galaxy power
spectrum could be utilized as a standard ruler. The BAO have the same origin as the acoustic
peaks in the anisotropies of the CMB. Before recombination, baryons and photons
were tightly coupled. Gravitation and radiation pressure
produced acoustic oscillations in this hot plasma; during the expansion of the
Universe, the plasma then cooled and finally nuclei and electrons recombined. The released
photons propagated through the expanding Universe and are observed by
ourselves as
the highly redshifted radiation of the CMB; in contrast, the baryons followed
the clustering of the dark matter and eventually collapsed to form
galaxies. Since the dark matter did not participate
in the acoustic oscillations, the oscillatory feature in the galaxy power
spectrum is far less pronounced than for the CMB photons
(Bond & Efstathiou 1984; Holtzman 1989; Peebles & Yu 1970; Sunyaev & Zeldovich 1970; Eisenstein & Hu 1998; Hu & Sugiyama 1996).
When the physical scale of the BAO has been calibrated using precise CMB measurements, it can be applied as a standard ruler for measuring the angular
diameter distance
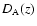 and Hubble parameter H(z).
In contrast to supernovae Ia, the scale of the BAO is a more reliable
standard ruler at high redshifts. As the number of unperturbed peaks
and troughs corresponding to the BAO in the power spectra increases,
the wavelength of the BAO can be determined more accurately.
On scales where structure growth is already nonlinear, the oscillations
cannot be easily discerned (Springel et al. 2005; Gottlöber et al. 2006; Eisenstein et al. 2007b). Hence, with
decreasing redshift the uncertainty in the observed scale of the BAO
increases. To have good statistics for the first peaks a large volume has to
be surveyed. The BAO have been detected in the present-day largest galaxy
redshift surveys (Cole et al. 2005; Eisenstein et al. 2005). Data sets studying larger volumes and higher redshifts are
however required to achieve tight
constraints on dynamical DE models. Galaxy redshift surveys at about
z=3, 1, or 0.5, like HETDEX (Hill et al. 2004), the WFMOS BAO survey (Bassett et al. 2005; Glazebrook et al. 2005), and BOSS (SDSS-III Collaboration 2008), are designed for measuring
the scale of the BAO and the EOS parameter w with a precision to
a few percent and thereby constrain a variety of DE models.
and Hubble parameter H(z).
In contrast to supernovae Ia, the scale of the BAO is a more reliable
standard ruler at high redshifts. As the number of unperturbed peaks
and troughs corresponding to the BAO in the power spectra increases,
the wavelength of the BAO can be determined more accurately.
On scales where structure growth is already nonlinear, the oscillations
cannot be easily discerned (Springel et al. 2005; Gottlöber et al. 2006; Eisenstein et al. 2007b). Hence, with
decreasing redshift the uncertainty in the observed scale of the BAO
increases. To have good statistics for the first peaks a large volume has to
be surveyed. The BAO have been detected in the present-day largest galaxy
redshift surveys (Cole et al. 2005; Eisenstein et al. 2005). Data sets studying larger volumes and higher redshifts are
however required to achieve tight
constraints on dynamical DE models. Galaxy redshift surveys at about
z=3, 1, or 0.5, like HETDEX (Hill et al. 2004), the WFMOS BAO survey (Bassett et al. 2005; Glazebrook et al. 2005), and BOSS (SDSS-III Collaboration 2008), are designed for measuring
the scale of the BAO and the EOS parameter w with a precision to
a few percent and thereby constrain a variety of DE models.
Many studies presented methods for extracting the scale of the BAO and
estimated the accuracy of its measurement achievable by future surveys. In
these analyses, Monte Carlo simulations
(Glazebrook & Blake 2005; Blake et al. 2006; Blake & Glazebrook 2003), Fisher matrix techniques
(Seo & Eisenstein 2003; Matsubara 2004; Hu & Haiman 2003; Seo & Eisenstein 2007; Linder 2003; Hütsi 2006b), N-body simulations
(White 2005; Angulo et al. 2008; Koehler et al. 2007; Angulo et al. 2005; Huff et al. 2007; Seo & Eisenstein 2005), and observational data
(Hütsi 2006a,2005,2006c; Eisenstein et al. 2005) were used.
In this article, we attempt to include all important (physical and observational)
effects for measuring the BAO and deriving constraints
on the EOS parameter w. Our perspective is that of an observer, i.e. the
starting point for the BAO measurement should be a galaxy catalog that
provides celestial coordinates and redshifts of the galaxies. Since we do not have in hand
the type of real observations that we require, we have first to generate mock
catalogs; we achieve this by completing ``observations'' on the data products of N-body simulations. Using these ``observations'', we are able to study for
the first time in detail the light-cone
effect and the accuracy of the scaling relations used to compensate the
cosmological distortion that arises by assuming an incorrect reference cosmology.
A crucial point for all BAO measurements is the fitting method. We develop
a method which uses only the oscillatory part of the power spectrum
in a way that produces unbiased and robust results.
Further, we compare the results of fitting the
angle-averaged one-dimensional power spectrum and anisotropic
two-dimensional power spectrum. Finally, we predict the
uncertainty with which proposed surveys will be able to measure the EOS
parameter w by assuming two different w-models.
The paper is structured as follows. In Sect. 2, we review how the EOS
parameter w is measured using BAO. In Sect. 3, we explain how we generate
the ``observed'' data from N-body simulations, and in Sect. 4, we describe the
power spectrum calculation and our fitting method. In Sect. 5, we present our
results, and finally we provide our conclusions in Sect. 6.
2 Cosmology with baryon acoustic oscillations
Knowledge of the true comoving scales, both parallel (
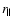 )
and transverse (
)
and transverse (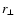 )
to the line of sight, of an observed physical property at a given
redshift z, in the case of BAO statistical properties of large-scale
structure, enables us to derive the Hubble parameter H(z) and angular diameter
distance
)
to the line of sight, of an observed physical property at a given
redshift z, in the case of BAO statistical properties of large-scale
structure, enables us to derive the Hubble parameter H(z) and angular diameter
distance
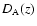 from the measured quantities (redshift
from the measured quantities (redshift 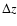 and
angle
and
angle
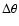 ):
):
|
|
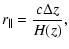 |
|
| |
|
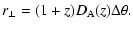 |
(1) |
In a flat Universe and for moderate redshifts at which the contribution of
radiation can be neglected, the Hubble parameter depends on three cosmological
parameters, the present-day Hubble parameter H0, fraction of matter
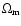 ,
and the dark energy EOS parameter w(z), in the following manner
,
and the dark energy EOS parameter w(z), in the following manner
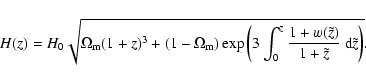 |
(2) |
The angular diameter distance
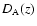 is a functional of the Hubble parameter
and is given by
is a functional of the Hubble parameter
and is given by
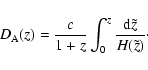 |
(3) |
Assuming that we know apart from w all important cosmological parameters
to significant precision from other
observations, especially from CMB precision measurements such as WMAP
(Spergel et al. 2007) and direct measurements of the Hubble constant H0 by the
HST Key project (Freedman et al. 2001), one can constrain the EOS parameter w using this chain of
equations. Since w appears in an integral over z in Eq. (2),
observations at a single redshift cannot be used to measure the value of w at
this redshift. A certain model for w has to be assumed before its value can be
measured. In this paper, we assume a constant w and a simple redshift-dependent parameterization
w=w0 + (1-a) wa; this parameterization is used frequently in the
literature (compare Dark Energy Task Force Report (Albrecht et al. 2006)) and advocated by Linder (2007) to be robust and applicable to a wide range of dark energy models.
One problem of using the scale of the BAO as a standard ruler is that the BAO appear in a
statistical quantity. We cannot measure 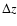 of the BAO, but we can measure
the redshifts of the galaxies and then, assuming a reference cosmology,
reconstruct their positions and derive their power spectrum. From this power
spectrum, we can determine the apparent scale of the BAO and compare this
with its true value. If they agree, we have used the correct cosmology. In
principle, for every trial cosmology we have to recalculate the distances and
recompute the power spectrum. A more efficient method is to scale
appropriately the power spectrum derived for the reference cosmology using
the following approximations (Glazebrook & Blake 2005; Seo & Eisenstein 2003)
of the BAO, but we can measure
the redshifts of the galaxies and then, assuming a reference cosmology,
reconstruct their positions and derive their power spectrum. From this power
spectrum, we can determine the apparent scale of the BAO and compare this
with its true value. If they agree, we have used the correct cosmology. In
principle, for every trial cosmology we have to recalculate the distances and
recompute the power spectrum. A more efficient method is to scale
appropriately the power spectrum derived for the reference cosmology using
the following approximations (Glazebrook & Blake 2005; Seo & Eisenstein 2003)
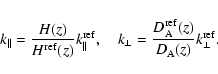 |
(4) |
In this paper, we test if these approximations are still sufficiently accurate for
very large surveys where z varies substantially within the survey.
We achieve this by using three reference cosmologies, which differ only in the EOS
parameter
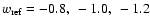 .
We use the relation (4)
to scale the derived power spectra and compare the results. For convenience, we
define the following scaling factors parallel and transverse to the line of
sight and an isotropic one for the one-dimensional angle-averaged power spectrum
.
We use the relation (4)
to scale the derived power spectra and compare the results. For convenience, we
define the following scaling factors parallel and transverse to the line of
sight and an isotropic one for the one-dimensional angle-averaged power spectrum
| |
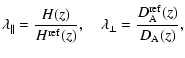 |
|
| |
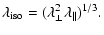 |
(5) |
In Fig. 1, we show the dependence of the scaling factors on a
constant w for redshift z=3 (solid line) and z=1 (dotted line). As a
reference value, we chose
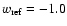 .
We also show the derivatives of
the scaling factors with respect to w. The higher the value of the
derivative, the more accurately
we can constrain the constant w for a given uncertainty in the scaling
factor. Since the derivatives decrease with decreasing w, the uncertainty
in w will be, in general, higher towards lower w values. The derivative
of
.
We also show the derivatives of
the scaling factors with respect to w. The higher the value of the
derivative, the more accurately
we can constrain the constant w for a given uncertainty in the scaling
factor. Since the derivatives decrease with decreasing w, the uncertainty
in w will be, in general, higher towards lower w values. The derivative
of
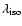 around w=-1 at redshift z=1 is
around w=-1 at redshift z=1 is 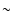 1.5 times
higher than at z=3, that is although we can probably measure the scale of
the BAO less accurately at redshift z=1 than at z=3 (due to nonlinear
evolution), this does not need to be the case for the EOS parameter w.
1.5 times
higher than at z=3, that is although we can probably measure the scale of
the BAO less accurately at redshift z=1 than at z=3 (due to nonlinear
evolution), this does not need to be the case for the EOS parameter w.
![\begin{figure}
\par\includegraphics[angle=-90,width=4.4cm,clip]{7688f01a.ps}\inc...
...688f01e.ps}\includegraphics[angle=-90,width=4.4cm,clip]{7688f01f.ps}\end{figure}](/articles/aa/full/2008/31/aa7688-07/Timg42.gif) |
Figure 1:
The scaling factors
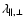 and
and
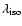 and their derivatives are shown as a function of w for
the redshifts z=3 (solid line) and z=1 (dotted line).
and their derivatives are shown as a function of w for
the redshifts z=3 (solid line) and z=1 (dotted line). |
| Open with DEXTER |
To derive realistic samples of large galaxy surveys, we first completed an N-body
simulation in a large box (
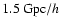 )
and constructed
the corresponding dark matter distribution on a light cone by interpolating
between about 20 snapshots. We calculated the redshifts, which would
be observed including the effect of peculiar velocities. Assuming a certain
cosmology, we converted these redshifts into distances. Finally, we selected a
certain number of particles by applying a simple bias scheme and defining them as
galaxies. In the following subsections, we describe each step of this procedure.
)
and constructed
the corresponding dark matter distribution on a light cone by interpolating
between about 20 snapshots. We calculated the redshifts, which would
be observed including the effect of peculiar velocities. Assuming a certain
cosmology, we converted these redshifts into distances. Finally, we selected a
certain number of particles by applying a simple bias scheme and defining them as
galaxies. In the following subsections, we describe each step of this procedure.
Our principal N-body simulation consists of 5123 dark matter particles of a mass
of 2 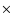
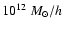 in a
in a
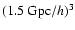 box. The
initial power spectrum was produced by CMBfast (Seljak & Zaldarriaga 1996). Starting from
a glass distribution, the particles were displaced according to second order
Lagrangian perturbation theory by using the code of Sirko (2005). As
cosmological parameters, we chose
box. The
initial power spectrum was produced by CMBfast (Seljak & Zaldarriaga 1996). Starting from
a glass distribution, the particles were displaced according to second order
Lagrangian perturbation theory by using the code of Sirko (2005). As
cosmological parameters, we chose
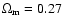 ,
,
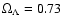 ,
h=0.7,
,
h=0.7,
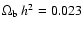 ,
,
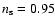 ,
,
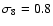 and w=-1.0.
The simulation was performed with GADGET-2 (Springel 2005) using a softening
length of comoving
and w=-1.0.
The simulation was performed with GADGET-2 (Springel 2005) using a softening
length of comoving
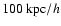 .
The starting redshift was z=20.
.
The starting redshift was z=20.
We also completed twelve 2563 dark matter particles simulations with
the same cosmological parameters but different realizations of the initial
conditions. We used these simulations to investigate systematic effects.
Especially, we tested if our fitting procedure provides unbiased results.
An observer at the present epoch t0 (z(t0)=0) identifies the galaxy
distribution on his past light cone. He receives photons emitted at t<t0that have traversed the comoving distance
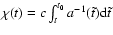 .
To construct a light-cone survey, we follow an approach used by
Evrard et al. (2002). We identify for each particle two consecutive
snapshots between which it crosses the light cone and interpolate between
them to find the position and velocity of that particle
on the light cone. Expressed in formulas, the interpolated position is given by
.
To construct a light-cone survey, we follow an approach used by
Evrard et al. (2002). We identify for each particle two consecutive
snapshots between which it crosses the light cone and interpolate between
them to find the position and velocity of that particle
on the light cone. Expressed in formulas, the interpolated position is given by
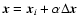 where
where 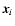 is the position
of the particle in snapshot i and
is the position
of the particle in snapshot i and
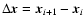 ,
and
,
and 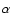 is determined by requiring that
is determined by requiring that
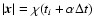 with
with 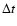 being the time step between the two snapshots. After a Taylor
expansion for the last term, we can solve for
being the time step between the two snapshots. After a Taylor
expansion for the last term, we can solve for 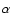
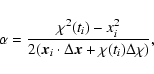 |
(6) |
with
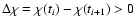 .
The interpolated velocity is
then given by
.
The interpolated velocity is
then given by
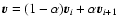 .
.
For the galaxy sample at redshift z=3, we place the center of the simulation
box at redshift z=3, i.e.
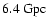 comoving distance away from the virtual observer.
The orientation of the box is such that the line connecting the center of the
box with the observer is parallel to the z-axis.
The
comoving distance away from the virtual observer.
The orientation of the box is such that the line connecting the center of the
box with the observer is parallel to the z-axis.
The
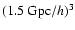 box then extends from redshift 2.1 to 4.7, i.e. from 5.3 Gpc to 7.6 Gpc in
comoving distances. For this redshift range, we have 17 snapshots at different
times, i.e. of different expansion factors:
box then extends from redshift 2.1 to 4.7, i.e. from 5.3 Gpc to 7.6 Gpc in
comoving distances. For this redshift range, we have 17 snapshots at different
times, i.e. of different expansion factors:
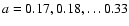 .
The
box centered at redshift z=1 ranges from redshift 0.6 to 1.7. For this
interval, we use 27 snapshots with
.
The
box centered at redshift z=1 ranges from redshift 0.6 to 1.7. For this
interval, we use 27 snapshots with
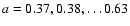 for the light
cone construction.
for the light
cone construction.
3.3 ``Observation''
Our virtual observer is at redshift z=0 and the simulation box
is centered on redshift z=3 and z=1, respectively. To derive a redshift for
each particle, we compute the comoving distance 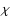 to the observer
and solve the following equation numerically for the expansion factor a,
to the observer
and solve the following equation numerically for the expansion factor a,
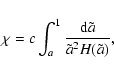 |
(7) |
where H is the ``true'' Hubble parameter of the simulation
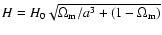 .
The corresponding redshift is then
.
The corresponding redshift is then
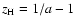 .
In addition to this redshift
caused by the Hubble expansion of the Universe, there is also a Doppler
redshift caused by the peculiar velocity of the particle. Hence, the total
observed redshift is
.
In addition to this redshift
caused by the Hubble expansion of the Universe, there is also a Doppler
redshift caused by the peculiar velocity of the particle. Hence, the total
observed redshift is
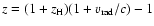 ,
where
,
where
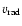 is the radial velocity of the particle. The accuracy of the
simulation and the numerical algorithm of the integral equation above, implies
an uncertainty of
is the radial velocity of the particle. The accuracy of the
simulation and the numerical algorithm of the integral equation above, implies
an uncertainty of
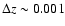 .
.
We next convert the observed redshifts to distances by assuming different reference cosmologies, where the dark energy EOS parameter w has the values
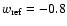 ,
-1.0, and -1.2. In this case, the Hubble parameter becomes
,
-1.0, and -1.2. In this case, the Hubble parameter becomes
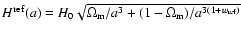 .
.
Since the mass resolution of our simulation is too low for identifying galaxy-sized
friends-of-friends halos, we use a simple bias scheme
to compile mock galaxy samples from the dark matter distribution (Cole et al. 1998; Yoshida et al. 2001).
Using the initial density field, we define a probability function by
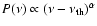 if
if 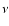 is above the threshold
is above the threshold
 and zero otherwise. The dimensionless variable
and zero otherwise. The dimensionless variable 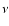 is given
by the density contrast normalized by its root-mean-square on the
grid
is given
by the density contrast normalized by its root-mean-square on the
grid 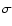 ,
i.e.
,
i.e.
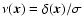 .
The density contrast
.
The density contrast
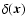 of each particle is computed in the following way. First, we assign the
particles with the cloud in cell (CIC) scheme to a 5123 grid
(Hockney & Eastwood 1988) to obtain the density
of each particle is computed in the following way. First, we assign the
particles with the cloud in cell (CIC) scheme to a 5123 grid
(Hockney & Eastwood 1988) to obtain the density 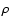 on the grid points. Then, we
calculate the density contrast
on the grid points. Then, we
calculate the density contrast
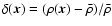 on the grid points and interpolate it to the positions of the particles.
on the grid points and interpolate it to the positions of the particles.
In the next step, we Poisson sample the dark matter particles according to the
probability function and track these ``galaxies''
throughout the snapshots and the constructed light cones.
As parameters, we use (
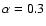 ,
,
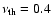 )
for a strongly
biased sample and (
)
for a strongly
biased sample and (
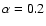 ,
,
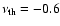 )
for a more weakly biased
sample. We calculate the corresponding galaxy bias to be the square root of
the ratio of the galaxy power spectrum to the dark matter power spectrum
in real space:
)
for a more weakly biased
sample. We calculate the corresponding galaxy bias to be the square root of
the ratio of the galaxy power spectrum to the dark matter power spectrum
in real space:
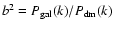 .
The bias of the mock galaxies decreases with decreasing redshift (Fig. 2)
as expected in the model. We select primarily particles in high-density
regions of the initial density field, which occupy less
prominent structures at later times due to the further development of gravitational
clustering. The bias has a mild scale dependence due to the schematic
procedure of grid-based density estimation and the specific probability
selection function.
.
The bias of the mock galaxies decreases with decreasing redshift (Fig. 2)
as expected in the model. We select primarily particles in high-density
regions of the initial density field, which occupy less
prominent structures at later times due to the further development of gravitational
clustering. The bias has a mild scale dependence due to the schematic
procedure of grid-based density estimation and the specific probability
selection function.
The parameters 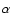 and
and
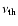 were chosen such that
the strong bias sample at redshift z=3 is consistent with the expected bias
of the target galaxies of HETDEX (Hill et al. 2004). The bias of this sample is very similar to the
friends-of-friends halo sample with a halo mass higher than
were chosen such that
the strong bias sample at redshift z=3 is consistent with the expected bias
of the target galaxies of HETDEX (Hill et al. 2004). The bias of this sample is very similar to the
friends-of-friends halo sample with a halo mass higher than
 4
4 
 obtained from the Mare Nostrum
simulation (Gottlöber et al. 2006). As observations of the target galaxies of
HETDEX, namely Lyman-
obtained from the Mare Nostrum
simulation (Gottlöber et al. 2006). As observations of the target galaxies of
HETDEX, namely Lyman-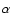 emitting galaxies (LAE), suggest
(Gawiser et al. 2007; Gronwall et al. 2007), this expected value for the bias might be too
optimistic. Therefore, we also use the weaker bias sample at z=3,
which matches the measured bias of LAE observed by the MUSYC
collaboration (Gawiser et al. 2007; Gronwall et al. 2007).
emitting galaxies (LAE), suggest
(Gawiser et al. 2007; Gronwall et al. 2007), this expected value for the bias might be too
optimistic. Therefore, we also use the weaker bias sample at z=3,
which matches the measured bias of LAE observed by the MUSYC
collaboration (Gawiser et al. 2007; Gronwall et al. 2007).
For z=1, we use the ``weaker'' bias sample, which is
fairly consistent with the expected bias of the target galaxies of WFMOS
(the KAOS Purple Book 2003; Bassett et al. 2005).
The bias of the strongly biased sample at z=1 is too high for these galaxies and we do not use this sample in the rest of the paper.
For the survey centered on z=3, we generate several mock catalogs of one million galaxies from the strongly and weakly biased light cones in redshift space using the entire
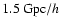 box, which has a volume of
box, which has a volume of
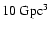 .
These numbers are at the upper limit of the current baseline of the HETDEX project.
.
These numbers are at the upper limit of the current baseline of the HETDEX project.
For the mock catalogs at z=1, we use only the galaxies on the light cone
around z=1 in redshift space with a bias of
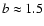 .
As a number
of tracers, we choose one and two million galaxies in the entire box.
.
As a number
of tracers, we choose one and two million galaxies in the entire box.
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{7688f02.ps}\end{figure}](/articles/aa/full/2008/31/aa7688-07/Timg91.gif) |
Figure 2:
Galaxy bias for the two different parameter sets at
redshift z=3 and z=1. To construct this plot, we used 15 million galaxies to reduce
the shot noise. |
| Open with DEXTER |
We analyze the mock catalogs first by calculating the power spectrum and then
by fitting the extracted BAO. In the following two subsections, we describe how
we calculate the power spectrum and provide details about the fitting procedure.
Since we use an FFT to complete the Fourier transformation, we first have to assign
the particles to a regular grid. We consider a 10243 regular grid and
select the CIC scheme to complete the mass assignment. After converting the density field
 to the density contrast
to the density contrast
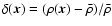 and
performing the FFT to evaluate the Fourier transform (FT)
and
performing the FFT to evaluate the Fourier transform (FT)
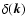 ,
we
compute the raw isotropic (one-dimensional) and anisotropic (two-dimensional)
power spectrum by averaging
,
we
compute the raw isotropic (one-dimensional) and anisotropic (two-dimensional)
power spectrum by averaging
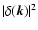 over spherical shells
over spherical shells
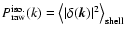 and rings
and rings
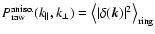 ,
respectively. These raw
power spectra are related to the true power spectrum in the following way (Jing 2005):
,
respectively. These raw
power spectra are related to the true power spectrum in the following way (Jing 2005):
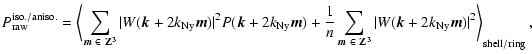 |
|
|
(8) |
where 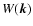 is the FT of the mass assignment function,
is the FT of the mass assignment function,
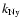 the
Nyquist frequency, and n the number density of tracers for the density
field. The first term in the equation above reflects the convolution of the
density field with the mass assignment function. The second term corresponds
to the shot noise. The summation over all integer vectors
the
Nyquist frequency, and n the number density of tracers for the density
field. The first term in the equation above reflects the convolution of the
density field with the mass assignment function. The second term corresponds
to the shot noise. The summation over all integer vectors 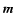 takes
care of the aliasing. In the case of the CIC scheme,
takes
care of the aliasing. In the case of the CIC scheme, 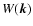 takes the
following form
takes the
following form
![\begin{displaymath}%
W({\vec k})=\left[ \prod_i {\frac{ \sin\left( \frac{\pi k_i...
...Ny}}
\right) }{ \frac{\pi k_i}{2k_{\rm Ny}} }}\right] ^2\cdot
\end{displaymath}](/articles/aa/full/2008/31/aa7688-07/img101.gif) |
(9) |
To derive a good estimate of the true power spectrum from its raw form,
we first subtract the shot noise and then follow an iterative method
for the correction of deconvolution and aliasing as proposed by Jing (2005).
We subtract only for the galaxy samples shot noise, since
we do not detect any shot noise for the dark matter densities.
We estimate the error in the power spectrum by counting the number of independent modes used in the calculation of
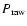 ,
which corresponds approximately to
,
which corresponds approximately to
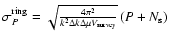 and
and
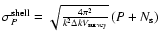 (Feldman et al. 1994)
for the anisotropic and isotropic power spectrum, respectively. Here,
(Feldman et al. 1994)
for the anisotropic and isotropic power spectrum, respectively. Here, 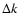 denotes the thickness of the rings and shells we averaged over.
For the anisotropic power spectrum, there is additionally the parameter
denotes the thickness of the rings and shells we averaged over.
For the anisotropic power spectrum, there is additionally the parameter
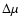 which is the range in the values of the cosine of the angle between the wave vector and the line
of sight. The shot noise is denoted by
which is the range in the values of the cosine of the angle between the wave vector and the line
of sight. The shot noise is denoted by 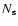 .
All the power
spectra in this paper have independent bins with a bin width of
.
All the power
spectra in this paper have independent bins with a bin width of
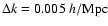 .
.
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{7688f03.ps}\end{figure}](/articles/aa/full/2008/31/aa7688-07/Timg110.gif) |
Figure 3:
Power spectrum of the dark matter distribution at z=3
(lower curves) and z=1 (upper curves). The dashed lines are the linearly
evolved initial power spectrum. In the case of redshift space,
the linear power spectrum was multiplied in addition by
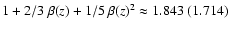 for z=3 (1).
for z=3 (1). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{7688f04.ps}\end{figure}](/articles/aa/full/2008/31/aa7688-07/Timg111.gif) |
Figure 4:
Fractional difference of the light-cone power spectrum
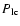 and the power spectrum at the corresponding snapshot
and the power spectrum at the corresponding snapshot
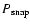 .
The horizontal lines show the predicted shifts from linear theory in real space (dashed) and redshift space (solid). .
The horizontal lines show the predicted shifts from linear theory in real space (dashed) and redshift space (solid). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{7688f05.ps}\end{figure}](/articles/aa/full/2008/31/aa7688-07/Timg112.gif) |
Figure 5:
Fractional difference of the galaxy light-cone power
spectrum
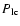 and the galaxy power spectrum at the corresponding snapshot
and the galaxy power spectrum at the corresponding snapshot
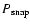 . . |
| Open with DEXTER |
In Fig. 3, we show the isotropic dark matter power spectra at
redshift z=3 and z=1 obtained by assuming the correct cosmology with
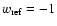 .
If not stated otherwise, we always use as the reference cosmology the cosmology of
the simulation, i.e. we assume that
.
If not stated otherwise, we always use as the reference cosmology the cosmology of
the simulation, i.e. we assume that
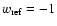 .
The linear redshift distortion
(Kaiser 1987) amplifies the power by
.
The linear redshift distortion
(Kaiser 1987) amplifies the power by
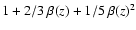 with
with
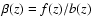 ,
where f(z) is the linear growth rate and b(z)
the bias parameter. In the case of dark matter we have b=1.
For scales shown, the nonlinear evolution is still mild. The
deviations in the real-space power spectra from the linearly evolved initial
power spectra (plotted as dashed lines) start around
,
where f(z) is the linear growth rate and b(z)
the bias parameter. In the case of dark matter we have b=1.
For scales shown, the nonlinear evolution is still mild. The
deviations in the real-space power spectra from the linearly evolved initial
power spectra (plotted as dashed lines) start around
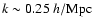 and
and
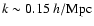 for z=3 and z=1, respectively. The
nonlinear redshift distortions (``finger of God'' effects) in redshift space
lead to a suppression of power on small scales, which almost balances
the increase in power due to nonlinear clustering at z=1 (filled squares in Fig. 3). The BAO can be seen as tiny wiggles in
the power spectrum. Their amplitudes are
for z=3 and z=1, respectively. The
nonlinear redshift distortions (``finger of God'' effects) in redshift space
lead to a suppression of power on small scales, which almost balances
the increase in power due to nonlinear clustering at z=1 (filled squares in Fig. 3). The BAO can be seen as tiny wiggles in
the power spectrum. Their amplitudes are 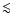
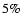 of P(k).
of P(k).
We do not show the light-cone power spectra, since they lie almost exactly
on the corresponding snapshot power spectra. The fractional differences in
the power spectra derived from the light cone and the corresponding snapshot
are instead plotted in Fig. 4. On linear scales, the fractional
differences are 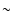
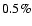 and
and 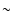
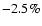 at z=3 and z=1, respectively.
The reason for these differences is that the value of the growth function at
the mean redshift is not equal to the mean growth function.
The stated numbers can be understood by averaging the square of the
redshift-dependent growth function multiplied by an appropriate geometrical
factor over the survey box (Yamamoto et al. 1999).
Numerical calculations for our survey designs are shown as dashed (real space)
and solid (redshift space) lines. The deviations at larger k are due
to nonlinear effects. The question of whether these light-cone effects alter
the fitting of the BAO is addressed in Sect. 5.
at z=3 and z=1, respectively.
The reason for these differences is that the value of the growth function at
the mean redshift is not equal to the mean growth function.
The stated numbers can be understood by averaging the square of the
redshift-dependent growth function multiplied by an appropriate geometrical
factor over the survey box (Yamamoto et al. 1999).
Numerical calculations for our survey designs are shown as dashed (real space)
and solid (redshift space) lines. The deviations at larger k are due
to nonlinear effects. The question of whether these light-cone effects alter
the fitting of the BAO is addressed in Sect. 5.
In Fig. 5, we compare the biased galaxy power spectra
derived from the light cones with those evaluated for the corresponding
snapshots. Qualitatively, we observe the same behavior as in the dark matter
case. The larger scatter is due to higher shot noise and the means are
shifted slightly, since, as happened before for the growth function, the bias at
the mean redshift is not equal to the bias averaged over the appropriate
redshift range.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.3cm,clip]{7688f06a.ps}\hsp...
...pace*{3mm}
\includegraphics[angle=-90,width=8.3cm,clip]{7688f06d.ps}\end{figure}](/articles/aa/full/2008/31/aa7688-07/Timg122.gif) |
Figure 6:
The left upper panel shows the oscillatory part of the
power spectrum at redshift z=3 obtained from real space and its best-fit
function including the suppression factor (dashed line). The dotted line
corresponds to the oscillatory part of the initial power spectrum. The solid
line is the best-fit of the reconstructed data.
At the bottom left, we present the same in redshift space. On the right the
corresponding plots for z=1 are shown. |
| Open with DEXTER |
Our fitting method attempts to remove all the information
apart from the BAO themselves. This is easily achieved by dividing the power
spectrum by a smoothed version of itself. The advantage of this is that one does
not need to model all the physical processes that alter the power spectrum
such as redshift distortion, nonlinear evolution, and galaxy bias or uncertainties
in cosmological parameters, such as 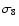 ,
,
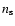 ,
and massive neutrinos,
which affect the overall shape of the power spectrum but have little effect
on the BAO.
,
and massive neutrinos,
which affect the overall shape of the power spectrum but have little effect
on the BAO.
The extracted BAO of the reference power spectra were then fitted to the
extracted BAO, allowing the scaling factors
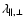 or
or
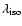 to vary.
In an additional fitting attempt, our free parameter is instead the EOS parameter w and we derive the scaling factors
to vary.
In an additional fitting attempt, our free parameter is instead the EOS parameter w and we derive the scaling factors
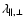 or
or
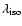 by applying Eq. (5).
by applying Eq. (5).
The fitting parameters are determined by Monte Carlo Markov
chain (MCMC) techniques. We use the Metropolis-Hastings algorithm
(Metropolis et al. 1953; Hastings 1970) to build up the Markov chain.
In the following, we describe each step of the fitting procedure.
There are previous proposals to use only the oscillatory part of the power
spectrum for measuring the scale of the BAO
(Glazebrook & Blake 2005; Hütsi 2006a; Koehler et al. 2007; Hütsi 2005; Angulo et al. 2008; Blake & Glazebrook 2003; Percival et al. 2007b).
All of them divide the power spectrum by (or subtract from it) a non-oscillating
fit. The methods used to derive the smooth fit range from deriving a semi-analytic
zero-baryon reference power spectrum, fitting with a quadratic polynomial
in log-log space, or using a cubic spline, to fitting with a non-oscillating
phenomenological function. In this paper, we generate a smoothed power spectrum in an
almost parameter-free way, by computing for each point the arithmetic mean
in log space of its neighbors in a range of 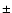
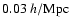 in k. In the
two-dimensional case, we smooth radially in the direction of |k|. This
smoothing length is the only parameter in our smoothing method, which, for all input power spectra, we select to have the same value of approximately equal to the wavelength of the BAO.
in k. In the
two-dimensional case, we smooth radially in the direction of |k|. This
smoothing length is the only parameter in our smoothing method, which, for all input power spectra, we select to have the same value of approximately equal to the wavelength of the BAO.
By dividing the measured power spectrum by its smoothed version, we derive the
purely oscillatory part of the power spectrum
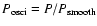 (see Fig. 6).
(see Fig. 6).
In place of fitting the extracted BAO by a (modified) sine function
(Glazebrook & Blake 2005; Blake & Glazebrook 2003) or using a periodogram (Hütsi 2005)
to measure the scale of the BAO, we compare the BAO with a range of different oscillatory reference
power spectra
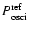 produced from thousands of linear
power spectra generated with CMBfast, which differ in the cosmological
parameters
produced from thousands of linear
power spectra generated with CMBfast, which differ in the cosmological
parameters
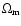 ,
,
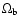 ,
,
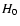 ,
and
,
and 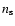 .
.
We prefer this method since the BAO are not exactly harmonic
(Koehler et al. 2007; Eisenstein & Hu 1998) and the uncertainties in the aforementioned
cosmological parameters can easily be included. As priors on these
cosmological parameters we use the predicted uncertainties for the
Planck mission (The Planck Bluebook 2005).
For the Hubble constant H0, we combine the Planck priors with constraints
provided by large-scale structure (Percival et al. 2007a) and include measurements from the HST Key project (Freedman et al. 2001):
| |
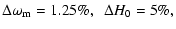 |
|
| |
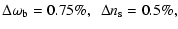 |
(10) |
where
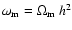 and
and
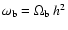 .
We assume throughout this article that the Universe is spatially flat.
.
We assume throughout this article that the Universe is spatially flat.
We determine the scaling factors
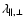 or
or
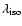 by fitting a scaled
by fitting a scaled
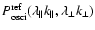 or
or
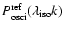 to
to
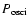 .
.
Since nonlinear structure growth diminishes the amplitudes of the wiggles
(Eisenstein et al. 2007b), we can improve the fitting by adding a suppression factor
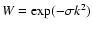 to our fitting function
to our fitting function
![\begin{displaymath}%
P_{\rm osci}(k)=W \left[P_{\rm osci}^{\rm ref}(\lambda_{\rm iso} k) - 1\right] +1.
\end{displaymath}](/articles/aa/full/2008/31/aa7688-07/img138.gif) |
(11) |
For the two-dimensional redshift-space power spectrum, we have to introduce
two suppression parameters
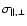 ,
since the redshift space
distortion increases suppression along the line of sight. The suppression
factor then becomes
,
since the redshift space
distortion increases suppression along the line of sight. The suppression
factor then becomes
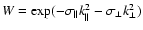 .
.
If the density field is known accurately, i.e. the shot noise is small and the
galaxy bias is known, it is possible to use reconstruction techniques
(see e.g. Narayanan & Croft 1999, for a comparison of methods) to undo, at least
in part, the suppression of the wiggles (Eisenstein et al. 2007a). We applied the PIZA
method (Croft & Gaztanaga 1997) to the dark matter distributions. We attempted a similar
technique for the mock catalogs but due to shot noise and galaxy
bias our results were unsatisfactory. Further efforts are required to achieve
this goal. In Fig. 6, we indicate the BAO extracted from the data by
crosses. The dashed lines show the best-fit functions and the dotted lines depict
the corresponding non-damped reference
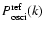 .
We observe that the suppression of the BAO is higher in redshift space and
increases with time. Additionally, the results of the reconstructed density
fields are plotted (data as filled circles and the best-fits as solid lines).
The amplitude of the BAO could not be reestablished completely but to a
significant fraction.
.
We observe that the suppression of the BAO is higher in redshift space and
increases with time. Additionally, the results of the reconstructed density
fields are plotted (data as filled circles and the best-fits as solid lines).
The amplitude of the BAO could not be reestablished completely but to a
significant fraction.
The k range over which we use the data for our fitting plays an important role.
In the fitting procedure we use a minimum wave number
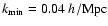 ,
since for the points with
,
since for the points with
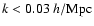 the smoothing
is not well defined, and the error due to sample variance is high. As the
maximum wave number, we select
the smoothing
is not well defined, and the error due to sample variance is high. As the
maximum wave number, we select
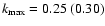 ,
for redshift z=1 (3).
Although nonlinear evolution has already started on these scales, the BAO
are still clearly visible (see Fig. 6).
,
for redshift z=1 (3).
Although nonlinear evolution has already started on these scales, the BAO
are still clearly visible (see Fig. 6).
5 Results
The most important measurements in our analysis are the marginalized probability
distribution functions (PDF) of the scaling factors and the EOS parameter w.
To determine their values, we marginalize the joint PDF produced via the MCMC
technique over all other fitting parameters. From these functions, we can derive
the best-fit values and the accuracy of both the scaling factors and the EOS w.
With the twelve 2563 simulations we assess the robustness of our fitting
method and the presence of systematic effects. We determine the best-fitting
scaling factors, both parallel and transverse to the line of sight, for the dark matter power
spectrum in real and redshift space for all twelve simulations at redshift
z=10, 3, and 1. For all redshifts, we find that the mean value
of the twelve simulations is clearly less than 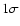 (standard deviation)
away from unity. Hence, our fitting method provides unbiased results within the
margins of error (see Table 1).
(standard deviation)
away from unity. Hence, our fitting method provides unbiased results within the
margins of error (see Table 1).
Table 1:
Results for the scaling factors
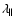 and
and
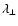 obtained from the dozen 2563 simulations.
obtained from the dozen 2563 simulations.
The differences between results for real and redshift space in each simulation
do not show a systematic trend. The mean difference is in fact consistent with zero. The
error in the scale factor parallel to the line of sight
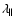 is
larger in redshift space, since the damping of the BAO is stronger in redshift
space (see Fig. 6).
is
larger in redshift space, since the damping of the BAO is stronger in redshift
space (see Fig. 6).
To understand the degeneracies in the scaling factor for the
cosmological parameters included in our method, we complete the fitting
by keeping all cosmological parameters fixed to the value of the simulation
apart from the parameter under consideration, for which we calculate
the PDF of
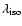 for different values of this parameter.
The corresponding
for different values of this parameter.
The corresponding 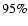 confidence lines for the dark matter power
spectrum at z=3 (solid) and at z=1 (dotted) are shown in
Fig. 7
confidence lines for the dark matter power
spectrum at z=3 (solid) and at z=1 (dotted) are shown in
Fig. 7![[*]](/icons/foot_motif.gif) .
Since the sound horizon imprinted in the power spectrum is redshift
independent, we expect that the derived degeneracies are also
redshift independent. This is indeed the case for our fitting method.
The only difference with respect to z is the larger uncertainty in
.
Since the sound horizon imprinted in the power spectrum is redshift
independent, we expect that the derived degeneracies are also
redshift independent. This is indeed the case for our fitting method.
The only difference with respect to z is the larger uncertainty in
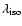 at lower redshifts due to the suppression of the
BAO by nonlinear evolution.
at lower redshifts due to the suppression of the
BAO by nonlinear evolution.
The interval of cosmological parameters plotted in Fig. 7
was chosen to be centered on the values of the simulation and in the range of
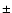
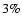 .
In this way, we can immediately assess the degree of degeneracy.
We find that if we alter one of the cosmological parameters by
.
In this way, we can immediately assess the degree of degeneracy.
We find that if we alter one of the cosmological parameters by 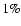 the scaling factor changes by
the scaling factor changes by 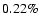 for
for
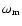 ,
,
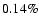 for
for
 ,
,
 for H0, and
for H0, and 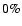 for
for 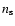 .
These numbers agree well with those given by the fitting
formula for the sound horizon by Eisenstein & Hu (1998):
.
These numbers agree well with those given by the fitting
formula for the sound horizon by Eisenstein & Hu (1998):
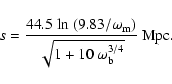 |
(12) |
![\begin{figure}
\par\hspace*{-0.2cm}\includegraphics[width=4.3cm,clip]{7688f07a.p...
...c.ps}\hspace*{0.5cm}
\includegraphics[width=4.2cm,clip]{7688f07d.ps}\end{figure}](/articles/aa/full/2008/31/aa7688-07/Timg155.gif) |
Figure 7:
Dependence of the fitted
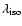 on the
cosmological parameters
on the
cosmological parameters
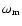 , ,
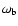 ,
H0, and ,
H0, and 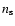 at redshift z=3 (solid) and z=1 (dotted).
at redshift z=3 (solid) and z=1 (dotted). |
| Open with DEXTER |
More interesting are the dependences of the equation of state w on the
cosmological parameters, in particular the dependence on
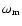 and H0,
which enter the relation between the scaling factors and w. For a constant w model (w=w0), we indicate the derived correlations in Fig. 8, where
the solid line corresponds to z=3 and the dotted line to z=1. In contrast
to the previous case, these correlations are redshift dependent, for example
at z=1 the dependence of both the sound horizon and the Hubble parameter H(z) on
and H0,
which enter the relation between the scaling factors and w. For a constant w model (w=w0), we indicate the derived correlations in Fig. 8, where
the solid line corresponds to z=3 and the dotted line to z=1. In contrast
to the previous case, these correlations are redshift dependent, for example
at z=1 the dependence of both the sound horizon and the Hubble parameter H(z) on
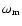 almost exactly cancel each other, whereas at z=3 the
effect originating in the Hubble parameter H(z) is stronger.
Among the cosmological parameters the largest uncertainty in w0 originates in
H0, in particular at lower redshifts.
almost exactly cancel each other, whereas at z=3 the
effect originating in the Hubble parameter H(z) is stronger.
Among the cosmological parameters the largest uncertainty in w0 originates in
H0, in particular at lower redshifts.
We have already mentioned that the power spectra derived from the light cone output
and corresponding snapshot at the mean redshift are almost
on top of each other. The more evolved parts of the light-cone sample
compensate almost precisely the less evolved parts, such that its power spectrum
is almost identical to that at the mean redshift (see Fig. 4).
In Fig. 9 we show the corresponding PDFs of the scaling factors. The lines show the 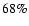 and
and 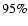 confidence levels obtained
from the dark matter snapshot (dashed) and light-cone (dotted) power spectra
at redshift z=3 (left) and z=1 (right) in real (top) and redshift space
(bottom). The differences in the error ellipses derived from the light-cone and snapshot
data are overall small. Hence, light-cone effects in this survey volume and at these redshifts are unimportant to our fitting.
confidence levels obtained
from the dark matter snapshot (dashed) and light-cone (dotted) power spectra
at redshift z=3 (left) and z=1 (right) in real (top) and redshift space
(bottom). The differences in the error ellipses derived from the light-cone and snapshot
data are overall small. Hence, light-cone effects in this survey volume and at these redshifts are unimportant to our fitting.
The error ellipses for the reconstructed samples are shown in
Fig. 9 as solid lines. We observe that for data at z=1 in
redshift space the reconstruction of the BAO shrinks the error ellipses by a
factor of three. For this reason, it would be desirable to develop a
reconstruction method that can be applied to noisy and biased density
fields. For surveys at redshift z=3, this effect is less important.
The errors in the scaling factors originate in two different sources. One source is
the errors in the power spectrum; the other source is the
uncertainties in the cosmological parameters
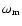 and
and
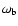 ,
which produce an uncertainty in the sound horizon, i.e. the scale of the BAO.
If the principal error could be attributed to the uncertainty in the physical
sound horizon, the orientation of the ellipse would be approximately in the
direction of the line defined by
,
which produce an uncertainty in the sound horizon, i.e. the scale of the BAO.
If the principal error could be attributed to the uncertainty in the physical
sound horizon, the orientation of the ellipse would be approximately in the
direction of the line defined by
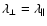 .
For a low signal-to-noise
ratio power spectrum for which the scale of the BAO in the power spectrum
cannot be determined accurately, the orientation of the error ellipse is
instead in the direction of the line of
.
For a low signal-to-noise
ratio power spectrum for which the scale of the BAO in the power spectrum
cannot be determined accurately, the orientation of the error ellipse is
instead in the direction of the line of
![$\sqrt[3]{\lambda_\bot^2\lambda_{\vert\vert}}={\rm const}$](/articles/aa/full/2008/31/aa7688-07/img158.gif) .
.
![\begin{figure}
\par\includegraphics[width=4.1cm,clip]{7688f09a.ps}\hspace*{0.5cm...
...c.ps}\hspace*{0.5cm}
\includegraphics[width=4.1cm,clip]{7688f09d.ps}\end{figure}](/articles/aa/full/2008/31/aa7688-07/Timg159.gif) |
Figure 9:
The marginalized probability distribution functions (PDF) of the scaling factors at redshifts z=3 ( left) and z=1 ( right) in real space ( top) and redshift space ( bottom) derived from the light cone (dotted), snapshot (dashed), and
``reconstructed'' light cone (solid). |
| Open with DEXTER |
We assess if the approximations to compensate for an incorrect reference
cosmology i.e. the scaling relations given in Eq. (4), are sufficiently
accurate for our simulated surveys. We calculate the distances
assuming three reference cosmologies that differ only in terms of
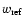 and compute the corresponding power spectra.
and compute the corresponding power spectra.
As an example, the oscillatory parts of the dark matter power spectra at z=3
in real space are shown in Fig. 10. We observe
that the scale of the oscillations is compressed and stretched for
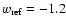 and
and
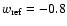 ,
respectively.
,
respectively.
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{7688f10.ps}\end{figure}](/articles/aa/full/2008/31/aa7688-07/Timg161.gif) |
Figure 10:
The oscillatory part of the real space power spectra at redshift z=3 derived for three
different cosmologies and its best-fit function. For display purposes, the
power spectrum for
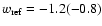 is shifted
+0.2(-0.2) along the
y-axis.
is shifted
+0.2(-0.2) along the
y-axis. |
| Open with DEXTER |
We scale the one-dimensional power spectra according to the scaling
relation, i.e.
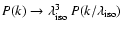 ,
where the factor
,
where the factor
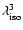 is due to the scaled volume element.
The fractional difference of these scaled power spectra with respect
to that of the correct cosmology, i.e. w=-1, is shown in Fig. 11.
The data points for w=-1.2 (squares) and w=-0.8 (plus signs) are shifted
by
is due to the scaled volume element.
The fractional difference of these scaled power spectra with respect
to that of the correct cosmology, i.e. w=-1, is shown in Fig. 11.
The data points for w=-1.2 (squares) and w=-0.8 (plus signs) are shifted
by 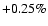 and
and 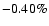 ,
respectively, to center them on the zero line.
These small shifts have a similar origin as in the light-cone versus snapshot
comparison; we calculate the scaling factor at the mean redshift, which is
not equal to the mean scaling factor. The noise in the scaled power
spectra is substantially smaller on large scales than the error, which is
already implicit in the power spectrum due to cosmic variance (dashed line)
and additional shot noise (solid line). To determine if this
(additional) noise impairs the fitting of the BAO and
with it the measurement of the equation of state w, we fit the corresponding data of the
twelve 2563 simulations by assuming a constant w. We find that the best-fit
value for w0 varies among the different reference cosmologies for a
single simulation by not more than
,
respectively, to center them on the zero line.
These small shifts have a similar origin as in the light-cone versus snapshot
comparison; we calculate the scaling factor at the mean redshift, which is
not equal to the mean scaling factor. The noise in the scaled power
spectra is substantially smaller on large scales than the error, which is
already implicit in the power spectrum due to cosmic variance (dashed line)
and additional shot noise (solid line). To determine if this
(additional) noise impairs the fitting of the BAO and
with it the measurement of the equation of state w, we fit the corresponding data of the
twelve 2563 simulations by assuming a constant w. We find that the best-fit
value for w0 varies among the different reference cosmologies for a
single simulation by not more than 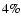 ,
and is typically
,
and is typically 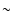
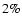 .
This
should be compared with the standard deviation for a single w0 measurement,
which is about
.
This
should be compared with the standard deviation for a single w0 measurement,
which is about 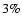 .
All PDFs scatter about the mean value of
w0=-1, no systematic effects are noticeable. We conclude that the scaling
relations do not introduce a noticeable bias or enlarge the error in w.
For real data, a consistency check would be
to recalculate the distances and corresponding power spectrum and
redo the analysis using the measured w as the reference
value for the assumed cosmology.
.
All PDFs scatter about the mean value of
w0=-1, no systematic effects are noticeable. We conclude that the scaling
relations do not introduce a noticeable bias or enlarge the error in w.
For real data, a consistency check would be
to recalculate the distances and corresponding power spectrum and
redo the analysis using the measured w as the reference
value for the assumed cosmology.
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{7688f11.ps}\end{figure}](/articles/aa/full/2008/31/aa7688-07/Timg168.gif) |
Figure 11:
The fractional difference of the scaled real-space
power spectra at redshift z=3 is shown for the three different reference
cosmologies. Note that the data points for w=-1.2 and w=-0.8 are shifted
vertically by +0.0025 and -0.0040, respectively, to enhance the visibility
of the scatter. The lines show the intrinsic error in the power
spectrum due to cosmic variance (dashed line) plus shot noise (solid line). |
| Open with DEXTER |
The two-dimensional power spectrum provides the possibility to measure
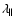 and
and
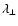 ,
instead of the combination
,
instead of the combination
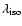 only, as in the case of the one-dimensional power spectrum.
Since both scaling factors depend on w in different ways, we expect that wis more accurately constrained by the two-dimensional
power spectrum. In the case of a simple constant w, this is not the case:
both the mean values and the errors are similar to those derived from the
one-dimensional power spectra. For more complex models of w, the measurement of
only, as in the case of the one-dimensional power spectrum.
Since both scaling factors depend on w in different ways, we expect that wis more accurately constrained by the two-dimensional
power spectrum. In the case of a simple constant w, this is not the case:
both the mean values and the errors are similar to those derived from the
one-dimensional power spectra. For more complex models of w, the measurement of
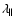 and
and
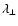 is very helpful as we see from
Fig. 12, where we applied the model
w=w0+(1-a) wa.
For display purposes, we performed a coordinate transformation of the
parameters to the ``pivot'' system
is very helpful as we see from
Fig. 12, where we applied the model
w=w0+(1-a) wa.
For display purposes, we performed a coordinate transformation of the
parameters to the ``pivot'' system
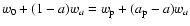 where we chose
where we chose
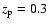 as discussed below.
The left (right) panel indicates the constraints obtained from the dark
matter light-cone power spectrum around z=3 (z=1) in real space. One sees
that for z=3 the contour lines are open towards negative wa even for the
two-dimensional case. Nevertheless, in both redshift cases the use of the
anisotropic power spectrum tightens the constraints substantially.
as discussed below.
The left (right) panel indicates the constraints obtained from the dark
matter light-cone power spectrum around z=3 (z=1) in real space. One sees
that for z=3 the contour lines are open towards negative wa even for the
two-dimensional case. Nevertheless, in both redshift cases the use of the
anisotropic power spectrum tightens the constraints substantially.
For a prediction of how well upcoming observations will enable w to be measured,
we analyze the mock galaxy catalogs introduced above, namely the weakly and
strongly biased one million galaxy catalogs at redshift z=3 and the one and
two million galaxy catalogs at z=1. In Fig. 13, we present
typical fitting results of the scaling factors for each type of
catalogs. For the solid lines, we used the aforementioned priors on the
cosmological parameters, whereas for the dashed lines we fixed these parameters.
![\begin{figure}
\par\includegraphics[width=4cm,clip]{7688f12a.ps}\hspace*{0.8cm}
\includegraphics[width=4cm,clip]{7688f12b.ps}\end{figure}](/articles/aa/full/2008/31/aa7688-07/Timg170.gif) |
Figure 12:
This plot shows the 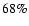 and
and 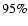 confidence levels
for the redshift-dependent w model obtained from the one-dimensional
(dashed lines) and two-dimensional (solid lines) dark matter power spectrum
at redshift z=3 ( left) and z=1 ( right) in real space.
confidence levels
for the redshift-dependent w model obtained from the one-dimensional
(dashed lines) and two-dimensional (solid lines) dark matter power spectrum
at redshift z=3 ( left) and z=1 ( right) in real space. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=4cm,clip]{7688f13a.ps}\hspace*{0.4cm}
...
...13c.ps}\hspace*{0.4cm}
\includegraphics[width=4cm,clip]{7688f13d.ps}\end{figure}](/articles/aa/full/2008/31/aa7688-07/Timg171.gif) |
Figure 13:
Typical contour plots of the joint PDF of
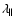 and
and
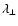 obtained from the mock catalogs at redshift z=3 ( left: weak ( top) and strong ( bottom) bias) and z=1 ( right: 1 million ( top) and 2 million ( bottom) galaxies) are shown. The contour lines correspond to 68% and 95% confidence level. The dashed
line shows the results when the cosmological parameters are fixed at the values of the simulation.
obtained from the mock catalogs at redshift z=3 ( left: weak ( top) and strong ( bottom) bias) and z=1 ( right: 1 million ( top) and 2 million ( bottom) galaxies) are shown. The contour lines correspond to 68% and 95% confidence level. The dashed
line shows the results when the cosmological parameters are fixed at the values of the simulation. |
| Open with DEXTER |
Since the error in the scaling factors is dominated by the errors in the power
spectrum, improving the accuracy of the cosmological parameters to higher than
that of the assumed priors does not significantly reduce the error in the scaling
factors. However, it tightens the constraints on w (see Fig. 14 for
constant w): the uncertainty in H0, in particular, degrades the measurement of w.
For the strongly biased sample at z=3 of one million galaxies in
a volume of
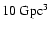 ,
the mean
,
the mean![[*]](/icons/foot_motif.gif) uncertainties in the Hubble
parameter (
uncertainties in the Hubble
parameter (
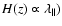 and angular diameter
distance (
and angular diameter
distance (
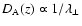 )
are
)
are 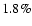 and
and
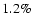 (
(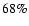 c.l.), respectively. This corresponds to an error of
c.l.), respectively. This corresponds to an error of 
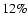 for a constant w. By keeping the cosmological parameters fixed, the
uncertainty in w is lowered to
for a constant w. By keeping the cosmological parameters fixed, the
uncertainty in w is lowered to 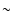
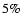 .
.
The corresponding numbers for the two million galaxy mock catalog at z=1
are 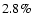 and
and 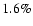 for the Hubble parameter and angular diameter
distance, respectively. In this case, we derive an accuracy of
for the Hubble parameter and angular diameter
distance, respectively. In this case, we derive an accuracy of 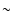
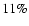 and
and 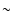
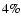 for a constant w with Planck priors and fixed cosmology, respectively.
for a constant w with Planck priors and fixed cosmology, respectively.
![\begin{figure}
\par\includegraphics[angle=-90,width=4.3cm,clip]{7688f14a.ps}\hspace*{0.2cm}
\includegraphics[angle=-90,width=4.3cm,clip]{7688f14b.ps}\end{figure}](/articles/aa/full/2008/31/aa7688-07/Timg178.gif) |
Figure 14:
PDFs for constant w derived from the one million
strongly biased galaxy sample at z=3 ( left) and from the two million
galaxy at z=1 ( right). |
| Open with DEXTER |
To translate the results for the scaling factors into constraints
of the redshift-dependent w-model
w=w0+(1-a)wa, we combine the data
of the strongly biased one million galaxy catalog at z=3 and two
million galaxy catalog at z=1 with 192 SN Ia observations
(Astier et al. 2006; Wood-Vasey et al. 2007; Davis et al. 2007; Riess et al. 2007). In addition we include constraints from
CMB measurements by holding the ratio of the distance to the last
scattering surface and the sound horizon fixed:
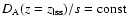 .
.
The confidence contours for w0 and wa are shown in the upper panels of Fig. 15. In the lower panels, the confidence contours are presented in the pivot variable
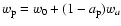 ,
where we choose
,
where we choose 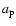 such that the error ``ellipse'' from the combined datasets (solid line) is least tilted; we find
such that the error ``ellipse'' from the combined datasets (solid line) is least tilted; we find
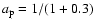 .
One sees that the intersection angle
of the BAO contours with respect to the error ellipse derived from SN data
varies with redshift (see also Fig. 16).
For z=3, the orientation is very similar to the CMB contours,
whereas for z=1, it is more aligned with the SN ellipse. Measurements at both
redshifts would therefore constrain the parameters of this model significantly
more than two (or twice a good) measurements at a single redshift.
.
One sees that the intersection angle
of the BAO contours with respect to the error ellipse derived from SN data
varies with redshift (see also Fig. 16).
For z=3, the orientation is very similar to the CMB contours,
whereas for z=1, it is more aligned with the SN ellipse. Measurements at both
redshifts would therefore constrain the parameters of this model significantly
more than two (or twice a good) measurements at a single redshift.
![\begin{figure}
\par\includegraphics[width=4.1cm,clip]{7688f15a.ps}\hspace*{0.7cm...
...15c.ps}\hspace*{0.8cm}
\includegraphics[width=4cm,clip]{7688f15d.ps}\end{figure}](/articles/aa/full/2008/31/aa7688-07/Timg183.gif) |
Figure 15:
The 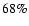 and
and 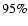 confidence level for the
parameters of the model
w=w0+(1-a) wa obtained from SN (dotted), SN+CMB
(dashed), and SN+CMB+BAO (solid). Results for the strongly biased one
million galaxy sample are shown at z=3 ( left) and for the weakly biased
two million galaxy sample at z=1 ( right). At the bottom, we show the same results but transformed to the pivot system
confidence level for the
parameters of the model
w=w0+(1-a) wa obtained from SN (dotted), SN+CMB
(dashed), and SN+CMB+BAO (solid). Results for the strongly biased one
million galaxy sample are shown at z=3 ( left) and for the weakly biased
two million galaxy sample at z=1 ( right). At the bottom, we show the same results but transformed to the pivot system
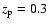 . . |
| Open with DEXTER |
In Fig. 16, we show the constraints on w derived alone from BAO measurements at two different redshifts, namely z=1 (dashed lines) and z=3 (dotted lines), and the combination of both measurements (solid lines). The redshift-dependent shape and orientation of the contour lines is clearly evident in the pivot system (right panel).
For all confidence contours in Figs. 15 and 16, the above stated priors for the cosmological parameters
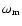 ,
,
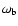 ,
,
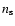 ,
and H0 were used.
,
and H0 were used.
![\begin{figure}
\par\includegraphics[width=4.15cm,clip]{7688f16a.ps}\hspace*{0.6cm}
\includegraphics[width=4cm,clip]{7688f16b.ps}\end{figure}](/articles/aa/full/2008/31/aa7688-07/Timg184.gif) |
Figure 16:
The 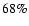 and
and 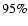 confidence level for the parameters of the model
w=w0+(1-a) wa obtained from the BAO measurements in the strongly biased one million galaxy sample at z=3 (dotted) and in the weakly biased two million galaxy sample at z=1 (dashed). The solid lines show the combination of both BAO measurements. On the right, the contours are transformed to the pivot system of the combined dataset
confidence level for the parameters of the model
w=w0+(1-a) wa obtained from the BAO measurements in the strongly biased one million galaxy sample at z=3 (dotted) and in the weakly biased two million galaxy sample at z=1 (dashed). The solid lines show the combination of both BAO measurements. On the right, the contours are transformed to the pivot system of the combined dataset
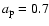 . . |
| Open with DEXTER |
We have simulated large redshift surveys by ``observing'' mock galaxies on a light
cone obtained from an N-body simulation with 5123 dark matter
particles in a
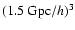 box. By fitting the apparent
scale of the BAO in the power spectrum, we have derived constraints on the
EOS parameter w.
box. By fitting the apparent
scale of the BAO in the power spectrum, we have derived constraints on the
EOS parameter w.
Our fitting method uses only the oscillatory part of the power spectrum and is
therefore insensitive to changes in the power spectrum due to nonlinear
evolution, redshift distortions, and scale-dependent galaxy bias. Fitting
methods that use the overall shape of the power spectrum suffer in general
from these complicated physical effects (unless they are accurately
modeled) and tend to provide biased results (Smith et al. 2007).
The drawback of fitting only the oscillatory part is that it is insensitive to
information provided by the overall shape of the power
spectrum. Determining the growth function would be
interesting in particular for dark energy constraints (Sapone & Amendola 2007; Amendola et al. 2005).
It is unclear how to extract the BAO from the power spectrum in the most
appropriate and accurate way. Our simple smoothing method works fairly well. It is essentially
parameter-free and produces unbiased and robust results.
We analyzed the degeneracies in the EOS w with other cosmological
parameters. Given the expected accuracies in the cosmological parameters involved,
we found that more accurate measurements of H0 would have the largest effect on lowering the
uncertainties in w, especially for observations at lower redshifts.
Comparing the results of the light-cone power spectrum with
those of the power spectrum of the snapshot at the corresponding
redshift, we did not find evidence for substantial differences. For the surveys under consideration, light cone effects therefore do not play a role in determining w with our fitting method.
This is in addition true, when we include redshift-dependent galaxy
bias. Fitting methods, sensitive to the overall shape of the power spectrum,
in particular to the growth function, must include explicitly the light-cone effects to produce unbiased results.
The PIZA technique (Croft & Gaztanaga 1997), which is used to reconstruct the linear
density field and thereby the amplitude of the BAO, is effective if the density field is
known to sufficient accuracy. In the case of substantial shot noise and
unknown galaxy bias, more sophisticated reconstruction techniques are required.
To investigate the cosmological distortion due to an incorrect reference
cosmology, we adopted three different reference cosmologies with different values for
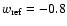 ,
-1.0, and -1.2. Employing the usual scaling relations
(see Eq. (5)), we found in all three cases similar fitting
results within the margins of error. We conclude that even for this large survey
volume the simple scaling of the power spectrum is fairly accurate.
Nevertheless, for real data we propose to use an iterative scheme;
after measuring w for an assumed reference cosmology, one would then repeat
the analysis for the updated reference cosmology, using the measured value of w for
,
-1.0, and -1.2. Employing the usual scaling relations
(see Eq. (5)), we found in all three cases similar fitting
results within the margins of error. We conclude that even for this large survey
volume the simple scaling of the power spectrum is fairly accurate.
Nevertheless, for real data we propose to use an iterative scheme;
after measuring w for an assumed reference cosmology, one would then repeat
the analysis for the updated reference cosmology, using the measured value of w for
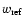 .
.
By fitting the two-dimensional power spectrum, we can determine independently both scaling factors. For a constant w, the two-dimensional fitting does not improve the constraints on w significantly. For models of w that are not so tightly constrained, independent measurements of the Hubble parameter (
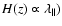 and the angular diameter
distance (
and the angular diameter
distance (
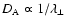 )
will however be very helpful. For the model
w=w0+(1-a)wa, this is especially true at lower redshifts.
)
will however be very helpful. For the model
w=w0+(1-a)wa, this is especially true at lower redshifts.
Our estimates for future surveys show that BAO measurements around redshifts
z=3 and z=1 in combination with SN and CMB data tighten the constraints on
dynamical dark energy substantially and that these redshift surveys deliver
complementary results. For a constant w-model the BAO measurements from our
two mock catalogs at z=3 and z=1 alone will constrain w0 to an accuracy of 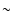
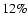 and
and 
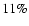 ,
respectively.
,
respectively.
To achieve more realistic predictions, the survey geometry, i.e. the
window function, has to be taken into account. A more realistic galaxy
bias scheme, tailored in particular for the target galaxies, should also be
developed. For such a study, large-volume simulations of far higher mass resolution are needed.
Acknowledgements
We are grateful to Jochen Weller for advice concerning the Monte Carlo Markov
chain sampling method and dark energy models. We thank Karl Gebhardt and
Eiichiro Komatsu for helpful discussion and useful comments on the draft.
We acknowledge useful and constructive remarks by the anonymous referee.
- Albrecht, A.,
Bernstein, G., Cahn, R., et al. 2006
[arXiv:astro-ph/0609591]
(In the text)
- Amendola, L.,
Quercellini, C., & Giallongo, E. 2005, MNRAS, 357, 429 [NASA ADS] [CrossRef]
- Angulo, R., Baugh,
C. M., Frenk, C. S., et al. 2005, MNRAS, 362,
L25 [NASA ADS] [CrossRef]
- Angulo,
R. E., Baugh, C. M., Frenk, C. S., & Lacey,
C. G. 2008, MNRAS, 383, 755 [NASA ADS]
- Astier, P., Guy, J.,
Regnault, N., et al. 2006, A&A, 447, 31 [NASA ADS] [CrossRef] [EDP Sciences]
- Bassett, B. A.,
Nichol, B., & Eisenstein, D. J. 2005, Astron. Geophys.,
46, 26 [CrossRef]
- Blake, C.,
& Glazebrook, K. 2003, ApJ, 594, 665 [NASA ADS] [CrossRef]
-
Blake, C., Parkinson, D., Bassett, B., et al. 2006, MNRAS,
365, 255 [NASA ADS] [CrossRef]
- Bond, J. R., &
Efstathiou, G. 1984, ApJ, 285, L45 [NASA ADS] [CrossRef]
- Carroll, S. M. 2001,
Living Reviews in Relativity, 4, 1 [NASA ADS]
(In the text)
- Cole, S., Hatton, S.,
Weinberg, D. H., & Frenk, C. S. 1998, MNRAS, 300,
945C [NASA ADS] [CrossRef]
- Cole, S., Percival,
W. J., Peacock, J. A., et al. 2005, MNRAS, 362,
505 [NASA ADS] [CrossRef]
- Croft, R. A. C.,
& Gaztanaga, E. 1997, MNRAS, 285, 793 [NASA ADS]
(In the text)
- Davis, T. M.,
Mörtsell, E., Sollerman, J., et al. 2007, ApJ, 666,
716 [NASA ADS] [CrossRef]
- Eisenstein, D. J.,
& Hu, W. 1998, ApJ, 496, 605 [NASA ADS] [CrossRef]
- Eisenstein,
D. J., Hu, W., & Tegmark, M. 1998, ApJ, 504, L57 [NASA ADS] [CrossRef]
- Eisenstein,
D. J., Hu, W., & Tegmark, M. 1999, ApJ, 518, 2 [NASA ADS] [CrossRef]
- Eisenstein, D. J.,
Zehavi, I., Hogg, D. W., et al. 2005, ApJ, 633, 560 [NASA ADS] [CrossRef]
-
Eisenstein, D. J., Seo, H.-J., Sirko, E., & Spergel,
D. N. 2007a, ApJ, 664, 675 [NASA ADS] [CrossRef]
(In the text)
- Eisenstein,
D. J., Seo, H.-J., & White, M. 2007b, ApJ, 664, 660 [NASA ADS] [CrossRef]
- Evrard,
A. E., MacFarland, T. J., Couchman, H. M. P.,
et al. 2002, ApJ, 573, 7 [NASA ADS] [CrossRef]
(In the text)
- Feldman, H. A.,
Kaiser, N., & Peacock, J. A. 1994, ApJ, 426, 23 [NASA ADS] [CrossRef]
(In the text)
- Freedman, W. L., Madore,
B. F., Gibson, B. K., et al. 2001, ApJ, 553, 47 [NASA ADS] [CrossRef]
(In the text)
- Gawiser, E., Francke,
H., Lai, K., et al. 2007, ApJ, 671, 278 [NASA ADS] [CrossRef]
- Glazebrook, K., &
Blake, C. 2005, ApJ, 631, 1 [NASA ADS] [CrossRef]
-
Glazebrook, K., Eisenstein, D., Dey, A., Nichol, B., & The
WFMOS Feasibility Study Dark Energy Team 2005
[arXiv:astro-ph/0507457]
-
Gottlöber, S., Yepes, G., Wagner, C., & Sevilla, R. 2006,
in From Dark Halo to Light, ed. S. Maurogordato, J. Tran
Thanh Van, & L. Tresse, Proc. XLI Moriond (Gioi
publishers), 309
- Gronwall, C.,
Ciardullo, R., Hickey, T., et al. 2007, ApJ, 667, 79 [NASA ADS] [CrossRef]
- Hastings, W. 1970,
Biometrika, 57, 97 [CrossRef]
- Hill, G. J.,
Gebhardt, K., Komatsu, E., & MacQueen, P. J. 2004, AIP
Conf. Proc., 743, 224 [NASA ADS]
(In the text)
- Hockney, R. W.,
& Eastwood, J. W. 1988, Computer simulation using
particles (Bristol: Hilger)
(In the text)
- Holtzman,
J. A. 1989, ApJS, 71, 1 [NASA ADS] [CrossRef]
- Hu, W., & Haiman, Z.
2003, Phys. Rev. D, 68, 063004 [NASA ADS] [CrossRef]
- Hu, W., &
Sugiyama, N. 1996, ApJ, 471, 542 [NASA ADS] [CrossRef]
- Huff, E., Schulz,
A. E., White, M., Schlegel, D. J., & Warren,
M. S. 2007, Astropart. Phys., 26, 351 [NASA ADS] [CrossRef]
-
Hütsi, G. 2005 [arXiv:astro-ph/0507678]
- Hütsi,
G. 2006a, A&A, 449, 891 [NASA ADS] [CrossRef] [EDP Sciences]
- Hütsi, G.
2006b, A&A, 446, 43 [NASA ADS] [CrossRef] [EDP Sciences]
-
Hütsi, G. 2006c, A&A, 459, 375 [NASA ADS] [CrossRef] [EDP Sciences]
- Jing, Y. P. 2005, ApJ,
620, 559 [NASA ADS] [CrossRef]
(In the text)
- Kaiser, N. 1987, MNRAS,
227, 1 [NASA ADS]
(In the text)
- Koehler, R. S.,
Schuecker, P., & Gebhardt, K. 2007, A&A, 462, 7 [NASA ADS] [CrossRef] [EDP Sciences]
- Linder, E. V.
2003, Phys. Rev. D, 68, 083504 [NASA ADS] [CrossRef]
- Linder, E. V.
2007 [arXiv:0708.0024]
(In the text)
- Matsubara, T.
2004, ApJ, 615, 573 [NASA ADS] [CrossRef]
- Metropolis, N.,
Rosenbluth, A., Rosenbluth, M., Teller, A., & Teller, E. 1953,
J. Chem. Phys., 21, 1087 [NASA ADS] [CrossRef]
- Narayanan,
V. K., & Croft, R. A. C. 1999, ApJ, 515,
471 [NASA ADS] [CrossRef]
(In the text)
- Peebles,
P. J. E., & Yu, J. T. 1970, ApJ, 162, 815 [NASA ADS] [CrossRef]
- Percival,
W. J., Cole, S., Eisenstein, D. J., et al. 2007a,
MNRAS, 381, 1053 [NASA ADS] [CrossRef]
(In the text)
- Percival,
W. J., Nichol, R. C., Eisenstein, D. J., et al.
2007b, ApJ, 657, 51 [NASA ADS] [CrossRef]
- Perlmutter, S.,
Aldering, G., Goldhaber, G., et al. 1999, ApJ, 517, 565 [NASA ADS] [CrossRef]
- Riess, A. G.,
Filippenko, A. V., Challis, P., et al. 1998, AJ, 116,
1009 [NASA ADS] [CrossRef]
- Riess,
A. G., Strolger, L.-G., Casertano, S., et al. 2007, ApJ,
659, 98 [NASA ADS] [CrossRef]
- Sapone, D., &
Amendola, L. 2007 [arXiv:0709.2792]
- SDSS-III Collaboration
2008, http://www.sdss3.org/cosmology.php
(In the text)
- Seljak, U., &
Zaldarriaga, M. 1996, ApJ, 469, 437 [NASA ADS] [CrossRef]
(In the text)
- Seo, H.-J., &
Eisenstein, D. J. 2003, ApJ, 598, 720 [NASA ADS] [CrossRef]
- Seo, H.-J., &
Eisenstein, D. J. 2005, ApJ, 633, 575 [NASA ADS] [CrossRef]
- Seo, H.-J., &
Eisenstein, D. J. 2007, ApJ, 665, 14 [NASA ADS] [CrossRef]
- Sirko, E. 2005, ApJ, 634,
728 [NASA ADS] [CrossRef]
(In the text)
- Smith, R. E.,
Scoccimarro, R., & Sheth, R. K. 2007
[arXiv:astro-ph/0703620]
(In the text)
- Spergel, D. N.,
Verde, L., Peiris, H. V., et al. 2003, ApJS, 148,
175 [NASA ADS] [CrossRef]
- Spergel, D. N.,
Bean, R., Doré, O., et al. 2007, ApJS, 170, 377 [NASA ADS] [CrossRef]
- Springel, V. 2005,
MNRAS, 364, 1105 [NASA ADS] [CrossRef]
(In the text)
- Springel, V.,
White, S. D. M., Jenkins, A., et al. 2005, Nature,
435, 629 [NASA ADS] [CrossRef]
- Sunyaev, R. A.,
& Zeldovich, Y. B. 1970, Ap&SS, 7, 3 [NASA ADS]
- The KAOS Purple
Book 2003, http://www.noao.edu/kaos/KAOS_Final.pdf
- The Planck Bluebook
2005, http://www.rssd.esa.int/SA/PLANCK/docs/Bluebook-ESA-SCI
(In the text)
- White, M. 2005,
Astropart. Phys., 24, 334 [NASA ADS] [CrossRef]
- Wood-Vasey, W. M.,
Miknaitis, G., Stubbs, C. W., et al. 2007, ApJ, 666,
694 [NASA ADS] [CrossRef]
- Yamamoto, K., Nishioka,
H., & Suto, Y. 1999, ApJ, 527, 488 [NASA ADS] [CrossRef]
(In the text)
- Yoshida, N., Colberg,
J., White, S. D. M., et al. 2001, MNRAS, 325, 803 [NASA ADS] [CrossRef]
Copyright ESO 2008
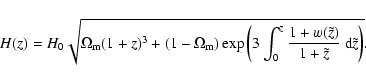
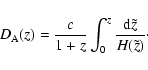
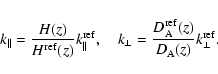
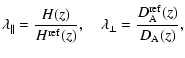
![\begin{figure}
\par\includegraphics[angle=-90,width=4.4cm,clip]{7688f01a.ps}\inc...
...688f01e.ps}\includegraphics[angle=-90,width=4.4cm,clip]{7688f01f.ps}\end{figure}](/articles/aa/full/2008/31/aa7688-07/Timg42.gif)
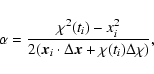
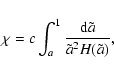
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{7688f02.ps}\end{figure}](/articles/aa/full/2008/31/aa7688-07/Timg91.gif)
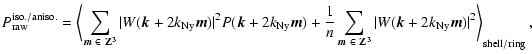
![\begin{displaymath}%
W({\vec k})=\left[ \prod_i {\frac{ \sin\left( \frac{\pi k_i...
...Ny}}
\right) }{ \frac{\pi k_i}{2k_{\rm Ny}} }}\right] ^2\cdot
\end{displaymath}](/articles/aa/full/2008/31/aa7688-07/img101.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{7688f03.ps}\end{figure}](/articles/aa/full/2008/31/aa7688-07/Timg110.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{7688f04.ps}\end{figure}](/articles/aa/full/2008/31/aa7688-07/Timg111.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{7688f05.ps}\end{figure}](/articles/aa/full/2008/31/aa7688-07/Timg112.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=8.3cm,clip]{7688f06a.ps}\hsp...
...pace*{3mm}
\includegraphics[angle=-90,width=8.3cm,clip]{7688f06d.ps}\end{figure}](/articles/aa/full/2008/31/aa7688-07/Timg122.gif)
![\begin{displaymath}%
P_{\rm osci}(k)=W \left[P_{\rm osci}^{\rm ref}(\lambda_{\rm iso} k) - 1\right] +1.
\end{displaymath}](/articles/aa/full/2008/31/aa7688-07/img138.gif)
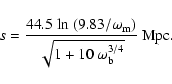
![\begin{figure}
\par\hspace*{-0.2cm}\includegraphics[width=4.3cm,clip]{7688f07a.p...
...c.ps}\hspace*{0.5cm}
\includegraphics[width=4.2cm,clip]{7688f07d.ps}\end{figure}](/articles/aa/full/2008/31/aa7688-07/Timg155.gif)
![\begin{figure}
\par\hspace*{-0.2cm}\includegraphics[width=4.3cm,clip]{7688f08a.p...
...c.ps}\hspace*{0.4cm}
\includegraphics[width=4.2cm,clip]{7688f08d.ps}\end{figure}](/articles/aa/full/2008/31/aa7688-07/Timg156.gif)
![\begin{figure}
\par\includegraphics[width=4.1cm,clip]{7688f09a.ps}\hspace*{0.5cm...
...c.ps}\hspace*{0.5cm}
\includegraphics[width=4.1cm,clip]{7688f09d.ps}\end{figure}](/articles/aa/full/2008/31/aa7688-07/Timg159.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{7688f10.ps}\end{figure}](/articles/aa/full/2008/31/aa7688-07/Timg161.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{7688f11.ps}\end{figure}](/articles/aa/full/2008/31/aa7688-07/Timg168.gif)
![\begin{figure}
\par\includegraphics[width=4cm,clip]{7688f13a.ps}\hspace*{0.4cm}
...
...13c.ps}\hspace*{0.4cm}
\includegraphics[width=4cm,clip]{7688f13d.ps}\end{figure}](/articles/aa/full/2008/31/aa7688-07/Timg171.gif)
![\begin{figure}
\par\includegraphics[width=4.1cm,clip]{7688f15a.ps}\hspace*{0.7cm...
...15c.ps}\hspace*{0.8cm}
\includegraphics[width=4cm,clip]{7688f15d.ps}\end{figure}](/articles/aa/full/2008/31/aa7688-07/Timg183.gif)