P. Hennebelle¹ - R. Banerjee² - E. Vázquez-Semadeni³ - R. S. Klessen² - E. Audit⁴

1 - Laboratoire de radioastronomie, UMR 8112 du CNRS, École normale supérieure et Observatoire de Paris, 24 rue Lhomond, 75231 Paris Cedex 05, France
2 - Zentrum für Astronomie der Universitat Heidelberg, Institut für Theoretische Astrophysik, 69120 Heidelberg, Germany
3 - Centro de Radioastronomía y Astrofísica, Universidad Autónoma de México, Apdo Postal 3-72 Morelia, 58089, México
4 - Service d'Astrophysique, CEA/DSM/DAPNIA/SAp, Centre d'Études de Saclay, l'Orme les Merisiers, 91191 Gif-sur Yvette Cedex, France

Abstract
Context. It has been proposed that giant molecular complexes form at the sites of streams of diffuse warm atomic gas that collide at transonic velocities.
Aims. We study the global statistics of molecular clouds formed by large scale colliding flows of warm neutral atomic interstellar gas under pure hydrodynamic and ideal MHD conditions. The flows deliver material as well as kinetic energy and trigger thermal instability leading eventually to gravitational collapse.
Methods. We perform adaptive mesh refinement MHD simulations that, for the first time in this context, treat cooling and self-gravity self-consistently.
Results. The clouds formed in the simulations develop a highly inhomogeneous density and temperature structure, with cold dense filaments and clumps condensing from converging flows of warm atomic gas. 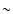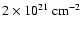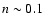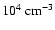In the clouds, the column density probability density distribution (PDF) peaks at $\sim$ $2 \times 10^{21} {\rm ~cm}^{-2}$ and decays rapidly at higher values; the magnetic intensity correlates weakly with density between $n \sim 0.1$ and $10^4 {\rm ~cm}^{-3}$ , and then varies roughly as n^1/2 for higher densities.
Conclusions. The global statistical properties of such molecular clouds are reasonably consistent with observational measurements. Our numerical simulations suggest that molecular clouds form by the moderately supersonic collision of warm atomic gas streams.

Key words: magnetohydrodynamics (MHD) - instabilities - ISM: kinematics and dynamics - ISM: structure - ISM: clouds

1 Introduction

Recently, large multi-dimensional non-magnetic numerical simulations have been performed (Hennebelle & Audit 2007; Vázquez-Semadeni et al. 2007; Heitsch et al. 2008, the last two including self-gravity) to study in detail the formation of dense gas from a large flow of warm neutral medium, resolving structure down to the star forming scales.

$\begin{figure} \par\includegraphics[width=17.5cm,clip]{0165fig1.eps} \end{figure}$

Figure 1: Left column shows the column density PDF for the hydrodynamical simulation ( top panel) and the MHD one ( bottom panel). The solid, dotted, dashed, and dash-dotted lines show the distributions at times t=3.5, 7.7, 9.8 and 11.5 Myr (hydro case) and t=3.5, 7.35, 11.41 and 13.11 Myr (MHD case). Middle column shows the density PDF for the hydrodynamical case ( top panel) and the MHD one ( bottom panel). Right column shows the temperature in the MHD simulation and the magnetic intensity as a function of gas density. In the top panel, the straight line, shows a distribution proportional to n^1/2.

Open with DEXTER

We present the first results of large adaptive mesh refinement (AMR) MHD simulations completed using the codes RAMSES (Teyssier 2002; Fromang et al. 2006) and FLASH (Fryxell et al. 2000). These are the first simulations that, starting from the WNM, include magnetic field, cooling, self-gravity, and according to the AMR scheme, have sufficient spatial resolution to resolve individual, high density, clouds. The molecular clouds that we observe in these simulations are self-consistently generated by thermal instabilities, turbulence, and gravitational contraction. We emphasize that the internal structure and the turbulent properties of these molecular clouds are not the result of an ad hoc assumption about the external turbulent driving. By performing these numerical simulations, we expect to tackle unsolved, outstanding questions such as what drives turbulence in molecular clouds; what is the gas density and temperature distribution, and what is the structure of the magnetic field in these objects? In this letter we consider the most important global properties of the clouds. In a subsequent article (Banerjee et al. 2008), we provide a more detailed analysis of the cloud formation, structure, and evolution.

In Sect. 2, we describe the numerical setup and the initial conditions whereas in Sect. 3 we present our results and preliminary comparisons with observations. Section 4 concludes this paper.

2 Numerical setup and initial conditions

The numerical simulations that we present in this letter have been performed with the AMR code RAMSES using the HLL solver. RAMSES is a second order Godunov scheme and uses the constraint transport method to ensure 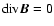${\rm div} \vec{B} =0$ (see Fromang et al. 2006). Starting with an initial resolution of 256³ cells, two levels of refinement are allowed during the calculation, producing an effective 1024³ numerical simulation. The criterion used to refine the grid is a simple density threshold of 50 cm^-3 for the first level and 200 cm^-3for the second level. This ensures that the dense gas is uniformly resolved. With the box size being about 50 pc, this corresponds to a spatial resolution of about 0.05 pc. 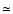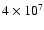The total numbers of cells in the simulations are about $\simeq$ $4 \times 10^7$ . About 25 000 timesteps have been performed for a total of 30 000 cpu hours.

To mimic a large scale, turbulent converging flow (e.g. Audit & Hennebelle 2005), a converging velocity field is imposed on the left and right faces of the simulation box, on top of which transverse and longitudinal velocity modulations have been superimposed. The velocity of each incoming flow is twice the sound speed of the WNM, leading to a total velocity difference of about 40 km s^-1 within the box. The amplitude of the modulation is about a factor of two, leading to velocities ranging from 0 to 40 km s^-1, and it is periodic with a spatial frequency of 10 pc. This produces strong fluctuations at the boundaries. The boundary conditions are periodic for the 4 remaining faces. Initially, the density and temperature are respectively 1 cm^-3 and about 8000 K, which are also the values imposed on the left and right faces. The velocity is initially equal to zero throughout the box. In the following, we present both a hydrodynamical and a MHD simulation for which the magnetic field is uniform initially and parallel to the x-axis, therefore aligned with the incoming velocity field and has an intensity of about 5 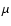$\mu$ G, corresponding to equipartition between magnetic and thermal pressure initially. The cooling is due to atomic species as described by Audit & Hennebelle (2005). Molecular cooling and H₂ formation are not modeled at this stage. As we will see, this nevertheless leads to reasonable temperature and density distributions.

$\begin{figure} \par\mbox{\includegraphics[width=5.5cm]{0165fig2.eps}\includegrap... ...=5.5cm]{0165fig6.eps}\includegraphics[width=5.5cm]{0165fig7.eps} }\end{figure}$

Figure 2: Top ( bottom) panel of left column shows the column density of the hydro (MHD) case. Top ( bottom) panel of middle column shows the density and velocity fields in the z=0 plane of the hydro (MHD) case. Top panel of right column shows the magnetic intensity and its xy-components (indicated as arrows) in the z=0 plane. Bottom panel of right column shows the temperature in the z=0 plane of the MHD case.

Open with DEXTER

3 Results

Figure 1 shows the column density and density pdf for the hydrodynamical case at time 3.5, 7.7, 9.83 and 11.5 Myr and for the MHD case at time 3.5, 7.35, 11.41, and 13.11 Myr. It displays also the temperature for the MHD run and magnetic intensity as a function of density. Because of the mass injection, the total mass increases continuously within the simulation box from about 3000 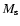$M_{\rm s}$ initially to roughly 10 times this value when the simulations are stopped. For the two first time frames, the evolution of the two runs is very similar. The mass of the gas increases in the box, increasing both the mean and the highest value of density.

As shown by the third timesteps displayed, gravity eventually takes over and triggers gravitational collapse producing far higher densities. Interestingly, this happens roughly 1.5-2 Myr earlier in the hydrodynamical simulations than in the MHD one indicating that the magnetic support has delayed the gravitational collapse. Thus the cloud should begin to form stars roughly 10 Myr after the collision of the converging flow has occurred (the collision between the flow arises at about 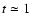$t\simeq 1$ Myr) for the hydrodynamical case and about 12 Myr in the MHD one.

As time advances, the cloud continues to form stars, while the total mass continues to increase. This agrees qualitatively with the observations of Blitz et al. (2007) for the LMC, that the masses of GMCs with little star formation activity are smaller than those of GMCs with strong activity. We note that the duration of 7 Myr, which they infer for the first massive starless phase, is similar to the timescale of our MHD simulation as estimated between time 7.35 Myr and 13.11 Myr. We emphasize, however, that defining precisely the ``birth'' time of the molecular cloud in our simulation is an elusive task since the cloud mass is an increasing function of time.

In both cases, the mass weighted PDF of the column density distribution peaks at about 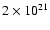$2 \times 10^{21}$ cm^-2and declines rapidly at higher densities. It is interesting to note that this is similar to what has recently been inferred by Goldsmith et al. (2008) for the Taurus molecular cloud (see their Fig. 8).

The temperature declines rapidly for densities between 3 and 30 cm^-3 at which it reaches a value of about 50 K. It then slowly decreases to about 10 K for densities above 10⁴ cm^-3. Since UV shielding and molecular cooling are not considered in this study, we note that the temperature in the dense gas is probably overestimated. This would imply that the average density of the cold clumps should probably be a little higher. Explicitly treating H₂ formation would have the same effect (Glover & Mac Low 2007).

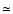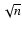For densities smaller than $\simeq$ 1000 cm^-3, the magnetic intensity increases smoothly with density, whereas for densities higher than $\simeq$ 1000 cm^-3, it is roughly proportional to $\sqrt{n}$ . Indeed, the lower density gas is magnetically sub-critical and mainly flows along the magnetic field lines without compressing the magnetic flux. On the other hand, the high density gas is supercritical and the magnetic flux is compressed along with the dense gas under the influence of the gravitational force. Future studies will have to investigate whether ambipolar diffusion modifies this behaviour significantly. We note that the dependence of the magnetic intensity on density appears to be similar to that measured by observations (Troland & Heiles 1986; Crutcher 1999)

Figure 2 shows the column density along the z-axis and the density and velocity field at z=0, for both cases, at time t=7.7 Myr (hydro) and t=7.35 Myr (MHD). Temperature and magnetic field at z=0 are also displayed for the MHD case. We note that the low column density patterns observed at the edge of the computational domain are due to the periodic forcing described previously.

The column density reveals that in both, the hydrodynamic and the MHD case, the cloud has a complex internal structure consisting of filaments and dense clumps of density between 100-1000 cm^-3, embedded in a more diffuse phase. This is even more clearly apparent in the density and temperature cuts that indicate the clumps are relatively isolated and embedded in the warm diffuse phase. This suggests that molecular clouds are not homogeneous isothermal media, but are instead closer to being isobaric, although with large density fluctuations provided by a combination of cooling and turbulent compressions.

The column density and density cuts reveal, however, noticeable differences between the results of hydrodynamical and MHD simulations. The first appears to be more fragmented into smaller clumps than the MHD one. The shape of the clumps also appears to be different.

Interestingly, the density of the warm gas embedded in the molecular cloud is higher than in the outer medium ( 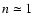$n \simeq 1$ cm^-3) and can be as large as 3-4 cm^-3. Indeed, this gas has been previously shocked and is in the process of cooling as it moves towards the dense cold regions (Vázquez-Semadeni et al. 2006; Hennebelle & Audit 2007). From a comparison between the column density and temperature in the z=0 plane, we note that the warm gas is deeply embedded in the molecular cloud. Note that in this work, the UV field is assumed to be constant. Although this is obviously not a good assumption for the dense gas, we see that since the filling factor of the cloud appears to be small, this is certainly a fair assumption for the WNM even when it is deeply embedded inside the cloud. Moreover, the higher temperatures are sometimes found at the edge of the clumps at the onset of the accretion shocks which occurs when the WNM flow encounters a dense clump. This clearly indicates that the dissipation of mechanical energy plays an important role in the heating of the warm phase. This is similar to the picture proposed by Hennebelle & Inutsuka (2006) except that the mechanical energy that heats the warm phase is the kinetic energy of the shocks instead of the energy of the MHD waves (possibly underestimated in this work since the ion-neutral drift is not treated). Note that the interclump medium being low density atomic hydrogen (n<4-10 cm^-3) is consistent with the estimate of Williams et al. (1995) for the Rosette molecular cloud.

Figure 2 shows the magnetic intensity in the z=0 plane as well as its xy-components. In the external medium, the magnetic field remains far more uniform than in the dense regions, where its direction fluctuates significantly. Since the field was initially uniform, this implies that the turbulent motions are able to significantly distort the field.

4 Conclusion

We have presented the results of AMR MHD simulations aiming to describe self-consistently the formation of a molecular cloud from a converging flow of warm diffuse atomic hydrogen. Our simulation results suggest that molecular clouds consist of a complex network of (colder) density fluctuations embedded in a warmer, more diffuse atomic phase. The simulations reproduce reasonably well the observed variations of magnetic intensity with density and the column density distribution. Finally, we suggest that star formation may begin in the cloud while it is still accreting material. This would imply that the mass of GMCs vary with time, in good agreement with recent observations (Blitz et al. 2007), and with the results of previous non-magnetic simulations of the phenomenon.

From the warm magnetized atomic medium to molecular clouds

1 Introduction

2 Numerical setup and initial conditions

3 Results

4 Conclusion

References