A&A 486, 837-841 (2008)
DOI: 10.1051/0004-6361:200809669
Non-thermal bremsstrahlung from supernova remnants and the effect of
Coulomb losses
(Research Note)
Jacco Vink
Astronomical Institute Utrecht, Utrecht University,
PO Box 80000 3508TA, Utrecht, The Netherlands
Received 27 February 2008 / Accepted 28 May 2008
Abstract
Aims. We investigate the shape of the electron cosmic ray spectrum in the range up to 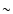 1000 keV, assuming that the acceleration process at the shock results in a power law in momentum, and that downstream of the shock the spectrum is affected by Coulomb interactions with background electrons only.
1000 keV, assuming that the acceleration process at the shock results in a power law in momentum, and that downstream of the shock the spectrum is affected by Coulomb interactions with background electrons only.
Methods. In the non-relativistic regime one can analytically determine the energy of an electron starting with a certain energy, and use this result to produce an electron cosmic ray spectrum, modified by Coulomb losses.
Results. An analytic expression for the electron spectrum is obtained that depends on the parameter
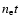 ,
which can be estimated from a similar parameter used to characterize the line spectra of supernova remnants.
,
which can be estimated from a similar parameter used to characterize the line spectra of supernova remnants.
Conclusions. For the brightest supernova remnants
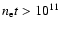 cm-3 s, and most of the electrons accelerated to <100 keV have lost their energy. Because of its high radio flux, Cas A is the most likely candidate for non-thermal bremsstrahlung. Although it has
cm-3 s, and most of the electrons accelerated to <100 keV have lost their energy. Because of its high radio flux, Cas A is the most likely candidate for non-thermal bremsstrahlung. Although it has

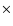 1011 cm-3 s, one may expect to pick up non-thermal bremsstrahlung above 100 keV with current hard X-ray detectors.
1011 cm-3 s, one may expect to pick up non-thermal bremsstrahlung above 100 keV with current hard X-ray detectors.
Key words: ISM: cosmic rays - acceleration of particles - ISM: supernova remnants - X-rays: ISM - shock waves - radiation mechanisms: non-thermal
Over the last five years there has been considerable progress in
our understanding of high energy cosmic ray acceleration by supernova
remnants (SNRs).
The spatial distribution and spectral shape of
X-ray synchrotron emission from all historical SNRs and some
other SNRs has made it clear that electron can be accelerated to
energies up to 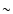 100 TeV (Koyama et al. 1995),
that diffusive shock acceleration works very efficiently, with diffusion
close to the Bohm limit (Vink et al. 2006; Vink 2005; Stage et al. 2006; Parizot et al. 2006), and that
magnetic fields are amplified by cosmic ray streaming
(Vink & Laming 2003; Bamba et al. 2005; Völk et al. 2005; Berezhko et al. 2003). Moreover, the
morphology of Tycho's SNR shows that at least in this remnant, but
also probably in Kepler's SNR, cosmic ray acceleration is so efficient that
it gives rise to enhanced compression ratios (Warren et al. 2005; Ellison et al. 2004).
In addition, considerable progress has been made in the field of
TeV astronomy, with many SNRs being established as sources
of TeV
100 TeV (Koyama et al. 1995),
that diffusive shock acceleration works very efficiently, with diffusion
close to the Bohm limit (Vink et al. 2006; Vink 2005; Stage et al. 2006; Parizot et al. 2006), and that
magnetic fields are amplified by cosmic ray streaming
(Vink & Laming 2003; Bamba et al. 2005; Völk et al. 2005; Berezhko et al. 2003). Moreover, the
morphology of Tycho's SNR shows that at least in this remnant, but
also probably in Kepler's SNR, cosmic ray acceleration is so efficient that
it gives rise to enhanced compression ratios (Warren et al. 2005; Ellison et al. 2004).
In addition, considerable progress has been made in the field of
TeV astronomy, with many SNRs being established as sources
of TeV 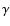 -rays (e.g. Albert et al. 2007; Aharonian et al. 2005,2004).
However, it has not yet been firmly established whether the
-rays (e.g. Albert et al. 2007; Aharonian et al. 2005,2004).
However, it has not yet been firmly established whether the 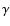 -ray emission is dominated by inverse Compton scattering from TeV electrons,
or from neutral pion decay, caused by TeV ion cosmic rays.
-ray emission is dominated by inverse Compton scattering from TeV electrons,
or from neutral pion decay, caused by TeV ion cosmic rays.
In contrast, little has happened concerning observations of low energy cosmic rays.
This is unfortunate, since from a theoretical perspective, the initial
stages of the acceleration process, from thermal energies up to energies where
Fermi acceleration efficiently operates, is complex
and not well understood (see e.g. Malkov & Drury 2001, for a review).
In fact, the processes by which particles are injected
into the Fermi acceleration process, are likely to be
different for electrons and ions, unlike Fermi acceleration itself.
Our current understanding of the initial stages of acceleration
is largely based on either in situ observations of
inter-planetary shocks, and on computer modeling using hybrid or particle in cell codes
(e.g. Bykov & Uvarov 1999; Lee et al. 2004; Schmitz et al. 2002).
There was some hope that hard X-ray observations of SNRs
might provide observational information on at least the electron component
of low energy cosmic rays (Vink & Laming 2003; Favata et al. 1997; Asvarov et al. 1990; Vink et al. 1997).
However, it is generally agreed that the non-thermal hard X-ray emission
from SNRs such as Cas A (Allen et al. 1997; Vink & Laming 2003; Renaud et al. 2006b; The et al. 1996; Favata et al. 1997),
SN1006 (Kalemci et al. 2006; Allen et al. 1999), Tycho (Allen et al. 1999),
Kepler and RCW 86 (Allen et al. 1999) is due to X-ray synchrotron from the highest energy electron cosmic rays, rather than from bremsstrahlung from low energy electrons.
Nevertheless, the issues remains of interest as current and future
hard X-ray detectors push the detection of hard X-ray emission
to higher photon energies. At high enough energies, the steepening
X-ray synchrotron spectrum is likely to be overtaken by non-thermal bremsstrahlung.
In this paper, I discuss the shape of the low energy
cosmic ray electron spectra, given the importance of Coulomb-losses.
These Coulomb losses in general alter the shape of the low electron cosmic
ray spectrum as generated near the shock front. Note that a
similar situation was investigated by Sarazin (1999)
for higher energy electrons in clusters of galaxies.
Supra-thermal electrons loose energy through various processes:
bremsstrahlung losses, Coulomb losses (collisions with electrons/ions),
and ionization losses![[*]](/icons/foot_motif.gif) .
In the hot plasmas inside SNR shells Coulomb
losses are likely to be the dominant source of energy losses of
electrons, in particular through electron-electron collisions
(e.g. Haug 2004). Electron-electron collisions are most efficient
at low electron energies. For SNRs we are interested in the bremsstrahlung
emission of supra-thermal electron with energies in the range of
.
In the hot plasmas inside SNR shells Coulomb
losses are likely to be the dominant source of energy losses of
electrons, in particular through electron-electron collisions
(e.g. Haug 2004). Electron-electron collisions are most efficient
at low electron energies. For SNRs we are interested in the bremsstrahlung
emission of supra-thermal electron with energies in the range of
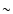 10-1000 keV. The problem with this energy range is that neither
the non-relativistic, nor the relativistic approximations for Coulomb
losses are completely valid. However, I will show that for most SNRs the
non-relativistic approximation is sufficient.
10-1000 keV. The problem with this energy range is that neither
the non-relativistic, nor the relativistic approximations for Coulomb
losses are completely valid. However, I will show that for most SNRs the
non-relativistic approximation is sufficient.
The energy loss rate for an electron with
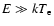 is given by
(e.g. Haug 2004; Huba 2002):
is given by
(e.g. Haug 2004; Huba 2002):
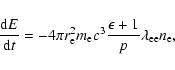 |
(1) |
with 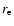 the classical electron radius,
and
the classical electron radius,
and 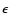 and p the kinetic energy and momentum in dimensionless units,
and p the kinetic energy and momentum in dimensionless units,
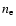 the electron density, and
the electron density, and
 the Coulomb logarithm,
given by (Huba 2002):
the Coulomb logarithm,
given by (Huba 2002):
![\begin{displaymath}%
\lambda_{\rm ee} = 30.9 -
\ln\left[ n_{\rm e}^{1/2} \left(\frac{1~{\rm keV}}{kT_{\rm e}} \right) \right]\cdot
\end{displaymath}](/articles/aa/full/2008/30/aa09669-08/img23.gif) |
(2) |
For the non-relativistic limit (
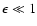 )
Eq. (1) gives:
)
Eq. (1) gives:
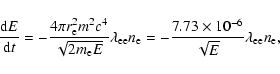 |
(3) |
with energies, E in units of eV.
The solution to this differential equation is:
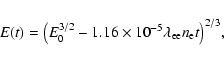 |
(4) |
with E0 the energy of the electron at t=0.
In fact, the correct equation, Eq. (1), can also be solved, but only gives
an implicit function for E(t):
Figure 1 shows both the full solution
and the non-relativistic approximation. As expected, the
non-relativistic approximation fails at high energies. For energies 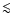 400 keV the approximation is reasonable, with errors in the loss timescale of less than 30%.
400 keV the approximation is reasonable, with errors in the loss timescale of less than 30%.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.8cm,clip]{09669fig01.ps}\end{figure}](/articles/aa/full/2008/30/aa09669-08/Timg31.gif) |
Figure 1:
The electron energy as a function of
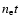 (
(
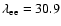 )
for different values of energy at t=0 s
(50 keV, 100 keV, 200 keV...6400 keV). The solid lines show the exact, but implicit solutions to
Eq. (1), i.e. Eq. (5).
The dotted lines are the non-relativistic solutions to Eq. (1),
i.e. Eq. (4). )
for different values of energy at t=0 s
(50 keV, 100 keV, 200 keV...6400 keV). The solid lines show the exact, but implicit solutions to
Eq. (1), i.e. Eq. (5).
The dotted lines are the non-relativistic solutions to Eq. (1),
i.e. Eq. (4). |
| Open with DEXTER |
The advantage of an explicit function (Eq. (4)) is that
it can be easily used to calculate the evolution of the electron spectrum,
using the transformation
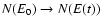 ,
if an analytic approximation is known. This can be done
by inverting Eq. (4) and insert the result in N(E),
taking into account that
,
if an analytic approximation is known. This can be done
by inverting Eq. (4) and insert the result in N(E),
taking into account that
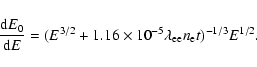 |
(6) |
A simple example is when N(E) can be approximated by a power law
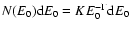 .
After some time t the spectrum
will be approximated by:
.
After some time t the spectrum
will be approximated by:
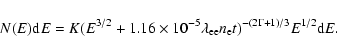 |
(7) |
A more interesting function in this context is the power law in momentum
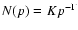 ,
since the simplest version of first order
Fermi acceleration predicts that this is the spectrum of cosmic rays.
Changing this into a function of energy
(
,
since the simplest version of first order
Fermi acceleration predicts that this is the spectrum of cosmic rays.
Changing this into a function of energy
(
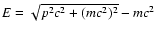 )
gives (see Asvarov et al. 1990):
)
gives (see Asvarov et al. 1990):
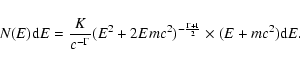 |
(8) |
Inserting Eqs. (4) and (6) in this expression gives:
One of the important aspects of this solution is that it depends almost
entirely on one parameter
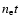 ,
since
,
since
 only
weakly depends on the plasma density and temperature. This parameter
is familiar to anyone investigating X-ray emission from SNRs, as
it is the key parameter for non-ionization equilibrium
(NEI, see Liedahl 1999) and for the equilibration of electrons and ions.
In both cases the parameter is a measure for the number of collisions with
background electrons.
only
weakly depends on the plasma density and temperature. This parameter
is familiar to anyone investigating X-ray emission from SNRs, as
it is the key parameter for non-ionization equilibrium
(NEI, see Liedahl 1999) and for the equilibration of electrons and ions.
In both cases the parameter is a measure for the number of collisions with
background electrons.
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{09669fig02.ps}\end{figure}](/articles/aa/full/2008/30/aa09669-08/Timg44.gif) |
Figure 2:
Low energy electron cosmic rays as expected from first order
Fermi acceleration, including the effects of Coulomb losses (Eq. (9)). The solid line gives the expected spectrum near the shock front,
whereas the other lines show the models for different values of
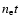 . . |
| Open with DEXTER |
Figure 2 shows the electron distributions for
values of
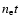 covering the relevant range for SNRs,
109-1012 cm-3 s. Figure 1 shows that for young SNRs
the non-relativistic approximation is expected to be valid, as large
errors only appear for
covering the relevant range for SNRs,
109-1012 cm-3 s. Figure 1 shows that for young SNRs
the non-relativistic approximation is expected to be valid, as large
errors only appear for
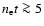
 1011 cm-3 s.
Moreover, the errors mostly affect the spectral shapes above 500 keV.
1011 cm-3 s.
Moreover, the errors mostly affect the spectral shapes above 500 keV.
As explained above the shape of the non-thermal electron spectrum below
1000 keV depends on the parameter
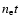 ,
which is the same
parameter that governs the ionization state of the SNR. However,
it depends on the details of the shock acceleration history, whether one can
safely assume that the average
,
which is the same
parameter that governs the ionization state of the SNR. However,
it depends on the details of the shock acceleration history, whether one can
safely assume that the average
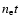 of the hot plasma corresponds
to the
of the hot plasma corresponds
to the
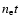 governing the shape of the low energy electron cosmic
rays. A close correspondence is likely if
shock heating results always in a fixed ratio of heated and accelerated
electrons at the shock front. Realistically, one should
take into account the variation of
governing the shape of the low energy electron cosmic
rays. A close correspondence is likely if
shock heating results always in a fixed ratio of heated and accelerated
electrons at the shock front. Realistically, one should
take into account the variation of
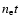 throughout the SNR, and
the evolution with time. However, in practise
one or two values for
throughout the SNR, and
the evolution with time. However, in practise
one or two values for
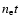 characterizes the overall plasma characteristics reasonably well
(e.g. Vink et al. 1996).
characterizes the overall plasma characteristics reasonably well
(e.g. Vink et al. 1996).
For young SNRs like Cas A, Tycho, Kepler and SN1006, the
X-ray spectra are dominated by line emission from ejecta, shock heated by
the reverse shock. This means that also
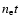 is determined
mostly by the plasma heated by the reverse shock, rather than by the
forward shock heated plasma.
It is often assumed that the reverse shock has
a low magnetic field and therefore does not efficiently accelerate
cosmic rays. However, Helder & Vink (2008)
showed recently that the
reverse shock of Cas A is responsible for most of the X-ray synchrotron
emission, this implies that the reverse shock is capable of accelerating
particles as well. This is a confirmation of recent theoretical calculations
by Ellison et al. (2005). Nevertheless, it is not quite clear what the
ratio is of the electrons accelerated by the forward shock, as opposed to
the reverse shock. Moreover, the initial acceleration process for electrons
may be different: the reverse shocked plasma is
dominated by metals.
In that case, a sizable fraction of the accelerated electrons
may originate from ionization of (mildly) accelerated ions.
is determined
mostly by the plasma heated by the reverse shock, rather than by the
forward shock heated plasma.
It is often assumed that the reverse shock has
a low magnetic field and therefore does not efficiently accelerate
cosmic rays. However, Helder & Vink (2008)
showed recently that the
reverse shock of Cas A is responsible for most of the X-ray synchrotron
emission, this implies that the reverse shock is capable of accelerating
particles as well. This is a confirmation of recent theoretical calculations
by Ellison et al. (2005). Nevertheless, it is not quite clear what the
ratio is of the electrons accelerated by the forward shock, as opposed to
the reverse shock. Moreover, the initial acceleration process for electrons
may be different: the reverse shocked plasma is
dominated by metals.
In that case, a sizable fraction of the accelerated electrons
may originate from ionization of (mildly) accelerated ions.
Apart from the plasma
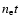 there is another reason why
the
there is another reason why
the
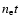 for the accelerated electrons is expected to be high
in Cas A: most of the electrons seem to
have been accelerated in the early life of the SNR. The best
evidence for this is the
for the accelerated electrons is expected to be high
in Cas A: most of the electrons seem to
have been accelerated in the early life of the SNR. The best
evidence for this is the 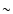 1%/yr decline in its radio flux,
which is best explained by adiabatic expansion of the relativistic electron
gas (Shklovsky 1968). Cas A may be a special case since it is evolving
into a red super giant wind, which has a density falling of with radius as r-2. This means that the particle flux entering the forward shock at any
radius is more or less constant, whereas the shock velocity is dropping
with radius. As a result particle acceleration was more efficient early on,
suggesting a high
1%/yr decline in its radio flux,
which is best explained by adiabatic expansion of the relativistic electron
gas (Shklovsky 1968). Cas A may be a special case since it is evolving
into a red super giant wind, which has a density falling of with radius as r-2. This means that the particle flux entering the forward shock at any
radius is more or less constant, whereas the shock velocity is dropping
with radius. As a result particle acceleration was more efficient early on,
suggesting a high
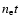 .
.
Unfortunately, this also means that it is quite unlikely that the
non-thermal X-ray emission of Cas A below  100 keV is dominated by
non-thermal bremsstrahlung, either from the forward shock, or
from internal shocks, as assumed by (Laming 2001a; Vink & Laming 2003; Laming 2001b).
The reason is that all the emission must then come from a limited fraction
of the total shock heated plasma for which
100 keV is dominated by
non-thermal bremsstrahlung, either from the forward shock, or
from internal shocks, as assumed by (Laming 2001a; Vink & Laming 2003; Laming 2001b).
The reason is that all the emission must then come from a limited fraction
of the total shock heated plasma for which
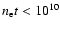 cm-3 s
(see Willingale et al. 2002; Yang et al. 2007, for the spatial distribution of
cm-3 s
(see Willingale et al. 2002; Yang et al. 2007, for the spatial distribution of
 ).
If I simply assume a linear relation between age and
).
If I simply assume a linear relation between age and
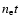 ,
less than 5% of the plasma has
,
less than 5% of the plasma has
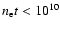 cm-3 s.
The lower hybrid wave model propagated by
Laming (2001a) remains an attractive
option for the injection of electrons into the Fermi acceleration process
itself (see also Ghavamian et al. 2007).
cm-3 s.
The lower hybrid wave model propagated by
Laming (2001a) remains an attractive
option for the injection of electrons into the Fermi acceleration process
itself (see also Ghavamian et al. 2007).
![\begin{figure}
\par\includegraphics[angle=-90,width=8.2cm,clip]{09669fig03a.ps}\includegraphics[angle=-90,width=8.2cm,clip]{09669fig03b.ps}\end{figure}](/articles/aa/full/2008/30/aa09669-08/Timg51.gif) |
Figure 3:
Left: spectral energy distribution of Cas A, as measured with
BeppoSAX-PDS (Vink et al. 2001, red) and INTEGRAL-IBIS (Renaud et al. 2006b, green),
assuming a magnetic field of   G, a spectral energy index
of -2.56 (corresponding to a radio-spectral index of G, a spectral energy index
of -2.56 (corresponding to a radio-spectral index of
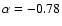 ),
and a background plasma with ),
and a background plasma with
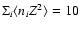 cm-3.
The bremsstrahlung spectra were calculated
using the analytic cross sections of Haug (1997).
The model spectra are shown for cm-3.
The bremsstrahlung spectra were calculated
using the analytic cross sections of Haug (1997).
The model spectra are shown for
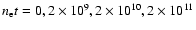 and
and
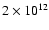 cm-3 s ( from top to bottom).
Right: spectral energy distribution of Tycho's SNR, as measured by the
BeppoSAX-PDS. The theoretical curves are for cm-3 s ( from top to bottom).
Right: spectral energy distribution of Tycho's SNR, as measured by the
BeppoSAX-PDS. The theoretical curves are for 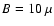 G, G,
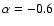 ,
and ,
and
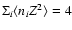 cm-3. The different curves are
for cm-3. The different curves are
for
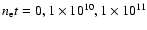 cm-3 s. cm-3 s. |
| Open with DEXTER |
Nevertheless, Cas A remains one of the most important targets for
searching for non-thermal bremsstrahlung, but only above  100 keV, where
the spectrum is less affected by Coulomb losses. The reason is
that Cas A is by far the brightest Galactic SNR in the radio.
This implies the ample presence of relativistic electrons, in combination
with a relatively high magnetic field of
100 keV, where
the spectrum is less affected by Coulomb losses. The reason is
that Cas A is by far the brightest Galactic SNR in the radio.
This implies the ample presence of relativistic electrons, in combination
with a relatively high magnetic field of
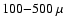 G
(Vink & Laming 2003; Shklovsky 1968; Berezhko & Völk 2004). This is illustrated in
Fig. 3, which suggests that with INTEGRAL-ISGRI we may be close
to a detection, or even that part of the flux density around
100 keV is caused by non-thermal bremsstrahlung (cf. the CGRO-OSSE
detection, The et al. 1996). No deep Suzaku Hard X-ray Detector (HXD)
(Takahashi et al. 2007)
of Cas A exist, but a deep observation with this sensitive instrument, may
also be able to detect emission above 100 keV.
G
(Vink & Laming 2003; Shklovsky 1968; Berezhko & Völk 2004). This is illustrated in
Fig. 3, which suggests that with INTEGRAL-ISGRI we may be close
to a detection, or even that part of the flux density around
100 keV is caused by non-thermal bremsstrahlung (cf. the CGRO-OSSE
detection, The et al. 1996). No deep Suzaku Hard X-ray Detector (HXD)
(Takahashi et al. 2007)
of Cas A exist, but a deep observation with this sensitive instrument, may
also be able to detect emission above 100 keV.
The normalization of the spectrum in Fig. 3 is determined from
the radio flux, and assuming a mean magnetic field of 
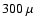 G.
The bremsstrahlung also depends on the emission measure:
G.
The bremsstrahlung also depends on the emission measure:
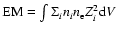 ,
with
,
with 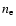 being,
here, the density of the accelerated electrons.
For Cas A the accelerated electrons are present in both
the forward shock heated plasma, with
being,
here, the density of the accelerated electrons.
For Cas A the accelerated electrons are present in both
the forward shock heated plasma, with
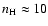 cm-3,
and in the reverse shock heated plasma, which consists
of pure metals, probably dominated by almost completely ionized oxygen
(e.g. Vink et al. 1996). The emitting volume of the forward shock heated plasma
is
cm-3,
and in the reverse shock heated plasma, which consists
of pure metals, probably dominated by almost completely ionized oxygen
(e.g. Vink et al. 1996). The emitting volume of the forward shock heated plasma
is
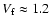
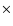 1057 cm3, based on a
shock radius of 2.6 pc and a contact discontinuity at
1057 cm3, based on a
shock radius of 2.6 pc and a contact discontinuity at  2 pc.
The reverse shock radius is
2 pc.
The reverse shock radius is  1.9 pc (Helder & Vink 2008), thus
1.9 pc (Helder & Vink 2008), thus
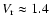
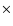 1056 cm3.
Conservatively assuming that there is
1056 cm3.
Conservatively assuming that there is 
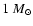 of
ionized oxygen (Vink et al. 1996) and that the other metals contribute
little to the bremsstrahlung, one finds for the shocked ejecta
of
ionized oxygen (Vink et al. 1996) and that the other metals contribute
little to the bremsstrahlung, one finds for the shocked ejecta
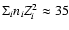 cm-3. For the volume averaged
normalization one finds
cm-3. For the volume averaged
normalization one finds
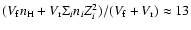 cm-3. Note that both the bremsstrahlung and synchrotron luminosity
scale with the emitting volume.
It is not unreasonable to assume that the synchrotron emitting
volume is equal to the volume of the shock heated plasma.
However, it is uncertain how the accelerated electron density
and magnetic field is distributed over this volume.
So the normalization of
cm-3. Note that both the bremsstrahlung and synchrotron luminosity
scale with the emitting volume.
It is not unreasonable to assume that the synchrotron emitting
volume is equal to the volume of the shock heated plasma.
However, it is uncertain how the accelerated electron density
and magnetic field is distributed over this volume.
So the normalization of
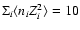 cm-3 used in Fig. 3
should be considered as a reasonable guess.
For a constant non-thermal bremsstrahlung emissivity a higher value
of
cm-3 used in Fig. 3
should be considered as a reasonable guess.
For a constant non-thermal bremsstrahlung emissivity a higher value
of
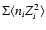 implies a higher magnetic field.
implies a higher magnetic field.
In contrast, for Tycho's SNR, due to its much lower radio luminosity,
one only expects a detection of the non-thermal
bremsstrahlung, if the magnetic field turns out to be unexpectedly low:
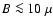 G. This is roughly the value
of the compressed average ISM magnetic field, whereas
estimates for the magnetic field in Tycho
indicates
G. This is roughly the value
of the compressed average ISM magnetic field, whereas
estimates for the magnetic field in Tycho
indicates
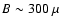 G (Völk et al. 2005).
G (Völk et al. 2005).
Finally, one could also consider SNRs in which the densities and
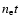 values are modest, and for which also the magnetic fields
are low; for example SN1006 (
values are modest, and for which also the magnetic fields
are low; for example SN1006 (
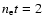
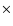 109 cm-3 s, Vink et al. 2003)
and the Northeast of RCW 86
(
109 cm-3 s, Vink et al. 2003)
and the Northeast of RCW 86
(
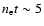
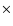 109 cm-3 s, Vink et al. 2006).
The advantage is that although the bremsstrahlung may be weaker, the low
109 cm-3 s, Vink et al. 2006).
The advantage is that although the bremsstrahlung may be weaker, the low
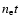 ensures non-thermal bremsstrahlung at lower photon energies.
Unfortunately, both these SNRs have also X-ray synchrotron radiation,
which may be hard to distinguish from non-thermal bremsstrahlung. However,
with imaging spectroscopy above 10 keV one may isolate regions where
non-thermal bremsstrahlung is important and X-ray synchrotron radiation
absent. Moreover, high spectral resolution spectra
may reveal departures from Maxwellian electron distributions.
This type of research will have to wait till the emergence of
high resolution, high throughput, X-ray imaging spectroscopy with
XEUS (Parmar et al. 2006).
ensures non-thermal bremsstrahlung at lower photon energies.
Unfortunately, both these SNRs have also X-ray synchrotron radiation,
which may be hard to distinguish from non-thermal bremsstrahlung. However,
with imaging spectroscopy above 10 keV one may isolate regions where
non-thermal bremsstrahlung is important and X-ray synchrotron radiation
absent. Moreover, high spectral resolution spectra
may reveal departures from Maxwellian electron distributions.
This type of research will have to wait till the emergence of
high resolution, high throughput, X-ray imaging spectroscopy with
XEUS (Parmar et al. 2006).
I have derived an analytic expression for the low energy electron
cosmic ray spectrum, assuming that the cosmic ray spectrum, as produced
by the diffusive acceleration process,
is a power law in momentum, and is only affected by
Coulomb losses downstream of the shock.
As may be expected, the parameter
governing the Coulomb losses depends on
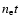 ,
the product
of (background) electron density and the age of the accelerated
electron population. This parameter is similar to the ionization
time scale of the hot, shock heated plasma, and can be easily estimated
from the line spectra of SNRs.
,
the product
of (background) electron density and the age of the accelerated
electron population. This parameter is similar to the ionization
time scale of the hot, shock heated plasma, and can be easily estimated
from the line spectra of SNRs.
For the SNRs with high densities, and large
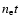 ,
one does not expect a large
population of accelerated electrons below 100 keV. This is in particular
the case for the very bright radio source Cas A. Nevertheless, Cas A
remains a good candidate for searching for non-thermal bremsstrahlung,
because of its high ion density and because its radio brightness indicates
a large amount of accelerated electrons.
Based on reasonable, but somewhat uncertain, assumptions,
the results presented here
imply that only above
,
one does not expect a large
population of accelerated electrons below 100 keV. This is in particular
the case for the very bright radio source Cas A. Nevertheless, Cas A
remains a good candidate for searching for non-thermal bremsstrahlung,
because of its high ion density and because its radio brightness indicates
a large amount of accelerated electrons.
Based on reasonable, but somewhat uncertain, assumptions,
the results presented here
imply that only above  100 keV one expects to pick up the non-thermal
bremsstrahlung component from Cas A.
This may be accomplished with future deep Suzaku HXD
observations, or additional deep INTEGRAL observations.
100 keV one expects to pick up the non-thermal
bremsstrahlung component from Cas A.
This may be accomplished with future deep Suzaku HXD
observations, or additional deep INTEGRAL observations.
Acknowledgements
I am grateful to Prof. Ishida and Dr Bamba for inviting me
for a short stay at ISAS, Japan in November 2007. The discussion on
Suzaku HXD data of Cas A led to the results reported here.
J.V. is financially supported by a Vidi grant from
the Netherlands Organization for
Scientific Research (NWO).
- Aharonian,
F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2005,
A&A, 437, L7 [NASA ADS] [CrossRef] [EDP Sciences]
- Aharonian,
F. A., Akhperjanian, A. G., Aye, K.-M., et al. 2004,
Nature, 432, 75 [NASA ADS] [CrossRef]
- Albert, J., Aliu,
E., Anderhub, H., et al. 2007, A&A, 474, 937 [NASA ADS] [CrossRef] [EDP Sciences]
- Allen, G. E.,
Keohane, J. W., Gotthelf, E. V., et al. 1997, ApJ, 487,
L97 [NASA ADS] [CrossRef]
- Allen, G. E.,
Gotthelf, E. V., & Petre, R. 1999, in the Proceedings of
the 26th International Cosmic Ray Conference
[arXiv:astro-ph/9908209]
- Asvarov,
A. I., Guseinov, O. H., Kasumov, F. K., &
Dogel', V. A. 1990, A&A, 229, 196 [NASA ADS]
- Bamba, A., Yamazaki,
R., Yoshida, T., Terasawa, T., & Koyama, K. 2005, ApJ, 621,
793 [NASA ADS] [CrossRef]
- Berezhko,
E. G., & Völk, H. J. 2004, A&A, 419,
L27 [NASA ADS] [CrossRef] [EDP Sciences]
- Berezhko,
E. G., Ksenofontov, L. T., & Völk, H. J.
2003, A&A, 412, L11 [NASA ADS] [CrossRef] [EDP Sciences]
- Bykov, A. M.,
& Uvarov, Y. A. 1999, JETP, 88, 465 [NASA ADS] [CrossRef]
- Drury, L. O.,
Duffy, P., Eichler, D., & Mastichiadis, A. 1999, A&A, 347,
370 [NASA ADS]
- Ellison,
D. C., Decourchelle, A., & Ballet, J. 2004, A&A, 413,
189 [NASA ADS] [CrossRef] [EDP Sciences]
- Ellison,
D. C., Decourchelle, A., & Ballet, J. 2005, A&A, 429,
569 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Favata, F., Vink,
J., dal Fiume, D., et al. 1997, A&A, 324, L49 [NASA ADS]
- Ghavamian,
P., Laming, J. M., & Rakowski, C. E. 2007, ApJ, 654,
L69 [NASA ADS] [CrossRef]
(In the text)
- Haug, E. 1997, A&A,
326, 417 [NASA ADS]
(In the text)
- Haug, E. 2004, A&A,
423, 793 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Helder, E., &
Vink, J. 2008, ApJ, accepted, [arXiv:0806:3748]
(In the text)
- Huba, J. D.
2002, NRL Plasma Formulary
- Kalemci, E.,
Reynolds, S. P., Boggs, S. E., et al. 2006, ApJ,
644, 274 [NASA ADS] [CrossRef]
- Koyama, K., Petre,
R., Gotthelf, E. V., et al. 1995, Nature, 378, 255 [NASA ADS] [CrossRef]
(In the text)
- Laming,
J. M. 2001a, ApJ, 546, 1149 [NASA ADS] [CrossRef]
- Laming,
J. M. 2001b, ApJ, 563, 828 [NASA ADS] [CrossRef]
- Lee, R. E., Chapman,
S. C., & Dendy, R. O. 2004, ApJ, 604, 187 [NASA ADS] [CrossRef]
- Liedahl,
D. A. 1999, Lecture Notes in Physics (Berlin: Springer
Verlag), 520, 189 [NASA ADS]
(In the text)
- Malkov, M. A.,
& Drury, L. 2001, Rep. Progr. Phys., 64, 429 [NASA ADS] [CrossRef]
(In the text)
- Parizot, E.,
Marcowith, A., Ballet, J., & Gallant, Y. A. 2006, A&A,
453, 387 [NASA ADS] [CrossRef] [EDP Sciences]
- Parmar, A. N.,
Arnaud, M., Barcons, X., et al. 2006, in Proc. SPIE, 6266,
50
(In the text)
- Renaud, M., Vink,
J., Decourchelle, A., et al. 2006b, ApJ, 647, L41 [NASA ADS] [CrossRef]
- Sarazin,
C. L. 1999, ApJ, 520, 529 [NASA ADS] [CrossRef]
(In the text)
- Schmitz, H.,
Chapman, S. C., & Dendy, R. O. 2002, ApJ, 579,
327 [NASA ADS] [CrossRef]
- Shklovsky,
J. S. 1968, Supernovae, Interscience Monographs and Texts in
Physics and Astronomy (London: Wiley)
(In the text)
- Stage, M. D.,
Allen, G. E., Houck, J. C., & Davis, J. E. 2006,
Nature Phys., 2, 614 [NASA ADS] [CrossRef]
- Takahashi,
T., Abe, K., Endo, M., et al. 2007, PASJ, 59, 35
(In the text)
- The, L.-S., Leising, M.
D., Kurfess, J. D., et al. 1996, A&AS, 120, C357 [NASA ADS] [CrossRef]
- Völk,
H. J., Berezhko, E. G., & Ksenofontov, L. T.
2005, A&A, 433, 229 [NASA ADS] [CrossRef] [EDP Sciences]
- Vink, J. 2005, in
High Energy Gamma-Ray Astronomy, ed. F. A. Aharonian,
H. J. Völk, & D. Horns, AIP Conf. Proc., 745,
160
- Vink, J., &
Laming, J. M. 2003, ApJ, 584, 758 [NASA ADS] [CrossRef]
- Vink, J., Kaastra,
J. S., & Bleeker, J. A. M. 1996, A&A, 307,
L41 [NASA ADS]
(In the text)
- Vink, J., Kaastra,
J. S., & Bleeker, J. A. M. 1997, A&A, 328,
628 [NASA ADS]
- Vink, J., Laming, J.
M., Kaastra, J. S., et al. 2001, ApJ, 560, L79 [NASA ADS] [CrossRef]
(In the text)
- Vink, J., Laming,
J. M., Gu, M. F., Rasmussen, A., & Kaastra, J. 2003,
ApJ, 587, 31 [NASA ADS] [CrossRef]
(In the text)
- Vink, J., Bleeker,
J., van der Heyden, K., et al. 2006, ApJ, 648, L33 [NASA ADS] [CrossRef]
- Warren, J. S.,
Hughes, J. P., Badenes, C., et al. 2005, ApJ, 634, 376 [NASA ADS] [CrossRef]
- Willingale,
R., Bleeker, J. A. M., van der Heyden, K. J.,
Kaastra, J. S., & Vink, J. 2002, A&A, 381, 1039 [NASA ADS] [CrossRef] [EDP Sciences]
- Yang, X.-J., Lu, F.-J.,
& Chen, L. 2007 [arXiv:0712.1071]
Copyright ESO 2008
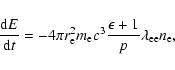
![\begin{displaymath}%
\lambda_{\rm ee} = 30.9 -
\ln\left[ n_{\rm e}^{1/2} \left(\frac{1~{\rm keV}}{kT_{\rm e}} \right) \right]\cdot
\end{displaymath}](/articles/aa/full/2008/30/aa09669-08/img23.gif)
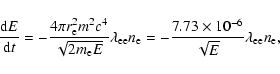
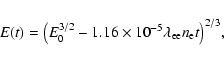
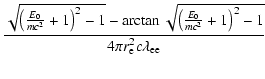
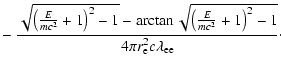
![\begin{figure}
\par\includegraphics[angle=-90,width=7.8cm,clip]{09669fig01.ps}\end{figure}](/articles/aa/full/2008/30/aa09669-08/Timg31.gif)
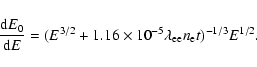
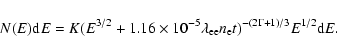
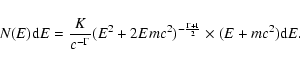
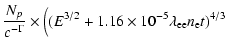
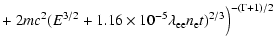
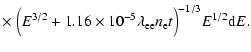
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{09669fig02.ps}\end{figure}](/articles/aa/full/2008/30/aa09669-08/Timg44.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=8.2cm,clip]{09669fig03a.ps}\includegraphics[angle=-90,width=8.2cm,clip]{09669fig03b.ps}\end{figure}](/articles/aa/full/2008/30/aa09669-08/Timg51.gif)