A&A 486, 971-984 (2008)
DOI: 10.1051/0004-6361:200809568
Two extremely luminous WN stars in the Galactic center with circumstellar emission from dust and gas
A. Barniske - L. M. Oskinova - W.-R. Hamann
Potsdam University, Am Neuen Palais 10, Potsdam 14469, Germany
Received 12 February 2008 / Accepted 22 May 2008
Abstract
Context. The central region of our Galaxy contains a large population of young massive stars. These stars are concentrated in three large star clusters, as well as being scattered in the field. Strong ionizing radiation and stellar winds of massive stars are the essential feedback agents that determine the physics of the ISM in the Galactic center.
Aims. The aim is to study relatively isolated massive WN-type stars in the Galactic center in order to explore their properties and their influence on the ISM.
Methods. The K-band spectra of two WN stars in the Galactic center, WR 102ka and WR 102c, are exploited to infer the stellar parameters and to compute synthetic stellar spectra using the Potsdam Wolf-Rayet (PoWR) model atmosphere code. These models are combined with dust-shell models for analyzing the Spitzer IRS spectra of these objects. Archival IR images complement the interpretation.
Results. We report that WR 102ka and WR 102c are among the most luminous stars in the Milky Way. They critically influence their immediate environment by strong mass loss and intense UV radiation, and thus set the physical conditions for their compact circumstellar nebula. The mid-IR continua for both objects are dominated by dust emission. For the first time we report the presence of dust in the close vicinity of WN stars. Also for the first time, we have detected lines of pure-rotational transitions of molecular hydrogen in a massive-star nebula. A peony-shaped nebula around WR 102ka is resolved at 24  m by the Spitzer MIPS camera. We attribute the formation of this IR-bright nebula to the recent evolutionary history of WR 102ka.
m by the Spitzer MIPS camera. We attribute the formation of this IR-bright nebula to the recent evolutionary history of WR 102ka.
Key words: stars: Wolf-Rayet - HII regions - Galaxy: center - stars: individual: WR 102ka - stars: individual: WR 102c
Visual light cannot penetrate the dust clouds obscuring the innermost
part of our Galaxy, whereas infrared astronomy opens extraordinary
views on this environment. Three very massive star clusters have been
discovered in the Galactic center (GC) during the last decade. The
central cluster is located within 1 pc from the central black hole
(Krabbe et al. 1995). Two other massive star clusters, the
Arches and the Quintuplet, are located within 30 pc projected distance
from Sgr A* (Serabyn et al. 1998; Figer et al. 1999b). While the Arches cluster is younger and contains many OB-type stars, the more evolved Quintuplet cluster (3-5 Myr old) harbors many Wolf-Rayet (WR) stars. Besides these compact stellar conglomerates, many high-mass stars whose association with stellar clusters is not obvious are scattered in the GC. Among these
are the rather isolated WR type stars WR 102ka and WR 102c - our program stars.
Massive stars severely influence their environment by strong ionizing
radiation, mass and kinetic energy input (Freyer et al. 2003).
The thermal Arched Filaments in the vicinity of the Arches and the
Sickle nebula in the vicinity of the Quintuplet are thought to be
powered by the combined action of hot massive stars located in these
clusters (Simpson et al. 2007, and references therein). However,
radio (e.g. Yusef-Zadeh & Morris 1987) and infrared (Price et al. 2001; Rodríguez-Fernández et al. 2001;
Simpson et al. 2007) surveys of the GC reveal a
complex structure of the ionized gas with many small-scale compact
sources of thermal emission. In this paper we investigate the emission
from such nebulae around our program stars.
A star with initial mass over 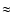 20
20 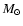 settles on the
main sequence as an O-type. Stars more massive than
settles on the
main sequence as an O-type. Stars more massive than
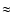 30
30 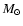 evolve off the main sequence at more or less
constant luminosity, but their mass-loss rate increases significantly.
Stars with initial masses above
evolve off the main sequence at more or less
constant luminosity, but their mass-loss rate increases significantly.
Stars with initial masses above 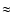 40
40 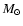 pass through a
short (
pass through a
short (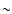 105 yr) luminous blue variable (LBV) evolutionary stage
that is characterized by high mass-loss rates and violent eruptions.
The ejected material, up to several
105 yr) luminous blue variable (LBV) evolutionary stage
that is characterized by high mass-loss rates and violent eruptions.
The ejected material, up to several 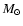 ,
is often observed in
the form of an associated nebula - one famous example is the
Homunculus nebula around the LBV star
,
is often observed in
the form of an associated nebula - one famous example is the
Homunculus nebula around the LBV star 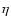 Car. The most massive
stars with initial masses
Car. The most massive
stars with initial masses
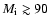
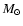 are thought to
lose enough mass during their life on the main-sequence to evolve to
the WR stage without ever becoming an LBV.
are thought to
lose enough mass during their life on the main-sequence to evolve to
the WR stage without ever becoming an LBV.
Stars that display CNO-processed matter in a strong stellar wind are classified as WR stars of the nitrogen sequence (WN type). The cooler, late WN subtypes (WNL) usually contain some rest of hydrogen in their atmospheres, while the hotter, early subtypes (WNE) are hydrogen free (Hamann et al. 1991). The WNL evolutionary stage can, in fact, precede the LBV stage (Langer et al. 1994; Smith & Conti 2008). Typically, WNL stars are significantly more luminous than WNE stars (Hamann et al. 2006). The WN phase may be followed by the WC stage, when the products of helium burning appear in the stellar atmosphere. Wolf-Rayet stars end their lives with a super- or hypernova explosion.
During its evolution a massive star loses a considerable fraction of its initial mass. This material accumulates in the circumstellar environment (e.g. Freyer et al. 2003). Recently, concerns
were raised that the empirically derived stellar mass-loss rates need to be drastically reduced (Fullerton et al. 2006). However, when the inhomogeneous nature of stellar winds is accounted for, the analyses of optical, UV, and X-ray spectra of massive stars consistently yield mass-loss rates that are only factor of two lower than inferred under the ``standard'' assumption of smooth winds (Oskinova et al. 2007).
Infrared (IR) spectra of H II regions around main-sequence stars are
composed of nebular emission lines and a dust-dominated continuum
(Dopita et al. 2005). However, in the vicinity of WR stars
dust is rarely found, except for WC-type stars in the inner,
metal-rich parts of galaxies (e.g. Crowther et al. 2006).
These stars are surrounded by dust shells, and it appears that the
metal-rich environment of the GC is favorable to the formation of
circumstellar dust. For WN stars, however, it is generally believed
that the chemical composition and strong radiation prohibit the
formation of dust in their vicinity.
We secured the mid-IR spectra of WN-type stars WR 102ka and WR 102c with the
Spitzer Space Telescope. Our program stars are sufficiently
isolated to allow high-resolution spectroscopy with the
Spitzer infrared spectrograph IRS. The basic strategy for the
analysis is to model the stellar spectrum using a stellar atmosphere
code, and then use the synthetic stellar spectrum as input for
modeling the circumstellar nebula.
This paper is organized as follows. Stellar parameters and synthetic stellar spectra of our program stars are obtained in Sect. 2 from the analysis of K-band spectra. Infrared spectroscopic and imaging observations are presented in Sect. 3. The analysis and modeling of the mid-IR Spitzer IRS spectra are conducted in Sect. 4. A discussion is presented in Sect. 5, followed by the summary in Sect. 6.
2 Program stars WR 102ka and WR 102c
Figure 1 shows the location of our program stars relative to the three massive clusters in the GC - the Central Cluster, the Arches cluster, and the Quintuplet cluster.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{9568fig1.ps}\end{figure}](/articles/aa/full/2008/30/aa09568-08/Timg21.gif) |
Figure 1:
Spitzer IRAC 8  m archive image of the GC. Arrows point to the locations of our program stars, the Arches, the Quintuplet, and the Central clusters. North is to the top and east to the left. m archive image of the GC. Arrows point to the locations of our program stars, the Arches, the Quintuplet, and the Central clusters. North is to the top and east to the left. |
| Open with DEXTER |
WR 102ka has a projected distance of 19 pc from Sgr A and apparently does not belong to any star cluster. It was first observed during a near-infrared survey in the GC by Homeier et al. (2003). By comparing the K-band spectrum of WR 102ka with the spectra of two WR stars in the LMC, WR 102ka was classified as a WN10 spectral subtype.
and apparently does not belong to any star cluster. It was first observed during a near-infrared survey in the GC by Homeier et al. (2003). By comparing the K-band spectrum of WR 102ka with the spectra of two WR stars in the LMC, WR 102ka was classified as a WN10 spectral subtype.
WR 102c lies in the outskirts of the Quintuplet cluster, in a large arc of diffuse emission called the Sickle nebula. The star was discovered during a survey by Figer et al. (1999a), and classified as WN6 subtype because the similarity of its K-band spectrum with the well-studied WN6 type star WR 115. It should be noted that the WN6 classification criteria can be met by either hydrogen-free WNE subtypes or by WNL stars with hydrogen. As WR 102c shows hydrogen in its spectrum (cf. Sect. 2.2), it belongs to the WNL subclass.
The coordinates of WR 102ka from the discovery paper are in agreement with the 2MASS point source catalog. For WR 102c, however, we report a difference of 0
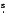 3 in RA between the coordinates given in Figer et al. (1999a) and the 2MASS point source catalog. For our Spitzer observation we used the latter coordinates (cf. Table 3). These coordinates agree with the catalog of point sources from Spitzer IRAC observations of the central part of the Galaxy (Ramírez et al. 2008). Throughout this paper we assume the distance to our program stars as d=8 kpc (Reid 1993).
3 in RA between the coordinates given in Figer et al. (1999a) and the 2MASS point source catalog. For our Spitzer observation we used the latter coordinates (cf. Table 3). These coordinates agree with the catalog of point sources from Spitzer IRAC observations of the central part of the Galaxy (Ramírez et al. 2008). Throughout this paper we assume the distance to our program stars as d=8 kpc (Reid 1993).
The only available part of the stellar spectrum of WR 102ka is the near-IR K-band spectrum obtained with SOFI at the ESO 3.6 m New Technology Telescope (Homeier et al. 2003). As can be seen in Fig. 2, the spectrum is dominated by strong emission lines of He I and He II + Br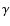 .
A small, flat-topped emission feature is present at the wavelength of the He II 10-7 transition. However, this feature appears broader than the
other lines and has a different spectral shape. Neither nebular (forbidden) lines nor H2 fluorescent emission is visible in the K-band spectrum of WR 102ka. The measured equivalent widths are listed in Table 1.
.
A small, flat-topped emission feature is present at the wavelength of the He II 10-7 transition. However, this feature appears broader than the
other lines and has a different spectral shape. Neither nebular (forbidden) lines nor H2 fluorescent emission is visible in the K-band spectrum of WR 102ka. The measured equivalent widths are listed in Table 1.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{9568fig2.ps}\end{figure}](/articles/aa/full/2008/30/aa09568-08/Timg25.gif) |
Figure 2:
K-band spectrum of WR 102ka (blue solid line) together with the best-fitting PoWR model spectrum (red dashed line). |
| Open with DEXTER |
The Potsdam Wolf-Rayet (PoWR) stellar atmosphere models are employed for the analysis of the K-band spectrum. The PoWR code solves the non-LTE radiative transfer in a spherically expanding atmosphere, consistently with the statistical equations and energy conservation. Iron-line
blanketing and wind clumping in first approximation are taken into account (Hamann et al. 2004). Grids of models for WN stars can be found on the Potsdam Wolf-Rayet (PoWR) models web-site![[*]](/icons/foot_motif.gif) .
.
All lines that can be definitely identified in the K-band spectrum of WR 102ka
are due to helium and hydrogen; therefore we cannot determine other element abundances. We adopt mass fractions that are typical for Galactic WN stars - N: 0.015, C: 0.0001, Fe: 0.0014 (Hamann et al. 2004) - throughout this paper.
The terminal wind velocity in WR 102ka,
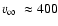 km s-1, is inferred from fitting the He I line profiles. To assess the hydrogen abundance, we use the line blend He II + Br
km s-1, is inferred from fitting the He I line profiles. To assess the hydrogen abundance, we use the line blend He II + Br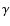 .
Our models show that whenever the strong observed He I lines are reproduced, the He II emissions are very small. Thus the strong emission at 2.165
.
Our models show that whenever the strong observed He I lines are reproduced, the He II emissions are very small. Thus the strong emission at 2.165  m must be mainly due to hydrogen; we obtain a hydrogen mass fraction of 0.2 for WR 102ka, which is typical for late-type WN (WNL) stars.
m must be mainly due to hydrogen; we obtain a hydrogen mass fraction of 0.2 for WR 102ka, which is typical for late-type WN (WNL) stars.
For a given chemical composition and stellar temperature 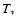 ,
synthetic spectra from WR model atmospheres of different mass-loss rates, stellar radii and terminal wind velocities yield almost the same emission line equivalent widths, if they agree in their ``transformed radius''
,
synthetic spectra from WR model atmospheres of different mass-loss rates, stellar radii and terminal wind velocities yield almost the same emission line equivalent widths, if they agree in their ``transformed radius'' 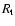 defined as
defined as
![\begin{displaymath}R_{\rm t} = R_*
\left[\frac{\varv_\infty}{2500~{\rm km}~{\rm...
...t M}{10^{-4}~M_\odot~{\rm yr^{-1}}}\right]^{2/3} \right. \cdot
\end{displaymath}](/articles/aa/full/2008/30/aa09568-08/img29.gif) |
(1) |
For the clumping contrast we adopt D=4 as a typical value for WN stars (Hamann et al. 1998). Note that 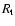 is inversely correlated with the mass-loss rate, i.e. the smaller the transformed radius the higher is the density in the stellar wind.
is inversely correlated with the mass-loss rate, i.e. the smaller the transformed radius the higher is the density in the stellar wind.
Table 1:
Measured equivalent widths in the K-band spectral lines of
WR 102ka.
In order to derive the fundamental stellar parameters of WR 102ka in a
systematic way, we 1) calculate a reasonably fine grid of models in the
adequate parameter range; 2) evaluate the equivalent widths
(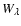 )
of model lines; 3) compare modeled
)
of model lines; 3) compare modeled 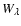 with
measured ones and choose the model which is capable to simultaneously
reproduce the measured equivalent widths.
with
measured ones and choose the model which is capable to simultaneously
reproduce the measured equivalent widths.
Contours of constant line emission in the model grid are shown in Fig. 3. Figure 3 shows a remarkable difference between the two He I lines in the K-band (compare Panels A and B). While the He I
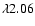
 m singlet
line is sensitive to both model parameters
m singlet
line is sensitive to both model parameters 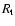 and
and 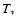 ,
the singlet/triplet blend He I
,
the singlet/triplet blend He I
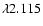
 m has a
m has a 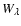 which is nearly independent of
which is nearly independent of 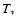 .
.
![\begin{figure}
\par\includegraphics[width=18cm]{9568fig3.ps}\end{figure}](/articles/aa/full/2008/30/aa09568-08/Timg39.gif) |
Figure 3:
Contours of constant line emission of helium in the
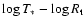 plane. All other parameters are kept constant (
plane. All other parameters are kept constant (
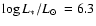 , ,
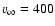 km s-1). Dots indicate the calculated grid models. The interpolated contour
lines are labeled with the equivalent width in Å. The solid red lines correspond to the measured value of km s-1). Dots indicate the calculated grid models. The interpolated contour
lines are labeled with the equivalent width in Å. The solid red lines correspond to the measured value of
 .
Panel A): He I .
Panel A): He I
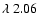  m;
B): He I m;
B): He I
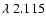  m; C): He II (?) m; C): He II (?)
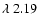  m.
The contours corresponding to the measured m.
The contours corresponding to the measured
 are shown
together in panel D). The large triangle indicates the adopted final
model for WR 102ka (see text).
are shown
together in panel D). The large triangle indicates the adopted final
model for WR 102ka (see text). |
| Open with DEXTER |
Figure 3D reveals that no consistent fit is possible for the three considered helium lines. We attribute the problem to the line at 2.189  m, tentatively identified with the He II 10-7 transition. Considering that the small observed
m, tentatively identified with the He II 10-7 transition. Considering that the small observed
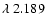
 m feature is broader than other lines, that it has a different line profile, and that the available spectrum is quite noisy, we conclude that the
m feature is broader than other lines, that it has a different line profile, and that the available spectrum is quite noisy, we conclude that the
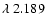
 m feature cannot be due to He II emission from that star.
m feature cannot be due to He II emission from that star.
Therefore we chose as our best-fitting model the grid point that lies closest to the intersection point of the contours for the strong He I
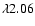
 m and He I
m and He I
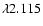
 m lines. The parameters are
T* = 25.1 kK and
m lines. The parameters are
T* = 25.1 kK and
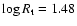 (large
triangle in the panels of Fig. 3).
(large
triangle in the panels of Fig. 3).
After we have derived
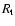 and
and 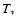 from the normalized line spectrum, the absolute values of L,
from the normalized line spectrum, the absolute values of L, 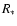 and
and 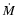 are obtained by fitting the spectral energy distribution (SED). The absolute flux scales proportional to
are obtained by fitting the spectral energy distribution (SED). The absolute flux scales proportional to 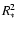 which in turn means that for a fixed value of
which in turn means that for a fixed value of 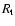 the mass loss rate
the mass loss rate 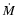 is proportional to L3/4. For convenience we calculate our models with a ``generic'' luminosity of
is proportional to L3/4. For convenience we calculate our models with a ``generic'' luminosity of
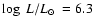 and scale it to match the observations.
and scale it to match the observations. 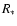 and
and 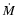 are then scaled along with the luminosity using the relations mentioned above.
are then scaled along with the luminosity using the relations mentioned above.
To account for the interstellar absorption we adopt the reddening law by Moneti et al. (2001), which was obtained for the Quintuplet cluster region and is therefore suitable for our program stars. In this law, the ratio between the V- and K-band extinctions is
AV/AK = 8.9.
By scaling the luminosity (logarithmic shift) and simultaneously varying EB-V, we adjust the synthetic SED to the 2MASS and the Spitzer IRAC photometry marks (see Sect. 3.2). The best fit is obtained with
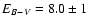 mag and is shown in Fig. 4. The stellar parameters of WR 102ka are compiled in Table 2. With a bolometric luminosity of
mag and is shown in Fig. 4. The stellar parameters of WR 102ka are compiled in Table 2. With a bolometric luminosity of
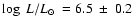 ,
WR 102ka is one of the most luminous stars in the Galaxy!
,
WR 102ka is one of the most luminous stars in the Galaxy!
According to its location in the
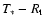 plane (cf. Hamann et al. 2004), WR 102ka has a spectral type later than WN8. The mass-loss rate and wind velocity of WR 102ka found from our modeling are very similar to the parameters of Ofpe/WN9 stars in the GC as determined by Martins
et al. (2007). Their Ofpe/WN9 objects cover a temperature range form
plane (cf. Hamann et al. 2004), WR 102ka has a spectral type later than WN8. The mass-loss rate and wind velocity of WR 102ka found from our modeling are very similar to the parameters of Ofpe/WN9 stars in the GC as determined by Martins
et al. (2007). Their Ofpe/WN9 objects cover a temperature range form
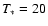 kK ... 23 kK, terminal velocities lie between 450 and 700 km s-1, and the mass-loss rates are
kK ... 23 kK, terminal velocities lie between 450 and 700 km s-1, and the mass-loss rates are
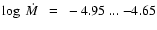 .
Hence we adopt the spectral classification
Ofpe/WN9 for WR 102ka.
.
Hence we adopt the spectral classification
Ofpe/WN9 for WR 102ka.
As discussed above, our final model for WR 102ka cannot reproduce the weak emission feature at 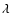 2.189
2.189  m. Instead, a small absorption feature from He II is predicted at this
wavelength. Moreover, there is a weak emission feature around 2.103
m. Instead, a small absorption feature from He II is predicted at this
wavelength. Moreover, there is a weak emission feature around 2.103  m visible in the observed spectrum of WR 102ka, which could be the emission wing of a P-Cygni profile from N V
m visible in the observed spectrum of WR 102ka, which could be the emission wing of a P-Cygni profile from N V 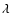 2.099
2.099  m; however, the appearance of this line is also not predicted by our final model. Therefore we must consider the possibility that WR 102ka is actually a binary system, and the spectrum is contaminated by a hotter but fainter companion. The N V lines at 2.099
m; however, the appearance of this line is also not predicted by our final model. Therefore we must consider the possibility that WR 102ka is actually a binary system, and the spectrum is contaminated by a hotter but fainter companion. The N V lines at 2.099  m appears in models for hot WNE stars, as demonstrated in Fig. 5 by adding a spectrum from a corresponding model (
m appears in models for hot WNE stars, as demonstrated in Fig. 5 by adding a spectrum from a corresponding model (
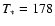 kK,
kK,
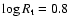 ). The presence of a WNE-type companion with fast stellar wind could also explain the appearance of the He II
). The presence of a WNE-type companion with fast stellar wind could also explain the appearance of the He II 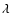 2.189
2.189  m line (see right panel in Fig. 5).
m line (see right panel in Fig. 5).
The contribution of the hot companion has been scaled down by a factor
of ten in order to match the weak He II and N V features
in the observation. It is plausible that a hot WNE-type companion would
contribute only little to the composite IR flux. WNE stars are generally
not that luminous, and even for same bolometric luminosity a companion
twice as hot as the primary would be 50% fainter in the Rayleigh-Jeans
domain of a black-body spectrum. We conclude that WR 102ka may be an
Ofpe/WN9+WNE binary system. However, the limited quality of the K-band
data (Fig. 2) does not allow this question to be settled.
Figer et al. (1999a) published a K-band spectrum of WR 102c,
unfortunately plotted with an unspecified offset, and assigned to it a K-band magnitude of 11.6 mag. This value is not consistent with the more recently available 2MASS and the Spitzer IRAC point source catalogs. We have to assume that, most plausibly, the K-band spectrum shown in Figer et al. (1999a) in fact belongs to a much brighter star (K-band magnitude 9.93 mag) which we identify with WR 102c. This assumption is validated by the consistent picture which emerges from (i) the photometry marks from 2MASS and Spitzer IRAC catalogs that are well matched by the (reddened) spectral energy distribution of a luminous WNL star (see Figs. 6 and 15), (ii) the location of WR 102c in the region of the IRAC color-color diagram populated by WN stars (Hadfield et al. 2007).
![\begin{figure}
\par\includegraphics[width=8.5cm]{9568fig4.ps}\end{figure}](/articles/aa/full/2008/30/aa09568-08/Timg53.gif) |
Figure 4:
Spectral energy distribution for WR 102ka. The thick red line gives the reddened model flux (see Table 2 for the parameters). Boxes give observed 2MASS magnitudes (labels). Triangles correspond to the flux in the four IRAC channels, which we extracted from the archival images (see
Sect. 3.2 and Table 5). |
| Open with DEXTER |
Table 2:
Stellar parameters of WR 102ka and WR 102c.
Table 3:
Spitzer IRS observations of WR 102ka and WR 102c.
![\begin{figure}
\par\includegraphics[width=8.8cm]{9568fig5.ps}\end{figure}](/articles/aa/full/2008/30/aa09568-08/Timg74.gif) |
Figure 5:
Features in the WR 102ka spectrum that indicate the possible presence of a companion. Observations (blue ragged line) are compared to the synthetic spectrum for our final model of WR 102ka (red dashed line). The black dotted line represents the spectrum of a hot WNE model, scaled down by a factor of ten. By superimposing both models, the N V (?), He I, and He II lines can be reproduced simultaneously. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.5cm]{9568fig6.ps}\end{figure}](/articles/aa/full/2008/30/aa09568-08/Timg75.gif) |
Figure 6:
Spectral energy distribution for WR 102c. The solid line represents the reddened model flux (see Table 2 for the parameters). Boxes give the observed 2MASS magnitudes (labels). Triangles correspond to the flux in the four IRAC channels, which we extracted from the archival images (see Sect. 3.2 and Table 5). |
| Open with DEXTER |
Figer et al. (1999a) classified WR 102c as a WN6 subtype, due to the similarity of its
K-band spectrum with WR 115. Taking this comparison at face value,
we adopt from the analysis of WR 115 by Hamann et al. (2006) the temperature
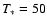 kK and terminal wind velocity
kK and terminal wind velocity
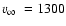 km s-1. To set upper and lower limits to the temperature, we qualitatively compare the K-band spectrum of WR 102c with the PoWR models. We can exclude a
km s-1. To set upper and lower limits to the temperature, we qualitatively compare the K-band spectrum of WR 102c with the PoWR models. We can exclude a 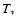 below 40 kK, since
cooler models do not show the He II emission line at
below 40 kK, since
cooler models do not show the He II emission line at
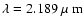 .
.
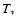 above 60 kK can be excluded because the He I singlet line at
above 60 kK can be excluded because the He I singlet line at
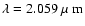 is not visible in hotter models. Despite of the WN-early classification, the relative strength of the He II/Br
is not visible in hotter models. Despite of the WN-early classification, the relative strength of the He II/Br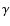 blend, compared to un-blended helium lines, requires a model with some hydrogen (
blend, compared to un-blended helium lines, requires a model with some hydrogen (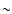 20% by mass as a very rough estimate). The WR 115 comparison star is actually hydrogen-free, but apart from the hydrogen lines this has only little influence on the stellar spectrum.
20% by mass as a very rough estimate). The WR 115 comparison star is actually hydrogen-free, but apart from the hydrogen lines this has only little influence on the stellar spectrum.
The luminosity of WR 102c is derived by scaling the spectral
energy distribution of the model to the photometry marks. The extinction
is simultaneously adjusted, yielding
AV = 25.7 mag. This estimate
is consistent with the extinction in the Sickle nebular region
determined by Cotera et al. (2000) and Schultheis et al. (1999). The latter work provides an extinction map which shows
strong spatial variation of AV, typically 1 mag, in a 1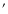 radius around WR 102c. We take this scatter as error estimate for the
adopted AV value. In the K-band this corresponds to
radius around WR 102c. We take this scatter as error estimate for the
adopted AV value. In the K-band this corresponds to
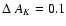 mag. Using model grids for WNE and WNL stars, we inspected the bolometric correction relative to the K-band magnitude for
the range of WN5-WN7 stars analyzed in Hamann et al. (2006), finding a scatter of about 0.65 mag which transforms into a luminosity uncertainty of
mag. Using model grids for WNE and WNL stars, we inspected the bolometric correction relative to the K-band magnitude for
the range of WN5-WN7 stars analyzed in Hamann et al. (2006), finding a scatter of about 0.65 mag which transforms into a luminosity uncertainty of 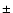 0.26 dex. Together with the scatter of
0.26 dex. Together with the scatter of
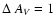 mag from the extinction map, the total uncertainty in luminosity amounts to
mag from the extinction map, the total uncertainty in luminosity amounts to 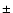 0.3 dex. The derived luminosity of WR 102c,
0.3 dex. The derived luminosity of WR 102c,
![$\log(L)~[L_\odot]\approx 6.3$](/articles/aa/full/2008/30/aa09568-08/img83.gif) ,
is typical for WNL-type stars (see Hamann et al. 2006).
,
is typical for WNL-type stars (see Hamann et al. 2006).
Figure 6 shows that the correspondingly reddened stellar model flux does not perfectly fit to the 2MASS and IRAC photometric observations. However, it should be noted that WR 102c resides in a crowded sky region which makes photometry measurements difficult. For instance, the quality flags in the 2MASS All Sky Catalog of Point Sources indicate difficulties in the photometry determination. Since we fit our synthetic SED to these photometric observations, this
induces some uncertainty to the derived luminosity. Some further error margins arise from the poorly constrained model parameters. The adopted stellar parameters of WR 102c are listed in
Table 2.
We obtained IR spectra of WR 102ka and WR 102c with the IRS spectrograph of the Spitzer Space Telescope (the observation log is shown in Table 3). In addition, our program stars were observed by various imaging mid-IR instruments (Spitzer IRAC, Spitzer MIPS, and MSX) that performed surveys of the GC. These observations are briefly described below.
The Spitzer Infrared Spectrograph (IRS) Short-High (SH) module covers the wavelength range 9.9-19.6  m and provides a moderate spectral resolving power of
m and provides a moderate spectral resolving power of
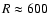 with a slit
aperture of
with a slit
aperture of
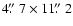 (Houck et al. 2004).
(Houck et al. 2004).
Already the first inspection of the pipe-line extracted spectra of
both program stars revealed a strong mid-IR flux (far above the flux
expected from the synthetic stellar SEDs) increasing towards longer
wavelength. The intensity along the slit does not vary between the
two ``nodding'' positions (in each exposure cycle, the target is
displaced towards one or the other end of the slit in turn).
Therefore we conclude that in both cases the mid-IR emission is not
due to a stellar point source, but emerges from an extended area
larger than the spectrograph slit. Hence we extracted the IRS spectra
(using the SPICE ver. 1.3 software) under the assumption of an
extended emission region with uniform surface brightness.
After the data reduction with SPICE, the individual echelle
orders of the IRS spectra do not match at their wavelength
overlap. For cosmetic reasons we slightly tilted each spectral order
until they fit perfectly. The resulting spectra are shown in
Figs. 7 and 8. The spectra display prominent forbidden
emission lines. Relatively weaker lines of H2, H I,
He II as well as SiC and/or PAH features are also present. The
equivalent widths and the line strengths of the individual emission
lines are compiled in Table 4 for both objects.
![\begin{figure}
\par\includegraphics[width=8.5cm]{9568fig7.ps}\end{figure}](/articles/aa/full/2008/30/aa09568-08/Timg86.gif) |
Figure 7:
Spitzer IRS SH spectrum of WR 102ka with line identifications. Since the emission region is more extended than the spectrograph slit, the flux is given in terms of surface brightness. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.5cm]{9568fig8.ps}\end{figure}](/articles/aa/full/2008/30/aa09568-08/Timg87.gif) |
Figure 8:
Spitzer IRS SH spectrum of WR 102c with line identifications. Since the emission region is more extended than the spectrograph slit, the flux is given in terms of surface
brightness. |
| Open with DEXTER |
The immediate question is whether the IRS spectra are merely dominated
by the GC background or do we indeed measure emission from
circumstellar nebulae physically associated with the program stars.
To answer this key question we retrieve and examine all available
mid-IR images of WR 102ka and WR 102c.
Table 4:
Equivalent widths, intensities, and intensity ratios of the prominent emission lines in the IRS spectra of WR 102ka and WR 102c.
3.2 IRAC and MSX images and photometry of WR 102ka and WR 102c
Spitzer IRAC observations of the central part of the Galaxy were presented by Stolovy et al. (2006). IRAC has high angular resolution (pixel size
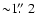 )
and sensitivity (Fazio et al. 2004). It provides simultaneous
)
and sensitivity (Fazio et al. 2004). It provides simultaneous
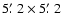 images in four channels (cf. Table 5).
images in four channels (cf. Table 5).
We have retrieved and analyzed the archival IRAC images of the fields containing WR 102ka and WR 102c. For illustration, Figs. 9 and 10 show these images in the first and the forth IRAC channel. Both WR 102c and WR 102ka are detected at all four wavelengths. To
extract photometric fluxes the current version of the mopex software was used (see Table 5). For the IRAC magnitudes and colors we adopted the calibration by Reach et al. (2005). The IRAC color indices of WR 102ka and WR 102c agree well with those of other galactic WR stars as presented by Hadfield et al. (2007) on basis of the IRAC GLIMPSE survey.
Images of the WR 102ka and WR 102c fields at wavelengths longer than those covered by IRAC were obtained with the Midcourse Space Experiment (MSX). The intrinsic angular resolution of this instrument - limited by its pixel size - is only 20
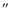 ,
which corresponds to 0.8 pc linear extent at the distance of the GC (Price et al. 2001). Figure 11 displays the archival MSX E-band image of the GC region. Both our objects show up as bright structures far above the general background, albeit in different morphological context.
,
which corresponds to 0.8 pc linear extent at the distance of the GC (Price et al. 2001). Figure 11 displays the archival MSX E-band image of the GC region. Both our objects show up as bright structures far above the general background, albeit in different morphological context.
WR 102ka coincides with an isolated, unresolved source visible in the wavelength bands C, D and E (see Fig. 12), as already noticed by Clark et al. (2005). The fluxes from the MSX point source catalog are included in Table 6.
WR 102c resides in an IR-bright, extended H II region, the Sickle
nebula. Figure 13 shows its MSX images. The unresolved
Quintuplet cluster is the dominant source in the A-band (8.28  m).
However, towards longer wavelengths the emission from the Sickle nebula
embedding WR 102c is strongly increasing. Remarkably, in the E-band
(18.2-25.1
m).
However, towards longer wavelengths the emission from the Sickle nebula
embedding WR 102c is strongly increasing. Remarkably, in the E-band
(18.2-25.1  m) the region centered on WR 102c is significantly brighter
than the whole Quintuplet cluster. The Sickle nebula appears as an
extended complex even with the poor resolution of MSX. The MSX point
source catalog lists a couple of sources that coincide with WR 102c within the resolution. The closest entry, G000.1668-00.0434, is offset
from the 2MASS coordinates of WR 102c by 7
m) the region centered on WR 102c is significantly brighter
than the whole Quintuplet cluster. The Sickle nebula appears as an
extended complex even with the poor resolution of MSX. The MSX point
source catalog lists a couple of sources that coincide with WR 102c within the resolution. The closest entry, G000.1668-00.0434, is offset
from the 2MASS coordinates of WR 102c by 7
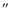 .
Somewhat arbitrarily
we identify this source with WR 102c and adopt the corresponding fluxes
(cf. Table 6).
.
Somewhat arbitrarily
we identify this source with WR 102c and adopt the corresponding fluxes
(cf. Table 6).
The MSX bands cover the wavelength range of our Spitzer IRS
spectra. Because both program stars are detected as MSX point sources
in all bands we conclude that the IRS spectra probe emission
originating from nebulae physically associated with WR 102ka and WR 102c.
For MSX with its 20
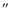
 20
20
 pixels these objects
remain unresolved point sources. However, we had concluded that the
emission sources are more extended than the Spitzer IRS slit of
pixels these objects
remain unresolved point sources. However, we had concluded that the
emission sources are more extended than the Spitzer IRS slit of
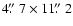 .
When multiplying the measured surface
flux with the slit area, we obtain the flux covered by the slit and
plot it in Figs. 14 and 15. The MSX point
source fluxes lie higher by a factor 5 to 7 for both program stars.
This is consistent with the above conclusion that both sources are
more extended than the area covered by the IRS slit.
.
When multiplying the measured surface
flux with the slit area, we obtain the flux covered by the slit and
plot it in Figs. 14 and 15. The MSX point
source fluxes lie higher by a factor 5 to 7 for both program stars.
This is consistent with the above conclusion that both sources are
more extended than the area covered by the IRS slit.
Table 5:
IRAC fluxes, magnitudes, and IR colors of WR 102ka and WR 102c.
![\begin{figure}
\par\includegraphics[width=13.2cm,clip]{9568fig9.ps}\end{figure}](/articles/aa/full/2008/30/aa09568-08/Timg93.gif) |
Figure 9:
Spitzer IRAC archive image at 3.6  ( left) and 8
( left) and 8  ( right) of the field around WR 102ka. The image size is
( right) of the field around WR 102ka. The image size is
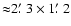 .
North is to the top and east to the left. The white circles have a radius of 10 .
North is to the top and east to the left. The white circles have a radius of 10
 and are centered on the coordinates of WR 102ka.
and are centered on the coordinates of WR 102ka. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=13.2cm,clip]{9568fig10.ps}\end{figure}](/articles/aa/full/2008/30/aa09568-08/Timg94.gif) |
Figure 10:
Spitzer IRAC archive image at 3.6  ( left) and 8
( left) and 8  ( right) of the field around WR 102c. The image size is
( right) of the field around WR 102c. The image size is
 .
North is to the top and east to the left. The white circles have a radius of 10 .
North is to the top and east to the left. The white circles have a radius of 10
 and are centered on the coordinates of WR 102c.
and are centered on the coordinates of WR 102c. |
| Open with DEXTER |
4 Analysis of mid-IR spectra and images
4.1 Temperature and mass of the dust around WR 102ka and WR 102c
As illustrated in Figs. 12, 13 and Table 6, the flux is increasing towards longer wavelengths and is strongest in the E band for both objects. The emission in this band is mostly due to dust grains heated by starlight (Cohen & Green 2001).
In order to determine the temperature, the mass, and the composition of the circumstellar dust around WR 102ka and WR 102c, we use the publicly available code DUSTY (Ivezic & Elitzur 1997) for modeling the continuum emission. This code treats the continuum radiative transfer in dust for a spherical circumstellar nebula, irradiated by a central star with a given emergent flux. For the optical properties of the dust, the theoretical grain model from Draine et al. (1984) is implemented. By suitable transformation to scale-free
quantities, DUSTY requires the following free parameters to be specified:
- i)
- The radiation field of the central star. This parameter
is determined by model stellar spectra obtained from our spectral
analyses (Sect. 2).
- ii)
- T1, the temperature at the inner boundary.
This parameter mainly influences the wavelength of flux maximum.
DUSTY assumes that the dust temperature is in radiative equilibrium
with the radiation field. Hence, T1 implicitly also fixes the inner
radius of the dust shell, r1.
- iii)
- Y=r2/r1, the radial extent of the dust shell. This parameter gives the outer boundary r2 in units of the inner boundary r1. Y influences the temperature stratification. In the optically thin case (which is relevant for our objects), a thin shell is nearly isothermal.
- iv)
- The radial density profile of the dust shell. For simplicity, we assume
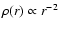 for stationary expansion at constant velocity.
for stationary expansion at constant velocity.
- v)
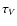 ,
the radial optical depth of the
dust shell at 5500 Å. This parameter governs the brightness of the dust emission. In the
optically thin regime, the fraction of stellar radiation which is converted by the dust into IR emission depends roughly linearly on
,
the radial optical depth of the
dust shell at 5500 Å. This parameter governs the brightness of the dust emission. In the
optically thin regime, the fraction of stellar radiation which is converted by the dust into IR emission depends roughly linearly on 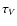 .
.
- vi)
- The grain size distribution. We adopt a usual power-law distribution,
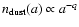 ,
for the grain size a, parameterized by the exponent q and limits for the smallest and largest dust grain diameter,
,
for the grain size a, parameterized by the exponent q and limits for the smallest and largest dust grain diameter,
 and
and
 .
For the exponent we take q=3.5 after Mathis et al. (1977). The cut-off values influence the temperature and optical properties of the dust.
.
For the exponent we take q=3.5 after Mathis et al. (1977). The cut-off values influence the temperature and optical properties of the dust.
- vii)
- The composition of dust. We assume a chemical composition as usually adopted for the standard ISM (Draine 2004), i.e. 47% of graphite and 53% of silicate grains.
A series of models with various choices of the parameters T1, Y,
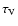 and grain size (
and grain size (
 ,
,
 )
were computed and fitted to the observed IR SED of our program stars.
)
were computed and fitted to the observed IR SED of our program stars.
![\begin{figure}
\par\includegraphics[width=8.5cm]{9568fig11.ps}\end{figure}](/articles/aa/full/2008/30/aa09568-08/Timg102.gif) |
Figure 11:
MSX band E image (histogram equalization scale). Positions of nebulae around WR 102ka and WR 102c are indicated by the arrows. |
| Open with DEXTER |
The cut-off values of the grain size distribution,
 and
and
 ,
have strong influence on the dust spectral energy distribution. Lowering
,
have strong influence on the dust spectral energy distribution. Lowering
 increases the amount of flux blueward 8.3
increases the amount of flux blueward 8.3  m. Very small grains (VSG) with diameter
m. Very small grains (VSG) with diameter
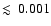
 m, increase the portion of scattered light and heat up more rapidly by the absorption of one energetic photon compared to larger grains. The DUSTY code, however, does not account for the detailed physics of the VSG. The upper cut-off value
m, increase the portion of scattered light and heat up more rapidly by the absorption of one energetic photon compared to larger grains. The DUSTY code, however, does not account for the detailed physics of the VSG. The upper cut-off value
 is difficult to constrain since the large grains contribute mostly to longer wavelengths where no data are available.
is difficult to constrain since the large grains contribute mostly to longer wavelengths where no data are available.
As it was mentioned earlier, the inner parts of the dusty nebulae around our program stars are covered by the Spitzer IRS slit (
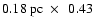 pc at the distance of the GC), while the MSX pixels correspond to a larger area (
pc at the distance of the GC), while the MSX pixels correspond to a larger area (
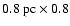 pc).
The DUSTY code provides only the total flux and cannot be used to compute angle-dependent intensities. Therefore we approximate an extended nebula by stacking together two DUSTY models: an ``inner part'' that roughly fits into the Spitzer slit, and an
``outer part'' that adds to the total flux observed with MSX. While the temperature T1 in the ``inner part'' model is a parameter, for the ``outer part'' model T1 is fixed by the temperature profile in the dust shell, such that there is continuous temperature distribution
across both the ``inner'' and the ``outer'' part.
pc).
The DUSTY code provides only the total flux and cannot be used to compute angle-dependent intensities. Therefore we approximate an extended nebula by stacking together two DUSTY models: an ``inner part'' that roughly fits into the Spitzer slit, and an
``outer part'' that adds to the total flux observed with MSX. While the temperature T1 in the ``inner part'' model is a parameter, for the ``outer part'' model T1 is fixed by the temperature profile in the dust shell, such that there is continuous temperature distribution
across both the ``inner'' and the ``outer'' part.
Figures 14 and 15 display our best fit to the measurements. The input model parameters and inferred quantities are compiled in Table 7. The ``inner part'' model fits well to the continuum emission in the IRS aperture, while the MSX photometry is reproduced by the co-added flux from both the ``inner'' and the ``outer'' part.
Our analysis reveals dust remarkably close to the WN stars. In case of WR 102ka the dust is found as close as 1000 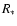 from the stellar surface! In case of the hotter WR 102c the inner boundary of the dust envelope is at 5000
from the stellar surface! In case of the hotter WR 102c the inner boundary of the dust envelope is at 5000 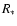 .
To our knowledge, this is the first detection of dust in such close proximity to a WN-type star.
.
To our knowledge, this is the first detection of dust in such close proximity to a WN-type star.
![\begin{figure}
\par\includegraphics[width=12.6cm,clip]{9568fig12.ps}\end{figure}](/articles/aa/full/2008/30/aa09568-08/Timg106.gif) |
Figure 12:
Archival MSX images of the sky field around WR 102ka, from left to right in the A-band (8.28  m), C-band (12.13 m), C-band (12.13  m), D-band (14.65 m), D-band (14.65  m), and E-band (21.34 m), and E-band (21.34  m). Each image has a size of m). Each image has a size of
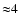 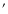 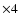 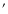 .
North is to the top and east to the left. The circles have a radius of 20 .
North is to the top and east to the left. The circles have a radius of 20
 and are centered on the coordinates of WR 102ka.
and are centered on the coordinates of WR 102ka. |
| Open with DEXTER |
To infer the mass of dust we first compute the density using the information on the dust opacity. According to Li (2005), the mass absorption coefficient of the Draine et al. (1984) grain model is given by
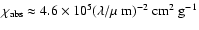 .
For
.
For
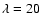
 m this yields
m this yields
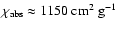 .
It should be remembered that the absolute value of the mass absorption coefficient depends strongly on the underlying grain model and can differ in extreme cases by an order of magnitude.
.
It should be remembered that the absolute value of the mass absorption coefficient depends strongly on the underlying grain model and can differ in extreme cases by an order of magnitude.
We denote the dust opacity by
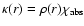 .
The inverse square dilution of
the density yields
.
The inverse square dilution of
the density yields
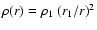 .
The radial optical depth is
.
The radial optical depth is
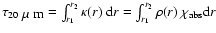 .
Integrating and rearranging for the density results in
.
Integrating and rearranging for the density results in
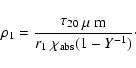 |
(2) |
The dust mass is given by the integral over the volume, i.e.
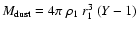 .
The inferred dust masses are listed in Table 7. The inner dust shell (observed with Spitzer IRS) contains only about one percent to the total mass in both objects, but contributes roughly one sixths to the mid-IR flux because of its higher temperature. The total dust mass of WR 102c is much higher than of WR 102ka, reflecting its much stronger IR flux.
.
The inferred dust masses are listed in Table 7. The inner dust shell (observed with Spitzer IRS) contains only about one percent to the total mass in both objects, but contributes roughly one sixths to the mid-IR flux because of its higher temperature. The total dust mass of WR 102c is much higher than of WR 102ka, reflecting its much stronger IR flux.
4.2 Molecular hydrogen diagnostics
In the next two sections we discuss the emission lines in the Spitzer IRS spectra that trace the gaseous material.
Emission from warm molecular hydrogen is routinely detected in
photo-dissociation regions (PDRs) (e.g. Parmar et al. 1991).
Models of H II/PDR regions predict a thin skin around the
ionized bubble, where hydrogen is mainly in atomic state (Kaufman
et al. 2006). The PDR is adjacent to it. The PDR starts with a
transition region of warm (
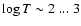 )
molecular hydrogen
mixed with atomic H I, which has
)
molecular hydrogen
mixed with atomic H I, which has  10% of the
spatial extend of the H II region. In the outer layers of the
PDR, the hydrogen becomes cooler (
10% of the
spatial extend of the H II region. In the outer layers of the
PDR, the hydrogen becomes cooler (
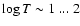 )
and
predominantly molecular. The size of the H II region and,
consequently, the distance between the ionizing star and the zone
where the warm H2 is located, depends on the number of ionizing
photons and on the electron density. For a star with
)
and
predominantly molecular. The size of the H II region and,
consequently, the distance between the ionizing star and the zone
where the warm H2 is located, depends on the number of ionizing
photons and on the electron density. For a star with
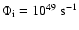 and electron density
and electron density
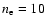 cm-3, the PDR starts at
cm-3, the PDR starts at
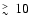 pc from the ionizing
source (Kaufman et al. 2006). Ultracompact and compact
H II regions with radii
pc from the ionizing
source (Kaufman et al. 2006). Ultracompact and compact
H II regions with radii 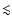 1 pc are observed around
new-born massive stars located in dense environments with
1 pc are observed around
new-born massive stars located in dense environments with
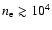 cm-3 (Dopita et al. 2006).
cm-3 (Dopita et al. 2006).
In the close vicinity of an evolved massive star the presence of
molecular hydrogen is very rare. Smith (2002) reported a
discovery of a ro-vibrational line
( -0) S(1)
-0) S(1)  2.12
2.12  m of H2 in the Homunculus
nebula around
m of H2 in the Homunculus
nebula around 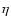 Carinae. Here, we identify lines of
pure-rotational (
Carinae. Here, we identify lines of
pure-rotational (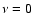 )
transitions of molecular hydrogen at
)
transitions of molecular hydrogen at
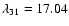
 m [J = 3-1] and
m [J = 3-1] and
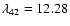
 m [J = 4-2] in the Spitzer spectra of WR 102ka and WR 102c (cf. Figs. 7, 8 and Table 4).
To our knowledge, this is the first detection of pure-rotational
transitions of molecular hydrogen in massive star nebulae.
m [J = 4-2] in the Spitzer spectra of WR 102ka and WR 102c (cf. Figs. 7, 8 and Table 4).
To our knowledge, this is the first detection of pure-rotational
transitions of molecular hydrogen in massive star nebulae.
A method to infer the excitation temperature and column density of
molecular hydrogen from the measured intensities of pure-rotational
lines was applied by Parmar et al. (1991) to the Orion Bar.
When gas has sufficiently high density, collisions maintain the lowest
pure rotational levels of H2 in thermal equilibrium (Burton et al. 1990). Hence, the lowest rotational transitions of H2provide a thermometer for the warm gas. Rotational
transitions in the IRS band have small Einstein coefficients (
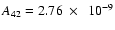 s-1 and
s-1 and
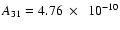 s-1, Turner et al. 1977) and thus are optically thin.
s-1, Turner et al. 1977) and thus are optically thin.
![\begin{figure}
\par\includegraphics[width=12.6cm,clip]{9568fig13.ps}\end{figure}](/articles/aa/full/2008/30/aa09568-08/Timg128.gif) |
Figure 13:
Archival MSX images of the sky field around WR 102c, from left to right in the A-band (8.28  m), C-band (12.13 m), C-band (12.13  m), D-band (14.65 m), D-band (14.65  m), and E-band (21.34 m), and E-band (21.34  m). Each image has a size of m). Each image has a size of
    .
North is to the top and east to the left. The circles have a radius of 20 .
North is to the top and east to the left. The circles have a radius of 20
 and are centered on the coordinates of WR 102c. The Quintuplet cluster can be seen in the lower left part of the images.
and are centered on the coordinates of WR 102c. The Quintuplet cluster can be seen in the lower left part of the images. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=15cm]{9568fig14.ps}\end{figure}](/articles/aa/full/2008/30/aa09568-08/Timg129.gif) |
Figure 14:
Spectrum of WR 102ka. Boxes, triangles and diamonds correspond to photometric measurements with 2MASS, Spitzer IRAC, and MSX, respectively (cf. Tables 5 and 6).
The thin blue line is the spectrum observed with Spitzer IRS. It contains only the flux from those parts of the extended object which have been covered by the spectrograph slit. The thick red line gives the flux of our stellar model. The model of the circumstellar shell adds dust emission. The dash-dotted line represents emission from the inner part of the circumstellar nebula that would be covered by the Spitzer IRS slit, while the long-dashed line contains the
simulated emission from the whole object. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=15cm]{9568fig15.ps}\end{figure}](/articles/aa/full/2008/30/aa09568-08/Timg130.gif) |
Figure 15:
Synthetic stellar spectrum (WNE subtype) of WR 102c (thick red line).
Boxes, triangles and diamonds correspond to photometric measurements with
2MASS, Spitzer IRAC, and MSX, respectively (cf. Tables 5 and 6). The thin blue line is the spectrum observed with Spitzer IRS. It contains only the flux from
those parts of the extended object which have been covered by the spectrograph slit. The model of the circumstellar shell adds dust emission. The dash-dotted line represents emission from the inner part of the circumstellar nebula that would be covered by the Spitzer IRS slit,
while the long-dashed line contains the simulated emission from the whole object. |
| Open with DEXTER |
Table 6:
MSX photometry of WR 102ka and WR 102c from the MSXC6 Catalog.
Since the interstellar extinction at 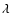 17.04
17.04  m and
m and 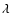 12.28
12.28  m is similar, the ratio of intensities of these two optically thin lines is
m is similar, the ratio of intensities of these two optically thin lines is
![\begin{displaymath}\frac{I_{[3-1]}}{I_{[4-2]}}~=~\frac{N_{J~=~3}}{N_{J~=~4}}\frac{A_{31}}{A_{42}} \frac{\lambda_{42}}{\lambda_{31}},
\end{displaymath}](/articles/aa/full/2008/30/aa09568-08/img132.gif) |
(3) |
where NJ is the column density of H2 in level J. Using the
Boltzmann equation for the ratio of the column densities, one can express the
temperature as a function of the observed line intensities:
![\begin{displaymath}kT = \left( E_{J~=~4}-E_{J~=~3}\right )/
{\ln{\left( {\cal A}\frac{I_{[3-1]}}{I_{[4-2]}} \right)}},
\end{displaymath}](/articles/aa/full/2008/30/aa09568-08/img133.gif) |
(4) |
where EJ is energy of upper level; for the two lines considered here,
EJ = 4/k = 1682 K and
EJ = 3/k = 1015 K. The quantity 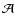 contains the constants for the considered line ratio,
contains the constants for the considered line ratio,
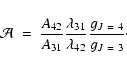 |
(5) |
The statistical weights follow from
g J=(2J+1)(2In+1), where  is the nuclear spin quantum number.
is the nuclear spin quantum number. 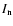 is 0 for even J (para), and 1 for odd J (ortho), giving
gJ = 4 = 9 and
gJ = 3 = 21 for the upper levels of the considered transitions. Combining all constants yields
is 0 for even J (para), and 1 for odd J (ortho), giving
gJ = 4 = 9 and
gJ = 3 = 21 for the upper levels of the considered transitions. Combining all constants yields
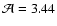 in our case.
in our case.
Inserting the line intensities from Table 4 in Eq. (4), the temperature of warm molecular hydrogen gas in the vicinity of WR 102ka equals 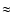 460 K. A higher temperature of the H2 gas is inferred from the IRS spectrum of WR 102c,
460 K. A higher temperature of the H2 gas is inferred from the IRS spectrum of WR 102c,
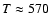 K. It should be noted that the above results hold for a uniform density and temperature, and therefore can be considered
only as a rough estimates.
K. It should be noted that the above results hold for a uniform density and temperature, and therefore can be considered
only as a rough estimates.
The column density of the molecular hydrogen can be estimated from the observed intensity in the H2 lines. The line intensity per steradian is given by
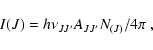 |
(6) |
where NJ is the column density of molecules in the upper level J. The column density of the total molecular hydrogen is inferred from the Boltzmann equation,
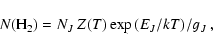 |
(7) |
where Z(T) is the partition function (Herbst et al. 1996):
![\begin{displaymath}Z(T) = 0.0247\ T \left[ 1 - \exp\frac{-6000{\rm K}}{T} \right]^{-1}\cdot
\end{displaymath}](/articles/aa/full/2008/30/aa09568-08/img141.gif) |
(8) |
The interstellar extinction is estimated for our program stars from fitting the SED with stellar atmosphere models (see Table 2). For the given wavelengths of the molecular emission lines and the previously determined EB - V, the extinction weakens the intensity from the program stars by a factor
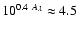 .
.
The de-reddened line intensities now enter Eq. (6), and
the obtained number densities of the corresponding upper levels are
inserted into the Boltzmann Eq. (7) yielding the
total H2 column density. The resulting column density of warm
molecular hydrogen in the vicinity of WR 102ka is
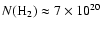 cm-2, and in the vicinity WR 102c
cm-2, and in the vicinity WR 102c
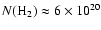 cm-2.
cm-2.
We can estimate the thickness of the warm PDR zone. In the layer of warm molecular hydrogen, the H II/PDR models predict roughly the same number density for hydrogen in atomic form and for H2 molecules (Kaufman et al. 2006). Taking thus the H2 value for the H column
density, and
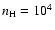 ... 105, the zone of warm molecular hydrogen has only a width of 10-3 ... 10-2 pc.
... 105, the zone of warm molecular hydrogen has only a width of 10-3 ... 10-2 pc.
Furthermore, the information on the column density can be used to derive the total mass of molecular hydrogen that is contained in the column defined by the aperture of the Spitzer IRS instrument. The size of the spectrograph slit corresponds to an area of
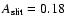 pc
pc 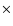 0.43 pc =
0.43 pc =
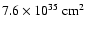 .
The mass of H2,
.
The mass of H2,
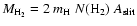 ,
results as
,
results as
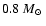 for WR 102ka and
for WR 102ka and
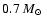 for WR 102c.
for WR 102c.
Since the spectral energy distribution of the ionizing source is known, we can constrain the distance of the PDR from the central star using the combined H II region/PDR models presented by Kaufman et al. (2006). For specified gas-phase elemental abundances
and grain properties, the parameters of a model are the density of H nuclei, 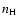 ,
and the incident ``FUV'' flux,
,
and the incident ``FUV'' flux,
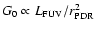 ,
where G0 is expressed in units of
,
where G0 is expressed in units of
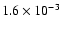 erg s-1 cm-2. ``Far ultra violet'' (FUV) means energies above 6 eV, but below the Lyman edge (13.6 eV), and
erg s-1 cm-2. ``Far ultra violet'' (FUV) means energies above 6 eV, but below the Lyman edge (13.6 eV), and
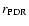 denotes the distance between the ionizing source and the PDR. Using the emergent flux from our atmosphere models, we estimate
denotes the distance between the ionizing source and the PDR. Using the emergent flux from our atmosphere models, we estimate
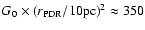 and
and 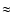 210 for WR 102ka and WR 102c, respectively.
210 for WR 102ka and WR 102c, respectively.
Kaufman et al. (2006) calculated intensities of the pure rotational H2 lines S(1) and S(2) as function of the hydrogen density and the radiation-field parameter G0 (see their Figs. 5 and 6). Now we enter these diagrams with the measured S(1) and S(2) line intensities for our program stars (Table 4). Because the numbers are very similar for both stars, we do not distinguish between them in the following order-of-magnitude estimates.
The observed line intensities are only reproduced for high density
and high radiation flux. Intensities of both H2 lines, being
mutually consistent within a factor of two, allow a stripe in the
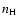 -G0 parameter plane between
-G0 parameter plane between
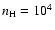 cm-3,
G0 = 105 and
cm-3,
G0 = 105 and
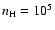 cm-3,
G0 = 103 (higher densities are not plausible and not covered by the
Kaufman et al. models). By comparison with the
cm-3,
G0 = 103 (higher densities are not plausible and not covered by the
Kaufman et al. models). By comparison with the
 values for the stellar radiation deduced above, the models require a distance between star and PDR in the range 0.6 pc ... 6 pc.
values for the stellar radiation deduced above, the models require a distance between star and PDR in the range 0.6 pc ... 6 pc.
Table 7:
Parameters of the dust models for WR 102ka and WR 102c. The ``inner part'' model is designed to reproduce the SED as observed through the aperture of the Spitzer IRS spectrograph, while the emission from the ``outer part'' model matches the SED constrained by the MSX photometric measurements (see text for details).
4.3 Parameters of the H II regions ionized by WR 102ka and
WR 102c
Recently, Simpson et al. (2007) presented Spitzer IRS (10-38  m) spectra obtained at 38 positions in the GC. The position 11 - ``the Bubble Rim'' - is
m) spectra obtained at 38 positions in the GC. The position 11 - ``the Bubble Rim'' - is
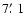 away
from WR 102ka, while the position 22 - ``the Sickle Handle'' - is only
away
from WR 102ka, while the position 22 - ``the Sickle Handle'' - is only
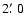 away from WR 102c.
away from WR 102c.
In the Spitzer SH IRS range, the line ratios [Ne III]15.5  m/[Ne II]12.8
m/[Ne II]12.8  m and [S IV]10.5
m and [S IV]10.5  m/[S III]18.7
m/[S III]18.7  m are indicative of the excitation in the nebula. In the IRS spectrum of WR 102c these ratios (see Table 4) are more than two times higher than those measured by Simpson et al. only
m are indicative of the excitation in the nebula. In the IRS spectrum of WR 102c these ratios (see Table 4) are more than two times higher than those measured by Simpson et al. only
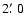 away in the Sickle Handle, or anywhere else in their fields (see their Table 3). Additionally, the continuum flux in the IRS spectrum of WR 102c is a few times higher compared to the observation of the Sickle Handle. This is in agreement with the IRAC and MSX images of the field around WR 102c shown in Figs. 10 and 13. Also, Lang et al. (1997) comment on the unusually high and unexplained (if only the Quintuplet cluster
ionizing stars are accounted for) ratio of H92
away in the Sickle Handle, or anywhere else in their fields (see their Table 3). Additionally, the continuum flux in the IRS spectrum of WR 102c is a few times higher compared to the observation of the Sickle Handle. This is in agreement with the IRAC and MSX images of the field around WR 102c shown in Figs. 10 and 13. Also, Lang et al. (1997) comment on the unusually high and unexplained (if only the Quintuplet cluster
ionizing stars are accounted for) ratio of H92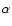 (8.31 GHz) and H115
(8.31 GHz) and H115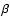 (8.43 GHz) radio recombination lines in the southwest Sickle (l=0.17, b=-0.40) where WR 102c is located. WR 102c produces
(8.43 GHz) radio recombination lines in the southwest Sickle (l=0.17, b=-0.40) where WR 102c is located. WR 102c produces
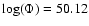 [s-1] ionizing photons, while the entire Quintuplet cluster produces
[s-1] ionizing photons, while the entire Quintuplet cluster produces
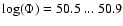 [s-1] (Figer et al. 1999a). WR 102c is located at 3.5 pc projected distance from the Quintuplet, therefore the ionizing flux from WR 102c dominates in a region of at least 1 pc around the star considering only geometrical dilution. We conclude that WR 102c is the principle ionizing source of the surrounding localized nebula that is located in the Sickle Handle region and is probed by our Spitzer IRS spectrum.
[s-1] (Figer et al. 1999a). WR 102c is located at 3.5 pc projected distance from the Quintuplet, therefore the ionizing flux from WR 102c dominates in a region of at least 1 pc around the star considering only geometrical dilution. We conclude that WR 102c is the principle ionizing source of the surrounding localized nebula that is located in the Sickle Handle region and is probed by our Spitzer IRS spectrum.
Similarly, the excitation ratios measured from our IRS spectra of WR 102ka are higher than those measured by Simpson et al. at the Bubble Rim location. From the IRAC and MSX images of the field with WR 102ka (Figs. 9 and 12) it is evident that the nebula is centered on this WN9 type star. Given the high temperature and luminosity of WR 102ka it is safe to conclude that this star powers the IR emission from the surrounding H II region.
To estimate the physical conditions in the H II regions around WR 102ka and WR 102c we use the dusty photoionization models calculated by Dopita et al. (2006). Comparing the observed spectra with the model spectra from Dopita et al., we roughly estimate the presure of ionized gas to
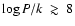 [cm-3 K]. This is in agreement with the location of WR 102ka and WR 102c in the
([Ne III]/[S III]-[Ne III]/[Ne II])
and
([Si IV]/[S III]-[Ne III]/[Ne
II]) model diagrams. Based on the available IRAC and MSX images and the
H2 measurements, the size of the H II region around WR 102ka is not larger than 0.6 ... 6 pc. According to the relationship between the radius of the H II bubble and the pressure in the ISM (Dopita et al. 2005), a bubble of such size around evolved stars is
only possible when the ISM pressure is large,
[cm-3 K]. This is in agreement with the location of WR 102ka and WR 102c in the
([Ne III]/[S III]-[Ne III]/[Ne II])
and
([Si IV]/[S III]-[Ne III]/[Ne
II]) model diagrams. Based on the available IRAC and MSX images and the
H2 measurements, the size of the H II region around WR 102ka is not larger than 0.6 ... 6 pc. According to the relationship between the radius of the H II bubble and the pressure in the ISM (Dopita et al. 2005), a bubble of such size around evolved stars is
only possible when the ISM pressure is large,
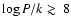 [cm-3 K]. This is significantly larger than the ISM pressure in the GC on average (see e.g. Simpson et al. 2007). Our measurements of the temperature and the density of the H2 (see Sect. 4.2) yielded
[cm-3 K]. This is significantly larger than the ISM pressure in the GC on average (see e.g. Simpson et al. 2007). Our measurements of the temperature and the density of the H2 (see Sect. 4.2) yielded
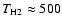 K and
K and
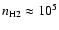 cm-3, resulting in
cm-3, resulting in
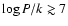 [cm-3 K] in the PDR, where H2 most likely resides.
[cm-3 K] in the PDR, where H2 most likely resides.
According to the diameter-density relationship from Dopita et al. (2006) the density in the H II region is
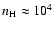 cm-3 around WR 102c and somewhat lower around the cooler star WR 102ka. A lower limit to the mass of ionized gas is obtained
from
cm-3 around WR 102c and somewhat lower around the cooler star WR 102ka. A lower limit to the mass of ionized gas is obtained
from
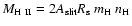 ,
where
,
where
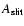 is the area of the Spitzer IRS slit, and
is the area of the Spitzer IRS slit, and 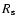 is the Strömgen radius. The lower limit to the mass of photoionized gas around WR 102ka is
is the Strömgen radius. The lower limit to the mass of photoionized gas around WR 102ka is 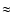 5
5
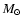 and around WR 102c
and around WR 102c 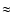 10
10
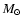 .
.
5 Discussion
Figer et al. (1998) presented evolutionary tracks for very massive stars based on the code by Langer et al. (1994). According to these tracks, the initial stellar mass is
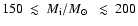 for WR 102ka and
for WR 102ka and
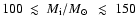 for WR 102c. Thus, both our program stars were initially among the most massive stars of the Galaxy.
for WR 102c. Thus, both our program stars were initially among the most massive stars of the Galaxy.
Our analysis of WR 102ka yields an unconventionally high luminosity at a
relatively low stellar temperature (cf. Table 2). In the
HR-diagram (see Fig. 16) WR 102ka is located above the
Humphreys-Davidson limit, in the region populated by the LBV
stars. WR 102ka is of spectral type Ofpe/WN9. This class of objects
is often considered as either LBV candidates or LBVs in quiescence
(Crowther et al. 1995; Morris et al. 1996). From the
analysis of the K-band spectrum, the surface mass fraction of hydrogen
in WR 102ka is 0.2. This is lower than the hydrogen mass fraction 0.3 ... 0.4 found in known LBVs (Stothers & Chin 2000). The complimentary helium mass fraction in WR 102ka
is significantly higher than found for e.g. the Pistol star (
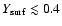 ). This indicates a more advanced evolutionary stage of
the former, compared to ``normal'' LBV stars. Interestingly, Maeder
et al. (2008) discussed possible filiations of Pop. I
massive stars. They suggest that stars with initial masses
). This indicates a more advanced evolutionary stage of
the former, compared to ``normal'' LBV stars. Interestingly, Maeder
et al. (2008) discussed possible filiations of Pop. I
massive stars. They suggest that stars with initial masses
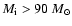 do not pass through an LBV stage, but have high enough
mass loss to get rid of their envelopes on the main
sequence. According to this scenario, it is possible that WR 102ka has not
been a classical LBV, but evolved directly from the Of to the WNL stage.
do not pass through an LBV stage, but have high enough
mass loss to get rid of their envelopes on the main
sequence. According to this scenario, it is possible that WR 102ka has not
been a classical LBV, but evolved directly from the Of to the WNL stage.
![\begin{figure}
\par\includegraphics[width=8.8cm]{9568fig16.ps}\end{figure}](/articles/aa/full/2008/30/aa09568-08/Timg197.gif) |
Figure 16:
Hertzsprung-Russel diagram with the location of some known LBVs, LBV candidates and our program stars. The thick line indicates the Humphreys-Davidson limit (according Eq. (2) in Lamers & Fitzpatrick 1988). The diamonds marks LBVs with time averaged observations, squares shows the location of the LBV at the maximum, circles at the minimum. The small triangles represent LBV candidates, while the big triangles indicate the locations of WR 102ka and WR 102c. Except of WR 102ka and WR 102c, stellar parameters are from Figer et al. (1998), van Genderen (2001),
Najarro (2006), Groh et al. (2006). |
| Open with DEXTER |
In the HR-diagram WR 102c is located in the same region as the outstandingly luminous WN6(h) ... WN8(h) type stars WR 22, WR 24, and WR 25 (Hamann et al. 2006). An
orbital solution for the eclipsing binary WR 22 yields
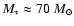 (Rauw et al. 1996) in agreement with an elaborate analysis based on the theory of optically thick winds
(Gräfener & Hamann 2008).
(Rauw et al. 1996) in agreement with an elaborate analysis based on the theory of optically thick winds
(Gräfener & Hamann 2008).
A crude estimate of the present stellar mass of WR 102c can be obtained by using the scaling between
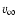 and the escape velocity
and the escape velocity
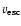 known for WN stars,
known for WN stars,
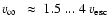 (Lamers & Cassinelli 1999). The escape
velocity is given by
(Lamers & Cassinelli 1999). The escape
velocity is given by
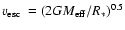 ,
where
,
where
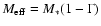 ,
and
,
and 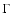 is the Eddington factor. Using stellar parameters and abundances of WR 102c from Table 2 we estimate the present stellar mass to
45 ... 55
is the Eddington factor. Using stellar parameters and abundances of WR 102c from Table 2 we estimate the present stellar mass to
45 ... 55 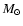 .
.
Because the scaling between
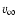 and the
and the
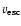 is not
established for stars located above the Humphreys-Davidson limit, the
same method cannot be applied to constrain the present mass of WR 102ka.
is not
established for stars located above the Humphreys-Davidson limit, the
same method cannot be applied to constrain the present mass of WR 102ka.
A vast amount of chemically enriched material has been lost during
recent stellar evolution of WR 102ka and WR 102c, and has contributed to the
nebulae around these stars. Interestingly, the evolutionary tracks
(Meynet et al. 2003) predict that the carbon to oxygen
mass-ratio on the surface is larger than unity already in the WN phase
for stars with
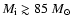 .
Thus one may speculate
that the PAH features observed in the spectra of our program stars and
elsewhere in the GC reflect the carbon enrichment of the
ISM by the stellar winds from initially very massive stars.
.
Thus one may speculate
that the PAH features observed in the spectra of our program stars and
elsewhere in the GC reflect the carbon enrichment of the
ISM by the stellar winds from initially very massive stars.
Neither WR 102ka nor WR 102c belong to the central parts of stellar
clusters. They may have been either dynamically ejected from parental
clusters, or formed in isolation. Conspicuously, WR 102ka is located at
the Bubble Rim, where the ISM could be pressurized by the expanding hot
bubble. WR 102c is located in the Sickle nebula at the edge of a dense
molecular cloud that is ionized by the Quintuplet cluster (Simpson et al. 1997). The Quintuplet cluster is 3-5 Myr old and contains a large population of WC-type stars that are older than WR 102c. Moreover, the radial velocity of the Quintuplet cluster, 130 km s-1 (Figer et al. 1999a), is quite different from the average radial velocity of the Sickle nebula, 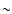 35 km s-1 (Lang et al. 1997). Hence, most likely formation of WR 102c is not linked to the Quituplet cluster.
35 km s-1 (Lang et al. 1997). Hence, most likely formation of WR 102c is not linked to the Quituplet cluster.
Recently, the Spitzer MIPS survey of the GC at 24  m became
publically available. The 24
m became
publically available. The 24  m image of WR 102ka and its nebula is
shown in Fig. 17. It confirms what was already obvious
from the less sensitive MSX observation - the presence of a compact
dusty nebula centered on WR 102ka. The MIPS image resolves its roughly
spherical shape, resembling a Peony flower. The radius of the ``peony
nebula'' in 24
m image of WR 102ka and its nebula is
shown in Fig. 17. It confirms what was already obvious
from the less sensitive MSX observation - the presence of a compact
dusty nebula centered on WR 102ka. The MIPS image resolves its roughly
spherical shape, resembling a Peony flower. The radius of the ``peony
nebula'' in 24  m image is about 50
m image is about 50
 (
( 1.5 pc),
i.e. nearly two times larger than the size of the unresolved image in
the MSX E-band. This is because the MIPS camera is
1.5 pc),
i.e. nearly two times larger than the size of the unresolved image in
the MSX E-band. This is because the MIPS camera is  104 times more sensitive. Unfortunately, the MIPS image is saturated in central parts, and therefore fluxes cannot be extracted for modeling purposes. Intriguingly, the two brightest, saturated parts of the ``peony nebula'' coincide with the point-like central star and with the fuzzy, feather-like feature north of the star, visible in the 8
104 times more sensitive. Unfortunately, the MIPS image is saturated in central parts, and therefore fluxes cannot be extracted for modeling purposes. Intriguingly, the two brightest, saturated parts of the ``peony nebula'' coincide with the point-like central star and with the fuzzy, feather-like feature north of the star, visible in the 8  m IRAC image (right panel of Fig. 9). This spatial coincidence is interesting, because the IRAC 8
m IRAC image (right panel of Fig. 9). This spatial coincidence is interesting, because the IRAC 8  m images trace the emission from PAH, while the MIPS 24
m images trace the emission from PAH, while the MIPS 24  m image shows the emission from small grains. For our Spitzer observation the slit was centered on WR 102ka, and therefore our spectrum samples the central part of the nebula.
m image shows the emission from small grains. For our Spitzer observation the slit was centered on WR 102ka, and therefore our spectrum samples the central part of the nebula.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{9568fig17.ps}\end{figure}](/articles/aa/full/2008/30/aa09568-08/Timg208.gif) |
Figure 17:
Spitzer MIPS 24  m image of WR 102ka and its peony-shaped nebula. The spatial resolution is m image of WR 102ka and its peony-shaped nebula. The spatial resolution is
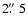 .
The nebula has a radius of about 50 .
The nebula has a radius of about 50
 .
The colors are chosen such that the background appears black. The image is shown on linear scale, as well as the contours. Two central parts of the image are saturated, and are shown in white for cosmetic reasons. North is up, east to the left. .
The colors are chosen such that the background appears black. The image is shown on linear scale, as well as the contours. Two central parts of the image are saturated, and are shown in white for cosmetic reasons. North is up, east to the left. |
| Open with DEXTER |
Unfortunately, the spectrum covers only the short-wavelength range and does not allow a detailed study of the chemical composition and the dynamics of the WR 102ka nebula. The available part of the nebula spectrum is similar to the spectra of known LBV nebulae (cf. Voors et al. 2000). As discussed above, WR 102ka is either a post-LBV star or a star that suffered high mass loss already on the main sequence. It is natural to suggest that the photoionized
peony-shaped nebula contains stellar material that was lost by WR 102ka during LBV-type eruptions and/or its strong stellar wind.
Table 8 compiles some of the results discussed in the previous sections.
Table 8:
Masses and radii. All numbers must be considered as rough estimates.
- 1)
- WR 102c and WR 102ka are among the most luminous and initially most
massive stars in the Galaxy.
- 2)
- In the HR diagram, WR 102c shares its location with the overluminous, very massive WN-type stars WR 22, WR 24, and WR 25.
- 3)
- WR 102ka is located above the Humphreys-Davidson limit in the HR diagram. Its initial mass plausibly was in excess of
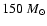 .
The K-band spectrum of WR 102ka shows indications that the star is a WNE+Of/WN9 binary. A hypothetical WNE companion has a higher effective temperature but lower luminosity than the primary.
.
The K-band spectrum of WR 102ka shows indications that the star is a WNE+Of/WN9 binary. A hypothetical WNE companion has a higher effective temperature but lower luminosity than the primary.
- 4)
- The Spitzer IRS spectra of WR 102ka and WR 102c are dominated by emission of a dusty nebulae powered by the stellar radiation of their respective central stars. Based on the modeling of the spectral energy distribution, the inner radius of the circumstellar dust shells is
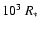 .
This is the first detection of dust so close to the surface of a WN-type star.
.
This is the first detection of dust so close to the surface of a WN-type star.
- 5)
- The lines of pure-rotational transitions of molecular hydrogen are detected in the nebular spectra of WR 102ka and WR 102c. To our knowledge, this is the first detection of pure-rotational transitions of warm H2 in the spectra of nebulae around evolved massive stars. The mass
of the warm molecular hydrogen is about one solar mass in each nebulae.
- 6)
- Assuming that H2 lines originate in the PDRs, the radii of the H II regions around WR 102ka and WR 102c are in the range 0.6 ... 6 pc. These radii are significantly smaller than normally expected for evolved hot massive stars, and probably reflect the high density and pressure in the respective H II regions and the ISM.
- 7)
- WR 102c is the dominant ionizing source of the rather compact H II region located in the Sickle Handle. This demonstrates the importance of individual massive stars scattered in the field as excitation sources in the GC.
- 8)
- The nebula powered by WR 102ka is resolved in the MIPS 24
 m image. This ``Peony nebula'' contains dust and warm molecular hydrogen. We suggest that the formation of the nebula is a result of strong recent mass loss by WR 102ka.
m image. This ``Peony nebula'' contains dust and warm molecular hydrogen. We suggest that the formation of the nebula is a result of strong recent mass loss by WR 102ka.
Acknowledgements
This work is based on observations obtained with the Spitzer Space Telescope, which is operated by the Jet Propulsion Laboratory, California Institute of Technology under a contract with NASA. This work has extensively used the NASA/IPAC Infrared Science Archive, the
NASA's Astrophysics Data System, and the SIMBAD database, operated at CDS, Strasbourg, France. The comments of an anonymous referee helped to improve the clarity of the paper. The
authors thank Nicole Homeier for providing the K-band spectrum of WR 102ka, and M.W. Pound and M. Wolfire for their advices regarding the PDR Toolbox (http://dustem.astro.umd.edu).
- Burton, M., Hollenbach,
D. J., & Tielens, A. G. G. M. 1990, ApJ, 365, 620 [NASA ADS] [CrossRef]
(In the text)
- Clark, J. S.,
Larionov, V. M., & Arkharov, A. 2005, A&A, 435, 239 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Cohen, M., & Green, A.
J. 2001, MNRAS, 325, 531 [NASA ADS] [CrossRef]
(In the text)
- Cotera, A. S., Simpson,
J. P., Erickson, E. F., et al. 2000, ApJS, 129, 123 [NASA ADS] [CrossRef]
(In the text)
- Crowther, P. A., Hillier,
D. J., & Smith, L. J. 1995, A&A, 293, 172 [NASA ADS]
(In the text)
- Crowther, P. A., Morris, P.
W., & Smith, J. D. 2006, ApJ, 636, 1033 [NASA ADS] [CrossRef]
(In the text)
- Dopita, M. A., Groves, B.
A., Fischera, J., et al. 2005, ApJ, 619, 755 [NASA ADS] [CrossRef]
(In the text)
- Dopita, M. A., Fischera,
J., Crowley, O., et al. 2006, ApJ, 639, 788 [NASA ADS] [CrossRef]
(In the text)
- Draine, B. T., 2004, in
Origin and Evolution of the Elements, Carnegie Observatories
Centennial Symposia, ed. A. McWilliam, & M. Rauch, 317
(In the text)
- Draine, B. T., & Lee,
H. M. 1984, ApJ, 285, 89 [NASA ADS] [CrossRef]
(In the text)
- Fazio, G. G., Hora, J. L.,
Allen, L. E., et al. 2004, ApJS, 154, 10 [NASA ADS] [CrossRef]
(In the text)
- Figer, D. F., Najarro,
F., Morris, M., et al. 1998, ApJ, 506, 384 [NASA ADS] [CrossRef]
(In the text)
- Figer, D. F., McLean, I.
S., & Morris, M. 1999a, ApJ, 514, 202 [NASA ADS] [CrossRef]
(In the text)
- Figer, D. F., Kim, S.
S., Morris, M., et al. 1999b, ApJ, 525, 750 [NASA ADS] [CrossRef]
(In the text)
- Freyer, T., Hensler, G.,
& Yorke, H. W. 2003, ApJ, 594, 888 [NASA ADS] [CrossRef]
(In the text)
- Fullerton, A. W., Massa,
D. L., & Prinja, R. K. 2006, ApJ, 637, 1025 [NASA ADS] [CrossRef]
(In the text)
- Gräfener, G., &
Hamann, W.-R. 2008, A&A, 482, 945 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Groh, J. H., Damineli,
A., Teodoro, M., & Barbosa, C. L. 2006, A&A, 457, 591 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Hadfield, L. J., van Dyk,
S. D., Morris, P. W., et al. 2007, MNRAS, 376, 248 [NASA ADS] [CrossRef]
(In the text)
- Hamann, W.-R., &
Koesterke, L. 1998, A&A, 333, 251 [NASA ADS]
(In the text)
- Hamann, W.-R., &
Gräfener, G. 2004, A&A, 427, 697 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Hamann, W.-R.,
Dünnebeil, G., Koesterke, L., Schmutz, W., & Wessolowski,
U. 1991, A&A, 249, 443 [NASA ADS]
(In the text)
- Hamann, W.-R.,
Gräfener, G., & Liermann, A. 2006, A&A, 457, 1015 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Herbst, T. M., Beckwith,
S. V. W., Glindemann, A., et al. 1996, ApJ, 111, 2403 [NASA ADS]
(In the text)
- Homeier, N. L., Blum, R. D.,
Pasquali, A., Conti, P. S., & Damineli, A. 2003, A&A, 408,
153 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Houck, J. R.,
Roellig, T. L., van Cleve, J., et al. 2004, ApJS, 154, 18 [NASA ADS] [CrossRef]
(In the text)
- Ivezic, Z., &
Elitzur, M. 1997, MNRAS, 287, 799 [NASA ADS]
(In the text)
- Kaufman, M. J., Wolfire,
M. G., & Hollenbach, D. J. 2006, ApJ, 644, 283 [NASA ADS] [CrossRef]
(In the text)
- Krabbe, A., Genzel, R.,
Eckart, A., et al. 1995, ApJ, 447, L95 [NASA ADS] [CrossRef]
(In the text)
- Lamers, H. J. G. L. M.,
& Fitzpatrick, E. L. 1988, ApJ, 324, 279 [NASA ADS] [CrossRef]
(In the text)
- Lamers, H. J. G. L. M.,
& Cassinelli, J. P. 1999, Introduction to Stellar Winds, ed. H.
J. G. L. M. Lamers, & J. P. Cassinelli (Cambridge, UK:
Cambridge University Press), 49
(In the text)
- Lang, C. C., Goss, W.
M., & Wood, D. O. S. 1997, ApJ, 474, 275 [NASA ADS] [CrossRef]
(In the text)
- Langer, N., Hamann,
W.-R., Lennon, M., et al. 1994, A&A, 290, 819 [NASA ADS]
(In the text)
- Li, A. 2005, AIPC, 761,
123 [NASA ADS]
(In the text)
- Maeder, A., Meynet, G.,
Ekström, S., Hirschi, R., & Georgy, C. 2008,
[arXiv:0801.4712]
(In the text)
- Meynet, G., & Maeder,
A. 2003, A&A, 404, 975 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Martins, F., Genzel, R.,
Hillier, D. J., et al. 2007, A&A, 468, 233 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Mathis, J. S., Rumpl, W.,
& Nordsieck, K. H. 1977, ApJ, 217, 425 [NASA ADS] [CrossRef]
(In the text)
- Moneti, A., Stolovy, S.,
Bommart, J. A. D. L, et al. 2001, A&A, 366, 106 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Morris, P. W., Eenens, P.
R. J, Hanson, M. M., et al. 1996, ApJ, 470, 597 [NASA ADS] [CrossRef]
(In the text)
- Najarro, F. 2006, J.
Phys. Conf. Ser., 54, 224 [NASA ADS] [CrossRef]
(In the text)
- Oskinova, L. M., Hamann,
W.-R., & Feldmeier, A. 2007, A&A, 476, 1331 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Parmar, P. S., Lacy, J.
H., & Achtermann, J. M. 1991, ApJ, 372, 25 [NASA ADS] [CrossRef]
(In the text)
- Price, S. D., Egan, M.
P., Carey, S. J., Mizuno, D. R., & Kuchar, T. A. 2001, AJ, 121,
2819 [NASA ADS] [CrossRef]
(In the text)
- Rauw, G., Vreux, J.-M.,
Gosset, E., et al. 1996, A&A, 306, 771 [NASA ADS]
(In the text)
- Reach, W., Megeath, S.
T., Cohen, M., et al. 2005, PASP, 117, 978 [NASA ADS] [CrossRef]
(In the text)
- Reid, M. J., ARA&A, 31,
345
(In the text)
- Ramírez, S. V.,
Arendt, R. G., Sellgren, K., et al. 2008, ApJS, 175, 147 [NASA ADS] [CrossRef]
(In the text)
- Rodriguez-Fernández,
N. J., Martín-Pintado, J., & de Vicente, P. 2001, A&A,
377, 631 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Schultheis, M., Ganesh,
S., Simon, G., et al. 1999, A&A, 349, L69 [NASA ADS]
(In the text)
- Serabyn, E., Shupe, D.,
& Figer, D. F. 1998, Nature, 394, 448 [NASA ADS] [CrossRef]
(In the text)
- Simpson, J. P., Colgan,
S. W. J., Cotera, A. S., et al. 1997, ApJ, 487, 689 [NASA ADS] [CrossRef]
(In the text)
- Simpson, J., Colgan, S.
W. J., Cotera, A. S., et al. 2007, ApJ, 670, 1115 [NASA ADS] [CrossRef]
(In the text)
- Smith, N. 2002,
MNRAS, 337, 1252 [NASA ADS] [CrossRef]
(In the text)
- Smith, N., &
Conti, P. S. 2008, ApJ, 679, 1467 [NASA ADS] [CrossRef]
(In the text)
- Stolovy, S., Ramirez, S.,
Arendt, R. G., et al. 2006, JPhCS, 54, 176 [NASA ADS] [CrossRef]
(In the text)
- Stothers, R. B.,
& Chin, C. W. 2000, ApJ, 540, 1041 [NASA ADS] [CrossRef]
- Turner, J., Kirby-Docken,
K., & Dalgarno, A. 1977, ApJS, 35, 281 [NASA ADS] [CrossRef]
(In the text)
- van Genderen, A. M. 2001,
A&A, 366, 508 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Voors, R. H. M., Waters,
L. B. F. M., de Koter, A., et al. 2000, A&A, 356, 501 [NASA ADS]
(In the text)
- Yusef-Zadeh, F., &
Morris, M. 1987, ApJ, 320, 545 [NASA ADS] [CrossRef]
(In the text)
Copyright ESO 2008
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{9568fig1.ps}\end{figure}](/articles/aa/full/2008/30/aa09568-08/Timg21.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{9568fig2.ps}\end{figure}](/articles/aa/full/2008/30/aa09568-08/Timg25.gif)
![\begin{displaymath}R_{\rm t} = R_*
\left[\frac{\varv_\infty}{2500~{\rm km}~{\rm...
...t M}{10^{-4}~M_\odot~{\rm yr^{-1}}}\right]^{2/3} \right. \cdot
\end{displaymath}](/articles/aa/full/2008/30/aa09568-08/img29.gif)
![\begin{figure}
\par\includegraphics[width=18cm]{9568fig3.ps}\end{figure}](/articles/aa/full/2008/30/aa09568-08/Timg39.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm]{9568fig4.ps}\end{figure}](/articles/aa/full/2008/30/aa09568-08/Timg53.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm]{9568fig6.ps}\end{figure}](/articles/aa/full/2008/30/aa09568-08/Timg75.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm]{9568fig7.ps}\end{figure}](/articles/aa/full/2008/30/aa09568-08/Timg86.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm]{9568fig8.ps}\end{figure}](/articles/aa/full/2008/30/aa09568-08/Timg87.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm]{9568fig11.ps}\end{figure}](/articles/aa/full/2008/30/aa09568-08/Timg102.gif)
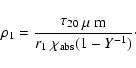
![\begin{figure}
\par\includegraphics[width=15cm]{9568fig14.ps}\end{figure}](/articles/aa/full/2008/30/aa09568-08/Timg129.gif)
![\begin{figure}
\par\includegraphics[width=15cm]{9568fig15.ps}\end{figure}](/articles/aa/full/2008/30/aa09568-08/Timg130.gif)
![\begin{displaymath}\frac{I_{[3-1]}}{I_{[4-2]}}~=~\frac{N_{J~=~3}}{N_{J~=~4}}\frac{A_{31}}{A_{42}} \frac{\lambda_{42}}{\lambda_{31}},
\end{displaymath}](/articles/aa/full/2008/30/aa09568-08/img132.gif)
![\begin{displaymath}kT = \left( E_{J~=~4}-E_{J~=~3}\right )/
{\ln{\left( {\cal A}\frac{I_{[3-1]}}{I_{[4-2]}} \right)}},
\end{displaymath}](/articles/aa/full/2008/30/aa09568-08/img133.gif)
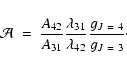
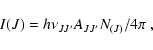
![\begin{displaymath}Z(T) = 0.0247\ T \left[ 1 - \exp\frac{-6000{\rm K}}{T} \right]^{-1}\cdot
\end{displaymath}](/articles/aa/full/2008/30/aa09568-08/img141.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm]{9568fig16.ps}\end{figure}](/articles/aa/full/2008/30/aa09568-08/Timg197.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{9568fig17.ps}\end{figure}](/articles/aa/full/2008/30/aa09568-08/Timg208.gif)