A&A 486, 763-769 (2008)
DOI: 10.1051/0004-6361:200809395
Are dry mergers of ellipticals the way to reconcile model predictions with downsizing?
A. Pipino1 - F. Matteucci2,3
1 - Astrophysics, University of Oxford, Denys Wilkinson Building, Keble Road, Oxford OX1 3RH, UK
2 - Dipartimento di Astronomia, Universita di Trieste, via G.B. Tiepolo, 11, 34100 Trieste, Italy
3 - INAF - Trieste, via G.B. Tiepolo 11, 34100 Trieste, Italy
Received 14 January 2008 / Accepted 6 May 2008
Abstract
Aims. We show that the bulk of the star formation and the galaxy assembly should occur simultaneously in order to reproduce at the same time the downsizing and the chemical properties of present-day massive spheroids within one effective radius.
Methods. By means of chemical evolution models, we create galactic building blocks of several masses and different chemical properties. We then construct a sample of possible merger histories going from a multiple minor merger scenario to a single major merger event aimed at reproducing a single massive elliptical galaxy. We compare our results against the mass-[Mg/Fe] and the mass-metallicity relations.
Results. We found that a series of multiple dry mergers (no star formation in connection with the merger) involving building-blocks that have been created ad hoc to satisfy the [Mg/Fe]-mass relation cannot fit the mass-metallicity relation and viceversa. A major dry merger, instead, does not make the agreement with observations worse if it happens between galaxies that already obey both the mass(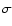 )-[Mg/Fe] and the mass(
)-[Mg/Fe] and the mass(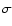 )-metallicity relations. However, this process alone cannot explain the physical reasons for these trends.
)-metallicity relations. However, this process alone cannot explain the physical reasons for these trends.
Conclusions. Dry mergers alone are not be the way to reconcile the need of a more efficient star formation in the most massive galaxies with the late-time assembly suggested in the hierarchical paradigm to recover the galaxy downsizing.
Key words: galaxies: elliptical and lenticular, cD - galaxies: abundances - galaxies: formation - galaxies: stellar content - galaxies: evolution
The scenario describing the formation of elliptical galaxies
in the framework of the hierarchical clustering scenario, namely of a major merger involving
two spirals at late time (e.g., Kauffmann & White 1993) has been questioned
several times (e.g., Ostriker 1980) since its original formulation.
Recent studies (e.g., Thomas & Kauffmann 1999; Pipino & Matteucci 2006; Naab & Ostriker 2007), emphasised a tension between the observed photo-chemical properties and the predicted properties. From the dynamical view point, however, the situation is different. In fact,
at least the medium-sized fast-rotating ellipticals (Emsellem et al. 2007) have
global morphological and kinematical properties which resemble
those of a spiral-spiral merger remnant (e.g., Naab & Burkert 2003; Cox et al. 2006; Robertson et al. 2006). On the other hand, the most massive ojects are better represented by the outcome of a dissipationless merger (Khochfar & Burkert 2005; Naab et al. 2006).
From a more general perspective, to reconcile at the same time the anti-hierarchical behaviour of Active Galactic Nuclei (AGNs; e.g., Hasinger et al. 2005),
the evolution of luminosity function with redshift (e.g., Bundy et al. 2006), as well as the
evidences from the analysis of the stellar populations inhabiting ellipticals (e.g.,
Thomas et al. 2002), a substantial modification of baryons' behaviour,
whith respect to the behaviour of the Dark Matter, seems to be required.
In particular, more massive ellipticals are older and form faster with
respect to smaller objects (Thomas et al. 2005).
This is so-called downsizing (Cowie 1996). Further independent evidence supports the well-known downsizing in the chemical
properties of ellipticals, namely the increase of mean stellar [Mg/Fe] with galaxy mass (see Matteucci 1994). For instance, the very recent observations of the evolution of the mass-gas metallicity relation with redshift (Maiolino et al. 2008)
and the study of the present-day ratio between stars and gas
(Calura et al. 2007), both favour the earlier and faster completion of the SF process for the most massive spheroids, with respect to the low-mass spheroids.
Hierarchical modelling, in its latest versions, partly accounts for
the downsizing. In pratice, the mass assembly still occurs at late times,
but most of the stars have been formed at high redshift in small subunits.
The preferred mechanism for the assembly of massive spheroids
is a sequence of dry mergers![[*]](/icons/foot_motif.gif) (e.g., Khochfar & Burkert 2003; De Lucia et al. 2006). Dry mergers have been observed (Tran et al. 2005; Bell et al. 2006; Rines et al. 2007; and in more extended samples, by van Dokkum 2005),
although the criteria used to define a dry-merger observationally have
been questioned by, e.g., Donovan et al. (2007).
Dry mergers between spheroidal systems are also invoked to explain
the so-called boxy ellipticals (e.g., Naab et al. 2006).
However, if we restrict ourselves to the most massive elliptical galaxies (L > L*),
they seem to be in place and do not show any signs of significant evolution
in mass since
(e.g., Khochfar & Burkert 2003; De Lucia et al. 2006). Dry mergers have been observed (Tran et al. 2005; Bell et al. 2006; Rines et al. 2007; and in more extended samples, by van Dokkum 2005),
although the criteria used to define a dry-merger observationally have
been questioned by, e.g., Donovan et al. (2007).
Dry mergers between spheroidal systems are also invoked to explain
the so-called boxy ellipticals (e.g., Naab et al. 2006).
However, if we restrict ourselves to the most massive elliptical galaxies (L > L*),
they seem to be in place and do not show any signs of significant evolution
in mass since 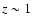 (Scarlata et al. 2006; Brown et al. 2007).
A great deal of work has been done in the field of dynamical simulations,
but so far the consequences on the chemical properties
of the final stellar populations have not been tested.
(Scarlata et al. 2006; Brown et al. 2007).
A great deal of work has been done in the field of dynamical simulations,
but so far the consequences on the chemical properties
of the final stellar populations have not been tested.
On the other hand, in the revised monolithic scenario (Larson 1974; Matteucci 1994; Chiosi & Carraro 2002; Merlin & Chiosi 2006) both the mass(or 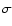 )-[Mg/Fe] (MFMR, hereafter) and the mass(or
)-[Mg/Fe] (MFMR, hereafter) and the mass(or 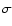 )-metallicity (MMR) relations are naturally explained, as shown by
Pipino & Matteucci (2004, PM04 hereafter). In particular, in PM04 for the first time, the inverse
wind scenario (Matteucci 1994) plus an initial infall episode, are adopted within a multi-zone formulation. Under reasonable assumptions on the behaviour of the infall timescale
and the star formation (SF) efficiency with galactic mass, PM04
showed how this kind of model can reproduce
the whole set of chemical and photometric observables simultaneously.
)-metallicity (MMR) relations are naturally explained, as shown by
Pipino & Matteucci (2004, PM04 hereafter). In particular, in PM04 for the first time, the inverse
wind scenario (Matteucci 1994) plus an initial infall episode, are adopted within a multi-zone formulation. Under reasonable assumptions on the behaviour of the infall timescale
and the star formation (SF) efficiency with galactic mass, PM04
showed how this kind of model can reproduce
the whole set of chemical and photometric observables simultaneously.
In particular, it is necessary that both the bulk of the star formation
and the galactic assembly proceed in lockstep.
The same conclusion was reached by Cimatti et al. (2006), who showed that the downsizing trend should also be extended to the mass assembly in the sense that the most massive ellipticals should have assembled before the less massive ones. This conclusion was based on a re-analysis of the rest frame B-band COMBO-17 and DEEP2 luminosity functions.
The aim of this paper is to show that this has not yet been taken
into account in models based on the hierarchical clustering paradigm.
We create galactic building blocks of different mass
and chemical properties. We then construct a sample of possible merger histories
running from a multiple minor merger scenario to a single major merger event aimed at reproducing
a single massive elliptical galaxy. We compare the results against the MFMR and the MMR.
In the absence of full a dynamical treatment, we cannot undertake a deeper
analysis of the mass- and [
 ]-
]-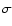 relations. In the following, we will refer to the stellar velocity dispersion as a mass tracer, unless otherwise stated.
relations. In the following, we will refer to the stellar velocity dispersion as a mass tracer, unless otherwise stated.
The chemical code adopted here is described
in PM04 to which we point the reader for more details. In particular,
this model is characterised by: Salpeter (1955) initial mass function (IMF); Thielemann et al. (1996), yields for massive stars; Nomoto et al. (1997), yields for type Ia SNe; and
van den Hoek & Groenewegen (1997), yields for low-
and intermediate-mass stars (the case with
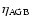 varying with metallicity).
varying with metallicity).
We will use this model for producing ad hoc progenitors of present-day galaxies
to investigate whether the final composite stellar population (CSP) in the merger remnant has
properties that match those of observed ellipticals.
In particular, for each of them, we list star formation efficiency, infall timescale,
and average stellar properties, such as the mass-weighted abundances and abundance ratios
(see PM04 for their definition). We define, according to Pagel & Patchett (1975; see also PM04 and Pipino et al. 2006, hereafter PMC06), the stellar
metallicity distribution,
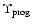 ,
as the fraction of stars
formed in a given metallicity (Fe/H or Mg/Fe) bin.
,
as the fraction of stars
formed in a given metallicity (Fe/H or Mg/Fe) bin.
The possibility to predict
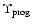 properties is important
in the context of this study because it allows us to infer
the average abundance ratios in the stars. These ratios are useful
when we want to compare our theoretical predictions to the observations,
often given in terms of SSP-equivalent values, namely
luminosity-weighted measures of the properties in the stellar component (see PMC06).
The fact that we deal with old objects without any merger-induced
SF guarantees that mass-weighted and luminosity-weighted values are
very similar in the more massive ellipticals (e.g., Arimoto & Yoshi 1987; Matteucci et al. 1998).
properties is important
in the context of this study because it allows us to infer
the average abundance ratios in the stars. These ratios are useful
when we want to compare our theoretical predictions to the observations,
often given in terms of SSP-equivalent values, namely
luminosity-weighted measures of the properties in the stellar component (see PMC06).
The fact that we deal with old objects without any merger-induced
SF guarantees that mass-weighted and luminosity-weighted values are
very similar in the more massive ellipticals (e.g., Arimoto & Yoshi 1987; Matteucci et al. 1998).
The assumed galactic building blocks have the following characteristics:
- A:
- a
 5
5 
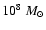 building block (luminous mass) that resembles a sort of present-day dwarf spheroidal galaxy (dSph). It has been obtained by assuming a star formation efficiency of
building block (luminous mass) that resembles a sort of present-day dwarf spheroidal galaxy (dSph). It has been obtained by assuming a star formation efficiency of
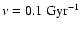 ,
while the infall timescale is
,
while the infall timescale is
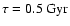 in agreement with the prescriptions of Lanfranchi & Matteucci (2004, 2007).
For this model, we predict [
in agreement with the prescriptions of Lanfranchi & Matteucci (2004, 2007).
For this model, we predict [
 ] = 0.28 dex and [
] = 0.28 dex and [
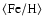 ] = -1.2 dex, and a stellar metallicity distribution
function
] = -1.2 dex, and a stellar metallicity distribution
function
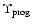 shown in Fig. 1. The star formation in this block lasts 2.4 Gyr, which is the time at which a supernovae-driven galactic wind occurs.
shown in Fig. 1. The star formation in this block lasts 2.4 Gyr, which is the time at which a supernovae-driven galactic wind occurs.
- A+:
- a
 5
5 
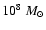 building block has been obtained by assuming a higher star formation efficiency with respect to the previous case
of
building block has been obtained by assuming a higher star formation efficiency with respect to the previous case
of
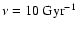 ,
while the infall timescale is
,
while the infall timescale is
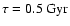 .
.
For this model, we predict [
 ] = 0.57 dex and [
] = 0.57 dex and [
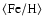 ] = -0.9 dex. The star formation here lasts only 130 Myr due to the faster occurrence of a galactic wind.
] = -0.9 dex. The star formation here lasts only 130 Myr due to the faster occurrence of a galactic wind.
- B:
- a
 5
5 
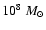 building block has been obtained by assuming a star formation efficiency of
building block has been obtained by assuming a star formation efficiency of
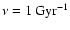 ,
while the infall timescale is
,
while the infall timescale is
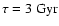 .
.
For this model, we predict [
 ] = -0.1 dex and [
] = -0.1 dex and [
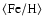 ] = 0.63 dex, and a stellar metallicity distribution
] = 0.63 dex, and a stellar metallicity distribution
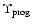 function shown in Fig. 2. The star formation here lasts 1.8 Gyr.
function shown in Fig. 2. The star formation here lasts 1.8 Gyr.
- E:
- a
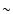
 elliptical galaxy that
matches both the MMR and the MFMR as well as the colour-magnitude relation (CMR, Bower et al.
1992). We refer to PM04's model IIb for the same mass.
For this model, we predict an overall [
elliptical galaxy that
matches both the MMR and the MFMR as well as the colour-magnitude relation (CMR, Bower et al.
1992). We refer to PM04's model IIb for the same mass.
For this model, we predict an overall [
 ] = 0.25 dex and [
] = 0.25 dex and [
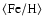 ] = 0.04 dex. The stellar metallicity distribution is presented in Fig. 3 (solid line). We refer the reader to PMC06 for a more detailed description of the
stellar metallicity distributions
] = 0.04 dex. The stellar metallicity distribution is presented in Fig. 3 (solid line). We refer the reader to PMC06 for a more detailed description of the
stellar metallicity distributions
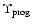 for such a model.
for such a model.
![\begin{figure}
\par\includegraphics[height=6.7cm,width=6.6cm,clip]{9395f1.eps}\end{figure}](/articles/aa/full/2008/30/aa09395-08/Timg19.gif) |
Figure 1:
Predicted stellar metallicity distribution
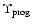 as a function of [Fe/H] for the progenitor A.
as a function of [Fe/H] for the progenitor A. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[height=6.7cm,width=6.4cm,clip]{9395f2.eps}\end{figure}](/articles/aa/full/2008/30/aa09395-08/Timg20.gif) |
Figure 2:
Predicted stellar metallicity distribution
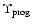 as a function of [Fe/H] for the progenitor B.
as a function of [Fe/H] for the progenitor B. |
| Open with DEXTER |
The final massive elliptical (F) we want to simulate is a 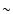 2
2 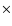
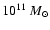 galaxy. In particular, we expect it to have [
galaxy. In particular, we expect it to have [
 ] = 0.27 dex
according to PM04's model IIb predictions for the same mass.
] = 0.27 dex
according to PM04's model IIb predictions for the same mass.
For the sake of simplicity, we will assume that our model galaxies do not have
radial gradient in 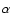 -enhancement.
As shown by Pipino et al. (2008), in fact, even though
most ellipticals form outside-in, the expected strong and positive [
-enhancement.
As shown by Pipino et al. (2008), in fact, even though
most ellipticals form outside-in, the expected strong and positive [
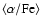 ]
gradient can be affected by the metal rich gaseous flows inside the galaxy acting together
with the SFR. We also recall that observations suggest that the observed gradient slope in the [
]
gradient can be affected by the metal rich gaseous flows inside the galaxy acting together
with the SFR. We also recall that observations suggest that the observed gradient slope in the [
 ]
has a null mean value (e.g., Mehlert et al. 2003).
Therefore, we will refer to a one-zone model in which the metallicity and
the
]
has a null mean value (e.g., Mehlert et al. 2003).
Therefore, we will refer to a one-zone model in which the metallicity and
the 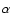 enhancement do not vary with radius. In general, we will expect that mergers cannot account for the steep metallicity gradient observed in the majority of ellipticals (e.g., Carollo et al. 1993), and we postpone to a forthcoming paper the analysis of
the gradients survival to several dry-mergers.
enhancement do not vary with radius. In general, we will expect that mergers cannot account for the steep metallicity gradient observed in the majority of ellipticals (e.g., Carollo et al. 1993), and we postpone to a forthcoming paper the analysis of
the gradients survival to several dry-mergers.
Under these assumptions, we predict the properties of the CSP of the merger remnant in a straightforward manner. In fact, the stellar metallicity distribution function for the end product
of a dry-merger is simply
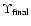 summed over all progenitors
and can be written as:
summed over all progenitors
and can be written as:
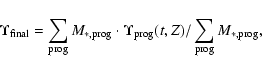 |
(1) |
where
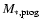 is the stellar mass of the single progenitors.
Similar equations hold for other distributions as functions of either [Mg/Fe] or [Fe/H].
We stress again that this is possible because we are studying dry merger
remnants, i.e., systems where no further SF is allowed to occur.
is the stellar mass of the single progenitors.
Similar equations hold for other distributions as functions of either [Mg/Fe] or [Fe/H].
We stress again that this is possible because we are studying dry merger
remnants, i.e., systems where no further SF is allowed to occur.
We also emphasise that we present an exercise whose assumptions
are rather extreme (i.e., galaxies formed only via dry mergers)
and without taking into account the observed merger rate
and its relation with redshift, environment, and possibly the morphology
of the progenitors (e.g., Lin et al. 2008).
![\begin{figure}
\par\includegraphics[height=6.7cm,width=6.7cm,clip]{9395f3.eps}\end{figure}](/articles/aa/full/2008/30/aa09395-08/Timg25.gif) |
Figure 3:
Shaded hystogram: predicted stellar metallicity distribution
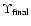 as a function of [Fe/H] for the case in which 50% of the final massive galaxy is made of progenitor A-like building blocks and the rest of progenitors B. For comparison, the prediction for the
as a function of [Fe/H] for the case in which 50% of the final massive galaxy is made of progenitor A-like building blocks and the rest of progenitors B. For comparison, the prediction for the
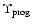 of the PM04 best model (case E) is presented (solid line).
of the PM04 best model (case E) is presented (solid line). |
| Open with DEXTER |
Let us first assume the extreme case in which our massive elliptical
has been made by merging of several progenitors of the kind A only, as expected
from galaxy formation models that assume a short SF process
at high redshift, but let the galaxy assembly happen much later (e.g., De Lucia et al. 2006; Kobayashi et al. 2007).
In order to have the right final mass, we need 400 of such small building blocks.
Since progenitor A has been built to yield the final correct 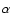 enhancement, our massive spheroid will have a Mg enhancement of 0.28 dex and will match
the average observational value for galaxies of the same mass fairly well.
We can infer from Eq. (1) that the final stellar metallicity distribution
will still look like Fig. 1, therefore its final
metallicity in terms of [Fe/H] will remain very low, thus not
matching either the MMR or the CMR.
enhancement, our massive spheroid will have a Mg enhancement of 0.28 dex and will match
the average observational value for galaxies of the same mass fairly well.
We can infer from Eq. (1) that the final stellar metallicity distribution
will still look like Fig. 1, therefore its final
metallicity in terms of [Fe/H] will remain very low, thus not
matching either the MMR or the CMR.
The predicted value of the SFR per unit mass is 0.02/Gyr for the progenitor of kind A.
Again, we can infer that the final spheroid will have the same value,
at variance with the results from Thomas et al. (2005), which
require this factor to be at least 2-3/Gyr, namely a factor of one hundred higher.
Such a high SFR is needed also to reproduce the observed SFR in
Lyman Break (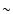
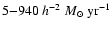 ,
Shapley et al. 2001) and SCUBA (e.g., Swinbank et al. 2004) galaxies.
,
Shapley et al. 2001) and SCUBA (e.g., Swinbank et al. 2004) galaxies.
On the other hand, a quasi-monolithic model can naturally have
the required SFR per unit mass. In fact, the prediction by PM04 (Fig. 4)
is in good agreement for what concerns shape, timescale, and mean redshift of formation
with those inferred by Thomas et al. (2005, see their Fig. 10),
the only difference being the sharp truncation due to the galactic wind.
It should be noted that many models based on the hierarchical clustering, which claim to have incorporated downsizing (e.g., De Lucia et al. 2006; Kobayashi et al. 2007), have an average SFR per unit mass lower at least by a factor of 3-5 than what is required from chemical evolution studies and line-strenght indices analysis to reproduce the [Mg/Fe] in massive ellipticals;
according to our calculations, with such a low SFR per unit mass is possible to reproduce only a very modest 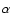 -enhancement (if any).
In fact, such a value for the SFR per unit mass (
-enhancement (if any).
In fact, such a value for the SFR per unit mass (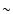
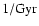 )
will only
suffice to explain the [
)
will only
suffice to explain the [
 ]
] 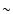 0.1 dex of the less massive spheroids.
0.1 dex of the less massive spheroids.
We tried to overcome the problem of having a too low SFR by introducing another ad hoc building block, namely the progenitor A+, which has a SFR per unit mass of the order of unity.
In this case, however, the lack of agreement with the MMR is much more evident,
and also the predicted [
 ]
is too high.
We note in passing that if we allow for a subsequent gas-rich merger
triggering a substantial episode of SF, we may be able to reproduce the MFMR,
but we fail in obtaining other properties, such as the CMRs or the MMR, as shown by
Pipino & Matteucci (2006, see, e.g., the models discussed in their Sect. 3.3).
]
is too high.
We note in passing that if we allow for a subsequent gas-rich merger
triggering a substantial episode of SF, we may be able to reproduce the MFMR,
but we fail in obtaining other properties, such as the CMRs or the MMR, as shown by
Pipino & Matteucci (2006, see, e.g., the models discussed in their Sect. 3.3).
![\begin{figure}
\par\includegraphics[height=7cm,width=7.2cm,clip]{9395f4.eps}\end{figure}](/articles/aa/full/2008/30/aa09395-08/Timg28.gif) |
Figure 4:
Predicted SFR per unit mass for several masses, PM04's best model.
The model E is represented by a solid line. |
| Open with DEXTER |
On the other hand, there can exist the extreme case in which
the galaxy is created by several progenitors of the kind B. The results of this analysis show that this model can reproduce the MMR, but it predicts an underabundance of 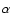 -elements relative to Fe, at variance with observations.
-elements relative to Fe, at variance with observations.
We conclude that we cannot form massive spheroids from a sequence of
several dry mergers between building blocks of the same kind (similar mass and chemical properties),
even if the progenitors are chosen to have the correct 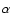 -enhancement.
For the same reason, present-day, low-mass ellipticals, which satisfy both the MMR
and the MFMR, cannot be the building blocks of massive ones.
This conclusion can be extended to the CMR, since the colour differences
are mainly driven by metallicity.
Remarkably, similar conclusions have been obtained by Ciotti et al. (2007)
by studying the dynamical properties of ellipticals. Therefore, pure dissipationless
merger of similar stellar systems cannot change the metallicity, the
-enhancement.
For the same reason, present-day, low-mass ellipticals, which satisfy both the MMR
and the MFMR, cannot be the building blocks of massive ones.
This conclusion can be extended to the CMR, since the colour differences
are mainly driven by metallicity.
Remarkably, similar conclusions have been obtained by Ciotti et al. (2007)
by studying the dynamical properties of ellipticals. Therefore, pure dissipationless
merger of similar stellar systems cannot change the metallicity, the 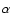 -enhancement, the colours, and the virial velocity dispersion.
-enhancement, the colours, and the virial velocity dispersion.
Now we relax the extreme assumption of the previous section and allow for two
or more kinds of progenitors for our massive elliptical.
If, for simplicity sake, there is a fraction f= 50% of the final mass coming from progenitors
of the type A and 1-f= 50% from progenitors B, the final stellar metallicity distribution (shaded hystogram in Fig. 3) will be closer to the one
expected for a normal elliptical (solid line in Fig. 3)and the outcome will match the CMR and the MMR, being its final [
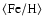 ] = 0.66 dex, but the predicted [
] = 0.66 dex, but the predicted [
 ] = 0.06 dex is still too low.
Moreover, this scenario cannot represent a solution for the still too low SFR per unit mass.
] = 0.06 dex is still too low.
Moreover, this scenario cannot represent a solution for the still too low SFR per unit mass.
If we repeat the same exercise with model A+ and B,
these latter quantities agree better with the values
inferred from the observations, and
we also notice an improvement for [
 ], which now amounts to 0.1 dex.
], which now amounts to 0.1 dex.
We admit that the portion of the parameter space that we are investigating is quite
small - although the choice of the models is sensible - the main aim of this investigation
being the study of a few clear and extreme cases.
Such examples serve to probe to what extent the random nature of
the merger process models can be accommodated within the observational
uncertainties. A more comprehensive analysis featuring a proper merger history based on the
hierachical growth of structure and a self-consistent chemical evolution
is in preparation.
However, even in the case in which either two more suitable progenitors can be found, or
a different mixture of several progenitors can predict the right final chemical
properties for a given final galactic mass, several questions arise: i) why are only dSph (i.e., progenitor A) still observable in the local universe? (but see Robertson et al. 2005);
ii) why is the fraction f such that none of the two classes is predominant?; and
iii) since the [
 ]
correlates with the final galactic mass, one should expect progenitors with different initial (i.e., pre-merger) properties, which scale accordingly to the final mass of the object, to live in the early universe. How it is possible that
they know in advance what they are about to build later on? Finally, even if a selection mechanism is at work and it leads to an agreement
between model and observed chemical properties, it must be able
to account for other scaling relations, such as the Faber-Jackson (Faber & Jackson 1976) and the Kormendy (1977) relations as well as the Fundamental Plane (e.g., Dressler et al. 1987).
]
correlates with the final galactic mass, one should expect progenitors with different initial (i.e., pre-merger) properties, which scale accordingly to the final mass of the object, to live in the early universe. How it is possible that
they know in advance what they are about to build later on? Finally, even if a selection mechanism is at work and it leads to an agreement
between model and observed chemical properties, it must be able
to account for other scaling relations, such as the Faber-Jackson (Faber & Jackson 1976) and the Kormendy (1977) relations as well as the Fundamental Plane (e.g., Dressler et al. 1987).
It is also interesting to note that Bournaud et al. (2007) claimed that
repeated minor mergers - such as the ones studied in this section - can theoretically form massive boxy elliptical galaxies without major mergers, being more frequent than the latter, in particular at moderate redshifts. The mechanism put forward by Bournaud et al. (2007) could explain the morphology and the dynamical properties
of the merger remnant; in particular, it might be a viable alternative to overcome the issues
in the major-merger scenario (Naab & Ostriker 2007)
to explain the high boxiness of massive ellipticals. Unfortunately,
Bournaud et al. (2007) explored only too narrow a mass range to understand
whether their argument helps in reproducing the observed scaling relations
for elliptical galaxies.
At variance with the previous section, we now test the scenario in which the final
galaxy is built via a series of a minor dry mergers, namely adding
several progenitors of either type (A-like or B-like) to a galaxy like progenitor
E until we double its mass (therefore, we need roughly 200 small building blocks).
Since the model E stars contain the right amount of 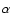 -enhancement and mean metallicity,
this case will help us in assessing whether the accretion of several progenitors of either types A or B can worsen the agreement with observations.
Following the same line of reasoning as in the previous sections, we first assume
that we want to build the final galaxy as the sum of E and only type A+ progenitors.
We obtain the
-enhancement and mean metallicity,
this case will help us in assessing whether the accretion of several progenitors of either types A or B can worsen the agreement with observations.
Following the same line of reasoning as in the previous sections, we first assume
that we want to build the final galaxy as the sum of E and only type A+ progenitors.
We obtain the
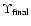 for model F according to Eq. (1), and
we find that the final [
for model F according to Eq. (1), and
we find that the final [
 ] = 0.26 does not exceed the observational boundaries. If we assume that F is the result of a progenitor like E plus roughly
two hundreds building blocks of the type B, we predict [
] = 0.26 does not exceed the observational boundaries. If we assume that F is the result of a progenitor like E plus roughly
two hundreds building blocks of the type B, we predict [
 ] = 0.13,
which is on the lower observational boundary (see Fig. 5, upper panel).
The two cases presented above bracket a region of the paramenter
space in which the final galaxy F can be obtained through a series
of dry mergers involving a galaxy like E and progenitors like A, A+, and B,
in different mixtures. Three main conclusions can be drawn from a scenario featuring multiple small
progenitors accreted by a medium-sized ellipticals until it doubles its
mass: i) multiple minor dry mergers cannot be ruled out on the basis
of current observations, but they are only small perturbations
for a massive elliptical which formed monolithically; ii) they may explain the observed scatter in the [
] = 0.13,
which is on the lower observational boundary (see Fig. 5, upper panel).
The two cases presented above bracket a region of the paramenter
space in which the final galaxy F can be obtained through a series
of dry mergers involving a galaxy like E and progenitors like A, A+, and B,
in different mixtures. Three main conclusions can be drawn from a scenario featuring multiple small
progenitors accreted by a medium-sized ellipticals until it doubles its
mass: i) multiple minor dry mergers cannot be ruled out on the basis
of current observations, but they are only small perturbations
for a massive elliptical which formed monolithically; ii) they may explain the observed scatter in the [
 ] values at a given galactic mass, although it can also be explained in the framework of the revised monolithic scheme by small differences in either the
star formation efficiency or the infall timescale with respect
to the PM04 best value (tuned to represent the average galaxy);
and iii) in any case, they cannot explain the trend of [
] values at a given galactic mass, although it can also be explained in the framework of the revised monolithic scheme by small differences in either the
star formation efficiency or the infall timescale with respect
to the PM04 best value (tuned to represent the average galaxy);
and iii) in any case, they cannot explain the trend of [
 ]
with
]
with
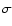 ,
because, even if they may lead to a modest increase
in [
,
because, even if they may lead to a modest increase
in [
 ], the stellar
velocity dispersion does not increase (Ciotti et al. 2007).
], the stellar
velocity dispersion does not increase (Ciotti et al. 2007).
It is obvious that a few events like the ones depicted in this section
can occur, for instance, in a dense environment such
as a cluster of galaxies where a residual ongoing SF is also detected
in massive ellipticals and cD (Bildfell et al. 2008).
The amount of SF inferred from UV spectra (Kaviraj et al. 2007)
from redshift 1 to the present-day (and consistent with the merger rate by Khochfar & Burkert 2006) will lead to a modest increase (1-5 percent) in the stellar mass, even tough
no SNII explosions have been detected to-date (Mannucci et al. 2007, but they might
still occur in S0; e.g., Pastorello et al. 2007);
therefore, we consider it either as an accident or a consequence of the
environment, rather than a signature of any particular galaxy formation scenario.
In fact, according to our previous calculations (Pipino & Matteucci 2006),
such a low-intensity late SF episode cannot significantly lower
the [
 ] ratio.
] ratio.
![\begin{figure}
\par\includegraphics[height=8.2cm,width=7.1cm,clip]{9395f5.eps}\end{figure}](/articles/aa/full/2008/30/aa09395-08/Timg29.gif) |
Figure 5:
Predicted evolutionary paths (solid: allowed by the analysis of the chemical properties; dashed: not allowed, see text) in the [
 ]- ]-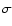 ( upper panel) and [
( upper panel) and [
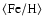 ]- ]-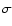 ( lower panel) planes.
The initial, intermediate, and final points are marked according to the galaxy (progenitor) type
and the merger end-product, respectively. The shaded areas encompass the observations (Nelan et al. 2006), whose average trends with the velocity dispersion are given by the black dotted lines.
( lower panel) planes.
The initial, intermediate, and final points are marked according to the galaxy (progenitor) type
and the merger end-product, respectively. The shaded areas encompass the observations (Nelan et al. 2006), whose average trends with the velocity dispersion are given by the black dotted lines. |
| Open with DEXTER |
Interestingly, recent observational evidences (Daddi et al. 2005; Trujillo et al. 2007) favour an increase in the size ellipticals by a factor of about 4 since redshift z=1, plausibly associated with the occurrence of dry mergers.
However, the simulations show that this kind of accretion occurs mainly outside one effective radius
(Naab et al. 2007) and it might be due to accretion of small satellites (Daddi et al. 2005); therefore, we do not expect them to affect the properties
of the galactic core, whose stars obey the MMR and the MFMR.
Again, even in the framework of the revised-monolithic scenario,
these episodes are unavoidable either in a dense environment or
considering the fact the massive ellitpicals are 12 Gyr old. Therefore, they
had enough time to interact with their satellites.
Finally, we want to test the feasibility of a major dry merger
between two massive spheroids of the kind E to produce the galaxy F.
In this case, the final elliptical will double its mass and keep
a mean [
 ] = 0.25 dex, which does not differ much from the value
expected by model F. Nevertheless, a problem arises from the fact that, for a pure dissipationless merger between two objects of equal mass and same velocity dispersion
] = 0.25 dex, which does not differ much from the value
expected by model F. Nevertheless, a problem arises from the fact that, for a pure dissipationless merger between two objects of equal mass and same velocity dispersion 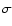 ,
the final object will double its mass, but preserve
,
the final object will double its mass, but preserve 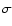 (Ciotti et al. 2007).
Therefore, we cannot move along the direction of the observed
[
(Ciotti et al. 2007).
Therefore, we cannot move along the direction of the observed
[
 ]-
]-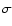 relation. This also seems to be the case when
the stellar central velocity dispersion is allowed to (modestly) increase
due to non-homology effects (Nipoti et al. 2003).
We stress that this clear and straightforward consequence
of the virial theorem is often neglected in works
that aim at reconciling the prediction from the hierarchical
clustering scenario with the evidences coming from the chemistry.
relation. This also seems to be the case when
the stellar central velocity dispersion is allowed to (modestly) increase
due to non-homology effects (Nipoti et al. 2003).
We stress that this clear and straightforward consequence
of the virial theorem is often neglected in works
that aim at reconciling the prediction from the hierarchical
clustering scenario with the evidences coming from the chemistry.
Nonetheless, we exploit the [
 ]-mass relation to infer some
constraints on the number of major dry mergers involving massive
spheroids. From Thomas et al. (2005), we know that
]-mass relation to infer some
constraints on the number of major dry mergers involving massive
spheroids. From Thomas et al. (2005), we know that
![$[ \langle {\rm Mg/Fe} \rangle ]=-0.459+0.062 \log(M_*)$](/articles/aa/full/2008/30/aa09395-08/img30.gif) with an intrinsic scatter of
with an intrinsic scatter of 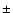 0.05 dex.
This means that an elliptical galaxy that satisfies the average trend,
can undergo either
0.05 dex.
This means that an elliptical galaxy that satisfies the average trend,
can undergo either 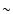 2-4 major dry mergers (if only one has mass ratio 1:1, the rest being either 1:2 or 1:3) or
2-4 major dry mergers (if only one has mass ratio 1:1, the rest being either 1:2 or 1:3) or 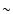 2-3 major dry-mergers (if the mass ratio is always 1:1, i.e., in the first step, we create two galaxies, each one via a merger
of two units like model E (2xE), and then we let them merge together), before crossing the boundary set by observations. Remarkably, such a limit is in agreement with recent observational estimates for the average number of major mergers experienced by elliptical galaxies since redshift 1.2 (e.g., Lin et al. 2008). Unfortunately, the nature of our exercise does not allow us either to put precise constraints or to make predictions on the merger rate. However, if we take into account the fact that the dry-merger rate seems to decline quite strongly with redshift, we may
argue that the maximum major-merger rate allowed by the MFMR is 0.2-0.3/Gyr
in agreement with Bell et al. (2006)'s estimate. In any case, following the same argument of the previous sections, no arbitrary sequence of dry mergers of a model E galaxy
with similar progenitor can ever form a
2-3 major dry-mergers (if the mass ratio is always 1:1, i.e., in the first step, we create two galaxies, each one via a merger
of two units like model E (2xE), and then we let them merge together), before crossing the boundary set by observations. Remarkably, such a limit is in agreement with recent observational estimates for the average number of major mergers experienced by elliptical galaxies since redshift 1.2 (e.g., Lin et al. 2008). Unfortunately, the nature of our exercise does not allow us either to put precise constraints or to make predictions on the merger rate. However, if we take into account the fact that the dry-merger rate seems to decline quite strongly with redshift, we may
argue that the maximum major-merger rate allowed by the MFMR is 0.2-0.3/Gyr
in agreement with Bell et al. (2006)'s estimate. In any case, following the same argument of the previous sections, no arbitrary sequence of dry mergers of a model E galaxy
with similar progenitor can ever form a
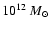 spheroid with the highest observed [
spheroid with the highest observed [
 ]
for that mass.
]
for that mass.
Before drawing our final remarks, we summarise the results
obtained in the studied case by means of Fig. 5, where the
average [
 ]
and the average [
]
and the average [
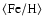 ]
are plotted versus
]
are plotted versus
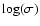 .
In this figure, we sketch the allowed paths as solid lines
whereas we plot as dashed lines what is impossible on the basis
of stellar population arguments.
We compare them with the observations by Nelan et al. (2006):
the black dotted line being the mean value,
and the shaded area brackets the observational scatter reported
by the authors. These values are in agreement with the previous analysis
by Thomas et al. (2005), although in Nelan et al. (2006)
the slope of the MFMR is somewhat flatter at high velocity dispersions.
.
In this figure, we sketch the allowed paths as solid lines
whereas we plot as dashed lines what is impossible on the basis
of stellar population arguments.
We compare them with the observations by Nelan et al. (2006):
the black dotted line being the mean value,
and the shaded area brackets the observational scatter reported
by the authors. These values are in agreement with the previous analysis
by Thomas et al. (2005), although in Nelan et al. (2006)
the slope of the MFMR is somewhat flatter at high velocity dispersions.
As done in the previous sections, we follow the merger history that
links progenitors A to the intermediate stage E
to the massive elliptical F as an example of a possible accretion history,
which may lead to the creation of a massive spheroid from small subunits.
With 400xA, we name the outcome of the multiple mergers
described in Sect. 3.1. We already know that some of the chemical properties of
such a galaxy will differ from those featured by model F.
We assume that the progenitors of type A inhabit the upper (lower) left
corner in the upper (lower) panel, without any further specification
on their initial 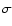 and on the dynamical outcome of the multiple mergers.
To be conservative, in fact, we assume that they can somehow
increase their
and on the dynamical outcome of the multiple mergers.
To be conservative, in fact, we assume that they can somehow
increase their 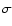
![[*]](/icons/foot_motif.gif) ,
but we recall that, where the build-up of model 400xA a sequence of pure parabolic mergers
,
but we recall that, where the build-up of model 400xA a sequence of pure parabolic mergers![[*]](/icons/foot_motif.gif) between collisionless systems, its final
between collisionless systems, its final 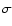 would
be equal to the maximum value of the stellar velocity dispersion
among the progenitors (Ciotti et al. 2007; see also Nipoti et al. 2003, for the effects of non-homology). This means that the remnant merger would probably lie very close to A in the upper panel of Fig. 5, without moving leftward as we assume in our
simple sketch. From the upper panel of Fig. 5, we notice
that the model 400xA is fairly close to the model that we want to reproduce
through the sequence of mergers (F). Therefore,
we mark this path (solid line) in the [Mg/Fe]-
would
be equal to the maximum value of the stellar velocity dispersion
among the progenitors (Ciotti et al. 2007; see also Nipoti et al. 2003, for the effects of non-homology). This means that the remnant merger would probably lie very close to A in the upper panel of Fig. 5, without moving leftward as we assume in our
simple sketch. From the upper panel of Fig. 5, we notice
that the model 400xA is fairly close to the model that we want to reproduce
through the sequence of mergers (F). Therefore,
we mark this path (solid line) in the [Mg/Fe]-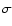 plane as allowed,
meaning that, on a pure chemical evolution basis, it is possible
to create a massive spheroid, which satisfies the MFMR starting from
plane as allowed,
meaning that, on a pure chemical evolution basis, it is possible
to create a massive spheroid, which satisfies the MFMR starting from
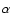 -enhanced building blocks.
On the other hand, the lower panel of Fig. 5 tells
us that the galaxy of type 400xA falls short in reproducing the MMR by more than
two orders of magnitude. A path joining A with E and F (dashed line)
is impossible if we want to satisfy both the observed relationships.
We do not show here the paths leading to a final F galaxy from building blocks
of type B. It is intuitive that they will be allowed
on the metallicity-
-enhanced building blocks.
On the other hand, the lower panel of Fig. 5 tells
us that the galaxy of type 400xA falls short in reproducing the MMR by more than
two orders of magnitude. A path joining A with E and F (dashed line)
is impossible if we want to satisfy both the observed relationships.
We do not show here the paths leading to a final F galaxy from building blocks
of type B. It is intuitive that they will be allowed
on the metallicity-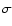 plane, but they will be outside the region delimited by the observations in the
[Mg/Fe]-
plane, but they will be outside the region delimited by the observations in the
[Mg/Fe]-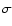 plane. If we allow galaxies to form through a sequence of mergers involving
different progenitors, given the random nature of the hierarchical assembly, it is natural
to expect a scatter in the predicted MMR and the MFMR much larger
than the observed ones and no slope at all.
We also expect this to happen in the most recent models based
on the hierarchical assembly, and even if they features
several gestures toward the downsizing,
as it has indeed been shown by Nagashima et al. (2005).
plane. If we allow galaxies to form through a sequence of mergers involving
different progenitors, given the random nature of the hierarchical assembly, it is natural
to expect a scatter in the predicted MMR and the MFMR much larger
than the observed ones and no slope at all.
We also expect this to happen in the most recent models based
on the hierarchical assembly, and even if they features
several gestures toward the downsizing,
as it has indeed been shown by Nagashima et al. (2005).
This fact and our previous works on the quasi-monolitic formation
of massive ellipticals (PM04) as well as the effect of major wet mergers
(Pipino & Matteucci 2006) allow us to derive the first important conclusions:
- i)
- the diagnostic power of the MMR and MFMR relies on the fact
that the mechanisms required to satisfy the former tend to worsen
the agreement with the latter, and viceversa;
- ii)
- only when most of the star formation process and the galactic assembly occur
at roughly the same time and the same place can both relations be fulfilled.
As expected from the discussion of Sect. 3.4, the outcome (called 2xE in Fig. 5) of a major dry merger involving two massive ellipticals,
will occupy the same place of its progenitor E and does not
move to where it is expected (i.e., at F), therefore we mark
this path as not allowed.
Moreover, the model E has been designed to represent an average
elliptical of medium size, although the observations tell us that there are
galaxies of the same mass, but lower 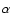 -enhacement (as low as
0.1 dex, lower boundary of the shaded region - Fig. 5, upper panel).
This means that, in principle, we should also be able to observe giant
ellipticals with [
-enhacement (as low as
0.1 dex, lower boundary of the shaded region - Fig. 5, upper panel).
This means that, in principle, we should also be able to observe giant
ellipticals with [
 ]
as low as
]
as low as 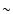 0.1 dex.
Since this is not the case, we are not only in need of a way to increase
0.1 dex.
Since this is not the case, we are not only in need of a way to increase
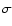 without having any substantial wet mergers (and further SF),
but also in need of a way to invoke some selective mergers.
Other constraints will come from the study of the joint evolution of
the MFMR and MMR with redshift.
without having any substantial wet mergers (and further SF),
but also in need of a way to invoke some selective mergers.
Other constraints will come from the study of the joint evolution of
the MFMR and MMR with redshift.
In conclusion, it seems hard to reproduce all giant ellipticals
either via a pure sequence of multiple minor dry mergers, or via major dry mergers.
However, the scatter of the MFMR is such that
the occurrence of 1-3 major-dry mergers during the galactic lifetime
cannot be ruled out and, indeed, it is in agreement with the observations
(e.g., Bell et al. 2006). For the same reason, several accretion episodes of small
satellites onto a massive ``monolithic'' elliptical galaxy,
can be classified as perturbations that may help explain
the observational scatter. Moreover, it is still to be understood whether a mixed (namely including
both wet and dry mergers) model that tracks the observed evolution
of the merger rates amongst different galactic morphologies (e.g., Lin et al. 2008)
can overcome the above difficulties![[*]](/icons/foot_motif.gif) . This is beyond the scope of the present paper, which (along with PM06)
aims at being only a first step into a quantitative analysis
of the chemical properties of merger remnants. We stress that we present some rather extreme cases (i.e., galaxies formed only via dry mergers) as opposed to PM06 where we presented only wet mergers.
Results by a semi-analytical model, which incorporates
several gestures toward the reproduction of the downsizing
as well as the galactic colour bimodality,
with a full and self-consistent treatment of the chemical evolution,
will be presented in a forthcoming paper (Pipino et al., in preparation).
. This is beyond the scope of the present paper, which (along with PM06)
aims at being only a first step into a quantitative analysis
of the chemical properties of merger remnants. We stress that we present some rather extreme cases (i.e., galaxies formed only via dry mergers) as opposed to PM06 where we presented only wet mergers.
Results by a semi-analytical model, which incorporates
several gestures toward the reproduction of the downsizing
as well as the galactic colour bimodality,
with a full and self-consistent treatment of the chemical evolution,
will be presented in a forthcoming paper (Pipino et al., in preparation).
Acknowledgements
We acknowledge useful discussions with T. Naab. We thank the referee for the careful reading.
L. Ciotti is warmly thanked for a timely reading of the paper
and many enlightening comments.
- Arimoto, N., &
Yoshii, Y. 1987, A&A, 173, 23 [NASA ADS]
(In the text)
- Bell, E. F., Naab, T.,
McIntosh, D. H., et al. 2006, ApJ, 640, 241 [NASA ADS] [CrossRef]
(In the text)
- Bildfell, C., Hoekstra,
H., Babul, A., & Mahdavi, A. 2008
[arXiv:0802.2712]
(In the text)
- Bournaud, F., Jog, J.,
& Combes, F. 2007, A&A, 476, 1179 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Bower, R. G., Lucey, J.
R., & Ellis, R. S. 1992, MNRAS, 254, 589 [NASA ADS]
(In the text)
- Brown, M. J. J, Dey,
A., Jannuzi, B. T., et al. 2007, ApJ, 654, 858 [NASA ADS] [CrossRef]
(In the text)
- Bundy, K., Ellis, R.
S., & Conselice, C. J. 2005, ApJ, 625, 621 [NASA ADS] [CrossRef]
- Calura, F., Jimenez,
R., Panter, B., Matteucci, F., & Heavens, A. F. 2007, ApJ, in
press [arXiv:0707.1345]
(In the text)
- Carollo, C. M.,
Danziger, I. J., & Buson, L. 1993, MNRAS, 265, 553 [NASA ADS]
(In the text)
- Cimatti, A., Daddi, E.,
Renzini, A., et al. 2004, Nature, 430, 184 [NASA ADS] [CrossRef]
- Cimatti, A., Daddi, E.,
& Renzini, A. 2006, A&A, 453, 29 [NASA ADS] [CrossRef]
(In the text)
- Ciotti, L., Lanzoni,
B., & Volonteri, M. 2007, ApJ, 658, 65 [NASA ADS] [CrossRef]
(In the text)
- Cox, T. J., Dutta, S. N.,
Di Matteo, T., et al. 2006, ApJ, 650, 791 [NASA ADS] [CrossRef]
(In the text)
- Cowie, L. L., Songaila,
A., Hu, E. M., & Cohen, J. G. 1996, AJ, 112, 839 [CrossRef]
- Daddi, E., Renzini, A.,
Pirzkal, N., et al. 2005, ApJ, 626, 680 [NASA ADS] [CrossRef]
(In the text)
- De Lucia, G., Springel,
V., White, S. D. M., Croton, D., & Kauffmann, G. 2006, MNRAS,
366, 499 [NASA ADS] [CrossRef]
(In the text)
- Donovan, J. L.,
Hibbard, J. E., & van Gorkom, J. H. 2007
[arXiv:0706.0734]
(In the text)
- Dressler, A.,
Lynden-Bell, D., Burnstein, D., et al. 1987, ApJ, 313, 42 [NASA ADS] [CrossRef]
(In the text)
- Emsellem, E.,
Cappellari, M., Krajnovic', D., et al. 2007, MNRAS, 379, 401 [NASA ADS] [CrossRef]
(In the text)
- Faber, S. M., &
Jackson, R. E. 1976, ApJ, 204, 668 [NASA ADS] [CrossRef]
(In the text)
- Hasinger, G., Miyaji,
T., & Schmidt, M. 2005, A&A, 441, 417 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Kauffmann, G., &
White, S. D. M. 1993, MNRAS, 261, 921 [NASA ADS]
(In the text)
- Kaviraj, S., Peirani,
S., Khochfar, S., Silk, J., & Kay, S. 2007
[arXiv:0711.1493]
(In the text)
- Khockfar, S., &
Burkert, A. 2003, ApJ, 597L, 117 [NASA ADS] [CrossRef]
(In the text)
- Khockfar, S., &
Burkert, A. 2005, MNRAS, 359, 1379 [NASA ADS] [CrossRef]
(In the text)
- Khockfar, S., &
Burkert, A. 2006, A&A, 445, 403 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Kobayashi, C.,
Springel, V., & White, S. D. M. 2007, MNRAS, 376, 1465 [NASA ADS] [CrossRef]
(In the text)
- Kormendy, J. 1977, ApJ,
218, 333 [NASA ADS] [CrossRef]
(In the text)
- Lanfranchi, G. A.,
& Matteucci, F. 2004, MNRAS, 351, 1338 [NASA ADS] [CrossRef]
(In the text)
- Lanfranchi, G. A.,
& Matteucci, F. 2007, A&A, 468, 927 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Larson, R. B. 1974,
MNRAS, 166, 585 [NASA ADS]
(In the text)
- Maiolino, R., et al.
2008, to appear on the proceedings of A Century of Cosmology: Past,
Present and Future [arXiv:0712.2880]
(In the text)
- Matteucci, F. 1994,
A&A, 288, 57 [NASA ADS]
(In the text)
- Matteucci, F., Ponzone,
R., & Gibson, B. K. 1998, A&A, 335, 855 [NASA ADS]
(In the text)
- Mannucci, F., Maoz, D.,
Sharon, K., et al. 2007, MNRAS, tmp, 1132
(In the text)
- Mehlert, D., Thomas,
D., Saglia, R. P., Bender, R., & Wegner, G. 2003, A&A, 407,
423 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Merlin, E., &
Chiosi, C. 2006, A&A, 457, 437 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Naab, T., & Ostriker,
J. P. 2007 [arXiv:astro-ph/0702535]
(In the text)
- Naab, T., Khochfar, S.,
& Burkert, A. 2006, ApJ, 636, L81 [NASA ADS] [CrossRef]
(In the text)
- Naab, T., Johansson, P.
H., Ostriker, J. P., & Efstathiou, G. 2007, ApJ, 658, 710 [NASA ADS] [CrossRef]
(In the text)
- Nagashima, M., Lacey,
C. G., Okamoto, T., et al. 2005, MNRAS, 363L, 31 [NASA ADS]
(In the text)
- Nelan, J. E., Smith, R.
J., Hudson, M. J., et al. 2005, ApJ, 632, 137 [NASA ADS] [CrossRef]
- Nipoti, C., Londrillo,
P., & Ciotti, L. 2003, MNRAS, 342, 501 [NASA ADS] [CrossRef]
(In the text)
- Nomoto, K., Hashimoto,
M., Tsujimoto, T., et al. 1997, Nucl. Phys. A, 621, 467 [NASA ADS] [CrossRef]
(In the text)
- Ostriker, J. P. 1980,
ComAp, 8, 177 [NASA ADS]
(In the text)
- Pastorello, A., Della
Valle, M., Smartt, S. J., et al. 2007, Nature, 449, 1 [NASA ADS] [CrossRef]
(In the text)
- Pagel, B. E. J., &
Patchett, B. E. 1975, MNRAS, 172, 13 [NASA ADS]
(In the text)
- Pipino, A., &
Matteucci, F. 2004, MNRAS, 347, 968 [NASA ADS] [CrossRef] (PM04)
(In the text)
- Pipino, A., &
Matteucci, F. 2006, MNRAS, 365, 1114 [NASA ADS]
(In the text)
- Pipino, A., Matteucci,
F., & Chiappini, C. 2006, ApJ, 638, 739 [NASA ADS] [CrossRef] (PMC06)
(In the text)
- Pipino, A., D'Ercole,
A., & Matteucci, F. 2008, A&A, 484, 679 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Rines, K., Finn, R.,
& Vikhlinin, A. 2007 [arXiv:0708.0011]
(In the text)
- Robertson, B.,
Bullock, J. S., Font, A. S., Johnston, K. V., & Hernquist, L.
2005, ApJ, 632, 872 [NASA ADS] [CrossRef]
(In the text)
- Robertson, B., Cox,
T. J., Hernquist, L., et al. 2006, ApJ, 641, 21 [NASA ADS] [CrossRef]
(In the text)
- Salpeter, E. E. 1955,
ApJ, 121, 161 [NASA ADS] [CrossRef]
(In the text)
- Scarlata, C., Carollo,
C. M., Lilly, S. J., et al. 2007, ApJS, 172, 494 [NASA ADS] [CrossRef]
- Shapley, A. E.,
Steidel, C., Adelberger, K. L., et al. 2001, ApJ, 562, 95 [NASA ADS] [CrossRef]
(In the text)
- Swinbank, A. M., Smail,
I., Chapman, S. C., et al. 2004, ApJ, 617, 64 [NASA ADS] [CrossRef]
(In the text)
- Thielemann, F. K.,
Nomoto, K., & Hashimoto, M. 1996, ApJ, 460, 408 [NASA ADS] [CrossRef]
(In the text)
- Thomas, D., &
Kauffmann, G. 1999, in Spectroscopic dating of stars and galaxies,
ed. I. Hubeny, S. Heap, & R. Cornett, ASP Conf. Ser., 192,
261
(In the text)
- Thomas, D., Maraston,
C., & Bender, R. 2002, Ap&SS, 281, 371 [NASA ADS] [CrossRef]
(In the text)
- Thomas, D., Maraston,
C., Bender, R., & Mendes de Oliveira, C. 2005, ApJ, 621,
673 [NASA ADS] [CrossRef]
(In the text)
- Thornton, K., Gaudlitz,
M., Janka, H.-T., & Steinmetz, M. 1998, ApJ, 500, 95 [NASA ADS] [CrossRef]
- Trager, S. C., Faber,
S. M., Worthey, G., & Gonzalez, J. J. 2000, AJ, 119, 1654 [NASA ADS] [CrossRef]
- Tran, K.-V. H., van
Dokkum, P., Franx, M., et al. 2005, ApJ, 627, L25 [NASA ADS] [CrossRef]
(In the text)
- Trujillo, I.,
Conselice, C. J., Bundy, K., et al. 2007, MNRAS, 382, 109 [NASA ADS] [CrossRef]
(In the text)
- van den Hoek, L. B.,
& Groenewegen, M. A. T. 1997, A&AS, 123, 305 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- van Dokkum, P. G. 2005,
AJ, 130, 2647 [NASA ADS] [CrossRef]
(In the text)
- Worthey, G., Faber, S.
M., & Gonzalez, J. J. 1992, ApJ, 398, 69 [NASA ADS] [CrossRef]
Copyright ESO 2008
![\begin{figure}
\par\includegraphics[height=6.7cm,width=6.6cm,clip]{9395f1.eps}\end{figure}](/articles/aa/full/2008/30/aa09395-08/Timg19.gif)
![\begin{figure}
\par\includegraphics[height=6.7cm,width=6.4cm,clip]{9395f2.eps}\end{figure}](/articles/aa/full/2008/30/aa09395-08/Timg20.gif)
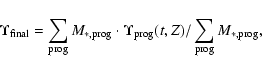
![\begin{figure}
\par\includegraphics[height=6.7cm,width=6.7cm,clip]{9395f3.eps}\end{figure}](/articles/aa/full/2008/30/aa09395-08/Timg25.gif)
![\begin{figure}
\par\includegraphics[height=7cm,width=7.2cm,clip]{9395f4.eps}\end{figure}](/articles/aa/full/2008/30/aa09395-08/Timg28.gif)
![\begin{figure}
\par\includegraphics[height=8.2cm,width=7.1cm,clip]{9395f5.eps}\end{figure}](/articles/aa/full/2008/30/aa09395-08/Timg29.gif)