A&A 486, L5-L8 (2008)
DOI: 10.1051/0004-6361:200809847
LETTER TO THE EDITOR
A reinterpretation of the energy balance in active region loops following new results from Hinode EIS
S. J. Bradshaw
Space and Atmospheric Physics, Blackett Laboratory, Imperial College London, Prince
Consort Road, SW7 2BZ, London, UK
Received 26 March 2008 / Accepted 27 May 2008
Abstract
Context. New observations made by the Hinode EUV Imaging Spectrometer have revealed persistent redshifts in solar active region loops in the temperature range
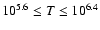 K. The presence of redshifts, interpreted as bulk downflows, indicates that the loops are undergoing radiative cooling rather than continuous heating. This has significant consequences for current ideas regarding the physics of the ubiquitous 1 MK loops observed by instruments such as TRACE and SoHO-EIT.
K. The presence of redshifts, interpreted as bulk downflows, indicates that the loops are undergoing radiative cooling rather than continuous heating. This has significant consequences for current ideas regarding the physics of the ubiquitous 1 MK loops observed by instruments such as TRACE and SoHO-EIT.
Aims. The aim of this work is to assess the validity of the radiative cooling interpretation of the physics governing these loops.
Methods. This interpretation requires an enthalpy flux to balance the radiative energy loss in order to avoid catastrophic cooling. An analytical model is developed and used to find the downflows needed to drive an enthalpy flux sufficient to balance the known radiative loss rates, which are then compared with the observationally measured redshifts.
Results. The model results are found to be in good agreement with the observed redshifts.
Conclusions. Based upon the current analysis it appears that the majority of active region loops observed in the temperature range
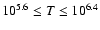 K are in the radiative cooling phase of their lifecycle.
K are in the radiative cooling phase of their lifecycle.
Key words: Sun: corona - Sun: transition region - Sun: UV radiation
1 Introduction
In a recent paper Del Zanna (2008) showed new observations made by the Hinode EUV Imaging Spectrometer (EIS, Culhane et al. 2007) of an active region (NOAA 10926) as it crossed the centre of the solar disk. Dopplergrams of the active region revealed persistent redshifts, more pronounced in cooler emission lines (20-30 km s-1 in Fe VIII, 5-10 km s-1 in Fe XII and  5 km s-1 in Fe XV), in almost all of the loop structures that were observed in the temperature range
5 km s-1 in Fe XV), in almost all of the loop structures that were observed in the temperature range
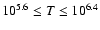 K. Observations of active regions made within this temperature range by imaging instruments such as TRACE and SoHO-EIT, which cannot resolve individual spectral lines, have in the past been interpreted in terms of static, steady-state loop structures undergoing some form of constant heating (Aschwanden et al. 2001; Aschwanden & Schrijver 2002), whereas EIS has now revealed significant dynamic activity which calls these previous interpretations into question.
K. Observations of active regions made within this temperature range by imaging instruments such as TRACE and SoHO-EIT, which cannot resolve individual spectral lines, have in the past been interpreted in terms of static, steady-state loop structures undergoing some form of constant heating (Aschwanden et al. 2001; Aschwanden & Schrijver 2002), whereas EIS has now revealed significant dynamic activity which calls these previous interpretations into question.
The presence of redshifts, interpreted as bulk downflows, indicates that the loops are in the radiative cooling phase of their lifecycle (Bradshaw & Cargill 2005) and not the heating/thermal conduction phase that would be associated with upflows (chromospheric evaporation). This leads to a significant re-interpretation of the nature of the energy balance and the key physical processes that operate within these ubiquitous structures. If the loops are indeed in their radiative cooling phase, the following two conditions must be satisfied: (a) the downflow must drive an enthalpy flux sufficient to balance the optically-thin radiative losses from the lower corona/transition region, otherwise the loops would be radiatively unstable and undergo catastrophic cooling in contradiction to their observed lifetimes of the order of hours (Lenz et al. 1999a; Lenz et al. 1999b); and (b) the magnitude of the downflow associated with the required enthalpy flux must be consistent with the observationally measured redshifts.
In the present work an analytical model is developed and used to assess the validity of the radiative cooling interpretation. In Sect. 2 an equation for the critical downflow velocity needed for an enthalpy flux to balance the radiative losses is derived and applied to a selection of loops with varying temperature and density structures. The results are compared with Del Zanna (2008). Conclusions are drawn and work to follow is discussed in Sect. 3.
2 An analytical model for a radiatively cooling loop
An optically thin, radiating plasma cools on a timescale given by
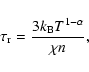 |
(1) |
where
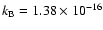 is the Boltzmann constant in cgs units, T is the plasma temperature and n is the plasma number density. The values
is the Boltzmann constant in cgs units, T is the plasma temperature and n is the plasma number density. The values
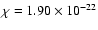 and
and 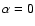 are taken from the power-law fit to the radiative emissivity
are taken from the power-law fit to the radiative emissivity
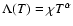 given by Klimchuk & Cargill (2001) for
given by Klimchuk & Cargill (2001) for
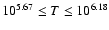 .
For average lower corona/transition region values of
T = 105.8 K and
n = 1010 cm-3,
.
For average lower corona/transition region values of
T = 105.8 K and
n = 1010 cm-3,
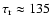 s. Since loops persist for significantly longer than a few minutes there must be a supply of energy to these regions in order to sustain the radiative emission. Bradshaw & Cargill (2005) showed that during radiative cooling the key physical processes operating within a loop are the transport of mass and energy by advection and, of course, the energy loss due to radiative emission. Thus,
s. Since loops persist for significantly longer than a few minutes there must be a supply of energy to these regions in order to sustain the radiative emission. Bradshaw & Cargill (2005) showed that during radiative cooling the key physical processes operating within a loop are the transport of mass and energy by advection and, of course, the energy loss due to radiative emission. Thus,
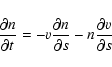 |
(2) |
and
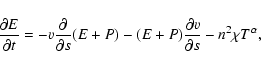 |
(3) |
where s is the field-aligned spatial position, v is the velocity of the bulk flow,
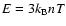 is the total energy of the plasma (neglecting the kinetic energy, which is several orders of magnitude less than the thermal energy when the Mach number
is the total energy of the plasma (neglecting the kinetic energy, which is several orders of magnitude less than the thermal energy when the Mach number 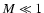 )
and
)
and
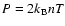 is the plasma pressure. Substituting
is the plasma pressure. Substituting
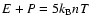 into Eq. (3) gives
into Eq. (3) gives
hence,
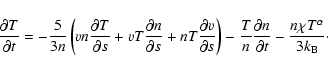 |
(4) |
Substituting Eq. (2) into Eq. (4) gives
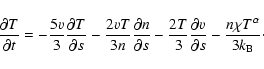 |
(5) |
In order to estimate the temperature gradient let us assume that the temperature structure at and above the location of the lower corona/transition region, where s=s0, has the form
and
![\begin{displaymath}\frac{\partial T}{\partial s} = \frac{T_{\rm a}}{\lambda_T} \exp \left[ - \frac{s}{\lambda_T} \right],
\end{displaymath}](/articles/aa/full/2008/29/aa09847-08/img20.gif) |
(6) |
where
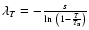 is the temperature scale-length such that
T=T(s=s0) and
is the temperature scale-length such that
T=T(s=s0) and
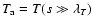 (the apex temperature of the loop).
(the apex temperature of the loop).
Let us assume that the plasma is gravitationally stratified at and above s=s0. Thus,
where
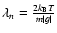 is the density scale-length (
is the density scale-length (
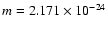 g and
g and
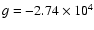 cm s-2) and
cm s-2) and
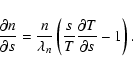 |
(7) |
Finally, an expression for the velocity is required. Following Bradshaw & Cargill (2005),
where
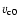 and
and
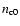 are the velocity and coronal density at the beginning of the radiative cooling phase. Differentiating,
are the velocity and coronal density at the beginning of the radiative cooling phase. Differentiating,
and substituting Eq. (7), gives
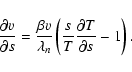 |
(8) |
Substituting Eqs. (6)-(8) into Eq. (5) yields
![\begin{displaymath}\frac{\partial T}{\partial t} =
\frac{v}{3} \Bigg[ \left( \...
...a)}{k_{\rm B}} \Bigg] - \frac{n\chi T^\alpha}{3k_{\rm B}}\cdot
\end{displaymath}](/articles/aa/full/2008/29/aa09847-08/img33.gif) |
(9) |
Let
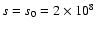 cm be the field-aligned position of the lower corona/transition region and
T=T(s0)=105.8 K (the temperature of peak Fe VIII abundance at equilibrium). The value of
cm be the field-aligned position of the lower corona/transition region and
T=T(s0)=105.8 K (the temperature of peak Fe VIII abundance at equilibrium). The value of 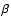 can be found from
Eqs. (12) and (13) of Bradshaw & Cargill (2005) where it was shown that
can be found from
Eqs. (12) and (13) of Bradshaw & Cargill (2005) where it was shown that
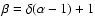 and
and
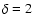 .
In the current work
.
In the current work 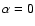 which gives
which gives 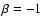 and so the
and so the 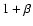 terms drop out of Eq. (9). Bradshaw & Cargill (2005) found values of order 1 for the magnitude of
terms drop out of Eq. (9). Bradshaw & Cargill (2005) found values of order 1 for the magnitude of 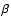 and so
and so
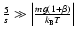 for the chosen values of s and T. Thus the
for the chosen values of s and T. Thus the 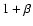 terms can be safely neglected for a realistic range of
terms can be safely neglected for a realistic range of 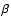 ,
although they will be retained in the following analysis for completeness.
,
although they will be retained in the following analysis for completeness.
In order for the lower corona/transition region radiative emission to be sustained, the condition
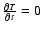 must be satisfied in these regions. This implies, from Eq. (8),
must be satisfied in these regions. This implies, from Eq. (8),
![\begin{displaymath}v ~ \Bigg[ \left( \frac{5}{s} + \frac{m\vert g\vert(1+\beta)}...
...eta)}{k_{\rm B}} \Bigg]= \frac{n\chi T^\alpha}{k_{\rm B}}\cdot
\end{displaymath}](/articles/aa/full/2008/29/aa09847-08/img42.gif) |
(10) |
Note that the upper corona is assumed to continue to radiatively cool (
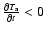 ), but does so slowly. For example, using Eq. (1) and the appropriate values for
), but does so slowly. For example, using Eq. (1) and the appropriate values for 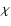 and
and 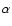 from Klimchuk & Cargill (2001) it can be seen that a loop with an upper corona temperature of 5 MK and density
from Klimchuk & Cargill (2001) it can be seen that a loop with an upper corona temperature of 5 MK and density
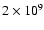 cm-3 will radiatively cool on a timescale of about 5 h. As long as
cm-3 will radiatively cool on a timescale of about 5 h. As long as
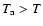 the upper corona can continue to supply energy via an enthalpy flux to the lower corona/transition region.
the upper corona can continue to supply energy via an enthalpy flux to the lower corona/transition region.
The critical parameter in Eq. (9) is the velocity of the plasma,
![\begin{displaymath}v_{\rm critical} =
\frac{n\chi T^\alpha}{k_{\rm B}} \Bigg[ ...
...ight)
+ \frac{m\vert g\vert(1+\beta)}{k_{\rm B}} \Bigg]^{-1},
\end{displaymath}](/articles/aa/full/2008/29/aa09847-08/img48.gif) |
(11) |
where
 is the velocity that one would expect to observe at spatial position s, where the temperature is T and the density is n, for the enthalpy flux to sustain a radiative energy loss of
is the velocity that one would expect to observe at spatial position s, where the temperature is T and the density is n, for the enthalpy flux to sustain a radiative energy loss of
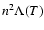 erg cm-3 s-1, given an upper corona temperature characterised by the value of
erg cm-3 s-1, given an upper corona temperature characterised by the value of 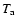 .
.
Table 1:
The critical velocity that the downflow must reach in order to drive an enthalpy flux sufficient to sustain the radiative emission.
Table 1 shows values of
 for a range of n=n(s0) and
for a range of n=n(s0) and 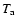 .
The value of s is held fixed at
.
The value of s is held fixed at
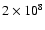 cm (a height of about 2000 km for the lower corona/transition region) and
T = 105.8 K (the temperature of peak Fe VIII abundance in equilibrium). Thus, the values in Table 1 are the velocities one would expect to observe from Doppler shifts in Fe VIII emission lines if the enthalpy flux sustains the radiative emission. This parameter space was chosen to allow for direct comparison with the Dopplergrams of Del Zanna (2008). Note that
cm (a height of about 2000 km for the lower corona/transition region) and
T = 105.8 K (the temperature of peak Fe VIII abundance in equilibrium). Thus, the values in Table 1 are the velocities one would expect to observe from Doppler shifts in Fe VIII emission lines if the enthalpy flux sustains the radiative emission. This parameter space was chosen to allow for direct comparison with the Dopplergrams of Del Zanna (2008). Note that
 depends sensitively on
depends sensitively on
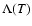 erg cm3 s-1, the optically-thin radiative emissivity.
erg cm3 s-1, the optically-thin radiative emissivity.
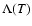 depends most sensitively on the values selected for the element abundances, which highlights the need for accurate spectroscopic determinations of these quantities.
depends most sensitively on the values selected for the element abundances, which highlights the need for accurate spectroscopic determinations of these quantities.
During radiative cooling
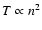 (Bradshaw & Cargill 2005) and so the corona cools more rapidly than it drains (for example, a factor of 2 decrease in n corresponds to a factor 4 decrease in T). Table 1 shows that
(Bradshaw & Cargill 2005) and so the corona cools more rapidly than it drains (for example, a factor of 2 decrease in n corresponds to a factor 4 decrease in T). Table 1 shows that
 is weakly dependent on
is weakly dependent on 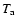 (and thus on the temperature structure of the loop) and strongly dependent on n; therefore, after significant cooling and only moderate draining the value of
(and thus on the temperature structure of the loop) and strongly dependent on n; therefore, after significant cooling and only moderate draining the value of
 can substantially decrease. For example, consider a coronal loop of moderate temperature
can substantially decrease. For example, consider a coronal loop of moderate temperature
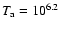 K and density
K and density
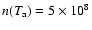 cm-3 rising by a factor of 10 to
cm-3 rising by a factor of 10 to
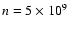 cm-3 in the lower corona/transition region: the radiative cooling timescale in the coronal part of the loop is about
cm-3 in the lower corona/transition region: the radiative cooling timescale in the coronal part of the loop is about
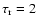 h and a coronal temperature of order 106 K and a density ratio of 0.1 implies a loop length of order 105 km (in the case of gravitational stratification) which, according to Table 1, implies a draining timescale of about
h and a coronal temperature of order 106 K and a density ratio of 0.1 implies a loop length of order 105 km (in the case of gravitational stratification) which, according to Table 1, implies a draining timescale of about 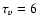 h. Therefore, while the loop remains bright at EUV temperatures it should not catastrophically empty and sufficient plasma remains in the corona to act as a reservoir for the energy needed to sustain the radiative emission from lower-lying cooler and denser plasma.
h. Therefore, while the loop remains bright at EUV temperatures it should not catastrophically empty and sufficient plasma remains in the corona to act as a reservoir for the energy needed to sustain the radiative emission from lower-lying cooler and denser plasma.
In order to compare the critical velocities in Table 1 with the redshifts shown in the Dopplergrams of Del Zanna (2008) (for example, his Fig. 2), some idea of the range of densities is required. There are no density maps corresponding to the Dopplergrams in Del Zanna (2008); however, Young et al. (2007) analysed Hinode-EIS observations of an active region and used a Mg VII (
T=105.8 K) diagnostic to find a density of
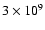 cm-3 at the foot-point of a loop visible in the TRACE 171 Å channel and Tripathi et al. (2008) found densities of up to 1010.5 cm-3 in the core of an active region. Assuming that these properties do not vary too markedly from active region to active region then values of a few 109 cm-3 for loop foot-point densities and a few 1010 cm-3 for active region core densities would appear to be reasonable choices. The critical velocities in Table 1 that correspond to this density range are in good agreement with the redshifts measured by Del Zanna (2008). For example, in Fig. 2 of Del Zanna (2008) the redshifts in the Fe VIII emission from the active region core are between 24 and 40 km s-1, and Table 1 predicts downflow speeds of around 30 km s-1 for a density of
cm-3 at the foot-point of a loop visible in the TRACE 171 Å channel and Tripathi et al. (2008) found densities of up to 1010.5 cm-3 in the core of an active region. Assuming that these properties do not vary too markedly from active region to active region then values of a few 109 cm-3 for loop foot-point densities and a few 1010 cm-3 for active region core densities would appear to be reasonable choices. The critical velocities in Table 1 that correspond to this density range are in good agreement with the redshifts measured by Del Zanna (2008). For example, in Fig. 2 of Del Zanna (2008) the redshifts in the Fe VIII emission from the active region core are between 24 and 40 km s-1, and Table 1 predicts downflow speeds of around 30 km s-1 for a density of
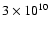 cm-3 (1010.5 cm-3). Moving out from the active region core to regions of lower density, the redshifts in the Fe VIII emission fall to values of
cm-3 (1010.5 cm-3). Moving out from the active region core to regions of lower density, the redshifts in the Fe VIII emission fall to values of 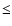 10 km s-1, as also predicted by Table 1.
10 km s-1, as also predicted by Table 1.
These results may also explain the origin and longevity of the ubiquitous active region moss (Berger et al. 1999), now thought to be the relatively cool (1 MK) emission from the upper transition regions of hot (3-10 MK) coronal loops (Martens et al. 2000). Given typical moss values of order T=106 K and
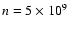 cm-3 (Berger et al. 1999) then in the range 3 MK
cm-3 (Berger et al. 1999) then in the range 3 MK
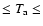 10 MK Eq. (11) gives 3.4 km s
10 MK Eq. (11) gives 3.4 km s
 km s-1. Such gentle downflows could explain the apparent stability of the moss emission in the imaging observations made by TRACE while also providing an explanation for its longevity. Furthermore, Gray & Kilkenny (1980) showed that thermal conduction can be strongly attenuated from its classical value (Spitzer & Härm 1953) at high temperatures, which may explain the lack of a significant role for thermal conduction in the energy balance.
km s-1. Such gentle downflows could explain the apparent stability of the moss emission in the imaging observations made by TRACE while also providing an explanation for its longevity. Furthermore, Gray & Kilkenny (1980) showed that thermal conduction can be strongly attenuated from its classical value (Spitzer & Härm 1953) at high temperatures, which may explain the lack of a significant role for thermal conduction in the energy balance.
3 Summary and conclusions
An analytical model has been developed and used to assess the validity of a radiative cooling interpretation for the physics of active region loops observed in the temperature range
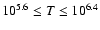 K. These loops have previously been interpreted in terms of a static, steady-state model, in which their properties and evolution were understood in terms of an energy balance between heating and thermal conduction. In the new model the key physical processes lead to an energy balance between optically-thin radiative emission and a mechanical transport of energy (an enthalpy flux). The critical velocities predicted by the model and needed to drive an enthalpy flux sufficient to balance the radiative losses were found to be in good agreement with the observationally measured redshifts in the Dopplergrams of Del Zanna (2008). Thus, one may conclude that the majority of these loops are in the radiative cooling phase of their lifecycle.
K. These loops have previously been interpreted in terms of a static, steady-state model, in which their properties and evolution were understood in terms of an energy balance between heating and thermal conduction. In the new model the key physical processes lead to an energy balance between optically-thin radiative emission and a mechanical transport of energy (an enthalpy flux). The critical velocities predicted by the model and needed to drive an enthalpy flux sufficient to balance the radiative losses were found to be in good agreement with the observationally measured redshifts in the Dopplergrams of Del Zanna (2008). Thus, one may conclude that the majority of these loops are in the radiative cooling phase of their lifecycle.
Moreover, the radiative cooling interpretation is in agreement with Warren et al. (2002) who suggested that coronal loops are made up of many strands heated separately to X-ray temperatures and detected at EUV temperatures as they cool through the sensitivity range of the observing instrument's wavelength filters. This process also provides a natural explanation for the observed overdensity of EUV loops compared with the density predicted by static, steady-state scaling laws (Rosner et al. 1978; Serio et al. 1981), as confirmed by the numerical work of Spadaro et al. (2003).
Pneuman & Kopp (1977, 1978) reached similar conclusions to those presented here after they showed that a downflow of spicular material can provide an enthalpy flux to the transition region that is significantly greater than the energy supplied by thermal conduction from the corona.
The observational study will be extended in forthcoming work to include more active regions and density maps will be produced to accompany Dopplergrams for a larger number of emission lines. This will facilitate an improved comparison with the analytical model and allow the generality of the results and conclusions presented here to be determined.
Acknowledgements
The author is grateful to Dr. Giulio Del Zanna for bringing these observational results to his attention and to Professor Peter Cargill for insightful discussions during the preparation of this work. Thanks also to the referee for their detailed and interesting comments. The author is supported by a Post-Doctoral Fellowship awarded by the STFC.
-
Aschwanden, M. J., & Schrijver, C. J. 2002, ApJS, 142, 269
In the text
-
Aschwanden, M. J., Schrijver, C. J., & Alexander, D. 2001, ApJ, 550,
1036
In the text
-
Berger, T. E., de Pontieu, B., Schrijver, C. J., & Title, A. M. 1999,
ApJ, 519, L97
In the text
-
Bradshaw, S. J., & Cargill, P. J. 2005, A&A, 437, 311
In the text
-
Culhane, J. L., Harra, L. K., James, A. M., et al. 2007, Sol. Phys., 243,
19
In the text
-
Del Zanna, G. 2008, A&A, 481, L49
In the text
-
Gray, D. R., & Kilkenny, J. D. 1980, Plasma Phys., 22, 81
In the text
-
Klimchuk, J. A., & Cargill, P. J. 2001, ApJ, 553, 440
In the text
-
Lenz, D. D., Deluca, E. E., Golub, L., Rosner, R., & Bookbinder,
J. A. 1999a, ApJ, 517, L155
In the text
-
Lenz, D. D., Deluca, E. E., Golub, L., et al. 1999b,
Sol. Phys., 190, 131
In the text
-
Martens, P. C. H., Kankelborg, C. C., & Berger, T. E. 2000, ApJ, 537,
471
In the text
-
Pneuman, G. W., & Kopp, R. A. 1977, A&A, 55, 305
In the text
-
Pneuman, G. W., & Kopp, R. A. 1978, Sol. Phys., 57, 49
In the text
-
Rosner, R., Tucker, W. H., & Vaiana, G. S. 1978, ApJ, 220, 643
In the text
-
Serio, S., Peres, G., Vaiana, G. S., Golub, L., & Rosner, R. 1981,
ApJ, 243, 288
In the text
-
Spadaro, D., Lanza, A. F., Lanzafame, A. C., et al. 2003, ApJ, 582,
486
In the text
-
Spitzer, L., & Härm, R. 1953, Phys. Rev., 89, 977
In the text
-
Tripathi, D., Mason, H. E., Young, P. R., & Del Zanna, G. 2008, A&A,
481, L53
In the text
-
Warren, H. P., Winebarger, A. R., & Hamilton, P. S. 2002, ApJ, 579,
L41
In the text
-
Young, P. R., Del Zanna, G., Mason, H. E., et al. 2007, PASJ, 59, 727
In the text
Copyright ESO 2008
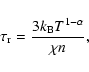
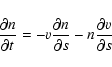
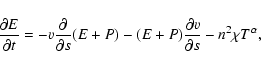
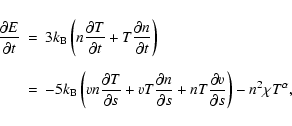
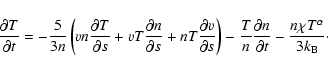
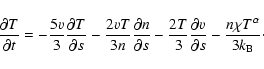
![\begin{displaymath}T = T_{\rm a} \left( 1 - \exp \left[ - \frac{s}{\lambda_T} \right] \right)
\end{displaymath}](/articles/aa/full/2008/29/aa09847-08/img19.gif)
![\begin{displaymath}\frac{\partial T}{\partial s} = \frac{T_{\rm a}}{\lambda_T} \exp \left[ - \frac{s}{\lambda_T} \right],
\end{displaymath}](/articles/aa/full/2008/29/aa09847-08/img20.gif)
![\begin{displaymath}n = n_0 \exp \left[ - \frac{s}{\lambda_n} \right],
\end{displaymath}](/articles/aa/full/2008/29/aa09847-08/img23.gif)
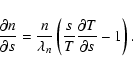
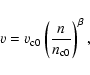
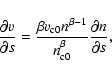
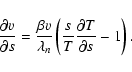
![\begin{displaymath}\frac{\partial T}{\partial t} =
\frac{v}{3} \Bigg[ \left( \...
...a)}{k_{\rm B}} \Bigg] - \frac{n\chi T^\alpha}{3k_{\rm B}}\cdot
\end{displaymath}](/articles/aa/full/2008/29/aa09847-08/img33.gif)
![\begin{displaymath}v ~ \Bigg[ \left( \frac{5}{s} + \frac{m\vert g\vert(1+\beta)}...
...eta)}{k_{\rm B}} \Bigg]= \frac{n\chi T^\alpha}{k_{\rm B}}\cdot
\end{displaymath}](/articles/aa/full/2008/29/aa09847-08/img42.gif)
![\begin{displaymath}v_{\rm critical} =
\frac{n\chi T^\alpha}{k_{\rm B}} \Bigg[ ...
...ight)
+ \frac{m\vert g\vert(1+\beta)}{k_{\rm B}} \Bigg]^{-1},
\end{displaymath}](/articles/aa/full/2008/29/aa09847-08/img48.gif)