A&A 486, 427-435 (2008)
DOI: 10.1051/0004-6361:200809805
The contribution of red dwarfs and white dwarfs to the halo
dark matter
S. Torres1,2 - J. Camacho1 -
J. Isern3,2 - E. García-Berro1,2
1 - Departament de Física Aplicada, Escola Politécnica Superior de Castelldefels, Universitat Politècnica de Catalunya, Avda. del Canal Olímpic 15, 08860 Castelldefels, Spain
2 - Institute for Space Studies of Catalonia, c/Gran Capità 2-4, Edif. Nexus 104,
08034 Barcelona, Spain
3 - Institut de Ciències de l'Espai, CSIC, Campus UAB, Facultat de Ciències, Torre C-5, 08193 Bellaterra, Spain
Received 18 March 2008 / Accepted 9 April 2008
Abstract
Context. The nature of the several microlensing events observed by the MACHO team towards the LMC still remains controversial. Low-mass substellar objects and stars with masses larger than 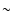 1
1
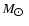 have been ruled out as major components of a MACHO Galactic halo, while stars of half solar masses are the most probable candidates.
have been ruled out as major components of a MACHO Galactic halo, while stars of half solar masses are the most probable candidates.
Aims. We assess jointly the relative contributions of both red dwarfs and white dwarfs to the mass budget of the Galactic halo.
Methods. We use a Monte Carlo simulator that incorporates up-to-date evolutionary sequences of both red dwarfs and white dwarfs as well as detailed descriptions of both our Galaxy and the LMC. We explore a complete mass range between 0.08 and 1
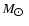 of possible microlensing candidates and we compare the synthetic populations obtained with our simulator with the results obtained by the MACHO and EROS experiments.
of possible microlensing candidates and we compare the synthetic populations obtained with our simulator with the results obtained by the MACHO and EROS experiments.
Results. The contribution of the red-dwarf population is insufficient to explain the number of events claimed by the MACHO team; this is even though the optical depth measured for the white-dwarf population alone, increases by a factor of two, after the addition of the red-dwarf population.
Conclusions. We find that the contribution to the halo dark matter of the entire population under study, is smaller than 10%, at the 95% confidence level.
Key words: stars: luminosity function, mass function - stars: white dwarfs - Galaxy: halo - stars: low-mass, brown dwarfs - Galaxy: stellar content - galaxies: structure
Several cosmological observations show compelling evidence that
baryons represent only a small fraction of the total matter in our
Universe and that non-baryonic dark matter dominates over
baryons. Within the standard cosmological model, this naturally leads
to the existence of a type of unknown energy, the dark energy, which
is the predominant component,
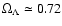 ,
and a
dark-matter component, for which
,
and a
dark-matter component, for which
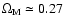 ,
in
contrast to the baryonic component, for which
,
in
contrast to the baryonic component, for which
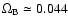 .
Moreover, most of the baryons are non-luminous, since the
density of luminous matter is
.
Moreover, most of the baryons are non-luminous, since the
density of luminous matter is
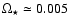 .
In the case
of the Galaxy, it was found that the virial mass, out to 100 kpc, is
.
In the case
of the Galaxy, it was found that the virial mass, out to 100 kpc, is
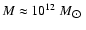 ,
while the baryonic mass in the form of
stars is
,
while the baryonic mass in the form of
stars is
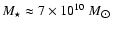 ,
which
implies that the baryon fraction of the Galaxy is at most 8% (Klypin
et al. 2007). This paradox is known as the missing-baryon problem
- see the review of Silk (2007) for a complete, interesting
discussion of this issue - and its resolution is critical to our
understanding of how the Galaxy (and, in addition, by extension other
galaxies) were formed and subsequently evolve. Three alternative
solutions can be envisaged: (i) these baryons are in the outer regions
of our Galaxy; (ii) they were never present in the protogalaxy; or
(iii) they may have been ejected from the Milky Way. The
most-promising explanation, and presently the most favored one, is the
first of these options.
,
which
implies that the baryon fraction of the Galaxy is at most 8% (Klypin
et al. 2007). This paradox is known as the missing-baryon problem
- see the review of Silk (2007) for a complete, interesting
discussion of this issue - and its resolution is critical to our
understanding of how the Galaxy (and, in addition, by extension other
galaxies) were formed and subsequently evolve. Three alternative
solutions can be envisaged: (i) these baryons are in the outer regions
of our Galaxy; (ii) they were never present in the protogalaxy; or
(iii) they may have been ejected from the Milky Way. The
most-promising explanation, and presently the most favored one, is the
first of these options.
Since the pioneering proposal of Paczynski (1986) that gravitational
microlensing could be used to clarify the nature of Galactic dark
matter, considerable observational and theoretical efforts have been
invested in this issue. Among the most likely candidates for
building-up the baryonic, dark-matter density are massive, baryonic
halo-objects, or MACHOs. From the theoretical point of view it has
been suggested that MACHOs could be planets (
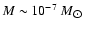 ), brown and red dwarfs (with masses ranging from
), brown and red dwarfs (with masses ranging from 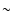 0.01 to
0.01 to  1
1
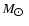 ), primordial black holes (
), primordial black holes (
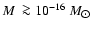 ), molecular clumps (
), molecular clumps (
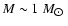 ), and old
white dwarfs (
), and old
white dwarfs (
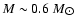 ). From the observational
perspective, the MACHO (Alcock et al. 1997, 2000), EROS (Lasserre et al. 2001; Goldman et al. 2002; Tisserand et al. 2007), OGLE (Udalski et al. 1994), MOA (Muraki et al. 1997), and SuperMACHO (Becker et al. 2005) teams have monitored millions of stars during
several years, in both the Large Magellanic Cloud (LMC) and the Small
Magellanic Cloud (SMC), to search for microlensing events. However,
only the MACHO team and the EROS group have reported their results.
Although differences were initially found between the results,
agreement has now been reached in some of the most important points.
For instance, no microlensing candidates were found by the MACHO team
or the EROS group with event durations between a few hours and 20
days. This implied that the Galactic halo could contain no more than
a 10% of dark objects in the mass range
). From the observational
perspective, the MACHO (Alcock et al. 1997, 2000), EROS (Lasserre et al. 2001; Goldman et al. 2002; Tisserand et al. 2007), OGLE (Udalski et al. 1994), MOA (Muraki et al. 1997), and SuperMACHO (Becker et al. 2005) teams have monitored millions of stars during
several years, in both the Large Magellanic Cloud (LMC) and the Small
Magellanic Cloud (SMC), to search for microlensing events. However,
only the MACHO team and the EROS group have reported their results.
Although differences were initially found between the results,
agreement has now been reached in some of the most important points.
For instance, no microlensing candidates were found by the MACHO team
or the EROS group with event durations between a few hours and 20
days. This implied that the Galactic halo could contain no more than
a 10% of dark objects in the mass range
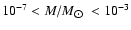 .
This ruled out planets and brown dwarfs as the
major contributors to the mass budget of the dark halo. Moreover, the
MACHO collaboration detected
.
This ruled out planets and brown dwarfs as the
major contributors to the mass budget of the dark halo. Moreover, the
MACHO collaboration detected 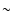 15 microlensing events during
their 5.7 yr analysis of 11.9 million stars in the LMC (Alcock et al.
2000). In their analysis, they derived an optical depth towards the
LMC of
15 microlensing events during
their 5.7 yr analysis of 11.9 million stars in the LMC (Alcock et al.
2000). In their analysis, they derived an optical depth towards the
LMC of
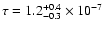 or, equivalently, a halo
fraction
0.08<f<0.50, at the
or, equivalently, a halo
fraction
0.08<f<0.50, at the 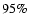 confidence level, with a MACHO
mass in the range
confidence level, with a MACHO
mass in the range
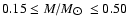 ,
depending on the
halo model. On the other hand, the non-detections reported by the EROS
collaboration provided an upper limit. The EROS team presented an
analysis of a subsample of bright stars belonging to the LMC
(Tisserand et al. 2007), to minimize source confusion and blending
effects. Their results implied that the optical depth towards the LMC
was
,
depending on the
halo model. On the other hand, the non-detections reported by the EROS
collaboration provided an upper limit. The EROS team presented an
analysis of a subsample of bright stars belonging to the LMC
(Tisserand et al. 2007), to minimize source confusion and blending
effects. Their results implied that the optical depth towards the LMC
was
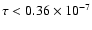 ,
at the 95% confidence level,
corresponding to a fraction of the halo mass of less than 7%. This
result was 4 times smaller than that obtained by the MACHO team.
Consequently, this started discussion about the location and nature of
the lenses. In particular, LMC models were used to ascertain if
possible asymmetries in the space distribution of the microlensed
stars could be related to Galactic halo objects or LMC ones. In fact,
different studies indicate that a sizeable fraction of the microlensed
events are due to LMC self-lensing (Sahu 1994; Gyuk et al.
2000; Calchi Novati et al. 2006). Moreover, a full variety of
possible explanations were proposed to reproduce the microlensing
events: tidal debris or a dwarf galaxy toward the LMC (Zhao 1998), a
Galactic-extended shroud population of white dwarfs (Gates & Gyuk
2001), blending effects (Belokurov et al. 2003, 2004),
spatially-varying mass-functions (Kerins & Evans 1998; Rahvar 2005), and other explanations (Holopainen et al. 2006). However, all of
these proposals were received with some criticism because none fully
explained the observed microlensing results.
,
at the 95% confidence level,
corresponding to a fraction of the halo mass of less than 7%. This
result was 4 times smaller than that obtained by the MACHO team.
Consequently, this started discussion about the location and nature of
the lenses. In particular, LMC models were used to ascertain if
possible asymmetries in the space distribution of the microlensed
stars could be related to Galactic halo objects or LMC ones. In fact,
different studies indicate that a sizeable fraction of the microlensed
events are due to LMC self-lensing (Sahu 1994; Gyuk et al.
2000; Calchi Novati et al. 2006). Moreover, a full variety of
possible explanations were proposed to reproduce the microlensing
events: tidal debris or a dwarf galaxy toward the LMC (Zhao 1998), a
Galactic-extended shroud population of white dwarfs (Gates & Gyuk
2001), blending effects (Belokurov et al. 2003, 2004),
spatially-varying mass-functions (Kerins & Evans 1998; Rahvar 2005), and other explanations (Holopainen et al. 2006). However, all of
these proposals were received with some criticism because none fully
explained the observed microlensing results.
Other observational pieces of evidence were added to help resolve the
present puzzle, such as the search for very faint objects in the
Hubble Deep Field or the search for the microlensing events towards
the Galactic bulge or towards very crowded fields such as M 31. In
particular, the Hubble Deep Field provided an opportunity to test the
contribution of white dwarfs to the Galactic dark matter. Ibata et al. (1999) and Kilic et al. (2005) claimed the detection of some
white-dwarf candidates among several faint blue objects. These objects
exhibit significant proper motion and are, thus, assumed to belong to
the thick disk or the halo populations. Despite the increasing number
of surveys that are searching for white dwarfs - such as the Sloan
Digital Sky Survey (Eisenstein et al. 2006), the 2 Micron All Sky Survey (Cutri et al. 2003), the SuperCosmos Sky Survey (Hambly et al. 2001), the 2dF QSO Redshift Survey (Vennes et al.
2002), and other observational searches (Knox et al. 1999; Ibata et al. 1999; Oppenheimer et al. 2001; Majewski & Siegel 2002; Nelson et al. 2002) - and the numerous theoretical studies (Isern et al. 1998; Reylé et al. 2001; Flynn et al. 2003; Hansen & Liebert 2003; García-Berro et al. 2004), the problem still remains open.
Despite the fact that, for obvious reasons, no information about the
halo could be derived from the microlensing events towards the
Galactic bulge, the results obtained so far indicate the primordial
role played by low-mass stars rather than other objects.
In two previous papers, we extensively analyzed the role played by the
carbon-oxygen (CO) white-dwarf population (García-Berro et al.
2004) in addition to the contribution of oxygen-neon (ONe) white
dwarfs (Camacho et al. 2007). We performed a thorough study of a
wide range of Galactic inputs, including different initial mass
functions and halo ages, and several density profiles corresponding to
different halo models. The calculations indicated that a sizeable
fraction of the halo dark matter cannot be locked in the form of white
dwarfs. We found that the contribution of white dwarfs is, in fact,
approximately a modest 5% in the most optimistic case. This
contribution is mainly due to old CO white dwarfs with hydrogen-rich
atmospheres and the contribution of ONe white dwarfs is minor, because
although ONe white dwarfs can reach faint magnitudes more rapidly than
CO white dwarfs, their contribution is heavily suppressed by the
initial mass function.
In this paper, we analyze, in a comprehensive way, a significant range
of masses
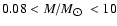 likely to produce microlensing events
towards the LMC and, thus, to contribute to the halo dark matter. This
mass range represents almost 90% of the stellar content, including
the red-dwarf regime (
likely to produce microlensing events
towards the LMC and, thus, to contribute to the halo dark matter. This
mass range represents almost 90% of the stellar content, including
the red-dwarf regime (
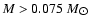 ), the CO white-dwarf
population, and the population of massive ONe white dwarfs. The paper
is organized as follows. In Sect. 2. we summarize the main
ingredients of our Monte Carlo code and other basic assumptions and
procedures necessary to evaluate the microlensing optical depth
towards the LMC. Section 3 is devoted to describing our main results,
including the contribution of red dwarfs and white dwarfs to the
microlensing optical depth towards the LMC, and we compare our results
to those of the MACHO and EROS teams. In this section, we also
estimate the probability that a microlensing event could be assigned
to one or another of the populations under study and we discuss the
contribution of red and white dwarfs to the baryonic content of the
Galaxy. In Sect. 4, our we summarize our major findings and draw our
conclusions.
), the CO white-dwarf
population, and the population of massive ONe white dwarfs. The paper
is organized as follows. In Sect. 2. we summarize the main
ingredients of our Monte Carlo code and other basic assumptions and
procedures necessary to evaluate the microlensing optical depth
towards the LMC. Section 3 is devoted to describing our main results,
including the contribution of red dwarfs and white dwarfs to the
microlensing optical depth towards the LMC, and we compare our results
to those of the MACHO and EROS teams. In this section, we also
estimate the probability that a microlensing event could be assigned
to one or another of the populations under study and we discuss the
contribution of red and white dwarfs to the baryonic content of the
Galaxy. In Sect. 4, our we summarize our major findings and draw our
conclusions.
A detailed description of our Monte Carlo simulator was presented in
Torres et al. (2002), García-Berro et al. (2004), and Camacho et al. (2007). We summarize its most important features and inputs. The basic ingredient of any Monte Carlo simulator is a
random-number-generator algorithm that must ensure a non-correlated
sequence and a good set of statistical properties. We used a
random-number-generator algorithm (James 1990) that provides a uniform
probability density within the interval (0,1) and ensures a
repetition period of
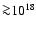 ,
which is sufficient for our
purposes. Each one of the Monte Carlo simulations presented here
consists of an ensemble of
,
which is sufficient for our
purposes. Each one of the Monte Carlo simulations presented here
consists of an ensemble of
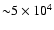 independent realizations
of the synthetic-star population, for which the average of any
observational quantity, along with its corresponding standard
deviation, were computed. Here the standard deviation means the
ensemble mean of the sample dispersions for a typical sample.
independent realizations
of the synthetic-star population, for which the average of any
observational quantity, along with its corresponding standard
deviation, were computed. Here the standard deviation means the
ensemble mean of the sample dispersions for a typical sample.
The Galactic halo was modeled assuming a spherically-symmetric halo. In particular, the model used here is an isothermal sphere of radius 5 kpc also referred to as the ``S-model'', which was used extensively by the MACHO collaboration (Alcock et al. 2000; Griest 1991). The position of each synthetic star was randomly chosen according to this density profile. We have not used other profiles, such as the exponential power-law model, the Navarro et al. (1997) density profile, and others, because their inclusion would not have significantly changed the final results (García-Berro et al. 2004). This reasoning is also applicable to the non-standard Galactic halo models, such as flattened profiles, oblate halo models, and others, which are beyond the scope of the present study.
The mass distribution of synthetic stars was computed using two
different initial mass functions, the standard initial mass function
of Scalo (1998) and the biased log-normal initial mass function
proposed by Adams & Laughlin (1996), the latter being representative
of other non-conventional initial mass functions, such as that of
Chabrier et al. (1996). We note, however, that these biased initial
mass functions appear to be incompatible with the observed properties
of the halo white-dwarf population (Isern et al. 1998; García-Berro et al. 2004), with the contribution of thermonuclear
supernovae to the metallicity of the Galactic halo (Canal et al. 1997), and with the observations of galactic halos in deep galaxy surveys (Charlot & Silk 1995). For the sake of completeness we prefer, however, to include a representative example of these biased
mass functions to illustrate the role played by the red dwarf
population when a biased initial mass function is adopted.
The main-sequence mass is obtained by drawing a pseudo-random number,
according to the adopted initial mass function. The time at which a
star was born is randomly choosen, previously assuming that the halo
was formed 14 Gyr ago in an intense burst of star formation of
duration  1 Gyr. The main-sequence lifetime, as a function of
the mass in the main sequence, is that of Iben & Laughlin (1989). As
soon as the mass of a synthetic star is chosen, its main-sequence
lifetime is inferred and we are the able to determine which stars are
able to evolve into white dwarfs or remain on the main sequence as red
dwarfs. We considered red dwarfs to have masses in the range
1 Gyr. The main-sequence lifetime, as a function of
the mass in the main sequence, is that of Iben & Laughlin (1989). As
soon as the mass of a synthetic star is chosen, its main-sequence
lifetime is inferred and we are the able to determine which stars are
able to evolve into white dwarfs or remain on the main sequence as red
dwarfs. We considered red dwarfs to have masses in the range
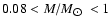 .
For these stars, we adopted the evolutionary
models of Baraffe et al. (1998). Stars with such small masses have
large main-sequence lifetimes; no post-main-sequence evolutionary
tracks of these stars were, therefore, required. Effective
temperatures, luminosities, and colors were derived for stars that had
time to enter the white-dwarf cooling track, given a set of
theoretical cooling-sequences and an initial-to-final-mass
relationship (Iben & Laughlin 1989). The cooling sequences adopted
here depend on the mass of the white dwarf. White dwarfs with masses
smaller than
.
For these stars, we adopted the evolutionary
models of Baraffe et al. (1998). Stars with such small masses have
large main-sequence lifetimes; no post-main-sequence evolutionary
tracks of these stars were, therefore, required. Effective
temperatures, luminosities, and colors were derived for stars that had
time to enter the white-dwarf cooling track, given a set of
theoretical cooling-sequences and an initial-to-final-mass
relationship (Iben & Laughlin 1989). The cooling sequences adopted
here depend on the mass of the white dwarf. White dwarfs with masses
smaller than
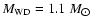 are expected to have a CO
core and for these we adopt the cooling tracks of Salaris et al.
(2000). White dwarfs with masses larger than
are expected to have a CO
core and for these we adopt the cooling tracks of Salaris et al.
(2000). White dwarfs with masses larger than
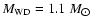 probably have ONe cores; for these white dwarfs, we adopt
the cooling sequences of Althaus et al. (2007). Both sets of cooling
sequences incorporate the most accurate physical inputs for the
stellar interior (including neutrinos, crystallization, phase
separation and Debye cooling) and reproduce the blue turn at low
luminosities (Hansen 1998).
probably have ONe cores; for these white dwarfs, we adopt
the cooling sequences of Althaus et al. (2007). Both sets of cooling
sequences incorporate the most accurate physical inputs for the
stellar interior (including neutrinos, crystallization, phase
separation and Debye cooling) and reproduce the blue turn at low
luminosities (Hansen 1998).
The kinematical properties of the halo population were modeled using
Gaussian laws (Binney & Tremaine 1987) with radial and tangential
velocity dispersions that were related by the Jean's equation to
reproduce the flat rotation curve of our Galaxy. We adopted standard
values for the circular velocity
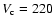 km s-1, in addition to
the peculiar velocity of the Sun
km s-1, in addition to
the peculiar velocity of the Sun
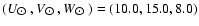 km s-1 (Dehnen & Binney 1998). We discarded stars that had
velocities smaller than 250 km s-1, which were not considered as halo
members. We also rejected stars of velocities larger than 750 km s-1,
because these velocities exceeded 1.5 times the escape velocity.
Since white dwarfs do not usually have radia-component determinations
of their velocities, the radial velocity of each model star is not
considered when a comparison with observational data is completed.
km s-1 (Dehnen & Binney 1998). We discarded stars that had
velocities smaller than 250 km s-1, which were not considered as halo
members. We also rejected stars of velocities larger than 750 km s-1,
because these velocities exceeded 1.5 times the escape velocity.
Since white dwarfs do not usually have radia-component determinations
of their velocities, the radial velocity of each model star is not
considered when a comparison with observational data is completed.
To compare simulated results with observations, a normalization criterion should be used. We proceeded as in our previous papers (Camacho et al. 2007; García-Berro et al. 2004), that is, we normalized our simulations to the local density of halo white dwarfs obtained from the halo white dwarf luminosity function of Torres et al. (1998), we also took account the new halo white-dwarf candidates in the SDSS Stripe 82 (Vidrih et al. 2007).
To reproduce the microlensing experiments towards the LMC, we followed
the detailed LMC descriptions of Gyuk et al. (2000) and Kallivayalil
et al. (2006). Our model takes account of parameters such as the
scale length and scale height of the LMC, its inclination, and its
kinematical properties. This model provides a synthetic population of
stars representative of the monitored point sources. After each
simulation was completed, we evaluated which star of the Galactic halo
could be responsible for a microlensing event. We considered only
stars that fulfilled a series of criteria. First, the lensing star
should be fainter than a certain magnitude limit. In a second step,
we checked whether the lens was inside the Einstein tube of the
monitored star, that is, if the angular distance between the lens and
monitored star was smaller than the Einstein radius. We recall here
that the Einstein radius is given by
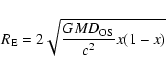 |
(1) |
where
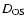 is the observer-source distance and
is the observer-source distance and
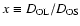 .
Third, we filter those stars that
are candidates to produce a microlensing event with the detection
efficiency function,
.
Third, we filter those stars that
are candidates to produce a microlensing event with the detection
efficiency function,
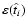 ,
where
,
where 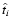 is the
Einstein ring diameter crossing time. The detection efficiency depends
on the particular characteristics of the experiment. We reproduced the
MACHO and EROS experiments. In the case of the MACHO project, we
adopted
is the
Einstein ring diameter crossing time. The detection efficiency depends
on the particular characteristics of the experiment. We reproduced the
MACHO and EROS experiments. In the case of the MACHO project, we
adopted
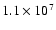 stars during 5.7 yr over
stars during 5.7 yr over
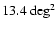 ,
whereas the detection efficiency was modeled according to:
,
whereas the detection efficiency was modeled according to:
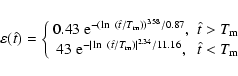 |
(2) |
where
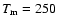 days. This expression provides a good
fit to the results of Alcock et al. (2000). For the EROS experiment,
we used
days. This expression provides a good
fit to the results of Alcock et al. (2000). For the EROS experiment,
we used
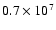 stars over a wider field of
stars over a wider field of
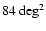 and a period of 6.7 yr. To evaluate the detection efficiency, we
adopted a numerical fit to the results of Tisserand et al. (2007).
and a period of 6.7 yr. To evaluate the detection efficiency, we
adopted a numerical fit to the results of Tisserand et al. (2007).
For all of the simulations, we extract parameters required to
characterize the microlensing experiments. A complete description of
parameters important to a discussion of gravitational microlensing can be
found in Mollerach & Roulet (2002) and Schneider et al. (2004). The
most important parameter, for our purposes, is probably the optical
depth, 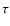 ,
which measures the probability that, at a given time, a
star is magnified by a lens by more than a factor of 1.34.
Observationally, an estimate of this parameter can be obtained using
the expression (Alcock et al. 2000):
,
which measures the probability that, at a given time, a
star is magnified by a lens by more than a factor of 1.34.
Observationally, an estimate of this parameter can be obtained using
the expression (Alcock et al. 2000):
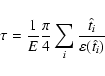 |
(3) |
where E is the total exposure in star-years. The optical
depth is independent of both the lens motion and mass distribution.
Since the experiments measure the number of events and their
durations, additional information can be however obtained using the
microlensing rate, 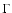 ,
and its distribution as a function of
event duration. The microlensing rate represents the flux of lenses
inside the microlensing tube. Finally, an estimate of the expected
number of events can be evaluated using the expression
,
and its distribution as a function of
event duration. The microlensing rate represents the flux of lenses
inside the microlensing tube. Finally, an estimate of the expected
number of events can be evaluated using the expression
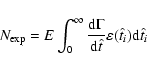 |
(4) |
As previously mentioned, the optical depth provides the most obvious
and basic information about the microlensing experiments. Even so,
the optical depth plays a critical role in our analysis, since it
provides a wealth of information about the Galactic halo and the
presence of dark matter. We compare results obtained using our Monte
Carlo simulator with those derived by the MACHO collaboration. In
Fig. 1, we present the contribution of the different simulated
populations, to the optical depth, for the two initial mass functions
studied, as a function of the adopted magnitude cut. Our simulations
were normalized to the value of the optical depth derived by Alcock et al. (2000),
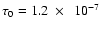 .
.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{9805fig01.eps}\end{figure}](/articles/aa/full/2008/29/aa09805-08/Timg42.gif) |
Figure 1:
Microlensing optical depth towards the LMC as a function of the limiting magnitude. Solid and open squares represent the CO and ONe white-dwarf populations, respectively. Red dwarfs are represented using open triangles, while the entire population is shown using open circles. |
| Open with DEXTER |
The white-dwarf populations
are represented by solid and open squares for the CO and ONe white
dwarfs, respectively. Open triangles indicate the contribution of red
dwarfs, while the contribution of the three populations is represented
by open circles. The first remarkable result is that, for the
standard initial mass function (top panel of Fig. 1), the combined
contribution of red dwarfs and white dwarfs is at most one third of
the observed optical depth, when a totally-unrealistic magnitude cut
is adopted,
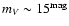 .
We note, in addition, that there
is a clearly-decreasing trend as the magnitude-cut adopted is
increased. This is because fewer objects contribute to the optical
depth measured as the magnitude cut increases. Furthermore, the slope
of the distributions is different for the three types of objects
considered. For instance, the contribution of red dwarfs decreases
faster than the contribution of CO white dwarfs as the magnitude cut
increases, which, in turn, decreases faster than the contribution of
ONe white dwarfs. This reflects the fact that, in general, red dwarfs
are brighter than regular, CO white dwarfs. Finally, ONe white dwarfs
cool rapidly (Althaus et al. 2007) and thus, for realistic halo ages,
are faint objects. Consequently, their contribution remains almost
constant. We note that the optical depth, measured for the entire
population, almost doubles that obtained when the white-dwarf
population alone is considered. The value measured remains, however,
far below the observed value, which agrees with other studies; it is
clear that the mass of a Galactic halo population cannot fully explain
the results of the MACHO team. Even for different initial mass
functions, for example that of Adams & Laughlin (1996), we are able
to predict that
.
We note, in addition, that there
is a clearly-decreasing trend as the magnitude-cut adopted is
increased. This is because fewer objects contribute to the optical
depth measured as the magnitude cut increases. Furthermore, the slope
of the distributions is different for the three types of objects
considered. For instance, the contribution of red dwarfs decreases
faster than the contribution of CO white dwarfs as the magnitude cut
increases, which, in turn, decreases faster than the contribution of
ONe white dwarfs. This reflects the fact that, in general, red dwarfs
are brighter than regular, CO white dwarfs. Finally, ONe white dwarfs
cool rapidly (Althaus et al. 2007) and thus, for realistic halo ages,
are faint objects. Consequently, their contribution remains almost
constant. We note that the optical depth, measured for the entire
population, almost doubles that obtained when the white-dwarf
population alone is considered. The value measured remains, however,
far below the observed value, which agrees with other studies; it is
clear that the mass of a Galactic halo population cannot fully explain
the results of the MACHO team. Even for different initial mass
functions, for example that of Adams & Laughlin (1996), we are able
to predict that
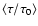 is, at most, 0.3, which
is evaluated for unrealistic magnitude cuts (see the bottom panel of
Fig. 1). The results obtained using the non-standard initial mass
function deserve two additional comments. In particular, we note that
the largest contribution to the optical depth measurement is made
by the CO white-dwarf population and, secondly, that the contribution
of red dwarfs is negligible for magnitude cuts larger than
is, at most, 0.3, which
is evaluated for unrealistic magnitude cuts (see the bottom panel of
Fig. 1). The results obtained using the non-standard initial mass
function deserve two additional comments. In particular, we note that
the largest contribution to the optical depth measurement is made
by the CO white-dwarf population and, secondly, that the contribution
of red dwarfs is negligible for magnitude cuts larger than
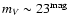 ,
which is a reasonable value for current surveys. Both
facts are unsurprising, since this particular initial mass function
was tailored to produce a large population of
,
which is a reasonable value for current surveys. Both
facts are unsurprising, since this particular initial mass function
was tailored to produce a large population of
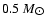 white
dwarfs. In summary, we find that, for the mass range considered, a
model stellar halo produces a microlensing optical-depth that is at
most one third of that measured by the MACHO team, independently of
the adopted initial mass function.
white
dwarfs. In summary, we find that, for the mass range considered, a
model stellar halo produces a microlensing optical-depth that is at
most one third of that measured by the MACHO team, independently of
the adopted initial mass function.
Table 1:
Summary of the results obtained for the entire simulated population of microlenses in the direction of the LMC for a halo age of 14 Gyr, different model initial mass functions,
and several magnitude cuts.
In Table 1, we summarize the average values of parameters of the
entire population for two initial mass functions and four magnitude
cuts, that is, we present the number of microlensing events, the average
mass of the microlenses, their average proper motion, distance and
tangential velocity, the corresponding Einstein crossing times and,
finally, the contribution to the microlensing optical depth. It is
clear that some parameters are dependent of the magnitude cut. For
instance, the average distance of the sample increases as the
magnitude cut increases. This is a natural consequence of selecting
more distant objects which, in turn, implies longer Einstein crossing
times. This behavior is independent of the assumed initial mass
function. However, there are characteristics which do not change as
the magnitude cut increases, for instance, the expected number of
events or the average mass of the sample. In the case of a standard
initial mass function, no more than one microlensing event should be
expected at the 1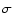 confidence level, while for a log-normal
mass function up to 5 events might be expected. In any case, the
expected number of microlensing events is far from the 17 events
claimed by the MACHO experiment.
confidence level, while for a log-normal
mass function up to 5 events might be expected. In any case, the
expected number of microlensing events is far from the 17 events
claimed by the MACHO experiment.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{9805fig02.eps}\end{figure}](/articles/aa/full/2008/29/aa09805-08/Timg61.gif) |
Figure 2:
Contribution to the optical depth as a function of lens mass. |
| Open with DEXTER |
As already mentioned, the average mass of the microlenses depends on
the assumed initial mass function. To investigate this further in
Fig. 2, the contribution of the microlenses to the optical depth as a
function of the mass of the lens object, for both initial mass
functions, is shown. The results obtained with our Monte Carlo
simulator clearly show that for a standard initial mass function
(shown in the top panel of Fig. 2) there are two peaks centered at
masses
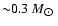 and
and
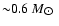 ,
respectively.
These masses correspond to the average masses of red dwarfs and CO
white dwarfs, respectively. We note that, in the case of a standard
initial mass function, the contribution of ONe white dwarfs appears as
an extended tail in the case of a standard initial mass function.
This agrees with studies of the distribution of masses of the
white-dwarf population (Finley et al. 1997; Liebert et al.
2005). These studies indicate that a narrow, sharp peak exists close
to
,
respectively.
These masses correspond to the average masses of red dwarfs and CO
white dwarfs, respectively. We note that, in the case of a standard
initial mass function, the contribution of ONe white dwarfs appears as
an extended tail in the case of a standard initial mass function.
This agrees with studies of the distribution of masses of the
white-dwarf population (Finley et al. 1997; Liebert et al.
2005). These studies indicate that a narrow, sharp peak exists close
to
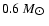 ,
with a tail extending towards larger masses, and
that several white dwarfs with spectroscopically-determined masses
occupy the mass interval between 1.0 and 1.2
,
with a tail extending towards larger masses, and
that several white dwarfs with spectroscopically-determined masses
occupy the mass interval between 1.0 and 1.2
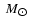 .
The
situation is different for the non-standard initial mass function,
which is shown in the bottom panel of Fig. 2. The log-normal initial
mass function considered here cannot produce red dwarfs with masses
below
.
The
situation is different for the non-standard initial mass function,
which is shown in the bottom panel of Fig. 2. The log-normal initial
mass function considered here cannot produce red dwarfs with masses
below
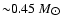 and thus the peak at
and thus the peak at
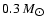 previously found is absent in this case.
previously found is absent in this case.
Table 2:
Summary of the results obtained for the population of red dwarf microlenses towards the LMC for an age of the halo of 14 Gyr, different model initial mass functions, and several
magnitude cuts.
A more detailed analysis of the role played by the red-dwarf
population is possible. In Table 2, we summarize the average parameter
values of the red-dwarf population for both initial mass functions.
Similar sets of data for the white-dwarf population can be found in
our previous studies (Camacho et al. 2007; García-Berro et al.
2004). As seen in Table 2, the red-dwarf population constitutes
roughly 10% of the observed MACHO optical depth for a standard
initial mass function. It is also important to discuss the other
parameters shown in Table 2. For instance, the average mass clearly
decreases when the magnitude cut increases, which is the opposite of
what occurs for the white-dwarf population. We should expect to find
less massive objects for larger magnitude cuts, because the more
massive the red dwarf, the brighter it will be. This result is
reinforced by the fact that the average distance increases for
increasing magnitude cuts. Since the average tangential velocity
remains constant, the combined effect a mass that decreases on average
and a distance that increases on average is that the Einstein
crossing-time remains almost constant. The characteristics of the
red-dwarf population differ significantly when the initial mass
function of Adams & Laughlin (1996) is used, since in this case the
production of low-mass red dwarfs is heavily suppressed. Accordingly,
in our simulations, we did not produce red dwarfs with masses smaller
than 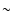 0.45
0.45
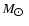 .
Thus, since the masses on average are
larger, we also find brighter stars. We therefore expect no
contribution at all for magnitude cuts above
.
Thus, since the masses on average are
larger, we also find brighter stars. We therefore expect no
contribution at all for magnitude cuts above
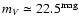 ,
while for brighter magnitude cuts the average mass expected is
,
while for brighter magnitude cuts the average mass expected is
 0.7
0.7
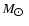 ,
which is even larger than expected for CO white
dwarfs.
,
which is even larger than expected for CO white
dwarfs.
For the standard initial mass function, a double-peaked profile is
found, as already observed; but the peak amplitude, however, should be
analyzed in more detail. The ratio of the contribution to the optical
depth of a typical red dwarf with respect to the contribution of a
typical CO white dwarf is
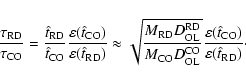 |
(5) |
This value depends on the adopted initial mass function and
on the magnitude cut used. For the standard initial mass function and
a magnitude cut of
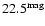 ,
the average values of the mass
and distance of a red dwarf are, respectively,
,
the average values of the mass
and distance of a red dwarf are, respectively,
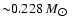 and 4.88 kpc, while for a typical CO white dwarf, the average mass
is
and 4.88 kpc, while for a typical CO white dwarf, the average mass
is
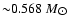 and the average distance is 3.14 kpc.
For these values, the ratio of the optical depths is equal to
and the average distance is 3.14 kpc.
For these values, the ratio of the optical depths is equal to
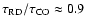 .
Thus, although the samples
of red dwarfs and white dwarfs differ, their contribution to the
optical depth, per object, remains the same. For instance, the
red-dwarf population has a smaller average mass than that of white
dwarfs but, in contrast, the average distance is larger. The total
contribution of both populations is therefore the number of
microlenses. To clarify this issue, we evaluated the fraction of
microlenses, for the different populations, as a function of the
adopted magnitude cut. The results are shown in Fig. 3 for both the
standard initial mass function (top panel) and the log-normal initial
mass function (bottom panel). For the standard initial mass function,
the relative contribution of red dwarfs decreases with increasing
value of magnitude cuts, while that of the CO white dwarfs increases.
Both contributions are equal for a magnitude cut of
.
Thus, although the samples
of red dwarfs and white dwarfs differ, their contribution to the
optical depth, per object, remains the same. For instance, the
red-dwarf population has a smaller average mass than that of white
dwarfs but, in contrast, the average distance is larger. The total
contribution of both populations is therefore the number of
microlenses. To clarify this issue, we evaluated the fraction of
microlenses, for the different populations, as a function of the
adopted magnitude cut. The results are shown in Fig. 3 for both the
standard initial mass function (top panel) and the log-normal initial
mass function (bottom panel). For the standard initial mass function,
the relative contribution of red dwarfs decreases with increasing
value of magnitude cuts, while that of the CO white dwarfs increases.
Both contributions are equal for a magnitude cut of
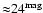 .
Finally, the contribution of ONe white dwarfs remains roughly
constant and only becomes significant for large magnitude cuts. These
trends can be attributed to the fact that red dwarfs are more numerous
at bright magnitudes than white dwarfs, for which typical luminosities
are of the order of
.
Finally, the contribution of ONe white dwarfs remains roughly
constant and only becomes significant for large magnitude cuts. These
trends can be attributed to the fact that red dwarfs are more numerous
at bright magnitudes than white dwarfs, for which typical luminosities
are of the order of
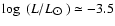 .
The situation is
completely different when the
.
The situation is
completely different when the 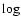 -normal initial mass function of
Adams & Laughlin (1996) is used. As can be seen in the bottom panel
of Fig. 3, the number of microlenses is practically dominated by the
CO white-dwarf contribution, while the contribution of red dwarfs and
ONe white dwarfs is negligible.
-normal initial mass function of
Adams & Laughlin (1996) is used. As can be seen in the bottom panel
of Fig. 3, the number of microlenses is practically dominated by the
CO white-dwarf contribution, while the contribution of red dwarfs and
ONe white dwarfs is negligible.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{9805fig03.eps}\end{figure}](/articles/aa/full/2008/29/aa09805-08/Timg79.gif) |
Figure 3:
Fraction of microlenses with respect to the entire population, as a function of the magnitude cut. |
| Open with DEXTER |
As previously pointed out, the contribution to the optical depth for a
standard initial mass function is doubled when the red dwarf
population is considered. We have also shown that for a standard
initial mass function the contributions of red dwarfs and CO white
dwarfs are roughly the same. It is natural to ask whether there are
differences that can help us to discern the contribution of one or
another population, using the observational data of the MACHO
experiment. To answer this question we analyzed the microlensing rate
as a function of event duration. The results of our simulations, for
a standard initial mass function, are shown in Fig. 4. Each of the
panels is clearly labelled with the adopted magnitude cut and the population of microlenses. In the left panels of Fig. 4, we adopted a magnitude cut of
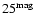 ,
whilst for the right panels a magnitude cut of
,
whilst for the right panels a magnitude cut of
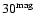 was adopted. In all cases, the simulated microlensing rate is shown using solid lines, while the observational data obtained by the MACHO team is shown using a dotted line. All distributions are normalized to unit area. The red-dwarf and the white-dwarf distributions present some differences. For a magnitude cut of
was adopted. In all cases, the simulated microlensing rate is shown using solid lines, while the observational data obtained by the MACHO team is shown using a dotted line. All distributions are normalized to unit area. The red-dwarf and the white-dwarf distributions present some differences. For a magnitude cut of
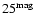 ,
the white-dwarf population presents a wider distribution, even though both the red-dwarf population and the white-dwarf populations show a peak located at nearly
,
the white-dwarf population presents a wider distribution, even though both the red-dwarf population and the white-dwarf populations show a peak located at nearly 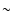 20 days. When a magnitude cut of
20 days. When a magnitude cut of
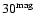 is adopted, the differences are more pronounced and it is clear that the distribution peak for the CO white-dwarf population moves to longer durations (
is adopted, the differences are more pronounced and it is clear that the distribution peak for the CO white-dwarf population moves to longer durations ( 70 days); in contrast, the peak of the red-dwarf population does not move appreciably.
70 days); in contrast, the peak of the red-dwarf population does not move appreciably.
![\begin{figure}
\par\includegraphics[width=11.5cm,clip]{9805fig04.eps}\end{figure}](/articles/aa/full/2008/29/aa09805-08/Timg82.gif) |
Figure 4:
Differential event rate normalized to unit area as a function of the Einstein crossing-time for the populations under study and different magnitude cuts (solid lines). The observational event distribution from Alcock et al. (2000) is represented as a dotted line in each panel. |
| Open with DEXTER |
To be able to attain more quantitative estimates, we performed a Z2statistical test of the compatibility of the different populations
with the observed data. The Z2 statistical test (Lucy 2000)
represents an improvement to the standard 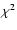 statistical test
and was specially developed for small data sets. In Table 3, we show
the Z2 probability that the different simulated populations are
compatible with the distribution of Einstein times, obtained by the
MACHO experiment. It should be clarified that this probability
represents an estimate of the degree to which the observed event-rate
distribution can be derived from a single population of stars. As can
be seen in Table 3, the CO white-dwarf population provides the most
appropriate description of the observational data, given that its
compatibility is as high as 0.90 for the faintest magnitude cut.
Moreover, the compatibility of this population with the observational
data increases at fainter magnitude bins. In sharp contrast, the
population of red dwarfs presents a decreasing trend as the magnitude
cut increases and, additionally, the compatibility with the
observational data is, at most, 0.70. With regard to the ONe
white-dwarf population, the compatibility presents an almost constant
value of around 0.70, independently of the magnitude cut. These
results indicate that the CO white-dwarf population can reproduce the
observed distribution of microlensing event-rates. Even more, they
dominate the behavior of the entire population, as can be seen from
the final row of Table 3, in which we analyze the compatibility of the
entire population of simulated stars. Therefore, even if the expected
number of microlensing events obtained in our simulations is
considerable smaller than the
statistical test
and was specially developed for small data sets. In Table 3, we show
the Z2 probability that the different simulated populations are
compatible with the distribution of Einstein times, obtained by the
MACHO experiment. It should be clarified that this probability
represents an estimate of the degree to which the observed event-rate
distribution can be derived from a single population of stars. As can
be seen in Table 3, the CO white-dwarf population provides the most
appropriate description of the observational data, given that its
compatibility is as high as 0.90 for the faintest magnitude cut.
Moreover, the compatibility of this population with the observational
data increases at fainter magnitude bins. In sharp contrast, the
population of red dwarfs presents a decreasing trend as the magnitude
cut increases and, additionally, the compatibility with the
observational data is, at most, 0.70. With regard to the ONe
white-dwarf population, the compatibility presents an almost constant
value of around 0.70, independently of the magnitude cut. These
results indicate that the CO white-dwarf population can reproduce the
observed distribution of microlensing event-rates. Even more, they
dominate the behavior of the entire population, as can be seen from
the final row of Table 3, in which we analyze the compatibility of the
entire population of simulated stars. Therefore, even if the expected
number of microlensing events obtained in our simulations is
considerable smaller than the 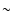 15 events claimed by the MACHO
team, the event rate distribution of the CO white-dwarf population is
in fair agreement with the observed distribution. This result places
doubt on how well the characteristics of the halo white-dwarf
population are known and if there are other ways to produce a larger
number of old white dwarfs in the stellar halo.
15 events claimed by the MACHO
team, the event rate distribution of the CO white-dwarf population is
in fair agreement with the observed distribution. This result places
doubt on how well the characteristics of the halo white-dwarf
population are known and if there are other ways to produce a larger
number of old white dwarfs in the stellar halo.
Table 3:
Compatibility, as obtained using the Z2 statistical test, of the observed MACHO distribution of Einstein crossing times and those of the different simulated populations.
Table 4:
Summary of the results obtained for the simulation of microlenses towards the LMC for the EROS experiment for an age of the halo of 14 Gyr, different model initial mass functions, and several magnitude cuts.
While the MACHO team claim the identification of up to 17 observed
events, the EROS collaboration have not found any microlensing event
towards the LMC and one candidate event towards the SMC. Adopting a
standard halo model and assuming
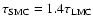 ,
the EROS results imply an optical depth
,
the EROS results imply an optical depth
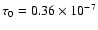 (Tisserand et al. 2007), which is four times smaller than that
obtained by the MACHO team. We performed a set of simulations
emulating the conditions of the EROS experiment with inputs similar to
those described in Sect. 2. Although only minor differences should be
expected in the analysis of the main results, it is clear as well that
a joint study of both experiments, using a controlled set of
prescriptions, represents a test of the robustness of our numerical
procedure.
(Tisserand et al. 2007), which is four times smaller than that
obtained by the MACHO team. We performed a set of simulations
emulating the conditions of the EROS experiment with inputs similar to
those described in Sect. 2. Although only minor differences should be
expected in the analysis of the main results, it is clear as well that
a joint study of both experiments, using a controlled set of
prescriptions, represents a test of the robustness of our numerical
procedure.
In Table 4, we summarized the results obtained in this second set of
Monte Carlo simulations of microlenses towards the LMC, for the EROS
experiment. Our simulations show that, for the standard initial mass
function, the expected optical depth could be 70% of the value
found by the EROS team. The value obtained, when only the white-dwarf
population was considered, was previously found to be 50% (Camacho
et al. 2007). Our simulations reproduce the results of the EROS
experiment more effectively. The red-dwarf population is obviously
responsible for this increase. When a non-standard initial mass
function is adopted, the results show, however, only marginal
differences with respect to those obtained for a white-dwarf
population, given that in this case the role of red dwarfs is
limited. In summary, our results are in fair agreement with those
obtained by the EROS experiment, and appear to indicate that the
microlensing optical depth, obtained by the MACHO collaboration, is an
overestimate.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9805fig05.eps}\end{figure}](/articles/aa/full/2008/29/aa09805-08/Timg90.gif) |
Figure 5:
Halo dark-matter fraction as a function of the mass lens. We
plot, using a solid line, the 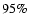 confidence-level curve
for the MACHO experiment and the
confidence-level curve
for the MACHO experiment and the 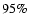 confidence-level
upper-limit for the EROS experiment.
confidence-level
upper-limit for the EROS experiment. |
| Open with DEXTER |
Using the information presented in this paper, we are able to assess
the contribution of stellar populations, for the mass range studied,
to the mass of the baryonic dark-matter halo. Based on their 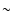 15 microlensing events, the MACHO collaboration derived an estimate of
the halo fraction of dark matter f, as well as the MACHO mass m,
using maximum-likelihood techniques. A similar analysis was completed
by the EROS team, but with the significant difference that, in that
case, no event was reported for the LMC, which implies that only an
upper limit to the halo mass fraction can be obtained. To compare the
results of the MACHO and EROS collaborations with our Monte Carlo
simulations, we adopted, as our reference model, the isothermal sphere
of core radius 5 kpc, with a value of
15 microlensing events, the MACHO collaboration derived an estimate of
the halo fraction of dark matter f, as well as the MACHO mass m,
using maximum-likelihood techniques. A similar analysis was completed
by the EROS team, but with the significant difference that, in that
case, no event was reported for the LMC, which implies that only an
upper limit to the halo mass fraction can be obtained. To compare the
results of the MACHO and EROS collaborations with our Monte Carlo
simulations, we adopted, as our reference model, the isothermal sphere
of core radius 5 kpc, with a value of
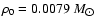 pc-3 for the local dark-matter density and disregarding the contribution of the LMC halo. Using this model, we obtained that the optical depth towards the LMC is
pc-3 for the local dark-matter density and disregarding the contribution of the LMC halo. Using this model, we obtained that the optical depth towards the LMC is
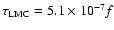 .
The different estimates of the halo mass fraction f, as a function of mass, are plotted in Fig. 5. As a solid line we show the curve of the MACHO 95% confidence level, as taken from Alcock et al. (2000), and the EROS 95% confidence-level upper-limit, based on
no observed events in the EROS-1 and EROS-2 data (Tisserand et al. 2007). We also represent the individual contributions of each population studied and the entire population, in addition to the corresponding 95% confidence level error bars. It is remarkable
that the value obtained for the entire halo simulated-population
agrees within the 95% confidence level curves of both observational
estimates. Our results therefore predict that the range of stellar
masses within 0.08 and
.
The different estimates of the halo mass fraction f, as a function of mass, are plotted in Fig. 5. As a solid line we show the curve of the MACHO 95% confidence level, as taken from Alcock et al. (2000), and the EROS 95% confidence-level upper-limit, based on
no observed events in the EROS-1 and EROS-2 data (Tisserand et al. 2007). We also represent the individual contributions of each population studied and the entire population, in addition to the corresponding 95% confidence level error bars. It is remarkable
that the value obtained for the entire halo simulated-population
agrees within the 95% confidence level curves of both observational
estimates. Our results therefore predict that the range of stellar
masses within 0.08 and
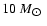 ,
provides f=0.05 and an
average mass of
,
provides f=0.05 and an
average mass of
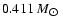 to the halo dark matter, in
agreement with the observational data. This result corroborates our
previous estimates of the limited contribution of both CO white dwarfs
and ONe white dwarfs (García-Berro et al. 2004; Camacho et al. 2007).
to the halo dark matter, in
agreement with the observational data. This result corroborates our
previous estimates of the limited contribution of both CO white dwarfs
and ONe white dwarfs (García-Berro et al. 2004; Camacho et al. 2007).
We have extended our previous studies of the contribution to the halo
dark matter of the white-dwarf population and included the Galactic
population of red dwarfs. We have estimated the contribution of these
objects to the microlensing optical depth towards the LMC and compared
our estimate with the measurements of the MACHO and EROS
collaborations. Our estimate is based on a series of Monte Carlo
simulations that incorporate the most up-to-date evolutionary tracks
for red dwarfs, CO white dwarfs, and ONe white dwarfs, and reliable
models of our Galaxy and the LMC. In a first set of simulations, we
have found that the contribution of the red-dwarf population
practically doubles the contribution found so far for the white-dwarf
population. Our results indicate that the entire population of these
stars can account for at most 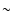 0.3 of the optical depth found by
the MACHO team. This value implies that the contribution of the full
range of masses between 0.08 and
0.3 of the optical depth found by
the MACHO team. This value implies that the contribution of the full
range of masses between 0.08 and
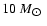 represents 5% of
the halo dark matter with an average mass of
represents 5% of
the halo dark matter with an average mass of
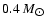 .
Although this result is in partial agreement with the 95% confidence level MACHO estimate for a standard isothermal sphere and no halo LMC contribution, the expected number of events
obtained by our simulations (3 events at the 95% confidence level)
is substantially below the 13 to 17 observed MACHO events. These
arguments reinforce the idea, previously pointed out by other studies,
that the optical depth found by the MACHO team should be an
overstimate, probably due to contamination of self-lensing objects,
variable stars and others. Moreover, we have assessed the
compatibility between the observed event rate distribution and the
ones obtained for the different populations under study. Our results
show that the CO white-dwarf population can reproduce fairly well the
observed event-rate distribution although, as mentioned earlier, the
expected number of events is considerable smaller. On the other hand,
the negative results obtained by the EROS team towards the LMC are in
agreement with our standard halo simulation. Finally, and for the
sake of completeness, we have studied the effects of a log-normal
biased initial mass function. In this case, the contribution of the
red-dwarf population is only marginal given that the production of
low-mass stars is strongly inhibited. Accordingly, the total
contribution to the microlensing optical depth is not different from
that found in previous studies of the white-dwarf contribution.
.
Although this result is in partial agreement with the 95% confidence level MACHO estimate for a standard isothermal sphere and no halo LMC contribution, the expected number of events
obtained by our simulations (3 events at the 95% confidence level)
is substantially below the 13 to 17 observed MACHO events. These
arguments reinforce the idea, previously pointed out by other studies,
that the optical depth found by the MACHO team should be an
overstimate, probably due to contamination of self-lensing objects,
variable stars and others. Moreover, we have assessed the
compatibility between the observed event rate distribution and the
ones obtained for the different populations under study. Our results
show that the CO white-dwarf population can reproduce fairly well the
observed event-rate distribution although, as mentioned earlier, the
expected number of events is considerable smaller. On the other hand,
the negative results obtained by the EROS team towards the LMC are in
agreement with our standard halo simulation. Finally, and for the
sake of completeness, we have studied the effects of a log-normal
biased initial mass function. In this case, the contribution of the
red-dwarf population is only marginal given that the production of
low-mass stars is strongly inhibited. Accordingly, the total
contribution to the microlensing optical depth is not different from
that found in previous studies of the white-dwarf contribution.
Acknowledgements
Part of this work was supported by the MEC grants AYA05-08013-C03-01 and 02, by the European Union FEDER funds and by the AGAUR.
- Adams, F. C., & Laughlin, G. 1996, ApJ, 468, 686
In the text
- Alcock, C., Allsman, R. A., Alves, D. R., et al. 1997, ApJ, 486, 69
In the text
- Alcock, C., Allsman, R. A., Alves, D. R., et al. 2000, ApJ, 542, 281
In the text
- Althaus, L. G., García-Berro, E., Isern, J., Córsico, A. H., & Rohrmann, R. D. 2007, A&A, 465, 249
In the text
- Baraffe, I., Chabrier, G., Allard, F., & Hauschildt, P. H. 1998, A&A, 337, 403
In the text
- Becker, A. C., Rest, A., Stubbs, C., et al. 2005, IAU Symp., 225, 357
In the text
- Belokurov, V., Evans, N. W., & Le Du, Y. 2003, MNRAS, 341, 1373
In the text
- Belokurov, V., Evans, N. W., & Le Du, Y. 2004, MNRAS, 352, 233
In the text
- Binney, J., & Tremaine, H. 1987, Galactic Dynamics (Princeton: Princeton Univ. Press)
In the text
- Calchi, N. S., de Luca, F., Jetzer, P., & Scarpetta, G. 2006, A&A, 459, 407
In the text
- Camacho, J., Torres, S., Isern, J., Althaus, L. G., & García-Berro, E. 2007, A&A, 471, 151
In the text
- Canal, R., Isern, J., & Ruiz-Lapuente, P. 1997, ApJ, 488, L35
In the text
- Chabrier, G. 2004, ApJ, 611, 315
- Chabrier, G., Segretain, L., & Méra, D. 1996, ApJ, 468, 21
In the text
- Charlot, S., & Silk, J. 1995, ApJ, 445, 124
In the text
- Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, 2MASS All Sky Catalog of point sources, Univ. of Massachusetts and IPAC/California Institute
of Technology
In the text
- Dehnen, W., & Binney, J. 1998, MNRAS, 298, 387
In the text
- Eisenstein, D. J., Liebert, J., Harris, H. C., et al. 2006, ApJS, 167, 40
In the text
- Finley, D. S., Koester, D., & Basri, G. 1997, ApJ, 488, 375
In the text
- Flynn, C., Holopainen, J., & Holmberg, J. 2003, MNRAS, 339, 817
- García-Berro, E., Torres, S., Isern, J., & Burkert, A. 2004, A&A, 418, 53
In the text
- Gates, E. I., & Gyuk, G. 2001, ApJ, 547, 786
In the text
- Goldman, B., Afonso, A., Alard, Ch., et al. 2002, A&A, 389, 69
In the text
- Griest, K. 1991, ApJ, 366, 412
In the text
- Gyuk, G., Dalal, N., & Griest, K. 2000, ApJ, 535, 90
In the text
- Hambly, N. C., Irwin, M. J., & MacGillivray, H. T. 2001, MNRAS, 326, 1295
In the text
- Hansen, B. M. S. 1998, Nature, 394, 860
In the text
- Hansen, B. M. S., & Liebert, J. 2003, ARA&A, 41, 465
In the text
- Holopainen, J., Flynn, C., Knebe, A., Gill, S. P., & Gibson, B. K. 2006, MNRAS, 368, 1209
In the text
- Ibata, R. A., Richer, H. B., Gilliland, R. L., & Scott, D. 1999, ApJ, 524, L95
In the text
- Iben, I., & Laughlin, G. 1989, ApJ, 341, 312
In the text
- Isern, J., García-Berro, E., Hernanz, M., Mochkovitch, R., & Torres, S. 1998, ApJ, 503, 239
In the text
- James, F. 1990, Comput. Phys. Commun., 60, 329
In the text
- Kallivayalil, N., van der Marel, R. P., Alcock, C., et al. 2006, ApJ, 638, 772
In the text
- Kerins, E., & Evans, N. W. 1998, ApJ, 503, 75
In the text
- Kilic, M., Mendez, R. A., Von Hippel, T., & Winget, D. E. 2005, ApJ, 633, 1126
In the text
- Klypin, A., Zhao, H., & Somerville, R. 2002, ApJ, 573, 597
- Knox, R. A., Hawkins, M. R. S., & Hambly, N. C. 1999, MNRAS, 306, 736
In the text
- Lasserre, T., Afonso, C., Albert, J. N., et al. 2001, A&A, 355, L39
In the text
- Liebert, J., Dahn, C. C., & Monet, D. G. 1989, in White Dwarfs, ed. G. Wegner (Berlin: Springer), 15
- Liebert, J., Bergeron, P., & Holberg, J. 2005, ApJS, 156, 47
In the text
- Lucy, L. 2000, MNRAS, 318, 92
In the text
- Majewski, S. R., & Siegel, M. H. 2002, ApJ, 569, 432
In the text
- Mollerach, S., & Roulet, E. 2002, Gravitational Lensing and Microlensing (Singapore: World Scientific)
In the text
- Muraki, Y., Sumi, T., Abe, F., et al. 1997, ApJ, 490, 493
In the text
- Nelson, C. A., Cook, K. H., Axelrod, T. S., Mould, J. R., & Alcock, C. 2002, ApJ, 573, 644
In the text
- Oppenheimer, B. R., Hambly, N. C., Digby, A. P., Hodgkin, S. T., & Saumon, D. 2001, Science, 292, 698
In the text
- Paczynski, B. 1986, ApJ, 304, 1
In the text
- Rahvar, S. 2005, MNRAS, 356, 1127
In the text
- Reylé, C., Robin, A. C., & Créze, M. 2001, A&A, L53
In the text
- Sahu, K. 1994, Nature, 370, 275
In the text
- Salaris, M., García-Berro, E., Hernanz, M., Isern, J., & Saumon, D. 2000, ApJ, 544, 1036
In the text
- Scalo, J. 1998, in The Stellar Initial Mass Function, ed. G. Gilmore, & D. Howell (San Francisco: PASP Conf. Ser.), 142, 201
In the text
- Schneider, P., Kochanek, C. S., & Wambsganss, J. 2004, in Saas-Fee lectures on Gravitational Lensing
In the text
- Silk, J. 2007, in The invisible universe: dark matter and dark energy, Proc. of the Third Aegean Summer School (Berlin: Springer Verlag), Lect. Not. Phys. 720, 101
In the text
- Tisserand, P., Le Guillou, L., Afonso, et al. 2007, A&A, 469, 387
In the text
- Torres, S., García-Berro, E., & Isern, J. 1998, ApJ, 508, L71
In the text
- Torres, S., García-Berro, E., Burkert, A., & Isern, J. 2002, MNRAS, 336, 971
In the text
- Udalski, A., Szymanski, M., Kaluzny, J., et al. 1994, Acta Astron., 44, 1
In the text
- Vennes, S., Smith, R. J., Boyle, J., et al. 2002, MNRAS, 335, 673
In the text
- Vidrih, S., Bramich, D. M., Hewett, P. C., et al. 2007, MNRAS, 382, 515
In the text
- Zhao, H. S. 1998, MNRAS, 294, 139
In the text
Copyright ESO 2008
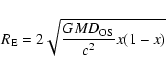
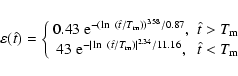
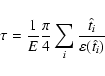
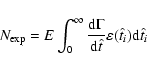
![\begin{figure}
\par\includegraphics[width=7cm,clip]{9805fig01.eps}\end{figure}](/articles/aa/full/2008/29/aa09805-08/Timg42.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{9805fig02.eps}\end{figure}](/articles/aa/full/2008/29/aa09805-08/Timg61.gif)
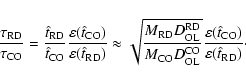
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{9805fig03.eps}\end{figure}](/articles/aa/full/2008/29/aa09805-08/Timg79.gif)
![\begin{figure}
\par\includegraphics[width=11.5cm,clip]{9805fig04.eps}\end{figure}](/articles/aa/full/2008/29/aa09805-08/Timg82.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9805fig05.eps}\end{figure}](/articles/aa/full/2008/29/aa09805-08/Timg90.gif)