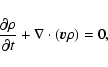A&A 486, 655-662 (2008)
DOI: 10.1051/0004-6361:200809800

Magnetohydrodynamic code for gravitationally-stratified media

S. Shelyag - V. Fedun - R. Erdélyi

Solar Plasma Physics Research Centre, Department of Applied Mathematics, University of Sheffield, Hicks Building, Hounsfield Rd., Sheffield, S7 3RH, UK

Received 17 March 2008 / Accepted 8 May 2008

Abstract
Aims. We describe a newly-developed magnetohydrodynamic (MHD) code with the capacity to simulate the interaction of any arbitrary perturbation (i.e., not necessarily limited to the linearised limit) with a magnetohydrostatic equilibrium background.
Methods. By rearranging the terms in the system of MHD equations and explicitly taking into account the magnetohydrostatic equilibrium condition, we define the equations governing the perturbations that describe the deviations from the background state of plasma for the density, internal energy and magnetic field. We found it was advantageous to use this modified form of the MHD equations for numerical simulations of physical processes taking place in a stable gravitationally-stratified plasma. The governing equations are implemented in a novel way in the code. Sub-grid diffusion and resistivity are applied to ensure numerical stability of the computed solution of the MHD equations. We apply a fourth-order central difference scheme to calculate the spatial derivatives, and implement an arbitrary Runge-Kutta scheme to advance the solution in time.
Results. We have built the proposed method, suitable for strongly-stratified magnetised plasma, on the base of the well-documented Versatile Advection Code (VAC) and performed a number of one- and multi-dimensional hydrodynamic and MHD tests to demonstrate the feasibility and robustness of the code for applications to astrophysical plasmas.

Key words: methods: numerical - magnetohydrodynamcs (MHD) - plasmas - Sun: general

1 Introduction

Plasma embedded in magnetic field can often be described by the equations of compressible magnetohydrodynamics (Alfvén 1942). Due to the highly non-linear nature and intrinsic complexity of these equations, numerical simulations are often the only way to obtain an in-depth knowledge about macroscopic physical processes taking place in magnetised non-uniform turbulent plasmas (e.g., Brandenburg 2003; Nordlund 1985; Chan et al. 1982).

Various numerical schemes have been proposed for MHD simulations and are circulating in the literature. The wide range of methods is mainly down to their challenging imperfectness: on the one hand, one has to care about the numerical stability of a solution, whereas on the other hand, the solution has to be physically correct. Without pretending to construct the only perfect method to solve the MHD equations numerically, we aim to find a technique that will allow us to perform simulations of non-linear processes in a magnetised plasma with the presence of external gravitational field.

In general, the numerical schemes working on a spatial domain may be divided into several types based on the way the schemes keep up with numerical stability and resolve the physical processes within the domain. Riemann type solvers successfully exploit an analytical solution obtained locally (Roe 1981; Dai & Woodward 1994). The need to develop a new Riemann solver when additional physics is necessary (e.g., for new types of wave modes) is often called to be the main disadvantage of these numerical schemes (Nordlund & Galsgaard 1995). Total variation diminishing (TVD) schemes (Tóth 1996; Harten 1983; van Leer 1979) aim at maintaining numerical stability of the solution by preserving its monotonicity, however, these schemes are often too diffusive, which results in the computational solution being smeared over the spatial domain (Tóth et al. 1998).

The possibility of controlled diffusion acting only on small scales, introduced to assure numerical stability of a computational solution at the lowest possible spatial scales for turbulent high Reynolds number plasma, has been demonstrated and is used widely (Vögler 2003; Vögler et al. 2005; Caunt & Korpi 2001; Nordlund & Galsgaard 1995; Stein & Nordlund 1998). However, in the case of a stable, gravitationally-stratified plasma, especially in regions of strong stable stratification that occurs, for example, in the upper photosphere or at the transition region of the Sun, this approach, as well as others, such as TVD or Riemann solver based numerical schemes, introduce a small but unavoidable large scale numerical diffusion. Consequently, this diffusion often leads to the violation of the desired magnetohydrostatic equilibrium in the model and to the generation of an unphysical flux tending to smear the background model (Tóth 1996; Boris & Book 1973). Flux corrected transport (FCT) schemes with strong anti-diffusion terms have shown a better behaviour (Boris & Book 1973; Erdélyi & James 2004). However, due to the larger and multi-dimensional numerical stencil (Zalesak 1979), these schemes may be more difficult for domain decomposition for parallelisation purposes. Also, it has been reported that some spurious oscillations may occur when using such a scheme (Tóth 1996).

The inevitable diffusion may forbid the robust advancement of the simulation of a non-linear phenomenon in gravitationally-stratified plasma, causing MHD simulations of such a plasma often to be referred to as ``black art''. This is definitely not the case for linear MHD simulations, since they mainly describe small deviations from a stable background state (Khomenko & Collados 2006; Parchevsky & Kosovichev 2007). Mixing the two approaches of hyperdiffusion and linearised MHD simulations, and removing the linear limit requirement, we aim to construct a novel method that will allow us to perform simulations of both linear and non-linear processes in strongly-stratified media from fluids to magnetised plasmas.

We describe a numerical MHD tool that allows us to simulate the interaction of any arbitrary perturbation (not necessarily limited to the linearised regime) with the background plasma in magnetohydrostatic equilibrium. The MHD equations for the perturbations of density, internal energy and magnetic field strength are redefined by taking into account the magnetohydrostatic equilibrium condition. Hyperdiffusion and hyperresistivity are implemented to achieve numerical stability of the computed solution of the MHD equations. We found it advantageous to use this, apparently more complex form of the MHD equations for numerical simulations of processes in a stable gravitationally-stratified plasma and implemented the method on the base of the well-known Versatile Advection Code (VAC; Tóth 1996). A number of standard tests are performed to demonstrate the feasibility and robustness of the technique. The imminently planned scientific application of the code is to use it in studies of propagation of (magneto)acoustic waves in the solar sub-photosphere in the presence of time- and spatially-dependent background flows or sound speed perturbations (Shelyag et al. 2007,2006), and conversion of linear to non-linear waves in the stratified solar corona (Fedun & Erdélyi 2008).

The paper is organized as follows. In the next section we describe the modified MHD equations and their proposed numerical implementation. Numerical tests of the code are presented in the third section of the paper. A range of future use of the method is discussed briefly in the last section.

2 Equations and numerical methods

The governing equations of full ideal compressible MHD in their conservative form are:

$$% \frac{\partial \rho}{\partial t} + \nabla \cdot \left({\vec v} \rho \right)=0,$$ (1)

$$% \frac{\partial{\left(\rho{\vec v}\right)}}{\partial t}+\nab... ...{\vec v}-{\vec B}{\vec B}\right)+\nabla p_{t}=\rho {{\vec g}},$$ (2)

$$% \frac{\partial{e}}{\partial{t}}+\nabla \cdot \left( {{\vec ... ...vec v}}+{{\vec v}}p_t\right)=\rho {{\vec g}} \cdot {{\vec v}},$$ (3)

$$% \frac{\partial{{\vec B}}}{\partial{t}}+\nabla\cdot\left(\vec{vB}-\vec{Bv}\right)=0,$$ (4)

$$% p_k=\left( \gamma-1 \right) \left(e - \frac{\rho {{\vec v}}^2}{2} - \frac{{{\vec B}}^2}{2} \right),$$ (5)

and

$$% p_{\rm t}=p_{\rm k} + \frac{{{\vec B}}^2}{2},$$ (6)

where $\rho$ is the density, ${{\vec v}}$ is the velocity vector, e is the total energy density per unit volume, ${{\vec B}}$ is the magnetic field vector, $p_{\rm k}$ is the kinetic gas pressure, $p_{\rm t}$ is the total (magnetic + kinetic) pressure, $\gamma$ is the gas adiabatic index, and ${{\vec g}}$ is the external gravitational field vector. In these equations, the magnetic permeability of the plasma is set to unity. Equation (5) in the MHD system is the equation of state of an ideal gas, which connects the internal energy of the gas to its kinetic pressure. There are no terms of physical viscosity and magnetic resistivity included in the description, however they can be added to the system.

Without loss of generality we split the variables $\rho$, e, and ${{\vec B}}$ into their background and perturbed components:

$$% \rho=\tilde{\rho}+\rho_{\rm b},$$ (7)

$$% e=\tilde{e}+e_{\rm b},$$ (8)

and

$$% {{\vec B}}=\tilde{{{\vec B}}}+{{\vec B}}_{\rm b},$$ (9)

where the tilde denotes a perturbed quantity. We assume that the background components of the variables  $\rho_{\rm b}$, $e_{\rm b}$ and ${{\vec B}}_{\rm b}$ do not change in time.

Also, we assume a magnetohydrostatic equilibrium of the background state of the magnetised plasma in the computational domain with the presence of an external gravity field ${{\vec g}}$:

$$% \nabla p_{\rm kb} + \nabla \frac{{{\vec B}}_{\rm b}^2}{2} -... ...rm b} \nabla\right) {{\vec B}}_{\rm b}=\rho_{\rm b}{{\vec g}}.$$ (10)

Equation (10), describing the magnetohydrostatic equilibrium, is now scalarly multiplied by the velocity vector ${{\vec v}}$:

$$% \left( \nabla p_{\rm kb} + \nabla \frac{{{\vec B}}_{\rm b}^... ...right) \cdot {{\vec v}}=\rho_{\rm b}{\vec g} \cdot {{\vec v}}.$$ (11)

Substracting Eqs. (10) and (11) from the equations of momentum Eq. (2) and energy Eq. (3), and adding the diffusive source terms D to the right-hand side of the equations (they are introduced for numerical stability reasons and will be described below), the system of MHD equations for an arbitrary perturbation of density, energy, and magnetic field can be written:

$$% \frac{\partial \tilde{\rho}}{\partial t} + \nabla \cdot \le... ...lde{\rho}\right) \right]=0+D_{\rho}\left(\tilde{\rho} \right),$$ (12)

 

$$% \frac{\partial{\left[\left(\rho_{\rm b}+\tilde{\rho}\right){\ve... ...ec D}}_{\rho v}\left[\left(\tilde{\rho}+ \rho_{\rm b} \right){{\vec v}}\right],$$ (13)

 

$$% \frac{\partial{\tilde{e}}}{\partial{t}}+\nabla \cdot \left[ {{\... ...}} =\tilde{\rho} {{\vec g}} \cdot {{\vec v}} +D_{\rm e}\left(\tilde{e} \right),$$ (14)

$$% \frac{\partial{\tilde{{\vec B}}}}{\partial{t}}+\nabla\cdot\... ...ec v}}\right]=0 + {{\vec D}}_{B}\left(\tilde{{\vec B}}\right),$$ (15)

where $\tilde{p}_{\rm t}$ is the perturbation to the total pressure

$$% \tilde{p}_{\rm t}=\tilde{p}_{\rm k}+\frac{{\tilde{{\vec B}}}^2}{2}+{{\vec B}}_{\rm b}{\tilde{{\vec B}}},$$ (16)

or, in terms of perturbed energy density per unit volume $\tilde{e}$,

$$% \tilde{p}_{\rm k}=\left(\gamma-1\right)\left(\tilde{e}-\fra... ...m b} {\tilde{{\vec B}}}-\frac{{\tilde{{\vec B}}}^2}{2}\right),$$ (17)

and

$$% \tilde{p}_{\rm t}=\left(\gamma-1\right)\left[\tilde{e}-\fra... ...}{\tilde{{\vec B}}}+\frac{{\tilde{{\vec B}}}^2}{2}\right)\cdot$$ (18)

Here $p_{\rm tb}$ denotes the total background pressure

$$% p_{\rm tb}=p_{\rm kb}+\frac{{{\vec B}}_{\rm b}^2}{2},$$ (19)

which, in terms of background conservative variables, gives

$$% p_{\rm kb}=\left(\gamma-1\right)\left(e_{\rm b}-\frac{{{{\vec B}}}_{\rm b}^2}{2}\right),$$ (20)

and

$$% p_{\rm tb}=\left(\gamma-1\right) e_{\rm b} - \left(\gamma-2\right)\frac{{{{\vec B}}}_{\rm b}^2}{2}\cdot$$ (21)

This form of the MHD equations, despite being perhaps more complicated, is in fact much more convenient for numerical purposes, since they do not govern the behaviour of the entire plasma itself. Instead, they describe the interference of a perturbation with an exact equilibrium background state, and they have no terms with background variables without having multiplied by velocity or its derivative. Also, it is straightforward to see that the form of the equations with respect to the perturbed variables  $\tilde{\rho}$, $\tilde{e}$, and $\tilde{{\vec B}}$ remains unchanged. Thus, setting the background variables to zero, the equations turn into their canonical form, which will be very useful for testing the code. Another advantage of this form of the MHD equations is that there is a certain amount of freedom in setting the background properly, and less care might be taken about the numerical precision of the background state, since the equations above do not have any forces or fluxes inherited from the background. However, this advantage has to be exploited carefully, since an improper non-equilibrium background will still produce a numerical solution that may not even be completely physical.

A fourth order central difference scheme is applied for the spatial derivatives and second or fourth order Runge-Kutta time advance scheme is implemented in the code. Central difference schemes are conservative due to their symmetry, and conserve the divergence of magnetic field  $\nabla \cdot {{\vec B}}$ (Vögler et al. 2005). Also, central difference schemes applied to hyperbolic equations almost always produce a spurious oscillatory behaviour, caused by the accumulation of energy on scales smaller than the grid cell size, and thus some additional stabilisation of the numerical scheme is necessary.

Numerical diffusion and resistivity are often used to stabilise computational solutions. The method has already proven its robustness and feasibility (Vögler et al. 2005; Caunt & Korpi 2001; Stein & Nordlund 1998). Even though it is described in detail in the literature, we recall briefly the main points for completeness and rewrite the method here in the terms we use to define the system of MHD Eqs. (12)-(15).

The term D in the energy equation consists of three parts:

$$% D_{\rm e}=D^{\rm di{ff}usive}_{\rm e}+D^{\rm viscous}_{\rm e}+D^{\rm ohmic}_{\rm e},$$ (22)

which describe thermal diffusion, viscous and ohmic heating of plasma, respectively.

The hyperdiffusive terms for scalar quantities are written as follows:

$$% D_\rho=\sum_i \frac{\partial}{\partial x_i} \nu_i\left(\rho\right) \frac{\partial}{\partial x_i} \tilde{\rho},$$ (23)

$$% D_{\rm e}^{\rm di{ff}usive}=\sum_i \frac{\partial}{\partial... ...left(e\right) \frac{\partial}{\partial x_i} \tilde{\epsilon}.$$ (24)

The derivatives in Eqs. (23) and (24) are applied in a way that the outer derivative is taken forward, while the inner derivative is taken backward, and the viscosity coefficient is interpolated backward on the grid cell interface. Thus, the diffusion terms remain spatially centred. In Eq. (24), $\tilde{\epsilon}$ is the thermal energy perturbation $\tilde{\epsilon}=\tilde{e}-(\tilde{\rho}+\rho_{\rm b}){{\vec v}}^2/2-{\tilde{{\vec B}}}^2/2$.

The hyperviscous terms for vector quantities are more complicated, i.e.:

$$% {{\vec D}}_{\rho {{\vec v}}} = \nabla \cdot \tau,$$ (25)

and

$$% {{\vec D}}_{{\vec B}} = - \nabla \times \mathcal{E}.$$ (26)

The hyperviscous and ohmic heating terms in Eq. (22) are set as follows:

$$% D_{\rm e}^{\rm visc}=\nabla \cdot \left({{\vec v}} \cdot \tau \right)$$ (27)

and

$$% D_{\rm e}^{\rm ohmic}=\nabla \cdot \left({{\vec B}} \times \mathcal{E}\right).$$ (28)

The viscous tensor $\tau$ is given by

$$% \tau_{kl}=\frac{1}{2}\left(\tilde{\rho}+\rho_{\rm b}\right)... ...nu_l\left(v_k\right)\frac{\partial v_k}{\partial x_l} \right],$$ (29)

the vector quantity $\mathcal{E}$ is defined as

$$% \mathcal{E}_k=\epsilon_{klm}~\left[\nu_l\left(\tilde{B}_m\right)\frac{\partial \tilde{B}_m}{\partial x_l}\right],$$ (30)

where $\epsilon_{klm}$ is the Levi-Civita symbol, and the summation is over l and m indices.

The derivatives in the expressions Eqs. (25)-(28) are such that if the direction of the outer derivative is the same as the direction of the inner derivative, then they are calculated using the same principle as the derivatives in Eqs. (23)-(24). If the direction of the outer derivative is different from the direction of the inner derivative, then both derivatives are evaluated using a second order central difference scheme, and the viscous coefficients are interpolated to the grid cell centres.

The viscous coefficient $\nu$ for the variable u in the ith direction is expressed as

$$% \nu_i\left(u\right)=c_2^u \Delta x_i v_{\rm t} \frac{\max\l... ...}{\max\left\vert\Delta_i^1 u \right\vert} + c_1^u \nu_{\rm s},$$ (31)

where $v_{\rm t}=v_{\rm a}+v_{\rm s}$ is the sum of maximum Alfvén and sound speeds in the domain, operators $\Delta_3$ and $\Delta_1$ are the forward differences of the third and first order taken in the ith direction, and $\Delta x_i$ are the spatial resolutions. The maxima are taken over five grid cell stencils in the ith direction. Coefficients c₁^u and c₂^u can be defined separately for each variable and are selected in the way that the hyperdiffusion ensures numerical stability of the solution, and the solution is not influenced strongly by the diffusion. The shock viscosity  $\nu_{\rm s}$ is defined in the following way:

 

$$% \nu_{\rm s}=\Delta x_i^2 \left\vert \nabla \cdot {{\vec v}} \right\vert,~\nabla \cdot {{\vec v}} \le 0,$$

$$\nu_{\rm s}=0,~\nabla \cdot {{\vec v}} > 0,$$ (32)

and ensures that regions with strong compression remain resolved by the numerical scheme (von Neumann & Richtmyer 1950).

	Figure 1: Standard Riemann shock tube problem snapshot at time t=0.2. The density, velocity, thermal energy density per unit mass and pressure are shown.
Open with DEXTER

The time step is limited by the standard CFL condition and by the hyperdiffusion time scale, given by the following expression:

$$% \Delta t=\frac{k \Delta x^2}{\max\left(\nu\right)}\cdot$$ (33)

Here the coefficient k is an equivalent to the constant coefficient of the CFL condition and is less than one to ensure the stability of the solution.

The above outlined approach of variable separation also allows the use of more simple boundary conditions than it was necessary when the non-split variables have been implemented. The ``transparent'' boundary condition for the energy perturbation now does not contain the requirement of magnetohydrostatic equilibrium, and can be simply written as $\partial \tilde{e}/ \partial x=0$ at the boundary. This boundary condition, in terms of the values of the function defined on the grid, can be expressed as follows:

 

f_N+i=f_N-i, (34)

where N is the position of the last grid cell in the working part of the domain, and the function is symmetrically copied from the working part of the domain to the ghost cells. Two layers of the ghost cells are necessary for the fourth-order central difference numerical scheme used in the code.

Similar boundary conditions are introduced for the other variables, however, in cases when a strong gradient of the background density, thermal energy, or magnetic field is peculiar to the model, we found it reasonable to apply the boundaries written for the primitive variables rather than for the conservative ones to improve the robustness of the code. Also, it should be mentioned that it is definitely possible and may even be necessary to define some higher order boundary conditions for higher precision calculations.

We use the MPI VAC code (Tóth 1996) as the basis for the implementation of the above described procedure. This version of VAC already has the MPI domain decomposition extension which, however, needed to be expanded since the hyperdiffusion and hyperresistivity modules require one additional grid cell to be copied from each neighbouring subdomain due to a larger 7-point stencil applied there.

	Figure 2: Strong shock tube problem snapshot, taken at the time t=0.12. Density, velocity, thermal energy density per unit mass and pressure are shown.
Open with DEXTER

	Figure 3: Snapshot of Brio & Wu problem, taken at the time t=0.11. Density, velocity, thermal pressure, and the y component of magnetic field are shown.
Open with DEXTER

3 Numerical tests

In order to demonstrate the ability of the approach outlined in the previous section to solve the equations of magnetohydrodynamics accurately, we have performed a number of standard one-, two- and three-dimensional hydrodynamic and magnetohydrodynamic tests and compare the output with known analytical solutions or with results obtained earlier by alternative numerical schemes.

3.1 Standard Riemann shock tube problem

The standard one-dimensional Riemann shock tube problem is simulated as the first stage of testing (Caunt & Korpi 2001; Sod 1978). The initial conditions contain a discontinuity located at x=0.5 in this problem. To the left of the discontinuity, pressure p₁=1, density $\rho_1=1$, whereas pressure and density to the right of the discontinuity are p₂=0.1, and $\rho_2=0.125$, and the compression ratio is 10. The adiabatic index $\gamma$ is set to 1.4. Magnetic field is set to zero. Density, velocity, thermal energy density per unit mass, and pressure for time t=0.2 are shown in Fig. 1. The physical domain size is equal to unity, the resolution is 256 grid cells in the direction of the shock wave propagation.

Figure 1 shows that the shock front is resolved with 3-4 grid cells, however, some unavoidable smoothing in the contact discontinuity and the rarefaction wave is present. Despite this fact, the amplitudes and the positions of the shock tube features are correct and agree well with other tests shown in the literature (e.g. Caunt & Korpi 2001; Sod 1978). Also, some small amplitude oscillations can be seen behind the shock front. These oscillations do not grow in time since they are successfully suppressed by the hyperdiffusion.

3.2 Strong shock tube problem

The strong shock tube test (Fig. 2) is more difficult for the numerical scheme. This case differs from the weak Riemann shock tube test described above by setting p₁=10 and $\rho_1=10$, thus the compression ratio is now 100. Again, most of the shock features are represented and resolved well with the simulation. The shock front is smeared over 3-4 grid cells as in the previous case. Small scale oscillations are more pronounced, however, the hyperdiffusion still ensures the stability of the model. It should also be mentioned that this realisation of the hyperdiffusion has resolved the high-energy plateau around x=0.8 more successfully, which was the problem for some previous attempts (Caunt & Korpi 2001).

3.3 Brio & Wu shock tube

Next, a test of the formation of magnetohydrodynamic shock waves is performed. The initial condition has a discontinuity at x=0.5. Parameters to the left and right of the discontinuity are set as: p₁=1, p₂=0.1, $\rho_1=1$, $\rho_2=0.125$, B_y1=1, B_y2=-1, B_x=0.75. The adiabatic index $\gamma$ is set to 2. The grid resolution is set to 800 grid cells to precisely compare our results with the original work of Brio & Wu (1988). Figure 3 shows density, velocity in the direction across the discontinuity, gas pressure and the component of magnetic field along the discontinuity taken at t=0.11. The slow compound wave at x=0.475 and the contact discontinuity at x=0.55 are resolved well. The slow shock at x=0.65 is also well resolved within 3-4 grid points, and the slow shock and the fast rarefaction wave at x=0.85 and x=0.9 are noticeable. The amplitudes of the waves in the presented simulations are in perfect agreement with the amplitudes given by Brio & Wu (1988).

3.4 Ország-Tang vortex

	Figure 4: Snapshot of the plasma density of the Ország-Tang vortex problem simulation at t=0.5.
Open with DEXTER

The Ország-Tang vortex (Ország & Tang 1979) is a more complicated test often used to validate a full non-linear MHD solver in two dimensions. A complex two-dimensional interaction of various types of non-linear shock waves travelling at different speeds and transition to the MHD turbulence regime imply rigorous requirements for the resolution and stability of the numerical scheme used to perform the test.

The horizontal and vertical dimensions of the domain are set to unity, and the resolution of the simulation box is 256 $\times$ 256 for this test problem. The adiabatic index is set to 5/3, the density and gas pressure are constants, i.e., $\rho=25/36\pi$ and $p=5/12\pi$, the magnetic field $B_x=-B_0\sin(4\pi y)$; $B_y=B_0\sin(2\pi x)$; where $B_0=1/\sqrt{4\pi}$ (the magnetic permeability is set to unity); the initial velocity is $V_x=\sin(2\pi y)$; $V_y=\sin(2\pi x)$. The boundaries of the domain are periodic. Also, to validate the approach of splitting the variables into their background and perturbed components, we assign the background variables to contain the density, magnetic field, and magnetic and thermal energy, leaving only the kinetic component of the total energy in the perturbed component. Figure 4 shows the density snapshot at the time t=0.5. The features in the image show precise agreement with earlier simulations by, e.g., Ryu et al. (1995), Dai & Woodward (1998) or by Londrillo & Del Zanna (2000).

3.5 Strong explosion in 3D non-uniform media

Kontorovich & Shelyag (2002) have calculated analytically the shape of a shock caused by a strong uniform off-centre explosion in a non-uniform medium with background density dependence

$$% \rho_{\rm b}=C_1/r^2+C_2.$$ (35)

We have compared the numerical solution produced by the code with the analytical solution, derived by Kontorovich & Shelyag (2002). The numerical setup for the problem is as follows. A three-dimensional box with physical size of 3000³ light years is resolved by 192³ grid cells. The explosion, represented by adding $10^{48}~{\rm J}$ of thermal energy to the perturbed energy density variable $\tilde{e}$, is located at $500~{\rm Ly}$ off the centre of the density inhomogeneity, located in the centre of the simulation box. In Eq. (35), the coefficient C₂ represents the density of the interstellar medium far from the density singularity, and is equal to $10^{-22}~{\rm kg/m^3}$. The coefficient C₁ characterises how the density increases towards the centre of the domain and is set in the way that the density at the distance of $0.5~{\rm Ly}$ from the centre is equal to $10^{-21}~{\rm kg/m^3}$. The adiabatic index $\gamma$ is 5/3. A snapshot of the three-dimensional shape of the shock front is shown in Fig. 5. The two-dimensional cut through the axis defined by the explosion point and the centre of the domain is shown in Fig. 6. The data for Figs. 5 and 6 are taken at $t \sim 30000~{\rm years}$, thus the figures can be directly compared with Fig. 3 in Kontorovich & Shelyag (2002). The comparison shows a perfect agreement with the analytical solution.

	Figure 5: Strong shock front caused by the explosion with energy $e=10^{48}~{\rm J}$ in non-uniform media. The figure shows the shape of the shock at the time $t \sim 30~000~{\rm years}$.
Open with DEXTER

	Figure 6: Two-dimensional shape of the shock front. The explosion, which caused the shock wave, is marked by cross at the point with the coordinates $\left (0,-0.5\right )$ in the figure.
Open with DEXTER

3.6 Conversion of linear waves into non-linear waves in the magnetised and stratified 3D solar atmosphere

	Figure 7: Snapshot of the vertical velocity structure of the simulation of the wave propagation and conversion in the non-magnetic solar chromosphere and corona taken at $t=230~{\rm s}$. Conversion of the linear waves into non-linear ones is seen at the height above $z=2000~{\rm km}$.
Open with DEXTER

Since we are planning to use the code presented here mainly in applications to study the physics of the magnetically-coupled solar interior, atmosphere and corona, we performed test simulations of conversion of linear waves into non-linear ones for non-magnetic and magnetic models of the strongly-stratified solar photosphere, chromosphere, transition region and corona (Fedun & Erdélyi 2008). For these simulations, the background density is taken from the VAL IIIC model (Vernazza et al. 1981) for the lower solar atmosphere that is extended towards the solar corona using the model by McWhirter et al. (1975). Then the (magneto-) hydrostatic equilibrium condition Eq. (10) is applied to obtain the background pressure  $p_{\rm tb}$. Next, the background internal energy density $e_{\rm b}$ is determined according to Eq. (21). The physical size of the simulation domain is $8~{\rm Mm}$ in the vertical direction and $8{-}8~{\rm Mm}$ in both horizontal directions. The resolution is 1024 $\times$ 128 $\times$ 128 grid points. A harmonic acoustic driver is implemented just above the temperature minimum level of the initial equilibrium. The driver acts vertically with the period $T=30~{\rm s}$. The spatial extent of the driver is a smoothed Gaussian ellipsoid with the vertical axis of $0.1~{\rm Mm}$ and horizontal axes of $3~{\rm Mm}$ each.

The structure of the vertical velocity component is shown in Fig. 7 as two orthogonal vertical cuts through the three-dimensional computational domain. The snapshot captures the propagation of linear acoustic waves generated by the driver in the lower part of the non-magnetised solar chromosphere and their conversion into non-linear waves in the upper region of the model, caused by the decrease of the density and pressure there.

The vertical component of the velocity in the computational domain taken along the intersection of the cuts in Fig. 7 is shown in Fig. 8. The non-linear character of the wave propagation is clearly observed above the transition region ( $z>2~{\rm Mm}$) in the figure. Also, note a change in the linear propagation of the acoustic wave at the height $z=1.5~{\rm Mm}$ that is caused by a partial reflection of the upward-propagating waves from the transition region. The qualitative comparison of earlier studies in one- (De Pontieu et al. 2004), two- (Erdélyi et al. 2007; Malins & Erdélyi 2007) and the three-dimensional (Fedun & Erdélyi 2008), non-magnetic simulations with our test results shown here are in a very good agreement.

	Figure 8: Vertical velocity profile, taken at the centre of the simulation box, from the simulation of the wave conversion in the solar corona taken at $t=230~{\rm s}$. The conversion of linear waves into non-linear occurs at $z=2000~{\rm km}$.
Open with DEXTER

	Figure 9: Snapshot from the simulation of the wave propagation and conversion in magnetic solar chromosphere and corona taken at $t=209~{\rm s}$. The magnetic field, which is sketched by a cylinder in the figure, acts as a waveguide and suppresses the energy propagation outside the magnetic flux concentration.
Open with DEXTER

	Figure 10: Vertical velocity profile taken at the centre of the simulation box from the simulation of the wave conversion in the solar corona taken at $t=209~{\rm s}$. The conversion of linear waves into non-linear occurs at $z=2000~{\rm km}$.
Open with DEXTER

Finally, for testing the code for MHD wave propagation in a vertically-stratified plasma embedded in magnetic field, we select the magnetic field configuration to be a straight vertical cylinder with radius of $1.2~{\rm Mm}$. The strength of the magnetic field imposed in the simulation is $B_{\rm b}^z=4~{\rm G}$, which corresponds to plasma $\beta=0.29$ at the upper layers of domain representing the solar corona.

Figure 9 demonstrates that the magnetic field acts as an excellent waveguide for the magneto-acoustic oscillations generated by the photospheric driver in the model. In agreement with previous simulations (e.g., Fedun & Erdélyi 2008), the magnetic cylinder suppresses the propagation of the waves laterally outwards from the magnetic field region, thus causing larger amplitudes of the vertical velocity profile (Figs. 9 and 10) generated by the driver of the same amplitude as in the case of the non-magnetic simulation (Figs. 7 and 8). Even a quick qualitative comparison confirms this expectation clearly.

4 Discussion

We have presented a number of test simulations of the fully non-linear MHD code developed on the basis of the well-known VAC platform. The code, as presented here, is able to handle all standard tests well, and the produced numerical solutions are identical either to the known analytical solutions wherever such solutions are available, or to known numerical results of other authors.

The main advantage of the proposed numerical technique is that the code allows us to simulate robustly the macroscopic processes in gravitationally stratified (non-)magnetised plasmas. Not all of the presented tests are realisable with conventional numerical schemes. Particularly, the test with the strong shock wave in non-uniform media was not possible due to the enhanced numerical diffusion of the density inhomogeneity in the domain. Because of the intrinsic robustness of the proposed re-written equations derived for the perturbed variables, it is now achievable to implement a more complicated, e.g., analytically-defined magnetic field configurations such as potential or self-similar magnetic fields (e.g. Gordovskyy & Jain 2007), or even to use real magnetic structures extrapolated from the observational data (for example, derived from MDI instrument of the SOHO satellite; Marsh & Walsh 2006).

It should be pointed out that the code has no limitations of simulation length in time imposed by complications originating from the upper boundary, as, for example, occurred in similar simulations of the solar atmosphere of Hasan & van Ballegooijen (2008), where up to the first 130 s our test computations are in excellent agreement with their results. Neither do we need to implement special procedures, as has been the case in, e.g., Khomenko & Collados (2006), to treat the upper boundaries.

Since we are planning to use the code mainly for the forward modelling of helioseismological processes and for the coupling processes in the solar interior, photosphere, and corona, we have demonstrated the ability of the code to perform simulations of linear and non-linear wave propagation in the strongly-stratified solar atmosphere with the presence of magnetic field therein. Strictly speaking, it might not be necessary to have a non-linear MHD solver for helioseismological applications due to the linear nature of the solar acoustic modes, however, the code is able to properly handle this kind of physical problem, and additional filtering (Hanasoge et al. 2007) is not expected to be necessary to produce forward simulated data with high signal to noise ratios. Of course, when a magnetic coupling of the solar interior to the corona is present, non-linearity is unavoidable.

Finally, we note that there are also foreseen encouraging ways to expand the code due to its modular structure inherited from VAC, which allows us to modify and add new physics easily. To treat localised regions with strong stratification more precisely, non-uniform and time-dependent mesh should be included by using spatially and temporarily dependent weight coefficients in the finite difference representation of the derivatives in the MHD equations. For more involved small-scale simulations of the solar interior, atmosphere and corona, where the ionisation flux is large and cannot be neglected anymore, the equation of state should be expanded to incorporate the description of ionization processes in the plasma. Also, simplified constant flux boundary conditions might be replaced with more involved ones using, for example, the method of characteristics (Hansteen 2007; Rosenthal et al. 2002).

Acknowledgements

The authors thank Rony Keppens for helpful discussions and advice. This work was supported by the ${\rm SP^2RC}$ Rolling Grant of Science and Technology Facilities Council (STFC, UK). R.E. acknowledges M. Kéray for patient encouragement and is also grateful to NSF, Hungary (OTKA, Ref. No. K67746).

References

 
• Alfvén, H. 1942, Nature, 150, 405 In the text  
• Boris, J. P., & Book, D. L. 1973, J. Comput. Phys., 11, 38 In the text  
• Brandenburg, A. 2003, Adv. Nonlinear Dyna., 269 In the text  
• Brio, M., & Wu, C. C. 1988, J. Comput. Phys., 75, 400 In the text  
• Caunt, S. E., & Korpi, M. J. 2001, A&A, 369, 706 In the text  
• Chan, K. L., Sofia, S., & Wolff, C. L. 1982, ApJ, 263, 935 In the text  
• Dai, W., & Woodward, P. R. 1994, J. Comput. Phys., 111, 354 In the text  
• Dai, W., & Woodward, P. R. 1998, ApJ, 494, 317 In the text  
• De Pontieu, B., Erdélyi, R., & James, S. P. 2004, Nature, 430, 536 In the text  
• Erdélyi, R., & James, S. P. 2004, A&A, 427, 1055 In the text  
• Erdélyi, R., Malins, C., Tóth, G., & de Pontieu, B. 2007, A&A, 467, 1299 In the text  
• Fedun, V., & Erdélyi, R. 2008, Solar Phys., submitted In the text  
• Gordovskyy, M., & Jain, R. 2007, ApJ, 661, 586 In the text  
• Hanasoge, S. M., Duvall, T. L., Jr., & Couvidat, S. 2007, ApJ, 664, 1234 In the text  
• Hansteen, V. 2007, private communication. In the text  
• Harten, A. 1983, J. Comput. Phys., 49, 357 In the text  
• Hasan, S. S., & van Ballegooijen, A. A. 2008 [arXiv:0802.3509] In the text  
• Hasan, S. S., van Ballegooijen, A. A., Kalkofen, W., & Steiner, O. 2005, ApJ, 631, 1270  
• Khomenko, E., & Collados, M. 2006, ApJ, 653, 739 In the text  
• Kontorovich, V. M., & Shelyag, S. I. 2002, Soviet J. Exper. Theor. Phys. Lett., 76, 115 In the text  
• van Leer, B. 1979, J. Comput. Phys., 32, 101 In the text  
• Londrillo, P., & Del Zanna, L. 2000, ApJ, 530, 508 In the text  
• Malins, C., & Erdélyi, R. 2007, Sol. Phys., 246, 41 In the text  
• Marsh, M. S., & Walsh, R. W. 2006, ApJ, 643, 540 In the text  
• McWhirter, R. W. P., Thonemann, P. C., & Wilson, R. 1975, A&A, 40, 63 In the text  
• von Neumann, J., & Richtmyer, R. D. 1950, J. Appl. Phys., 21, 232 In the text  
• Nordlund, A. 1985, Sol. Phys., 100, 209 In the text  
• Nordlund, A., & Galsgaard, K. 1995, Tech. Rep., Astronomical Observatory, Copenhagen University, 1997 In the text  
• Ország, S. A., & Tang, C.-M. 1979, J. Fluid Mech., 90, 129 In the text  
• Parchevsky, K. V., & Kosovichev, A. G. 2007, ApJ, 666, 547 In the text  
• Roe, P. L. 1981, J. Comput. Phys., 43, 357 In the text  
• Rosenthal, C. S., Bogdan, T. J., Carlsson, M., et al. 2002, ApJ, 564, 508 In the text  
• Ryu, D., Jones, T. W., & Frank, A. 1995, ApJ, 452, 785 In the text  
• Shelyag, S., Erdélyi, R., & Thompson, M. J. 2006, ApJ, 651, 576 In the text  
• Shelyag, S., Erdélyi, R., & Thompson, M. J. 2007, A&A, 469, 1101 In the text  
• Sod, G. A. 1978, J. Comput. Phys., 27, 1 In the text  
• Stein, R. F., & Nordlund, A. 1998, ApJ, 499, 914 In the text  
• Tóth, G. 1996, Astrophys. Lett. & Commun., 34, 245 In the text  
• Tóth, G., Keppens, R., & Botchev, M. A. 1998, A&A, 332, 1159 In the text  
• Vernazza, J. E., Avrett, E. H., & Loeser, R. 1981, ApJS, 45, 635 In the text  
• Vögler, A. 2003, Three-dimensional simulations of magneto-convection on the solar photosphere, Ph.D. Thesis, Göttingen In the text  
• Vögler, A., Shelyag, S., Schüssler, M., et al. 2005, A&A, 429, 335 In the text  
• Zalesak, S. T. 1979, J. Comput. Phys., 31, 335 In the text