A&A 486, 437-452 (2008)
DOI: 10.1051/0004-6361:200809446
A. Kayser1,2 - M. Hilker3,4 - E. K. Grebel1,2 - P. G. Willemsen3
1 - Astronomisches Institut der Universität Basel, Venusstrasse 7, 4102 Binningen, Switzerland
2 -
Astronomisches Rechen-Institut, Zentrum für Astronomie, Universität Heidelberg, Mönchhofstraße 12-14, 69120 Heidelberg, Germany
3 -
Argelander-Institut für Astronomie, Auf dem Hügel 71, 53121 Bonn, Germany
4 -
ESO, Karl-Schwarzschild-Str. 2, 85748 Garching bei München, Germany
Received 24 January 2008 / Accepted 14 April 2008
Abstract
Our work focuses on the understanding of the origin of CNO-anomalies, which
have been detected in several Galactic globular clusters.
The novelty and advantage of this study is that it is based on a homogeneous
data set of hundreds of medium-resolution spectra of stars in eight Galactic
globular clusters (M 15, M 22, M 55, NGC 288, NGC 362, NGC 5286,
Palomar 12, and Terzan 7). Two of the clusters (Palomar 12 and Terzan 7)
are believed to be former members of the Sagittarius dwarf spheroidal
(Sgr dSph) galaxy. The large homogeneous data set allows for a detailed
differential study of the line strengths in the stellar spectra of the
observed clusters. Our sample comprises stars in different evolutionary
states, namely the main-sequence turn-off (MSTO) region, the subgiant branch
(SGB) and the base of the red giant branch (RGB). We compare the relative CN
and CH line strengths of stars in the same evolutionary states (with similar
log g and
![]() ). The majority of the examined clusters show significant
variations in their CN and CH abundances at the base of the RGB. We confirm
the presence of a bimodal distribution in CN for the second parameter pair of the clusters
(NGC 288 and NGC 362). The two probable former Sgr dSph clusters do not
exhibit any CN-strong stars. Overall, our results suggest that the environment in which the
clusters formed is responsible for the existence of CN-strong stars.
We can confirm the known anticorrelation between CN and CH for most of the
observed clusters. Although the signal of CN absorption is weaker for the
hotter stars on the MSTO and SGB, we observed the same anticorrelation in these
less evolved stars for the CN-bimodal clusters.
Including structural parameters taken from the literature reveals
that the existence of the CN-bifurcation seems to be independent of most other
cluster characteristics. In particular, we do not confirm the correlation
between cluster ellipticity and number of CN-strong stars.
However, there may be a trend toward an increased percentage of CN-strong stars
with increasing cluster tidal radius and total luminosity.
We argue that our findings are consistent with
pollution by intermediate AGB stars and/or fast rotating massive stars
and two generations of star formation in luminous clusters with larger tidal radii
at greater Galactocentric distances.
). The majority of the examined clusters show significant
variations in their CN and CH abundances at the base of the RGB. We confirm
the presence of a bimodal distribution in CN for the second parameter pair of the clusters
(NGC 288 and NGC 362). The two probable former Sgr dSph clusters do not
exhibit any CN-strong stars. Overall, our results suggest that the environment in which the
clusters formed is responsible for the existence of CN-strong stars.
We can confirm the known anticorrelation between CN and CH for most of the
observed clusters. Although the signal of CN absorption is weaker for the
hotter stars on the MSTO and SGB, we observed the same anticorrelation in these
less evolved stars for the CN-bimodal clusters.
Including structural parameters taken from the literature reveals
that the existence of the CN-bifurcation seems to be independent of most other
cluster characteristics. In particular, we do not confirm the correlation
between cluster ellipticity and number of CN-strong stars.
However, there may be a trend toward an increased percentage of CN-strong stars
with increasing cluster tidal radius and total luminosity.
We argue that our findings are consistent with
pollution by intermediate AGB stars and/or fast rotating massive stars
and two generations of star formation in luminous clusters with larger tidal radii
at greater Galactocentric distances.
Key words: stars: abundances - Galaxy: globular clusters: general
Over the last three decades spectroscopic studies of the CN and CH absorption bands often revealed a bimodality in CN that is accompanied by a broadened distribution in CH. For the majority of the CN-bimodal clusters (e.g., M 2, M 3, M 5, M 13, 47 Tuc) a CN-CH anticorrelation was detected (e.g., Smith et al. 1996). Since CN is a double-metal molecule, it can be more easily observed in stars with a higher metallicity. Nevertheless, the CN-CH anticorrelation seems to be present also in the very metal-poor cluster M 15 where no clear bimodality of CN could be detected so far (Lee 2000).
Although this topic has been studied extensively in the last decades no self-consistent model has been found to satisfactorily explain the observed chemical variations. Two main scenarios are discussed as possible origins of these abundance patterns:
The ``self-enrichment'' scenario also is strengthened by the recent findings of multiple subgiant branches (SGB) and main sequences (MS) in several massive GCs (Piotto et al. 2007; Bedin et al. 2004), which require stellar populations with distinct abundance patterns (and ages) within the clusters. Interestingly, the multiple SGBs and MSs can best be explained by a large helium enhancement in the second/third subpopulation of a cluster (D'Antona et al. 2005), which is consistent with the expected abundances of ejecta from intermediate-mass AGB stars (e.g., D'Antona et al. 2002). Actually, these AGB stars need not have been members of the same star cluster. Bekki et al. (2007) recently suggested that massive GCs might have formed in low mass dwarfs embedded in a dark matter halo. In this scenario, the second/third generation of stars then was created out of ejecta from the external ``field'' AGB stars. Since products of H burning are released by fast rotating massive stars in slow winds, also this class of stars may provide the He-enhancement required to explain multiple sequences observed in globular clusters.
Coming back to the overall CNO abundances, the work by Smith et al. (1996) has
shown that the total
![]() for giants in the globular clusters M 3 and M 13 is
the same for both CN-strong and CN-weak stars, which would be expected from
deep mixing, dredging up CNO processed material to the stellar surfaces.
Thus although mixing effects are not existent in unevolved stars they
seem to play a role for red giants when studying the CN and CH bands.
The challenge is to disentangle the primordial contribution to the C, N abundances from the one resulting from normal evolutionary changes.
On the one hand, some basic evolution of low mass population II stars is clearly
a common feature in both field and cluster stars.
Smith & Martell (2003) showed that halo field giants and
globular cluster giants share the same pattern of declining C as a function of
increasing magnitude. The same two mixing mechanisms (first dredge-up and a
second mixing episode after the RGB-bump) are acting in all population II giants.
On the
other hand, field stars behave very differently from cluster stars as far as
``heavier'' light elements (namely O, Na) are concerned (Gratton et al. 2000).
for giants in the globular clusters M 3 and M 13 is
the same for both CN-strong and CN-weak stars, which would be expected from
deep mixing, dredging up CNO processed material to the stellar surfaces.
Thus although mixing effects are not existent in unevolved stars they
seem to play a role for red giants when studying the CN and CH bands.
The challenge is to disentangle the primordial contribution to the C, N abundances from the one resulting from normal evolutionary changes.
On the one hand, some basic evolution of low mass population II stars is clearly
a common feature in both field and cluster stars.
Smith & Martell (2003) showed that halo field giants and
globular cluster giants share the same pattern of declining C as a function of
increasing magnitude. The same two mixing mechanisms (first dredge-up and a
second mixing episode after the RGB-bump) are acting in all population II giants.
On the
other hand, field stars behave very differently from cluster stars as far as
``heavier'' light elements (namely O, Na) are concerned (Gratton et al. 2000).
If the environment in which a cluster formed (e.g., in the disk of a galaxy vs. the
center of a dark matter substructure) defines the enrichment history of a cluster,
the observed abundance patters would provide an indication of the origin of the cluster.
In his groundbreaking work Zinn proposed that the Galactic globular
cluster system consists of various sub-systems (Zinn 1993,1985):
bulge/disk (BD), old halo (OH), young halo (YH) globular clusters. He furthermore
suggested that most YH clusters might have been accreted from satellite
galaxies.
However, the Milky Way companions have been found to show, on average,
systematically lower [
![]() ]
ratios than Galactic halo stars and
globular clusters (e.g., Sbordone et al. 2007; Pritzl et al. 2005; Shetrone et al. 2001; Fulbright 2002).
Hence the present-day dwarfs do not seem to have contributed in a significant
way to the build-up of the Galactic halo and to the YH clusters.
]
ratios than Galactic halo stars and
globular clusters (e.g., Sbordone et al. 2007; Pritzl et al. 2005; Shetrone et al. 2001; Fulbright 2002).
Hence the present-day dwarfs do not seem to have contributed in a significant
way to the build-up of the Galactic halo and to the YH clusters.
The aim of this work is to gain further insight into the mechanism responsible for the strong CN enhancement in some stars. We therefore concentrate on regions in the color magnitude diagrams (CMDs) where stars are believed to be unaffected by mixing effects, i.e. stars on the MS, MSTO, SGB, and lower RGB. In particular, we investigate whether there is a dependence of the CN enhancement on the overall globular cluster properties and/or the sub-class they are belonging to. We investigate if CN-CH variations are different in genuine halo clusters as compared to possibly accreted globular clusters.
This article is structured as follows. Section 2 describes our data and their reduction. Section 3 explains the measurements of the CN and CH band strength and the definition of the cyanogen excess parameter. Sections 4 and 5 present the investigation of the CN/CH anticorrelation and the search for correlations between other cluster properties and the number ratio of CN-strong/CN-weak stars. The final Sect. 6 gives our summary and conclusions.
Table 1: Log of observations.
The spectroscopic data were obtained in May 2002 and July 2004 at the VLT/UT4 at ESO/Paranal (Chile) with the multi-slit spectroscopy instrument FORS2/MXU.
FORS2 provides a field of view of
![]() .
The observations of M 55 were obtained in 2002 and were also used for calibration purposes in a study of
.
The observations of M 55 were obtained in 2002 and were also used for calibration purposes in a study of ![]() Cen (Kayser et al. 2006; Willemsen et al. 2005; Hilker et al. 2004).
The observations obtained in 2004 were dedicated to CN and CH measurements in seven further Galactic globular clusters (M 15, M 22, M 55, NGC 288, NGC 362, NGC 5286, Palomar 12, and Terzan 7) spanning a large range in metallicity (
Cen (Kayser et al. 2006; Willemsen et al. 2005; Hilker et al. 2004).
The observations obtained in 2004 were dedicated to CN and CH measurements in seven further Galactic globular clusters (M 15, M 22, M 55, NGC 288, NGC 362, NGC 5286, Palomar 12, and Terzan 7) spanning a large range in metallicity (
![]() ).
Two of the clusters (Palomar 12 and Terzan 7) are suggested to have originated from the Sagittarius dwarf spheroidal (Sgr dSph) galaxy (Bellazzini et al. 2003; Sbordone et al. 2005).
).
Two of the clusters (Palomar 12 and Terzan 7) are suggested to have originated from the Sagittarius dwarf spheroidal (Sgr dSph) galaxy (Bellazzini et al. 2003; Sbordone et al. 2005).
For both observing runs, the candidate stars for the spectroscopy were selected from pre-images in Johnson B and V. We selected target stars from the upper MS, the SGB, and the lower RGB in the cluster CMDs. On the RGB we focused on stars fainter than the RGB bump, the point where deep mixing is believed to set in (Charbonnel 1995; Sweigart & Mengel 1979).
We chose the grating with the ESO denotation 660I+25 (second order) with a dispersion of
![]() .
The spectral region covers
.
The spectral region covers ![]() 3700 to
3700 to
![]() including the CN band at
including the CN band at
![]() and the G-band at
and the G-band at
![]() .
The final actual wavelength coverage depends on the location of the star/slit on the mask with respect to the dispersion direction.
Typically we defined one slit mask per region of the CMD per cluster, containing
.
The final actual wavelength coverage depends on the location of the star/slit on the mask with respect to the dispersion direction.
Typically we defined one slit mask per region of the CMD per cluster, containing ![]() 50-70 slits.
We selected slit lengths of 4-8
50-70 slits.
We selected slit lengths of 4-8
![]() to make local sky subtraction possible.
The slit width was fixed to
to make local sky subtraction possible.
The slit width was fixed to
![]() .
The total exposure time per mask varied between 360 and
.
The total exposure time per mask varied between 360 and
![]() depending on the cluster and the brightness of the target stars.
To facilitate cosmic ray removal the observations were split into multiple (2-3) exposures.
The central coordinates of the observed fields as well as the total exposure times are listed in Table 1.
In addition to the science exposures, we obtained bias, flatfield and wavelength calibration observations.
depending on the cluster and the brightness of the target stars.
To facilitate cosmic ray removal the observations were split into multiple (2-3) exposures.
The central coordinates of the observed fields as well as the total exposure times are listed in Table 1.
In addition to the science exposures, we obtained bias, flatfield and wavelength calibration observations.
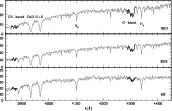 |
Figure 1: Typical spectrum of a RGB ( top panel), a SGB ( middle panel), and a MS ( bottom panel) star in the globular cluster NGC 288. The regions of the measured indices are marked by darker lines. Furthermore the positions of the prominent CaII H and K and Hydrogen lines are indicated in the top panel. |
| Open with DEXTER | |
![\begin{figure}
\par\hspace*{3mm}
\begin{tabular}[]{c c c}
\hspace*{-0.6cm}\psfig...
...rx=195mm,bbury=246mm}\hspace*{3cm}
\vspace*{0.9cm}\\
\end{tabular}
\end{figure}](/articles/aa/full/2008/29/aa09446-08/Timg32.gif) |
Figure 2:
The color magnitude diagrams for the globular clusters
in our sample. Those stars for which line strength measurements are available
are marked in color. We distinguish between stars of different evolutionary
states. MS stars are indicated by blue squares, SGB stars by green triangles,
and RGB stars by red circles. CN-weak and CN-strong stars are denoted by open
and filled symbols, respectively. Note that in all diagrams the calibrated
pre-image B and V magnitudes are shown. Our sample comprises clusters
spanning a wide range in metallicity (
|
| Open with DEXTER | |
Table 2: Reddening, distance modulus, and photometric parameters of the MSTO for our sample GCs.
The photometric data are based on the pre-image observations of the target fields in the B and V band, taken several months prior to the spectroscopic observations with FORS2 at the VLT/UT4. The identification and psf-photometry was performed on the pipeline reduced images (provided by ESO) using the the IRAF package DAOPHOT. B and V magnitudes were matched to create the CMDs. For this work, a precise photometric calibration is not necessary since we are mainly interested in a comparative study of stars in different evolutionary states, which can easily be identified in the CMDs. A rough calibration was done by adjusting the zeropoints such that the MSTO (B-V) colors and V magnitudes taken from the literature were matched (see Table 2).
Based on the location in the CMDs we assigned stars to the MS, SGB, and RGB. Figure 2 shows the CMDs for all clusters in our sample. The stars with available spectra are symbol-coded according to their position in the CMD. Only those stars are shown that were identified as radial velocity members and that passed our quality check of the spectra. For the two Sgr clusters Ter 7 and Pal 12 some stars near the RGB bump have been observed. These stars are included in the Figs. 2-4 but neglected in the further analysis.
The data reduction was carried out using standard routines within
IRAF![]() . This included bias correction and flatfielding. The
cleaning for cosmic rays was done with bclean from the
STARLINK package. Before sky subtraction was performed the spectra
from the individual exposures were stacked to improve the signal-to-noise
ratio. In most cases, object and sky could be extracted from the same slit.
The wavelength calibration was achieved using the emission spectra of the
He-Ne-Hg-Cd arc lamps taken after each set of observations. Note that the
final spectra were neither flux-calibrated nor normalized by the continuum.
All spectra were binned to a spectral scale of
. This included bias correction and flatfielding. The
cleaning for cosmic rays was done with bclean from the
STARLINK package. Before sky subtraction was performed the spectra
from the individual exposures were stacked to improve the signal-to-noise
ratio. In most cases, object and sky could be extracted from the same slit.
The wavelength calibration was achieved using the emission spectra of the
He-Ne-Hg-Cd arc lamps taken after each set of observations. Note that the
final spectra were neither flux-calibrated nor normalized by the continuum.
All spectra were binned to a spectral scale of
![]() .
Considering the seeing the final spectral resolution (FWHM) for narrow
lines is
.
Considering the seeing the final spectral resolution (FWHM) for narrow
lines is ![]()
![]() .
Typical spectra of a RGB, a SGB and a MS stars in NGC 288 are shown in
Fig. 1.
.
Typical spectra of a RGB, a SGB and a MS stars in NGC 288 are shown in
Fig. 1.
For all spectra we measured radial velocities by cross-correlating them with
five high quality template spectra taken from the ![]() Cen dataset using
IRAF/fxcor. We adopted the mean value of the five measurements as the
radial velocity of the star and corrected for the measured Doppler shift. The
scatter of the velocity measurements is of the order of
Cen dataset using
IRAF/fxcor. We adopted the mean value of the five measurements as the
radial velocity of the star and corrected for the measured Doppler shift. The
scatter of the velocity measurements is of the order of
![]() ,
which
reflects the uncertainties given by the spectral resolution. In the resulting
velocity distributions the globular clusters clearly stand out against the
Galactic foreground. Possible non cluster member stars were identified by
their radial velocities and rejected from the further analysis. In a final
step, we examined each spectrum individually and rejected those spectra with
bad quality (e.g., due to tracing errors). In total about 500 spectra are
suitable for our analysis, whereof 120 spectra are from lower RGB stars.
,
which
reflects the uncertainties given by the spectral resolution. In the resulting
velocity distributions the globular clusters clearly stand out against the
Galactic foreground. Possible non cluster member stars were identified by
their radial velocities and rejected from the further analysis. In a final
step, we examined each spectrum individually and rejected those spectra with
bad quality (e.g., due to tracing errors). In total about 500 spectra are
suitable for our analysis, whereof 120 spectra are from lower RGB stars.
Note that NGC 5286 and M 22 have quite a high foreground extinction, and probably differential reddening is broadening the giant branches (e.g., Richter et al. 1999). Most of the radial velocity members of NGC 5286 lie on the red side of the RGB sequence which might reflect their biased location west of the cluster center (pointing of the spectroscopic mask).
In the Appendix, magnitude limited samples of cluster member stars that were used for our analysis are presented (Table A.1). Only the brightest five stars of each cluster are contained in this table. The full table of all cluster stars only is available in the online version of the article.
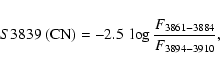 |
(1) |
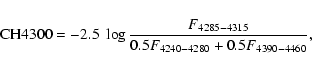 |
(2) |
 |
Figure 3: The distribution of the stars of the different clusters in the CN vs. MV diagram. The left upper panel illustrates the overall distribution of our sample stars. In the lower panel we distinguished between different evolutionary states of the stars. The color coding of the data points corresponds to stars from the different clusters as indicated in the figure legend in the upper right. Whereas for the MS all clusters show roughly the same distribution, for the RGB the distribution shows a large scatter. For the clusters NGC 288 and NGC 362, a bimodal distribution in CN band strength is visible. In the lower left corner of the bottom panels the median errors of the measurements are shown. |
| Open with DEXTER | |
In order to investigate the behavior of the strengths of the CN index as a function of evolutionary state (or stellar mass) we plotted CN against the absolute V magnitude, MV, for all clusters (Fig. 3). We adopted the distance moduli and extinction values of Harris (1996).
Looking at the whole sample of stars a wide spread in CN and a continuous
increase of CN with decreasing MV can be seen in the upper panel of this
figure. This is caused by the fact that the formation of molecules in stellar
atmospheres strongly depends on the effective temperature,
![]() ,
and the
surface gravity, log g of the stars. The efficiency of CN formation is
higher in stars with lower
,
and the
surface gravity, log g of the stars. The efficiency of CN formation is
higher in stars with lower
![]() and lower log g.
To further illustrate this effect we subdivided our sample into MS
(log g
and lower log g.
To further illustrate this effect we subdivided our sample into MS
(log g ![]() ,
,
![]()
![]() ), SGB (log g
), SGB (log g![]() 4.5-3,
4.5-3,
![]()
![]() 5000-6000
5000-6000![]() ), and RGB stars (log g
), and RGB stars (log g ![]() ,
,
![]()
![]() ). The different distributions for the different evolutionary
states are shown in the lower panels. One can clearly see that the line
strengths of CN on average increase as stars evolve from the MS to the RGB.
This can be understood by the augmented formation of molecules in cooler
atmospheres.
). The different distributions for the different evolutionary
states are shown in the lower panels. One can clearly see that the line
strengths of CN on average increase as stars evolve from the MS to the RGB.
This can be understood by the augmented formation of molecules in cooler
atmospheres.
Looking at the globular clusters individually one recognizes that they show very different behaviors in the MV vs. CN diagram. Whereas for the MS and the SGB all clusters show roughly the same pattern, the distributions on the RGB deviate between the clusters. For some clusters like e.g., NGC 288 and NGC 362, we clearly see a bifurcation in CN band strengths as we reach the RGB. Either part of the bifurcation contains roughly equal numbers of stars. This is worth to keep in mind as the two clusters are a so called ``second-parameter pair'': both clusters have similar metallicities but show a very distinct horizontal branch morphology. In NGC 288, most of the core helium burning stars can be found on the blue horizontal branch whereas almost no stars are located on the red part. Exactly the opposite is the case for NGC 362. For this cluster the red part of the horizontal branch is densely populated. Some authors proposed that deep mixing and the consequently increased mass loss could be an explanation for the different horizontal branch morphologies as well as the observed abundance anomalies (e.g., Weiss et al. 2000). For other second parameter pairs like e.g., M 3 and M 13, which also show differences in light abundance elements this might be a possible explanation for the observed patterns. Both clusters have similar ages and metallicities. However, the RGB in M 3 is dominated by CN-weak stars, whereas the majority of stars in M 13 are found to be CN-strong (e.g., Suntzeff 1981).
Nevertheless, the fact that we do not observe significant differences in the CN distributions indicates that deep mixing cannot be a major cause of the horizontal branch morphology. Similarly, based on the CN and CH measurements of stars in the second parameter globular cluster NGC 7006, Harbeck et al. (2003b) argued against the hypothesis that CN-variations are directly correlated with the second parameter effect. They found the scatter in CN to be similar to those in other GCs of the same metallicity but different horizontal branch ratios.
In contrast to NGC 288 and NGC 362, the clusters Ter 7, Pal 12, and M 55 seem to exhibit no or only very few stars with strong CN band strengths. In the clusters NGC 5286, M 22, and M 15, stars can be found on both the CN-weak and the CN-strong regime in this diagram. For M 15 and M 22, the majority of the stars are associated with the CN-weak group. For NGC 5286, we have only six measurements. Four of these stars are found to be CN-strong and two CN-weak.
We cannot assess whether similar abundance variations on the SGB and the
MS region are not present or can not be detected due to a too weak signal caused
by the higher effective temperatures of these stars. The observed scatter in
the CN measurements of MS and SGB stars (rms ![]() 0.13 and 0.14,
respectively) is found to be of the same order as the errors in the index
measurements (0.17 and 0.13, respectively).
0.13 and 0.14,
respectively) is found to be of the same order as the errors in the index
measurements (0.17 and 0.13, respectively).
CN as a double-metal molecule is easier to observe in more metal-rich clusters due to the stronger equivalent widths at higher metallicities. Our work as well as former studies on the RGB show that whatever process is responsible for the formation of the CN-strong stars, it seems to occur in the majority of Galactic globular clusters. In contrast to this, in both fairly metal-rich Sgr dSph clusters (Pal 12 and Ter 7) we found no sign for this process to be present. All stars in these clusters are located in the CN-weak branch in Fig. 3. From the fact that, if present, CN-strong stars should show up easily in these clusters we infer that they actually lack those stars. This suggests that probably the environment in which the clusters formed had an effect on the presence or absence of the CN variations. However we point out that possible effects of the small sample size cannot be ruled out. Preliminary results from low resolution spectra of seven giants in Arp 2 and Ter 7 suggest star to star variations in the CN band strength in these clusters (Briley et al. 2007).
| |
Figure 4: The distribution of the stars in the CN vs. CH diagram for the RGB star in our sample clusters. The stars of different clusters are indicated by different colors as listed in Fig. 3. The left panel illustrates the overall distribution of our sample stars, with a typical error given in the lower right corner. The solid line indicated a possible differentiation between CN-strong and CN-weak stars in this diagram, drawn by eye. In right panel we calculated the mean CN and CH of both the CN-strong and CN-weak stars. The original overall distribution is plotted in gray, while the mean values are color-coded as defined before. |
| Open with DEXTER | |
Interestingly, the stars in M 15, which showed no indication for a bifurcation
in Fig. 3, show a weak indication
of a bimodal distribution (two clumps separated at
![]() )
in the
CN-CH plane (Fig. 4). However,
this needs further confirmation since the observational errors of such weak
lines are large compared to the separation of the two clumps. Assuming that
the clump at
)
in the
CN-CH plane (Fig. 4). However,
this needs further confirmation since the observational errors of such weak
lines are large compared to the separation of the two clumps. Assuming that
the clump at
![]() and
and
![]() defines the CN-rich population,
this would strongly change the number ratio of CN-strong to CN-weak stars in
M 15 (see next section). In order to further illustrate the dichotomy in this
plot we separated CN-strong from CN-weak stars (see Fig. 4 right
panel) and calculated the mean CN- and CH-indices for each sub-population in
the different clusters (large dots).
defines the CN-rich population,
this would strongly change the number ratio of CN-strong to CN-weak stars in
M 15 (see next section). In order to further illustrate the dichotomy in this
plot we separated CN-strong from CN-weak stars (see Fig. 4 right
panel) and calculated the mean CN- and CH-indices for each sub-population in
the different clusters (large dots).
As we introduced earlier, one of the scenarios proposed to explain the variations in C and N in RGB stars in globular clusters is the dredge-up of material processed in the CNO cycle. In our case, the origin of the observed patterns/bimodalities can not only lie in such mixing effects as the analyzed stars are considerably fainter than the red bump at which the deep mixing mechanism is expected to set in. Although we did not find evidence for CN bimodalities among our SGB and MS stars (cf. Harbeck et al. 2003a) we favor a scenario in which the cluster formed out of chemically inhomogeneous material that was polluted by the outflows of fast rotating massive stars or AGB stars (e.g., Ventura et al. 2001; Cottrell & Da Costa 1981; Decressin et al. 2007).
As a measure to quantify the wide range of CN line strengths we used a CN
excess parameter (
![]() )
similar to the one introduced by Norris & Smith (1981).
This minimizes the effects of effective temperature and surface gravity
existent in the CN measurements. The
)
similar to the one introduced by Norris & Smith (1981).
This minimizes the effects of effective temperature and surface gravity
existent in the CN measurements. The
![]() parameter is defined as the
CN strength with respect to a baseline. This baseline is defined by the lower
envelope fitted for each individual cluster in the CN vs. MV distribution.
The left panel in Fig. 5 illustrates the baseline fit and the right panel
shows the resulting
parameter is defined as the
CN strength with respect to a baseline. This baseline is defined by the lower
envelope fitted for each individual cluster in the CN vs. MV distribution.
The left panel in Fig. 5 illustrates the baseline fit and the right panel
shows the resulting
![]() vs. MV distribution for the cluster NGC 288.
vs. MV distribution for the cluster NGC 288.
In the previous sections we saw that the bimodality is only clearly detected for stars on the lower RGB. Therefore, in the following we concentrate on this part of the CMD. Figure 6 shows the histograms of the CN excess parameter for the RGB stars in all eight globular clusters in our sample, sorted by their metallicity. We selected a bin width of 0.13, comparable to the median uncertainties of the CN index for these stars.
| |
Figure 5:
Left: the MV vs. CN diagram for the RGB (red), SGB
(green), and MS (blue) stars for the cluster NGC 288. The bimodal distribution
is clearly visible. The dashed line illustrates the lower envelope fitted to
this distribution. Right: plotted is MV vs. the CN excess parameter
|
| Open with DEXTER | |
![\begin{figure}
\par\hspace*{1.5cm}\scalebox{1}[1]{\includegraphics*[viewport=30 45 499 547]{9446fig13.ps}}
\end{figure}](/articles/aa/full/2008/29/aa09446-08/Timg53.gif) |
Figure 6:
Distributions of CN-band strength in the RGB stars
of our sample clusters. The histograms of the CN-excess parameter
|
| Open with DEXTER | |
Most of the metal-poor clusters (M 15, M 55, and M 22) show a distinct main
CN-weak peak with a weak extension towards higher
![]() values. For NGC 5286,
we observe a fairly flat distribution. However, due to the small sample size
we cannot definitely comment on any distribution pattern. For NGC 288 and
NGC 362, which have similar intermediate metallicities, the bimodal
distribution clearly shows up in these plots. Both peaks are roughly equally
pronounced. The two probable Sgr dSph clusters (Pal 12 and Ter 7) show a
single peak and a fairly broad distribution around the CN-weak peak.
The spanned ranges in
values. For NGC 5286,
we observe a fairly flat distribution. However, due to the small sample size
we cannot definitely comment on any distribution pattern. For NGC 288 and
NGC 362, which have similar intermediate metallicities, the bimodal
distribution clearly shows up in these plots. Both peaks are roughly equally
pronounced. The two probable Sgr dSph clusters (Pal 12 and Ter 7) show a
single peak and a fairly broad distribution around the CN-weak peak.
The spanned ranges in
![]() of about 0.45 and 0.53 for Ter 7 and Pal 12
are comparable with the ranges of 0.54 and 0.48 for M 55 and M 15 (excluding
the extremely CN-strong outlier in the last cluster) which at first glance
might point to a similar enrichment history of those clusters, despite their
very different metallicities and environments they live in. However, the
apparent broadness observed in M 15 and M 55 is mainly due to the metal-poor
nature of these clusters, resulting in larger errors in determining their
CN strength. In contrast, for the metal-rich clusters Pal 12 and Ter 7,
CN-strong stars and a bimodality are expected to clearly show up in these
diagrams, if present. This makes the chemical patters of the Sgr clusters
appear different from those of galactic clusters of similar metallicities
(e.g., 47 Tuc) that show more pronounced CN spreads and/or bimodality.
of about 0.45 and 0.53 for Ter 7 and Pal 12
are comparable with the ranges of 0.54 and 0.48 for M 55 and M 15 (excluding
the extremely CN-strong outlier in the last cluster) which at first glance
might point to a similar enrichment history of those clusters, despite their
very different metallicities and environments they live in. However, the
apparent broadness observed in M 15 and M 55 is mainly due to the metal-poor
nature of these clusters, resulting in larger errors in determining their
CN strength. In contrast, for the metal-rich clusters Pal 12 and Ter 7,
CN-strong stars and a bimodality are expected to clearly show up in these
diagrams, if present. This makes the chemical patters of the Sgr clusters
appear different from those of galactic clusters of similar metallicities
(e.g., 47 Tuc) that show more pronounced CN spreads and/or bimodality.
In Fig. 7 we show combined histograms for the
![]() measurements
of the clusters in our sample. We distinguish between a histogram of all eight
clusters and one where we did not include the two Sgr dSph clusters, Ter 7 and
Pal 12. In both cases a clear bimodal distribution is visible.
As Ter 7 and Pal 12 are of extragalactic origin
we focused on the histogram based on six globular clusters. This
distribution was used for the differentiation between CN-strong and CN-weak
stars. We fitted a double Gaussian to the distribution and selected the
minimum as the differential criteria between CN-strong and CN-weak stars.
CN-strong stars are then those that have a CN excess greater than
measurements
of the clusters in our sample. We distinguish between a histogram of all eight
clusters and one where we did not include the two Sgr dSph clusters, Ter 7 and
Pal 12. In both cases a clear bimodal distribution is visible.
As Ter 7 and Pal 12 are of extragalactic origin
we focused on the histogram based on six globular clusters. This
distribution was used for the differentiation between CN-strong and CN-weak
stars. We fitted a double Gaussian to the distribution and selected the
minimum as the differential criteria between CN-strong and CN-weak stars.
CN-strong stars are then those that have a CN excess greater than
![]() = 0.46.
= 0.46.
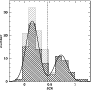 |
Figure 7:
Combined histograms of the CN-excess parameter for
the clusters in our sample. The gray histogram comprises all eight clusters.
In the black histogram Pal 12 and Ter 7, which are believed to belong to the
Sgr dSph, are not included. Here we only consider stars on the lower RGB.
|
| Open with DEXTER | |
To quantify the observed bimodality in the CN line strength, we
determined the parameter r introduced by Norris (1987). It gives the number
ratio of CN-strong to CN-weak stars,
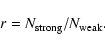 |
(3) |
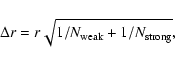 |
(4) |
Table 3: CN number ratios.
For subsequent analysis, we included two additional data from literature sources. Briley (1997) determined the ratio of CN-strong to CN-weak stars for stars on the RGB in 47 Tuc. He distinguishes between RGB stars below and above the RGB bump and found very similar values of 1.9 and 1.8, respectively. For this work, we adopted the value of 1.9. Penny et al. (1992) and Lee (2005) find the r-parameter in the cluster M 71 for stars on the lower RGB to be 0.8 and 0.69, respectively. We adopted the more recent result by Lee (2005). The measurements of the number ratio of CN-strong stars on the upper RGB of M 71 range between 0.3 (Penny et al. 1992), 0.63 (Cohen 1999), and 1.0 (Lee 2005). The average value is 0.64, similar to those found on the lower RGB. Nevertheless, we have to keep in mind that the additional r-parameters are based on observations obtained with a different instrument and different index definitions.
In the upper part of Table 3, an overview of the number of stars identified as CN-strong and CN-weak is given. In the third column the r-parameters for the lower RGB of our clusters and M 71 and 47 Tuc are listed. The r-parameters range from 0.0 for Ter 7 to 2.00 for NGC 5286. The uncertainties vary from 0.07 for Pal 12 to 1.73 for NGC 5286. The large uncertainty for NGC 5286 is due to the small sample size. If one divided the stars of M 15 into CN-weak and CN-strong according to Fig. 4, its r-parameter would be 0.6 (given in brackets in Table 3). For those clusters that were part of previous studies, the r-parameters for the upper RGB are given in the last column. We find for two out of the three clusters of our sample, for which RGB studies exist, good agreement of the number ratios found on the SGB with those on the RGB. The values for NGC 362 differ by a factor of 2. The reason for this remains unclear and requires the repetition of the measurement on the RGB.
To examine possible CN-CH anticorrelations we used the distinction criteria between CN-strong and CN-weak RGB stars as described in Sect. 3.1. Although no clear bimodality in CN absorption strength was detected on the SGB and MS, we observe scatter in CN more than expected from measurement errors alone in all evolutionary states.
Since CN dichotomies have been detected before on the MS on M 13 (Briley et al. 2004), 47 Tuc
(Harbeck et al. 2003a), and M 71 (Cohen 1999), it is quite conceivable that
abundance variations among the less evolved stars exist in our sample as well.
At the precision of our measurements, however, the signal might simply be too
weak due to the higher temperatures and/or low metallicities, which inhibit the
formation efficiency of the CN molecule.
Nevertheless, to check for anticorrelations, we determined the CN
excess parameter for the SGB and MS stars analogously to the RGB stars.
The resulting
![]() distributions are shown in Fig. 8.
In analogy to the RGB analysis we neglected the Sgr clusters Pal 12 and
Ter 7. The median
distributions are shown in Fig. 8.
In analogy to the RGB analysis we neglected the Sgr clusters Pal 12 and
Ter 7. The median
![]() values were found to be 0.20 both for the SGB and MS.
The standard deviation is 0.08 in both cases.
We considered those stars with
values were found to be 0.20 both for the SGB and MS.
The standard deviation is 0.08 in both cases.
We considered those stars with
![]() higher than
higher than ![]() above and below the
median as CN-strong and CN-weak, i.e. CN-strong:
above and below the
median as CN-strong and CN-weak, i.e. CN-strong:
![]() >
>
![]() ;
CN-weak:
;
CN-weak:
![]() <
<
![]() .
.
| |
Figure 8:
The combined distributions of the CN excess
parameters measured for stars on the SGB and MS. The gray histogram
comprises all eight clusters. In the black histogram Pal 12 and Ter 7 are
not included. The solid lines indicate the median values of the distributions.
The dashed lines indicate the selection limits for CN-strong and CN-weak
stars. Stars with
|
| Open with DEXTER | |
A comparison of CN vs. MV and CH vs. MV is shown in Fig. 9. We
differentiate between RGB, SGB, and MS stars for all clusters.
Furthermore, we distinguish between stars with strong, weak, and intermediate
CN absorption band features.
A bimodal
distribution in CH is not detected for any of the clusters. Note that even for
NGC 288 and NGC 362, which showed the strongest dichotomy in CN, we do not
observe a bimodality in CH.
However, the CN-strong RGB stars of these two GCs clearly have smaller
CH indices than the CN-weak RGB stars of similar MV. This is not seen for the
other clusters, except maybe for NGC 5286. In the case of M 22, larger
uncertainties due to the significant differential reddening (Richter et al. 1999) might
dilute a possible CN-CH anticorrelation.
In the very metal-poor cluster, M 15, one RGB star with high CN absorption
bands was identified, which also seems to be quite rich in CH. This CN-
and
CH-strong star in M 15 stands out from the rest of the datapoints by more
than 1 in
![]() .
Since this star lies slightly off the RGB, we suggest
that this star is not a cluster member (although it has the right radial
velocity).
.
Since this star lies slightly off the RGB, we suggest
that this star is not a cluster member (although it has the right radial
velocity).
Moving from the RGB to the SGB and the MS, the CN-CH anticorrelation is still visible for NGC 288 and NGC 362. Due to the lower signal to noise ratio, it is less pronounced but on average the more CN-strong stars are CH-weaker. For the other clusters, no clear statement can be made.
We conclude that, in the case of clearly bimodal clusters like NGC 288 and NGC 362, the differences in the band strengths and the CN/CH anticorrelation do exist among stars of all evolutionary states. Deep mixing is believed to set in at the level of the RGB bump and does not take place in stars on the lower RGB, SGB, and MS. Furthermore, low-mass MS stars burn hydrogen only in their cores. Thus the observed patterns cannot be caused by the transport of CNO cycle processed material from the interior to the stellar surfaces. We can therefore rule out evolutionary effects within the stars as the origin of the observed anticorrelation.
![\begin{figure}
\par\hspace*{2mm}
\begin{tabular}[]{c c}
\psfig{figure=9446fig16....
...t=18cm,bbllx=110mm,bblly=60mm,bburx=550mm,bbury=246mm}\end{tabular}
\end{figure}](/articles/aa/full/2008/29/aa09446-08/Timg76.gif) |
Figure 9:
The CN vs. MV and CH vs. MV diagrams for the eight
clusters in our sample. We differentiate between RGB, SGB, and MS stars for
all clusters. The CN-strong and CN-weak stars are marked by filled and open
symbols, respectively. SGB and MS stars with intermediate
|
| Open with DEXTER | |
Table 4: Global parameters of globular clusters of our sample.
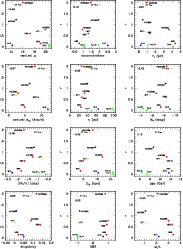 |
Figure 10: The number ratio of CN-strong to CN-weak stars (r-parameter) vs. various cluster parameters (see Table 4). Our targets are indicated by the filled circles. The two results taken from the literature are marked by open triangles. Red, blue, yellow, and green colors indicate OH, YH, BD, and Sgr GCs, respectively. In the upper left corner the calculated Spearman rank correlation coefficient is given. |
| Open with DEXTER | |
To explore possible correlations of the CN distribution with global
parameters of the globular clusters, we combine our observations to quantities
available in the literature. A similar analysis has been done before by, e.g.,
Norris (1987), Smith & Mateo (1990), Smith (2002), and Harbeck et al. (2003b). However their
studies were based on compilations of upper RGB star measurements in various
clusters from different sources and therefore different techniques. We now
provide a sample that is based on a very homogeneous data set of eight star
clusters. The cluster quantities were selected from the 2003 version of the
McMaster (Harris 1996) and Pryor & Meylan (1993) globular cluster
catalogs![]() .
As no ellipticity is listed in these catalogs for NGC 288, we adopted the
value given by Frenk & Fall (1982). The age estimates were adopted from
Rosenberg et al. (1999) and Buonanno et al. (1998). Moreover, we adopted the subdivision of our
globular clusters into objects belonging to different Galactic components
(namely OH, YH, BD, and those accreted from the Sgr dSph (SG)) from
Mackey & van den Bergh (2005). Table 4 gives an overview of the extracted
parameters.
.
As no ellipticity is listed in these catalogs for NGC 288, we adopted the
value given by Frenk & Fall (1982). The age estimates were adopted from
Rosenberg et al. (1999) and Buonanno et al. (1998). Moreover, we adopted the subdivision of our
globular clusters into objects belonging to different Galactic components
(namely OH, YH, BD, and those accreted from the Sgr dSph (SG)) from
Mackey & van den Bergh (2005). Table 4 gives an overview of the extracted
parameters.
To quantify the statistical significance of possible correlations
between the number ratio of CN-strong stars with various structural parameters,
we computed the Spearman coefficient of rank correlation (![]() )
for each parameter.
This correlation coefficient is a technique that can be used to
characterize the strength and direction of a relationship of two random
variables.
The values of
)
for each parameter.
This correlation coefficient is a technique that can be used to
characterize the strength and direction of a relationship of two random
variables.
The values of ![]() lie between +1 and -1, the extremes where the rank
sequences completely coincide and are completely opposite, respectively.
For the clusters in our sample we do not find a clear correlation between the
majority of the cluster parameters and the percentage of CN-strong stars
(Fig. 10).
lie between +1 and -1, the extremes where the rank
sequences completely coincide and are completely opposite, respectively.
For the clusters in our sample we do not find a clear correlation between the
majority of the cluster parameters and the percentage of CN-strong stars
(Fig. 10).
Norris (1987) observed a correlation between the percentage of CN-rich stars and the apparent flattening of the individual clusters, which he proposed is associated with the clusters' rotation. He suggested that the high systematic cluster rotation is linked via exchange of angular momentum to a higher initial angular momentum of the individual stars. Within giants the rotation may drive circulation currents that are capable of cycling the material in the envelope through the interior hydrogen-burning shell where the CNO process is active (Sweigart & Mengel 1979). Consequently a higher percentage of CN-strong stars is expected to be observed in clusters with higher mean stellar rotation velocities and thus higher overall cluster rotational velocities and hence possibly higher ellipticities. Since there is little information on cluster rotation for the globulars in our sample, we use ellipticity as a proxy for rotation. This correlation was confirmed by Smith & Mateo (1990) and Smith (2002). The computed Spearman rank coefficient of 0.26 suggests that the number ratio of CN-strong stars is mostly independent of the cluster ellipticity. We conclude that the effect proposed by Sweigart & Mengel (1979) is probably not as relevant as thought so far.
Another correlation detected by Smith & Mateo (1990) is between the r-parameter and
the central velocity dispersion. Our analysis reveals
![]() ,
which
makes such a correlation rather unlikely. Furthermore, Smith & Mateo (1990) found
the highest percentages of CN-strong stars to be restricted to the more
luminous/massive clusters. They suggest an inter-cluster self-pollution
scenario as a possible origin. Due to the higher binding energies in more
massive clusters, the ability to retain enriched ejecta of massive and
intermediate-mass stars is expected to be higher than in lower mass clusters.
Our cluster sample supports the correlation with the total absolute
magnitude (MV).
The calculated Spearman coefficient of
,
which
makes such a correlation rather unlikely. Furthermore, Smith & Mateo (1990) found
the highest percentages of CN-strong stars to be restricted to the more
luminous/massive clusters. They suggest an inter-cluster self-pollution
scenario as a possible origin. Due to the higher binding energies in more
massive clusters, the ability to retain enriched ejecta of massive and
intermediate-mass stars is expected to be higher than in lower mass clusters.
Our cluster sample supports the correlation with the total absolute
magnitude (MV).
The calculated Spearman coefficient of
![]() is actually among the highest
found in our analysis.
is actually among the highest
found in our analysis.
We furthermore determined the Spearman rank correlation coefficients
using the alternative higher number ratio of M 15 (see Sect. 3.2).
Although most of the changes are small, some correlations show a higher significance,
in particular for MV with
![]() .
Since the results for NGC 5286 suffer from small number statistics and thus a large
error in
.
Since the results for NGC 5286 suffer from small number statistics and thus a large
error in ![]() ,
we decided to also recalculate the correlation coefficients by neglecting
this cluster (using the original value for M 15).
The resulting values are comparable to those considering all clusters.
An overview of the computed Spearman rank coefficients is given in Table 5.
,
we decided to also recalculate the correlation coefficients by neglecting
this cluster (using the original value for M 15).
The resulting values are comparable to those considering all clusters.
An overview of the computed Spearman rank coefficients is given in Table 5.
For a more statistically complete investigation, we combined our results with those by Smith (2002) and Harbeck et al. (2003b). In Sect. 3.1 we have seen that for the majority of the studied clusters the r-parameter on the upper RGB is consistent with those on the lower RGB. We are thus confident that we may combine our results with those from the literature. Nevertheless we keep in mind that this leads to a more heterogeneous sample, since values of different evolutionary states and different measurements are combined.
For most parameters the lack of any clear trends is confirmed. In particular,
the inclusion of our results with those listed in Smith (2002) and
Harbeck et al. (2003b) further confirms the lack of a correlation between cluster
ellipticity ![]() and the number ratio of CN-strong stars.
We observe a large scatter in Fig. 11 (lower right panel). It can,
however, not be ruled out that some clusters with low
and the number ratio of CN-strong stars.
We observe a large scatter in Fig. 11 (lower right panel). It can,
however, not be ruled out that some clusters with low ![]() and high
r values are actually more elliptical but appear round due to projection
effects. This would dilute a possible correlation. GCs with high
and high
r values are actually more elliptical but appear round due to projection
effects. This would dilute a possible correlation. GCs with high ![]() and low r values would then be clear outliers.
and low r values would then be clear outliers.
We see a possible connection between the r-parameter and the tidal radius (Fig. 11, lower left panel). Clusters with larger tidal radii seem to possess a higher percentage of CN-strong stars. Interestingly, those clusters that do not follow this trend are those that are thought to be linked to the Sgr dSph (Palomar 12 and Terzan 7), as well as the very metal-poor clusters M 15 and NGC 5272, which belong to the young halo GCs. We computed the Spearman coefficient including and excluding these cluster. The resulting values are 0.19 and 0.67, respectively. This is an interesting finding, since Zinn (1993) postulated that the young halo population of globular clusters was predominantly formed by accretion of extragalactic objects. We therefore put forward the hypothesis that, among other parameters, environmental differences due to different cluster formation sites may influence the today observed abundance patterns. Carretta (2006) showed that, apart from differences in the environmental properties during the time of formation also differences in the evolution of clusters have probably influenced the light element abundance ratios. Using a set of high-resolution spectroscopic abundance measurements he found that clusters with larger orbital semi major axes, i.e., extended orbits and revolution periods, exhibit a larger amount of inhomogeneities. From this he concluded that, for clusters on orbits reaching large Galactocentric distances, the lack of disturbance by the Galactic disk helps to retain pre-enriched material. In contrast, clusters close to the Galactic center might have suffered early and frequent disk/bulge shocks that enforced rapid gas loss and prohibited the formation of a second enriched subpopulation. Those clusters also show smaller tidal radii due to the even stronger tidal forces towards the center of the Galaxy.
In the upper right panel of Fig. 11, we plotted the r-parameter as a function of the absolute magnitude, representing the present-day cluster mass. It seems that the maximum number ratio of CN-strong to CN-weak stars increases with increasing MV (cf. Smith 2002). Only the brightest clusters have formed CN-strong stars. This supports the idea that the more massive objects can more efficiently retain processed material ejected from evolved stars.
The possible CN-bimodality of M 15 as described in Sect. 3.2 and
shown in Fig. 4 increases the r-parameter of this cluster to 0.6.
As a consequence the correlations of r with absolute magnitude, MV and tidal radius, ![]() become slightly more
significant with Spearman rank values of
become slightly more
significant with Spearman rank values of
![]() and -0.68,
respectively.
The low correlations with central velocity dispersion and ellipticity, however, remain nearly unchanged.
More accurate CN/CH index measurements of this very metal-poor
cluster are needed to confirm these findings.
and -0.68,
respectively.
The low correlations with central velocity dispersion and ellipticity, however, remain nearly unchanged.
More accurate CN/CH index measurements of this very metal-poor
cluster are needed to confirm these findings.
Table 5: Calculated Spearman rank correlation coefficients.
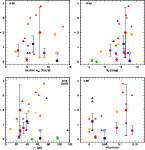 |
Figure 11:
Plot of the r-parameter vs. those globular cluster
parameters that showed a promising correlation in Fig. 10 or in previous studies by e.g., Smith (2002), such as
ellipticity, central velocity dispersion (
|
| Open with DEXTER | |
We analyzed the absorption bands of the CN and CH molecule in eight Galactic globular clusters via line index measurements. In each cluster, stars of various evolutionary stages were studied, from the lower RGB and SGB to the upper MS. Our sample comprises clusters belonging to different Milky Way components, e.g., young and old halos. In particular, two of our studied objects are associated with a disrupting Galactic companion, the Sagittarius dwarf spheroidal (Sgr dSph). We could show that the majority of the studied clusters shows significant CN/CH variations at the base of the RGB. For the two most prominent CN-bimodal GCs, NGC 288 and NGC 362, CN anticorrelates with CH. A weak signal for a CN/CH anticorrelation was detected also in the least evolved stars in these clusters. From this we conclude that purely evolutionary effects within the stellar interior cannot be the main driver of the observed abundance patterns. Our findings therefore favor a scenario in which a certain fraction of most clusters was formed out of material that was enriched or polluted by ejecta of a prior generation of massive stars. In fact, the existence of star-to-star variations among those slightly evolved stars favors self-enrichment as the probable origin. One possible explanation could be that the stars observed nowadays in globular clusters formed from protocluster material that was to some degree inhomogeneously enriched in light elements. Such a pollution might have originated from ejecta of a prior generation of massive and therefore fast evolving stars, either belonging to the cluster itself or to the field population of a larger (dwarf sized) galaxy in which the cluster was embedded (e.g., Bekki et al. 2007). Possible candidates for the polluters discussed in the literature are massive AGB stars (e.g., Ventura et al. 2001; Cottrell & Da Costa 1981) and more recently fast rotating massive stars (Decressin et al. 2007). AGBs eject material via slow winds that are processed through the hot CNO cycle but are not enriched in iron. Fast rotating massive stars lose large amounts of material through slow winds, which are also enriched in H-burning products.
For the clusters NGC 288 and NGC 362, we found a clear bimodal distribution in CN with similar numbers of CN-strong and CN-weak stars. As the two clusters are a second-parameter pair, we conclude that the horizontal branch morphology is not correlated with this phenomenon. A possible explanation for such a pronounced dichotomy is given by a prolonged star formation in these globular clusters. The second, enriched stellar population formed well after the first generation had expelled and homogeneously distributed their AGB ejecta. The existence of such multiple stellar populations within globular clusters is further supported by the recent discoveries of complex CMD morphologies (e.g., multiple SGBs and MSs with age spreads) in some massive objects (Piotto et al. 2007; Bedin et al. 2004).
The two probable former Sgr dSph clusters (Terzan 7 and Palomar 12) do not exhibit any CN-strong stars. They are the most metal-rich clusters in our sample, so the double metal molecule CN should be easy to detect. We conclude that these clusters might lack stars with strong CN absorption. Our results suggest that the accreted Sgr globular clusters might be more chemically homogeneous than those native to the Milky Way. This is supported by the abundance analysis of 21 elements for four Sgr stars by Cohen (2004), who do not find a significant star-to-star scatter. Probably environmental conditions during the formation of the clusters played a major role for the observed abundance pattern. However, we point out that all existing studies suffer from small number statistics. Thus it cannot be ruled out that CN-rich stars are simply missed in the sampling (see the preliminary results by Briley et al. 2007). For more conclusions a thorough investigation of the abundance patterns other probable Sgr clusters (M 54, Arp 2, Ter 7, Ter 8, and Pal 12) is desirable.
To search for possible drivers for the abundance anomalies we studied the ratio of CN-strong/CN-weak stars as a function of various cluster parameters. We do not confirm the correlation with the cluster ellipticity that was observed before (Norris 1987). Our study therefore does not support cluster rotation and the associated enhanced deep mixing (Sweigart & Mengel 1979) as a main source of the production of CN-strong stars. Although we hardly see correlations in the number ratio of CN-strong stars with the majority of cluster parameters, some dependencies do seem to exist. We find evidence of an increase in the CN-strong star fraction with cluster tidal radius. Since GCs with large tidal radii are mostly found in the weak tidal field of the Galaxy (well outside the bulge and disk potential), they might occupy orbits that avoid bulge/disk shocks. Thus they might keep their gas longer, which favors the build-up of a second generation of enriched stars. Furthermore, we find that preferably the more luminous/massive clusters exhibit a large number of CN-strong stars. This may be an indication that the CNO processed ejecta could be more efficiently retained by more massive objects, independent of their tidal radius. The picture emerges that there are two basic channels that lead to a high fraction of CN-rich stars in GCs: 1) the cluster formed and lived in a remote environment, which allowed it to keep/regain its gas; and 2) the gravitational potential of the cluster itself was large enough to trap the enriched ejecta of slow velocity winds out of which a new generation of stars was formed.
Interestingly, those clusters that do not follow the observed trend are either associated with the young halo or accreted from the Sgr dSph. This might indicate that, as third parameter, the environmental conditions in which the clusters formed might had a non-negligible influence on the abundance patterns we observe today.
Nevertheless we point out that our study is limited to a small sample of clusters. For a statistically better supported study, a larger cluster sample is necessary. Furthermore, a complete set of cluster parameters is needed to search for the significance of the CN-CH differences between genuine halo globular clusters and accreted objects.
Acknowledgements
The authors thank the referee for the useful comments and suggestions. A.K. and E.K.G. gratefully acknowledge support by the Swiss National Science Foundation through the grants 200020-105260 and 200020-113697. M.H. acknowledges support from a German Science Foundation Grant (DFG-Projekt HI-855/2).
The following table contains a magnitude limited list (five stars per cluster)
of our spectroscopic sample stars. They are ordered by increasing V
magnitude. The columns are as follows:
Column 1. Identification of the object, giving the name of the globular cluster followed by a number which is ordered with increasing V magnitude.
Column 2. Right ascension for the epoch 2000 in decimals.
Column 3. Declination (2000) in decimals.
Column 4. Apparent V magnitude as determined by PSF photometry with DAOPHOT II under IRAF.
Column 5. B-V color from PSF photometry.
Column 6. Measured CN band strength.
Column 7. Error in measured CN band strength.
Column 8. Measured CH band strength.
Column 9. Error in measured CH band strength.
Column 10. Calculated CN-excess parameter
![]() .
.
Column 11. Radial velocity as determined from cross-correlation with FXCOR under IRAF and not corrected for systematic errors. Thus, these velocities are only indicative.
Column 12. ``Type'' describes to which part of the CMD the star most
probably belongs: RGB = red giant branch, HB = horizontal branch,
SGB = sub giant branch, MS = main
sequence.
Note: The full table of analyzed stars only is available in the online version of the article.
Table A.1: List of spectroscopic sample stars, ordered by increasing V magnitude.
Table A.1: List of spectroscopic sample stars, ordered by increasing V magnitude.