A&A 486, 255-271 (2008)
DOI: 10.1051/0004-6361:20078786
D. N. Aguilera1,2 - J. A. Pons1 - J. A. Miralles1
1 - Department of Applied Physics, University of Alicante,
Apartado de Correos 99, 03080 Alicante, Spain
2 -
Theoretical Physics, Tandar Laboratory,
National Council on Atomic Energy (CNEA-CONICET), Av. Gral Paz 1499, 1650 San Martín,
Buenos Aires, Argentina
Received 3 October 2007 / Accepted 28 February 2008
Abstract
Context. Many thermally emitting, isolated neutron stars have magnetic fields that are larger than 1013 G. A realistic cooling model that includes the presence of high magnetic fields should be reconsidered.
Aims. We investigate the effects of an anisotropic temperature distribution and Joule heating on the cooling of magnetized neutron stars.
Methods. The 2D heat transfer equation with anisotropic thermal conductivity tensor and including all relevant neutrino emission processes is solved for realistic models of the neutron star interior and crust.
Results. The presence of the magnetic field affects significantly the thermal surface distribution and the cooling history during both, the early neutrino cooling era and the late photon cooling era.
Conclusions. There is a large effect of Joule heating on the thermal evolution of strongly magnetized neutron stars. Both magnetic fields and Joule heating play an important role in keeping magnetars warm for a long time. Moreover, this effect is important for intermediate field neutron stars and should be considered in radio-quiet isolated neutron stars or high magnetic field radio-pulsars.
Key words: stars: neutron - stars: magnetic fields - radiation mechanisms: thermal
Observation of thermal emission from neutron stars (NSs) can provide not only information on the physical properties such as the magnetic field, temperature, and chemical composition of the regions where this radiation is produced but also information on the properties of matter at higher densities deeper inside the star (Page et al. 2006; Yakovlev & Pethick 2004). To derive this information, we need to calculate the structure and evolution of the star, and compare the theoretical model with the observational data. Most previous studies assumed a spherically symmetric temperature distribution. However, there is increasing evidence that this is not the case for most nearby neutron stars whose thermal emission is visible in the X-ray band of the electromagnetic spectrum (Zavlin 2007; Haberl 2007). The anisotropic temperature distribution may be produced not only in the low density regions where the spectrum is formed and preliminary investigations had focused their attention, but also in intermediate density regions, such as the solid crust, where a complicated magnetic field geometry could cause a coupled magneto-thermal evolution. In some extreme cases, this anisotropy may even be present in the poorly known interior, where neutrino processes are responsible for the energy removal.
The observational fact that most thermally emitting isolated NSs have magnetic fields larger than 1013 G (Haberl 2007), which is sometimes confirmed by spin down measurements, leads to the conclusion that a realistic cooling model must not avoid the inclusion of the effects produced by the presence of high magnetic fields. The transport processes that occur in the interior are affected by these strong magnetic fields and their effects are expected to have observable consequences, in particular for highly magnetized NSs or magnetars. Moreover, the large surface magnetic field strengths inferred from the observations probably indicate that the interior field could reach even larger values, as theoretically predicted by some models (Thompson & Duncan 1993).
The presence of a magnetic field affects the transport properties of all plasma components, especially the electrons. In general, the motion of free electrons perpendicular to the magnetic field is quantized in Landau levels, and the thermal and electrical conductivities exhibit quantum oscillations. In the limit of a strongly quantizing field, in which almost all electrons populate the lowest level, such as in the envelope of a NS, a quantum description is necessary to calculate the thermal and electrical conductivities. Earlier calculations by Canuto & Chiuderi (1970) and Itoh (1975) concluded that the electron thermal conductivity is strongly suppressed in the direction perpendicular to the magnetic field and increased along the magnetic field lines, which reduces the thermal insulation of the envelope (heat blanketing). Thus, there is an anisotropic heat transport in the NS's envelope governed by the magnetic field geometry, that produces a non-uniform surface temperature.
The anisotropy in the surface temperature of a NS appears to be confirmed by the analysis of observational data
from isolated NSs (see Zavlin 2007 and Haberl 2007,
for reviews on the current status
of theory and observations). The mismatch between the extrapolation
to low energy of fits to the X-ray spectra,
and the observed Rayleigh-Jeans tail in the optical band (optical excess flux),
cannot be addressed using a unique temperature.
Several simultaneous fits to multiwavelength spectra of
RX J1856.5-3754 (Trümper et al. 2004; Pons et al. 2002),
RBS 1223 (Schwope et al. 2007,2005), and
RX J0720.4-3125 (Pérez-Azorín et al. 2006b) are explained by a small hot emitting
area ![]() 10-20 km2, and an extended cooler component.
Another piece of evidence that strongly supports the nonuniform temperature distribution are
pulsations in the X-ray signal of some objects of amplitudes
10-20 km2, and an extended cooler component.
Another piece of evidence that strongly supports the nonuniform temperature distribution are
pulsations in the X-ray signal of some objects of amplitudes ![]() 5-30
5-30![]() ,
some of which have
irregular light curves that point towards a non-dipolar temperature distribution.
All of these facts reveal that the idealized picture of a NS with a dipolar magnetic
field and uniform surface temperature is oversimplified.
,
some of which have
irregular light curves that point towards a non-dipolar temperature distribution.
All of these facts reveal that the idealized picture of a NS with a dipolar magnetic
field and uniform surface temperature is oversimplified.
In a pioneering work, Greenstein & Hartke (1983) obtained the temperature at the surface of a NS as a function of the magnetic field inclination angle in a simplified plane-parallel approximation. This model was applied to different magnetic field configurations and the observational consequences of a non-uniform temperature distribution were analyzed in the pulsars Vela and Geminga among others (Page 1995). Potekhin & Yakovlev (2001) improved the former calculations including realistic thermal conductivities. Nevertheless, the temperature anisotropy as generated in the envelope may be insufficiently to be consistent with the observed thermal distribution and, in this case, should originate deeper inside the NS (Pérez-Azorín et al. 2006a; Geppert et al. 2004).
Crustal confined magnetic fields could be responsible for the surface thermal anisotropy. In the crust, even if a strong magnetic field is present, the electrons occupy a large number of Landau levels and the classical approximation remains valid during a long time in the thermal evolution. The magnetic field limits the movement of electrons in the direction perpendicular to the field and, since they are the main carriers of the heat transport, the thermal conductivity in this direction is highly suppressed, while remaining almost unaffected along the field lines. Temperature distributions in the crust were obtained as stationary solutions of the diffusion equation with axial symmetry (Geppert et al. 2004). The approach assumes an isothermal core and a magnetized envelope as an inner and outer boundary condition, respectively. The results show important deviations from the crust isothermal case for crustal confined magnetic fields with strengths larger than 1013 G and temperatures below 108 K. Similar conclusions were obtained considering not only poloidal but also toroidal components for the magnetic field (Geppert et al. 2006; Pérez-Azorín et al. 2006a). This models succeeded in explaining simultaneously the observed X-ray spectrum, the optical excess, the pulsed fraction, and other spectral features for some isolated NS such as RX J0720.4-3125 (Pérez-Azorín et al. 2006b) and RX J1856.5-3754 (Geppert et al. 2006).
Non-uniform surface temperature in NSs
was studied by different authors using simplified models (Shibanov & Yakovlev 1996; Potekhin & Yakovlev 2001).
Although these models can provide useful information, a detailed
investigation of heat transport in 2D must be completed to obtain more solid conclusions.
However, this is not the only effect that must be revisited to study the cooling
of NSs.
For isolated NSs, different relevant magnetic field dissipation processes were
identified (Goldreich & Reisenegger 1992). The Ohmic dissipation rate is determined by
the finite conductivity of the constituent matter. In the crust, the electrical resistivity
is mainly due to electron-phonon and electron-impurity scattering processes
(Flowers & Itoh 1976), resulting in more efficient Ohmic dissipation than in the fluid interior.
The strong temperature dependence of the resistivity leads to rapid dissipation of the
magnetic energy in the outermost low-density regions during the early evolution of a hot NS,
which becomes less relevant as the star cools down.
Joule heating in the crustal layers due to Ohmic decay was thought to affect only
the late photon cooling era in old NS (![]() 107 yr), and to be an efficient mechanism
to maintain the surface temperature as high as
107 yr), and to be an efficient mechanism
to maintain the surface temperature as high as ![]() 104-5 K for a long time
(Miralles et al. 1998). Page et al. (2000) studied the 1-D thermal evolution of NSs
combined with an evolving Stokes function that defines a purely poloidal,
dipolar magnetic field.
The Joule heating rate was evaluated averaging the currents over the azimuthal angle.
However, for strongly magnetized NS, Joule heating
can be important much earlier in the evolution.
In a recent work, Kaminker et al. (2006) placed a heat source inside the outer crust
of a young, warm, magnetar of field strength
104-5 K for a long time
(Miralles et al. 1998). Page et al. (2000) studied the 1-D thermal evolution of NSs
combined with an evolving Stokes function that defines a purely poloidal,
dipolar magnetic field.
The Joule heating rate was evaluated averaging the currents over the azimuthal angle.
However, for strongly magnetized NS, Joule heating
can be important much earlier in the evolution.
In a recent work, Kaminker et al. (2006) placed a heat source inside the outer crust
of a young, warm, magnetar of field strength
![]() G.
To explain observations, they
concluded that the heat source should be located at a density
G.
To explain observations, they
concluded that the heat source should be located at a density
![]()
![]() g cm-3,
and the heating rate should be
g cm-3,
and the heating rate should be ![]() 1020 erg cm-3 s-1 for at least
1020 erg cm-3 s-1 for at least
![]() yr.
Anisotropic heat transport
is neglected in these simulations, which were performed in spherical symmetry,
assuming that
it will not affect the results in the early evolution.
Nevertheless we will show that, in 2D simulations, the effect of anisotropic
heat transport is important.
yr.
Anisotropic heat transport
is neglected in these simulations, which were performed in spherical symmetry,
assuming that
it will not affect the results in the early evolution.
Nevertheless we will show that, in 2D simulations, the effect of anisotropic
heat transport is important.
In addition to purely Ohmic dissipation, strongly magnetized NSs can also experience a
Hall drift with a drift velocity proportional to the magnetic field strength.
Although the Hall drift conserves the magnetic energy
and it is not a dissipative mechanism by itself, it can enhance the Ohmic decay by compressing
the field into small scales, or by displacing currents to regions with higher resistivity,
where Ohmic dissipation is more efficient.
Recently, the first 2D-long term simulations of the magnetic field evolution
in the crust studied the interplay of Ohmic dissipation and the Hall drift effect
(Pons & Geppert 2007).
It was shown that, for magnetar field strength, the characteristic timescale during which
Hall drift influences Ohmic dissipation is of about 104 yr. All of these studies
imply
that both field decay and Joule heating play a role in
the cooling of neutron stars born with field strengths ![]() 1013 G.
1013 G.
We will show that, during the neutrino cooling era and the early stages of the photon cooling era,
the thermal evolution is coupled to the magnetic field decay, since both cooling and magnetic
field diffusion proceed on a similar timescale (![]() 106 yr).
The energy released by magnetic field decay in the crust
could be an important heat source that modifies or even controls the thermal evolution of a NS.
Observational evidence of this fact is shown in Pons et al. (2007). They found a
strong correlation between the inferred
magnetic field and the surface temperature for a wide range of magnetic fields:
from magnetars (
106 yr).
The energy released by magnetic field decay in the crust
could be an important heat source that modifies or even controls the thermal evolution of a NS.
Observational evidence of this fact is shown in Pons et al. (2007). They found a
strong correlation between the inferred
magnetic field and the surface temperature for a wide range of magnetic fields:
from magnetars (![]() 1014 G), through radio-quiet isolated neutron stars
(
1014 G), through radio-quiet isolated neutron stars
(![]() 1013 G)
down to some ordinary pulsars (
1013 G)
down to some ordinary pulsars (![]() 1013 G). The main conclusion is that,
rather independently from the stellar structure and the matter composition,
the correlation can be explained by the decay of currents
on a timescale of
1013 G). The main conclusion is that,
rather independently from the stellar structure and the matter composition,
the correlation can be explained by the decay of currents
on a timescale of ![]() 106 yr.
106 yr.
The aim of the present work is to study in a more consistent way the cooling of a realistic NS under the effects of large magnetic fields, including the effects of an anisotropic temperature distribution and Joule heating in 2D simulations. As a first step towards a fully coupled magneto-thermal evolution, a phenomenological law for the magnetic field decay is considered.
This article is structured as follows. In Sect. 2 we discuss the equations governing the magnetic field structure and evolution, while Sect. 3 is devoted to the thermal evolution equations. Section 4 presents the microphysics inputs. Sections 5 and 6 contain our results for weakly and strongly magnetized NSs, respectively. In Sect. 7, we focus on the effects of field decay and Joule heating on the cooling history of a NS. Finally, in Sect. 8 we present the main conclusions and perspectives of the present work.
While the large-scale external structure of the magnetic field of NSs is usually represented by the vacuum solution of an external dipole, or sometimes a more complex magnetosphere, the structure of the magnetic field in the interior of NSs is poorly known. Results from MHD simulations show that stable configurations require the coexistence of both poloidal and toroidal components, approximately of the same strength (Braithwaite & Spruit 2004), although predominantly poloidal configurations may be stabilized by rapid rotation (Geppert & Rheinhardt 2006). In general, a realistic NS magnetic field model should contain both components, and their location and relative strength should vary. Moreover, two-dimensional simulations (Pons & Geppert 2007) showed that, while the initial magnetic field configuration determines the early evolution of the field (t<104 yr), at later stages a more stable configuration, consisting of a dipolar poloidal component and a higher order toroidal component, is preferred.
We consider the Newtonian approximation of a NS magnetic field because
general relativistic corrections are not important in our study.
In axial symmetry, the magnetic field
can be decomposed into poloidal and toroidal components (Raedler 2000)
| (1) |
| (2) | |||
| (3) |
Expanding the angular part of the scalar functions in Legendre polynomials,
we can write
From the above general form of the magnetic field components, different interesting cases can easily be recovered. We describe three possible configurations that we explored in this work.
One of the particular models we consider here are the force-free fields.
They satisfy:
If the magnetic field extends to the center of the NS, only the regular solutions at x=0
(jl) must be considered, i.e., we must set b=0, which directly
determines ![]() .
Due to the superconducting nature of the fluid core, the magnetic field
may be expelled and confined to the crustal region
(Jones 1987; Konenkov & Geppert 2001).
.
Due to the superconducting nature of the fluid core, the magnetic field
may be expelled and confined to the crustal region
(Jones 1987; Konenkov & Geppert 2001).
This is of course a simplification, since
in a type II superconductor the magnetic field would be organized in flux tubes with complex
geometries, but it suffices for our purposes to establish qualitative differences between
core- and crustal-fields.
In the case of magnetic fields confined to the crustal region, from the core
radius (
![]() )
to
)
to
![]() ,
one must adjust
,
one must adjust ![]() to have a vanishing radial component in the crust-core interface.
This can be done by solving
to have a vanishing radial component in the crust-core interface.
This can be done by solving
This force-free solution can easily be extended to higher order multipoles, e.g. quadrupole, by replacing the angular dependence by the corresponding Legendre polynomial and using the corresponding spherical Bessel functions of the same index l. From the above general expression of force-free fields, some of the cases usually considered in the literature can be recovered.
Table 1:
Central density
![]() ,
mass M, radius
,
mass M, radius
![]() ,
crust thickness
,
crust thickness
![]() ,
and
,
and ![]() parameter for the two cases used
in this work: low mass (LM) and
high mass (HM).
parameter for the two cases used
in this work: low mass (LM) and
high mass (HM).
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{8786fig1.ps}\end{figure}](/articles/aa/full/2008/28/aa8786-07/Timg88.gif) |
Figure 1:
Normalized magnetic field components for the force free case in the crust:
|
| Open with DEXTER | |
We consider another two
models with crustal-confined toroidal fields that obey
| (11) | |||
| (12) |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{8786fig2.ps}\end{figure}](/articles/aa/full/2008/28/aa8786-07/Timg93.gif) |
Figure 2:
Normalized toroidal field components
|
| Open with DEXTER | |
If we assume that the magnetic field is confined to the crust, and maintained by
purely toroidal currents, we can simply set
![]() and, from
Eq. (5), we have
and, from
Eq. (5), we have
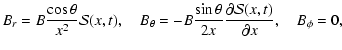 |
(13) |
The extension of the vacuum solution towards
the interior can be shown to correspond to the limit
![]() of the
non-regular function n1, explicitly,
of the
non-regular function n1, explicitly,
| (14) |
The induction equation that describes the evolution of the magnetic field
in the crust is
The first term in the bracket is purely diffusive (Ohmic) and the
second corresponds to the Hall term.
Taking the scalar product of ![]() by Eq. (15), and integrating over
the volume, it can be seen that the Hall term does not contribute to the dissipation
of energy, but it redistributes the magnetic energy from one place to another.
A force-free field satisfying
by Eq. (15), and integrating over
the volume, it can be seen that the Hall term does not contribute to the dissipation
of energy, but it redistributes the magnetic energy from one place to another.
A force-free field satisfying
![]() is not
subject to the Hall term and, if
is not
subject to the Hall term and, if ![]() is constant throughout the crust volume,
the induction equation is reduced to
is constant throughout the crust volume,
the induction equation is reduced to
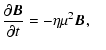 |
(16) |
In a realistic case the situation is more complex, since the non-linear evolution of the Hall term must be taken into account and the conductivity and electron density profiles are not constant. Even if we start from a force-free magnetic field, the effect of a resistivity gradient leads to a fast modification of its geometry, and the Hall term becomes immediately important.
For simplicity, and with the purpose of investigating qualitatively the effects
of magnetic field decay, we include phenomenologically a first stage with rapid
(non-exponential) decay, and a late stage with purely Ohmic dissipation
(exponential). We assume that the geometry of the field is fixed
and the temporal dependence is included only in the normalization
value B according to
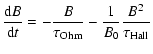 |
(18) |
If the field is anchored into the superconducting core, the results will be different. It is not the purpose of this paper to discuss such a possibility, which deserves a separate analysis, but to investigate the possible effects of crustal fields that enhance the surface temperature anisotropy and are subject to Ohmic dissipation and, consequently, Joule heating.
Assuming that deformations with respect to the spherically-symmetric case due
to rotation, magnetic field, and temperature distribution do not affect
the metric in the interior of a NS, we use the standard form (Misner et al. 1973)
| (24) |
The total conductivity tensor,
![]() ,
must include the contributions
of all relevant carriers, which are of interest in the solid crust: electrons, neutrons, protons and
phonons
,
must include the contributions
of all relevant carriers, which are of interest in the solid crust: electrons, neutrons, protons and
phonons
| (25) |
For magnetized NS, the electron thermal conductivity tensor becomes anisotropic:
in the direction perpendicular to the
magnetic field, its strength is strongly diminished, which causes a suppression of the heat flow
orthogonal to the magnetic field lines.
The ratio of conductivities along and orthogonal to the magnetic field can be defined in terms of
the magnetization parameter,
![]() ,
as
,
as
In spherical coordinates, and choosing the polar axis
to coincide with the axis of symmetry of the magnetic field,
the electron contribution can be written as follows
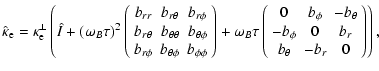 |
For numerical reasons, the thermal evolution equation is difficult to solve in
the thin layer which consist of the envelope, of a few meters depth, and the atmosphere, of a few centimeters, in which radiative equilibrium is established and the observed spectrum
is generated. Since this outer layer has a small scale and its thermal relaxation time
is much shorter than the overall evolutionary time, the usual approach is to use
results of stationary, plane-parallel, envelope models to obtain a phenomenological fit
that relates the temperature at the bottom of the envelope ![]() ,
with the surface
temperature
,
with the surface
temperature ![]() .
This ``
.
This ``
![]() relationship'' can be used to implement boundary
conditions, because the surface flux can then be calculated for a given temperature at the base of the
envelope, which corresponds to the outer point of the numerical grid in our cooling simulations.
relationship'' can be used to implement boundary
conditions, because the surface flux can then be calculated for a given temperature at the base of the
envelope, which corresponds to the outer point of the numerical grid in our cooling simulations.
Models assuming a non-magnetized envelope made of iron and iron-like nuclei
show that the surface temperature is related to ![]() as follows (Gudmundsson et al. 1983)
as follows (Gudmundsson et al. 1983)
![\begin{displaymath}T_{b,8}
=1.288
\left[ \frac{T_{s,6}^4}{g_{14}}
\right]^{~0.455}
\end{displaymath}](/articles/aa/full/2008/28/aa8786-07/img141.gif) |
(29) |
Since the magnetic field increases the heat permeability of the envelope in
regions where the magnetic field lines are radial but strongly suppresses it where
the magnetic field lines are almost
tangential (Potekhin & Yakovlev 2001), this implies a large anisotropic distribution
of ![]() ,
which depends on the magnetic field geometry.
In iron magnetized envelopes,
the surface temperature depends on the angle
,
which depends on the magnetic field geometry.
In iron magnetized envelopes,
the surface temperature depends on the angle ![]() that the magnetic field forms
with respect to the normal to the NS surface by means of a function
that the magnetic field forms
with respect to the normal to the NS surface by means of a function
![]() :
:
![\begin{displaymath}T_{\rm s}^{(0)} \approx 10^6 ~
g_{14}^{1/4}\left[(7\zeta)^{2.25}+(\zeta/3)^{1.25}\right]^{1/4}~ {\rm K},
\end{displaymath}](/articles/aa/full/2008/28/aa8786-07/img147.gif) |
(31) |
Strongly magnetized envelopes were revisited by Potekhin et al. (2007), who reconsidered
neutrino emission processes that are activated by strong fields, that is neutrino synchrotron.
These processes
were found to lower the surface temperature at a fixed ![]() .
To take this effect into account,
we introduce a maximum surface temperature
.
To take this effect into account,
we introduce a maximum surface temperature
![]() that can be reached for a given
that can be reached for a given ![]() ,
which we parameterize as a function of B to reproduce their results.
,
which we parameterize as a function of B to reproduce their results.
In this work, we assume an iron composition for the envelope and focus on the magnetic corrections to the transport due to the presence of a large field. Nevertheless, if light elements were present, which is very unlikely because the large magnetic field suppresses accretion, they strongly reduce the blanketing effect and the relations used here should be revised. Another possibility is that the gaseous atmosphere and the outer envelope condensates to a solid state due to the cohesive interaction between ions caused by the magnetic field. This condensed surface has different emission properties and, consequently, the boundary condition must be recalculated, as for example in Pérez-Azorín et al. (2006a). This scenario will be studied in future work.
To build the background NS model, we used a
Skyrme-type equation of state (EoS), at zero temperature to
describe both the NS crust and the liquid core, based on
the effective nuclear interaction SLy (Douchin & Haensel 2001).
The low density EoS, below the neutron drip point, employed is
that of Baym et al. (1971).
Throughout this work we use two models:
a low mass neutron star (LM) and a high mass (HM) NS,
which have the properties listed in Table 1.
For the chosen EoS, the crust-core interface is at
![]() ,
where
,
where
![]() g cm-3 is the nuclear saturation density,
and for both models the crust thickness is approximately 1 km,
which defines a characteristic length scale for the confinement of the crustal magnetic field.
g cm-3 is the nuclear saturation density,
and for both models the crust thickness is approximately 1 km,
which defines a characteristic length scale for the confinement of the crustal magnetic field.
In Fig. 3, the number of particles per baryon (
![]() )
and the fraction of nucleons
inside heavy nuclei (
)
and the fraction of nucleons
inside heavy nuclei (![]() )
are shown as a function of the density.
In the upper horizontal axis, the
scale shows the value of the radial coordinate that limits each region:
the outer and inner crust, and the outer and inner core,
for the LM and HM NS models.
We do not include muons in our equation of state.
)
are shown as a function of the density.
In the upper horizontal axis, the
scale shows the value of the radial coordinate that limits each region:
the outer and inner crust, and the outer and inner core,
for the LM and HM NS models.
We do not include muons in our equation of state.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.6cm,clip]{8786fig3.ps}\end{figure}](/articles/aa/full/2008/28/aa8786-07/Timg156.gif) |
Figure 3:
NS composition for the EoS employed. Number of particles per baryon as a function of the density: |
| Open with DEXTER | |
Pairing in nuclear matter can play an important role
in NS cooling, without affecting significantly the EoS, but strongly modifying
neutrino emissivities and specific heat.
In fact, for the paired component, these are suppressed by exponential Boltzmann
factors.
If superfluidity (SF) occurs inside NSs, i.e. when T is below a critical temperature
(![]() ),
the inclusion of these suppression factors will have important
consequences on the thermal evolution as we see in the following subsections.
We consider the pairing of neutrons in the crust in the n
),
the inclusion of these suppression factors will have important
consequences on the thermal evolution as we see in the following subsections.
We consider the pairing of neutrons in the crust in the n ![]() state,
protons in the core in the p
state,
protons in the core in the p ![]() state, and the n
state, and the n ![]() state, for neutrons in
the core.
Following Kaminker et al. (2001) and Andersson et al. (2005),
we use a phenomenological formula for the momentum dependence of the energy gap at zero
temperature
state, for neutrons in
the core.
Following Kaminker et al. (2001) and Andersson et al. (2005),
we use a phenomenological formula for the momentum dependence of the energy gap at zero
temperature
Table 2: Parameterization and references of the energy gaps for superfluid states.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{8786fig4.ps}\end{figure}](/articles/aa/full/2008/28/aa8786-07/Timg162.gif) |
Figure 4:
Energy gaps for superfluidity as a function of the density.
Lines denote: case a (thick solid), case b (short dashed),
and case c (long dashed) for n |
| Open with DEXTER | |
For the n ![]() pairing, the bare interaction predicts a maximum gap
pairing, the bare interaction predicts a maximum gap
![]() MeV (Schulze et al. 1998),
but the polarization effects reduce it by a factor 2-3, giving
MeV (Schulze et al. 1998),
but the polarization effects reduce it by a factor 2-3, giving
![]() MeV at
MeV at
![]() fm-1.
This is the case for
the approximation a, which in our NS models peaks at
fm-1.
This is the case for
the approximation a, which in our NS models peaks at
![]() g cm-3
in the inner crust (Fig. 4).
Although model calculations have found some agreement
about the value of the maximum energy gaps,
its precise location is uncertain and may vary in
the different approaches, as shown in cases b and c.
The corresponding critical temperatures for the s-wave
can be calculated approximately to be
g cm-3
in the inner crust (Fig. 4).
Although model calculations have found some agreement
about the value of the maximum energy gaps,
its precise location is uncertain and may vary in
the different approaches, as shown in cases b and c.
The corresponding critical temperatures for the s-wave
can be calculated approximately to be
![]() ,
which implies a maximum for neutrons of
,
which implies a maximum for neutrons of
![]() K,
for the case a. As shown later, this high temperature implies
that neutrons become superfluid in the crust during the
early cooling of a NS and the most important consequence is that the crustal
specific heat is suppressed.
K,
for the case a. As shown later, this high temperature implies
that neutrons become superfluid in the crust during the
early cooling of a NS and the most important consequence is that the crustal
specific heat is suppressed.
The calculations for the p ![]() pairing take into account the presence
of the neutron gas and depend also on the proton fraction through
the symmetry energy of the EoS. For different approaches, such as case e and f,
pairing take into account the presence
of the neutron gas and depend also on the proton fraction through
the symmetry energy of the EoS. For different approaches, such as case e and f,
![]() is located at about
is located at about
![]() fm-1,
which is much smaller than for neutrons, due to the smaller proton effective mass.
Nevertheless, due to the proton number density, the peak is shifted to
fm-1,
which is much smaller than for neutrons, due to the smaller proton effective mass.
Nevertheless, due to the proton number density, the peak is shifted to
![]() g cm-3
in the outer core of our NSs, as shown in Fig. 4. Most models agree that the proton
energy gap should vanish at
kF,p> 1.5 fm-1, i.e. at high densities inside the star
g cm-3
in the outer core of our NSs, as shown in Fig. 4. Most models agree that the proton
energy gap should vanish at
kF,p> 1.5 fm-1, i.e. at high densities inside the star
![]() g cm-3.
For the cases considered here,
g cm-3.
For the cases considered here,
![]() K, indicating
that also proton superfluidity
will be present from the very beginning of the NS thermal evolution.
Due to the charge of the protons,
the superfluid is also in a superconducting (SC) state.
K, indicating
that also proton superfluidity
will be present from the very beginning of the NS thermal evolution.
Due to the charge of the protons,
the superfluid is also in a superconducting (SC) state.
The situation for the pairing of neutrons in the core is more complicated,
because the ![]() state has coupled anisotropic gap equations.
Some calculations show that the energy gap should be reduced by a factor
of 2-3, as in the proton case, due to the lower neutron effective mass in very dense matter.
But relativistic effects become important and there is no conclusive approach to the problem.
Thus, in our calculations we considered three different cases that reflect this uncertainty:
h, k and m with
state has coupled anisotropic gap equations.
Some calculations show that the energy gap should be reduced by a factor
of 2-3, as in the proton case, due to the lower neutron effective mass in very dense matter.
But relativistic effects become important and there is no conclusive approach to the problem.
Thus, in our calculations we considered three different cases that reflect this uncertainty:
h, k and m with
![]() MeV, respectively (Table 2).
The location of the maximum varies as well, at
MeV, respectively (Table 2).
The location of the maximum varies as well, at
![]() -2 fm-1, i.e.
at
-2 fm-1, i.e.
at
![]() -
-
![]() g cm-3,
as plotted in Fig. 4, in which case m is omitted because it is not visible in this scale.
We note that for the p-wave we take that
g cm-3,
as plotted in Fig. 4, in which case m is omitted because it is not visible in this scale.
We note that for the p-wave we take that
![]() (Bailin & Love 1984),
which corresponds to a a wide range of
(Bailin & Love 1984),
which corresponds to a a wide range of
![]() -
-
![]() K for the chosen models.
K for the chosen models.
The temperature dependence of the energy gap that we use is the approximate
functional form given by Levenfish & Yakovlev (1994):
From these considerations, it is clear that a NS at the beginning of its cooling history should contain superfluid neutrons in the crust and superconducting protons in the core, while the occurrence of neutron pairing in the core is rather model dependent.
In NS cooling simulations, the thermal conductivity should be calculated over a
region covering a large range of densities,
from the core (![]() 1015 g cm-3) to the outer crust
(
1015 g cm-3) to the outer crust
(![]() 109 g cm-3).
109 g cm-3).
Schematically, the thermal conductivity tensor can be written for each carrier
in terms of the effective relaxation time tensor,
![]() (Urpin & Yakovlev 1980; Flowers & Itoh 1976; Itoh et al. 1984),
as follows,
(Urpin & Yakovlev 1980; Flowers & Itoh 1976; Itoh et al. 1984),
as follows,
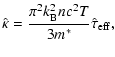 |
(34) |
In the inner liquid core, we include contributions from electrons, neutrons and protons (Baiko et al. 2001; Gnedin & Yakovlev 1995), without taking account of the effects of the magnetic field because of proton superconductivity: the field is either expelled from the core or confined into flux tubes that occupy a small fraction of its volume. We note that, if the magnetic field does not affect transport properties, a large thermal conductivity of matter is produced soon after birth in an isothermal core (Fig. 5), which implies that the precise value of the thermal conductivity is not important.
In the solid crust, only electron and phonon transport are considered.
While phonon conductivity is negligible in non-magnetic neutron stars,
this situation changes when the magnetization parameter becomes large.
Since electron transport is drastically suppressed in the direction transverse
to the magnetic field,
the phonon contribution may become dominant at low density as shown in Fig. 5.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{8786fig5.ps}\end{figure}](/articles/aa/full/2008/28/aa8786-07/Timg190.gif) |
Figure 5:
Thermal conductivity contributions as a function of the density for different fixed temperatures.
|
| Open with DEXTER | |
In our calculations, we use the non-quantizing electron conductivities from the public code
of Potekhin (1999)![]() .
The three electron scattering processes that play a role in our scenario are scattering
off ions, electron-phonon scattering, and scattering off impurities.
Semi-analytic expressions and fitting formulae for the relaxation time and thermal
conductivity along the magnetic field for all three processes, were derived
by Potekhin & Yakovlev (1996).
.
The three electron scattering processes that play a role in our scenario are scattering
off ions, electron-phonon scattering, and scattering off impurities.
Semi-analytic expressions and fitting formulae for the relaxation time and thermal
conductivity along the magnetic field for all three processes, were derived
by Potekhin & Yakovlev (1996).
At high temperatures, the phonon conductivity of the lattice is determined mainly by
Umklapp processes, and can be approximated by the expression
| (35) |
Chugunov & Haensel (2007) revised the ion
thermal conductivity in neutron star envelopes. They included the contribution of
electron-phonon scattering and improved the calculations of phonon-phonon scattering.
Our estimates for
![]() are larger than their results by a factor of a few,
depending on the density, which results in a smaller temperature anisotropy.
However their results are more applicable to the neutron star envelope,
than for the crust. The main reason is that,
at temperatures smaller than the Debye temperature,
the inclusion of the effect of impurities and defects in the crystal becomes necessary.
Given our limited knowledge of the impurity content of the inner crust, which
may affect the results, we do not include phonon-impurity interactions in our
simulations. In principle, its effect would be to reduce the phonon mean free path,
but it is unclear how to calculate accurately this contribution at low temperature.
are larger than their results by a factor of a few,
depending on the density, which results in a smaller temperature anisotropy.
However their results are more applicable to the neutron star envelope,
than for the crust. The main reason is that,
at temperatures smaller than the Debye temperature,
the inclusion of the effect of impurities and defects in the crystal becomes necessary.
Given our limited knowledge of the impurity content of the inner crust, which
may affect the results, we do not include phonon-impurity interactions in our
simulations. In principle, its effect would be to reduce the phonon mean free path,
but it is unclear how to calculate accurately this contribution at low temperature.
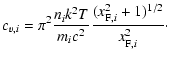 |
(36) |
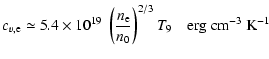 |
(37) |
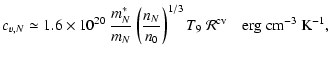 |
(38) |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{8786fig6.ps}\end{figure}](/articles/aa/full/2008/28/aa8786-07/Timg199.gif) |
Figure 6: Specific heat as a function of the enclosed volume V(r) within a radius r, and for different fixed T. We show the contribution of neutrons (long-dashed line), protons (short-dashed line), electrons (dotted-dashed line), and ions (brown solid line). Total cv is plotted using a black solid line. The dotted lines show the non-superfluid case. |
| Open with DEXTER | |
In our model we include the crustal specific heat, which has contributions from the neutron gas, the degenerate electron gas and the nuclear lattice (van Riper 1991); it is however negligible in comparison to the core contribution, due to the small volume of the crust.
During the first ![]() 105 yr, the so-called neutrino cooling era,
the evolution of a NS is governed by the
emission of neutrinos. Thereafter, photons
radiated from the surface control the evolution in the photon cooling era.
The path of a NS in a temperature-age diagram and the duration of the neutrino
cooling era is determined by the efficiency of the neutrino processes in their interior.
Typically, neutrino emissivities, at high densities, depend on
temperature to the power of a large number,
and weakly on density; a review is provided by Yakovlev et al. (2001).
In the so-called standard cooling scenario, the total emissivity is dominated by
slow processes in the core, such as modified Urca (MUrca) and nucleon-nucleon (N-N) Bremsstrahlung.
The minimal cooling model, in which pairing between nucleons
and the effects of superfluidity are both included (Page et al. 2004), is more realistic.
If fast neutrino processes, i.e. direct Urca (DUrca), occur, the evolution of a NS alters significantly,
leading to the enhanced cooling scenario.
Nevertheless, DUrca only operates above a critical proton fraction
105 yr, the so-called neutrino cooling era,
the evolution of a NS is governed by the
emission of neutrinos. Thereafter, photons
radiated from the surface control the evolution in the photon cooling era.
The path of a NS in a temperature-age diagram and the duration of the neutrino
cooling era is determined by the efficiency of the neutrino processes in their interior.
Typically, neutrino emissivities, at high densities, depend on
temperature to the power of a large number,
and weakly on density; a review is provided by Yakovlev et al. (2001).
In the so-called standard cooling scenario, the total emissivity is dominated by
slow processes in the core, such as modified Urca (MUrca) and nucleon-nucleon (N-N) Bremsstrahlung.
The minimal cooling model, in which pairing between nucleons
and the effects of superfluidity are both included (Page et al. 2004), is more realistic.
If fast neutrino processes, i.e. direct Urca (DUrca), occur, the evolution of a NS alters significantly,
leading to the enhanced cooling scenario.
Nevertheless, DUrca only operates above a critical proton fraction
![]() ,
that is only reached at high density (4-6)
,
that is only reached at high density (4-6) ![]() in the inner core of high mass NSs.
Since we assume a superfluid core with
in the inner core of high mass NSs.
Since we assume a superfluid core with ![]() paring for protons and
paring for protons and ![]() pairing for neutrons,
we account for the exponential suppression of these processes through reduction functions
pairing for neutrons,
we account for the exponential suppression of these processes through reduction functions
![]() (Yakovlev et al. 2001).
We include the Cooper Pair Breaking and Formation emissivity (CPBF),
although the effectivity of this process was questioned both,
by observational arguments (Cumming et al. 2006) and
by theoretical calculations (Leinson & Pérez 2006). In the latter work, the authors showed that
the neutron
(Yakovlev et al. 2001).
We include the Cooper Pair Breaking and Formation emissivity (CPBF),
although the effectivity of this process was questioned both,
by observational arguments (Cumming et al. 2006) and
by theoretical calculations (Leinson & Pérez 2006). In the latter work, the authors showed that
the neutron ![]() CPBF emissivity is suppressed, which is relevant in the crust,
but the proton
CPBF emissivity is suppressed, which is relevant in the crust,
but the proton ![]() and neutron
and neutron ![]() channels, which are relevant in the core, are not seriously altered.
Including or not this suppression has an effect on the
early relaxation of the crust, but has little imprint on the long term cooling evolution.
channels, which are relevant in the core, are not seriously altered.
Including or not this suppression has an effect on the
early relaxation of the crust, but has little imprint on the long term cooling evolution.
In our calculations, we consider all relevant neutrino emission processes listed in Table 3, which indicates the density and temperature dependence of the emissivity
for the different processes.
The factors that account for further corrections, due to for example effective masses and correlation effects,
can be found in the references listed in Table 3.
The table also includes the critical proton fraction
![]() that is required before some processes can operate.
In the enhanced cooling scenario,
we include the fast DUrca process. The efficiency of this fast reaction
is exponentially reduced when superfluidity is taken into account.
that is required before some processes can operate.
In the enhanced cooling scenario,
we include the fast DUrca process. The efficiency of this fast reaction
is exponentially reduced when superfluidity is taken into account.
Table 3:
Neutrino processes and their emissivities Q
in the core and in the crust.
Third column shows the onset for some processes to operate
(critical proton fraction
![]() ).
Detailed functions and precise factors can be found in the references
(last column).
).
Detailed functions and precise factors can be found in the references
(last column).
The neutrino energy losses from processes that occur inside the crust are
very important at the beginning
of thermal evolution, during the relaxation stage prior to the core-crust thermal coupling.
This stage lasts about 10-102 yr and was studied in detail by Gnedin et al. (2001).
These reactions occurs in a wide range of matter compositions,
which includes a strongly-coupled plasma of nuclei and electrons in the outer layers, a
lattice of neutron-rich nuclei, up to the crust-core interface with abundant free neutrons.
Thus, the resulting emissivities are complicated functions of the temperature and matter composition.
Considering that the free neutrons in the crust are very likely to pair in the ![]() state,
we account for, in addition, the superfluid corrections and the CPFB process in the crust.
state,
we account for, in addition, the superfluid corrections and the CPFB process in the crust.
Finally, we regard relativistic electrons that can emit neutrino pairs under the presence of a strong magnetic field, which is analogous to the synchrotron emission of photons, because our primary goal is to describe the cooling of magnetized NSs. This neutrino synchrotron emissivity is proportional to the field strength (Bezchastnov et al. 1997) and becomes important for B>1014 G.
The emissivities of the most relevant core and crust neutrino processes
for the minimal cooling scenario
are plotted in Fig. 7,
for three fixed temperatures of
![]() K,
K,
![]() K, and
K, and
![]() K.
K.
At
![]() K, in the early evolution, the plasmon decay dominates
the neutrino emission in the crust and the MUrca is the strongest energy
loss mechanism in the core, as seen in the upper panl of Fig. 7.
At this temperature, neutron superfluidity already exists in the crust, and
CPBF becomes important near the crust-core interface.
On the other hand, protons and neutrons in the core have not yet
condensed into a paired state in a significant volume in the core.
Later, at intermediate temperatures of
K, in the early evolution, the plasmon decay dominates
the neutrino emission in the crust and the MUrca is the strongest energy
loss mechanism in the core, as seen in the upper panl of Fig. 7.
At this temperature, neutron superfluidity already exists in the crust, and
CPBF becomes important near the crust-core interface.
On the other hand, protons and neutrons in the core have not yet
condensed into a paired state in a significant volume in the core.
Later, at intermediate temperatures of
![]() K (middle panel), plasmon decay is dominant
only in the outer crust, while electron-nuclei Bremsstrahlung becomes more efficient in
a large part of the crust volume.
In addition, there is an enhancement of the emissivities due to the CPBF, at densities between
1013-1014 g cm-3.
In the core,
K (middle panel), plasmon decay is dominant
only in the outer crust, while electron-nuclei Bremsstrahlung becomes more efficient in
a large part of the crust volume.
In addition, there is an enhancement of the emissivities due to the CPBF, at densities between
1013-1014 g cm-3.
In the core, ![]() proton superconductivity and
proton superconductivity and ![]() neutron superfluidity have a
twofold effect: suppression
of the otherwise dominant processes (MUrca and N-N Bremsstrahlung),
and enhanced emissivity from CPBF.
At later stages, when the temperature has fallen to T=108 K,
neutrino synchrotron
overcomes the other emissivities if a magnetic field of the order of
neutron superfluidity have a
twofold effect: suppression
of the otherwise dominant processes (MUrca and N-N Bremsstrahlung),
and enhanced emissivity from CPBF.
At later stages, when the temperature has fallen to T=108 K,
neutrino synchrotron
overcomes the other emissivities if a magnetic field of the order of
![]() G is present.
A narrow density window is still controlled by CPBF of neutrons in the crust.
G is present.
A narrow density window is still controlled by CPBF of neutrons in the crust.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{8786fig7.ps}\end{figure}](/articles/aa/full/2008/28/aa8786-07/Timg241.gif) |
Figure 7:
Neutrino processes in the crust and in the core for the
minimal cooling for different fixed T. Lines denote: MUrca (thick solid),
n-n Bremsstrahlung (long dashed), n-p Bremsstrahlung (short dashed dotted),
p-p Bremsstrahlung (double dashed dotted), e-A Bremsstrahlung (long dashed dotted),
Plasmon decay (solid with cross symbols), CPBF (thin solid) and
|
| Open with DEXTER | |
Our discussion in based on two baseline models (see Table 1)
that correspond to the minimal and
enhanced cooling scenarios. The first case
corresponds to low mass NSs
in which the central density is below
the critical density for the onset of the DUrca process, which is
![]() g cm-3 for our EoS.
The second case
describes the thermal evolution of a high mass star for
which the DUrca process operates in a finite volume in the core.
For both models, we solved the thermal diffusion Eq. (22)
using several magnetic field configurations described in Sect. 2 and the microphysics inputs presented in Sect. 4 including the effects of
superfluidity. We use a two-dimensional numerical grid containing 350 radial
and 60 angular points.
g cm-3 for our EoS.
The second case
describes the thermal evolution of a high mass star for
which the DUrca process operates in a finite volume in the core.
For both models, we solved the thermal diffusion Eq. (22)
using several magnetic field configurations described in Sect. 2 and the microphysics inputs presented in Sect. 4 including the effects of
superfluidity. We use a two-dimensional numerical grid containing 350 radial
and 60 angular points.
We address the timescale for both the crust formation and the growth of the core region where protons are in a superconducting state, because the temperature of a NS falls below 1010 K a few minutes after birth. The comparison of these two timescales is relevant to understand whether or not there is enough time to expel magnetic flux from the core before the crust is formed and the magnetic field is frozen into the solid lattice. If this is the case, after the crust is formed, the problem can be treated by assuming that the magnetic field evolves independently in the crust, without penetrating the core, while the thermal evolution of the core and the crust become coupled. In contrast, if a substantial part of the magnetic flux remains within the core, it is probably organized into superconducting flux tubes that have a complex interaction with the normal phase. This would be a much more difficult problem to solve and the evolution would depend on the interaction between the flux tubes and vortices and how they become attached to the lattice. The study of such a scenario is beyond the scope of this paper, and, for simplicity, we assume that either the magnetic field has been completely expelled from the core or that it penetrates into the core without considering superconducting effects.
We followed two indicators of the growth of the crust and the superconducting core:
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{8786fig8.ps}\end{figure}](/articles/aa/full/2008/28/aa8786-07/Timg255.gif) |
Figure 8:
Left panel: growth of the proton superconducting region in the core.
|
| Open with DEXTER | |
To evaluate whether all microphysics inputs are implemented properly in our
two-dimensional code, we revisit cooling curves for weakly magnetized neutron stars,
i.e. with field strengths
![]() G. We compare our results
considering that, for weak fields, the temperature profiles are almost spherically symmetric,
with previous one-dimensional calculations performed by other authors.
The most important deviations between models
arise, as expected, from the underlying microphysics. Major differences depend
on the occurrence of superfluidity and whether slow or fast neutrino emission processes
are taking place. We summarize these effects below.
G. We compare our results
considering that, for weak fields, the temperature profiles are almost spherically symmetric,
with previous one-dimensional calculations performed by other authors.
The most important deviations between models
arise, as expected, from the underlying microphysics. Major differences depend
on the occurrence of superfluidity and whether slow or fast neutrino emission processes
are taking place. We summarize these effects below.
We plot the surface temperature ![]() for the minimal and enhanced cooling
scenarios in Fig. 9.
In both cases, we explored different superfluidity models. The major uncertainties
come from the n
for the minimal and enhanced cooling
scenarios in Fig. 9.
In both cases, we explored different superfluidity models. The major uncertainties
come from the n ![]() pairing gap in the core; furthermore, this gap is expected to have
the strongest impact on the luminosities (Page et al. 2004).
Hereafter, we fix two models of the
n
pairing gap in the core; furthermore, this gap is expected to have
the strongest impact on the luminosities (Page et al. 2004).
Hereafter, we fix two models of the
n ![]() superfluidity in the crust and the p
superfluidity in the crust and the p ![]() in the core to the cases a and e, respectively.
We checked that replacing them with the other options listed in
Table 2, produces slight deviations in the cooling curves.
We only vary the gap model of the n
in the core to the cases a and e, respectively.
We checked that replacing them with the other options listed in
Table 2, produces slight deviations in the cooling curves.
We only vary the gap model of the n ![]() state between
three different limit cases: no pairing (no SF),
case h for high
state between
three different limit cases: no pairing (no SF),
case h for high
![]() (
(![]()
![]() K), and
case m for low
K), and
case m for low
![]() (
(![]()
![]() K).
K).
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{8786fig9.ps}\end{figure}](/articles/aa/full/2008/28/aa8786-07/Timg258.gif) |
Figure 9:
Cooling curves of weakly magnetized NS with
|
| Open with DEXTER | |
In the early stages of evolution (up to ![]() 102 yr) during the initial
thermal relaxation of the crust, the main effect of superfluidity
is the suppression of the specific heat of
free neutrons in the crust (see Fig. 6), which leads to a faster temperature
decrease compared to the
nonsuperfluid case (dotted lines). The following epoch (up to
102 yr) during the initial
thermal relaxation of the crust, the main effect of superfluidity
is the suppression of the specific heat of
free neutrons in the crust (see Fig. 6), which leads to a faster temperature
decrease compared to the
nonsuperfluid case (dotted lines). The following epoch (up to
![]() 104-105 yr)
is controlled by neutrino emission from the core. The MUrca and Bremsstrahlung processes
(or the DUrca process for model B)
are exponentially suppressed, in addition to the
heat capacities of neutrons and protons in the core.
Nevertheless, core CPFB is important and acts in the opposite direction, increasing
the emissivities but inside a narrow density window. The overall effect is a faster cooling
of the LM star.
The opposite effect is found for the HM star,
where a high
104-105 yr)
is controlled by neutrino emission from the core. The MUrca and Bremsstrahlung processes
(or the DUrca process for model B)
are exponentially suppressed, in addition to the
heat capacities of neutrons and protons in the core.
Nevertheless, core CPFB is important and acts in the opposite direction, increasing
the emissivities but inside a narrow density window. The overall effect is a faster cooling
of the LM star.
The opposite effect is found for the HM star,
where a high
![]() pairing of the n
pairing of the n ![]() ,
which covers all the core density region (case h), produces a significantly
higher
,
which covers all the core density region (case h), produces a significantly
higher ![]() with respect to the non-superfluid case. If the pairing has a
low
with respect to the non-superfluid case. If the pairing has a
low
![]() (case m)
or does not occupy the whole core volume, then the DUrca process is as efficient as in the nonsuperfluid case, leading to a very rapid cooling.
In the later cooling phase (from 105-106 yr),
when photon luminosity gradually overtakes the
neutrino luminosity, the most important effect of superfluidity is the reduction
of the core specific heat that makes the star cool faster.
(case m)
or does not occupy the whole core volume, then the DUrca process is as efficient as in the nonsuperfluid case, leading to a very rapid cooling.
In the later cooling phase (from 105-106 yr),
when photon luminosity gradually overtakes the
neutrino luminosity, the most important effect of superfluidity is the reduction
of the core specific heat that makes the star cool faster.
In brief, we confirm all previous results for the cooling of non-magnetized neutron stars and do not find any qualitative difference from earlier works (Page et al. 2006; Yakovlev & Pethick 2004).
We study now magnetized NSs with
![]() G.
After analyzing the effect of superfluidity on the cooling curves, we restrict further
study of magnetized neutron stars to two different limiting scenarios with fixed
superfluidity models, which can be
summarized as follows:
G.
After analyzing the effect of superfluidity on the cooling curves, we restrict further
study of magnetized neutron stars to two different limiting scenarios with fixed
superfluidity models, which can be
summarized as follows:
In Fig. 10, we plot temperature profiles across the star, for the
Model A, as a function of the density, and for different evolution times.
The magnetic field is confined to the crust (PC; Br and
![]() as in
Fig. 1) and
as in
Fig. 1) and
![]() G.
G.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{8786fig10.ps}\end{figure}](/articles/aa/full/2008/28/aa8786-07/Timg261.gif) |
Figure 10:
Evolution of the temperature as a function of the density
of a LM magnetized NS with
|
| Open with DEXTER | |
In Fig. 11, we show the magnetically induced anisotropic temperature distribution
for the same model.
The upper panels are the usual cooling curves (temperature vs. time), which
display the evolution of ![]() at the magnetic pole and the equator,
for two different field configurations: core dipolar (CD) and poloidal confined
to the crust (PC). For the latter configuration we show results for two field strengths.
The cooling curves do not show large deviations between models, although
the difference with respect to the non-magnetized case becomes larger with
increasing magnetic field strength.
The lower panel
shows the corresponding angular distribution of
at the magnetic pole and the equator,
for two different field configurations: core dipolar (CD) and poloidal confined
to the crust (PC). For the latter configuration we show results for two field strengths.
The cooling curves do not show large deviations between models, although
the difference with respect to the non-magnetized case becomes larger with
increasing magnetic field strength.
The lower panel
shows the corresponding angular distribution of ![]() ,
normalized to its
value at the pole, for three different ages.
,
normalized to its
value at the pole, for three different ages.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{8786fig11a.eps}\\
\vspace{1.05cm}
\includegraphics[width=8.8cm,clip]{8786fig11b.eps}\end{figure}](/articles/aa/full/2008/28/aa8786-07/Timg262.gif) |
Figure 11:
Cooling of strongly magnetized NSs for the Model A.
Upper panel: |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{8786fig12a.eps}\\
\vspace{1.05cm}
\includegraphics[width=8.8cm,clip]{8786fig12b.eps}\end{figure}](/articles/aa/full/2008/28/aa8786-07/Timg263.gif) |
Figure 12: Same as Fig. 11 but for the Model B. |
| Open with DEXTER | |
We reiterate that ![]() is the temperature at the bottom of the envelope, corresponding to
our outer point of integration at
is the temperature at the bottom of the envelope, corresponding to
our outer point of integration at
![]() g cm-3,
and the blanketing effect of the envelope
should be taken into account before comparison with observations.
To translate the temperature at the base of the envelope to the surface
temperature
g cm-3,
and the blanketing effect of the envelope
should be taken into account before comparison with observations.
To translate the temperature at the base of the envelope to the surface
temperature ![]() ,
we assumed a magnetized envelope as described in Sect. 3.2,
taking into account the angle that the magnetic field forms with respect to the
normal to the surface.
In Fig. 13, we plot
,
we assumed a magnetized envelope as described in Sect. 3.2,
taking into account the angle that the magnetic field forms with respect to the
normal to the surface.
In Fig. 13, we plot ![]() and
and
![]() vs. age
for the same three cases as in Fig. 11.
vs. age
for the same three cases as in Fig. 11.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{8786fig13a.eps}\\
\vspace{1.05cm}
\includegraphics[width=8.8cm,clip]{8786fig13b.eps}\end{figure}](/articles/aa/full/2008/28/aa8786-07/Timg268.gif) |
Figure 13:
Cooling of strongly magnetized NSs for the Model A.
Same as Fig. 11 but for the surface temperature |
| Open with DEXTER | |
If we compare our temperature angular distribution to former results (Pérez-Azorín et al. 2006a; Geppert et al. 2004), we find that our late time profiles coincide qualitatively with the stationary solutions obtained in previous works. However, the temperature distributions at early times are quite different. The reason is that stationary solutions cannot describe properly the temperature distribution in young NSs, because a NS is evolving and changing its thermodynamical conditions faster than, or on a similar timescale, to the time needed to reach the stationary state.
Despite our lack of direct information about the magnetic field geometry inside a neutron star, there is some agreement that several independent mechanisms can create strong toroidal fields, such as differential rotation during core collapse (Wheeler et al. 2002), or proto-neutron star dynamo. Hence, it is natural to investigate the effect of toroidal components on the surface temperature distribution. In particular, the inclusion of toroidal components was used to explain the small hot emitting areas observed in some isolated NSs (Pérez-Azorín et al. 2006b; Geppert et al. 2006). These works concluded that the surface temperature is determined more by the geometry rather than by the magnetic field strength. With this motivation, we include a toroidal component in our models and study its influence on the results.
In the remainder of this section, we focus on the effect of the toroidal
component on model A, but our qualitative conclusions can be generally extended to model B.
In Fig. 14, we compare the cooling curves in the upper panel, and the
angular temperature distribution in the lower panel, for
![]() G,
for the different toroidal field configurations.
The first conclusion is that the presence of crustal confined toroidal fields
(TC1 and TC2)
does not significantly change the results obtained with purely poloidal fields
(dotted lines in Fig. 14).
We omitted model TC2 in the upper panel because it was indistinguishable
from TC1; minor differences are visible only during the first 100 years of evolution
(see lower panel).
We found that the FF configuration exhibits larger
G,
for the different toroidal field configurations.
The first conclusion is that the presence of crustal confined toroidal fields
(TC1 and TC2)
does not significantly change the results obtained with purely poloidal fields
(dotted lines in Fig. 14).
We omitted model TC2 in the upper panel because it was indistinguishable
from TC1; minor differences are visible only during the first 100 years of evolution
(see lower panel).
We found that the FF configuration exhibits larger ![]() than the other
models in the late evolution (t>105 yr) because the heat transport was
suppressed by the toroidal component extended through the envelope, and the
insulating effect was more pronounced.
than the other
models in the late evolution (t>105 yr) because the heat transport was
suppressed by the toroidal component extended through the envelope, and the
insulating effect was more pronounced.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{8786fig14a.eps}\\
\vspace{1.05cm}
\includegraphics[width=8.8cm,clip]{8786fig14b.eps}\end{figure}](/articles/aa/full/2008/28/aa8786-07/Timg269.gif) |
Figure 14:
Cooling of strongly magnetized NSs with toroidal fields.
Upper panel: |
| Open with DEXTER | |
As we can see in the lower panel of Fig. 14
for the FF case, the toroidal field maintains, during the entire evolution,
a cooler and more extended
equatorial belt, while the hot polar region is shrunk in comparison to the other models.
Defining the angular size of our polar cap by the angle at which the radial
component of B becomes larger than the tangential component, this is
![]() ,
for a purely poloidal configuration, which implies a hot
area of about
,
for a purely poloidal configuration, which implies a hot
area of about ![]()
![]() .
For a FF model, this condition is
reached when
.
For a FF model, this condition is
reached when
![]() ,
which provides a smaller angular size
of about
,
which provides a smaller angular size
of about
![]() ,
which agrees with the estimated emitting area for
some isolated neutron stars (Pérez-Azorín et al. 2006b).
The same comment made at the end of the previous subsection about the comparison
with stationary models is valid when comparing these results to stationary temperature
distributions with toroidal fields (Geppert et al. 2006; Pérez-Azorín et al. 2006a).
,
which agrees with the estimated emitting area for
some isolated neutron stars (Pérez-Azorín et al. 2006b).
The same comment made at the end of the previous subsection about the comparison
with stationary models is valid when comparing these results to stationary temperature
distributions with toroidal fields (Geppert et al. 2006; Pérez-Azorín et al. 2006a).
In the previous section, we discussed the impact of strong magnetic fields on the cooling and the temperature distribution of NSs, keeping the field strength and geometry fixed throughout the entire evolution. But the existence of crustal confined fields supported by crustal currents is inconsistent with the assumption of non-evolving fields. Currents in the crust dissipate in a relatively short timescale, which may vary depending on the interaction of electrons with the lattice in different crustal regions. In any case, this leads to dissipation of the magnetic field on timescales at least comparable, if not shorter, than the cooling timescale. This effect is important while the crust is still hot because of the large temperature dependence of the electrical resistivity. At late times, that is after a few 106 years, when the crust temperature drops below 107 K, the conductivity increases significantly, although limited by electron-impurity or phonon-impurity scattering, and the magnetic field decays on a much longer timescale.
Since we are interested mostly in the evolution of NSs while their temperature is sufficiently high for them to be visible as thermal emitters, the effect of Joule heating by magnetic field decay cannot be ignored.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{8786fig15a.eps}\\
\vspace{1.05cm}
\includegraphics[width=8.8cm,clip]{8786fig15b.eps}\end{figure}](/articles/aa/full/2008/28/aa8786-07/Timg275.gif) |
Figure 15:
Cooling of strongly magnetized NSs with Joule heating with
|
| Open with DEXTER | |
Having fixed our background NS model and field geometry, we varied the parameters
that describe the typical timescales for Ohmic dissipation and a
fast initial decay induced by the Hall drift.
In Fig. 15, we show the cooling curves for three different pairs
of values
![]() yr, represented by
solid lines, dashed lines, and dash-dotted lines, respectively.
For comparison, the dotted lines show the evolution with constant field for
the same initial field (
yr, represented by
solid lines, dashed lines, and dash-dotted lines, respectively.
For comparison, the dotted lines show the evolution with constant field for
the same initial field (
![]() G).
G).
The decay of such a large field has an enourmous effect upon the surface temperature;
due to the heat released, the temperature remains
far higher than for a non-decaying magnetic field.
The strong imprint of the field decay is evident for all pairs of parameters chosen.
We note that the temperature of the initial plateau is higher for
shorter
![]() ,
but the duration of this stage, which has almost constant temperature, is also shorter.
This is a consequence of releasing a similar amount of heat in a shorter time:
at
,
but the duration of this stage, which has almost constant temperature, is also shorter.
This is a consequence of releasing a similar amount of heat in a shorter time:
at
![]() ,
B has decayed to about half of its initial value
and three quarters of the initial magnetic energy has dissipated. By
reducing
,
B has decayed to about half of its initial value
and three quarters of the initial magnetic energy has dissipated. By
reducing
![]() we can therefore maintain higher temperatures, but for shorter times.
After
we can therefore maintain higher temperatures, but for shorter times.
After
![]() ,
there is a noticeable drop in
,
there is a noticeable drop in ![]() due to the transition
from the fast Hall decay to the slower Ohmic decay.
due to the transition
from the fast Hall decay to the slower Ohmic decay.
The insulating effect of tangential magnetic fields operates in both directions: in
the absence of additional heating sources, it decouples low latitude regions from the
hotter core resulting in lower temperatures at the base of the envelope; conversely,
if heat is released in the crust, it prevents extra heat flowing into
the inner crust or the core where it is more easily lost in the form of neutrinos.
Indeed, our simulations that include Joule heating systematically indicate the presence
of a hot equatorial belt at the crust-envelope interface.
Kaminker et al. (2006) studied the effect of a localized heat source
at different depths inside a NS. They concluded that
only a heat source very close to the stellar surface can have observational
consequences. In this work, we find evidence for a far more important effect on the surface
temperature. The main reason for this apparent discrepancy is that our cooling
models are two-dimensional and include the insulating effect of the strong
tangential field in the crust, as opposed to the one-dimensional simulations studied by Kaminker et al. (2006).
However, as discussed in the previous section, this
inverted temperature distribution at the level of the crust
is not necessarily visible in the surface
temperature distribution because it is filtered by the magnetized envelope.
An analysis of the angular temperature distribution shown in the
lower panel of Fig. 15 shows an interesting feature
related to the heat deposition: the development of a middle latitude region
hotter than the pole at relatively late stages in the evolution (
![]() yr).
For a wide range of parameters we found this hot area. It would have implications
for the light curves of rotating NSs, that will differ substantially from the light curves
obtained with a typical model consisting of a hot polar cap with a cooler equatorial region.
yr).
For a wide range of parameters we found this hot area. It would have implications
for the light curves of rotating NSs, that will differ substantially from the light curves
obtained with a typical model consisting of a hot polar cap with a cooler equatorial region.
We conclude our discourse on the important impact of magnetic field decay
in the cooling history of a neutron star by reconsidering the enhanced cooling scenario,
in which the DUrca efficiently cools the star very quickly.
In Fig. 16, we compare our results for the cooling of low and high mass NS
(Models A and B), with and without magnetic fields. Neglecting the effect of
magnetic fields, the differences between the fast and slow cooling scenarios
(short dashed and dotted lines, respectively) are clearly
evident, although they can be reduced by strong superfluidity.
We consider, however, a limiting case that experiments a rapid cooling, which has no superfluidity in the inner core, to observe the significance of the magnetic field effects on the surface temperature (thick solid and dashed lines).
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{8786fig16.ps}\end{figure}](/articles/aa/full/2008/28/aa8786-07/Timg280.gif) |
Figure 16:
Comparison of the fast and slow cooling including Joule heating.
|
| Open with DEXTER | |
We have presented a thorough study of the thermal evolution of neutron stars including some of the most intriguing effects of magnetic fields. Our results were based on two-dimensional cooling simulations of realistic models that account for the anisotropy in the thermal conductivity tensor. In the first part of the paper, we revisited the classical scenario with low magnetic fields and presented the input microphysics, working assumptions, and the baseline models. As an interesting byproduct, we reconsidered the growth of the crust and of the superconducting region in the NS core, and found that there are situations in which both growth rates are comparable. The main body of the work was aimed at the discussion of the two principal effects of magnetic fields: the anisotropic surface temperature distribution and the additional heating by magnetic field decay. We found that, even for purely dipolar fields, an inverted temperature distribution is plausible at intermediate ages. Thus the surface temperature distribution of neutron stars with high magnetic fields, even in the axisymmetric case, may be quite different from the model with two hot polar caps and a cooler equatorial region. The irregular light curves of some isolated neutron stars, for instance RBS1223, (Schwope et al. 2005; Kaplan & van Kerkwijk 2005) are an indication of such complex structures.
The main result of this work is that, in NSs born as magnetars, Joule heating has an enormous effect on the thermal evolution. Moreover, this effect is important for intermediate field stars. If the magnetic field is supported by crustal currents, this effect can reach a maximum because two combined factors enhance the efficiency of the heating process: i) more heat is released into the crust, in the regions of higher resistivity close to the surface; and ii) large non radial components of the field channel the heat towards the surface, instead of being lost by neutrinos in the core. As expected, it becomes clear that magnetic fields and Joule heating are playing a key role keeping magnetars warm for a long time, but it is likely that the same effect, although quantitatively smaller, must be considered in radio-quiet isolated NSs or high magnetic field radio-pulsars.
Another aspect that should be considered when we try to explain observations using theoretical cooling curves is that for many objects the age is estimated assuming that the loss of angular momentum is entirely due to dipolar radiation from a magnetic dipole (spin-down age). In the case of a decaying magnetic field, the spin down age, seriously overestimates the true age (Gunn & Ostriker 1970). Therefore, the cooling evolution time should be corrected, according to the prescription for magnetic field decay, to compare our model accurately with observations. A detailed comparison of the cooling curves obtained in this work with observational sources can be found in Aguilera et al. (2008).
Our last striking remark is that the occurrence of direct URCA or, in general, fast neutrino cooling in NS may be hidden by a combination of effects due to strong magnetic fields. Our conclusion is that the most appropiate candidates to monitor as rapid coolers are NSs with fields lower than 1013 G. Otherwise, we may be misled in our interpretation of the temperature-age diagrams.
The main drawback of our work is that we are not yet able to return a fully consistent simulation of the magneto-thermal coupled evolution of temperature and magnetic field. In the near future, we plan to extend this study by coupling our thermal diffusion code to the consistent evolution of the magnetic field in the crust given by the Hall induction equation. That approach will permit the accurate evaluation of the heating rates, including the non-linear effects associated with the Hall-drift in the NS crust. We believe, however, that the phenomenological parameterization employed in this paper, reproduces qualitatively the results expected in a real case. We have provided another step towards understanding the cooling of neutron stars, by pointing out a number of important features that must be more carefully considered in future work.
Acknowledgements
This work has been supported by the Spanish MEC grant AYA 2007-67626-C03-C02. D.N.A was supported by VESF-VIRGO project number EGO-DIR-112/2005. We thank U. Geppert for carefully reading and valuable comments. D.N.A. acknowledges interesting discussions during the INT Neutron Star Crust and Surface Workshop, Seattle.