A&A 485, 695-705 (2008)
DOI: 10.1051/0004-6361:20079161

On the morphology of sigma-drop galaxies

S. Comerón¹ - J. H. Knapen¹ - J. E. Beckman^1,2

1 - Instituto de Astrofísica de Canarias, 38200 La Laguna, Spain
2 - Consejo Superior de Investigaciones Científicas, Spain

Received 28 November 2007 / Accepted 28 April 2008

Abstract
Context. Local reductions of the stellar velocity dispersion in the central regions of galaxies are known as sigma-drops ($\sigma$-drops). Knowing the origin of these features can lead to better understanding of inner galactic dynamics.
Aims. We present a sample of 20 $\sigma$-drop galaxies matched with a control sample of galaxies without $\sigma$-drop in order to search for correlations between $\sigma$-drops and the properties, primarily morphological, of the nuclear zones and discs of their host galaxies.
Methods. We study the dust and H$\alpha$ distribution at 0.1 arcsec scale, using Hubble Space Telescope imaging, in the circumnuclear zones of the two samples of galaxies, searching for differences and trying to establish a link between the nuclear kinematics and the host morphology. We have also considered the CO and H  I emission of the galaxies and their luminosity profiles.
Results. We classify the two samples following both morphological parameters and the luminosity profiles. We find a larger fraction of nuclear dust spirals and H$\alpha$ rings in the $\sigma$-drop sample. We also find that the fraction of Seyfert galaxies in the $\sigma$-drop sample is bigger than that of LINERs and that the reverse is true for the control sample.
Conclusions. Our findings are evidence that a $\sigma$-drop is very probably due to inflow-induced star formation in a dynamically cool disc, or in a gas ring, shock focused by an inner Lindblad resonance above a certain critical density level. The same mechanism that feeds the nuclear ring or the nuclear disc is probably reponsible for the higher rate of Seyfert galaxies among the $\sigma$-drop hosts.

Key words: Galaxy: kinematics and dynamics - galaxies: nuclei - galaxies: statistics

1 Introduction

It is normally considered physically reasonable that the stars closest to the centre of a galaxy, close to the bottom of the potential well, should have the highest velocity dispersions. In other words, a radial plot of velocity dispersion across a galaxy should peak on the nucleus. This prediction, however, would be predicated on the isotropy of the stellar orbits in a spheroid in equilibrium under gravity with its mass centrally concentrated. As the angular resolution of spectroscopic data has improved, detailed measurements on nearby galaxies have shown in some galaxies an unexpected drop in the stellar velocity dispersion as the nucleus is approached, a phenomenon referred to as a dispersion drop or $\sigma$-drop (Emsellem et al. 2001; Emsellem 2004). One of the first known examples of this phenomenon can be found in Jarvis et al. (1988), later results include those reported by Jarvis & Peletier (1991), Bottema (1993), van der Marel (1994), Bertola et al. (1996), Bottema & Gerritsen (1997), Fisher (1997), Simien & Prugniel (1997a,b,c), Héraudeau & Simien (1998), Simien & Prugniel (1998), Héraudeau et al. (1999), Simien & Prugniel (2000), Emsellem et al. (2001), Simien & Prugniel (2002), de Zeeuw et al. (2002), Aguerri et al. (2003), Márquez et al. (2003), Shapiro et al. (2003), Chung & Bureau (2004), Falcón-Barroso et al. (2006), Ganda et al. (2006), Emsellem et al. (2008), and Dumas et al. (2007).

The frequency of $\sigma$-drops in galaxy populations has still not been determined with precision, but estimates currently go as high as 50% of disc galaxies (from the previously cited articles). They have been found in a wide variety of galaxy types in both active and non-active galaxies. A few cases have been observed in lenticular and elliptical galaxies (Emsellem 2008).

Explanations have been proposed for this phenomenon with theoretical arguments and also using numerical simulations. For disc galaxies a scenario has been proposed in which the stellar population in a $\sigma$-drop galaxy was formed from a circumnuclear rapidly rotating dynamically cool gaseous component. The stars inherit the velocity pattern of the gas from which they form, so their velocity dispersion is lower than that of the older, `underlying' stars. A young stellar population dominates an older population in luminosity, so the resulting spectrum is dominated by the lower velocity dispersion of the younger stars (see, e.g., Wozniak et al. 2003, also Allard et al. 2005, 2006). This effect can be enhanced by a falling velocity dispersion of the gas towards the centre of a galaxy, due to a strong accumulation of gas in a dissipative disc that would cool the gas in a cold component (i.e., a cold disc as shown in Falcón-Barroso et al. 2006). Hydro/N-body simulations (Wozniak et al. 2003) have shown that a $\sigma$-drop can form in less than 500 Myr, but that its lifetime can exceed 1 Gyr if the nuclear zone is continually fed with gas to sustain star formation. This continued formation of stars is required to maintain a long term $\sigma$-drop, which in turn is required for the observed large $\sigma$-drop fraction among the galaxy population. When star formation ceases, dynamical relaxation will cause the $\sigma$-drop to dissipate in a time-scale that goes from a few hundred Myr for short-lived $\sigma$-drops (circumnuclear volume feeding during less than 500 Myr) to the order of 1 Gyr or even more for long-lived $\sigma$-drops (see Fig. 2 in Wozniak et al. 2003). It is worth keeping in mind that the phenomenon of $\sigma$-drops and that of gas inflow are both considered to be indications of the type of phenomena which occur in secular evolution (as reviewed by Kormendy & Kennicutt 2004).

Although this model is considered not only plausible but probable, there are a number of alternatives. A massive, concentrated dark matter halo could remove kinetic energy from the stellar component. Numerical simulations of this effect can be found in Athanassoula & Misiriotis (2002), their Fig. 13. In this model the massive halo gives rise to a strong bar, and the $\sigma$-peak is suppressed compared with galaxies having smaller halos. However, these numerical simulations are only done with particles (stars) and do not take into account the effects of gas concentration in the galactic centre. It has also been argued (Dressler & Richstone 1990) that a $\sigma$-drop might be a symptom of the absence of a central supermassive black hole, but van der Marel (1994) argues against this that a cause might even be the widening of spectral line wings in the presence of a black hole, giving rise to an apparent reduction in $\sigma$.

In this article we present a statistical study of 20 of these $\sigma$-drop galaxies, and match the sample with a control sample to see if we can identify characteristics which distinguish the overall morphologies of the $\sigma$-drop hosts.

In Sect. 2 we explain the sample selection criteria, and give a brief description of the resulting samples. In Sect. 3 we show how we processed the data, in Sect. 4 we study the $\sigma$-drop properties such as size, in Sect. 5 we describe the morphological classification adopted, in Sect. 6 we study the presence of activity in nuclei, and in Sect. 7 we show a test based on the use of luminosity profiles of the sample galaxies. In Sect. 8 we add H  I+CO radio observations to the previous optical and near-IR data sets, applying these to the task of differentiating $\sigma$-drop galaxies from the control sample, and in Sect. 9 we discuss the material presented in this article, and present our conclusions.

2 Sample selection

Table 1: Source of the velocity dispersion profiles or 2D maps that we used to construct the samples.

	Figure 1: Matching of the $\sigma$-drop and the control sample with respect to four parameters of the host galaxy: distance ( top left), B absolute magnitude ( top right), axis ratio d/D ( bottom left), and morphological type ( bottom right). The filled bars correspond to the $\sigma$-drop sample and the dashed bars denote the control sample.
Open with DEXTER

Our $\sigma$-drop galaxy sample is a sub-sample of the selection of galaxies listed by Emsellem (2008) as having spectroscopic evidence for the presence of a drop in the central stellar velocity dispersion. We added one galaxy, NGC 4826 (Héraudeau & Simien 1998) to bring the number up to 20 galaxies. We selected those galaxies that had been imaged with the Hubble Space Telescope (HST) and which were not classified as edge-on in the RC3 catalogue (de Vaucouleurs et al. 1991). For all of these galaxies we retrieved WFPC2 or ACS red images from the HST archive, and whenever available also H$\alpha$ images taken with the WFPC2 or ACS cameras.

We then constructed a control sample that matches almost exactly the $\sigma$-drop sample in the statistical distribution across four key parameters of the host galaxies. The four parameters are:

• distance (from radial velocity corrected for Virgo infall with a Hubble constant $H_{0}=70~\rm {km~s^{-1}~Mpc^{-1}}$ for galaxies with radial velocities greater than $1400~\rm {km~s^{-1}}$, and from distance determinations from the literature, where possible, in other cases);

• absolute magnitude (from the LEDA database), corrected for galactic extinction and internal extinction of the target galaxies;

• ratio of minor and major axis diameter, d/D, of the galaxy, which is directly related to the inclination (from LEDA, except for NGC 1097 and NGC 6814 where the axis ratio measurement given there is obviously biased by the strong bar. In the first case we determined the axis ratio by measuring the kpc-scale ring of star formation and assuming that it is intrinsically round. In the second case the inner morphology suggests that this is an almost face-on galaxy);

• morphological type of the galaxy in the Hubble sequence (from de Vaucouleurs et al. 1991).

We started the sample matching process by classifying the $\sigma$-drop host galaxies into several bins for each parameter. To create the control sample, we then selected from the HST archive all galaxies that have at least visible, red or near-IR imaging obtained with the WFPC2 and/or the ACS. Our control sample is made up of galaxies with evidence for the absence of a $\sigma$-drop in the literature. The stellar velocity dispersion profiles and 2D maps we used for this can be found in Jarvis et al. (1998), Bottema (1993), Fisher (1997), Héraudeau & Simien (1998), Héraudeau et al. (1999), Falcón-Barroso et al. (2006), Ganda et al. (2006), and Dumas et al. (2007), as detailed in Table 1. A possible caveat in our control sample is that several dispersion profiles are measured only along the major axis of the galaxies (Bottema 1993; Héraudeau & Simien 1998; Héraudeau et al. 1999; seven of our galaxies in total) while $\sigma$-drops sometimes only are detectable when measuring along the minor axis (Fisher 1997, in four of the seven galaxies with $\sigma$-drop), which could generate some contamination in our control sample. This contamination is probably below 20%, especially considering that in the kinematical studies the proportion of $\sigma$-drop hosts is around 50% and that only six galaxies in the control sample have only single-slit spectra.

It is easy to match a $\sigma$-drop sample with a control sample for early-type galaxies but it is much more difficult to do so for late-type galaxies. This is due to the lack of late-type galaxies without $\sigma$-drop in the literature; probably a selection effect because Fisher (1997), Simien & Prugniel (2002), de Zeeuw et al. (2002), Aguerri et al. (2003), and Falcón-Barroso et al. (2006) include only early-type galaxies, and the work of Ganda et al. (2006) is the only relevant one devoted to late-type galaxies. 19 of 20 of our $\sigma$-drops come from the list of Emsellem (2008), in which the selection is independent of morphological type, contrary to the works we used to make the control sample.

From the list produced by this first stage in the selection, we proceeded to take random galaxies and populate the bins until achieving the best possible match between the two samples. In some cases, several combinations of galaxies yielded similarly good overall matching. In those cases we favoured the distribution in morphological type over the other three parameters because we are primarily interested in investigating possible links between morphology and dynamics, and thus prefer to minimise any biases in that area. The limits of the bins we selected are (see also Fig. 1):

• for distance, we split the samples at distances R<10 Mpc, 10-20 Mpc, 20-30 Mpc, and 30-50 Mpc;
• for luminosity, we split the samples at magnitudes B<-21.00, -21.00<B<-20.00, -20.00<B<-19.00, and B>-19.00;
• for the axis ratio d/D we split the samples at d/D=0.2-0.4, 0.4-0.6, 0.6-0.8, and 0.8-1.0;
• for morphological type, we created a bin for the lenticular galaxies and further bins for galaxy types 0, 1, 2, 3, 4 and 5-6.

The final $\sigma$-drop and control samples are listed in Tables 2 and 3. Figure 1 and Table 4, which shows the mean and the median for each parameter and for each sub-sample, indicate that the two samples are very similar. The only noticeable differences are that the median luminosity and axis ratio for the control galaxies are smaller, and that the lower magnitude distribution end is sub-populated in the control sample. This is because there is only one galaxy without a $\sigma$-drop with B>-19 in the papers with velocity dispersion studies in the literature, and this galaxy has not been included because it is almost edge-on.

Table 2: Results of the morphological classification of dust structure and H$\alpha$ nuclear and circumnuclear structure of the 20 galaxies from the $\sigma$-drop sample. ID of the galaxy (Col. 1); morphological type (RC3, Col. 2); nuclear activity (from NED, Col. 3); distance in Mpc, (Col. 4); B magnitude (NED, Col. 5); axis ratio d/D (NED, except in NGC 1097 where we measured d/D from the H$\alpha$ ring and NGC 6814 that looks face-on), (Col. 6); dust structure within the radius r_c (Col. 7); nuclear H$\alpha$ structure (Col. 8); circumnuclear H$\alpha$ structure (Col. 9). Statements such as ``Ring+Patchy'' describe in which order we find each H$\alpha$ structure, starting at the nucleus.

Table 3: As Table 2, now for the 20 control sample galaxies.

Table 4: Statistical properties of the $\sigma$-drop and control samples, showing mean and median values of the four parameters used for matching the samples.

3 Data processing

3.1 Structure maps

The structure map technique (Pogge & Martini 2002) allows one to observe the distribution of structure, and in particular that of dust, in a galaxy on the scale of the PSF using only one image in one filter. The structure map is mathematically defined as

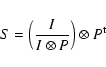$$S=\left(\frac{I}{I\otimes P}\right) \otimes P^{\rm t}$$ (1)

where S is the structure map, I is the image, P is the point-spread function (PSF), $P^{\rm t}$ is the transform of the PSF, and $\otimes$ is the convolution operator (Pogge & Martini 2002). We used synthetic PSFs which were created with the Tiny Tim software (Krist & Hook 1999).

We used images taken through green or red optical filters to apply the structure map operator, namely F547M, F606W, F791W, and F814W for WFPC2 images, and F625W and F814W for ACS images. The resulting images are shown in Appendices A (for the $\sigma$-drop sample) and B (for the control sample, the appendices are online-only).

3.2 H$\alpha$ images

For 10 of the 20 galaxies in our $\sigma$-drop sample and for ten more in our control sample we could retrieve H$\alpha$ narrow-band imaging from the HST archive. We used H$\alpha$ images taken through the narrow filters F656N or F658N, and a continuum image taken through a red broad-band filter. In the few cases where images taken through both H$\alpha$ filters were available in the archive, we chose the F658Nimage, because the H$\alpha$ line of our sample galaxies was better centred in its passband. The images used for the continuum subtraction were those from which we derived the structure maps.

After selecting the images from the archive, the continuum and narrow-band images were aligned using standard IRAF software. We then plotted for each pixel in the whole image the number of counts in the narrow-band filter versus that in the continuum filter. In the absence of H$\alpha$ line emission, the number of counts in the narrow-band filter will be proportional to the number of counts in the continuum, and the constant of proportionality is the factor by which the continuum has to be scaled before subtracting from the narrow-band image. Since even for a star-forming galaxy most pixels trace only continuum emission, those pixels without H$\alpha$ emission can easily be recognised in the graph, and a fit to them yields the continuum scaling factor (see Knapen et al. 2005, 2006, for details and a graphic illustration). In most cases, there is a contribution from the [N  II] line in the H$\alpha$ images but this is not a problem because we do not use the H$\alpha$ images for photometry, and [N  II] emission is unlikely to affect the morphology on the scales we are interested in here. The resulting continuum-subtracted H$\alpha$ images are shown in Appendices A and B (for the $\sigma$-drop and control samples, respectively; online only).

4 Size of the $\sigma$-drop region

Table 5: Sizes of the $\sigma$-drop and $r_{\rm {c}}$.

	Figure 2: In the left panel, radius of the $\sigma$-drop ( $r_{\sigma \rm {-drop}}$) versus the photometric radius $r_{\rm {c}}$, and in the right panel, the ratio of $r_{\sigma \rm {-drop}}$ and $r_{\rm {c}}$ versus $r_{\rm {c}}$.
Open with DEXTER

We have searched for correlations between size of the $\sigma$-drop region and other properties of their host galaxies, such as differences in morphology or in radio emission from gas (see further sections for details on how we study those properties). We have found no correlation between any of these properties and the size of the $\sigma$-drops.

We have also made a comparison between the radius of the $\sigma$-drop ( $r_{\sigma \rm {-drop}}$) and $r_{\rm {c}}$, a measure of radius which is directly related to the visible size of the galaxy and which we define as 2% of the radius of the galaxy (where the radius is half of D₂₅ as taken from the RC3). We use the definition for $r_{\rm {c}}$ because it is similar to the effective radius of the bulge of a spiral galaxy (Laurikainen et al. 2004) - it thus provides an objective but simple and effective working definition of the central region.

The data used appear in Table 5 and the plots are in Fig. 2. The radii of the $\sigma$-drops were taken from the velocity dispersion plots in the papers cited in Sect. 2. These dispersions are not always very well defined because in several papers the spectra are taken only along one axis of the galaxy (usually the major axis) and this does not provide as good a measure of the $\sigma$-drop radius as IFU spectroscopy. We note that the highest value of the ratio $r_{\sigma\rm {-drop}}/r_{\rm {c}}$, NGC 3593, is a ``strange'' galaxy with two counter-rotating discs (Bertola et al. 1996). We find some hint that higher $r_{\sigma\rm {-drop}}/r_{\rm {c}}$ ratios are found in smaller galaxies and vice versa. That would indicate that $r_{\sigma \rm {-drop}}$ is not directly related to the size of the galaxy, which is confirmed by the plot in the right panel of Fig. 2.

5 Morphological classification

5.1 Bars

Because we ignored bars in our sample selection procedure (Sect. 2), we can as a first step investigate the presence and properties of the bars in our $\sigma$-drop and control sample galaxies. The interest in this lies primarily in the fact that bars can facilitate the inflow of cool gas into the inner regions of galaxies by removing angular momentum from the gas in the outer parts. If $\sigma$-drops are related to star formation from dynamically cold gaseous material close to the nucleus, it is reasonable to conjecture that bars may play an important role in the process. In Tables 2 and 3 we therefore summarise the bar classification of the galaxies. This is based primarily on the RC3 catalogue (de Vaucouleurs et al. 1991), where, as is conventional, SA galaxies are those without a bar, SAB (also known as SX) are weakly or moderately barred, and SB galaxies have a prominent bar in the optical.

Although the RC3 is based on optical imaging and is therefore not optimal in recognising all bars, it is generally reliable in reporting well-defined bars. We did check the literature and images of individual galaxies though, and refined the classification in the following cases. Some galaxies are catalogued as non-barred in the RC3 but do in fact have weak and/or small bars. The first case is NGC 1068, part of our $\sigma$-drop sample, where a bar has been discovered from near-IR imaging (e.g., Scoville et al. 1988). Other galaxies with a bar discovered on the basis of modern imaging are the control sample galaxies NGC 3169 (Laurikainen & Salo 2002), NGC 3593 and NGC 3675 (Laurikainen et al. 2004), and NGC 2460, NGC 7331, and NGC 7742 (Laine et al. 2002). Fitting ellipses to a 2MASS image we also found strong evidence for a weak bar in NGC 2985.

The bar fractions in our $\sigma$-drop and control samples can thus be seen in Table 6, where we use Poisson statistics to give an estimate of the error in the numbers ( $\epsilon=\sqrt{f(1-f/N)}$, where f is the quantity that is measured and N is the sample size in which the quantity is searched). The conclusion from the numbers presented in Table 6 is that there are no statistically significant differences between the two samples. What is evident from this test, however, is that a bar is not needed to cause a $\sigma$-drop, and that, conversely, the presence of a bar does not automatically, or even preferentially, lead to a dip in the central stellar velocity dispersion. As for inner bars, we have found six of them in $\sigma$-drop galaxies (NGC 1068, NGC 1097, NGC 1808, NGC 2460, NGC 4303, and NGC 4725) and three in galaxies of the control sample (namely NGC 3169, NGC 3368, and NGC 7742). All of these inner bars have been reported independently by Laine et al. (2002) and/or Erwin (2004).

The difference between inner bar fraction in the $\sigma$-drop and control samples is not very significant, but points in the direction of a link between inner bars and $\sigma$-drops. It is worthy to note here that, except in the case of NGC 3593, $\sigma$-drops have a much smaller scale than outer bars. In the other hand, $\sigma$-drops occur on a size scale similar to that of inner bars (our nine inner bars have a mean size of 350 pc, compared to the mean radius of the $\sigma$-drops in the sample, which is 400 pc).

Table 6: Bars in the sample galaxies. The data come from the RC3 except in the cases that are explained in the text.

5.2 Dust classification

Dust is well traced by structure maps, and we thus used the structure maps we constructed for our sample galaxies to characterise the central dust morphology across our samples. The structure maps are shown in Appendices A and B (online only) for the $\sigma$-drop and control samples, respectively. We draw two ellipses that indicate the scale of each image, an inner ellipse that indicates  $r_{\rm {c}}$, as defined above, in Sect. 4, and an outer one which indicates the inner kiloparsec in radius.

We applied the classification criteria developed by Peeples & Martini (2006) to the central area ( $r_{\rm {c}}$) of each galaxy. Examples of each classification class are given in Fig. 2 of Peeples & Martini (2006). The classes are:

• Grand design (GD): two spiral arms with a 180$^{\circ}$ rotational offset between them. At least one arm must reach the unresolved centre of the galaxy and must be a dominant feature.

• Tightly wound (TW): a coherent spiral over a wide range of radius, with a pitch angle smaller than 10$^{\circ}$.

• Loosely wound (LW): a coherent spiral over a wide range of radius, with a pitch angle greater than 10$^{\circ}$.

• Chaotic spiral (CS): evidence of spiral arms with a unique sense of chirality, but not coherent over a wide radial range.

• Chaotic (C): no evidence of spiral structure.

• No structure (N): no dust seen.

The results of the classification for the $\sigma$-drop and the control sample are in Tables 2 and 3, respectively. One result that is obvious from the tables is that there is a correlation between the dust distribution and the axis ratio. Galaxies with ``chaotic'' dust distribution tend to have lower axis ratios (they are more highly inclined), which we interpret as being due to the dust in the disc obscuring the nucleus and the small-scale dusty features that are in the same plane as the external discs of dust. To quantify this we can compute the mean d/D for the 13 chaotic galaxies ( $\overline{d/D}=0.48$) and for the 40 studied galaxies ( $\overline{d/D}=0.65$)

	Figure 3: Comparison between the dust distribution in the two samples. Filled bars correspond to the $\sigma$-drop sample and dashed bars denote the control sample. The numbers at the top of each bin refer to the number of galaxies in each bin.
Open with DEXTER

Figure 3 summarises the dust morphology for the $\sigma$-drop and control samples. There is some correlation between the presence of a $\sigma$-drops and the morphology of the dust structure. Whereas galaxies with dust spirals (especially LW) are preferentially $\sigma$-drop hosts, the chaotic and chaotic spiral morphological classes have more control sample galaxies.

Figure 4: Comparison between the H$\alpha$ distribution in the two samples. Filled bars correspond to the $\sigma$-drop sample and dashed bars denote the control sample. In the histogram that shows the nuclei classification the ``other'' bars refer to the ``Peak+Bipolar Structure'', and ``Peak + Bipolar Structure + UCNR''. The numbers at the top of each bin refer to the number of galaxies in the bin and the number of galaxies in the subsample.

Open with DEXTER

When using broader bins, i.e., separating galaxies with clear spiral dust structure (classes LW, TW, and GD) from those without it (N, C, and CS), and thus to some extent overcoming the low-number statistics, the result is amplified. Eleven of the 20 $\sigma$-drop galaxies show clear dust spiral structure ( $55\% \pm 11\%$), versus only five ( $25\% \pm 10\%$) in the control sample .

Does this mean that galaxies without a $\sigma$-drop are preferentially chaotic? To test this idea we first have to remember how the sample was composed. The key matching parameter is morphological type, so axis ratio is not so well matched. This causes the mean and median axis ratios of the control sample to be slightly smaller than those of the $\sigma$ sample. This might explain part of the fraction of control galaxies in the C category whose inner structure is hidden by a dust disc seen edge-on. But CS galaxies clearly show the bulge dust structure and therefore are barely affected by disc dust so the size of the CS class is not overestimated. In summary, chaotic morphologies are indeed favoured by the control sample galaxies.

5.3 H$\alpha$ classification

The classification of the H$\alpha$ emission (images shown in Appendices A and B; online only) is based on the scheme developed by Knapen (2005). We classify the images separately for two radial regions, $r_{\rm {c}}$, as defined above, and the inner kpc. In the very central region ( $r_{\rm {c}}$) the H$\alpha$ emission can be dominated by the following features:

• Peak: a peaked emission region centred on the nucleus of the galaxy.

• Amorphous: clear H$\alpha$ emission, but without any significant peak.

• Peak+UCNR: a peaked emission region centred on the nucleus of the galaxy surrounded by an H$\alpha$-emitting Ultra-Compact Nuclear Ring (UCNR; Comerón et al. 2008) of a few tens of parsec in radius.

• Peak+Bipolar Structure+UCNR: a peak in the centre accompanied by both a bipolar structure and an UCNR. This appears only in NGC 4579 where the inner peak and the bipolar structure are surrounded by an extremely fuzzy UCNR ring of 130 pc in radius. Its existence has been confirmed from UV images (Comerón et al. 2008).

• Peak+Nuclear spiral: a peak in the centre surrounded by a short H$\alpha$ spiral that does not reach $r_{\rm {c}}$. NGC 3031 is the only example of this kind of galaxy in our samples.

In the zone between $r_{\rm {c}}$ and the inner kpc radius, we used the following classification criteria:

• Patchy: individual regions of H$\alpha$ emission, not centrally peaked, looking like the H  II regions that can be found in the discs of galaxies.

• Ring: H$\alpha$ emission organised in a well-defined ring of star formation bigger than a UCNR, which means that it measures, at least, two hundred parsecs in radius. We are classifying only the inner kpc in radius, so rings with bigger radii are not taken into account.

• Diffuse: H$\alpha$ emission is present but cannot be ascribed to individual and well-defined H  II regions.

• Filaments: H$\alpha$ emission distributed in long filaments of H  II regions.

• None: less than 1% of the area of the inner kiloparsec region has any H$\alpha$ emission.

This classification has been applied to the 10 $\sigma$-drop galaxies and the 10 control sample galaxies for which we have H$\alpha$ images. Results for the $\sigma$-drop sample are listed in Table 2, and for the control sample in Table 3, and are summarised as histograms in Fig. 4.

There are no significant differences at all in the very central H$\alpha$ emission morphology. For the inner 1 kpc region, however, we notice that star-forming activity is much higher in $\sigma$-drop galaxies than in control-sample galaxies. Patches and filaments in $\sigma$-drop host galaxies are more extended (covering a larger surface area) and more obvious in the images than in the control sample galaxies. Most of the control galaxies are devoid of H$\alpha$ formation or have a weak diffuse emission. Galaxies in the $\sigma$-drop sample often show strong starbursts with bright H$\alpha$ rings and patches.

The differences between these two subsamples could be due to the fact that they are not as well matched as the two samples of 20 galaxies. The mean axis ratio for the $\sigma$-drop galaxies is 0.56 while it is 0.62 for the control galaxies. Four $\sigma$-drop galaxies have axis ratios smaller than 0.4. Two of these galaxies (NGC 1808 and NGC 3593) show clear evidence of nuclear star-burst rings, which means that we are seeing the inner region without strong extinction. In the other two cases (NGC 3623 and NGC 3627) there is no H$\alpha$ emission, possibly due to dust obscuration. In the control sample dust seems to hide the inner regions in NGC 3169 (d/D=0.62 and diffuse circumnuclear emission) and in NGC 3718 (d/D=0.49 with no circumnuclear emission). It is difficult to explain using only obscuration the virtual absence of circumnuclear emission in the two other galaxies, NGC 3031 which shows a tiny nuclear spiral and the nearly face-on galaxy NGC 6340.

The other difference between the two subsamples is that the mean morphological type of the control sample is earlier than that of the $\sigma$-drop sample (mean Hubble morphological type 1.8 and 2.6, respectively). Both subsamples have galaxies with types ranging between zero and six. In Knapen et al. (2006) galaxies with no circumnuclear emission tend to be early type and patchy emission tends to be in later-type galaxies which is coherent with what we have found in the two subsamples. Diffuse emission is also more prevalent in the control sample. As the diffuse emission is an intermediate case between no emission and patchy emission, the overabundance of this type in the control sample is probably due to the fact that it contains earlier-type galaxies. But in Knapen et al. (2006) the nuclear starburst ring distribution peaks around T=1, so the control sample should have a higher number of nuclear rings, which is not the case. According to the statistics of Knapen et al. (2006), corrected for the nuclear ring fractions reported there for each morphological type of the host galaxy, four of our $\sigma$-drop galaxies and six control galaxies should have a circumnuclear ring - the actually observed numbers are five and zero. Therefore it is reasonable to think that the higher proportion of circumnuclear star-forming rings in $\sigma$-drop galaxies is a true effect correlated with the $\sigma$-drop.

6 Nuclear activity

From Tables 2 and 3 we can see that the proportion of galaxies in the $\sigma$-drop sample that have a Seyfert nucleus is $65\%\pm11\%$ while in the control sample it is $30\%\pm10\%$. On the other hand, LINERs make up $25\% \pm 10\%$ of the $\sigma$-drop sample but $60\%\pm11\%$ of the control sample. This points to a link between $\sigma$-drops and Seyferts, and links the other galaxies with a more reduced level of activity.

If this is indeed the case, assuming that Seyfert nuclei are more active than LINERs, we might intuitively think that more energetic phenomena are related to a bigger inflow of gas. This gas could have been partly spent in a generation of stars in the inner volume of the galaxies. The signature of this recent star formation would be a $\sigma$-drop. This result has to be handled with care because in both samples we have a proportion of AGN of around 80%, which is far higher than the proportion of active galaxies that is found in a randomly taken sample. A direct explanation might be that HST is usually employed to observe `interesting' objects, which implies an enhanced fraction of AGN in the galaxies that have been observed with the space telescope.

One possibility is that the inflow of gas giving rise to a $\sigma$-drop feeds the energetic phenomena detected as nuclear activity. When the inflow stops the activity fades, and the $\sigma$-drop gradually relaxes. As the timescale for the former is shorter than that for the latter, any correlation will be only partial.

A way to test if this correlation is indeed true is to study a bigger sample, for example all the galaxies from the papers from which we selected the control sample. That yields 85 $\sigma$-drop galaxies and 95 control galaxies. There are around 40 galaxies that are difficult to classify and therefore are not included in this test. We found that of the $\sigma$-drop galaxies $32\%\pm5\%$ are Seyfert hosts and $19\%\pm4\%$ are LINER hosts. For the control sample we find that $16\%\pm4\%$ are Seyfert hosts and $24\%\pm4\%$ are LINER hosts. These data must be taken with caution because they do not come from matched samples, so the effects that we see may be due to other effects such as differences in morphological type. More than a half of the galaxies used for this test (as performed on the total sample of 85+95 galaxies, defined above) come from the papers from Héraudeau & Simien (1998), Héraudeau et al. (1999), and Simien & Prugniel (1997a,b,c, 1998, 2000, 2002), which have dispersion profiles from galaxies that are so distant that in many cases they have not been studied in any survey of nuclear activity.

From this discussion we may tentatively conclude that $\sigma$-drop are preferably accompanied by Seyfert nuclei, and that both phenomena can be traced to increased gas inflow. Given the different spatial and time scales involved, exactly why and how this is so is slightly puzzling. We note that a similar, and similarly puzzling, relation has been reported in the literature between the presence of nuclear activity and that of nuclear rings (see Knapen 2005, in particular the discussion in Sect. 6 of that paper).

7 Luminosity profiles

As a way to check another possible connection between $\sigma$-drops and their host galaxies, we searched for a correlation between the presence of a $\sigma$-drop and the shape of the luminosity profiles of their host galaxies. Our aim here was to derive luminosity profiles from the nucleus to the outer parts of the galaxies or to use profiles obtained by other authors. We obtained Sloan Digital Sky Survey release 5 (SDSS5) (Adelman-McCarthy et al. 2007) r-band images to make the profiles. In several cases we had to join two or three SDSS frames to get a complete image of a galaxy. Each pixel in the SDSS images subtends 0.396 arcsec, obviously not nearly small enough to do an analysis at the same scale as we did for dust and H$\alpha$, so we concentrate on the host disc here.

We obtained 13 profiles for the $\sigma$-drop sample and 13 more for the control subsample. These subsamples are very well matched in morphological type. There are not so well matched in axis ratio but this is only marginally important because ellipse fitting and posterior deprojection allow good photometry. The biggest difference is in the galaxies' magnitudes. The $\sigma$-drop subsample is on average 0.23 magnitudes brighter than the control one.

To produce the luminosity profile, we start by subtracting the sky background contribution from the images. That was done using the average of sky measurements over outer parts of an image where the disc of the galaxy is well below the noise level. The sky measures were done by averaging circles of 10 pixels in radius. Once the sky had been subtracted, we fitted ellipses for increasing radius, which yielded, first of all, the position angle (PA) and the ellipticity of the outer regions of the galaxy. The radial profiles were usually featureless across the outer regions. We used this PA and ellipticity to measure surface photometry at increasing radii from the centre of the galaxy until the disc ``fades out''. More details about the method can be found in Erwin et al. (2008). The results are shown as radial surface brightness profiles for all the galaxies in Appendices C and D (online only), for the $\sigma$-drop and control samples, respectively. The fitted exponentials are overplotted. The vertical dashed-dotted lines correspond to the position of the end of the bar. When there are two vertical lines, they indicate a lower and an upper limit estimate of the end of the bar.

We classified each profile following Erwin et al. (2008), and thus divide the galaxies in three groups:

• Type I: the radial variation in disc surface brightness is described by a single exponential, allowing some irregularities due to structure (e.g., arms, big star-forming regions). This type of profile was established by Freeman (1970).

• Type II: galaxies with a break in the surface brightness characterised by a convex, steeper, outer slope ( truncation). This type of profile was also established by Freeman (1970). In barred galaxies the type II class can be subdivided into two subclasses, namely type II.i, where the break is inside the bar radius, and type II.o, where it is outside, as explained by Erwin et al. (2008). All the type II galaxies in this paper have the break outside the bar radius, so we ignored this subdivision.

• Type III: galaxies with a concave break followed by a less steep slope (antitruncation; Erwin et al. 2005).

In some cases, antitruncations and truncations appear in the same galaxy at different radii. That is the reason that we can have, for example, II+III and II+III+II galaxies. We fitted exponentials to every section of the surface brightness profile that was roughly straight in the plots, except in the case of features directly related to bars or dust rings, as judged from a visible comparison with the images.

Table 7: Luminosity profiles of the studied galaxies.

Table 7 summarises the classified shapes of the surface brightness profiles for all the galaxies of our samples that are either in the SDSS survey, or in Pohlen & Trujillo (2006; NGC 1068 and NGC 5806), in Erwin et al. (2008; NGC 3368 and NGC 4102), or in Gutiérrez et al. (2008, in preparation; NGC 2460, NGC 2775, and NGC 2985). NGC 4151 also appears in Erwin et al. (2008) but we have performed deeper photometry and have shifted the classification of this galaxy from type I to type II. In the latter two papers, the procedure for constructing the luminosity profiles is the same as that used in the current paper.

The data in Table 7 show that there is no apparent correlation between the presence of a $\sigma$-drop and the shape of the disc surface brightness profile.

We have also fitted a sersic+exponential profile to the 2MASS H-band profiles in order to find excess or lack of light in the circumnuclear zone. This excess or lack could be either related to a recent star-burst or to a high dust extinction. We find no differences between the two samples.

8 Analysis of radio data

The spatial resolution of radio observations is not generally good enough to allow us to see details in the centres of galaxies. It seems, nevertheless, reasonable to think that there may be a link between the total quantity of gas in a galaxy, as measured through their 21 cm emission in H  I, or the millimetre emission in CO, and the quantity of gas available in the central region. We thus investigate whether there are any statistical differences between the gas content of the $\sigma$-drop and the control galaxies.

8.1 Analysis of CO data

Table 8: Emission in CO and H  I by the sample galaxies. Both the fluxes and the errors are in units of 10⁵⁴ W km (Hz s)^-1 for CO, and of 10⁵² W km (Hz s)^-1 for H  I. The error column corresponds to the photometric error and does not take into account the uncertainty in the distance. In some cases, no error estimate is given for the H  I emission because this was not given in the literature. A hyphen (-) means that no data are available.

We have used data from two CO surveys (Young et al. 1995; and Helfer et al. 2003) to search for a correlation between CO emission and the presence of $\sigma$-drops. Not all the galaxies in our samples were included in the surveys; the CO fluxes and the uncertainties of those that do appear are listed in Table 8. Using the distance to each galaxy, we converted the observed flux values into the total emission of the galaxy in the CO line. We obtained CO emission data for 13 galaxies for the $\sigma$-drop sample and 12 more for the control sample. These two subsamples are well matched in axis ratio, morphological type, and brightness. They are not so well matched in distance which is not really important because we are interested in an integrated CO luminosity.

Table 9: Statistics of CO emission in the $\sigma$-drop and control samples. All data are in units of 10⁵⁴ W km (Hz s)^-1.

The statistical results for the CO are summarised in Table 9, which shows that there are no significant differences between the two samples. This is relevant because CO is a good tracer of molecular gas and $\sigma$-drops are thought to be related to accumulations of gas in the nuclear region. The absence of observed differences between the amount of gas in galaxies with and without $\sigma$-drops could thus be seen as evidence against this assumption, although our current data do not allow us to say anything about the level of concentration of the CO, and thus of the amount of gas in their nuclear regions.

8.2 Analysis of H I data

We obtained integrated H  I emission for our sample galaxies from LEDA, except for NGC 2639 where the data come from Springob et al. (2005). As in the case of the CO emission, we used the distance to each galaxy to derive the total emission. The results are listed in Table 8. We found data for 18 galaxies from the $\sigma$-drop sample and 19 for the control sample. The two subsamples of galaxies for which we have H  I data are well matched.

Table 10: Statistics of H  I emission in $\sigma$-drop and control samples. All data are in units of 10⁵² W km (Hz s)^-1.

The statistical results for the integral H  I emission are summarised in Table 10. Although the H  I emission of the $\sigma$-drop sample is more than two times lower than that of the control sample, this difference is not statistically significant. The conclusion from our analysis of both CO and H  I emission must be that there is no compelling evidence for either more or less gas in the $\sigma$-drop galaxies as compared to those without $\sigma$-drops.

9 Discussion and conclusions

In this paper we have presented an analysis of the morphology of dust and H$\alpha$ emission on scales smaller than 0.1 arcsec and within the central 1 kpc radius, of the disc surface brightness profiles, and of the CO and H  I emission of a sample of $\sigma$-drop host galaxies, and compared the results to those obtained for a matched control sample.

Our control sample is not guaranteed to be completely free of $\sigma$-drop galaxies, but we estimate (Sect. 2) that less than 20% of our control sample galaxies can be expected to host a $\sigma$-drop. This possible contamination somewhat weakens the significance of our results. Another factor that can weaken our results is that, even though this is the biggest $\sigma$-drop galaxy sample studied in such a consistent way, it is not big enough to avoid problems with small number statistics. In addition, to study correlations for several parameters we had to work with subsamples that were not as well matched.

Our overall conclusion is that $\sigma$-drops are related to nuclear dust spirals and nuclear star-forming rings. We find that the $\sigma$-drop radius is independent of the other tested parameters of the host galaxy. We note the possibility that Seyfert galaxies are related to $\sigma$-drops and find that LINERs are found more often in galaxies without this feature. We also find that bars, at least strong bars, are not likely to be a necessary feature to cause a $\sigma$-drop in a galaxy.

One of the theories for the creation of $\sigma$-drops is based on a massive and concentrated dark matter halo which can remove kinetic energy from the stellar component of galactic nuclei (Athanassoula & Misiriotis 2002). Such a dark matter halo would, however, have other effects on a galaxy's morphology and kinematics, such as the stimulation of a strong bar (Athanassoula & Misiriotis 2002). But in our $\sigma$-drop sample there are only three strongly barred and ten weakly barred galaxies, and these numbers are not significantly different for the control sample. This indicates that massive and compact dark matter halos are not likely to be the only $\sigma$-drop formation mechanism, and may well not affect this phenomenon at all.

There are other theories for $\sigma$-drops. Dressler & Richstone (1990) propose that $\sigma$-drops may be due to the lack of a central super-massive black hole and van der Marel (1994) suggests that a $\sigma$-drop may be due to the presence of a super-massive black hole that broadens emission lines and makes ``traditional'' line fitting overestimate the true velocity. These hypotheses can now be completely discarded, mainly because the presence of a $\sigma$-drop has been found to be a widespread phenomenon (in the literature cited in the introduction they are found in 30%-50% of the disc galaxies) and because $\sigma$-drops are not found only in galaxies whose velocity profiles indicate the presence of an anomalous super-massive black hole.

Another theory for $\sigma$-drop formation points to cold gas accumulation and a posterior starburst in the inner parts of the galaxy (e.g., simulations by Wozniak et al. 2003). Such a concentration of gas would start to create stars at a given density threshold. This critical density would probably only be related to local gas properties so the $\sigma$-drop size is independent of macroscopic galactic parameters. This is confirmed by our results. The huge dispersion in $\sigma$-drop sizes can be related to a reduction of their size when they become old or to the different extents of the cool gas volume at the moment it reached the critical density.

As we have shown in Sect. 4.2, $\sigma$-drop hosts have in more than 50% of the cases a clear inner dust system of spiral arms that probably trace the path of the inflowing material. In contrast, less than 20% of the control sample galaxies show such a clear spiral pattern. As there are no significant differences in bar characteristics between the two samples, it is safe to say that there is some correlation between $\sigma$-drops and inner dust spiral arms. This dust could trace the inflowing gas fuelling the $\sigma$-drop, or it could be the product of relatively recent star-formation.

We have also found that $\sigma$-drop galaxies often (in 50% of the cases) have a nuclear star-forming ring visible in H$\alpha$ with a size between 400 pc and 1 kpc and that there are no star-forming rings at those scales in the control sample. It thus seems reasonable to say that the rings are a manifestation of the same phenomena causing the $\sigma$-drops. The stars that compose the $\sigma$-drops can be formed in such nuclear starburst rings, usually due to shock focusing of gas near the location of one or more inner Lindblad resonances (ILRs; Schwarz 1984; Athanassoula 1992; Knapen et al. 1995; Heller & Shlosman 1996; see also Shlosman 1999; Knapen 2005, for reviews). The ILRs are thought to be related to bars or interactions between close galaxies. Four of our five galaxies with star-forming rings are barred. The fifth, NGC 6503, is so edge-on that a bar may be difficult to detect.

We have found that $\sigma$-drop galaxies are more often Seyfert than LINER hosts. On the other hand, control galaxies more often have LINER emission than Seyfert emission. Seyfert galaxies are more energetic phenomena, which probably implies a more continuous or more recent inflow of material to maintain the central activity. The dust spiral arms that are frequent in $\sigma$-drop galaxies are a plausible method to feed the central black hole. It is therefore possible to postulate that both $\sigma$-drops and Seyferts are due to a more efficient feeding of the inner parts of galaxies. As Seyferts are shorter lived than $\sigma$-drops (few 10⁸ yr versus 1 Gyr) the correlation can only hold partially.

We thus suggest the following model for the creation of a $\sigma$-drop. Gas is driven inwards by spiral arms and maybe by bars. The gas is focused by an ILR into a dynamically cold ring where the density increases until it reaches a critical value when star formation starts. These stars are dynamically cold and start to create a $\sigma$-drop. Alternatively, if there is no ILR, gas can be focused in a cold nuclear disc that also starts to create stars when it reaches the critical density. In both cases friction causes some gas to lose enough angular momentum to drift inwards to feed the super-massive black hole. This gas can be traced with the dust related to the relatively recent star formation. It is entirely possible that $\sigma$-drops are exclusively created in rings that disappear due to the transient nature of the bars and/or the inflow. As a $\sigma$-drop is a long-lived feature (as shown by modelling by Wozniak et al. 2003, and as indicated by the high fraction of galaxies that host them) it would survive long after the ring has disappeared. These conclusions should be strengthened in future work by improving the statistics and by further numerical modelling.

Acknowledgements

We thank Leonel Gutiérrez and Rebeca Aladro for their help with some of the luminosity profiles used in this study, Peter Erwin for his help in the classification of luminosity profiles, Paul Martini for letting us peruse his structure map IDL scripts, and the referee, Eric Emsellem, for comments that helped improve the paper. This work was supported by projects AYA 2004-08251-CO2-01 of the Ministerio de Educación y Ciencia and P3/86 and 3I2407 of the Instituto de Astrofísica de Canarias. Based on observations made with the NASA/ESA Hubble Space Telescope, obtained from the data archive at the Space Telescope Science Institute. STScI is operated by the Association of Universities for Research in Astronomy, Inc. under NASA contract NAS 5-26555. This work is also based in SDDS release 5.

References

 
• Adelman-McCarthy, J. K., Jennifer, K., Agüeros, M. A., et al. 2007, ApJS, 172, 634 In the text  
• Aguerri, J. A. L., Debattista, V. P., & Corsini, E. M. 2003, MNRAS, 338, 465 In the text  
• Allard, E., Peletier, R. F., & Knapen, J. H. 2005, ApJ, 633, 25 In the text  
• Allard, E., Knapen, J. H., Peletier, R. F., & Sarzi, M. 2006, MNRAS, 371, 1087 In the text  
• Athanassoula, E. 1992, MNRAS, 259, 345 In the text  
• Athanassoula, E., & Misiriotis, A. 2002, MNRAS, 330, 35 In the text  
• Bertola, F., Cinzano, P., Corsini, E. M., Pizzella, A., Persic, M., & Salucci, P. 1996, ApJ, 458, 67 In the text  
• Bottema, R. 1993, A&A, 275, 16 In the text  
• Bottema, R., & Gerritsen, J. P. E. 1997, MNRAS, 290, 585 In the text  
• Chung, A., & Bureau, M. 2004, AJ, 127, 3192 In the text  
• Comerón, S., Knapen, J. H., Beckman, J. E., & Shlosman, I. 2008, A&A, 478, 403 In the text  
• Dressler, A., & Richstone, D. O. 1990, ApJ, 348, 120 In the text  
• Dumas, G., Mundell, C. G., Emsellem, E., & Nagar, N. M. 2007, MNRAS, 379, 1249 In the text  
• Emsellem, E. 2004, ASSL, 319, 149 In the text  
• Emsellem, E. 2008, in Mapping the Galaxy and Nearby Galaxies, ed. K. Wada & F. Combes (New York: Springer), 139 In the text  
• Emsellem, E., Greusard, D., Combes, F., et al. 2001, A&A, 368, 52 In the text  
• Emsellem, E., Fathi, K., Wozniak, H., et al. 2006, MNRAS, 365, 367  
• Erwin, P. 2004, A&A, 415, 941 In the text  
• Erwin, P., Beckman, J. E., & Pohlen, M. 2005, ApJ, 626, 81 In the text  
• Erwin, P., Pohlen, M., & Beckman, J. E. 2008, AJ, 135, 20 In the text  
• Falcón-Barroso, J., Bacon, R., Bureau, M., et al. 2006, MNRAS, 369, 529 In the text  
• Fisher, D. 1997, AJ, 113, 950 In the text  
• Freeman, K. C. 1970, ApJ, 160, 811 In the text  
• Ganda, K., Falcón-Barroso, J., Peletier, R., et al. 2006, MNRAS, 367, 46 In the text  
• Helfer, T. T., Thornley, M. D., Regan, M. W., et al. 2003, ApJS, 145, 259 In the text  
• Heller, C. H., & Shlosman, I. 1996, MNRAS, 471, 143 In the text  
• Héraudeau, P., & Simien, F. 1998, A&A, 133, 317 In the text  
• Héraudeau, P., Simien, F., Maubon, G., & Prugniel, P. 1999, A&AS, 136, 509 In the text  
• Jarvis, B. J., & Peletier, R. F. 1991, A&A, 247, 315 In the text  
• Jarvis, B. J., Dubath, P., Martinet, L., & Bacon, R. 1988, Msngr, 53, 19 In the text  
• Knapen, J. H. 2005, A&A, 429, 141  
• Knapen, J. H., Beckman, J. E., Shlosman, I., et al. 1995, ApJ, 443, 73 In the text  
• Knapen, J. H., Mazzuca, L. M., Böker, T., et al. 2006, A&A, 448, 489 In the text  
• Kormendy, J., & Kennicutt, R. C. Jr. 2004, ARA&A, 42, 603 In the text  
• Krist, J. E., & Hook, R. N. 1999, The Tiny Tim User's Guide (ver. 5.0; Baltimore: STScI) In the text  
• Laine, S., Shlosman, I., Knapen, J. H., & Peletier, R. F. 2002, ApJ, 567, 97 In the text  
• Laurikainen, E., & Salo, H. 2002, MNRAS, 337, 1118 In the text  
• Laurikainen, E., Salo, H., Buta, R., & Vasylyev, S. 2004, MNRAS, 355, 1251 In the text  
• van der Marel, R. P. 1994, MNRAS, 270, 271 In the text  
• Márquez, I., Masegosa, J., Durret, F., et al. 2003, A&A, 409, 459 In the text  
• Peeples, M., & Martini, P. 2006, ApJ, 652, 1097P In the text  
• Pogge, R. W., & Martini, P. 2002, ApJ, 569, 624 In the text  
• Pohlen, M., & Trujillo, I. 2006, A&A, 454, 759 In the text  
• Schwarz, M. P. 1984, PASAu, 5, 464 In the text  
• Scoville, N. Z., Matthews, K., Carico, D. P., & Sanders, D. B. 1988, ApJ, 327, 61 In the text  
• Shapiro, K. L., Gerssen, J., & van der Marel, R. P. 2003, AJ, 126, 2707 In the text  
• Shlosman, I. 1999, ASPC, 187, 100 In the text  
• Simien, F., & Prugniel, Ph. 1997a, A&AS, 122, 521 In the text  
• Simien, F., & Prugniel, Ph. 1997b, A&AS, 126, 15  
• Simien, F., & Prugniel, Ph. 1997c, A&AS, 126, 519  
• Simien, F., & Prugniel, Ph. 1998, A&AS, 131, 287 In the text  
• Simien, F., & Prugniel, Ph. 2000, A&AS, 145, 263  
• Simien, F., & Prugniel, Ph. 2002, A&A, 384, 371  
• Springob, C. M., Haynes, M. P., Giovanelli, R., & Kent, B. R. 2005, ApJS, 160, 149 In the text  
• Tonry, J. L., Dressler, A., Blakeslee, J. P., et al. 2001, ApJ, 546, 681  
• Tully, R. B. 1988, Nearby galaxies catalog (Cambridge and New York: Cambridge University Press)  
• de Vaucouleurs, G., de Vaucouleurs, A., Corwin, H. G., Jr., et al. 1991, Third Reference Catalogue of Bright Galaxies (New York: Springer Verlag) (RC3) In the text  
• Wozniak, H., & Champavert, N. 2006, MNRAS, 369, 853  
• Wozniak, H., Combes, F., Emsellem, E., & Friedli, D. 2003, ASPC, 290, 563 In the text  
• Young, J. S., Xie, S., Tacconi, L., et al. 1995, ApJS, 98, 219 In the text  
• de Zeeuw, P. T., Xie, S., Tacconi, L., et al. 2002, MNRAS, 329, 513 In the text

 

  
Online Material

Appendix A: Structure maps and H$\alpha$ images of the $\sigma$-drop sample galaxies

Where two images for one galaxy are given on a row, the structure map is shown on the left, and the continuum-subtracted H$\alpha$ image on the right; where only one image is shown there is no H$\alpha$ image available. The orientation of the images is shown with pairs of arrows, where the longer indicates north and the shorter one east. The small ellipse indicates $r_{\rm {c}}$, as defined in the text, and the large one is at 1 kpc radius. Where one ellipse is drawn it indicates $r_{\rm {c}}$ - in those cases the image scale is such that the 1 kpc radius falls outside the image. Grey-scales are such that dark indicates more dust (less emission) in the structure maps, and more H$\alpha$ emission in the H$\alpha$ images. Each image has at the top left the name of the galaxy, the morphological classification given in NED and the activity, also given in NED.

	Figure A.1:
Open with DEXTER

	Figure A.1: continued.
Open with DEXTER

	Figure A.1: continued.
Open with DEXTER

	Figure A.1: continued.
Open with DEXTER

	Figure A.1: continued.
Open with DEXTER

	Figure A.1: continued.
Open with DEXTER

	Figure A.1: continued.
Open with DEXTER

Appendix B: As Appendix A, now for the control sample galaxies

	Figure B.1:
Open with DEXTER

	Figure B.1: continued.
Open with DEXTER

	Figure B.1: continued.
Open with DEXTER

	Figure B.1: continued.
Open with DEXTER

	Figure B.1: continued.
Open with DEXTER

	Figure B.1: continued.
Open with DEXTER

	Figure B.1: continued.
Open with DEXTER

Appendix C: Radial surface brightness profiles of the $\sigma$-drop sample galaxies

Exponential fits are indicated with dashed lines, while the dotted lines indicate the sky level for each galaxy. Vertical dashed-dotted lines correspond to the end of the bar. Where there are two vertical lines, they indicate the lower and the upper limit to the end of the bar. The squares show the limits of the intervals that we have used to fit the exponential discs.

	Figure C.1:
Open with DEXTER

	Figure C.1: continued.
Open with DEXTER

	Figure C.1: continued.
Open with DEXTER

	Figure C.1: continued.
Open with DEXTER

	Figure C.1: continued.
Open with DEXTER

Appendix D: As Appendix C, now for the control sample galaxies

	Figure D.1:
Open with DEXTER

	Figure D.1: continued.
Open with DEXTER

	Figure D.1: continued.
Open with DEXTER

	Figure D.1: continued.
Open with DEXTER

	Figure D.1: continued.
Open with DEXTER