A&A 485, 531-540 (2008)
DOI: 10.1051/0004-6361:20065685
A. M. Glauser1 - F. Ménard2 - C. Pinte4 - G. Duchêne2,3 - M. Güdel1 - J.-L. Monin2 - D. L. Padgett5
1 - Paul Scherrer Institut,
5232 Villigen PSI, Switzerland
2 -
Laboratoire d'Astrophysique
de Grenoble, CNRS/UJF UMR 5571, BP 53, 38041 Grenoble Cedex 9,
France
3 -
Astronomy Department, UC Berkeley, Berkeley CA
947209-3411, USA
4 -
School of Physics, University of Exeter,
Stocker Road, Exeter EX4 4QL, UK
5 - Caltech-JPL/IPAC,
Mail Code 100-22, Pasadena, CA 91125, USA
Received 24 May 2006 / Accepted 14 April 2008
Abstract
We present a study of the circumstellar environment of
IRAS 04158+2805 based on multi-wavelength observations and
models. Images in the optical and near-infrared, a polarisation map
in the optical, and mid-infrared spectra were obtained with
VLT-FORS1, CFHT-IR, and S PITZER-IRS. Additionally we used an
X-ray spectrum observed with Chandra. We interpret the observations
in terms of a central star surrounded by an axisymmetric
circumstellar disc, but without an envelope, to test the validity of
this simple geometry. We estimate the structural properties of the
disc and its gas and dust content. We modelled the dust disc with a
3D continuum radiative transfer code, MCFOST, based on a Monte-Carlo
method that provides synthetic scattered light images and
polarisation maps, as well as spectral energy distributions. We find
that the disc images and spectral energy distribution narrowly
constrain many of the disc model parameters, such as a total dust
mass of
![]() and an inclination of
and an inclination of
![]() .
The maximum grain size required to fit all
available data is of the order of
.
The maximum grain size required to fit all
available data is of the order of
![]() m although the
upper end of this range is loosely constrained. The observed optical
polarisation map is reproduced well by the same disc model,
suggesting that the geometry we find is adequate and the optical
properties are representative of the visible dust content. We
compare the inferred dust column density to the gas column density
derived from the X-ray spectrum and find a gas-to-dust ratio along
the line of sight that is consistent with the ISM value. To our
knowledge, this measurement is the first to directly compare dust
and gas column densities in a protoplanetary disc.
m although the
upper end of this range is loosely constrained. The observed optical
polarisation map is reproduced well by the same disc model,
suggesting that the geometry we find is adequate and the optical
properties are representative of the visible dust content. We
compare the inferred dust column density to the gas column density
derived from the X-ray spectrum and find a gas-to-dust ratio along
the line of sight that is consistent with the ISM value. To our
knowledge, this measurement is the first to directly compare dust
and gas column densities in a protoplanetary disc.
Key words: stars: circumstellar matter - stars: pre-main-sequence - stars: individual: IRAS 04158+2805 - stars: formation - stars: planetary systems: protoplanetary discs
Accretion discs are key elements in star and planet formation scenarios. They provide the material for accretion leading to star and planet building, they provide the energy and material for launching jets, and they are the medium through which angular momentum is transported away. Knowing their geometrical and physical properties is important for understanding these processes and their evolution.
Large-scale surveys have been performed to search for discs around young low-mass pre-main sequence stars (e.g., Stapelfeldt et al. 2003; Schneider et al. 2005), the so-called T Tauri stars. A few tens of discs have been imaged and, for many of them, images are available over a progressively broader wavelength range, enabling deeper studies of the disc properties.
However, the properties of discs around more massive stars and, of concern here, around the lower mass late M dwarfs and brown dwarfs remain poorly known, because images for these discs are still extremely rare. As a consequence, our knowledge of the circumstellar environment of these objects is based solely on spectral energy distribution (SED) fitting.
In this paper we present a study of IRAS 04158+2805, a low-mass star
located near the substellar boundary. The classification of
IRAS 04158+2805 varies in the literature, with most authors agreeing
on a late spectral type, implying a very low stellar mass. The
recent paper by Luhman (2006) concludes that its spectral type is
consistent with a low mass star close to the brown dwarf limit.
IRAS 04158+2805 is located at a distance of 140 pc, in the L1495 east
dark cloud, which is part of the Taurus molecular cloud complex. It
is surrounded by an extended reflection nebulosity seen in scattered
light. It propels a well-collimated, ionised atomic jet seen in
H![]() that extends at least out to 60 arcsec to the north.
The object is probably located in the foreground of the large
reflection nebulosity illuminated by V892 Tau, one of the rare
Herbig Ae stars of the Taurus cloud, because the disc of
IRAS 04158+2805 appears in silhouette over the reflection
nebulosity. This is the only such case in Taurus to our knowledge.
that extends at least out to 60 arcsec to the north.
The object is probably located in the foreground of the large
reflection nebulosity illuminated by V892 Tau, one of the rare
Herbig Ae stars of the Taurus cloud, because the disc of
IRAS 04158+2805 appears in silhouette over the reflection
nebulosity. This is the only such case in Taurus to our knowledge.
In this paper, we apply an axisymmetric, inclined-disc model to our
data, fitting near-infrared images, near- and mid-infrared
photometry, mid-infrared spectroscopy, millimeter photometry, and
near-infrared polarimetry to derive disc geometry, disc mass, and
dust composition. The large size of the disc derived from the
near-infrared images (radius of approximately 8 arcsec in the I band, corresponding to 1120 AU at a distance of 140 pc) is
intriguing, especially around a star of such a low mass. We will
show that the data are compatible with an inclined disc without any
need to invoke a larger envelope. The paper is organised as follows.
Section 2 presents the observations which are
further discussed in Sect. 3. In Sect. 4,
we discuss the modelling of the dust disc. We estimate the
structural model parameters of the circumstellar disc and we discuss
the quality and the uniqueness of the solution found in Sect. 5. We present our conclusions in Sect. 6.
![\begin{figure}
\par\includegraphics[width=17.2cm,clip]{5685fig1.eps}\end{figure}](/articles/aa/full/2008/26/aa5685-06/Timg14.gif) |
Figure 1:
I-, H- and K-band contour plots of IRAS 04158+2805.
The contour lines are on the levels
|
| Open with DEXTER | |
IRAS 04158+2805 was observed on December 12, 2001 in the I-band with
the FORS1/ IPOL instrument. The weather conditions were good
and the seeing was measured between 0
![]() 9 and 1'' over the
observation period. The total field of view (FOV) of
FORS1/ IPOL is
9 and 1'' over the
observation period. The total field of view (FOV) of
FORS1/ IPOL is
![]() in the Standard Resolution
mode with a focal scale of
in the Standard Resolution
mode with a focal scale of
![]() /pixel. Polarimetry was
performed by inserting a Wollaston prism in the beam. The prism
splits the incident light beam into two separate beams of orthogonal
polarisation states, the so-called ordinary (o) and extraordinary
(e) beams. A stepped half-wave plate retarder was placed at the
entrance of the incident beam and was rotated by steps of 22.5 degrees. The separation of the two o- and e-beams on the CCD is
performed by the Wollaston prism and overlap of the two beams is
avoided by inserting a 9-slit focal mask. Each slit in the mask
provided a
/pixel. Polarimetry was
performed by inserting a Wollaston prism in the beam. The prism
splits the incident light beam into two separate beams of orthogonal
polarisation states, the so-called ordinary (o) and extraordinary
(e) beams. A stepped half-wave plate retarder was placed at the
entrance of the incident beam and was rotated by steps of 22.5 degrees. The separation of the two o- and e-beams on the CCD is
performed by the Wollaston prism and overlap of the two beams is
avoided by inserting a 9-slit focal mask. Each slit in the mask
provided a ![]()
![]() FOV. Images of IRAS 04158+2805
were recorded at 8 retarder positions with an integration time of
3 minutes per frame. The images were then combined to yield the
Stokes parameters I, Q and U.
FOV. Images of IRAS 04158+2805
were recorded at 8 retarder positions with an integration time of
3 minutes per frame. The images were then combined to yield the
Stokes parameters I, Q and U.
A dedicated data reduction pipeline was written using
NOAO/IRAF (see, e.g., Monin et al. 2006). The images are first
corrected for bias and bad pixels, and then flat-fielded. In the
next step, the images went through a polarisation extraction routine
in which the normalised flux difference between the ordinary and
extraordinary images is calculated for every pixel of the image, and
a Fourier series was computed to derive the Stokes parameter I, Qand U![]() : We first computed the
normalised flux difference F from the target flux f:
: We first computed the
normalised flux difference F from the target flux f:
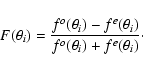 |
(1) |
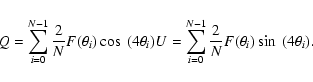 |
(2) |
We estimated carefully the instrumental polarisation at the centre
of the FORS1 field by measuring nearby (i.e., high proper motion)
unpolarised targets. We observed GJ 781.1 and GJ 2147, two high
proper motion stars. Because the immediate solar neighbourhood is
remarkably devoid of dust (e.g., Leroy 1993, 1999) the interstellar
polarisation of nearby stars can be considered null. The average of
4 measurements on both GJ objects gives
![]() .
We therefore believe that FORS1/IPOL instrumental
polarisation is very low on-axis, well below 0.1% at the centre of
the field, and we did not attempt to remove it from the
measurements.
.
We therefore believe that FORS1/IPOL instrumental
polarisation is very low on-axis, well below 0.1% at the centre of
the field, and we did not attempt to remove it from the
measurements.
On the other hand, Patat & Romaniello (2006) showed that FORS1 presents a spatially variable instrumental polarisation component. This component follows a radial pattern with an intensity scaling as 0.06 r2 (in % if r is in arcmin), ranging from 0.1% in the central region, one arcmin in radius, to 1% at the edge of the FOV. First, the absolute value of the instrumental polarisation is low (0.23% at the position of the source) compared to the observed polarisation of IRAS 04158+2805 which is always higher than 3%. Second, since the source is small compared to the FOV, we decided to neglect the spatial variation of the instrumental polarisation on the FORS1 detector because it does not vary significantly across the object.
On October 29 and 30, 2001, we used the near-infrared CFHT-IR camera
(Starr et al. 2000) at the Canada-France-Hawaii Telescope to obtain
H- and K-band images of IRAS 04158+2805 with a pixel scale of 0
![]() 211/pixel and a total FOV of 3
211/pixel and a total FOV of 3
![]() 6. Conditions were
non-photometric and the seeing during the observations was 0
6. Conditions were
non-photometric and the seeing during the observations was 0
![]() 65
at K-band and 0
65
at K-band and 0
![]() 9 at H-band, as measured from the average
FHWM of several unresolved point sources located in the FOV. With
each filter, two series of 10 jittered images were obtained in
separate sets. Each set of images was first reduced as an
independent dataset in the following manner. All images were
median-combined to create a sky frame, which was subtracted from
each image. The images were then flat-fielded, registered based on
the location of a bright point source in the field and
median-combined. The two independent images per filter resulting
from this procedure were then averaged together to produce the final
images presented in Fig. 1.
9 at H-band, as measured from the average
FHWM of several unresolved point sources located in the FOV. With
each filter, two series of 10 jittered images were obtained in
separate sets. Each set of images was first reduced as an
independent dataset in the following manner. All images were
median-combined to create a sky frame, which was subtracted from
each image. The images were then flat-fielded, registered based on
the location of a bright point source in the field and
median-combined. The two independent images per filter resulting
from this procedure were then averaged together to produce the final
images presented in Fig. 1.
We use archival data of the S PITZER Infrared Spectrograph
(IRS, see, e.g., Houck et al. 2004) observation from March 4, 2004
(program request 3534848) which was done in the spectral mapping
mode with the two low resolution channels: Short-Low (SL; 5.2-14 ![]() m,
m,
![]() )
and Long-Low (LL; 14-38
)
and Long-Low (LL; 14-38 ![]() m,
m,
![]() ). The mapping mode (3 exposures across the target for each slit and 2 nodding positions
each) was chosen due to the small mispointing of S PITZER in
the early mission. Therefore, the flux of the object is separated in
two or three observations. To recover the photometric information,
all three parallel exposures were summed for the SL while the
overlap of the FOV of the LL-slit is such that the full flux is
extractable by summing the first and last exposures.
). The mapping mode (3 exposures across the target for each slit and 2 nodding positions
each) was chosen due to the small mispointing of S PITZER in
the early mission. Therefore, the flux of the object is separated in
two or three observations. To recover the photometric information,
all three parallel exposures were summed for the SL while the
overlap of the FOV of the LL-slit is such that the full flux is
extractable by summing the first and last exposures.
We used the final products from the Spitzer Science Center's IRS data-reduction pipeline (post-BCD). To allow a background subtraction the two nodding observations were used to subtract them from each other. The data extraction was done with the Spitzer IRS Customer Extractor software (SPICE) provided by the Spitzer Science Center.
IRAS 04158+2805 was serendipitously observed by the Chandra X-ray
Observatory in a field pointing at the L1495 East dark cloud around
V410 Tauri. The observation was performed with ACIS-S on March 7, 2002 between 6:16 UT and 11:45 UT, with a useful total exposure time
of approximately 17 700 s. IRAS 04158+2805 was located 11
![]() 6
off-axis on the ACIS-S chip S1. This resulted in a rather distorted,
extended point spread function (PSF) with considerable background
contributions. The data were, however, sufficiently clean to extract
a useful spectrum (see Fig. 2).
6
off-axis on the ACIS-S chip S1. This resulted in a rather distorted,
extended point spread function (PSF) with considerable background
contributions. The data were, however, sufficiently clean to extract
a useful spectrum (see Fig. 2).
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{5685fig2.eps} \end{figure}](/articles/aa/full/2008/26/aa5685-06/Timg29.gif) |
Figure 2: X-ray spectrum of IRAS04158+2805 observed with Chandra. |
| Open with DEXTER | |
We reduced all ACIS-S data using standard analysis techniques
following the Chandra CIAO Science
Threads![]() .
Specifically, we flagged bad pixels, applied CCD charge transfer
inefficiency corrections to create a so-called level2 events file.
We extracted source counts from a circular area with a radius of
27
.
Specifically, we flagged bad pixels, applied CCD charge transfer
inefficiency corrections to create a so-called level2 events file.
We extracted source counts from a circular area with a radius of
27
![]() 6 around the source. To define a background spectrum, a
source-free circular area with a radius of 98
6 around the source. To define a background spectrum, a
source-free circular area with a radius of 98
![]() 4 was extracted
from the same chip. The counts were binned into a source and a
background spectrum. Appropriate responses were created using the
mkrmf task, and the ancillary file was obtained from mkarf.
4 was extracted
from the same chip. The counts were binned into a source and a
background spectrum. Appropriate responses were created using the
mkrmf task, and the ancillary file was obtained from mkarf.
Contour plots of IRAS 04158+2805 at I-, H- and K-bands are presented in Fig. 1. In the I-band, the object shows a bipolar reflection nebula geometry. The dark lane, tracing the equatorial plane, is seen in absorption over the background light. It separates a prominent triangular nebulosity located to the North from a low surface brightness elongated counter nebula to the south. The counter nebula is undetected at H- and K-bands. At these wavelengths, the triangular shape of the main nebula is still visible, but its extension decreases with increasing wavelength.
The maximum width of the northern nebula is measured to be
15
![]() 8, 14
8, 14
![]() 1 and 10
1 and 10
![]() 8 at I-, H- and K-band,
respectively. The northern nebula has a triangular shape whose
opening angle is
8 at I-, H- and K-band,
respectively. The northern nebula has a triangular shape whose
opening angle is ![]() 130
130![]() at all wavelengths. Finally, the
distance between the peak of the two nebulae at I-band is
at all wavelengths. Finally, the
distance between the peak of the two nebulae at I-band is
![]() arcsec. In Sect. 4.2, we define additional
morphological and photometric observables to compare models and
observations.
arcsec. In Sect. 4.2, we define additional
morphological and photometric observables to compare models and
observations.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{5685fig3.eps}\end{figure}](/articles/aa/full/2008/26/aa5685-06/Timg32.gif) |
Figure 3: Modeled SED (dashed line) compared to observed fluxes: IRS spectrum (solid line); Strom & Strom (1994, squares); Kenyon et al. (1990) and Kenyon & Hartmann (1995, circles); Luhman & Rieke (1998) and Luhman (2000, crosses); Motte & André (2001, diamonds); this paper, see Sect. 3.2 (triangle). The error bars of the photometric fluxes are smaller than their symbols and therefore not drawn. |
| Open with DEXTER | |
To construct the spectral energy distribution of IRAS 04158+2805
shown in Fig. 3, we use mid-infrared IRAS flux measurements
from Kenyon et al. (1990), optical and near-infrared photometry from
Kenyon et al. (1990), Strom & Strom (1994) and from the 2MASS point
source catalog. The 1.3 mm continuum flux is from Motte & André
(2001).
Because IRAS 04158+2805 is
extended, we suspect that the 2MASS photometry may be underestimated
since these fluxes are listed in the 2MASS All-Sky Point Source
Catalogue (PSC) and were obtained by PSF fitting. To check this
point, we extracted the photometry from our own near-infrared images
by using three point-like sources that have 2MASS photometry and use
them as relative photometric standards. We obtained K=11.04 and
H=12.10 for IRAS 04158+2805, with estimated uncertainties of
0.05 mag. For the H-band this is 0.28 mag brighter than the 2MASS
photometry and 0.13 mag for the K-band. While the brightness
profile of IRAS 04158+2805 is peaked in the near infrared and may
account for this discrepancy, we note that from our images we find a
difference of only 0.03 mag in the photometry when two apertures of
4
![]() 2 and 10
2 and 10
![]() 6 are used. Therefore, we attribute the
difference in photometry of IRAS 04158+2804 between 2MASS and our
images to intrinsic variability of the source rather than an
aperture size too small in 2MASS.
6 are used. Therefore, we attribute the
difference in photometry of IRAS 04158+2804 between 2MASS and our
images to intrinsic variability of the source rather than an
aperture size too small in 2MASS.
The S PITZER-IRS spectrum shows absorption features at ![]() 10
10 ![]() m and
m and ![]() 15.2
15.2 ![]() m. Both can be identified as
silicates and carbon dioxyde ice, respectively (see Fig. 3).
Similar features are seen for example in low-mass protostars, where
the cold envelope and/or outer disc cause the absorption (e.g.,
Watson et al. 2004). In IRAS 04158+2805, it is interesting to note
that the silicate absorption is maximum slightly short of 10 microns, around 9.5 microns. This is an indication for small dust
grains made of either amorphous or crystalline material such as
enstatite (Schegerer et al. 2006). We did not attempt to fit the
exact shape of the feature and cannot conclude about the exact
mineralogy of the grains. It is also interesting to find CO2 ice
signatures in absorption in a source where the disc appears to
dominate the SED (see Sect. 4.2.3), but the high
inclination, nearly edge-on, probably provides the needed column
density along the line of sight. However, it is beyond the scope of
this paper to discuss quantitatively the IRS spectrum. We will do so
in a forthcoming paper.
m. Both can be identified as
silicates and carbon dioxyde ice, respectively (see Fig. 3).
Similar features are seen for example in low-mass protostars, where
the cold envelope and/or outer disc cause the absorption (e.g.,
Watson et al. 2004). In IRAS 04158+2805, it is interesting to note
that the silicate absorption is maximum slightly short of 10 microns, around 9.5 microns. This is an indication for small dust
grains made of either amorphous or crystalline material such as
enstatite (Schegerer et al. 2006). We did not attempt to fit the
exact shape of the feature and cannot conclude about the exact
mineralogy of the grains. It is also interesting to find CO2 ice
signatures in absorption in a source where the disc appears to
dominate the SED (see Sect. 4.2.3), but the high
inclination, nearly edge-on, probably provides the needed column
density along the line of sight. However, it is beyond the scope of
this paper to discuss quantitatively the IRS spectrum. We will do so
in a forthcoming paper.
We extract the fluxes at 12 ![]() m and 25
m and 25 ![]() m and compare with IRAS
fluxes published in Kenyon et al. (1990). The difference is of the
order of 0.5% at 12
m and compare with IRAS
fluxes published in Kenyon et al. (1990). The difference is of the
order of 0.5% at 12 ![]() m and 1.3% at 25
m and 1.3% at 25 ![]() m and is negligible
therefore.
m and is negligible
therefore.
The light from the northern photometric nebulosity centre has a
linear polarisation of
![]() ,
averaged within a region of 2 arcsec (10 pixels) in diameter. Since neighbouring objects do not
show a significant polarisation rate, this is an indication that the
peak in the nebula is not arising from stellar photons seen directly
but, instead, from scattered light. The polarisation is maximum at
the corners of the triangular northern nebula and has values between
35
,
averaged within a region of 2 arcsec (10 pixels) in diameter. Since neighbouring objects do not
show a significant polarisation rate, this is an indication that the
peak in the nebula is not arising from stellar photons seen directly
but, instead, from scattered light. The polarisation is maximum at
the corners of the triangular northern nebula and has values between
35![]() and 41
and 41![]() (see Fig. 4). For this
determination we use the highest ``reliable'' value. We decided to use
only those pixels for which the polarisation rate topology shows a
certain smooth behaviour. This was quantified by determining the
standard deviation of the polarisation rate of each pixel and its 4 neighbours. If the standard deviation is higher than 20% (typical
noise level), the pixel is not used.
(see Fig. 4). For this
determination we use the highest ``reliable'' value. We decided to use
only those pixels for which the polarisation rate topology shows a
certain smooth behaviour. This was quantified by determining the
standard deviation of the polarisation rate of each pixel and its 4 neighbours. If the standard deviation is higher than 20% (typical
noise level), the pixel is not used.
![\begin{figure}
\par\includegraphics[width=17.4cm,clip]{5685fig4.eps}\end{figure}](/articles/aa/full/2008/26/aa5685-06/Timg35.gif) |
Figure 4: Polarisation maps of the observed ( left panel) and modelled ( middle panel) nebula. The vector length for 100% polarisation is indicated by the bar in the lower right corner. Right panel: comparison of the polarisation level as a function of position in the observed (solid) and modelled (dashed) nebula. These curves are estimated along the ridges (black curves) and symmetry axis (gray) of the nebula. |
| Open with DEXTER | |
The Chandra ACIS X-ray spectrum of IRAS 04158+2805 is shown in Fig. 2. The spectrum was binned such that the minimum number of counts per bin was 10 before background subtraction. The total number of counts in the 0.5-6 keV range was 100, which allowed for only a rather simplistic spectral model that is, however, sufficient to derive useful estimates of the absorption column density to the X-ray source. The source spectrum is obviously very strongly absorbed, with essentially no counts detected below 1.5 keV. The X-ray source is hard enough to produce counts up to 6 keV in the observation.
We fitted the spectral data in XSPEC (Arnaud et al. 1996), using the
vapec collisional-ionization equilibrium model and a
photoelectric absorption component, the latter essentially being
defined by the hydrogen column density ![]() between observer and
source. We first fitted the spectrum with a single thermal
component, assuming that all element abundances are at 0.3 times the
solar values, referring to the solar abundances of Anders &
Grevesse (1989). This corresponds to the elemental composition
typically measured in coronae of magnetically active stars (Güdel
2004).
between observer and
source. We first fitted the spectrum with a single thermal
component, assuming that all element abundances are at 0.3 times the
solar values, referring to the solar abundances of Anders &
Grevesse (1989). This corresponds to the elemental composition
typically measured in coronae of magnetically active stars (Güdel
2004).
We found a best-fit temperature of 5.8 keV or
![]() K, and
a best-fit value for
K, and
a best-fit value for ![]() of
of
![]() cm-2, where the error range refers to the 68%
confidence limit. Given that the spectrum reveals only the hard end
of the entire soft X-ray spectrum, the fit may be biased by fitting
a hot component only. This bias may be relieved somewhat by fitting
a continuous distribution of emission measures (EMD
cm-2, where the error range refers to the 68%
confidence limit. Given that the spectrum reveals only the hard end
of the entire soft X-ray spectrum, the fit may be biased by fitting
a hot component only. This bias may be relieved somewhat by fitting
a continuous distribution of emission measures (EMD![]() ). We adopted an EMD with a
prescribed shape such as found for less-absorbed T Tauri stars,
described in more detail by Telleschi et al. (2007). The EMD model
essentially consists of two power laws on each side of a peak.
Neither the location of the EMD peak nor the power-law slope toward
higher temperatures were well constrained, but the results for
). We adopted an EMD with a
prescribed shape such as found for less-absorbed T Tauri stars,
described in more detail by Telleschi et al. (2007). The EMD model
essentially consists of two power laws on each side of a peak.
Neither the location of the EMD peak nor the power-law slope toward
higher temperatures were well constrained, but the results for ![]() were robust and converged to
were robust and converged to
![]() cm-2.
cm-2.
To summarise these two approaches, irrespective of the uncertainties
in the intrinsic X-ray spectrum of IRAS 04158+2805, we find that the
X-rays, which are presumably emitted in the corona surrounding the
central star, are attenuated by a gas column density of
![]() cm-2, with a one sigma range of
cm-2, with a one sigma range of
![]() cm-2.
cm-2.
In this section we explore the parameter space of a simple model comprising the stellar photosphere and a power-law disc (see Sect. 4.1.1 below) to explain the observations of IRAS 04158+2805 and its associated reflection nebulosity.
Synthetic images, polarisation maps and spectral energy distributions are computed using MCFOST, a 3D radiative transfer code based on the Monte-Carlo method. MCFOST is described in details in Pinte et al. (2006). MCFOST solves the full polarised radiative transfer in dusty environment. It includes multiple scattering, passive heating of the dust disc and thermal re-emission by the dust to produce synthetic images in all four Stokes parameters at any wavelength, as well as SEDs. The dust temperature, the same for all grain sizes, is calculated assuming local thermal equilibrium.
We consider a flared density structure with a Gaussian vertical
profile
![]() ,
valid for a
well-mixed vertically isothermal, hydrostatic, non-self-gravitating
disc. We use power-law distributions for the surface density
,
valid for a
well-mixed vertically isothermal, hydrostatic, non-self-gravitating
disc. We use power-law distributions for the surface density
![]() and for the scale height
and for the scale height
![]() where r is the radial coordinate in
the equatorial plane and h0 is the scale height at the radius
r0 =50 AU. The disc extends from an inner cylindrical radius
where r is the radial coordinate in
the equatorial plane and h0 is the scale height at the radius
r0 =50 AU. The disc extends from an inner cylindrical radius
![]() to an outer limit
to an outer limit
![]() .
The central
star is represented by a point-like, isotropic source of photons.
.
The central
star is represented by a point-like, isotropic source of photons.
We consider homogeneous spherical grains and we use the dielectric
constants described by Mathis & Whiffen (1989) in their model A,
which accounts for the interstellar extinction law. Grain sizes are
distributed according to a power-law
![]() with
with
![]() and
and
![]() being the minimum and
maximum grain radii. The interstellar values from Mathis & Whiffen
(1989) are
being the minimum and
maximum grain radii. The interstellar values from Mathis & Whiffen
(1989) are
![]() m and
m and
![]() m. The mean grain density is 0.5 g cm-3 as a consequence
of the high porosity (80%) of the grains. In this work,
m. The mean grain density is 0.5 g cm-3 as a consequence
of the high porosity (80%) of the grains. In this work,
![]() is considered as a free model parameter to fit
for. Extinction and scattering opacities, scattering phase functions
and Mueller matrices are calculated using Mie theory. The dust and
gas are assumed to be perfectly mixed and the grain properties are
taken to be independent of position within the disc.
is considered as a free model parameter to fit
for. Extinction and scattering opacities, scattering phase functions
and Mueller matrices are calculated using Mie theory. The dust and
gas are assumed to be perfectly mixed and the grain properties are
taken to be independent of position within the disc.
In the process of extracting the disc geometric parameters from the
observations, we first attempt to fit the I-, H- and K-band images
simultaneously with a single disc model. This is presented in 4.2.1. We use
![]() ,
,
![]() ,
,
![]() ,
,
![]() and the inclination as free model parameters. The
I band image suggests a maximum disc radius of 8 arcsec, which
corresponds to 1120 AU at a distance of 140 pc. There must also be
an inner disc radius, which is typically at a few tenths of an AU.
These radii are poorly constrained by our I-, H, and K-band images;
we therefore fix them at the given values (inner radius is set to
0.5 AU), which will have little effect on our results. Since we do
not implement background illumination into our model, the appearance
of the dark lane and the counter nebula is expected to be slightly
different in the model.
and the inclination as free model parameters. The
I band image suggests a maximum disc radius of 8 arcsec, which
corresponds to 1120 AU at a distance of 140 pc. There must also be
an inner disc radius, which is typically at a few tenths of an AU.
These radii are poorly constrained by our I-, H, and K-band images;
we therefore fix them at the given values (inner radius is set to
0.5 AU), which will have little effect on our results. Since we do
not implement background illumination into our model, the appearance
of the dark lane and the counter nebula is expected to be slightly
different in the model.
We computed about 12 000 models covering a wide range of the free parameters. A handful of viable solutions remain after the image-fitting process (in Sect. 4.2.2). We explore the relative merits of these few solutions by calculating their respective SEDs (in Sect. 4.2.3), and I-band polarisation map (in Sect. 4.2.5) for comparison with the data.
To permit a direct comparison of the observed and modelled images,
observational effects must be added to the model images. First of
all, the pixel size of the model output is therefore chosen to match
the scale of the observation (0
![]() 200/pixel in the optical,
0
200/pixel in the optical,
0
![]() 211/pixel in NIR). The model images must be convolved with
the observed PSF and scaled to the same peak value as the observed
images which allows an addition of Poisson and background noise to
yield the same signal-to-noise ratio.
211/pixel in NIR). The model images must be convolved with
the observed PSF and scaled to the same peak value as the observed
images which allows an addition of Poisson and background noise to
yield the same signal-to-noise ratio.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{5685fig5.eps}\end{figure}](/articles/aa/full/2008/26/aa5685-06/Timg56.gif) |
Figure 5:
Definition of geometrical observables w, a, b, c and |
| Open with DEXTER | |
The width of the nebula is defined as the distance w between the two intersection points of the ridges with the contour at the level of a signal-to-noise ratio equal to 1 (shown in Fig. 5 as circles).
The next observable describes quantitatively whether the nebula
looks triangular or round. This observable, which we call the
triangularity, t, is determined for each contour level. In
Fig. 5 an example is shown for the contour level n=8.
The two ridges and the symmetry axis are intersected with the
contour line (shown as squares in the figure). The distance between
the intersection point of the symmetry axis with the contour line
and the triangle spanned by the peak and the two intersection points
of the contour line with the ridges is called b. The triangularity
is then defined as
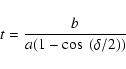 |
(3) |
Finally, the counter nebula is described by the peak-to-peak distance c, and the contrast is defined as the ratio between the maximum brightness of the nebula and the counter nebula.
For a given set
of free model parameters (![]() ,
,
![]() ,
...), we use the
following quality metric to estimate whether the model actually
reproduces the three images of the object. This metric is a
pseudo-
,
...), we use the
following quality metric to estimate whether the model actually
reproduces the three images of the object. This metric is a
pseudo-![]() ,
defined as follows:
,
defined as follows:
Table 1:
Weights
![]() of the pseudo-
of the pseudo-![]() function
(4).
function
(4).
Table 2: Disc model parameters for the best-fitting model and their acceptable range.
The exploration of the parameter space was performed iteratively. We first ran a series of models with only 2 variable model parameters. Once the best model in the series was identified, we fixed these model parameters and created a new series by varying two other parameters, and so on. The range of the explored parameter space is listed in the second column of Table 2. The first selection of the parameter range was chosen arbitrarily but reasonably. If the model behaviour suggested possible solutions outside the scanned range, the exploration was extended until the model diverged significantly from the observation. Among all these models, only a few provided good fits simultaneously to the images of IRAS 04158+2805. In addition, we note that fitting the images at each wavelength independently leads to models of similar parameters and quality. The combination of all images in a single fit allows, however, to narrow down the list of possible good models.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{5685fig6.eps}\end{figure}](/articles/aa/full/2008/26/aa5685-06/Timg77.gif) |
Figure 6: Examples of projections of f2 (Eq. (4)) to different model parameter planes. The contour is plotted in a logarithmic scale. White areas correspond to minimal values of f2. The colour range is identical in all four plots. The black cross shows the location of the best model, after the SED fitting. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{5685fig7.eps}\end{figure}](/articles/aa/full/2008/26/aa5685-06/Timg86.gif) |
Figure 7:
Comparison between observations ( left) and best fitting
model ( mid, see Table 2) in I-band ( top), H-band
( middle) and K-band ( bottom). For demonstration purposes, the right
column shows the images of the best fitting model but with doubled
dust disc mass (
|
| Open with DEXTER | |
We estimated the valid model parameter range by using one good-fitting parameter set and changed only one parameter until the f2 function showed a significant increase or until an eyeball comparison could clearly detect an unsatisfying model. This method does not include an estimation of the general solution range but gives an impression of the validity of the free model parameters at a certain minimum of f2.
Additionally we had to set an artificial upper limit for the valid
range of
![]() :
Fig. 6c shows a valley for
:
Fig. 6c shows a valley for
![]() and
and
![]() m.
This is a consequence of comparing the modelled with the observed
images only up to the K-band. Therefore, the fit is only mildly
sensitive to larger grains, and we set
m.
This is a consequence of comparing the modelled with the observed
images only up to the K-band. Therefore, the fit is only mildly
sensitive to larger grains, and we set
![]() m
with no further consequences for the solution.
m
with no further consequences for the solution.
Fitting the images for each wavelength individually delivers only
very small variations in
![]() and disc mass and is
consistent with the multi-wavelength solution within the valid model
parameter range.
and disc mass and is
consistent with the multi-wavelength solution within the valid model
parameter range.
To refine the model selection we fit the SED. The modelled SED includes photospheric emission, scattered light and thermal emission by assuming passive heating of the dust in the disc (Pinte et al. 2006). We use a 3000 K spectrum from Baraffe et al. (1998) in agreement with a spectral type of a low mass star. For each of the best image-fitting models there are only 2 extra free parameters to the SED fitting: the value of foreground extinction AV and the bolometric luminosity of the central source. The latter is a free parameter since we do not see the source directly. The foreground extinction AV describes the material between the observer and the outer limit of the star-disc system and is added to the model after the radiation transfer calculation.
It turns out that only one model is a simultaneous good fit to the
images and to the SED. We consider it our best model in the
following (see third column of Table 2). The SED for
this model is presented in Fig. 3. It includes AV=0.5mag and a stellar luminosity of ![]() 0.4
0.4 ![]() .
.
Photometric variations are observed for IRAS 04158+2805. It results
in a large spread in the SED data at a given wavelength in the
optical and NIR (e.g., ![]() 1.5 mag in the I-band between Strom &
Strom 1994; Luhman 2000). The calculated SED agrees well with the
data points and falls within the range of observed variations. The
estimated extinction is lower than the value estimated by Strom &
Strom (1994; AJ=0.7), Luhman & Rieke (1998; AJ=1.5), and
Luhman (2000, AH=1.5) in the NIR. However these estimations did
not take into account the fact that the object's colours are
strongly modified by the scattering in the circumstellar material.
We therefore believe that our estimate of the foreground
extinction is more robust than previous estimates.
1.5 mag in the I-band between Strom &
Strom 1994; Luhman 2000). The calculated SED agrees well with the
data points and falls within the range of observed variations. The
estimated extinction is lower than the value estimated by Strom &
Strom (1994; AJ=0.7), Luhman & Rieke (1998; AJ=1.5), and
Luhman (2000, AH=1.5) in the NIR. However these estimations did
not take into account the fact that the object's colours are
strongly modified by the scattering in the circumstellar material.
We therefore believe that our estimate of the foreground
extinction is more robust than previous estimates.
The
parameters of the best-fitting model are described in
Table 2 under ``best model''. To define the ``acceptable
range'' (see fourth column of Table 2) we calculated
series of images from the best model in which only one parameter at
a time was varied from its best fit value. This allowed us to define
a possible range of solutions, i.e., solutions with values of f2only moderately higher than the best model (
![]() )
or images that showed no obvious mismatches with the
observations by an eyeball comparison. These ranges give a feeling
of how tightly each parameter is constrained.
)
or images that showed no obvious mismatches with the
observations by an eyeball comparison. These ranges give a feeling
of how tightly each parameter is constrained.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{5685fig8.eps}\end{figure}](/articles/aa/full/2008/26/aa5685-06/Timg90.gif) |
Figure 8: Difference of observed and modelled polarisation percentage ( top) and polarisation direction ( bottom) along the ridges (black) and the symmetry line (grey). |
| Open with DEXTER | |
For the best-fitting model we compared the polarisation map with the data. Observational effects are applied to the model polarisation output in a similar manner as for the direct images.
To compare the model with the data, the polarisation values are
extracted along the ridges and the symmetry axis of the Northern
nebula (see Fig. 4 left and middle panel) and
compared as a function of distance from the central source (right
panel). The difference of the observed and the modelled polarisation
rate and orientation can be found in Fig. 8. The
observed polarisation rates are reproduced reasonably well along the
ridges by the model (
![]() )
except on the central
peak where the model predicts only a 1.2% polarisation instead of
the observed 3.3%. The large difference in polarisation orientation
close to the central peak is an artifact from the exact peak
placement and has no physical meaning. The upper limit of the
observed polarisation is also well reproduced (
)
except on the central
peak where the model predicts only a 1.2% polarisation instead of
the observed 3.3%. The large difference in polarisation orientation
close to the central peak is an artifact from the exact peak
placement and has no physical meaning. The upper limit of the
observed polarisation is also well reproduced (![]() 30%). Along
the symmetry axis of the nebula the general trend is also correct,
rising from central source to edge, but the model polarisation
appears to be systematically lower by a few percent compared to the
data. Nonetheless, the trends are well reproduced as well as the
observed maximum polarisation rates.
30%). Along
the symmetry axis of the nebula the general trend is also correct,
rising from central source to edge, but the model polarisation
appears to be systematically lower by a few percent compared to the
data. Nonetheless, the trends are well reproduced as well as the
observed maximum polarisation rates.
Table 3: Extracted observables of the observation and the best-fit model.
We were able to fit a dust disc model to the observations of IRAS 04158+2805 that matches the I-, H- and K-band images as well as the SED from visual to far-infrared and the I-band polarisation rate at different object positions. Since our model uses simple assumptions, such as homogeneous spherical grains, power-law distributions (grain size, surface density, flaring) and no dust settling, these results provide a useful insight on the geometry of the circumstellar environment.
We fitted the observation well in terms of the width of the nebula, opening angle and peak-to-peak distance and brightness contrast (see Table 3 for all observables). The triangularity tis well fitted for the I- and H-band but for the K-band the model is too triangular. At the centre of the object, the model predicts a polarisation rate which is slightly below the observed value. While this probably indicates that our grain model needs refinement (either in its size distribution, composition or grain shape), the former may indicate that we need a more complex geometry either for the disc or for the emitting source. For instance, K-band emission from the inner parts of the disc might be an important source of photons, which is neglected in our calculations. To check this possibility we calculated a K-band model image that includes the disc emission as a source for scattered photons for our best-fitting model. It turns out that the star is so cool that, at the 0.5 AU assumed inner radius, the dust reaches a temperature of only 400 K. As a consequence, roughly 99% of all K-band photons emitted by the system come from the star and, therefore, the resulting images are unchanged if we include or neglect the disc emission. Vertical settling could also play a role, as well as the presence of a remnant halo that could be responsible for the roundish 4-5''structure best highlighted at K-band, where the extinction of the material located in front becomes much lower.
By comparing the I-band observed and modelled images, the shape of the counter nebula and the dark lane between the two bright areas do not coincide exactly. The model did not take into account the absorption of background light in the dust lane. The artificial noise of the model images was produced by adding Poisson noise to the scattered light images and by superposing position-independent Gaussian-noise. This does not reflect the real nature of the background since IRAS 04158+2805 is illuminated by the large reflection nebulosity in the back. Therefore, we may expect a difference of the observation and the models at those wavelengths where the background light dominates the noise. In the H- and K-bands this dominance is not visible in the observed images.
The model underpredicts the millimeter flux by a factor of 3 but uncertainties are large regarding dust opacities in this regime, typically by a factor of 5. Also, the mm-data were obtained with an 11 arcsec beam and may suffer from background contamination, hence overestimate the true flux. Higher resolution millimeter data is needed to investigate this discrepancy further.
Nevertheless, one single model can describe accurately the scattered light images in three wavelength bands, the SED and the polarisation map of IRAS 04158+2805. The method applied here is therefore generally valid and promising to find parameters for relatively simply structured dust discs.
From our model, we can easily derive the column density
![]() by integrating the dust density structure along our
line of sight to the central source. We find
by integrating the dust density structure along our
line of sight to the central source. We find
![]() g cm-2. From
g cm-2. From
![]() we obtain a gas column density
we obtain a gas column density
![]() g cm-2 by assuming interstellar
abundances (Morrison & McCammon 1983). This provides an estimate of
the total gas-to-dust ratio in a protoplanetary disc, along the line
of sight that grazes the disc top layers in this case. To our
knowledge this is the first time it is obtained directly using
g cm-2 by assuming interstellar
abundances (Morrison & McCammon 1983). This provides an estimate of
the total gas-to-dust ratio in a protoplanetary disc, along the line
of sight that grazes the disc top layers in this case. To our
knowledge this is the first time it is obtained directly using ![]() rather than
rather than
![]() :
:
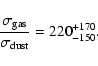 |
(5) |
In any case, we do find an upper limit to the gas-to-dust ratio
(albeit not a lower limit) of ![]()
![]() ,
which
provides clear evidence that the disc cannot be strongly (e.g. by an
order of magnitude) depleted of dust along the line of sight to the
star. Such dust depletion would be expected if strong settling of
dust toward the disc midplane had occurred.
,
which
provides clear evidence that the disc cannot be strongly (e.g. by an
order of magnitude) depleted of dust along the line of sight to the
star. Such dust depletion would be expected if strong settling of
dust toward the disc midplane had occurred.
We have shown that we can well reproduce all observational properties of IRAS04158 with a simple model of a nearly edge-on disc, i.e., that of a Class II source without substantial circumstellar envelope. This result confirms prior classifications by e.g. Park & Kenyon (2002) or Kenyon & Hartmann (1995). The flat SED of IRAS 04158+2805 can be interpreted in terms of a high inclination to the line of sight instead of invoking a highly embedded source, as a protostar would be. This work demonstrates the importance of understanding the circumstellar geometry to assess the nature of the central source. Here, an edge-on disc blocks our direct view towards the central object, flattening the shape of the SED. It is known that a classical T Tauri star can have a rising near- to mid-infrared SED. But only a few mimic an embedded source, as is the case for IRAS 04158+2805. Most sources such as HH30 (see, e.g., Wood et al. 2006), HK Tau B, or HV Tau C, do have a declining near- to mid-IR SED, and the second peak from thermal emission is found only at longer wavelengths.
Interestingly, IRAS 04158+2804 is just above the substellar limit,
based on its spectral type. If our model is correct, it hosts a
large massive disc implying that some of the lowest-mass T Tauri
stars, at least in Taurus, can be surrounded by ![]() 1000 AU-radius
discs. This object likely formed from the collapse of a small
pre-stellar core and is very unlikely to have undergone any violent
dynamical interaction, such as an ejection from an unstable multiple
system (e.g. Reipurth & Clarke 2001). This result adds support to
the idea that the ejection scenario is not the only mode to form VLM
T Tauri stars and brown dwarfs.
1000 AU-radius
discs. This object likely formed from the collapse of a small
pre-stellar core and is very unlikely to have undergone any violent
dynamical interaction, such as an ejection from an unstable multiple
system (e.g. Reipurth & Clarke 2001). This result adds support to
the idea that the ejection scenario is not the only mode to form VLM
T Tauri stars and brown dwarfs.
Also, considering the probable mass of the central star ![]()
![]() ,
the total dust-disc mass we derive
(
,
the total dust-disc mass we derive
(
![]() )
and the gas-to-dust ratio we derived
(
)
and the gas-to-dust ratio we derived
(![]() 220, assuming it is true throughout the disc and not only
along our line of sight), this implies a total disc/star mass ratio
of
220, assuming it is true throughout the disc and not only
along our line of sight), this implies a total disc/star mass ratio
of ![]() 0.1-0.2. In other words, the disc is close to the limit
against gravitational instability. Because collapse in these
gravitationally unstable discs is one suggested mode for planet
formation, it is of great importance to study IRAS 04158+2805
further: the estimation of both the gas and the dust masses need to
be refined. The gas mass estimation can be improved by much deeper
X-ray observations while the dust mass can be obtained better with
models witch use more free parameters and which are directly fitted
on the images, not just a handful of observables.
0.1-0.2. In other words, the disc is close to the limit
against gravitational instability. Because collapse in these
gravitationally unstable discs is one suggested mode for planet
formation, it is of great importance to study IRAS 04158+2805
further: the estimation of both the gas and the dust masses need to
be refined. The gas mass estimation can be improved by much deeper
X-ray observations while the dust mass can be obtained better with
models witch use more free parameters and which are directly fitted
on the images, not just a handful of observables.
In this paper we presented a multiwavelength study of
IRAS 04158+2805 and its circumstellar environment. We modelled the
shape and brightness profiles of the reflection nebulosity in three
optical and NIR bands (I-, H- and K-band) with MCFOST, a Monte Carlo
polarised radiative transfer code, and found a good agreement
between the model and the data. Many parameters of the final model
are well constrained (e.g., inclination,
![]() ,
,
![]() )
while a few remain poorly determined. The
scale height h and
)
while a few remain poorly determined. The
scale height h and ![]() are degenerate but the pair h-
are degenerate but the pair h-![]() is
relatively constrained.
is
relatively constrained.
The disc model parameters used to match the data are listed in
Table 2. They are 2 ![]() m for the maximum dust grain
size,
m for the maximum dust grain
size,
![]() for the dust disc mass, 1120 AU for
the outer disc radius, 1.2 for the exponent
for the dust disc mass, 1120 AU for
the outer disc radius, 1.2 for the exponent ![]() of the flaring
law, -1.0 for the exponent
of the flaring
law, -1.0 for the exponent ![]() of the radial dust density law,
a scale height of 8 AU at a radius of 50 AU and an inclination of 62.7
of the radial dust density law,
a scale height of 8 AU at a radius of 50 AU and an inclination of 62.7![]() .
.
The best model fits the observed SED well. However, it falls slightly short of producing the right amount of 1.3 mm continuum flux by about a factor of 3. The model also reproduces reasonably the observed I-band polarisation behaviour along the symmetry axis and ridges of the Northern nebula.
Combining dust disc models with X-ray spectroscopy allowed probing the gas-to-dust ratio in the disc. We found a value of 220+170-150 which is compatible with the ISM value and the value generally assumed in protoplanetary discs.
According to its spectral type, IRAS 04158+2805 has a mass slightly above the substellar limit. Clearly, stars with such a low mass keep being formed by accretion from a circumstellar disc whose properties do not seem to differ significantly from those of their more massive young counterparts. It would be interesting to push the search further for disc images around less massive objects, located well into the substellar regime.
Acknowledgements
This work is based in part on archival data obtained with the S PITZER Space Telescope, which is operated by the Jet Propulsion Laboratory, California Institute of Technology under a contract with NASA. Support for this work was provided in part by an award issued by JPL/Caltech and in part by Programme National de Physique Stellaire (PNPS) of CNRS/INSU (France). We are grateful to Sylvain Bontemps for obtaining the CFHTIR images presented here and to Jérome Bouvier for performing their basic data reduction. The CXC X-ray Observatory Center is operated by the Smithsonian Astrophysical Observatory for and on behalf of the NASA under contract NAS8-03060.