A&A 485, 33-39 (2008)
DOI: 10.1051/0004-6361:200809606
High-spatial resolution SED of NGC 1068 from near-IR to radio
Disentangling the thermal and non-thermal contributions
S. F. Hönig1 -
M. A. Prieto2 -
T. Beckert1
1 - Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
2 -
Instituto Astrofisica de Canarias, 38200 La Laguna, Tenerife, Spain
Received 19 February 2008 / Accepted 27 March 2008
Abstract
We investigate the idea that a sizable fraction of the interferometrically unresolved infrared emission of the nucleus of NGC 1068 might originate from processes other than thermal dust emission from the torus. We examine the contribution of free-free or synchrotron emission to the central mid- and near-IR parsec-scale emitting region of NGC 1068. Each mechanism is constrained using parsec scale radio data available for NGC 1068 in the
109 -1011 Hz regime, and compared with the highest-resolution interferometric data available in the mid-infrared. It is shown that the unresolved emission in the interferometric observation (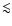 1 pc) is still dominated by dust emission and not by contributions from synchrotron or free-free emission. As previous studies suggest, the interferometric observations appear to infer a clumpy structure of the dust distribution. Extrapolation of the radio free-free or synchrotron emission to the IR indicates that their contribution is <20% even for the unresolved fraction of the interferometric flux.
1 pc) is still dominated by dust emission and not by contributions from synchrotron or free-free emission. As previous studies suggest, the interferometric observations appear to infer a clumpy structure of the dust distribution. Extrapolation of the radio free-free or synchrotron emission to the IR indicates that their contribution is <20% even for the unresolved fraction of the interferometric flux.
The slope of the available radio data is consistent with a power law exponent
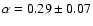 that we interpret in terms of either free-free emission or synchrotron radiation from quasi-monochromatic electrons. We apply emission models for both mechanisms to obtain physical parameters.
that we interpret in terms of either free-free emission or synchrotron radiation from quasi-monochromatic electrons. We apply emission models for both mechanisms to obtain physical parameters.
Furthermore, we attempt to quantify the possible contribution of the accretion disk to the near-infrared emission. It has been suggested, that the unresolved K-band flux in VLTI/VINCI interferometric observation at 46 m baseline (40% of the total K-band flux) might originate in the accretion disk. By using an accretion disk spectrum that has been adjusted to the luminosity and black hole mass of NGC 1068, we find that the expected accretion-disk flux in the K-band is negligible. Moreover, the scenario of detecting the accretion disk through holes in a clumpy torus is extremely unlikely. We conclude that all current IR data of NGC 1068 trace the torus dust emission, favoring a clumpy torus.
Key words: galaxies: Seyfert - galaxies: nuclei - galaxies: individual: NGC 1068 - infrared: galaxies - ISM: dust, extinction
1 Introduction
The nucleus of the nearby Seyfert 2 galaxy NGC 1068 - at a distance of
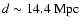 at which a scale of 10 mas corresponds to
at which a scale of 10 mas corresponds to 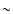 0.7 pc - has been the prime target of the most recent high spatial resolution studies of AGN at frequencies from the infrared (IR) to the radio (e.g., Weigelt et al. 2004; Gallimore et al. 2004; Jaffe et al. 2004; Wittkowski et al. 2004). For the first time, it is possible to construct a genuine nuclear spectrum of the immediate vicinity of the AGN. Near- (NIR) and mid-infrared (MIR) interferometric observations resolved the nuclear IR emission source (Weigelt et al. 2004; Wittkowski et al. 1998; Jaffe et al. 2004). It was proposed that the nuclear radio emission emanates from an accretion disk corona or an associated jet while the infrared emission is probably caused by thermal dust emission in the circumnuclear dusty torus (e.g., Gallimore et al. 2004; Hönig et al. 2006; Gallimore et al. 1996).
0.7 pc - has been the prime target of the most recent high spatial resolution studies of AGN at frequencies from the infrared (IR) to the radio (e.g., Weigelt et al. 2004; Gallimore et al. 2004; Jaffe et al. 2004; Wittkowski et al. 2004). For the first time, it is possible to construct a genuine nuclear spectrum of the immediate vicinity of the AGN. Near- (NIR) and mid-infrared (MIR) interferometric observations resolved the nuclear IR emission source (Weigelt et al. 2004; Wittkowski et al. 1998; Jaffe et al. 2004). It was proposed that the nuclear radio emission emanates from an accretion disk corona or an associated jet while the infrared emission is probably caused by thermal dust emission in the circumnuclear dusty torus (e.g., Gallimore et al. 2004; Hönig et al. 2006; Gallimore et al. 1996).
It is yet unclear, however, how each component contributes to the nuclear flux at different frequencies. MIR VLTI/MIDI interferometric observations by Jaffe et al. (2004) showed that approximately 20% of the MIR emission originates in an unresolved source of size
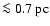 .
Wittkowski et al. (2004) reported that K-band interferometry acquired using the VLTI/VINCI instrument at 46 m baseline revealed a surprisingly high contribution of 40% to the entire nuclear flux by an unresolved source with a diameter
.
Wittkowski et al. (2004) reported that K-band interferometry acquired using the VLTI/VINCI instrument at 46 m baseline revealed a surprisingly high contribution of 40% to the entire nuclear flux by an unresolved source with a diameter 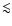
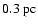 .
This can be explained by either radiation from a small compact source, which is associated with the nuclear radio spectrum (e.g., Wittkowski et al. 1998), or substructure inside a clumpy dust torus (Hönig et al. 2006).
.
This can be explained by either radiation from a small compact source, which is associated with the nuclear radio spectrum (e.g., Wittkowski et al. 1998), or substructure inside a clumpy dust torus (Hönig et al. 2006).
In this paper, we combine high spatial resolution photometry, radiative-transfer simulations in the IR, and emission models in the radio to compare the extrapolated radio emission with measurements at IR frequencies, in order to investigate the origin of the resolved and unresolved the near- and mid-infrared emission. In Sect. 2, we summarize the observational data used for our study. In Sect. 3, we describe the models which were used at radio and IR frequencies, respectively. In the following Sect. 4, we discuss the model results and analyse the maximum contributions of the radio component to the observed NIR and MIR emission of diffraction-limited and interferometric data.
In Sect. 5, the contribution of the accretion disk to the IR spectrum is quantified and compared to the interferometric VLTI/VINCI observations. In Sect. 6, we summarize our results.
2 Observational data
Table 1:
High spatial resolution observations of the nulear emission of NGC 1068 from radio to infrared frequencies.
The location of NGC 1068's nucleus in the radio is assumed to be at the center of a 0.8 pc-wide, disk-like structure known as S1, resolved at 5 and 8.4 GHz by Gallimore et al. (2004,1997). In the mid-IR, a Gaussian decomposition of VLTI/MIDI interferometry data places an upper limit of 0.7 pc 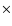 1 pc on the size of the central source at wavelengths
1 pc on the size of the central source at wavelengths
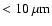 (Jaffe et al. 2004). At
(Jaffe et al. 2004). At
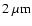 ,
the combination of speckle observations (Weigelt et al. 2004) and VLTI/VINCI interferometry (Wittkowski et al. 2004) confirm the presence of a compact core with Gaussian
,
the combination of speckle observations (Weigelt et al. 2004) and VLTI/VINCI interferometry (Wittkowski et al. 2004) confirm the presence of a compact core with Gaussian
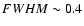 pc. Shortward of
pc. Shortward of
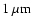 ,
the NGC 1068 nucleus is fully obscured and undetected.
,
the NGC 1068 nucleus is fully obscured and undetected.
The radio to IR to optical SED of NGC 1068's nucleus is extracted from subarcsec photometry currently available for this source. Overall, we sample spatial scales at radio, MIR and NIR wavelengths down to few parsecs. Radio data for the source S1, which is assumed to be the nucleus of NGC 1068, is taken from the VLA/MERLIN 65 mas beam (Gallimore et al. 2004; Muxlow et al. 1996) and VLBA-observation (Gallimore et al. 2004; Roy et al. 1998). Gallimore et al. (2004) reported that they resolved the nuclear source S1 at 5 and 8.4 GHz. S1 appears disk-like with a reference size of 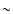 11 mas (for detailed sizes see Table 1). The millimeter data at 1 mm and 3 mm are taken from Krips et al. (2006) and correspond to a beam size of
11 mas (for detailed sizes see Table 1). The millimeter data at 1 mm and 3 mm are taken from Krips et al. (2006) and correspond to a beam size of
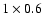 arcsec. Because of the possible contribution of the jet in the 3 mm data, only the peak value as specified by Krips et al. (2006) is considered.
arcsec. Because of the possible contribution of the jet in the 3 mm data, only the peak value as specified by Krips et al. (2006) is considered.
Data in the
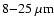 range are taken from Bock et al. (2000) and Tomono et al. (2001), using their reported fluxes in aperture diameters of
range are taken from Bock et al. (2000) and Tomono et al. (2001), using their reported fluxes in aperture diameters of 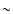 200 mas. This high resolution was obtained by deconvolving their 10 m Keck and 8.2 m Subaru images, respectively. It is important to note that both sets of deconvolved-extracted fluxes differ by <30%.
200 mas. This high resolution was obtained by deconvolving their 10 m Keck and 8.2 m Subaru images, respectively. It is important to note that both sets of deconvolved-extracted fluxes differ by <30%.
Interferometry data from VLTI/MIDI in the
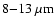 window are taken from Jaffe et al. (2004). For our study, we used the correlated fluxes from the 78 m baseline, which provides the highest resolution data currently available. The visibilities show that the silicate absorption feature becomes more pronounced with growing baseline. This was interpreted as an indication of clumpy substructure within the dust torus (Hönig et al. 2006; Jaffe et al. 2004). At the 78 m baseline, 5-20% of the total flux are unresolved.
window are taken from Jaffe et al. (2004). For our study, we used the correlated fluxes from the 78 m baseline, which provides the highest resolution data currently available. The visibilities show that the silicate absorption feature becomes more pronounced with growing baseline. This was interpreted as an indication of clumpy substructure within the dust torus (Hönig et al. 2006; Jaffe et al. 2004). At the 78 m baseline, 5-20% of the total flux are unresolved.
In the
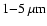 range
range![[*]](/icons/foot_motif.gif) , we use our adaptive optics images acquired using VLT/NACO, in addition to the L-band photometry, which was taken from literature (Marco & Brooks 2003). The spatial resolution achieved in these observations varies from
, we use our adaptive optics images acquired using VLT/NACO, in addition to the L-band photometry, which was taken from literature (Marco & Brooks 2003). The spatial resolution achieved in these observations varies from
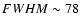 mas in the 1.3-
mas in the 1.3-
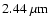 range to FWHM
range to FWHM  160 mas in the M-band. Nuclear fluxes were integrated in an aperture size comparable to those resolutions. These aperture sizes were selected as a compromise to minimize the contribution from the prominent IR diffuse emission surrounding the nucleus of NGC 1068. The
160 mas in the M-band. Nuclear fluxes were integrated in an aperture size comparable to those resolutions. These aperture sizes were selected as a compromise to minimize the contribution from the prominent IR diffuse emission surrounding the nucleus of NGC 1068. The
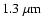 measurement should be considered as an upper limit. The corresponding frequency is the highest at which the core of NGC 1068 can be reliably distinguished from the strong extended emission.
measurement should be considered as an upper limit. The corresponding frequency is the highest at which the core of NGC 1068 can be reliably distinguished from the strong extended emission.
NGC 1068 is Compton-thick to X-ray photons. It shows prominent extended soft X-ray emission as seen by Chandra (Young et al. 2001). The extended emission is preferentially distributed along the ionization cone. XMM spectra show that most of this emission is resolved in multiple emission lines and not much continuum is detected (Kinkhabwala et al. 2002). Due to the Compton thickness of the source and extension of the emission, we do not include X-ray photometry in our modeling of the nucleus.
3 Models
We focused our modeling efforts on two components: (1) the near- and mid-infrared component in the range of 1013-1014 Hz, and (2) the radio component at frequencies from 109 Hz to 1011 Hz. Our aim is to quantify the contribution of each component to emission at different frequencies.
3.1 IR torus model
At infrared wavelengths of the NGC 1068 SED, we used the clumpy torus models of Hönig et al. (2006). With these models, we attempt to fit the photometric data from
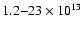 Hz, simultaneously with the 78 m baseline data observed with VLTI/MIDI. A grid of models was calculated where we tested (a) different radial cloud distributions (radial distribution function
Hz, simultaneously with the 78 m baseline data observed with VLTI/MIDI. A grid of models was calculated where we tested (a) different radial cloud distributions (radial distribution function
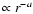 with
a=1.0,1.5,2.0), (b) inclination angles, and (c) average numbers of (optically thick) clouds, N0, in an equatorial line of sight. For each set of model parameters, we simulated 10 different random arrangements of clouds. This accounts for variations in the SEDs that occur due to the actual cloud distribution. Our best-fit model is shown as blue-dashed lines in Figs. 1 and 2.
with
a=1.0,1.5,2.0), (b) inclination angles, and (c) average numbers of (optically thick) clouds, N0, in an equatorial line of sight. For each set of model parameters, we simulated 10 different random arrangements of clouds. This accounts for variations in the SEDs that occur due to the actual cloud distribution. Our best-fit model is shown as blue-dashed lines in Figs. 1 and 2.
The modeled torus has a line-of-sight inclination of 90 deg, which corresponds to an edge-on view of the torus. In radial direction, the clouds are distributed according to a power law
of r-3/2, which is consistent with clumpy torus accretion scenarios where the torus is located in the sphere of influence of the central supermassive black hole (Beckert & Duschl 2004). We assume linear flaring throughout the torus, i.e. the height of the torus H increases with radius,
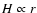 .
The half opening angle of our geometrical configuration is
.
The half opening angle of our geometrical configuration is 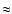 40 deg. Although a general power law
40 deg. Although a general power law
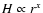 could have been chosen, it was already tested by Hönig et al. (2007,2006) where a more appropriate fit to the IR data could not be found. Furthermore, theoretical considerations and observational studies of clumpy tori seem to favor linear flaring geometries over stronger r-dependences of the torus height (Polletta et al. 2008; Hönig & Beckert 2007). The obscuration of the nucleus in the presented torus model is characterised by an average of N0=10 optically thick dust clouds in an equatorial line of sight. For the edge-on geometry that we model, this corresponds to an average number of clouds, N, which obscure the AGN along the line of sight towards the observer (i.e., N=N0=10, as used in Sect. 5).
could have been chosen, it was already tested by Hönig et al. (2007,2006) where a more appropriate fit to the IR data could not be found. Furthermore, theoretical considerations and observational studies of clumpy tori seem to favor linear flaring geometries over stronger r-dependences of the torus height (Polletta et al. 2008; Hönig & Beckert 2007). The obscuration of the nucleus in the presented torus model is characterised by an average of N0=10 optically thick dust clouds in an equatorial line of sight. For the edge-on geometry that we model, this corresponds to an average number of clouds, N, which obscure the AGN along the line of sight towards the observer (i.e., N=N0=10, as used in Sect. 5).
Table 2:
Parameters of the synchrotron models A, B, and C for the nuclear source S1 of NGC 1068: the linear scale s is the half thickness in model A & B and the radius of the emission spheres in model C. For the mean Lorentz factor
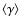 of the electron distributions (width
of the electron distributions (width
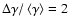 )
there are only lower limits derived form the assumed upper cut-off frequency
)
there are only lower limits derived form the assumed upper cut-off frequency
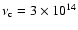 Hz of the synchrontron spectrum. The values for
Hz of the synchrontron spectrum. The values for
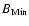 is the minimum energy B-field for the claimed size of s=5.6 mas in model A and upper limits for B and C. The electron density in the last column corresponds to
is the minimum energy B-field for the claimed size of s=5.6 mas in model A and upper limits for B and C. The electron density in the last column corresponds to
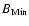 .
.
![\begin{figure}
\par\includegraphics[angle=0,width=14cm]{9606fig1.eps}
\end{figure}](/articles/aa/full/2008/25/aa09606-08/Timg88.gif) |
Figure 1:
High-spatial resolution SED of the nucleus of NGC 1068, in comparison to thermal dust emission from a torus in the IR and non-thermal synchrotron emission in the radio. The blue line shows the clumpy torus model that was used in this study to model the single-dish IR photometry (diamonds) and interferometric observations by VLTI/MIDI (orange solid line; model: dashed-dotted blue line). The radio data (diamonds) are modeled by a spectrum
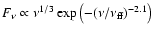 (Synchrotron emission + free-free absorption; green-dotted line) and extrapolated into the infrared. The dashed line shows the synchrotron spectrum attenuated by dust obscuration (
(Synchrotron emission + free-free absorption; green-dotted line) and extrapolated into the infrared. The dashed line shows the synchrotron spectrum attenuated by dust obscuration (
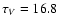 )
to reproduce the J-band data.
regimes. )
to reproduce the J-band data.
regimes. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[angle=0,width=14cm]{9606fig2.eps}
\end{figure}](/articles/aa/full/2008/25/aa09606-08/Timg89.gif) |
Figure 2:
Same as Fig. 1, but with our free-free emission model in the radio. The free-free spectrum was attenuated by dust with 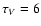 to reproduce the J-band data.
to reproduce the J-band data. |
| Open with DEXTER |
As compared to other model parameters in our grid, the presented model simultaneously reproduces (1) the NIR slope, (2) the depth of the silicate feature, (3) the slope from N-band to Q-band, and (4) the correlated MIDI flux. Due to the ambiguity in actual cloud arrangement, there is some degeneracy in the model parameter space (compare results in Hönig et al. 2006), especially when fitting the SED alone. On the other hand, the presented dust distribution parameters are the only set for which we could find good agreement with the SED properties (1-3) and the interferometric data (4). As a general guideline, a>1.5 produces bluer NIR colors and less Q-band flux, and vice versa for a<1.5 (see also discussion in Polletta et al. 2008).
The observed and modeled diameter of the dust torus is 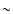 20-30 mas (
20-30 mas (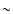 1.4-2 pc), depending on wavelength and orientation. To fit the observed fluxes, a bolometric luminosity of the central AGN of
1.4-2 pc), depending on wavelength and orientation. To fit the observed fluxes, a bolometric luminosity of the central AGN of
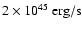 was used. We note that this model luminosity is larger than inferred from the measured fluxes assuming isotropic emission. The reasons for this are anisotropic emission of the torus (type 2 edge-on emission is smaller than type 1 face-on emission) as well as the covering factor of the torus which is smaller than unity, so that not all of the AGN bolometric luminosity is absorbed by the torus. Total discrepancies can be up to one order of magnitude.
was used. We note that this model luminosity is larger than inferred from the measured fluxes assuming isotropic emission. The reasons for this are anisotropic emission of the torus (type 2 edge-on emission is smaller than type 1 face-on emission) as well as the covering factor of the torus which is smaller than unity, so that not all of the AGN bolometric luminosity is absorbed by the torus. Total discrepancies can be up to one order of magnitude.
For radio frequencies lower than 1 THz, we used two different emission models to reproduce the observed high spatial resolution data. In order to study the possible influence of the radio emission sources on the observed IR emission, we assume that the model spectra reach near-IR frequencies without a high-frequency break. In a further step, the model spectra are attenuated by dust extinction so that the model fluxes are consistent with the observed near-IR fluxes. For that, we use different optical depths, 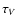 ,
so that the observed J-band flux at 1.2
,
so that the observed J-band flux at 1.2 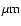 is reproduced only by the radio component (i.e., 100% flux contribution). This procedure provides a robust upper limit to the possible contribution of the radio source to the K-band data where high spatial resolution observations and interferometry is available. We compare the
is reproduced only by the radio component (i.e., 100% flux contribution). This procedure provides a robust upper limit to the possible contribution of the radio source to the K-band data where high spatial resolution observations and interferometry is available. We compare the 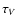 values used with the torus model and the estimated broad-line region obscuration in the next section.
values used with the torus model and the estimated broad-line region obscuration in the next section.
The radio data of NGC 1068 shows an inverted spectrum (
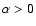 )
between 5-230 GHz with an apparent turnover at
)
between 5-230 GHz with an apparent turnover at 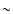 109 Hz. From a least squares fitting to the radio data, we obtain a slope of
109 Hz. From a least squares fitting to the radio data, we obtain a slope of
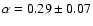 .
This is consistent with a power law index
.
This is consistent with a power law index
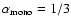 ,
which can be produced by optically thin synchrotron radiation coming from quasi-monoenergetic electrons (Beckert & Duschl 1997). In this scenario, the emission spectrum can be approximated by
,
which can be produced by optically thin synchrotron radiation coming from quasi-monoenergetic electrons (Beckert & Duschl 1997). In this scenario, the emission spectrum can be approximated by
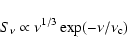 |
(1) |
with an exponential turnover,
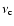 ,
at high frequencies. For the purpose of estimating the maximum possible NIR contribution of the radio source, we assume that
,
at high frequencies. For the purpose of estimating the maximum possible NIR contribution of the radio source, we assume that
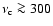 THz, so that the actual high-frequency cutoff can be neglected hereafter. At low frequencies, a turnover can occur, e.g. if the synchrotron source is located within dense plasma leading to thermal free-free absorption
THz, so that the actual high-frequency cutoff can be neglected hereafter. At low frequencies, a turnover can occur, e.g. if the synchrotron source is located within dense plasma leading to thermal free-free absorption
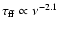 that produces a sharp turnover towards low frequencies (e.g., Beckert et al. 1996). As a result, the synchrotron spectrum is modified by a factor
that produces a sharp turnover towards low frequencies (e.g., Beckert et al. 1996). As a result, the synchrotron spectrum is modified by a factor
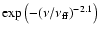 ,
with the low-frequency turnover at
,
with the low-frequency turnover at
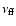 ,
so that the flux can be parameterised by
,
so that the flux can be parameterised by
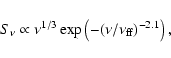 |
(2) |
neglecting the
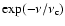 turnover at high frequencies.
turnover at high frequencies.
In Fig. 1, we compare the synchrotron model SED with observed radio fluxes. The low-frequency free-free absorption turnover occurs at
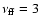 GHz, which is consistent with the upper limit on detections around 1.5 GHz. The spectrum was attentuated by standard ISM dust absorption of optical depth
GHz, which is consistent with the upper limit on detections around 1.5 GHz. The spectrum was attentuated by standard ISM dust absorption of optical depth
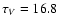 to reproduce the J-band observation.
to reproduce the J-band observation.
An alternative explanation for the low-frequency turnover is synchrotron self-absorption (SSA) within the source. This would result in a spectral turnover from the optically thin
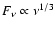 to the optically thick case
to the optically thick case
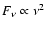 ,
which is less steep than in the case of free-free absorption as discussed above. The optically thick part behaves like a thermal Rayleigh-Jeans branch in contrast to the standard power law electron distribution which corresponds to
,
which is less steep than in the case of free-free absorption as discussed above. The optically thick part behaves like a thermal Rayleigh-Jeans branch in contrast to the standard power law electron distribution which corresponds to
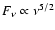 (e.g., Pacholczyk 1970). Given the detection of S1 in NGC 1068 at 5 GHz and the upper limits at
(e.g., Pacholczyk 1970). Given the detection of S1 in NGC 1068 at 5 GHz and the upper limits at 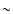 1.4 GHz, the turnover should occur inbetween. The observed lower limit for the power law index in this frequency range (
1.4 GHz, the turnover should occur inbetween. The observed lower limit for the power law index in this frequency range (
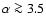 )
favors the free-free absorption scenario over SSA.
)
favors the free-free absorption scenario over SSA.
In a quantitative analysis, we inverted the low-frequency model approximation to synchrotron emission and self-absorption from quasi-monoenergetic electrons (Beckert & Duschl 1997). We suppose that the minimum energy assumption holds for our emission region to link B-field and electron density, 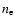 .
The emission region is assumed to be a ellipsoid with apparent axes r,s (volume
.
The emission region is assumed to be a ellipsoid with apparent axes r,s (volume
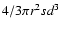 ,
and distance d to NGC 1068; disk-like if s<r). When the low-frequency turnover is due to SSA and the peak of the spectrum, at the end of the
,
and distance d to NGC 1068; disk-like if s<r). When the low-frequency turnover is due to SSA and the peak of the spectrum, at the end of the 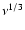 -part, can be determined from observations, it is generally possible to fix the main model parameters, i.e. the B-field strength, the electron density
-part, can be determined from observations, it is generally possible to fix the main model parameters, i.e. the B-field strength, the electron density 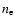 ,
and the Lorentz factor
,
and the Lorentz factor 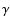 .
Here, we have no knowledge about the peak of the spectrum and only upper limits to the self-absorption frequency since we assume that the steep low-frequency turnover is due to free-free absorption rather than SSA. Thus, only limits on the physical parameters can be determined.
.
Here, we have no knowledge about the peak of the spectrum and only upper limits to the self-absorption frequency since we assume that the steep low-frequency turnover is due to free-free absorption rather than SSA. Thus, only limits on the physical parameters can be determined.
For reference, we use the radio flux of the partly resolved core S1 at 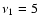 GHz from (Gallimore et al. 2004) of
GHz from (Gallimore et al. 2004) of
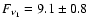 mJy. The size of the elliptical source is 16.6 and 11.2 mas for the major and minor axis, respectively. In Table 2, we use the half axis values, which correspond to radii in the source model.
mJy. The size of the elliptical source is 16.6 and 11.2 mas for the major and minor axis, respectively. In Table 2, we use the half axis values, which correspond to radii in the source model.
Here, we present three synchrotron models for S1. All are based on the 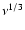 -power law spectrum as described above. In the first case (model A), we assume that the disk is resolved in the radial and vertical direction with a half major axis r = 8.3 mas and a half minor axis s = 5.6 mas. The corresponding source parameters are given in Table 2. In model B, we assume that the actual disk thickness is smaller than the minor axis, s < 5.6 mas, so that the observed vertical extension might be due to disk inclination or warping. In this case, we derive a lower limit for s from the absence of SSA down to 3 GHz. Thus, a lower limit for the mean Lorentz factor
-power law spectrum as described above. In the first case (model A), we assume that the disk is resolved in the radial and vertical direction with a half major axis r = 8.3 mas and a half minor axis s = 5.6 mas. The corresponding source parameters are given in Table 2. In model B, we assume that the actual disk thickness is smaller than the minor axis, s < 5.6 mas, so that the observed vertical extension might be due to disk inclination or warping. In this case, we derive a lower limit for s from the absence of SSA down to 3 GHz. Thus, a lower limit for the mean Lorentz factor 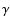 of the electron distribution is obtained, as well as an upper limit for both the corresponding B-field and the density of relativistic electrons in the radiating plasma (values see Table 2).
of the electron distribution is obtained, as well as an upper limit for both the corresponding B-field and the density of relativistic electrons in the radiating plasma (values see Table 2).
The alternative model C is motivated by the orientation of the major axis of S1, which is almost perpendicular to the large-scale radio jet in NGC 1068
(Gallimore et al. 2004; Muxlow et al. 1996). S1 may, therefore, be associated with a perpendicular shock front close to the base of an outflow or the corona of an accretion disk.
The large size of S1 and its low brightness temperature of
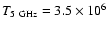 K argues against a large-scale shock. Instead, a corona above an accretion disk may be heated in localized regions through magnetic reconnection or small-scale shock fronts. The corresponding emission regions are much smaller than the size of the underlying disk. In this model C, we assume
K argues against a large-scale shock. Instead, a corona above an accretion disk may be heated in localized regions through magnetic reconnection or small-scale shock fronts. The corresponding emission regions are much smaller than the size of the underlying disk. In this model C, we assume
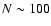 unresolved coronal emission regions which together form S1 and provide the appearance of a thick disk. For simplicity, we assume that the emission regions are spherical and use a size that is three times larger than implied by the SSA limit to avoid mutual absorption by emission regions superimposed on the sky. We obtain lower limits to the sphere radius s and a mean Lorentz factor
unresolved coronal emission regions which together form S1 and provide the appearance of a thick disk. For simplicity, we assume that the emission regions are spherical and use a size that is three times larger than implied by the SSA limit to avoid mutual absorption by emission regions superimposed on the sky. We obtain lower limits to the sphere radius s and a mean Lorentz factor
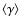 ,
and upper limits for the B-field and relativistic electron density
,
and upper limits for the B-field and relativistic electron density 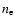 .
The results are summarized in Table 2. In this picture, the relatively large size of S1, when compared to the size of the small emission regions, might be due to electron scattering not directly connected to the small emission regions (e.g. surrounding medium) and provides only an upper size limit.
.
The results are summarized in Table 2. In this picture, the relatively large size of S1, when compared to the size of the small emission regions, might be due to electron scattering not directly connected to the small emission regions (e.g. surrounding medium) and provides only an upper size limit.
For NGC 1068, the possibility of synchrotron emission from quasi-monoenergetic electrons was already explored by Wittkowski et al. (1998) but with a smaller amount of available radio data. Similar models were suggested for other galactic nuclei like Sgr A* (Duschl & Lesch 1994; Beckert & Duschl 1997) or M 81 (Reuter & Lesch 1996). According to Wittkowski et al. (2004), such an emission mechanism would require a source size of the order of 100 AU and electron densities of
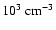 .
While the size is consistent with our estimates, we require lower electron densities in the present analysis.
.
While the size is consistent with our estimates, we require lower electron densities in the present analysis.
The fluxes at the highest radio frequencies >100 GHz are consistent with a flat spectrum. This opens the possibility that the radio spectrum is produced by thermal free-free emission, as already suggested by Gallimore et al. (2004,1997).
To investigate this possibility, we develop a free-free emission model. The flux from thermal free-free emission at frequency 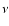 for a given electron temperature T is described by
for a given electron temperature T is described by
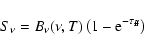 |
(3) |
where
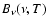 denotes the Planck function
denotes the Planck function
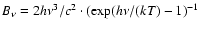 .
The optical depth for the free-free process can be described as
.
The optical depth for the free-free process can be described as
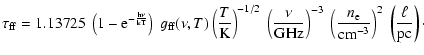 |
|
|
(4) |
Here, the emission measure
 is approximated by a slab with constant electron density
is approximated by a slab with constant electron density 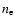 and a typical size
and a typical size 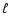 .
The function
.
The function
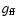 is the Gaunt factor that accounts for the difference between semi-classical and quantum mechanical treatment of free-free emission (Kramers 1923; Gaunt 1930). For low frequencies where
is the Gaunt factor that accounts for the difference between semi-classical and quantum mechanical treatment of free-free emission (Kramers 1923; Gaunt 1930). For low frequencies where
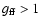 ,
we use the thermally-averaged approximation by Oster (1970,1961),
,
we use the thermally-averaged approximation by Oster (1970,1961),
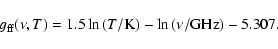 |
(5) |
For high frequencies, exact treatments show that
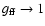 (e.g. Beckert et al. 2000), which we account for by a function that steps in when Eq. (5) would become
(e.g. Beckert et al. 2000), which we account for by a function that steps in when Eq. (5) would become 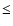 1.
1.
Table 3:
Parameters for the free-free emission model described in the text.
In Fig. 2, we show a free-free emission model fit to the radio SED of NGC 1068. The model parameters (noted as model F) are shown in Table 3. We attenuate the model with ISM dust of optical depth 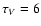 to be consistent with the NIR measurements, which concerns mainly the J-band data point in this case. The low-frequency cutoff occurs at the transition where the medium becomes optically thick to free-free emission. With our parameters, we obtain a cutoff frequency of
to be consistent with the NIR measurements, which concerns mainly the J-band data point in this case. The low-frequency cutoff occurs at the transition where the medium becomes optically thick to free-free emission. With our parameters, we obtain a cutoff frequency of
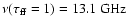 .
For the size of the emission region, we use the resolved core diameter determined using 5 and 8.4 GHz observations by Gallimore et al. (2004, semi-major axis )tex2html_wrap_inline1431#11 mas#. These authors also provide parameters for a free-free model, based on fluxes at their observed frequencies, which approximately agree with our model using a broader frequency range.
.
For the size of the emission region, we use the resolved core diameter determined using 5 and 8.4 GHz observations by Gallimore et al. (2004, semi-major axis )tex2html_wrap_inline1431#11 mas#. These authors also provide parameters for a free-free model, based on fluxes at their observed frequencies, which approximately agree with our model using a broader frequency range.
![\begin{figure}
\par\includegraphics[angle=0,width=13.5cm]{9606fig3.eps}
\end{figure}](/articles/aa/full/2008/25/aa09606-08/Timg135.gif) |
Figure 3:
Accretion disk contribution to the IR spectrum. A standard accretion disk spectrum
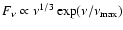 was adjusted for the assumed parameters
was adjusted for the assumed parameters
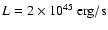 and
and
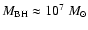 of NGC 1068 (green dotted line) and attenuated by dust obscuration (green dashed line) with
of NGC 1068 (green dotted line) and attenuated by dust obscuration (green dashed line) with
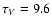 to be consistent with the NIR measurements.
to be consistent with the NIR measurements. |
| Open with DEXTER |
4 The influence of the radio components to the IR
Since there is a gap between the 100 GHz and 10 THz regime, it is difficult to judge how the IR and radio components are connected. In particular, a high frequency turnover for the radio component cannot be determined using existing data. As a consequence, the radio source either breaks before the IR or reaches IR frequencies and, thus, may contribute to the unresolved IR fluxes according to our models as discussed in the previous section. The latter possibility leaves two open questions: (1) Is the unresolved flux in the long-baseline MIR interferometric data from VLTI/MIDI coming from the central AGN, i.e. the radio source? (2) Can the radio source (especially a possible synchrotron source) be responsible for a significant fraction of the unresolved K band flux as observed by Wittkowski et al. (2004)? To address these questions, we extend the two investigated radio models into the IR regime, as discussed in the previous section (Figs. 1 and 2, green dotted lines).
We assume that the radio source is surrounded by the dusty torus. As a result, it suffers extinction by the dust within the torus (Figs. 1 and 2, green dashed lines). The extinction used to reproduce the J-band observation with the radio emission models was, however, much smaller than what is inferred from the lack of optical and infrared broad lines (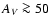 mag Lutz et al. 2000). Thus, the IR contribution of the radio emission source is probably lower than that derived from our analysis that reproduced the J-band data. This enforces the analysis in terms of obtaining strong upper limits for the contribution to the unresolved K-band and mid-IR flux.
mag Lutz et al. 2000). Thus, the IR contribution of the radio emission source is probably lower than that derived from our analysis that reproduced the J-band data. This enforces the analysis in terms of obtaining strong upper limits for the contribution to the unresolved K-band and mid-IR flux.
As can be seen from Figs. 1 and 2, the maximum possible extrapolated mid-IR flux of the synchrotron and free-free power law is still a factor of
5-10 below the unresolved 78 m baseline MIDI flux. As a conservative limit, we estimate the maximum flux contribution of the radio source to the MIR as
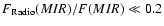 ,
if it is sychrotron emission. This means that the unresolved MIDI flux is most likely originating exclusively from thermal dust emission in the torus rather than from the radio component. As shown in the previous section (see also Hönig et al. 2007,2006), the unresolved emission can be fully interpreted in terms of a clumpy torus model.
,
if it is sychrotron emission. This means that the unresolved MIDI flux is most likely originating exclusively from thermal dust emission in the torus rather than from the radio component. As shown in the previous section (see also Hönig et al. 2007,2006), the unresolved emission can be fully interpreted in terms of a clumpy torus model.
In the near-IR, the constraints are even tighter since (1) the assumption
that 100% of the J-band flux is very conservative and (2) the difference in ``true'' (=broad-line region) and modeled extinction affects near-IR frequencies more than mid-IR frequencies. As can be seen in Figs. 1 and 2, the non-torus contribution to the K-band emission is certainly much less than 20%, no matter if the radio emission is due to synchrotron or free-free emission. This strong upper limit is important for the interpretation of the unresolved flux measured by Wittkowski et al. (2004) using VLTI/VINCI: even though the size of this unresoved emission is smaller than 0.3 pc, it must originate from the torus. Kishimoto el al. (2007) show that this size is consistent with the sublimation radius as expected from reverberation mapping of Type 1 objects and the assumption of a central AGN luminosity of 1045 erg/s. Alternatively, substructure in a clumpy torus can account for the unresolved flux (Hönig et al. 2007).
5 Quantifying the contribution of the accretion disk
An alternative interpretation of unresolved VLTI/VINCI flux is a contribution from the putative accretion disk in the center of NGC 1068, as discussed by Wittkowski et al. (2004). In that case, the torus must be clumpy so that the accretion disk can be seen through ``holes'' of low or no extinction within the torus.
In a clumpy medium with high optical depth of each dust cloud, the probability,
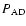 ,
that an accretion disk photon crosses all clouds without being absorbed can be estimated by Poisson statistics,
,
that an accretion disk photon crosses all clouds without being absorbed can be estimated by Poisson statistics,
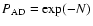 (N = number of clouds along the line-of-sight; Natta & Panagia 1984). From the edge-on torus model as presented in Sect. 3, we obtained N = 10. This corresponds to a probability that the accretion disk is seen through the torus clouds of
(N = number of clouds along the line-of-sight; Natta & Panagia 1984). From the edge-on torus model as presented in Sect. 3, we obtained N = 10. This corresponds to a probability that the accretion disk is seen through the torus clouds of
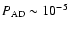 ,
which makes the scenario very unlikely. Nevertheless, we attempt to constrain the possible accretion disk contribution to the K-band flux. For that, we used a standard accretion disk spectrum of the shape
,
which makes the scenario very unlikely. Nevertheless, we attempt to constrain the possible accretion disk contribution to the K-band flux. For that, we used a standard accretion disk spectrum of the shape
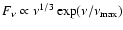 (e.g., Shakura & Sunyaev 1973). The turnover frequency,
(e.g., Shakura & Sunyaev 1973). The turnover frequency,
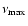 ,
is characterised by the accretion disk temperature at the innermost stable orbit (
,
is characterised by the accretion disk temperature at the innermost stable orbit (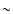
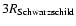 ), which can be inferred from the mass of the central black hole (
), which can be inferred from the mass of the central black hole (
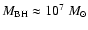 ,
Greenhill et al. 1996) and the modeled bolometric luminosity (
,
Greenhill et al. 1996) and the modeled bolometric luminosity (
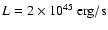 ,
see Sect. 3.1). For NGC 1068, we obtain
,
see Sect. 3.1). For NGC 1068, we obtain
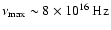 ,
which corresponds to a temperature of approximately
,
which corresponds to a temperature of approximately
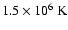 .
We extended the accretion disk spectrum to IR frequencies, such that the integrated accretion disk spectrum matches the bolometric luminosity as inferred from torus modeling. This enables the thermal emission from the accretion disk to be constrained, although it is completely obscured in the UV and optical.
.
We extended the accretion disk spectrum to IR frequencies, such that the integrated accretion disk spectrum matches the bolometric luminosity as inferred from torus modeling. This enables the thermal emission from the accretion disk to be constrained, although it is completely obscured in the UV and optical.
In Fig. 3, we show a comparison of the observed fluxes with the clumpy torus model (Sect. 3.1), and the accretion disk spectrum which is extrapolated from the UV to the MIR (dotted line) and attenuated by dust extinction with
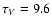 (dashed line) to reproduce the J-band flux. The obscured accretion disk spectrum is obviously unable to contribute significantly to the NIR or MIR emission. Again, we note that the actual extinction towards the broad-line region is much higher than that used to obtain an upper limit as described in the previous section. Thus, we safely conclude that the unresolved K-band flux as observed with VLTI/VINCI (40% of the total nuclear flux) does not originate from the accretion disk.
(dashed line) to reproduce the J-band flux. The obscured accretion disk spectrum is obviously unable to contribute significantly to the NIR or MIR emission. Again, we note that the actual extinction towards the broad-line region is much higher than that used to obtain an upper limit as described in the previous section. Thus, we safely conclude that the unresolved K-band flux as observed with VLTI/VINCI (40% of the total nuclear flux) does not originate from the accretion disk.
6 Summary and conclusions
We analysed the SED of NGC 1068 from 109 Hz to 1014 Hz. The SED was modeled by two components: (1) an IR component that is represented by a clumpy torus model, and (2) a radio component described either by synchrotron emission with
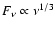 ,
or optically thin free-free emission. For the infrared, we used our clumpy torus model to reproduce simultaneously the high-resolution NIR-to-MIR SED and the VLTI/MIDI correlated fluxes at 78 m baseline. The model is characterized by a radial cloud density distribution
,
or optically thin free-free emission. For the infrared, we used our clumpy torus model to reproduce simultaneously the high-resolution NIR-to-MIR SED and the VLTI/MIDI correlated fluxes at 78 m baseline. The model is characterized by a radial cloud density distribution 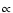 r-3/2 and a half opening angle of 40
r-3/2 and a half opening angle of 40
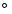 .
The central AGN is obscured by 10 dust clouds, on average, along a radial line of sight in the equatorial plane. For the radio source, we showed that the power law index of
.
The central AGN is obscured by 10 dust clouds, on average, along a radial line of sight in the equatorial plane. For the radio source, we showed that the power law index of
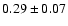 is consistent with a spectral slope proportional to
is consistent with a spectral slope proportional to 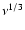 ,
which is expected from synchrotron emission by quasi-monoenergetic electrons. Further more, we showed that the radio emission can also originate from thermal free-free emission. Both radio models require a low-frequency turnover between 1 and 10 GHz where the spectral slope changes. The steepness in the range between 1-6 GHz suggests that the turnover is caused by a foreground screen of thermal plasma that becomes optically thick below
,
which is expected from synchrotron emission by quasi-monoenergetic electrons. Further more, we showed that the radio emission can also originate from thermal free-free emission. Both radio models require a low-frequency turnover between 1 and 10 GHz where the spectral slope changes. The steepness in the range between 1-6 GHz suggests that the turnover is caused by a foreground screen of thermal plasma that becomes optically thick below 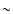 3-6 GHz
3-6 GHz
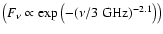 .
This can be connected to the gas in either the galaxy or the torus.
.
This can be connected to the gas in either the galaxy or the torus.
For both scenarios - synchrotron and free-free emission - we presented models to extract physical parameters from the radio SED, depending on the emission mechanism. The observed source sizes at 5 and 8.4 GHz are consistent with a scenario in which synchrotron emission emanates either from a disk (models A and B) or from small emission regions connected to the disk (e.g. magnetical reconnection zones in the disk corona), and possibly additional electron scattering in the surrounding medium (model C). The necessary Lorentz factors are
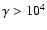 with B-field strengths of the order of 0.1-1 G. When the radio SED is attributed to thermal free-free emission (model F), the observed fluxes and source sizes require an electron density
with B-field strengths of the order of 0.1-1 G. When the radio SED is attributed to thermal free-free emission (model F), the observed fluxes and source sizes require an electron density
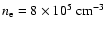 and a temperature
and a temperature
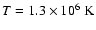 .
.
The main goal of this study was to disentangle the contribution of near- and mid-infrared torus dust emission from that of possible contamination by the radio source. For that, we extrapolated the free-free and synchrotron models to the infrared. It was possible to show that the radio source is contributing certainly <20% to the observed unresolved flux at 78 m baseline. A similar analysis shows that the unresolved K-band flux, as observed using VLTI/VINCI, originates in the torus and is almost uncontaminated by the radio source. We were able to argue against the possibility that in the K-band the accretion disk might be seen through holes in the clumpy torus. This means that all observed near- and mid-IR emission - resolved and unresolved - is thermal dust emission from the torus. This interpretation is consistent with the clumpy torus model that was presented. It is, however, not clear if the unresolved K-band flux represents emission from the inner boundary of the torus as indicated by Kishimoto el al. (2007), or is due to the clumpy substructure of the torus (Hönig et al. 2006; Hönig & Beckert 2007).
Acknowledgements
The authors would like to thank M. Kishimoto for fruitful discussions and Ian Robson for helpful comments and suggestions that improved the paper.
- Beckert, T., &
Duschl, W. J. 1997, A&A, 328, 95 [NASA ADS]
(In the text)
- Beckert, T., &
Duschl, W. J. 2004, A&A, 426, 445 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Beckert, T., Duschl,
W. J., Mezger, P. G., & Zylka, R. 1996, A&A, 307,
450 [NASA ADS]
(In the text)
- Beckert, T., Duschl,
W. J., & Mezger, P. G. 2000, A&A, 356, 1149 [NASA ADS]
(In the text)
- Bock, J. J.,
Neugebauer, G., Matthews, K., et al. 2000, AJ, 120, 2904 [NASA ADS] [CrossRef]
(In the text)
- Duschl , W. J., &
Lesch, H. 1994, A&A, 286, 431 [NASA ADS]
- Gallimore, J. F.,
Baum, S. A., O'Dea, C. P., & Pedlar, A. 1996, ApJ, 464,
198 [NASA ADS] [CrossRef]
- Gallimore, J. F.,
Baum, S. A., & O'Dea, C. P. 1997, Nature, 388, 852 [NASA ADS] [CrossRef]
- Gallimore, J. F.,
Baum, S. A., & O'Dea, C. P. 2004, ApJ, 613, 794 [NASA ADS] [CrossRef]
- Gaunt, J. A., Phil.
Trans. R. Soc. London, Ser. A, 229, 163
- Greenhill, L. J.,
Gwinn, C. R., Antonucci, R., & Barvainis, R. 1996, ApJ,
472, L21 [NASA ADS] [CrossRef]
(In the text)
- Hönig, S. F.,
Beckert, T., Ohnaka, K., & Weigelt, G. 2006, A&A, 452,
459 [NASA ADS] [CrossRef] [EDP Sciences]
- Hönig, S. F.,
Beckert, T., Ohnaka, K., & Weigelt, G. 2007, ASPC, 373, 487 [NASA ADS]
[arXiv:astro-ph/0611946]
- Hönig, S. F.,
& Beckert, T. 2007, MNRAS, 380, 1172 [NASA ADS] [CrossRef]
- Jaffe, W., Meisenheimer,
K., Röttgering, H. J. A., et al. 2004, Nature,
429, 47 [NASA ADS] [CrossRef]
- Kramers, H. A. 1923,
Phil. Mag., 46, 836
- Kinkhabwala, A., Sako,
M., Behar, E., Kahn, S. M., & Paerels, F. 2002, ApJ, 575,
732 [NASA ADS] [CrossRef]
(In the text)
- Kishimoto, M.,
Hönig, S. F., Beckert, T., & Weigelt, G. 2007,
A&A, 476, 713 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Krips, M., Eckart, A.,
Neri, R., et al. 2006, A&A, 446, 113 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Lutz, D., Genzel, R.,
Sturm, E., et al. 2000, ApJ, 530, L733 [NASA ADS] [CrossRef]
(In the text)
- Marco, O., & Brooks,
K. J. 2003, A&A, 398, 101 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Muxlow,
T. W. B., Pedlar, A., Holloway, A. J., Gallimore,
J. F., & Antonucci, R. R. J. 1996, MNRAS, 278,
854 [NASA ADS]
- Natta, A., & Panagia,
N. 1984, ApJ, 287, 228 [NASA ADS] [CrossRef]
(In the text)
- Oster, L. 1961, ApJ, 134,
1010 [NASA ADS] [CrossRef]
- Oster, L. 1970, A&A,
9, 318 [NASA ADS]
- Pacholczyk, A. G. 1970,
Radio astrophysics (San Francisco: Freeman)
(In the text)
- Polletta, M., Weedman,
D., Hönig, S. F., et al. 2007, ApJ, 675, 960 [NASA ADS] [CrossRef]
- Reuter, H.-P., &
Lesch, H. 1996, A&A, 310, L5 [NASA ADS]
(In the text)
- Roy, A. L., Colbert,
E. J. M., Wilson, A. S., & Ulvestad, J. S.
1998, ApJ, 504, 147 [NASA ADS] [CrossRef]
- Shakura, N. I.,
& Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS]
(In the text)
- Tomono, D., Doi, Y.,
Usuda, T., & Nishimura, T. 2001, ApJ, 557, 637 [NASA ADS] [CrossRef]
(In the text)
- Weigelt, G., Wittkowski,
M., Balega, Y. Y., et al. 2004, A&A, 425, 77 [NASA ADS] [CrossRef] [EDP Sciences]
- Wittkowski, M., Balega,
Y., Beckert, T., et al. 1998, A&A, 329, L45 [NASA ADS]
- Wittkowski, M., Kervella,
P., Arsenault, R., et al. 2004, A&A, 418, L39 [NASA ADS] [CrossRef] [EDP Sciences]
- Young, A. J.,
Wilson, A. S., & Shopbell, P. L. 2001, ApJ, 556,
6 [NASA ADS] [CrossRef]
(In the text)
Copyright ESO 2008
![\begin{figure}
\par\includegraphics[angle=0,width=14cm]{9606fig1.eps}
\end{figure}](/articles/aa/full/2008/25/aa09606-08/Timg88.gif)
![\begin{figure}
\par\includegraphics[angle=0,width=14cm]{9606fig2.eps}
\end{figure}](/articles/aa/full/2008/25/aa09606-08/Timg89.gif)
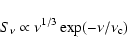
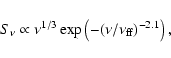
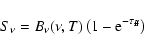
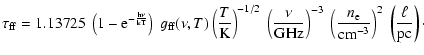
![\begin{figure}
\par\includegraphics[angle=0,width=13.5cm]{9606fig3.eps}
\end{figure}](/articles/aa/full/2008/25/aa09606-08/Timg135.gif)