A&A 485, 267-273 (2008)
DOI: 10.1051/0004-6361:200809351
Turbulent magnetic pumping in a Babcock-Leighton solar dynamo
model
G. Guerrero - E. M. de Gouveia Dal Pino
Astronomy Department, Instituto de Astronomia,
Geofísica e Ciências Atmosfêricas,
Universidade de São Paulo,
Rua do Matão 1226, São Paulo, Brazil
Received 3 January 2008 / Accepted 18 March 2000
Abstract
Context. The turbulent pumping effect corresponds to the transport of magnetic flux due to the presence of density and turbulence gradients in convectively unstable layers. In the induction equation it appears as an advective term and for this reason it is expected to be important in the solar and stellar dynamo processes.
Aims. We explore the effects of turbulent pumping in a flux-dominated Babcock-Leighton solar dynamo model with a solar-like rotation law.
Methods. As a first step, only vertical pumping has been considered through the inclusion of a radial diamagnetic term in the induction equation. In the second step, a latitudinal pumping term was included and then, a near-surface shear was included.
Results. The results reveal the importance of the pumping mechanism in solving current limitations in mean field dynamo modeling, such as the storage of the magnetic flux and the latitudinal distribution of the sunspots. If a meridional flow is assumed to be present only in the upper part of the convective zone, it is the full turbulent pumping that regulates both the period of the solar cycle and the latitudinal distribution of the sunspot activity. In models that consider shear near the surface, a second shell of toroidal field is generated above
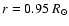 at all latitudes. If the full pumping is also included, the polar toroidal fields are efficiently advected inwards, and the toroidal magnetic activity survives only at the observed latitudes near the equator. With regard to the parity of the magnetic field, only models that combine turbulent pumping with near-surface shear always converge to the dipolar parity.
at all latitudes. If the full pumping is also included, the polar toroidal fields are efficiently advected inwards, and the toroidal magnetic activity survives only at the observed latitudes near the equator. With regard to the parity of the magnetic field, only models that combine turbulent pumping with near-surface shear always converge to the dipolar parity.
Conclusions. This result suggests that, under the Babcock-Leighton approach, the equartorward motion of the observed magnetic activity is governed by the latitudinal pumping of the toroidal magnetic field rather than by a large scale coherent meridional flow. Our results support the idea that the parity problem is related to the quadrupolar imprint of the meridional flow on the poloidal component of the magnetic field and the turbulent pumping positively contributes to wash out this imprint.
Key words: Sun: magnetic fields - Sun: activity
Flux-dominated Babcock-Leighton (FDBL) solar dynamos are mean field
models where the poloidal field is generated at the surface by the
transport and decay of bipolar magnetic regions (BMRs) which are
formed by twisted buoyant magnetic flux ropes. For this process to
occur, differential rotation must be able to develop intense
toroidal magnetic fields either at the tachocline or at the
convection zone. Numerical simulations have shown that magnetic flux
tubes with intensities around 104-105 G are able to become
buoyantly unstable and to emerge at the surface to form a bipolar
magnetic region with the appropriate tilt, in agreement with
Joy's law. One important limitation of this scenario is that
105 G results an energy density that is an order of magnitude
higher than the equipartition value, so that a stable layer is
required to store and amplify the magnetic fields. This raises
another problem with regard to the way in which the magnetic flux is
dragged down to deeper layers.
Given the lack of accurate observations of the flow at the
deeper layers, numerical simulations have shown that the penetration
of the plasma is restricted to only a few kilometers below the
overshoot layer (Rüdiger et al. 2005; Gilman & Miesch 2004). Nevertheless, the magnetic
fields can be transported, not only downwards, but also
longitudinally and latitudinally when strong density and turbulence
gradients are present in the medium due to the turbulent pumping
(Dorch & Nordlund 2001; Ziegler & Rüdiger 2003).
![\begin{figure}
\par\includegraphics[scale=.44]{9351f1.eps}\end{figure}](/articles/aa/full/2008/25/aa09351-08/Timg24.gif) |
Figure 1:
Radial and latitudinal profiles for 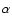 (continuous
line),
(continuous
line), 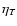 (dotted line) and for the pumping terms
(dotted line) and for the pumping terms 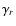 and
and
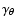 (dashed and dot-dashed lines,
respectively). All the profiles are normalized to their maximum
value.
(dashed and dot-dashed lines,
respectively). All the profiles are normalized to their maximum
value. |
| Open with DEXTER |
In axisymmetric mean field models of the solar cycle, the
effects of turbulent pumping rarely have been considered. A
first approach showing the importance of pumping in the solar
cycle was made by Brandenburg et al. (1992); since then few works have
incorporated the diamagnetic pumping component in the dynamo
equation as an extra diffusive term that provides a downward
velocity (Bonanno et al. 2002; Küker et al. 2001; Bonanno et al. 2006). More recently,
Käpylä et al. (2006b) have implemented simulations of mean field dynamos in
the distributed regime, including all the dynamo coefficients
previously evaluated in magneto-convection simulations
(Ossendrijver et al. 2002; Käpylä et al. 2006a). They have produced butterfly diagrams
that resemble observations. However, to our
knowledge no special efforts have been made to study the pumping
effects in the meridional plane (i.e., inside the convection zone)
or in an FDBL description. The latter has been found to be
particularly successful at reproducing most of the large scale
features of the solar cycle (Dikpati et al. 2004; Guerrero & de Gouveia Dal Pino 2007a,b; Dikpati & Charbonneau 1999, hereafter GDPa,b).
In this work, we explore the effects of turbulent
pumping on an FDBL model. In a first approximation, we include the
radial turbulent diamagnetism velocity term in the induction
equation as described by Kichatinov & Ruediger (1992), and then in a second approach
we add the pumping terms calculated in local magneto-convection
simulations (Ossendrijver et al. 2002; Käpylä et al. 2006a). This latter approximation
includes not only the radial but also the latitudinal contribution of
the pumping. We will also discuss the
implications of pumping when the near-surface radial shear layer
reported by Corbard & Thompson (2002) is considered. In the following sections,
we briefly present the model, our results and outline our
main conclusions.
Our model solves the mean field induction equation:
![\begin{displaymath}
\frac{\partial {\vec B}}{\partial t} = \nabla \times [{\vec ...
...es
{\vec B} + {\bf\cal{E}} - \eta_T \nabla \times {\vec B} ],
\end{displaymath}](/articles/aa/full/2008/25/aa09351-08/img25.gif) |
(1) |
where
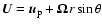 is the
observed velocity field,
is the
observed velocity field, 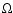 is the angular velocity,
is the angular velocity,
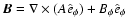 are the poloidal and toroidal components of the magnetic field,
are the poloidal and toroidal components of the magnetic field,
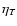 is the magnetic diffusivity and
is the magnetic diffusivity and
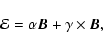 |
(2) |
corresponding to the first order terms of the expansion of the
electromotive force,
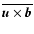 ,
and
representing the action of the small-scale fluctuations over the large
scales. The coefficients of (2) are the so-called dynamo
coefficients. Normally, the mean field models do not consider the
second term on the right hand side of the equation, i.e, the
turbulent pumping. The first term corresponds to the alpha effect
that has been considered in several ways in the literature. A pure
Babcock-Leighton model is an
,
and
representing the action of the small-scale fluctuations over the large
scales. The coefficients of (2) are the so-called dynamo
coefficients. Normally, the mean field models do not consider the
second term on the right hand side of the equation, i.e, the
turbulent pumping. The first term corresponds to the alpha effect
that has been considered in several ways in the literature. A pure
Babcock-Leighton model is an
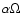 dynamo which represents a
large scale version of the
dynamo which represents a
large scale version of the
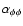 component of the
component of the
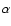 tensor. It should resemble the buoyant rising and
twisting of strong magnetic flux tubes, reproducing events of fast
emergence of them (see the continuous lines in the diagrams of
Fig. 1). We note that another source of poloidal fields may exist
inside the convection zone and at the tachocline, but for our purpose
we consider only the Babcock-Leighton
tensor. It should resemble the buoyant rising and
twisting of strong magnetic flux tubes, reproducing events of fast
emergence of them (see the continuous lines in the diagrams of
Fig. 1). We note that another source of poloidal fields may exist
inside the convection zone and at the tachocline, but for our purpose
we consider only the Babcock-Leighton 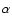 effect since it is
observed at the surface.
effect since it is
observed at the surface.
We solve Eq. (1) for A and 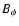 with
r and
with
r and 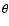 coordinates in the spatial ranges
coordinates in the spatial ranges
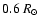 -
-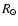 and 0-
and 0-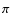 ,
respectively, in a
,
respectively, in a
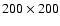 grid
resolution (see Guerrero & Muñoz 2004, for details of the numerical model).
grid
resolution (see Guerrero & Muñoz 2004, for details of the numerical model).
The velocity field (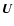 )
considered in the calculations below
corresponds to the analytical profiles of Eqs. (4) and (5) of
Dikpati & Charbonneau (1999). According to the Babcock-Leighton mechanism, the alpha
term (
)
considered in the calculations below
corresponds to the analytical profiles of Eqs. (4) and (5) of
Dikpati & Charbonneau (1999). According to the Babcock-Leighton mechanism, the alpha
term (
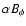 )
is concentrated between
)
is concentrated between
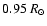 and
and
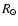 and at the latitudes where the sunspots appear (see the
continuous lines in Fig. 1). Since it must result in the emergence of
magnetic flux tubes, we consider this term as being proportional to
the toroidal field
and at the latitudes where the sunspots appear (see the
continuous lines in Fig. 1). Since it must result in the emergence of
magnetic flux tubes, we consider this term as being proportional to
the toroidal field
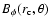 at the overshoot interface
at the overshoot interface
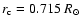 .
For the magnetic diffusion, we consider only one
gradient of diffusivity located at
.
For the magnetic diffusion, we consider only one
gradient of diffusivity located at 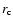 ,
which separates the
radiative stable region (with
,
which separates the
radiative stable region (with
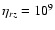 cm s-2) from
the convective turbulent one (with
cm s-2) from
the convective turbulent one (with
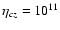 cm s-2) (see the dotted line in the upper panel of Fig. 1). The
non-dimensional parameters as defined in Dikpati & Charbonneau (1999) and employed
in the models have the following values:
cm s-2) (see the dotted line in the upper panel of Fig. 1). The
non-dimensional parameters as defined in Dikpati & Charbonneau (1999) and employed
in the models have the following values:
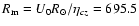 ,
,
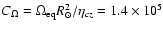 and
and
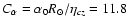 ,
where
,
where 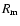 is the magnetic Reynolds number,
U0= is the maximum meridional flow velocity,
is the magnetic Reynolds number,
U0= is the maximum meridional flow velocity,
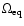 is
the angular velocity at the equator, and
is
the angular velocity at the equator, and 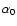 is the maximum
amplitude of the
is the maximum
amplitude of the 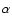 effect. In all the cases, the tachocline
thickness corresponds to 2% of the solar radii and is at a radius
effect. In all the cases, the tachocline
thickness corresponds to 2% of the solar radii and is at a radius
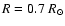 .
.
![\begin{figure}
\par\includegraphics[scale = 0.56]{9351f2a.eps}\\
\includegraphics[width = 8cm, height=6cm]{9351f2b.eps}\end{figure}](/articles/aa/full/2008/25/aa09351-08/Timg54.gif) |
Figure 2:
a) Butterfly diagram and latitudinal
snapshots for the
toroidal b) and the poloidal c) fields. The dark (blue) and light
(red) gray (color) scales represent positive and negative toroidal
fields, respectively; the continuous and dashed lines represent
the positive and negative poloidal fields. For this
model T=13.6 yr,
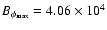 G and G and
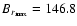 G. Only toroidal fields greater than G. Only toroidal fields greater than
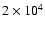 G (the most external contours) are shown in panels a)
and b). The dot-dashed line in panels b) and c) corresponds to the center of the overshoot layer. This model started with anti-symmetric
initial condition (see Sect. 3 for details). G (the most external contours) are shown in panels a)
and b). The dot-dashed line in panels b) and c) corresponds to the center of the overshoot layer. This model started with anti-symmetric
initial condition (see Sect. 3 for details). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[scale = 0.56]{9351f3a.eps}\\
\includegraphics[width = 8cm, height=6cm]{9351f3b.eps}\end{figure}](/articles/aa/full/2008/25/aa09351-08/Timg55.gif) |
Figure 3:
The same as in Fig. 2 but considering the
radial diamagnetic term. For this model T=13.6 year,
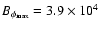 G and G and
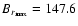 G. This model started with anti-symmetric
initial conditions. G. This model started with anti-symmetric
initial conditions. |
| Open with DEXTER |
In Fig. 2, the turbulent pumping is not considered. As
has been reported in GDPa and GDPb, the most important
contribution to the toroidal field comes from the latitudinal shear
term and therefore the field that is responsible for the observed
activity begins to be formed inside the convection zone. On the one hand,
it can be seen that the penetration into the stable layer is very weak,
on the other hand, the equartorward velocity is faster, so
that the time that the toroidal field has to amplify to the values
required by the magnetic flux tube simulations is probably short.
The upper panel of Fig. 2 shows the butterfly diagram
after a transient time of
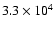 years. At this
time, the toroidal field
has almost reached a quadrupolar parity (i.e. the toroidal
field in both hemispheres has the same sign), which is in
contradiction to Hale's law. In the solar dynamo modelling
this problem is known as the parity problem and we will discuss this
in more detail in Sect. 5. In the next sections we
consider the turbulent magnetic pumping as an alternative mechanism of
penetration. The latitude of emergence of the toroidal field depends
on the stability criterion for the buoyancy
(e.g. see Ferriz-Mas et al. 1994, and their Figs. 1 and 2 for details).
years. At this
time, the toroidal field
has almost reached a quadrupolar parity (i.e. the toroidal
field in both hemispheres has the same sign), which is in
contradiction to Hale's law. In the solar dynamo modelling
this problem is known as the parity problem and we will discuss this
in more detail in Sect. 5. In the next sections we
consider the turbulent magnetic pumping as an alternative mechanism of
penetration. The latitude of emergence of the toroidal field depends
on the stability criterion for the buoyancy
(e.g. see Ferriz-Mas et al. 1994, and their Figs. 1 and 2 for details).
A way to describe the diamagnetic behaviour of a non-homogeneous
plasma based on a first order smoothing approximation (FOSA) was
outlined by Kichatinov & Ruediger (1992). If there is an inhomogeneous diffusivity
in a fluid, it causes transport of the magnetic field with an
effective velocity. We introduce this effect in the model by
changing the term
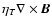 to
to
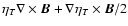 in Eq. (1). This new term increases the poloidal flux
that penetrates beneath the overshoot layer (Fig. 3) and, as a
consequence, more toroidal field is produced at all latitudes. The
toroidal field formed inside the convection zone penetrates the
stable layer where it is amplified by the radial shear at the
tachocline. The equartorward velocity of the magnetic flux inside
the stable layer is lower than the velocity right above the
overshoot interface, so that in the absence of latitudinal pumping,
the toroidal field would last longer at this layer. The radial
velocity corresponding to this effect at the overshoot region is
in Eq. (1). This new term increases the poloidal flux
that penetrates beneath the overshoot layer (Fig. 3) and, as a
consequence, more toroidal field is produced at all latitudes. The
toroidal field formed inside the convection zone penetrates the
stable layer where it is amplified by the radial shear at the
tachocline. The equartorward velocity of the magnetic flux inside
the stable layer is lower than the velocity right above the
overshoot interface, so that in the absence of latitudinal pumping,
the toroidal field would last longer at this layer. The radial
velocity corresponding to this effect at the overshoot region is
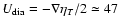 cm s-1 when a
variation of two orders of magnitude is considered for the
diffusivity in a thin region of
cm s-1 when a
variation of two orders of magnitude is considered for the
diffusivity in a thin region of
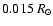 .
.
In a convectivelly unstable rotating plasma, the magnetic field is
not advected in the vertical direction only. The diamagnetic effect
may have components in all directions. Also, another pumping
effect due to density gradients can develop and in some conditions
can produce an upward transport that can balance the diamagnetic
effect (Ziegler & Rüdiger 2003). To investigate a more general
pumping advection, we will consider in this section the integration
of Eq. (1) with
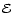 given by Eq. (2) and
given by Eq. (2) and
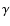 given by both contributions. The radial and latitudinal components
of this total
given by both contributions. The radial and latitudinal components
of this total
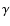 were computed numerically from
three-dimensional magneto-convection simulations by
Ossendrijver et al. (2002); Käpylä et al. (2006a). Similarly to Käpylä et al. (2006b), we use
the following profiles approximately fitted from the numerical
simulations:
were computed numerically from
three-dimensional magneto-convection simulations by
Ossendrijver et al. (2002); Käpylä et al. (2006a). Similarly to Käpylä et al. (2006b), we use
the following profiles approximately fitted from the numerical
simulations:
where
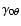 and
and
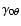 define the maximum
amplitudes of the pumping coefficients. The latitudinal pumping is
zero at the overshoot layer and assumes positive (negative) values at
the convection zone in the north (south) hemisphere; it is zero at the
poles and at the equator, with a
maximum value of 100 cm s-1 around
define the maximum
amplitudes of the pumping coefficients. The latitudinal pumping is
zero at the overshoot layer and assumes positive (negative) values at
the convection zone in the north (south) hemisphere; it is zero at the
poles and at the equator, with a
maximum value of 100 cm s-1 around  15
15 (see the
dot-dashed lines in Fig. 1). The radial pumping,
(see the
dot-dashed lines in Fig. 1). The radial pumping, 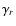 ,
is
negative at the convection zone, indicating downward transport
until r=0.7 (i.e., below the overshoot interface) and vanishes
below this value. Its maximum amplitude is 40 cm s-1 (see
dashed lines in Fig. 1). We do not consider the longitudinal
contribution of the pumping because it is small compared with the
longitudinal velocity term
,
is
negative at the convection zone, indicating downward transport
until r=0.7 (i.e., below the overshoot interface) and vanishes
below this value. Its maximum amplitude is 40 cm s-1 (see
dashed lines in Fig. 1). We do not consider the longitudinal
contribution of the pumping because it is small compared with the
longitudinal velocity term 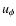 .
.
![\begin{figure}
\par\includegraphics[scale = 0.56]{9351f4a.eps}\\
\includegraphics[width = 8cm, height=6cm]{9351f4b.eps}\end{figure}](/articles/aa/full/2008/25/aa09351-08/Timg75.gif) |
Figure 4:
The same as in Fig. 2 for a model with the full turbulent
pumping terms obtained from magneto-convection simulations. For this
model T=8.2 yr,
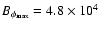 G and G and
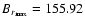 G. This model started
with anti-symmetric initial conditions. G. This model started
with anti-symmetric initial conditions. |
| Open with DEXTER |
Figure 4 shows that besides advecting the magnetic fields
towards the stable regions, the pumping terms lead to a distinct
latitudinal distribution of the toroidal fields when compared with
the results of Figs. 2 and 3. The turbulent and density
gradient levels present in a convectively unstable layer cause
pumping of the magnetic field both down and equartorward, allowing
its amplification within the stable layer and its later emergence at
latitudes very near the equator. This result is important for
dynamo modeling because it suggests that the pumping can not only
solve the problem of the storage of the toroidal fields in the
stable layer, but it can also help to provide a latitudinal
distribution that is in agreement with the observations.
![\begin{figure}
\par {\hspace*{1.5cm}\includegraphics[height = 5 cm]{9351f5a.eps}\hspace*{1.5cm}}\\
\includegraphics[scale = 0.55]{9351f5b.eps}\end{figure}](/articles/aa/full/2008/25/aa09351-08/Timg77.gif) |
Figure 5:
Meridional flow streamlines and the butterfly diagram for a
model with the full pumping term, but with a shallow meridional flow
penetration with a depth of only
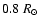 ,
U0=1300 cm s-1, ,
U0=1300 cm s-1,
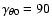 cm s-1 and cm s-1 and
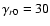 cm s-1. For this model we obtain T=10.8 yr, cm s-1. For this model we obtain T=10.8 yr,
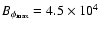 G and G and
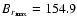 G. This model started with anti-symmetric initial
conditions. G. This model started with anti-symmetric initial
conditions. |
| Open with DEXTER |
As the pumping and the meridional flow are both advective
terms and in some regions inside the convection zone their radial
and latitudinal components have the same sign, when the total
pumping is considered the period of the cycle is strongly affected.
It goes from 13.6 yr in the models of Figs. 2 and 3, to 8.2 yr
in the model of Fig. 4. One way to reproduce the solar
period is to decrease the value of the diffusivity at the convection
zone. Another possibility is to decrease the depth of penetration of
the meridional flow. This is supported by recent helioseismic
results (Mitra-Kraev & Thompson 2007) that suggest that the return point of the
meridional circulation can be at 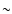
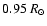 .
At lower regions,
beneath
.
At lower regions,
beneath 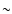
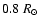 ,
a second weaker convection cell or even a
null large scale meridional flow can exist. In Fig. 5, we have
decreased the depth of penetration of the flow and found that the
period increases to the observed value at the same time that the
toroidal fields become more concentrated at lower latitudes. If we
further decrease the depth of penetration, the equatorward
concentration of the toroidal fields becomes larger and the period
longer. The reason is that no net magnetic flux is moving
poleward at the lower regions of the convective layer since it is
all moving to the equator with the pumping velocity. This result is
in agreement with Ossendrijver et al. (2002) who suggest than the equartorward
motion of the magnetic activity could not be the result of
meridional bulk motion, but due to the latitudinal pumping of the
toroidal mean magnetic field. A parametric analysis of the
simulations performed under the conditions above gives:
,
a second weaker convection cell or even a
null large scale meridional flow can exist. In Fig. 5, we have
decreased the depth of penetration of the flow and found that the
period increases to the observed value at the same time that the
toroidal fields become more concentrated at lower latitudes. If we
further decrease the depth of penetration, the equatorward
concentration of the toroidal fields becomes larger and the period
longer. The reason is that no net magnetic flux is moving
poleward at the lower regions of the convective layer since it is
all moving to the equator with the pumping velocity. This result is
in agreement with Ossendrijver et al. (2002) who suggest than the equartorward
motion of the magnetic activity could not be the result of
meridional bulk motion, but due to the latitudinal pumping of the
toroidal mean magnetic field. A parametric analysis of the
simulations performed under the conditions above gives:
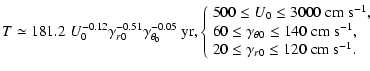 |
|
|
(5) |
This indicates that the pumping terms regulate the period of the
cycle, leading to a different class of dynamo that is
advection-dominated not by a deep meridional flow but by turbulent
pumping. Figure 5 shows a butterfly diagram with fiducial values for
the meridional flow which
result in a period of 10.8 yr. The agreement of this diagram with
the main features of the solar cycle, including the phase lag
between the field components, is clear.
![\begin{figure}
\par\includegraphics[scale = 0.55]{9351f6a.eps}\end{figure}](/articles/aa/full/2008/25/aa09351-08/Timg79.gif) |
Figure 6:
Butterfly diagram for a model with the same
parameters as
Fig. 2, but with near-surface shear layer. For this model T=15.6 yr
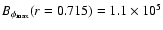 , ,
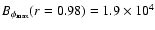 G and G and
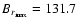 G. This model started with
symmetric initial conditions. G. This model started with
symmetric initial conditions. |
| Open with DEXTER |
Helioseismology inversions have identified a second
radial shear layer located below the solar photosphere in the upper
35 Mm of the sun (Corbard & Thompson 2002). It is possible that the solar
dynamo is operating in this region, as has been discussed
by Brandenburg (2005). The more attractive features
of an
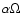 dynamo operating in this region are, among
others: (i) the intensity of the magnetic flux tubes in
this region does not need to be as large as 105 G in order to
form sunspots with the observed magnitudes, but 103 G is
sufficient; and (ii) with a near-surface
dynamo operating in this region are, among
others: (i) the intensity of the magnetic flux tubes in
this region does not need to be as large as 105 G in order to
form sunspots with the observed magnitudes, but 103 G is
sufficient; and (ii) with a near-surface 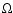 effect it is
possible to explain the
coincidence of the angular velocity of the sunspots in the
photosphere with the rotation velocity at
effect it is
possible to explain the
coincidence of the angular velocity of the sunspots in the
photosphere with the rotation velocity at
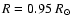 (see Fig. 2 of Brandenburg 2005), as well as the apparent disconnection between
the sunspot and its roots (Kosovichev 2002). The contribution
of a near-surface radial shear has been investigated in
interface-like dynamos (Mason et al. 2002), in distributed dynamos with a
turbulent
(see Fig. 2 of Brandenburg 2005), as well as the apparent disconnection between
the sunspot and its roots (Kosovichev 2002). The contribution
of a near-surface radial shear has been investigated in
interface-like dynamos (Mason et al. 2002), in distributed dynamos with a
turbulent 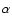 effect (Käpylä et al. 2006b), and also in advection
dominated dynamos (Dikpati et al. 2002). The latter authors have
discarded the radial shear layer
since it generates butterfly diagrams in which a positive toroidal
field gives rise to a negative radial field, which is exactly the
opposite to that observed. In this section, we include the radial
shear term in our FDBL model in order to explore the
contribution of pumping to this new configuration. We use the
analytical expression given in Eqs. (1)-(3) of Dikpati et al. (2002). The
near-surface shear described by these equations gives a
negative shear below
effect (Käpylä et al. 2006b), and also in advection
dominated dynamos (Dikpati et al. 2002). The latter authors have
discarded the radial shear layer
since it generates butterfly diagrams in which a positive toroidal
field gives rise to a negative radial field, which is exactly the
opposite to that observed. In this section, we include the radial
shear term in our FDBL model in order to explore the
contribution of pumping to this new configuration. We use the
analytical expression given in Eqs. (1)-(3) of Dikpati et al. (2002). The
near-surface shear described by these equations gives a
negative shear below
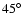 and a positive shear above
this latitude (see Fig. 1 of Dikpati et al. 2002)
and a positive shear above
this latitude (see Fig. 1 of Dikpati et al. 2002)![[*]](/icons/foot_motif.gif) .
.
![\begin{figure}
\par\includegraphics[scale = 0.56]{9351f7a.eps}\\
\includegraphics[width = 8cm, height=6cm]{9351f7b.eps}\end{figure}](/articles/aa/full/2008/25/aa09351-08/Timg82.gif) |
Figure 7:
The same as in Fig. 5 for a model with
near-surface shear
action. For this model T=16.3 yr
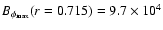 , ,
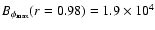 G and G and
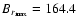 G. This model started with
symmetric initial conditions. G. This model started with
symmetric initial conditions. |
| Open with DEXTER |
With the assumption that the sunspots are formed in
the upper layers, the Babcock-Leighton poloidal source term, which
is concentrated in the same region (above
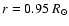 ), does
not have to be non-local any longer. For the same reason, the values of
both the radial and the toroidal fields in the butterfly diagram
can be taken at the same radial point (
), does
not have to be non-local any longer. For the same reason, the values of
both the radial and the toroidal fields in the butterfly diagram
can be taken at the same radial point (
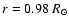 ). Using the
same parameters as in the model of Fig. 2, but considering a
near-surface shear, the results of Fig. 6 show two main branches
in the butterfly diagram. One is migrating poleward (at high
latitudes) and one is migrating equatorward (below
). Using the
same parameters as in the model of Fig. 2, but considering a
near-surface shear, the results of Fig. 6 show two main branches
in the butterfly diagram. One is migrating poleward (at high
latitudes) and one is migrating equatorward (below
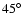 ). This
result is expected if the Parker-Yoshimura sign rule
(Yoshimura 1975; Parker 1955)
is considered. We note that the resulting parity is quadrupolar but
with the correct phase lag between the fields, which is opposite to
the result obtained in Dikpati et al. (2002). This difference probably
arises from the fact that we are
using a lower meridional circulation amplitude. Anyway, the
polar branches are strong enough to generate undesirable sunspots
close to the poles. The period increases to 15.6 y, which is due
to the fact that the dominant dynamo action at the surface goes in
the opposite direction to the meridional flow.
). This
result is expected if the Parker-Yoshimura sign rule
(Yoshimura 1975; Parker 1955)
is considered. We note that the resulting parity is quadrupolar but
with the correct phase lag between the fields, which is opposite to
the result obtained in Dikpati et al. (2002). This difference probably
arises from the fact that we are
using a lower meridional circulation amplitude. Anyway, the
polar branches are strong enough to generate undesirable sunspots
close to the poles. The period increases to 15.6 y, which is due
to the fact that the dominant dynamo action at the surface goes in
the opposite direction to the meridional flow.
In Fig. 7 the same parameters as in Fig. 5 have been
used, but this time considering the radial shear near the
surface. As the radial pumping has its maximum amplitude close to the
poles (see the dashed line in Fig. 1), the toroidal fields created
there are efficiently pushed down
before reaching a significant amplitude, so that only the
equatorial branches below
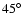 survive. This
scenario requires that the pumping be dominant over the buoyancy at
such latitudes. Also, the phase relation of
survive. This
scenario requires that the pumping be dominant over the buoyancy at
such latitudes. Also, the phase relation of
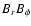 obtained in the model of Fig. 7 seems to be the one
observed, at least at the latitude of
activity. However, there is some overlap between one cycle and the
next. Results in better agreement with the observations
may be achieved if the parameters are finely tuned.
obtained in the model of Fig. 7 seems to be the one
observed, at least at the latitude of
activity. However, there is some overlap between one cycle and the
next. Results in better agreement with the observations
may be achieved if the parameters are finely tuned.
We note that the introduction of the radial
shear
close to the surface when a meridional flow cell penetrating down to
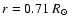 is considered, as in the model of Fig. 4, requires
an increase of the amplitude of
is considered, as in the model of Fig. 4, requires
an increase of the amplitude of 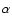 .
This result is in
agreement with that found by Käpylä et al. (2006b).
.
This result is in
agreement with that found by Käpylä et al. (2006b).
Even though it already has been explored by several
authors, the anti-symmetry (dipolar parity) or symmetry
(quadrupolar parity) of the toroidal magnetic fields across the
solar equator still constitutes one of the most challenging
questions in solar dynamo theory. This
is mainly because the resulting parity in a model is very sensitive
to a large parameter space. The solar-like (antisymmetric) solution
could result from the effective diffusive coupling of the poloidal
field in both hemispheres (Chatterjee et al. 2004), but it may also depend on
the position and amplitude of the 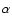 effect
(Bonanno et al. 2002; Dikpati & Gilman 2001), or be the result of the imprint of the
quadrupolar form of the meridional flow on the poloidal magnetic
field, as argued by Charbonneau (2007). Small variations in the parameter
space can switch one solution from a dipolar to a quadrupolar
one. Although the main goal of this work was not to
study the parity problem itself, but the contribution of the turbulent
magnetic pumping, it is interesting to take advantage of the full
sphere integration in order to see how the pumping affects the
parity.
effect
(Bonanno et al. 2002; Dikpati & Gilman 2001), or be the result of the imprint of the
quadrupolar form of the meridional flow on the poloidal magnetic
field, as argued by Charbonneau (2007). Small variations in the parameter
space can switch one solution from a dipolar to a quadrupolar
one. Although the main goal of this work was not to
study the parity problem itself, but the contribution of the turbulent
magnetic pumping, it is interesting to take advantage of the full
sphere integration in order to see how the pumping affects the
parity.
All the simulations presented in the previous sections
evolved 107 time steps up to  104 years. All
started with antisymetric (A) or with symmetric (S) toroidal
magnetic fields, but we have also performed tests with random (R)
fields. The parity of the solution is calculated, following
Chatterjee et al. (2004), with the equation below:
104 years. All
started with antisymetric (A) or with symmetric (S) toroidal
magnetic fields, but we have also performed tests with random (R)
fields. The parity of the solution is calculated, following
Chatterjee et al. (2004), with the equation below:
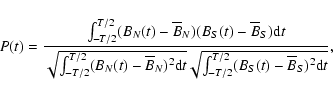 |
(6) |
where BN and BS are the values of the
toroidal magnetic field at
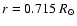 ,
and
,
and
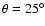 and
and
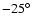 ,
respectively,
,
respectively,
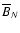 and
and
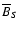 are their
respective temporal averages over one period. The value of P should
be between +1 (symmetric) and -1 (anti-symmetric) depending on the
parity of the fields. The results of our simulations with regard to the
parity can be summarized as follows:
are their
respective temporal averages over one period. The value of P should
be between +1 (symmetric) and -1 (anti-symmetric) depending on the
parity of the fields. The results of our simulations with regard to the
parity can be summarized as follows:
-
The models without pumping (e.g., Fig. 2), and those with diamagnetic
pumping (Fig. 3) result in quadrupolar solution. When beginning with a
dipolar initial condition they take several years before switching to
a quadrupolar solution (see Fig. 8a). This result diverges from the
one obtained by
Dikpati & Gilman (2001) or Chatterjee et al. (2004) in which
the change begins only after around 500 yr. This result
indicates the strong sensitivity of the parity to the initial
parameters, in such a way that, for example, the present parity
observed in the sun could be temporary, at least in the case that the
turbulent pumping is not relevant for the dynamo.
-
The models with full pumping (e.g., Fig. 5) conserve
the initial parity whether this is symmetric or anti-symmetric (see Fig.
8b). When initialized with a random field, the system tends first to
choose the quadrupolar parity, but then it tends to migrate to the
anti-symmetric (dipolar) parity (dot-dashed line of Fig 8b),
suggesting that the strong quadrupolar imprint due to meridional
circulation could be washed out when the full turbulent pumping is
switched on.
-
Models with full pumping plus a near-surface shear layer (e.g. Fig. 7)
tend to the dipolar parity from the first years of integration (see
continuous line of Fig. 8c). In these models we find that the
coupling of the polodial fields in both hemispheres is more
effective. This is probably due to the employment of a
local
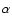 term. See, for example Chatterjee et al. (2004), where a
near-surface
term. See, for example Chatterjee et al. (2004), where a
near-surface 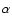 effect is combined with a buoyancy numerical
mechanism. They find a similar coupling. However this coupling alone is
not enough to ensure a dipolar parity (see Fig. 6 and the dashed line
of Fig. 8c). It is also necessary to eliminate the effect of the
quadrupolar shape of the meridional flow on the poloidal magnetic
component. This can be done by the action of the pumping in the entire
convection zone (as indicated by the continuous line of Fig. 8c).
effect is combined with a buoyancy numerical
mechanism. They find a similar coupling. However this coupling alone is
not enough to ensure a dipolar parity (see Fig. 6 and the dashed line
of Fig. 8c). It is also necessary to eliminate the effect of the
quadrupolar shape of the meridional flow on the poloidal magnetic
component. This can be done by the action of the pumping in the entire
convection zone (as indicated by the continuous line of Fig. 8c).
![\begin{figure}
\par\includegraphics[scale = 0.5]{9351f8a.eps}\\
\includegraphi...
...e = 0.5]{9351f8b.eps}\\
\includegraphics[scale = 0.5]{9351f8c.eps}\end{figure}](/articles/aa/full/2008/25/aa09351-08/Timg93.gif) |
Figure 8:
Parity curves for the three classes of models
considered,
i.e., a) for models without pumping (as e.g., in Fig. 2); b) for
models with full pumping (as e.g., in Fig. 5); and c) for models
with near-surface shear (as e.g., in Figs. 6 and 7). In
the panels a) and b), the continuous, dashed and dot-dashed lines
correspond to symmetric, anti-symmetric and random initial
conditions, respectively. In panel c), the continous
line is used for the model with turbulent pumping while the
dashed line is for the model without pumping. |
| Open with DEXTER |
We have performed 2D numerical simulations of BLFD solar dynamo
models including the turbulent pumping.
Our first set of simulations include a solar rotation profile but
without the a near-surface radial shear layer.
The results show that the pumping transport effect is
relevant in solar dynamo modelling, since it can solve two important
problems widely discussed in the
literature: the storage of the toroidal field at the stable layer and
its latitudinal distribution. A new class of dynamo is proposed in
which the meridional flow is important only near the surface layer in
order to make the Babcock-Leighton mechanism operate over the
toroidal fields, while in the inner layers, the advection is
dominated by the pumping velocity. Our results support the idea that
the equatorward migration of the sunspot activity is related to the
latitudinal pumping velocity at the overshoot layer and the
convection zone. Another attractive feature of this model is that a
large coherent meridional flow is no longer required.
In a second set of simulations, we have
included the shear layer
found by Corbard & Thompson (2002) in the upper 35 Mm of the sun. The results
show the formation of a second shell of a strong toroidal field just
below the photosphere when the full pumping is absent. The branches of
this field obey the
Parker-Yoshimura sign rule for a positive 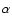 effect, i.e., they move poleward at high latitudes and equatorward
below
effect, i.e., they move poleward at high latitudes and equatorward
below
 .
The role of the pumping in this kind of models is
also interesting since it reduces the amplitude of the polar toroidal
fields, pushing them inwards (Fig. 7). These
models work better if a shallow meridional circulation profile
is used. When a deeper meridional flow going down to the tachocline is
considered, a strong
.
The role of the pumping in this kind of models is
also interesting since it reduces the amplitude of the polar toroidal
fields, pushing them inwards (Fig. 7). These
models work better if a shallow meridional circulation profile
is used. When a deeper meridional flow going down to the tachocline is
considered, a strong 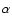 effect is required in order to excite
the dynamo.
effect is required in order to excite
the dynamo.
With regard to the parity problem, our
results show that a
simple
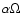 dynamo with the
dynamo with the 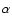 effect concentrated
near thesurface leads to a quadrupolar parity, although the switch
from dipolar to quadrupolar
parity takes longer than in previous studies.
The models with full pumping conserve the initial parity, and
when the initial condition is random, the system tends to switch to a
dipolar parity. All the models that combine full pumping with
near-surface shear prefer dipolar parity solutions too.
effect concentrated
near thesurface leads to a quadrupolar parity, although the switch
from dipolar to quadrupolar
parity takes longer than in previous studies.
The models with full pumping conserve the initial parity, and
when the initial condition is random, the system tends to switch to a
dipolar parity. All the models that combine full pumping with
near-surface shear prefer dipolar parity solutions too.
In summary, our results have demonstrated
the importance of
the pumping in the solar dynamo, and suggest that this effect must be
included in subsequent studies, even in those that employ multiple
convection cells (Jouve & Brun 2007; Bonanno et al. 2006). Also
it decreases the influence of the meridional flow in two important
aspects: the period of the cycle and the latitudinal
distribution of the toroidal fields. On the other hand, our results
indicate that in the presence of full pumping there are two possible
solutions to the question of where the dynamo operates: it could be
either at the convection zone with the magnetic flux tubes
emerging from the overshoot layer, or it could be at the layers near
the surface. Both possibilities have their pros and cons, however a
kinematic dynamo model only is not sufficient to reach a
definitive answer and we will explore this in more detail in
forthcoming work.
Acknowledgements
This work was supported by CNPq and FAPESP grants. G. Guerrero thanks
the MPI in Garching and the ALFA project for their kind hospitality
and support during the production of part of the present
paper. We would like to thank the anonymous referee for his/her
suggestions that have enriched this work.
- Bonanno, A., Elstner, D.,
Rüdiger, G., & Belvedere, G. 2002, A&A, 390, 673 [NASA ADS] [CrossRef] [EDP Sciences]
- Bonanno, A., Elstner, D.,
& Belvedere, G. 2006, Astron. Nachr., 327, 680 [NASA ADS] [CrossRef]
- Brandenburg, A. 2005,
ApJ, 625, 539 [NASA ADS] [CrossRef]
(In the text)
- Brandenburg,
A., Moss, D., & Tuominen, I. 1992, The Solar Cycle, ed.
K. L. Harvey, in ASP Conf. Ser., 27, 536
(In the text)
- Charbonneau, P. 2007,
Adv. in Space Res., 39, 1661 [NASA ADS] [CrossRef]
(In the text)
- Chatterjee, P., Nandy,
D., & Choudhuri, A. R. 2004, A&A, 427, 1019 [NASA ADS] [CrossRef] [EDP Sciences]
(In the text)
- Corbard, T., &
Thompson, M. J. 2002, Sol. Phys., 205, 211 [NASA ADS] [CrossRef]
(In the text)
- Dikpati, M., &
Charbonneau, P. 1999, ApJ, 518, 508 [NASA ADS] [CrossRef]
- Dikpati, M., &
Gilman, P. A. 2001, ApJ, 559, 428 [NASA ADS] [CrossRef]
- Dikpati, M.,
Corbard, T., Thompson, M. J., & Gilman, P. A. 2002,
ApJ, 575, L41 [NASA ADS] [CrossRef]
(In the text)
- Dikpati, M., de Toma, G.,
Gilman, P. A., Arge, C. N., & White, O. R. 2004,
ApJ, 601, 1136 [NASA ADS] [CrossRef]
- Dorch,
S. B. F., & Nordlund, Å. 2001, A&A, 365,
562 [NASA ADS] [CrossRef] [EDP Sciences]
- Ferriz-Mas, A.,
Schmitt, D., & Schuessler, M. 1994, A&A, 289, 949 [NASA ADS]
(In the text)
- Gilman, P. A., &
Miesch, M. S. 2004, ApJ, 611, 568 [NASA ADS] [CrossRef]
- Guerrero, G. A.,
& Muñoz, J. D. 2004, MNRAS, 350, 317 [NASA ADS] [CrossRef]
(In the text)
- Guerrero, G., & de
Gouveia Dal Pino, E. M. 2007a, A&A, 464, 341 [NASA ADS] [CrossRef] [EDP Sciences] (GDPa)
- Guerrero, G. A.,
& de Gouveia Dal Pino, E. M. 2007b, Astron. Nachr., 328,
1122 [NASA ADS] [CrossRef] (GDPb)
- Jouve, L., &
Brun, A. S. 2007, A&A, 474, 239 [NASA ADS] [CrossRef] [EDP Sciences]
- Käpylä,
P. J., Korpi, M. J., Ossendrijver, M., & Stix, M.
2006a, A&A, 455, 401 [NASA ADS] [CrossRef] [EDP Sciences]
- Käpylä,
P. J., Korpi, M. J., & Tuominen, I. 2006b, Astron.
Nachr., 327, 884 [NASA ADS] [CrossRef]
(In the text)
- Kichatinov, L. L.,
& Ruediger, G. 1992, A&A, 260, 494 [NASA ADS]
(In the text)
- Kosovichev, A. G.
2002, Astron. Nachr., 323, 186 [NASA ADS] [CrossRef]
(In the text)
- Küker, M.,
Rüdiger, G., & Schultz, M. 2001, A&A, 374, 301 [NASA ADS] [CrossRef] [EDP Sciences]
- Mason, J., Hughes,
D. W., & Tobias, S. M. 2002, ApJ, 580, L89 [NASA ADS] [CrossRef]
(In the text)
- Mitra-Kraev, U.,
& Thompson, M. J. 2007, ArXiv e-prints, 711
(In the text)
- Ossendrijver, M.,
Stix, M., Brandenburg, A., & Rüdiger, G. 2002, A&A,
394, 735 [NASA ADS] [CrossRef] [EDP Sciences]
- Parker, E. N.
1955, ApJ, 122, 293 [NASA ADS] [CrossRef]
- Rüdiger, G.,
Kitchatinov, L. L., & Arlt, R. 2005, A&A, 444,
L53 [NASA ADS] [CrossRef] [EDP Sciences]
- Yoshimura, H. 1975,
ApJ, 201, 740 [NASA ADS] [CrossRef]
- Ziegler, U., &
Rüdiger, G. 2003, A&A, 401, 433 [NASA ADS] [CrossRef] [EDP Sciences]
Copyright ESO 2008
![\begin{figure}
\par\includegraphics[scale=.44]{9351f1.eps}\end{figure}](/articles/aa/full/2008/25/aa09351-08/Timg24.gif)
![\begin{displaymath}
\frac{\partial {\vec B}}{\partial t} = \nabla \times [{\vec ...
...es
{\vec B} + {\bf\cal{E}} - \eta_T \nabla \times {\vec B} ],
\end{displaymath}](/articles/aa/full/2008/25/aa09351-08/img25.gif)
![\begin{figure}
\par\includegraphics[scale = 0.56]{9351f2a.eps}\\
\includegraphics[width = 8cm, height=6cm]{9351f2b.eps}\end{figure}](/articles/aa/full/2008/25/aa09351-08/Timg54.gif)
![\begin{figure}
\par\includegraphics[scale = 0.56]{9351f3a.eps}\\
\includegraphics[width = 8cm, height=6cm]{9351f3b.eps}\end{figure}](/articles/aa/full/2008/25/aa09351-08/Timg55.gif)
![$\displaystyle \gamma_{0\theta} \left[
1+{\rm erf}\left(\frac{r-0.8}{0.55}\right)\right]$](/articles/aa/full/2008/25/aa09351-08/img64.gif)
![$\displaystyle \times\left[1-{\rm erf}\left(\frac{r-0.98}{0.025}\right)\right]$](/articles/aa/full/2008/25/aa09351-08/img65.gif)
![$\displaystyle -\gamma_{0r} \left[
1+{\rm erf}\left(\frac{r-0.715}{0.015}\right) \right]$](/articles/aa/full/2008/25/aa09351-08/img68.gif)
![$\displaystyle \times \left[1- {\rm erf} \left(\frac{r-0.97}
{0.1}\right) \right]$](/articles/aa/full/2008/25/aa09351-08/img69.gif)
![$\displaystyle \times \left[ \exp \left(\frac{r-0.715}{0.015}\right)^2 \cos \theta
+ 1 \right],$](/articles/aa/full/2008/25/aa09351-08/img70.gif)
![\begin{figure}
\par\includegraphics[scale = 0.56]{9351f4a.eps}\\
\includegraphics[width = 8cm, height=6cm]{9351f4b.eps}\end{figure}](/articles/aa/full/2008/25/aa09351-08/Timg75.gif)
![\begin{figure}
\par {\hspace*{1.5cm}\includegraphics[height = 5 cm]{9351f5a.eps}\hspace*{1.5cm}}\\
\includegraphics[scale = 0.55]{9351f5b.eps}\end{figure}](/articles/aa/full/2008/25/aa09351-08/Timg77.gif)
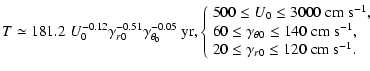
![\begin{figure}
\par\includegraphics[scale = 0.56]{9351f7a.eps}\\
\includegraphics[width = 8cm, height=6cm]{9351f7b.eps}\end{figure}](/articles/aa/full/2008/25/aa09351-08/Timg82.gif)
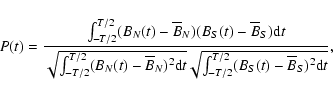
![\begin{figure}
\par\includegraphics[scale = 0.5]{9351f8a.eps}\\
\includegraphi...
...e = 0.5]{9351f8b.eps}\\
\includegraphics[scale = 0.5]{9351f8c.eps}\end{figure}](/articles/aa/full/2008/25/aa09351-08/Timg93.gif)