A&A 484, 879-885 (2008)
DOI: 10.1051/0004-6361:200809823
K. M. Aggarwal1 - K. Hamada2 - A. Igarashi2 - V. Jonauskas3 - F. P. Keenan1 - S. Nakazaki2
1 - Astrophysics Research Centre, School of Mathematics and Physics, Queen's University Belfast, Belfast BT7 1NN, Northern Ireland, UK
2 - Department of Applied Physics, Faculty of Engineering, University of Miyazaki, Miyazaki 889-2192, Japan
3 - Vilnius University Research Institute of Theoretical Physics and Astronomy, A. Gostauto 12, 01108 Vilnius, Lithuania
Received 20 March 2008 / Accepted 7 April 2008
Abstract
Aims. In this paper we report on calculations for energy levels, radiative rates, collision strengths, and effective collision strengths for transitions among the lowest 25 levels of the ![]() configurations of H-like Fe XXVI.
configurations of H-like Fe XXVI.
Methods. The general-purpose relativistic atomic structure package ( GRASP) and Dirac atomic R-matrix code ( DARC) are adopted for the calculations.
Results. Radiative rates, oscillator strengths, and line strengths are reported for all electric dipole (E1), magnetic dipole (M1), electric quadrupole (E2), and magnetic quadrupole (M2) transitions among the 25 levels. Furthermore, collision strengths and effective collision strengths are reported for all the 300 transitions among the above 25 levels over a wide energy (temperature) range up to 1500 Ryd (107.7 K). Comparisons are made with earlier available results and the accuracy of the data is assessed.
Key words: atomic data - atomic processes
This is in continuation of our work on generating atomic data (energy levels, radiative rates, collision strengths, and excitation rates) for iron ions, for which we have already reported our calculations for Fe IX (Aggarwal et al. 2006), Fe X (Aggarwal & Keenan 2004b, 2005b), Fe XI (Aggarwal & Keenan 2003a,b), Fe XIII (Aggarwal & Keenan 2004a,b), Fe XV (Aggarwal et al. 2001, 2003a), Fe XVI (Aggarwal & Keenan 2006, 2007, 2008), Fe XVII (Aggarwal et al. 2003b, 2004), Fe XVIII (Jonauskas et al. 2004), Fe XXI (Aggarwal & Keenan 1999, 2001), and Fe XXIV (McKeown et al. 2004). In this paper we report similar results for transitions in Fe XXVI.
Iron is an abundant element in solar and fusion plasmas, and its emission lines are observed over almost all ionization stages. To analyse the vast amount of observational data available from space missions such as SOHO, Chandra and XMM Newton, theoretical atomic data for Fe ions are required, because there is paucity of experimental results.
Emission lines of H-like Fe XXVI have been observed in astrophysical plasmas (Kato 1976), and have been helpful in estimating the radiative power loss in fusion
reactors (Summers & McWhirter 1979). A few calculations have been performed in the past, the most notable being those of Aggarwal & Kingston (1993), Kisielius
et al. (1996), and Ballance et al. (2002). Aggarwal & Kingston performed non-relativistic calculations in LS coupling for transitions among the ![]() states. They adopted the R-matrix program of Berrington et al. (1978), and resolved resonances in the threshold region in order to include their contribution in the
determination of effective collision strengths,
states. They adopted the R-matrix program of Berrington et al. (1978), and resolved resonances in the threshold region in order to include their contribution in the
determination of effective collision strengths, ![]() .
Since it is the fine-structure transitions which are observed in plasmas, their calculations were of limited
application. This deficiency was removed by Kisielius et al., who performed fully relativistic calculations in jj coupling. They too resolved resonances in the threshold
region, and employed the earlier version of the Dirac atomic R-matrix code ( DARC), as implemented by Ait-Tahar et al. (1996). However, their calculations
suffer from a few limitations. Firstly, their results for
.
Since it is the fine-structure transitions which are observed in plasmas, their calculations were of limited
application. This deficiency was removed by Kisielius et al., who performed fully relativistic calculations in jj coupling. They too resolved resonances in the threshold
region, and employed the earlier version of the Dirac atomic R-matrix code ( DARC), as implemented by Ait-Tahar et al. (1996). However, their calculations
suffer from a few limitations. Firstly, their results for ![]() were restricted to transitions among the
were restricted to transitions among the ![]() levels only, whereas transitions involving the n = 5levels have been observed (Dere et al. 2001). Secondly, they did not report results for ``elastic'' (i.e. allowed with
levels only, whereas transitions involving the n = 5levels have been observed (Dere et al. 2001). Secondly, they did not report results for ``elastic'' (i.e. allowed with ![]() n = 0) transitions. Thirdly, the
corresponding results for radiative rates were not reported. These are required, along with the excitation rates, in any modelling application. Finally, and most importantly,
their calculations for collision strengths (
n = 0) transitions. Thirdly, the
corresponding results for radiative rates were not reported. These are required, along with the excitation rates, in any modelling application. Finally, and most importantly,
their calculations for collision strengths (![]() )
were limited to an energy below 1000 Ryd, which is not sufficient for the determination of values of
)
were limited to an energy below 1000 Ryd, which is not sufficient for the determination of values of ![]() up to
up to
![]() K, the highest temperature considered by them. As a result, their reported values of
K, the highest temperature considered by them. As a result, their reported values of ![]() decrease with increasing temperature for (almost) all transitions, and are underestimated by up to
decrease with increasing temperature for (almost) all transitions, and are underestimated by up to ![]() 40%, particularly towards the higher end of the temperature range - see, for example, Fig. 1 of Ballance et al.
40%, particularly towards the higher end of the temperature range - see, for example, Fig. 1 of Ballance et al.
Table 1: Energy levels (in Ryd) of Fe XXVI.
All the above noted limitations in the work of Kisielius et al. (1996) were addressed by Ballance et al. (2002), who also adopted the R-matrix approach, but
in a semi-relativistic Breit-Pauli approximation. For all partial waves with angular momentum ![]() they performed Breit-Pauli calculations employing the R-matrix code
of Berrington et al. (1995), and for
they performed Breit-Pauli calculations employing the R-matrix code
of Berrington et al. (1995), and for
![]() they adopted the term coupling approach. However, this should not seriously affect the accuracy of their
calculations, because Fe XXVI is only a moderately heavy ion (Z = 26). This is further confirmed by a good agreement between their
they adopted the term coupling approach. However, this should not seriously affect the accuracy of their
calculations, because Fe XXVI is only a moderately heavy ion (Z = 26). This is further confirmed by a good agreement between their ![]() values and those of
Kisielius et al., particularly towards the lower end of the temperature range. Therefore, their results for
values and those of
Kisielius et al., particularly towards the lower end of the temperature range. Therefore, their results for ![]() are probably the best available today. However, past
experience for a number of Fe ions shows that often there are large discrepancies among various sets of calculations. This is in spite of adopting the same R-matrix approach,
including configuration interaction (CI) in constructing the wavefunctions, accounting for relativistic effects (in different approximations), and resolving resonances in the
threshold regions. Examples of large discrepancies are transitions in Fe X (Aggarwal & Keenan 2005b), Fe XI (Aggarwal & Keenan 2003a,b),
Fe XV (Aggarwal et al. 2001, 2003a), and Fe XVI (Aggarwal & Keenan 2006, 2008). Therefore, our aim is to perform yet another
calculation for Fe XXVI so that results for various atomic parameters can be rigorously compared, and their accuracy is assessed in order to apply those reliably. In
addition, we note that Ballance et al. have reported radiative rates (A-values) for electric dipole (E1) transitions alone, whereas corresponding results for other types of
transitions, namely electric quadrupole (E2), magnetic dipole (M1) and magnetic quadrupole (M2), are also required in the analysis of plasmas. Therefore, in this work we report
A-values for all types of transitions. Finally, our approach is fully relativistic, as for the generation of wavefunctions we employ the GRASP (general-purpose
relativistic atomic structure package) code of Grant et al. (1980), which has been updated by Dr. P. H. Norrington. Similarly, for the computations of
are probably the best available today. However, past
experience for a number of Fe ions shows that often there are large discrepancies among various sets of calculations. This is in spite of adopting the same R-matrix approach,
including configuration interaction (CI) in constructing the wavefunctions, accounting for relativistic effects (in different approximations), and resolving resonances in the
threshold regions. Examples of large discrepancies are transitions in Fe X (Aggarwal & Keenan 2005b), Fe XI (Aggarwal & Keenan 2003a,b),
Fe XV (Aggarwal et al. 2001, 2003a), and Fe XVI (Aggarwal & Keenan 2006, 2008). Therefore, our aim is to perform yet another
calculation for Fe XXVI so that results for various atomic parameters can be rigorously compared, and their accuracy is assessed in order to apply those reliably. In
addition, we note that Ballance et al. have reported radiative rates (A-values) for electric dipole (E1) transitions alone, whereas corresponding results for other types of
transitions, namely electric quadrupole (E2), magnetic dipole (M1) and magnetic quadrupole (M2), are also required in the analysis of plasmas. Therefore, in this work we report
A-values for all types of transitions. Finally, our approach is fully relativistic, as for the generation of wavefunctions we employ the GRASP (general-purpose
relativistic atomic structure package) code of Grant et al. (1980), which has been updated by Dr. P. H. Norrington. Similarly, for the computations of ![]() ,
and
subsequently of
,
and
subsequently of ![]() ,
we adopt the Dirac atomic R-matrix code ( DARC) of Norrington & Grant (private communication).
,
we adopt the Dirac atomic R-matrix code ( DARC) of Norrington & Grant (private communication).
The ![]() configurations of Fe XXVI give rise to 25 fine-structure levels, listed in Table 1. Our calculated energies obtained from the GRASP code, with
and without including the QED effects, are given in this table along with those from the experimental compilations of NIST (http://physics.nist.gov/PhysRefData),
and the earlier work of Kisielius et al. (1996) and Ballance et al. (2002). For our calculations, we have used the option of extended average level (EAL),
in which a weighted (proportional to 2j+1) trace of the Hamiltonian matrix is minimized. This produces a compromise set of orbitals describing closely lying states with moderate accuracy. The inclusion of QED effects lowers the energies by a maximum of 0.3 Ryd (
configurations of Fe XXVI give rise to 25 fine-structure levels, listed in Table 1. Our calculated energies obtained from the GRASP code, with
and without including the QED effects, are given in this table along with those from the experimental compilations of NIST (http://physics.nist.gov/PhysRefData),
and the earlier work of Kisielius et al. (1996) and Ballance et al. (2002). For our calculations, we have used the option of extended average level (EAL),
in which a weighted (proportional to 2j+1) trace of the Hamiltonian matrix is minimized. This produces a compromise set of orbitals describing closely lying states with moderate accuracy. The inclusion of QED effects lowers the energies by a maximum of 0.3 Ryd (![]() 0.06%). In the case of Coulomb energies, levels with same n and angular momentum J (such as 2/3 and 5/6) are quasi-degenerate, but split with the inclusion of QED effects (Lamb shift). As a result of this the level orderings change slightly, but we have retained the original orderings of the Coulomb energies, because these are the ones adopted in the subsequent tables. In general, the theoretical energies agree very well with the experimental ones. However, the level energies of Kisielius et al. are slightly lower, whereas ours are slightly higher (
0.06%). In the case of Coulomb energies, levels with same n and angular momentum J (such as 2/3 and 5/6) are quasi-degenerate, but split with the inclusion of QED effects (Lamb shift). As a result of this the level orderings change slightly, but we have retained the original orderings of the Coulomb energies, because these are the ones adopted in the subsequent tables. In general, the theoretical energies agree very well with the experimental ones. However, the level energies of Kisielius et al. are slightly lower, whereas ours are slightly higher (![]() 0.01 Ryd) in
comparison to the experimental ones. Similarly, the energy levels of Ballance et al. from the AutoStructure (AS) code of Badnell (1997) are slightly higher (by
0.01 Ryd) in
comparison to the experimental ones. Similarly, the energy levels of Ballance et al. from the AutoStructure (AS) code of Badnell (1997) are slightly higher (by ![]() 0.2 Ryd) than ours or the experimental results.
0.2 Ryd) than ours or the experimental results.
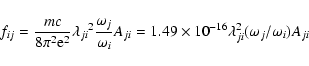 |
(1) |
For the electric dipole (E1) transitions
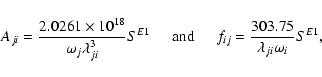 |
(2) |
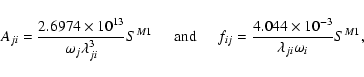 |
(3) |
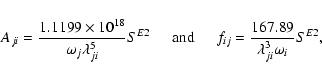 |
(4) |
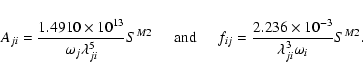 |
(5) |
The only other results available in the literature with which to compare are those of Ballance et al. (2002) for the E1 transitions. They have not reported the A-values in their paper (due to conciseness), but have posted their full results on their website at http://www-cfadc.phy.ornl.gov/data_and_codes/. In general, the two
sets of A-values agree closely (better than 20%), but for some (not all) weaker transitions (
![]() ), such as 1-17 and 4-18, the differences are larger. These
discrepancies arise mainly due to the different treatment of relativistic effects in the adopted programs.
), such as 1-17 and 4-18, the differences are larger. These
discrepancies arise mainly due to the different treatment of relativistic effects in the adopted programs.
For the computations of collision strengths, we have employed the DARC program, which includes the relativistic effects in a systematic way, in both the target description
and the scattering model. It is based on the jj coupling scheme, and uses the Dirac-Coulomb Hamiltonian in the R-matrix approach. However, because of the inclusion of
fine-structure in the definition of channel coupling, the matrix size of the Hamiltonian increases substantially. The R-matrix radius has been adopted to be 4.0 au, and 71 continuum orbitals have been included for each channel angular momentum for the expansion of the wavefunction. This allows us to compute ![]() up to an energy of 1600 Ryd.
The maximum number of channels for a partial wave is 110, and the corresponding size of the Hamiltonian matrix is 7848. In order to obtain convergence of
up to an energy of 1600 Ryd.
The maximum number of channels for a partial wave is 110, and the corresponding size of the Hamiltonian matrix is 7848. In order to obtain convergence of ![]() for all
transitions and at all energies, we have included all partial waves with angular momentum
for all
transitions and at all energies, we have included all partial waves with angular momentum ![]() ,
although a higher range would have been preferable for the convergence of
allowed transitions, in particular those with
,
although a higher range would have been preferable for the convergence of
allowed transitions, in particular those with
![]() .
However, to account for the inclusion of higher neglected partial waves, we have included a top-up, based on the
Coulomb-Bethe approximation for allowed transitions and geometric series for forbidden transitions.
.
However, to account for the inclusion of higher neglected partial waves, we have included a top-up, based on the
Coulomb-Bethe approximation for allowed transitions and geometric series for forbidden transitions.
In Figs. 1a-3a we show the variation of ![]() with angular momentum J at three energies of 700, 800 and 900 Ryd, and for three transitions, namely 2-3 (2s 2S1/2 -
2p 2P
with angular momentum J at three energies of 700, 800 and 900 Ryd, and for three transitions, namely 2-3 (2s 2S1/2 -
2p 2P
![]() ), 2-5 (2s 2S1/2-3p 2P
), 2-5 (2s 2S1/2-3p 2P
![]() )
and 6-7 (3s 2S1/2-3d 2D3/2), which are ``elastic'' (i.e. allowed with
)
and 6-7 (3s 2S1/2-3d 2D3/2), which are ``elastic'' (i.e. allowed with
![]() ), allowed (
), allowed (
![]() ), and forbidden, respectively. Similar results at higher energies of 1100, 1300 and 1500 Ryd are shown in Figs. 1b-3b. For the forbidden and allowed
transitions shown in Figs. 2 and 3, the values of
), and forbidden, respectively. Similar results at higher energies of 1100, 1300 and 1500 Ryd are shown in Figs. 1b-3b. For the forbidden and allowed
transitions shown in Figs. 2 and 3, the values of ![]() have fully converged at all energies, including the highest energy of our calculations. However, for the ``elastic'' transitions our range of partial waves is not sufficient for the convergence of
have fully converged at all energies, including the highest energy of our calculations. However, for the ``elastic'' transitions our range of partial waves is not sufficient for the convergence of ![]() ,
as shown in Fig. 1. For such transitions a top-up from the Coulomb-Bethe approximation is quite significant.
,
as shown in Fig. 1. For such transitions a top-up from the Coulomb-Bethe approximation is quite significant.
![\begin{figure}
\mbox{\includegraphics[angle=-90,width=8.8cm,clip]{fig1a.ps}\hspace{3mm}
\includegraphics[angle=-90,width=8.8cm,clip]{fig1b.ps} }
\end{figure}](/articles/aa/full/2008/24/aa09823-08/Timg32.gif) |
Figure 1:
Partial collision strengths for the 2s 2S1/2-2p 2P
|
| Open with DEXTER | |
![\begin{figure}
\mbox{\includegraphics[angle=-90,width=8.8cm,clip]{fig2a.eps}\hspace{3mm}
\includegraphics[angle=-90,width=8.8cm,clip]{fig2b.eps} }
\end{figure}](/articles/aa/full/2008/24/aa09823-08/Timg33.gif) |
Figure 2:
Partial collision strengths for the 2s 2S1/2-3p 2P
|
| Open with DEXTER | |
![\begin{figure}
\mbox{\includegraphics[angle=-90,width=8.8cm,clip]{fig3a.ps}\hspace{3mm}
\includegraphics[angle=-90,width=8.8cm,clip]{fig3b.eps} }
\end{figure}](/articles/aa/full/2008/24/aa09823-08/Timg34.gif) |
Figure 3: Partial collision strengths for the 3s 2S1/2-3d 2D3/2 (6-7) transition of Fe XXVI, at three energies of: (left panel) 700 Ryd (circles), 800 Ryd (triangles), and 900 Ryd (stars), (right panel) 1100 Ryd (circles), 1300 Ryd (triangles), and 1500 Ryd (stars). |
| Open with DEXTER | |
In Table 4 we present our results of ![]() for all transitions over a wider energy range (
for all transitions over a wider energy range (
![]() Ryd), but above thresholds. The indices adopted to represent
a transition are already given in Table 1. These results for
Ryd), but above thresholds. The indices adopted to represent
a transition are already given in Table 1. These results for ![]() are not directly applicable in any modelling work, but are very useful in assessing the accuracy of a
calculation. The only other results available in the literature with which to compare are from our earlier calculations in LS coupling (Aggarwal & Kingston 1993).
Those results for
are not directly applicable in any modelling work, but are very useful in assessing the accuracy of a
calculation. The only other results available in the literature with which to compare are from our earlier calculations in LS coupling (Aggarwal & Kingston 1993).
Those results for ![]() are confined to energies below 860 Ryd. However, a comparison of those results with the present ones shows excellent agreement (within 10%) for all
transitions, including those whose
are confined to energies below 860 Ryd. However, a comparison of those results with the present ones shows excellent agreement (within 10%) for all
transitions, including those whose ![]() values are very small (
values are very small (![]() 10-8), such as the 1s 2S-5g 2G transition. The only exception, for which the
present results are lower (by 30%), is the 4f 2F
10-8), such as the 1s 2S-5g 2G transition. The only exception, for which the
present results are lower (by 30%), is the 4f 2F![]() -5f 2F
-5f 2F![]() forbidden transition. This excellent agreement between the earlier non-relativistic and the present
relativistic calculations indicates that the relativistic effects for
forbidden transition. This excellent agreement between the earlier non-relativistic and the present
relativistic calculations indicates that the relativistic effects for ![]() in Fe XXVI are not too important, although their importance in accurately determining the
energy levels and radiative rates is clear, especially when we compare the energy levels in the present Table 1 with those of Aggarwal & Kingston.
in Fe XXVI are not too important, although their importance in accurately determining the
energy levels and radiative rates is clear, especially when we compare the energy levels in the present Table 1 with those of Aggarwal & Kingston.
In the absence of any other results for collision strengths for fine-structure transitions, we have performed another calculation using the Flexible Atomic Code ( FAC) of Gu (2003), which is available from the website http://kipac-tree.stanford.edu/fac. This is also a fully relativistic code which provides a variety of atomic parameters, and yields results comparable to GRASP and DARC, particularly for highly ionized elements and at higher energies. Thus results from FAC are helpful in assessing the accuracy of atomic parameters.
In Table 1 we have also included the energy levels obtained from the FAC code, which are comparable with the other calculations listed in this table, but are slightly
higher (by ![]() 0.04 Ryd) than the experimental ones. The A-values obtained from this code are also comparable with our calculations from GRASP for a majority of the E1
transitions. Similarly, the values of
0.04 Ryd) than the experimental ones. The A-values obtained from this code are also comparable with our calculations from GRASP for a majority of the E1
transitions. Similarly, the values of ![]() calculated from the FAC code agree very well (within 10%) with our corresponding results from DARC for (almost) all
transitions, including the weaker ones, such as: 1-15 (1s 2S1/2-4f 2F
calculated from the FAC code agree very well (within 10%) with our corresponding results from DARC for (almost) all
transitions, including the weaker ones, such as: 1-15 (1s 2S1/2-4f 2F
![]() ), 1-23 (1s 2S1/2-5g 2G7/2) and 1-25 (1s 2S1/2-5g 2G9/2). However, there are four transitions, namely 14-15 (4d 2D5/2-4f 2F
), 1-23 (1s 2S1/2-5g 2G7/2) and 1-25 (1s 2S1/2-5g 2G9/2). However, there are four transitions, namely 14-15 (4d 2D5/2-4f 2F
![]() ), 19-20 (5p 2P
), 19-20 (5p 2P
![]() -5d 2D3/2), 21-22 (5f
2F
-5d 2D3/2), 21-22 (5f
2F
![]() -5d 2D5/2), and 23-24 (5g 2G7/2-5f 2F
-5d 2D5/2), and 23-24 (5g 2G7/2-5f 2F
![]() ), for which the differences between the FAC and DARC calculations are
significant. The reason for the large differences becomes apparent when we have a closer look at the energy levels in Table 1. For the 14-15, 21-22 and 23-24 transitions, the
energy differences (
), for which the differences between the FAC and DARC calculations are
significant. The reason for the large differences becomes apparent when we have a closer look at the energy levels in Table 1. For the 14-15, 21-22 and 23-24 transitions, the
energy differences (![]() )
are zero in our GRASP and FAC calculations, and are very small for the 19-20 transition. Transitions such as the above ones are
``elastic'', i.e. allowed with
)
are zero in our GRASP and FAC calculations, and are very small for the 19-20 transition. Transitions such as the above ones are
``elastic'', i.e. allowed with
![]() and
and
![]() ,
and converge very slowly with partial waves, as demonstrated earlier by Igarashi et al. (2003).
Since both DARC and FAC codes include the contribution of higher neglected partial waves from the Coulomb-Bethe formulation of Burgess et al. (1970), which is
highly sensitive to the adopted
,
and converge very slowly with partial waves, as demonstrated earlier by Igarashi et al. (2003).
Since both DARC and FAC codes include the contribution of higher neglected partial waves from the Coulomb-Bethe formulation of Burgess et al. (1970), which is
highly sensitive to the adopted ![]() ,
we obtain differing values of
,
we obtain differing values of ![]() .
Therefore, in order to resolve the differences between FAC and DARC calculations,
and to determine the values of
.
Therefore, in order to resolve the differences between FAC and DARC calculations,
and to determine the values of ![]() as accurately as possible, we have performed yet another calculation using a combination of the close-coupling (CC) and Coulomb-Born (CB)
programs of Igarashi et al. (2003, 2005). These calculations are similar to those performed recently for elastic transitions in Al XIII (Aggarwal et al.
2008), and for which we have adopted the energy levels of NIST.
as accurately as possible, we have performed yet another calculation using a combination of the close-coupling (CC) and Coulomb-Born (CB)
programs of Igarashi et al. (2003, 2005). These calculations are similar to those performed recently for elastic transitions in Al XIII (Aggarwal et al.
2008), and for which we have adopted the energy levels of NIST.
In Fig. 4 we compare the ![]() values from FAC and CC+CB programs for three transitions, namely 14-15 (4d 2D5/2-4f 2F
values from FAC and CC+CB programs for three transitions, namely 14-15 (4d 2D5/2-4f 2F
![]() ), 21-22 (5f 2F
), 21-22 (5f 2F
![]() -5d 2D5/2), and 23-24 (5g 2G7/2 - 5f 2F
-5d 2D5/2), and 23-24 (5g 2G7/2 - 5f 2F
![]() ). Apart from the lowest common energy (
). Apart from the lowest common energy (![]() 700 Ryd), the
700 Ryd), the ![]() values from FAC are overestimated by up to
values from FAC are overestimated by up to ![]() 40%, for the reasons explained above. Therefore, for the 26 elastic transitions we have adopted the values of
40%, for the reasons explained above. Therefore, for the 26 elastic transitions we have adopted the values of ![]() from our CC+CB calculations, and from the DARC code for the other remaining 274 transitions.
from our CC+CB calculations, and from the DARC code for the other remaining 274 transitions.
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{fig4.ps}\end{figure}](/articles/aa/full/2008/24/aa09823-08/Timg39.gif) |
Figure 4:
Comparison of collision strengths for the 14-15 (4d 2D5/2-4f 2F
|
| Open with DEXTER | |
Since we have adopted a wide range of partial waves in order to obtain the convergence of ![]() values for the forbidden as well as the allowed transitions, including the elastic ones, we estimate our results for
values for the forbidden as well as the allowed transitions, including the elastic ones, we estimate our results for ![]() listed in Table 4 are accurate to
listed in Table 4 are accurate to ![]() 15%. This estimate is based on a variety of comparisons made among the different calculations.
15%. This estimate is based on a variety of comparisons made among the different calculations.
Effective collision strengths ![]() are obtained after integrating
are obtained after integrating ![]() over a Maxwellian distribution of electron velocities, i.e.
over a Maxwellian distribution of electron velocities, i.e.
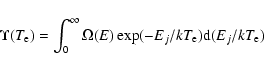 |
(6) |
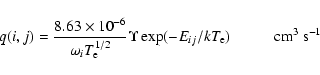 |
(7) |
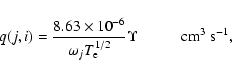 |
(8) |
Since the threshold energy region is dominated by numerous resonances, ![]() have been computed at a large number of energies in order to delineate these resonances. We have
performed our calculations of
have been computed at a large number of energies in order to delineate these resonances. We have
performed our calculations of ![]() at
at ![]() 18 400 energies in the threshold region. Close to thresholds (
18 400 energies in the threshold region. Close to thresholds (![]() 0.1 Ryd above a threshold) the energy mesh is 0.001 Ryd,
and away from thresholds is 0.002 Ryd. Thus care has been taken to include as many resonances as possible, and with as fine a resolution as is computationally feasible.
However, the energy gap between the n = 2 and 3 levels is very wide, i.e.
0.1 Ryd above a threshold) the energy mesh is 0.001 Ryd,
and away from thresholds is 0.002 Ryd. Thus care has been taken to include as many resonances as possible, and with as fine a resolution as is computationally feasible.
However, the energy gap between the n = 2 and 3 levels is very wide, i.e. ![]() 94 Ryd - see Table 1. Therefore, in this energy region the mesh has been gradually increased
to 0.01 Ryd. The density and importance of resonances can be appreciated from Figs. 5-7 in which we show our
94 Ryd - see Table 1. Therefore, in this energy region the mesh has been gradually increased
to 0.01 Ryd. The density and importance of resonances can be appreciated from Figs. 5-7 in which we show our ![]() values in the thresholds region for the 1-2 (1s
2S1/2-2s 2S1/2), 1-3 (1s 2S1/2-2p 2P
values in the thresholds region for the 1-2 (1s
2S1/2-2s 2S1/2), 1-3 (1s 2S1/2-2p 2P
![]() )
and 2-3 (2s 2S1/2-2p 2P
)
and 2-3 (2s 2S1/2-2p 2P
![]() )
transitions, respectively. Since for all of these
(as well as other) transitions, near-threshold resonances are very important,
)
transitions, respectively. Since for all of these
(as well as other) transitions, near-threshold resonances are very important, ![]() values for the 1-2 transition are shown in Figs. 5a,b in wider (510-650 Ryd) and a
narrow (511-513 Ryd) energy ranges. These near-threshold resonances enhance the
values for the 1-2 transition are shown in Figs. 5a,b in wider (510-650 Ryd) and a
narrow (511-513 Ryd) energy ranges. These near-threshold resonances enhance the ![]() values, particularly at lower temperatures.
values, particularly at lower temperatures.
![\begin{figure}
\par\subfigure[]{\includegraphics[angle=90,width=9cm,clip]{fig5a....
...
\subfigure[]{\includegraphics[angle=90,width=9cm,clip]{fig5b.ps} }
\end{figure}](/articles/aa/full/2008/24/aa09823-08/Timg44.gif) |
Figure 5: Collision strengths for the 1s 2S1/2-2s 2S1/2 (1-2) transition of Fe XXVI. |
| Open with DEXTER | |
Our calculated values of ![]() are listed in Table 5 over a wide temperature range of
are listed in Table 5 over a wide temperature range of
![]() K. A comparison with the similar results of Ballance et al. (2002) shows a satisfactory agreement for a majority of transitions, including the elastic ones, although 22 transitions (7%) differ by over 20%, mainly towards
the lower end of the temperature range. However for some transitions, such as 1-11, 1-18, 2-18, and 3-6, the two sets of
K. A comparison with the similar results of Ballance et al. (2002) shows a satisfactory agreement for a majority of transitions, including the elastic ones, although 22 transitions (7%) differ by over 20%, mainly towards
the lower end of the temperature range. However for some transitions, such as 1-11, 1-18, 2-18, and 3-6, the two sets of ![]() values differ over the entire temperature
range, and for four transitions, namely 3-6 (2p 2P
values differ over the entire temperature
range, and for four transitions, namely 3-6 (2p 2P
![]() -3s 2S1/2), 4-6 (2p 2P
-3s 2S1/2), 4-6 (2p 2P
![]() -3s 2S1/2), 20-24 (5d 2D3/2-5f 2F
-3s 2S1/2), 20-24 (5d 2D3/2-5f 2F
![]() ),
and 21-25 (5f 2F
),
and 21-25 (5f 2F
![]() -5g 2G9/2), the differences are up to 80%. For the 3-6 and 4-6 (allowed) transitions our values of
-5g 2G9/2), the differences are up to 80%. For the 3-6 and 4-6 (allowed) transitions our values of ![]() are higher whereas for the
(forbidden) 20-24 and 21-25 the
are higher whereas for the
(forbidden) 20-24 and 21-25 the ![]() values of Ballance et al. are higher. However, for the 3-6 and 4-6 transitions there is no discrepancy between our A-values and
those of Ballance et al. Similarly, there is no disagreement in the
values of Ballance et al. are higher. However, for the 3-6 and 4-6 transitions there is no discrepancy between our A-values and
those of Ballance et al. Similarly, there is no disagreement in the ![]() values between the DARC and FAC calculations. Therefore, the only source of differences
for the
values between the DARC and FAC calculations. Therefore, the only source of differences
for the ![]() values is the presence (or absence) of resonances. Although both 3-6 and 4-6 are allowed transitions, both show the presence of near-threshold resonances, as
illustrated in Fig. 8 for the 3-6 transition. It is possible that the calculations of Ballance et al. may not show such near-threshold resonances, as a result of which their
values of
values is the presence (or absence) of resonances. Although both 3-6 and 4-6 are allowed transitions, both show the presence of near-threshold resonances, as
illustrated in Fig. 8 for the 3-6 transition. It is possible that the calculations of Ballance et al. may not show such near-threshold resonances, as a result of which their
values of ![]() become lower particularly at the lower temperatures.
become lower particularly at the lower temperatures.
![\begin{figure}
\par\includegraphics[angle=90,width=9cm,clip]{fig6.ps}\end{figure}](/articles/aa/full/2008/24/aa09823-08/Timg46.gif) |
Figure 6:
Collision strengths for the 1s 2S1/2-2p 2P
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=90,width=9cm,clip]{fig7.ps}\end{figure}](/articles/aa/full/2008/24/aa09823-08/Timg47.gif) |
Figure 7:
Collision strengths for the 2s 2S1/2-2p 2P
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=90,width=9cm,clip]{fig8.ps}\end{figure}](/articles/aa/full/2008/24/aa09823-08/Timg48.gif) |
Figure 8:
Collision strengths for the 2p 2P
|
| Open with DEXTER | |
The two sets of calculations by us and Ballance et al. are quite similar, as both adopt the R-matrix approach, include relativistic effects in the construction of
wavefunctions as well as in the scattering process, include a wide range of partial waves to obtain converged ![]() ,
include a wide range of energy in order to determine
,
include a wide range of energy in order to determine
![]() values up to high temperatures, and finally include the contribution of resonances in order to improve upon the accuracy of the results for
values up to high temperatures, and finally include the contribution of resonances in order to improve upon the accuracy of the results for ![]() .
However,
there are also some differences. Firstly, our calculations are in the jj coupling scheme (in comparison to their LSJ approach), which particularly affects the accuracy of
transitions within the levels of a degenerate state. Secondly, we have adopted a single program to calculate the contribution of all partial waves with
.
However,
there are also some differences. Firstly, our calculations are in the jj coupling scheme (in comparison to their LSJ approach), which particularly affects the accuracy of
transitions within the levels of a degenerate state. Secondly, we have adopted a single program to calculate the contribution of all partial waves with ![]() ,
whereas they
have adopted different approaches for
,
whereas they
have adopted different approaches for ![]() and J > 10. Thirdly, our range of partial waves is wider (
and J > 10. Thirdly, our range of partial waves is wider (![]() in comparison to their
in comparison to their ![]() ), which affects the
accuracy of
), which affects the
accuracy of ![]() values particularly at higher energies. Finally, a comparison of their Figs. 2-4 with our Figs. 5-7 indicates that our energy mesh for resolving resonances
is finer. This affects the accuracy of the values of
values particularly at higher energies. Finally, a comparison of their Figs. 2-4 with our Figs. 5-7 indicates that our energy mesh for resolving resonances
is finer. This affects the accuracy of the values of ![]() at almost all temperatures, because the resonances are spread (for some transitions) over the entire range of the
threshold region of over 140 Ryd. Therefore, taking into account the above noted differences between the two sets of calculations, an agreement within 20% for a majority of
transitions between the corresponding
at almost all temperatures, because the resonances are spread (for some transitions) over the entire range of the
threshold region of over 140 Ryd. Therefore, taking into account the above noted differences between the two sets of calculations, an agreement within 20% for a majority of
transitions between the corresponding ![]() values is highly satisfactory.
values is highly satisfactory.
In the present work, results for energy levels, radiative rates, collision strengths, and effective collision strengths for transitions among the lowest 25 levels of Fe XXVI have been presented for all transitions. Additionally, results for radiative rates have been presented for four types of transitions, namely E1, E2, M1 and M2. A complete set of present results are likely to be useful for modelling of a variety of plasmas.
Additionally, our calculations have been performed in the jj coupling scheme, CI and relativistic effects have been included while generating wavefunctions, and a wide range of partial waves has been adopted in order to achieve convergence in ![]() values for a majority of transitions. Furthermore, resonances have been resolved in a fine energy
mesh in order to improve the accuracy of the derived values of
values for a majority of transitions. Furthermore, resonances have been resolved in a fine energy
mesh in order to improve the accuracy of the derived values of ![]() .
Similarly,
.
Similarly, ![]() have been computed over a wide energy range up to 1600 Ryd in order to determine
values of
have been computed over a wide energy range up to 1600 Ryd in order to determine
values of ![]() up to a temperature of 107.7 K. Based on comparisons made with earlier available data for several atomic parameters, our energy levels are assessed to
be accurate to
up to a temperature of 107.7 K. Based on comparisons made with earlier available data for several atomic parameters, our energy levels are assessed to
be accurate to ![]() 0.1%, whereas the accuracy of other parameters is probably better than 15%.
0.1%, whereas the accuracy of other parameters is probably better than 15%.
A comparison of our results for effective collision strengths with the corresponding data of Ballance et al. (2002) shows very good agreement for a majority of
transitions, both allowed as well as forbidden, which is highly satisfactory. This is in spite of the fact that they have included radiation damping in their calculations,
whereas we have not. Our present relativistic R-matrix calculations and those performed earlier by Kisielius et al. (1996) do not include radiation damping. However,
both sets of results for ![]() not only agree with each other, especially at lower temperatures which are considerably affected by resonances, but also with those of
Ballance et al., for a majority of transitions. We can therefore confidently state that radiation damping is not a significant contributing factor for transitions in Fe XXVI.
not only agree with each other, especially at lower temperatures which are considerably affected by resonances, but also with those of
Ballance et al., for a majority of transitions. We can therefore confidently state that radiation damping is not a significant contributing factor for transitions in Fe XXVI.
Acknowledgements
This work has been financed by the Engineering and Physical Sciences Research Council (EPSRC) and the Science and Technology Facilities Council (STFC) of the United Kingdom. We would like to thank Dr. Patrick Norrington for providing his GRASP and DARC codes prior to publication, and FPK is grateful to AWE Aldermaston for the award of a William Penney Fellowship. Finally, KMA would like to thank the University of Miyazaki for the hospitality enjoyed during a visit in December 2007.