A&A 484, 401-412 (2008)
DOI: 10.1051/0004-6361:20079312
L. Decin1,2,![]() - L. Blomme1 - M. Reyniers1,
- L. Blomme1 - M. Reyniers1,![]() - N. Ryde3,4 -
K. H. Hinkle5 - A. de Koter2
- N. Ryde3,4 -
K. H. Hinkle5 - A. de Koter2
1 -
Department of Physics and Astronomy, Institute of Astronomy,
K.U. Leuven, Celestijnenlaan 200D, 3001 Leuven, Belgium
2 - Sterrenkundig Instituut Anton Pannekoek, University of
Amsterdam, Kruislaan 4031098 Amsterdam, The Netherlands
3 - Department of Astronomy and Space Physics, Uppsala University, Box
515, 5120 Uppsala, Sweden
4 - Lund Observatory, Box 43, 22100 Lund, Sweden
5 - National Optical Observatories, PO Box 26732, Tucson, ZA
85726, USA
Received 21 December 2007 / Accepted 23 March 2008
Abstract
Context. The unusual Mira variable R Hya is well known for its declining period between AD 1770 and 1950, which is possibly attributed to a recent thermal pulse.
Aims. The goal of this study is to probe the circumstellar envelope (CSE) around R Hya and to check for a correlation between the derived density structure and the declining period.
Methods. We investigate the CSE around R Hya by performing an in-depth analysis of (1.) the photospheric light scattered by three vibration-rotation transitions in the fundamental band of CO at 4.6 ![]() m; and (2.) the pure rotational CO J = 1-0 through 6-5 emission lines excited in the CSE. The vibrational-rotational lines trace the inner CSE within 3.5
m; and (2.) the pure rotational CO J = 1-0 through 6-5 emission lines excited in the CSE. The vibrational-rotational lines trace the inner CSE within 3.5
![]() ,
whereas the pure rotational CO lines are sensitive probes of the cooler gas further out in the CSE.
,
whereas the pure rotational CO lines are sensitive probes of the cooler gas further out in the CSE.
Results. The combined analysis bear evidence of a change in mass-loss rate some 220 yr ago (at ![]() 150
150 ![]() or
or ![]() 1.9 arcsec from the star). While the mass-loss rate before AD 1770 is estimated to be
1.9 arcsec from the star). While the mass-loss rate before AD 1770 is estimated to be ![]()
![]()
![]() /yr, the present day mass-loss rate is a factor of
/yr, the present day mass-loss rate is a factor of ![]() 20 lower. The derived mass-loss history nicely agrees with the mass-loss rate estimates by Zijlstra et al. (2002) on the basis of the period decline. Moreover, the recent detection of an AGB-ISM bow shock around R Hya at 100 arcsec to the west by Wareing et al. (2006) shows that the detached shell seen in the 60
20 lower. The derived mass-loss history nicely agrees with the mass-loss rate estimates by Zijlstra et al. (2002) on the basis of the period decline. Moreover, the recent detection of an AGB-ISM bow shock around R Hya at 100 arcsec to the west by Wareing et al. (2006) shows that the detached shell seen in the 60 ![]() m IRAS images can be explained by a slowing-down of the stellar wind by surrounding matter and that no extra mass-loss modulation around 1-2 arcmin needs to be invoked.
m IRAS images can be explained by a slowing-down of the stellar wind by surrounding matter and that no extra mass-loss modulation around 1-2 arcmin needs to be invoked.
Conclusions. Our results give empirical evidence to the thermal-pulse model, which is capable of explaining both the period evolution and the mass-loss history of R Hya.
Key words: line: profiles - radiative transfer - stars: AGB and post-AGB - stars: circumstellar matter - stars: mass-loss - stars: individual: R Hya
The variability of R Hya (HR 5080, IRAS 13269-2301, HIP 65835) was first established in the early 1700s by Cassini's nephew Miraldi (Zijlstra et al. 2002) and was later classified as a Mira variable. Mira variables show a mono-periodic light curve with large visual amplitudes of more than 2.5 mag, and are usually found near the tip of the asymptotic giant branch (AGB). The s-process element technetium (99Tc) was detected in R Hya by Little et al. (1987) indicating that the star is in the thermal pulsing phase of the AGB. It is well established that AGB stars lose a significant amount of mass during the AGB phase due to a dust driven wind (e.g., Habing 1996).
The star R Hya belongs to the group of optically visible 1n M stars
in the IRAS-LRS catalog (Olnon et al. 1986). The (almost)
absence of the silicate feature around 10 ![]() m (see
Fig. 2) and its IRAS colours suggest that the dusty
circumstellar envelope is detached from the central star
(Hashimoto et al. 1990). From modelling the spectral
energy distribution (SED), Hashimoto et al. (1990)
derived an inner radius of 60
m (see
Fig. 2) and its IRAS colours suggest that the dusty
circumstellar envelope is detached from the central star
(Hashimoto et al. 1990). From modelling the spectral
energy distribution (SED), Hashimoto et al. (1990)
derived an inner radius of 60 ![]() (i.e.
(i.e. ![]() 1.8
1.8
![]() ), based
on a distance of 110 pc and a stellar radius
), based
on a distance of 110 pc and a stellar radius ![]() of
700
of
700 ![]() .
Moreover, R Hya is an unusual Mira variable,
being well known for its declining period between AD 1770 and 1950 (Zijlstra et al. 2002), possibly attributed
to a recent thermal pulse (Wood & Zarro 1981). The
gradual change in the period of R Hya implies that its
pulsation mode has remained constant over the last 345 years. The
period evolution should therefore be related to a change in stellar
parameters, causing a variation in the mass-loss rate during
the last few hundred years (using, e.g., the mass-loss equations
as derived by Vassiliadis & Wood 1993; Blöcker 1995).
.
Moreover, R Hya is an unusual Mira variable,
being well known for its declining period between AD 1770 and 1950 (Zijlstra et al. 2002), possibly attributed
to a recent thermal pulse (Wood & Zarro 1981). The
gradual change in the period of R Hya implies that its
pulsation mode has remained constant over the last 345 years. The
period evolution should therefore be related to a change in stellar
parameters, causing a variation in the mass-loss rate during
the last few hundred years (using, e.g., the mass-loss equations
as derived by Vassiliadis & Wood 1993; Blöcker 1995).
Apart from mass-loss rate variations being caused by an
internal mechanism (e.g., a thermal pulse or non-linearity
effects due to the pulsations), the interaction of the AGB wind with
the interstellar medium (ISM) forms another explanation for large
detached shells (Young et al. 1993). Recently,
Wareing et al. (2006) detected a bow shock around
R Hya: Spitzer images revealed a one-sided parabolic arc
100
![]() to the west, stretching from north to south.
to the west, stretching from north to south.
Thanks to the large cosmic abundances of carbon and oxygen and the high dissociation energy of carbon monoxide (CO), the CO molecule is ubiquitous in the CSE around evolved stars, being present both in the cool outer layers and in the warmer inner regions where the wind is initiated. CO studies have therefore been extensively used to trace the structure in the CSEs around evolved stars. Since the late seventies, low-excitation rotational CO emission lines were used to estimate the mass-loss rates during the AGB phase (e.g. Morris 1980; Knapp et al. 1980; Zuckermann et al. 1977).
The circumstellar shells can also be imaged in photospheric light
scattered by atomic or molecular resonance lines, including CO
(e.g., Plez & Lambert 1994; Gustafsson et al. 1997). Ryde et al. (2000)
have recently applied this latter technique to study the intermediate
regions of the CSE of o Ceti (Mira) using three
vibration-rotation transitions of the fundamental band of
12C16O between low-lying rotational levels in the ground and
first vibrationally excited state![]() . The infrared vibration-rotation lines of CO, as
an alternative to pure rotational CO lines at millimeter wavelengths,
allow us to study the regions closer to the star and they admit higher
spatial resolution in single-telescope studies. Vibration-rotation
lines are excited close to the star and are sensitive to the radiation
field, whereas pure rotational lines are usually more sensitive to the
temperature structure further out in the envelope. By combining
observations of pure rotational and vibration-rotation CO lines, one
may sample the gas located at
. The infrared vibration-rotation lines of CO, as
an alternative to pure rotational CO lines at millimeter wavelengths,
allow us to study the regions closer to the star and they admit higher
spatial resolution in single-telescope studies. Vibration-rotation
lines are excited close to the star and are sensitive to the radiation
field, whereas pure rotational lines are usually more sensitive to the
temperature structure further out in the envelope. By combining
observations of pure rotational and vibration-rotation CO lines, one
may sample the gas located at ![]() 1
1
![]() distance from the star
and beyond, and one might be able to put constraints on the
temperature and density stratification in the whole envelope, and
hence on possible mass-loss rate variations in the CSE of the studied
object.
distance from the star
and beyond, and one might be able to put constraints on the
temperature and density stratification in the whole envelope, and
hence on possible mass-loss rate variations in the CSE of the studied
object.
We seek to derive the mass-loss history of R Hya from the observations and in-depth modelling of pure rotational and vibrational-rotational CO lines emitted in the envelope around R Hya. In Sect. 2, we first discuss the scattered low-excitation vibrational-rotational transitions of the fundamental band of CO observed in the CSE around R Hya with the Phoenix spectrograph. Thereafter, in Sect. 2.2, we look at the pure rotational CO transitions emitted further out in the envelope of R Hya. In Sect. 3, both the vibrational-rotational and pure rotational CO lines are modelled using a non-LTE radiative transfer code. The results are discussed in Sect. 4 and some conclusions are drawn in Sect. 5.
The analysis is based on two sets of observations probing different
regions of the CSE. First, the CSE is imaged in photospheric light
scattered by low-excitation vibrational-rotational transitions of the
fundamental band of CO at an angular distance, ![]() ,
between
,
between ![]() 1
1
![]() -3.5
-3.5
![]() (see Sect. 2.1). Second, radio data of pure
rotational CO emission lines are analysed in detail (see
Sect. 2.2). The latter data provide constraints on the outer
regions of the CSE, out to approximately 2500
(see Sect. 2.1). Second, radio data of pure
rotational CO emission lines are analysed in detail (see
Sect. 2.2). The latter data provide constraints on the outer
regions of the CSE, out to approximately 2500 ![]() away from the star. Moreover, the circumstellar structure of R
Hya has been investigated in the IRAS survey scan data and the
spectral energy distribution (SED) has been modelled by
Hashimoto et al. (1998). Since the dust emission has
already been analysed by Hashimoto et al. (1998) and the
model fit was repeated and confirmed by
Zijlstra et al. (2002), we only summarise the most
important dust characteristics and the main results of the dust
analysis done by these two research groups in Sect. 2.3.
away from the star. Moreover, the circumstellar structure of R
Hya has been investigated in the IRAS survey scan data and the
spectral energy distribution (SED) has been modelled by
Hashimoto et al. (1998). Since the dust emission has
already been analysed by Hashimoto et al. (1998) and the
model fit was repeated and confirmed by
Zijlstra et al. (2002), we only summarise the most
important dust characteristics and the main results of the dust
analysis done by these two research groups in Sect. 2.3.
We observed on 26 February 2005 with the
Phoenix![]() spectrometer mounted on the 8 m Gemini South telescope. Phoenix is a
single-order, high spectral resolution (
spectrometer mounted on the 8 m Gemini South telescope. Phoenix is a
single-order, high spectral resolution (
![]() ),
near-IR (1-5
),
near-IR (1-5 ![]() m) spectrometer
(Hinkle et al. 1998). The slit length is 14
m) spectrometer
(Hinkle et al. 1998). The slit length is 14
![]() .
For
our observations, a slit width of 2 pixels (0.17
.
For
our observations, a slit width of 2 pixels (0.17
![]() )
is used,
resulting in a resolution of
)
is used,
resulting in a resolution of ![]() 75 000. The visual seeing was around
0.6
75 000. The visual seeing was around
0.6
![]() .
Assuming that the seeing is proportional to the
wavelength to the 1/5 power (Roddier 1981), the
seeing was better than 0.4
.
Assuming that the seeing is proportional to the
wavelength to the 1/5 power (Roddier 1981), the
seeing was better than 0.4
![]() at 4.6
at 4.6 ![]() m, the wavelength of
the observation.
m, the wavelength of
the observation.
Low-excitation lines of the vibration-rotation fundamental R-branch of
the electronic ground state of CO are observed. The
selected lines are the 1-0 R(1) (i.e.,
![]() and
and
![]() )
at
2150.86 cm-1; the 1-0 R(2) at 2154.60 cm-1; and the
1-0 R(3) at 2158.30 cm-1.
)
at
2150.86 cm-1; the 1-0 R(2) at 2154.60 cm-1; and the
1-0 R(3) at 2158.30 cm-1.
We used the same observational set-up as in
Ryde et al. (2000). The CSE of R Hya is
observed in a hashed configuration, resembling a perpendicular railway
crossing with the star in the middle (see Fig. 1).
The long slit was placed in the off-star position at 1
![]() from
the star. The four slit positions overlap at a distance of
from
the star. The four slit positions overlap at a distance of ![]() 1.4
1.4
![]() from the star. We were able to detect emission in the CSE
out to
from the star. We were able to detect emission in the CSE
out to ![]() 3.5
3.5
![]() .
.
![\begin{figure}
\par\includegraphics[angle=270,width=6.5cm,clip]{9312fig1.eps}\end{figure}](/articles/aa/full/2008/23/aa9312-07/Timg28.gif) |
Figure 1:
Slit positions for the Phoenix off-star observations of R Hya. All off-star slits are positioned at 1
|
| Open with DEXTER | |
The observed CO R(1), R(2), and R(3) lines suffer from telluric
absorption. Therefore, at the time of observation, the radial velocity
of the star combined with the heliocentric velocity of the Earth must
shift the star's CO lines away from the telluric ones. Otherwise, the
blending of the telluric and stellar lines severely compromises the
analysis of the faint circumstellar emission. From the pure rotational
CO lines, we deduce a
![]() = -10.4 km s-1 (see
Sect. 2.2). At the time of the observations and at Gemini
South, this corresponds to a geocentric radial velocity of
-33.5 km s-1.
= -10.4 km s-1 (see
Sect. 2.2). At the time of the observations and at Gemini
South, this corresponds to a geocentric radial velocity of
-33.5 km s-1.
The exposure times for the on-star observations were 1 s and were
30 s for each of the off-star observations. The total amount of
observing time was ![]() 5 h, of which some 650 s were
effective observing time on the target. We used the on-star exposures
to remove the scattered light from the off-star exposures. Since
Phoenix is a long-slit spectrograph, nodding along the slit is possible. This mode has been used to subtract the background (see also
Sect. 2.1.1). A logbook of the observations can be
found in Table A.1 in the online
Appendix A. We used the following nomenclature to
describe the off-star observations: ``EW-slit N1 E2.5'' indicates a
slit-position oriented in the east-west direction, which is offset by
1
5 h, of which some 650 s were
effective observing time on the target. We used the on-star exposures
to remove the scattered light from the off-star exposures. Since
Phoenix is a long-slit spectrograph, nodding along the slit is possible. This mode has been used to subtract the background (see also
Sect. 2.1.1). A logbook of the observations can be
found in Table A.1 in the online
Appendix A. We used the following nomenclature to
describe the off-star observations: ``EW-slit N1 E2.5'' indicates a
slit-position oriented in the east-west direction, which is offset by
1
![]() to the north from the star and which has been moved
2.5
to the north from the star and which has been moved
2.5
![]() in the east-direction along the slit (data sets 112 and
128 in Fig. 1). As can be seen in the logbook, we
have 16 off-star observations at our disposal: each time four
observations with a slit positioned 1
in the east-direction along the slit (data sets 112 and
128 in Fig. 1). As can be seen in the logbook, we
have 16 off-star observations at our disposal: each time four
observations with a slit positioned 1
![]() to the north, south,
east, and west away from the star were taken. The observing numbers of
the off-star data sets are listed in the logbook, and schematically
represented in Fig. 1.
to the north, south,
east, and west away from the star were taken. The observing numbers of
the off-star data sets are listed in the logbook, and schematically
represented in Fig. 1.
The data reduction is based on the standard procedures provided by the Image Reduction and Analysis Facility (IRAF). For a full description of the reduction procedure we refer to Ryde et al. (2000); only the most important steps and differences we outline here. Since the absolute flux calibration contains several steps, this part of the reduction process is outlined in a separate section. The pointing accuracy is discussed in Sect. 2.1.3.
Different steps are involved in the absolute flux calibration process of the on-star and off-star data. After the conversion factors are determined to convert the on-star data to physical flux units, the off-star data are scaled with the same factor.
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{9312fig2.ps}\end{figure}](/articles/aa/full/2008/23/aa9312-07/Timg31.gif) |
Figure 2:
The low-resolution ISO-SWS spectrum (
|
| Open with DEXTER | |
In Fig. 3, a comparison is shown between several
theoretical spectra to illustrate the effect of the effective
temperature on the infrared spectrum. We find that a theoretical
spectrum with
![]() = 2800 K already nicely reproduces the ISO-SWS
spectrum. Note that it is not our purpose to perfectly match the
ISO-SWS spectrum, especially since the hydrostatic MARCS model
atmosphere code does not account for the effects of pulsations in the
Mira-type star R Hya.
= 2800 K already nicely reproduces the ISO-SWS
spectrum. Note that it is not our purpose to perfectly match the
ISO-SWS spectrum, especially since the hydrostatic MARCS model
atmosphere code does not account for the effects of pulsations in the
Mira-type star R Hya.
![\begin{figure}
\par\includegraphics[angle=90,width=8.3cm,clip]{9312fig3.eps}\end{figure}](/articles/aa/full/2008/23/aa9312-07/Timg35.gif) |
Figure 3:
Comparison between the ISO-SWS spectrum of R Hya and
theoretical model spectra computed with the MARCS code. The
black curve represents the ISO-SWS spectrum, the purple curve a
MARCS spectrum at
|
| Open with DEXTER | |
In Fig. 4, the same theoretical spectrum as in
Fig. 3 (with
![]() = 2800 K) is compared with the
observed on-star Phoenix spectrum of R Hya. The general
features are well reproduced and are mainly due to
photospheric water and CO. Moreover, the agreement of the overall flux
level is astonishingly good: while Ryde et al. (2000)
have multiplied the model fluxes with a factor of 1.4 to adapt the
theoretical MARCS spectrum to the observed spectrum of
o Ceti, no (extra) shift needs to be applied to match the
observed Phoenix and theoretical MARCS spectrum of R Hya. Comparing the shift between the telluric and photospheric CO lines in
Fig. 4 yields a radial velocity of -32.3 km s-1, in
excellent agreement with the value derived in Sect. 2.1.
= 2800 K) is compared with the
observed on-star Phoenix spectrum of R Hya. The general
features are well reproduced and are mainly due to
photospheric water and CO. Moreover, the agreement of the overall flux
level is astonishingly good: while Ryde et al. (2000)
have multiplied the model fluxes with a factor of 1.4 to adapt the
theoretical MARCS spectrum to the observed spectrum of
o Ceti, no (extra) shift needs to be applied to match the
observed Phoenix and theoretical MARCS spectrum of R Hya. Comparing the shift between the telluric and photospheric CO lines in
Fig. 4 yields a radial velocity of -32.3 km s-1, in
excellent agreement with the value derived in Sect. 2.1.
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{9312fig4.ps}\end{figure}](/articles/aa/full/2008/23/aa9312-07/Timg36.gif) |
Figure 4:
Comparison between the on-star Phoenix spectrum of R Hya and the theoretical MARCS model spectrum computed with
the SCAN H2O linelist (red) and the AMES H2O
linelist (green) at a
|
| Open with DEXTER | |
The Gemini telescope guides using a wavefront sensor star that
is typically located about 5 arcmin from the target star. The
wavefront sensor star is held to 0.01
![]() drift in 1 h.
This star controls the offsets. So there is essentially no error
introduced by the offsetting.
drift in 1 h.
This star controls the offsets. So there is essentially no error
introduced by the offsetting.
To center a star on the slit, we first imaged the slit against the sky
with Phoenix in imaging mode (the grating is by-passed). Then the
star is imaged and centered at the middle of the slit position. One
then switches from imaging mode to spectroscopy mode, moves the star
to the correct starting position on the slit and starts taking
spectra. The plate scale has very small pixels allowing us to position
the star to better than 0.1
![]() on the slit. This peak-up happened
before the on-star exposure 108, before data set 123, before the
on-star exposure 137, before data set 149, and before data set 158.
on the slit. This peak-up happened
before the on-star exposure 108, before data set 123, before the
on-star exposure 137, before data set 149, and before data set 158.
The wavefront sensor (WFS) of Phoenix is not inside Phoenix, but in the telescope. This implies that there can be flexure between the Phoenix spectrometer and the telescope. From about 7 to 9 h UTC, we observed at a changing parallactic angle. As a result, observations in this time interval likely suffer from large flexure differences. They are on the order of 0.2 arcsec over an hour, but they may occur suddenly. To check this, after we had finished the sequence of observations 141 through 152, we repeated the offsets in an abbreviated way with data sets 158 through 161. As will be discussed in Sect. 2.1.5, flexure problems likely have occurred in data sets (149, 150).
To study the CO emission lines excited in the CSE, the on-star data are scaled to the off-star data and subtracted. This is illustrated in Fig. 5 for the EW-slit S1 W2.5 (data set 124). The scaled on-star spectrum at least approximately represents the radiation exciting the molecules. The CO and H2O lines dominate the photospheric spectrum (Aringer et al. 2002). The off-star spectrum consists of (1.) stellar light that is scattered in the Earth's atmosphere, the telescope, the spectrometer and/or dust grains in the CSE, leading to a spectrum resembling the on-star one; and (2.) the CO 1-0 R(1), R(2), and R(3) vibration-rotation emission lines. The circumstellar molecules are hence radiatively excited by the stellar light.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9312fig5.eps}\end{figure}](/articles/aa/full/2008/23/aa9312-07/Timg37.gif) |
Figure 5: Off-star (full line) and on-star (dashed line) spectrum of R Hya. The three off-star CO vibration-rotation emission lines, which are marked R(1), R(2), and R(3), are partly filled in by emission from the circumstellar CO lines compared to the on-star observations. Telluric CO lines are at 2150.86, 2154.60 and 2158.30 cm-1, telluric H2O lines at 2152.50 and 2156.50 cm-1. |
| Open with DEXTER | |
Figure 6 shows a typical example of the resulting CO emission lines integrated over the long slit for data set 128, being a EW-slit N1 E2.5. The CO emission lines from the other 15 data sets are displayed in Figs. A.1-A.4 in the online appendix. Note that the (co-)ordinate axes are put in the same scale in these plots to strengthen the (dis)similarities between the different off-star observations. Variations in the telluric lines between the object frame exposure and the background exposure, between two successive exposures used for background subtraction, and/or between the on-star and off-star exposure result in non-zero residuals in the continuum between the CO lines. The signal-to-noise ranges between 5 and 30.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9312fig6.eps}\end{figure}](/articles/aa/full/2008/23/aa9312-07/Timg38.gif) |
Figure 6: The resulting circumstellar CO vibration-rotation flux from the wind of R Hya for data set 128, being a EW-slit N1 E2.5. The intensity is integrated over the full slit area. |
| Open with DEXTER | |
In order to study the CO emission as a function of the angular
distance ![]() from the star, we divided the long-slit spectra into
38 sub-spectra. Each sub-spectrum covers 2 pixels in the spatial
direction. Thisway, the emission between 1
from the star, we divided the long-slit spectra into
38 sub-spectra. Each sub-spectrum covers 2 pixels in the spatial
direction. Thisway, the emission between 1
![]() and 3.5
and 3.5
![]() from the star can be measured (see, e.g.,
Fig. 7). For each of the 38 sub-spectra, the
wavelength-integrated intensity of the lines is measured, taken into
account the 2*2 pixel area. This way, each of the 16 off-star
data sets gives us the decline of the intensity of the three CO
emission lines as a function of the angular distance,
from the star can be measured (see, e.g.,
Fig. 7). For each of the 38 sub-spectra, the
wavelength-integrated intensity of the lines is measured, taken into
account the 2*2 pixel area. This way, each of the 16 off-star
data sets gives us the decline of the intensity of the three CO
emission lines as a function of the angular distance, ![]() ,
in two
directions, e.g., data set 112 taken at the north of R Hya yields the
decline in the north-east (NE) and north-west (NW)
direction
,
in two
directions, e.g., data set 112 taken at the north of R Hya yields the
decline in the north-east (NE) and north-west (NW)
direction![]() . The three CO
emission lines, R(1), R(2), and R(3) yield analogous results. By
adding the intensities of the three lines, the signal-to-noise is
increased. The decline of the intensity in the four slits positioned
at 1
. The three CO
emission lines, R(1), R(2), and R(3) yield analogous results. By
adding the intensities of the three lines, the signal-to-noise is
increased. The decline of the intensity in the four slits positioned
at 1
![]() to the north of R Hya is displayed in
Fig. 8. The results for the other three
directions are displayed in the Figs. A.5-A.7 in the online appendix. An overview of the
mean of the eight different directions, together with the overall mean
and standard deviation, is displayed in Fig. 9.
to the north of R Hya is displayed in
Fig. 8. The results for the other three
directions are displayed in the Figs. A.5-A.7 in the online appendix. An overview of the
mean of the eight different directions, together with the overall mean
and standard deviation, is displayed in Fig. 9.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9312fig7.eps}\end{figure}](/articles/aa/full/2008/23/aa9312-07/Timg39.gif) |
Figure 7:
Set of emission spectra at the east-position from R Hya (data set 142, being a NS-slit E1 S2.5). The spectra are
shifted vertically for reasons of clarity. The top spectrum is
measured closest to the star, i.e., at |
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\subfigure{\includegraphics[width=8cm,clip]{9312fig8a} ...
....5cm}
\subfigure{\includegraphics[width=8cm,clip]{9312fig8b.eps} }}
\end{figure}](/articles/aa/full/2008/23/aa9312-07/Timg40.gif) |
Figure 8:
Decline of the intensity of the circumstellar emission as a
function of angular distance |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9312fig9.eps}\end{figure}](/articles/aa/full/2008/23/aa9312-07/Timg41.gif) |
Figure 9:
Decline of the intensity of the circumstellar emission as a
function of the angular distance |
| Open with DEXTER | |
In this section, we first will discuss the decline of the intensity in the different scan directions and compare the different data sets tracing the same geometrical region in the circumstellar envelope. Thereafter, the mean over all directions will be compared to the mean of each individual direction. The data will be modelled and analysed in detail in Sect. 3.
Inspecting Fig. 8 and the online
Fig. A.5 displaying the circumstellar
CO vibration-rotation emission integrated over the slit
positioned at, respectively, 1
![]() north and south away from the star, it
is clear that the four data sets tracing the same region in the CSE
match nicely. The scatter between the data sets is mainly due to small
inaccuracies in the slit position and the (slightly) variable sky
conditions. The north-west (south-east) direction have a higher
intensity further out in the CSE than the north-east (south-west)
direction.
north and south away from the star, it
is clear that the four data sets tracing the same region in the CSE
match nicely. The scatter between the data sets is mainly due to small
inaccuracies in the slit position and the (slightly) variable sky
conditions. The north-west (south-east) direction have a higher
intensity further out in the CSE than the north-east (south-west)
direction.
Figure A.6, tracing the scans in the east
direction of the star, clearly shows a discrepancy between the (141,
142) and (158, 161) data sets in the east-south direction. This shift
in intensity is not seen in the east-north direction. The difference
between both pairs of data sets can also be seen in the online
Fig. A.3, where the (158, 161) data sets show a higher
flux peak in all three CO emission lines than the (141, 142)
data sets. Flexure between the telescope and the Phoenix slit (see
Sect. 2.1.3) is probably the cause for this discrepancy.
Note also that the nodding principle was used to subtract the sky from
the (141, 142) data set, while for the (158, 161) data set the sky was
subtracted using a sky frame exposure taken at 15
![]() from the
star.
from the
star.
A similar problem as for the east direction is seen in
Fig. A.7 tracing the westward region in the CSE. A
good match is found for the four data sets tracing the west-north
direction, but the west-south scans largely differ. While for the
east-south scans in Fig. A.6 only a shift in the
absolute integrated intensity valuebetween the different data sets is
noted, the intensity decline of the (159, 160) data sets is much
steeper than for the (149, 150) data sets. Inspecting the cross-over
points between the west-south and south-west direction around
1.4
![]() from the star clearly points towards problems with the
(149, 150) data sets (see Fig. A.8), possibly caused by a
sudden change in flexure between the telescope and the Phoenix
slit. Moreover, while all the other scan directions show the same
trend in intensity decline (see also next paragraph), the (149, 150)
data sets are a-typical. In the further analysis, the (149,
150) data sets have, therefore, been omitted. By comparing the
cross-overs of the other scan directions, a maximum uncertainty in
slit-position of 0.2
from the star clearly points towards problems with the
(149, 150) data sets (see Fig. A.8), possibly caused by a
sudden change in flexure between the telescope and the Phoenix
slit. Moreover, while all the other scan directions show the same
trend in intensity decline (see also next paragraph), the (149, 150)
data sets are a-typical. In the further analysis, the (149,
150) data sets have, therefore, been omitted. By comparing the
cross-overs of the other scan directions, a maximum uncertainty in
slit-position of 0.2
![]() is derived.
is derived.
In Fig. 9, the mean of the intensity decline over all directions is compared to the mean over all individual directions. Inspecting Fig. 9, we conclude that the measured emission-line intensities in the different directions from the star are consistent with a symmetric wind. The fact that the NW, NE, and SE intensities lie above the mean, while the SW, ES, EN, and WS lie below may be a (tentative) suggestion for a bipolar structure stretching from NW to SE.
![\begin{figure}
\par\includegraphics[angle=90,width=12cm,clip]{9312fig10.ps}\end{figure}](/articles/aa/full/2008/23/aa9312-07/Timg43.gif) |
Figure 10:
CO rotational line profiles of R Hya (plotted in
grey, see Table 1) compared with (i) black
dotted line: the model predictions based on the parameters as given
by Wannier & Sahai (1986), who derived a constant mass
loss of |
| Open with DEXTER | |
CO pure rotational line profiles (J = 2-1 and 3-2) have been
observed with the 15 m JCMT![]() . The observations were carried out using a
position-switching mode. The JCMT data reduction was performed with
the SPLAT devoted routines of STARLINK. A polynomial of first
order was fitted to an emission-free region of the spectral
baseline and subtracted. The antenna temperature,
. The observations were carried out using a
position-switching mode. The JCMT data reduction was performed with
the SPLAT devoted routines of STARLINK. A polynomial of first
order was fitted to an emission-free region of the spectral
baseline and subtracted. The antenna temperature,
![]() ,
was
converted to the main-beam temperature (
,
was
converted to the main-beam temperature (
![]() ),
using a main-beam efficiency
),
using a main-beam efficiency
![]() of 0.69 for the CO (2-1)
line and of 0.63 for the CO (3-2) line. The half-power beamwidth
(HPBW) of the different receivers was
of 0.69 for the CO (2-1)
line and of 0.63 for the CO (3-2) line. The half-power beamwidth
(HPBW) of the different receivers was
![]() for CO (2-1) and
for CO (2-1) and
![]() for CO (3-2) (Kemper et al. 2003). The
absolute flux calibration accuracy was estimated to be 10%. We note
that, in principle, pointing uncertainties, beam effects, atmospheric
seeing, and systematics at these frequencies can combine to produce an
error that is larger than 10%. For that reason, a conservative
absolute error estimate of 20% is adapted. The line shapes and
widths are, however, not very sensitive to pointing errors, etc.
for CO (3-2) (Kemper et al. 2003). The
absolute flux calibration accuracy was estimated to be 10%. We note
that, in principle, pointing uncertainties, beam effects, atmospheric
seeing, and systematics at these frequencies can combine to produce an
error that is larger than 10%. For that reason, a conservative
absolute error estimate of 20% is adapted. The line shapes and
widths are, however, not very sensitive to pointing errors, etc.
We complemented these data with CO pure rotational line profiles as available in the literature (see Table 1). The object R Hya was observed by different authors, resulting in a total of 10 line profiles covering 4 different transitions. Comparing the different line profiles of one rotational transition gives us information on the absolute flux uncertainties.
Table 1:
CO rotational line profiles as used in this
study. Consecutive columns list the transition, the
telescope, the half-power beamwidth ( HPBW), the main-beam
efficiency (
![]() ), the
absolute flux uncertainty (
), the
absolute flux uncertainty (
![]() ), and the literature
reference. The beam width, main-beam efficiency, and absolute flux
uncertainty listed in this table are the ones as found in the cited
paper. In case the absolute flux uncertainty was not given, an
uncertainty of 20% is assumed.
), and the literature
reference. The beam width, main-beam efficiency, and absolute flux
uncertainty listed in this table are the ones as found in the cited
paper. In case the absolute flux uncertainty was not given, an
uncertainty of 20% is assumed.
All available pure rotational CO emission data of the CSE around
R Hya are displayed in Fig. 10 and are compared
with a constant mass-loss model (see Sect. 3.2.1) based on
the parameters as given by Wannier & Sahai (1986). They
derived a constant mass-loss rate of ![]()
![]()
![]()
![]() yr-1, using a distance of 130 pc based on
CO(2-1) data obtained with the NRAO. While this constant mass-loss
rate model is capable of predicting the integrated intensities
of many of the pure rotational CO lines, it clearly is not able to
predict the line shapes correctly: the predictions show a
``two-horn'' line profile (indicative of an optically thin,
resolved emission line, Morris 1975) in contrast to
the sharp line profiles in the observational data. Comparing, however,
the different absolute intensity levels of one rotational transition
reveals clear differences (even after correcting for different beam
sizes and telescope diameters): the integrated intensities of the
CO(2-1) as obtained with the SEST, NRAO, and CSO are well-predicted
by the constant mass-loss model, while the same CO(2-1) line
observed with IRAM is over-predicted and the one observed with the
JCMT is by far under-predicted (see Fig. 10). An
analogous problem has been noted by Schöier et al. (2006)
for SiO(3-2) observations obtained with IRAM by
Bujarrabal et al. (1994), where the IRAM-data were
consistently a factor of two lower compared to model predictions matching
the other SiO-data. The observations are indeed taken at different
phases during the pulsation cycle. However, while the V-band
magnitude of R Hya varies between
yr-1, using a distance of 130 pc based on
CO(2-1) data obtained with the NRAO. While this constant mass-loss
rate model is capable of predicting the integrated intensities
of many of the pure rotational CO lines, it clearly is not able to
predict the line shapes correctly: the predictions show a
``two-horn'' line profile (indicative of an optically thin,
resolved emission line, Morris 1975) in contrast to
the sharp line profiles in the observational data. Comparing, however,
the different absolute intensity levels of one rotational transition
reveals clear differences (even after correcting for different beam
sizes and telescope diameters): the integrated intensities of the
CO(2-1) as obtained with the SEST, NRAO, and CSO are well-predicted
by the constant mass-loss model, while the same CO(2-1) line
observed with IRAM is over-predicted and the one observed with the
JCMT is by far under-predicted (see Fig. 10). An
analogous problem has been noted by Schöier et al. (2006)
for SiO(3-2) observations obtained with IRAM by
Bujarrabal et al. (1994), where the IRAM-data were
consistently a factor of two lower compared to model predictions matching
the other SiO-data. The observations are indeed taken at different
phases during the pulsation cycle. However, while the V-band
magnitude of R Hya varies between ![]() 4 and 10, the
amplitude of the variability is typically less in the near-infrared
than in the optical, and less in the mid-infrared than in the
near-infrared (Smith et al. 2002), and is not expected to
have that large an influence on the (sub)millimeter CO lines. When
modelling the data, we therefore will give a greater weight to the
line shape than to the integrated line intensity, and use the
statistical method as developed in Decin et al. (2007)
to select the best-fit model (see Sect. 3.2).
4 and 10, the
amplitude of the variability is typically less in the near-infrared
than in the optical, and less in the mid-infrared than in the
near-infrared (Smith et al. 2002), and is not expected to
have that large an influence on the (sub)millimeter CO lines. When
modelling the data, we therefore will give a greater weight to the
line shape than to the integrated line intensity, and use the
statistical method as developed in Decin et al. (2007)
to select the best-fit model (see Sect. 3.2).
R Hya is classified as an optically visible 1n M star in
the IRAS-LRS catalog (Olnon et al. 1986), showing (almost)
no silicate band feature around 10 ![]() m (see Fig. 2). A
large number of M-type stars classified as 1n have IRAS colours
indicating no or optically thin circumstellar dust envelopes with weak mass-loss activity, which explains the (almost) absence of the 10
m (see Fig. 2). A
large number of M-type stars classified as 1n have IRAS colours
indicating no or optically thin circumstellar dust envelopes with weak mass-loss activity, which explains the (almost) absence of the 10 ![]() m
silicate feature. Hashimoto et al. (1990), however, found
that a significant fraction of the optically visible 1n M stars show
remarkably red IRAS photometric colours, which indicate the presence of
circumstellar dust. Silicate emission forms close to the star and the
lack of it indicates a dust envelope being detached from the central
star (Hashimoto et al. 1990). The object R Hya is the
brightest source among the red 1n M stars. The IRAS images show that
the extended emission component around R Hya is almost
circular. From modelling the SED, Hashimoto et al. (1990)
derived an inner radius of 60
m
silicate feature. Hashimoto et al. (1990), however, found
that a significant fraction of the optically visible 1n M stars show
remarkably red IRAS photometric colours, which indicate the presence of
circumstellar dust. Silicate emission forms close to the star and the
lack of it indicates a dust envelope being detached from the central
star (Hashimoto et al. 1990). The object R Hya is the
brightest source among the red 1n M stars. The IRAS images show that
the extended emission component around R Hya is almost
circular. From modelling the SED, Hashimoto et al. (1990)
derived an inner radius of 60 ![]() based on a distance of 110 pc
and
based on a distance of 110 pc
and ![]() = 700
= 700 ![]() (i.e. at
(i.e. at
![]() 1.8
1.8
![]() ). Zijlstra et al. (2002) repeated the
SED model fit: at a distance of 165 pc, the inner radius scales to
). Zijlstra et al. (2002) repeated the
SED model fit: at a distance of 165 pc, the inner radius scales to
![]() cm, and the (pre-AD 1770) mass-loss rate,
cm, and the (pre-AD 1770) mass-loss rate,
![]() ,
is estimated to be
,
is estimated to be
![]()
![]() /yr
(assuming a gas-to-dust ratio of 200), with the
present-day mass-loss being at least a factor 10 smaller.
/yr
(assuming a gas-to-dust ratio of 200), with the
present-day mass-loss being at least a factor 10 smaller.
Interestingly, the IRAS 60 ![]() m image shows a detached shell around
a bright point source, with an inner radius of 1-2 arcmin (or
m image shows a detached shell around
a bright point source, with an inner radius of 1-2 arcmin (or
![]() cm at 165 pc). Hashimoto et al. (1990) cautioned for a
possible artefact in the deconvolution procedure, while
Zijlstra et al. (2002) considered the case that this ring
represents a much older mass-loss event, which was interrupted
cm at 165 pc). Hashimoto et al. (1990) cautioned for a
possible artefact in the deconvolution procedure, while
Zijlstra et al. (2002) considered the case that this ring
represents a much older mass-loss event, which was interrupted
![]() 5000 yr ago. Another possibility that should be considered is
the interaction of the AGB stellar wind with the interstellar medium
(ISM) resulting in a bow shock. Recently,
Wareing et al. (2006) imaged the structure around
R Hya with the Spitzer-telescope, revealing a
one-sided parabolic arc 100
5000 yr ago. Another possibility that should be considered is
the interaction of the AGB stellar wind with the interstellar medium
(ISM) resulting in a bow shock. Recently,
Wareing et al. (2006) imaged the structure around
R Hya with the Spitzer-telescope, revealing a
one-sided parabolic arc 100
![]() to the west, stretching from north
to south. Using three-dimensional hydrodynamic simulations, they
successfully modelled R Hya and its surroundings in terms of
a bow shock into the surrounding
ISM. Wareing et al. (2006) and Libert et al. (2007, considering the
carbon star Y CVn) proposed this
mechanism as another explanation of detached shells. The detached
shell is then the result from the slowing-down of the stellar wind by
surrounding matter.
to the west, stretching from north
to south. Using three-dimensional hydrodynamic simulations, they
successfully modelled R Hya and its surroundings in terms of
a bow shock into the surrounding
ISM. Wareing et al. (2006) and Libert et al. (2007, considering the
carbon star Y CVn) proposed this
mechanism as another explanation of detached shells. The detached
shell is then the result from the slowing-down of the stellar wind by
surrounding matter.
The decline of the intensity of the CO vibration-rotation emission lines offers a strong diagnostic tool to study the circumstellar density structure within the first few hundred stellar radii. In Sect. 3.1, we therefore first elaborate on the constraints posed by the CO vibrational-rotational emission lines and compare the decline with an analytical solution computed under the assumption of a spherically symmetric, optically thin wind with a constant mass loss and constant expansion velocity. Thereafter, the CO vibration-rotation intensity decline in combination with the pure CO rotational line profiles will be modelled in detail using the non-LTE radiative transfer code GASTRoNOoM (Sect. 3.2).
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{9312fig11.ps}\end{figure}](/articles/aa/full/2008/23/aa9312-07/Timg52.gif) |
Figure 11:
Dependence of the mean of the scattered
wavelength-integrated intensity of the circumstellar CO
vibration-rotation lines on the angular distance on
the sky, |
| Open with DEXTER | |
A simple analytical expression for the behaviour of the
wavelength-integrated intensity as a function of the angular distance,
![]() ,
can be constructed for a spherically symmetric and
homogeneous wind. The wind is assumed to be optically thin in the CO
lines along the line of sight, and has a constant mass-loss rate,
,
can be constructed for a spherically symmetric and
homogeneous wind. The wind is assumed to be optically thin in the CO
lines along the line of sight, and has a constant mass-loss rate,
![]() ,
and a constant expansion velocity
,
and a constant expansion velocity ![]() .
Under the assumption
of a pure scattering process, Gustafsson et al. (1997)
demonstrated that the ratio between the wavelength-integrated,
line-scattered intensity
.
Under the assumption
of a pure scattering process, Gustafsson et al. (1997)
demonstrated that the ratio between the wavelength-integrated,
line-scattered intensity
![]() (erg s-1 cm-2 arcsec-2) received in a scattering line and the observed
line-scattering stellar flux averaged across the line width,
(erg s-1 cm-2 arcsec-2) received in a scattering line and the observed
line-scattering stellar flux averaged across the line width,
![]() (erg s-1 cm-2 cm-1), can be
written as
(erg s-1 cm-2 cm-1), can be
written as
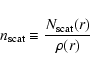 |
(2) |
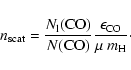 |
(3) |
Table 2:
Power-law dependence of the wavelength-integrated intensity
![]() on the angular distance
on the angular distance ![]() for the different
scan directions.
for the different
scan directions.
Ryde et al. (2000) derived a mean slope of the west,
east, and north positions for the scattered CO vibra-rotational emission in the
CSE of o Cet of
![]() = -2.8,
with individual dependencies of the different scan directions ranging
from -2.3 to -3.0. Although not used in the analysis by
Ryde & Schöier (2001), we note that also for o Cet a
``swing'' is visible around 3
= -2.8,
with individual dependencies of the different scan directions ranging
from -2.3 to -3.0. Although not used in the analysis by
Ryde & Schöier (2001), we note that also for o Cet a
``swing'' is visible around 3
![]() from the star.
from the star.
The observed circumstellar (vibrational-) rotational CO lines provide information on the thermodynamical structure of the outflow of R Hya. For a proper interpretation of both data sets, we have used our theoretical non-LTE radiative transfer code GASTRoNOoM (Decin et al. 2006). The code first (1.) calculates the kinetic temperature in the shell by solving the equations of motion of gas and dust and the energy balance simultaneously; then (2.) solves the radiative transfer equation in the co-moving frame using the Approximate Newton-Raphson operator as developed by Schönberg & Hempe (1986) and computes the non-LTE level-populations consistently; and finally (3.) determines the observable line profile by ray-tracing. The main assumption of the code is a spherically symmetric wind, which is confirmed to be a good approximation in case of the CSE of R Hya by the IRAS-images shown by Hashimoto et al. (1998). The mass-loss rate is allowed to vary with radial distance from the star. For a full description of the code we refer to Decin et al. (2006). In the code, complete angular and frequency redistribution (CRD) is assumed. As described by Ryde & Schöier (2001), the assumption of CRD is valid for the pure rotational CO transitions, since the collisions will have time to reset the frequency-memory of the excited atoms. For the vibrational-rotational CO transitions, this assumption can be problematic since the spontaneous de-excitation rates are of the order of 10 s-1. However, Ryde & Schöier (2001) demonstrated that for the low mass-loss rate models and the low optical depths occurring in the CSEs of stars, such as o Cet, and similarly of R Hya, the assumption of CRD is justified.
As explained in Sect. 2.2, the pure rotational CO line profiles show quite large differences in their absolute intensity level (after correction for different telescope size and HPBW) between the various observations of the same rotational transition, although the line shapes are similar. Decin et al. (2006) demonstrated that not only the integrated line intensities, but particularly the line shapes should be taken into account for a proper determination of the mass-loss history. To find the best-fit model and derive a 95% confidence interval for the model parameters, we will use the log-likelihood-method as developed in Decin et al. (2007). This method gives a greater weight to the line shapes than to the integrated line intensity. It turned out to be impossible to find a model structure for the envelope fulfilling the absolute flux criteria of all pure rotational CO lines (listed in Table 1) due to the large internal absolute flux differences. We therefore have opted to increase the absolute flux uncertainty to 40% on the IRAM and JCMT-data. Note that the log-likelihood method also accounts for the rms-noise on the data.
As shown in Fig. 10 a model with a constant mass-loss
rate fits quite nicely the integrated intensities
of the pure rotational line profiles, although the line shapes are
not well reproduced. In addition, the theoretically predicted
wavelength-integrated scattered line intensities of the CO
vibration-rotation emission lines show a
![]() -dependency
(see Fig. 12), being too steep and failing to
reproduce the observed ``swing''. To illustrate the sensitivity of the
intensity decline to the mass-loss rate, an increase of
-dependency
(see Fig. 12), being too steep and failing to
reproduce the observed ``swing''. To illustrate the sensitivity of the
intensity decline to the mass-loss rate, an increase of ![]() from
from
![]()
![]() /yr to
/yr to
![]()
![]() /yr results in the integrated CO intensity being well
represented by a
/yr results in the integrated CO intensity being well
represented by a ![]() power-law, with the exponent a rising
from -2.7 to -2.2. However, no ``swing'' is predicted.
power-law, with the exponent a rising
from -2.7 to -2.2. However, no ``swing'' is predicted.
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{9312fig12.ps}\end{figure}](/articles/aa/full/2008/23/aa9312-07/Timg70.gif) |
Figure 12:
Decline of the theoretically predicted integrated intensity
(in erg s-1 cm-2 arcsec-2) of the circumstellar CO
vibration-rotation emission as a function of angular distance
|
| Open with DEXTER | |
Using the statistical method outlined in
Decin et al. (2007), a grid of ![]() 400 000 models was
computed to find the best-fit model to both the pure rotational and
vibrational-rotational CO lines. This grid should constrain the mass-loss
history of R Hya. The grid was constructed around the stellar
parameters as deduced and discussed by
Zijlstra et al. (2002): an effective temperature
400 000 models was
computed to find the best-fit model to both the pure rotational and
vibrational-rotational CO lines. This grid should constrain the mass-loss
history of R Hya. The grid was constructed around the stellar
parameters as deduced and discussed by
Zijlstra et al. (2002): an effective temperature
![]() of 2830 K; a stellar mass of 2
of 2830 K; a stellar mass of 2 ![]() ;
a luminosity L of
;
a luminosity L of
![]()
![]() ;
and a radius R of 450
;
and a radius R of 450 ![]() (=
(=
![]() cm). Mass-loss rate values ranged between
cm). Mass-loss rate values ranged between
![]()
![]() /yr and
/yr and
![]()
![]() /yr, being either
constant throughout the envelope or showing variations with amplitudes
between a factor of 2 and 100. In case of a constant mass-loss rate, the value
of the outer photodissociation radius,
/yr, being either
constant throughout the envelope or showing variations with amplitudes
between a factor of 2 and 100. In case of a constant mass-loss rate, the value
of the outer photodissociation radius,
![]() ,
is set at the
radius where the CO abundance drops to 1% of its value at the
photosphere, using the photodissociation results of
Mamon et al. (1988). In the case of variations in the
mass-loss rate,
,
is set at the
radius where the CO abundance drops to 1% of its value at the
photosphere, using the photodissociation results of
Mamon et al. (1988). In the case of variations in the
mass-loss rate,
![]() is a free parameter in the theoretical code
with the constraint that
is a free parameter in the theoretical code
with the constraint that
![]() should be smaller than the
should be smaller than the
![]() -value obtained using the formula of
Mamon et al. (1988) for a value of the mass-loss rate equal to
that at the outermost radius point (see the
discussion in Decin et al. 2007).
-value obtained using the formula of
Mamon et al. (1988) for a value of the mass-loss rate equal to
that at the outermost radius point (see the
discussion in Decin et al. 2007).
When checking the decline of the scattered wavelength-integrated
intensities of the CO vibration-rotation emission lines, it turned out
that only a step in ![]() can reproduce the ``swing'' visible in the
observations. In case only the CO pure rotational lines would have been
at our disposal, it would have been impossible to remove the
degeneracy in models constraining the inner 3
can reproduce the ``swing'' visible in the
observations. In case only the CO pure rotational lines would have been
at our disposal, it would have been impossible to remove the
degeneracy in models constraining the inner 3
![]() region of the
envelope.
region of the
envelope.
Parameters characterising the CSE of the model with the best
goodness-of-fit are listed in Table 3. The derived
temperature profile, velocity structure, and mass-loss history are
displayed in Fig. 13; a comparison between the
observed rotational CO lines and theoretical predictions is shown in
Fig. 10; and the decline of the integrated intensity of the
CO vibrational-rotational emission lines is displayed in
Fig. 12. The 95% confidence intervals around
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
and the distance
to the star are determined from the modelling of the pure rotational
CO lines, while the vibrational-rotational CO lines constrain the
confidence intervals of
,
and the distance
to the star are determined from the modelling of the pure rotational
CO lines, while the vibrational-rotational CO lines constrain the
confidence intervals of
![]() and the amplitude of the jump
in
and the amplitude of the jump
in ![]() around 150
around 150 ![]() .
The derived confidence intervals
are statistical uncertainties, which should be interpreted in the
light of the model assumptions of a spherically symmetric wind with
a monotonically increasing velocity structure.
.
The derived confidence intervals
are statistical uncertainties, which should be interpreted in the
light of the model assumptions of a spherically symmetric wind with
a monotonically increasing velocity structure.
The photodissociation radius calculated using the formula of
Mamon et al. (1988) for ![]() =
=
![]()
![]() /yr and
/yr and ![]() = 8 km s-1 is
= 8 km s-1 is ![]() 2350
2350 ![]() .
Mainly
the CO J = 1-0 line is influenced by the outer radius. Due to
the suspected large absolute calibration uncertainty for the IRAM CO
J = 1-0 line of R Hya and the IRAM HPBW of 23
.
Mainly
the CO J = 1-0 line is influenced by the outer radius. Due to
the suspected large absolute calibration uncertainty for the IRAM CO
J = 1-0 line of R Hya and the IRAM HPBW of 23
![]() (
(![]() 1850
1850 ![]() ), the outer radius is only loosely constrained.
Moreover, it is unclear how the bow shock, as detected by
Wareing et al. (2006) around 100
), the outer radius is only loosely constrained.
Moreover, it is unclear how the bow shock, as detected by
Wareing et al. (2006) around 100
![]() (=
(=![]() 8000
8000 ![]() )
influences the CO-photodissociation radius and
the density structure in the outer envelope. The log-likelihood tests
yield acceptable
)
influences the CO-photodissociation radius and
the density structure in the outer envelope. The log-likelihood tests
yield acceptable
![]() -values between 2000 and 8000
-values between 2000 and 8000 ![]() .
The small differences between the log-likelihood values
of the best-fit model and the model with
.
The small differences between the log-likelihood values
of the best-fit model and the model with
![]() = 8000
= 8000 ![]() are due to the (very) small CO
abundance for r > 2300
are due to the (very) small CO
abundance for r > 2300 ![]() .
The gas temperature at
2000
.
The gas temperature at
2000 ![]() is still quite high and estimated to be around 180 K;
at 8000
is still quite high and estimated to be around 180 K;
at 8000 ![]() ,
the gas temperature is around 50 K.
,
the gas temperature is around 50 K.
Table 3: Parameters of the model with best goodness-of-fit for R Hya. In the second column the values of the best-fit model parameters are listed, in the third column the confidence interval around the parameter is specified. The numbers in italics are input parameters that have been kept fixed at the given values.
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{9312fig13.ps}\end{figure}](/articles/aa/full/2008/23/aa9312-07/Timg82.gif) |
Figure 13:
Upper: estimated temperature profile, middle:
estimated velocity structure, and bottom: estimated
mass-loss rate |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=90,width=16cm,clip]{9312fig14.ps}\par\end{figure}](/articles/aa/full/2008/23/aa9312-07/Timg83.gif) |
Figure 14: The CO vibra-rotational R(1), R(2), R(3) lines observed at different angular distance from the star (black) are compared with the theoretical model predictions (red) for the best-fit model with parameters as specified in Table 3. The displayed off-star data are for data set 128 (EW-slit N1 E2.5). |
| Open with DEXTER | |
Our best-fit model has an inner radius
![]() of
150
of
150 ![]() ,
representing the inner radius of a detached
envelope in which the dust condensed much closer to the star. This
is in nice agreement with the results of a detached dust shell by
Zijlstra et al. (2002) and
Hashimoto et al. (1998). In the theoretical model,
,
representing the inner radius of a detached
envelope in which the dust condensed much closer to the star. This
is in nice agreement with the results of a detached dust shell by
Zijlstra et al. (2002) and
Hashimoto et al. (1998). In the theoretical model,
![]() the gas kinetic temperature and velocity structure
beyond
the gas kinetic temperature and velocity structure
beyond
![]() are computed by solving simultaneously the
equations of motion of gas and dust and the energy balance. The
temperature structure between
are computed by solving simultaneously the
equations of motion of gas and dust and the energy balance. The
temperature structure between ![]() and
and
![]() is
described using a power law (
is
described using a power law (
![]() ), which holds
when both emission and absorption are optically thin (see
Fig. 13); the velocity law in this inner region is
approximated by the classical
), which holds
when both emission and absorption are optically thin (see
Fig. 13); the velocity law in this inner region is
approximated by the classical ![]() -law
(Decin et al. 2006). The region between
-law
(Decin et al. 2006). The region between ![]() and
and
![]() is the so-called ``quasi-stationary'' layer, where
molecules can reside at low expansion velocity, and (almost) no dust
is present to drive the wind. Possible reasons for the change in dust
mass, and hence mass-loss rate, at
is the so-called ``quasi-stationary'' layer, where
molecules can reside at low expansion velocity, and (almost) no dust
is present to drive the wind. Possible reasons for the change in dust
mass, and hence mass-loss rate, at
![]() are further
discussed in Sect. 4. Slightly beyond
are further
discussed in Sect. 4. Slightly beyond
![]() ,
the temperature increases due to gas-grain
collisional heating. Further outwards, the energy balance is
determined by the adiabatic expansion of the gas.
,
the temperature increases due to gas-grain
collisional heating. Further outwards, the energy balance is
determined by the adiabatic expansion of the gas.
Inspecting Fig. 10, we see a nice resemblance between
the observed rotational CO line profile shapes and the model
predictions. Note that if the displayed IRAM profiles would have been
in terms of the antenna temperature, the corrected main-beam
temperature would perfectly match the model predictions. A clear
asymmetry is visible in all radio CO line profiles. Quite often, this
kind of asymmetry is explained in terms of self-absorption along the
line of sight (e.g. Ryde & Schöier 2001), although an
asymmetric stellar atmosphere, unresolved bright spots or asymmetries
in the CSE-structure may explain this behaviour. Moreover, it is
unclear how the downstream of the detected bow shock around R Hya at ![]() 100
100
![]() influences the circumstellar structure
closer to the target.
influences the circumstellar structure
closer to the target.
The decline of the integrated intensity of the vibra-rotational CO emission lines as a function of the angular distance from the star is also reproduced quite well (see Fig. 12). Since the ``swing'' is somewhat canceled in the mean over all directions (grey line), likely due to variations in the exact slit position, the NE and NW-directions are also plotted to illustrate the strength of the ``swing''-behaviour. Furthermore, comparing the full vibra-rotational CO R(1), R(2), and R(3) line profiles (i.e., not only the integrated intensities) for the 38 sub-spectra extracted from each of the off-star data sets corroborates the quality of our best-fit theoretical model (see Fig. 14): at different angular distances from the star, the observed and theoretically predicted line strengths of the three CO vibra-rotational lines match nicely.
In addition, using the GASTRoNOoM-code, the Phoenix observations, done
with the 4 m Mayall telescope at Kitt Peak by
Ryde et al. (2000) for o Cet, have been simulated using
the stellar parameters and mass-loss rate history as derived by
Ryde & Schöier (2001). Using their ``cavity'' model, with an
inner radius at ![]() 50
50 ![]() (or
(or ![]() 1
1
![]() ), we obtain a
), we obtain a
![]() -dependence for the decline of the wavelength-integrated
intensity of the circumstellar CO vibration-rotation emission of
-dependence for the decline of the wavelength-integrated
intensity of the circumstellar CO vibration-rotation emission of
![]() = -2.4. No ``swing'' is
predicted, since the inner radius lies within the geometrical region
traced by the scattered light (i.e. being from 2
= -2.4. No ``swing'' is
predicted, since the inner radius lies within the geometrical region
traced by the scattered light (i.e. being from 2
![]() to 7
to 7
![]() ).
).
It is evident that the modelling of the pure rotational
CO emission lines in combination with the
scattered vibrational-rotational low-excitation CO
transitions has a strong diagnostic power for probing the temperature,
density, and velocity structure of the CSE of R Hya, and,
therefore, for studying the mass-loss history of this Mira-variable. The
main result from our in-depth analysis is that the mass-loss rate of
R Hya has changed at about 150 ![]() from the star (at
from the star (at ![]() 1.9
1.9
![]() or
or ![]() 220 yr ago for an expansion velocity of 8 km s-1) with a factor of
220 yr ago for an expansion velocity of 8 km s-1) with a factor of ![]() 20. The change of the mass-loss rate
as a function of time agrees with the predictions of
Zijlstra et al. (2002) who analysed the period evolution
of R Hya. They showed that the period of R Hya
decreased linearly between AD 1770 and 1950, and has
stabilised at 385 d since 1950. From fitting the SED,
Zijlstra et al. (2002) concluded that the mass-loss rate
should have changed with at least a factor of 10, while
Hashimoto et al. (1998) suggested that the SED and
IRAS-images should be interpreted in terms of a detached shell. The
presence of an SiO maser (Snyder & Buhl 1975), however,
proves that the mass-loss rate has not ceased completely. As
demonstrated by Zijlstra et al. (2002) the evolution of
the mass-loss rate as a function of period agrees with the mass-loss
formalism of Vassiliadis & Wood (1993), but is much
larger than predicted by
Blöcker (1995).
20. The change of the mass-loss rate
as a function of time agrees with the predictions of
Zijlstra et al. (2002) who analysed the period evolution
of R Hya. They showed that the period of R Hya
decreased linearly between AD 1770 and 1950, and has
stabilised at 385 d since 1950. From fitting the SED,
Zijlstra et al. (2002) concluded that the mass-loss rate
should have changed with at least a factor of 10, while
Hashimoto et al. (1998) suggested that the SED and
IRAS-images should be interpreted in terms of a detached shell. The
presence of an SiO maser (Snyder & Buhl 1975), however,
proves that the mass-loss rate has not ceased completely. As
demonstrated by Zijlstra et al. (2002) the evolution of
the mass-loss rate as a function of period agrees with the mass-loss
formalism of Vassiliadis & Wood (1993), but is much
larger than predicted by
Blöcker (1995).
We realize that a disadvantage of our analysis method of R Hya
is that the star is not allowed to evolve, in the sense that
the luminosity, effective temperature and stellar radius are kept
constant for the computation of the structure of the whole
envelope. The gradual change in period of R Hya implies that
its pulsation mode has remained constant, and that its evolution is
related to a change in stellar parameters. As discussed by
Zijlstra et al. (2002) various relations (such as the
period-luminosity relation, evolutionary tracks, colour-period
relation,
![]() -colour relation) are not mutually consistent. A
luminosity decrease of R Hya in the last 340 years is
possible, but not proven. Only a decrease in radius by 14-18%,
obtained from the period, appears well constrained.
-colour relation) are not mutually consistent. A
luminosity decrease of R Hya in the last 340 years is
possible, but not proven. Only a decrease in radius by 14-18%,
obtained from the period, appears well constrained.
The declining period of R Hya between AD 1770 and
1950 has been attributed by Wood & Zarro (1981) to a
possible recent thermal pulse. Wood & Zarro (1981) argued
that R Hya is presently in the luminosity decline following
the peak of the pulse, with the peak luminosity around AD
1750. The analysis of Zijlstra et al. (2002) places the
peak luminosity plateau around AD 1700. Since the detached
shell with inner radius of 1-2 arcmin found in the 60 ![]() m IRAS
images by Hashimoto et al. (1998) can be interpreted in
terms of an AGB-ISM bow shock (Wareing et al. 2006) and
no mass-loss variation around 1-2 arcmin from the star needs to be
invoked, the thermal-pulse model is capable of explaining the full
mass-loss history of R Hya. However, other causes, such as
envelope relaxation due to the non-linear pulsations
(Zijlstra et al. 2002), hydrodynamical oscillations due
to instabilities in the gas-dust coupling in the CSE while the star is
on the AGB (Simis et al. 2001) or a solar-like magnetic
activity cycle in the progenitor AGB star
(Soker 2000), cannot be ruled out.
m IRAS
images by Hashimoto et al. (1998) can be interpreted in
terms of an AGB-ISM bow shock (Wareing et al. 2006) and
no mass-loss variation around 1-2 arcmin from the star needs to be
invoked, the thermal-pulse model is capable of explaining the full
mass-loss history of R Hya. However, other causes, such as
envelope relaxation due to the non-linear pulsations
(Zijlstra et al. 2002), hydrodynamical oscillations due
to instabilities in the gas-dust coupling in the CSE while the star is
on the AGB (Simis et al. 2001) or a solar-like magnetic
activity cycle in the progenitor AGB star
(Soker 2000), cannot be ruled out.
For the first time, both the CO pure rotational emission
line profiles (J = 1-0 through J = 6-5) and the
CO vibrational-rotational scattered resonance lines from
the fundamental band of the unusual Mira variable R Hya are
analysed in detail using a non-LTE radiative transfer code. The
dependency of the CO vibra-rotational emission on the angular distance
on the sky clearly points towards a variation in the mass-loss
rate at ![]() 1.9
1.9
![]() from the star. An in-depth analysis of
the CO pure rotational emission line profiles and the vibra-rotational
circumstellar CO emission provides evidence for a drop in mass-loss
rate some 220 yr ago with a factor
from the star. An in-depth analysis of
the CO pure rotational emission line profiles and the vibra-rotational
circumstellar CO emission provides evidence for a drop in mass-loss
rate some 220 yr ago with a factor ![]() 20. This change in
mass-loss rate coincides with a period decline between AD 1770 and 1950, corroborating the analysis of
Zijlstra et al. (2002) and
Wood & Zarro (1981) that a He-flash may be the cause of
the period decline. A second mass-loss event originally suggested by
IRAS-images (Hashimoto et al. 1998; Zijlstra et al. 2002) may not be due to a change in mass-loss
rate, but may be caused by the AGB-ISM bow shock, detected in 2006 by
Wareing et al. (2006).
20. This change in
mass-loss rate coincides with a period decline between AD 1770 and 1950, corroborating the analysis of
Zijlstra et al. (2002) and
Wood & Zarro (1981) that a He-flash may be the cause of
the period decline. A second mass-loss event originally suggested by
IRAS-images (Hashimoto et al. 1998; Zijlstra et al. 2002) may not be due to a change in mass-loss
rate, but may be caused by the AGB-ISM bow shock, detected in 2006 by
Wareing et al. (2006).
The results point toward a mass-loss history during the last
![]() 2000 yr with a constant
2000 yr with a constant ![]() of
of ![]()
![]()
![]() /yr until
/yr until ![]() 220 yr ago, at which moment a He-flash
altered the internal stellar structure, resulting in a decrease of
220 yr ago, at which moment a He-flash
altered the internal stellar structure, resulting in a decrease of
![]() by a factor
by a factor ![]() 20. The period evolution, SED, and
cicrcumstellar CO pure-rotational and vibra-rotational emission lines
of R Hya can be explained by this mass-loss history.
20. The period evolution, SED, and
cicrcumstellar CO pure-rotational and vibra-rotational emission lines
of R Hya can be explained by this mass-loss history.
Acknowledgements
The observations are based on observations obtained at the Gemini Observatory, which is operated by the Association of Universities for Research in Astronomy, Inc., under a cooperative agreement with the NSF on behalf of the Gemini partnership: the National Science Foundation (US), the Science and Technology Facilities Council (UK), the National Research Council (Canada), CONICYT (Chile), the Australian Research Council (Australia), CNPq (Brazil) and SECYT (Argentina). The observations were obtained with the Phoenix infrared spectrograph, which was developed and is operated by the National Optical Astronomy Observatory. The spectra were obtained as part of program GS-2005A-C-8.L.D. and M.R. acknowledge financial support from the Fund for Scientific Research - Flanders (Belgium). N.R. is Royal Swedish Academy of Sciences Research Fellow supported by a grant from the Knut and Alice Wallenberg Foundation. The computations for this research have been done on the VIC HPC Cluster of the KULeuven. We are grateful to the LUDIT HPC team for their support. We would like to thank Remo Tilanus (JCMT) for his support during the observations and reduction of the data. Prof. J. R. Knapp and Dr. D. Teyssier are thanked for providing us the rotational CO emission profiles of R Hya obtained with the CSO and IRAM.
The logbook and extra figures of the CO vibrational-rotational lines excited in the CSE around R Hya are given in this appendix.
Table A.1 describes the logbook of the Phoenix CO vibrational-rotational transitions imaging the CSE of R Hya. Figures A.1-A.4 display the circumstellar CO vibration-rotation R(1), R(2), and R(3) emission lines integrated over the slit for the 16 off-star observations of R Hya. Inspecting Fig. A.3, it is clear that the CO emission lines in data sets (158, 161) are a factor 2 higher than in data sets (141, 142).
The decline of the intensity of the circumstellar CO emission as a
function of the angular distance ![]() in the south, east and west
position is given in Figs. A.5-A.7,
respectively. Omitting data sets (149, 150) in the westward scans in
the CSE of R Hya yield a better overlap between the mean of
the WS and SW scans, as illustrated in Fig. A.8 (we refer to
the paper for a discussion on this topic).
in the south, east and west
position is given in Figs. A.5-A.7,
respectively. Omitting data sets (149, 150) in the westward scans in
the CSE of R Hya yield a better overlap between the mean of
the WS and SW scans, as illustrated in Fig. A.8 (we refer to
the paper for a discussion on this topic).
Figure A.9 displays the dependence of the scattered wavelength-integrated intensities of the 3 CO vibration-rotation lines as a function of the angular distance for the different scan directions, together with the best-fit power law to the data.
Table A.1:
Logbook of the CO vibrational-rotational Phoenix observations
of R Hya. A notation ``EW-slit N1 E2.5'' indicates a
slit-position oriented in the east-west direction, which is 1
![]() offset
to the north from the star and which has been moved 2.5
offset
to the north from the star and which has been moved 2.5
![]() in the
east-direction along the slit. For the off-star observations, the
number of the data we used is also listed in the first
column.
in the
east-direction along the slit. For the off-star observations, the
number of the data we used is also listed in the first
column. ![]() Ori is a telluric reference star; the
observations of
Ori is a telluric reference star; the
observations of ![]() Vir are used to compute the slit loss (see the
paper for more details).
Vir are used to compute the slit loss (see the
paper for more details).
![\begin{figure}
\par\mbox{\subfigure[The CO~emission lines of data set~112, being...
...ludegraphics[width=7cm,height=4.6cm,angle=0]{9312figA1d.eps} }}
\par\end{figure}](/articles/aa/full/2008/23/aa9312-07/Timg85.gif) |
Figure A.1: The CO vibration-rotation emission lines north of R Hydrae, integrated over the slit. |
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\subfigure[The CO~emission lines of data set~116, being...
...ludegraphics[width=7cm,height=4.6cm,angle=0]{9312figA2d.eps} }}
\par\end{figure}](/articles/aa/full/2008/23/aa9312-07/Timg86.gif) |
Figure A.2: The CO vibration-rotation emission lines south of R Hydrae, integrated over the slit. |
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\subfigure[The CO~emission lines of data set~141, being...
...\includegraphics[width=7cm,height=4.6cm,angle=0]{9312figA3d.eps} }}
\end{figure}](/articles/aa/full/2008/23/aa9312-07/Timg87.gif) |
Figure A.3: The CO vibration-rotation emission lines east of R Hydrae, integrated over the slit. |
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\subfigure[The CO~emission lines of data set~149, being...
...ludegraphics[width=7cm,height=4.6cm,angle=0]{9312figA4d.eps} }}
\par\end{figure}](/articles/aa/full/2008/23/aa9312-07/Timg88.gif) |
Figure A.4: The CO vibration-rotation emission lines west of R Hydrae, integrated over the slit. |
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\subfigure{\includegraphics[width=8cm,clip]{9312figA5a....
...5cm}
\subfigure{\includegraphics[width=8cm,clip]{9312figA5b.eps} }}
\end{figure}](/articles/aa/full/2008/23/aa9312-07/Timg89.gif) |
Figure A.5:
Decline of the intensity of the circumstellar emission as a
function of angular distance |
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\subfigure{\includegraphics[width=8cm,clip]{9312figA6a....
...5cm}
\subfigure{\includegraphics[width=8cm,clip]{9312figA6b.eps} }}
\end{figure}](/articles/aa/full/2008/23/aa9312-07/Timg90.gif) |
Figure A.6:
Decline of the intensity of the circumstellar emission as a
function of angular distance |
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\subfigure{\includegraphics[width=8cm,clip]{9312figA7a....
...5cm}
\subfigure{\includegraphics[width=8cm,clip]{9312figA7b.eps} }}
\end{figure}](/articles/aa/full/2008/23/aa9312-07/Timg91.gif) |
Figure A.7:
Decline of the intensity of the circumstellar emission as a
function of angular distance |
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\subfigure{\includegraphics[width=8cm,clip]{9312figA8a....
...5cm}
\subfigure{\includegraphics[width=8cm,clip]{9312figA8b.eps} }}
\end{figure}](/articles/aa/full/2008/23/aa9312-07/Timg92.gif) |
Figure A.8:
Decline of the intensity of the circumstellar CO emission in
the south-west and west-south directions of R
Hya. Left: mean of the (116, 117, 123, 124) and (149, 150,
159, 160) data sets is displayed. At the cross-over points around
1.4
|
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\subfigure{\includegraphics[width=7cm]{9312figA9a.eps} ...
....5cm}
\subfigure{\includegraphics[width=7cm]{9312figA9h.eps} }}
\par\end{figure}](/articles/aa/full/2008/23/aa9312-07/Timg93.gif) |
Figure A.9:
Dependence of the scattered wavelength-integrated intensity
of the circumstellar CO vibration-rotation lines as a function of
the angular distance on the sky, |
| Open with DEXTER | |